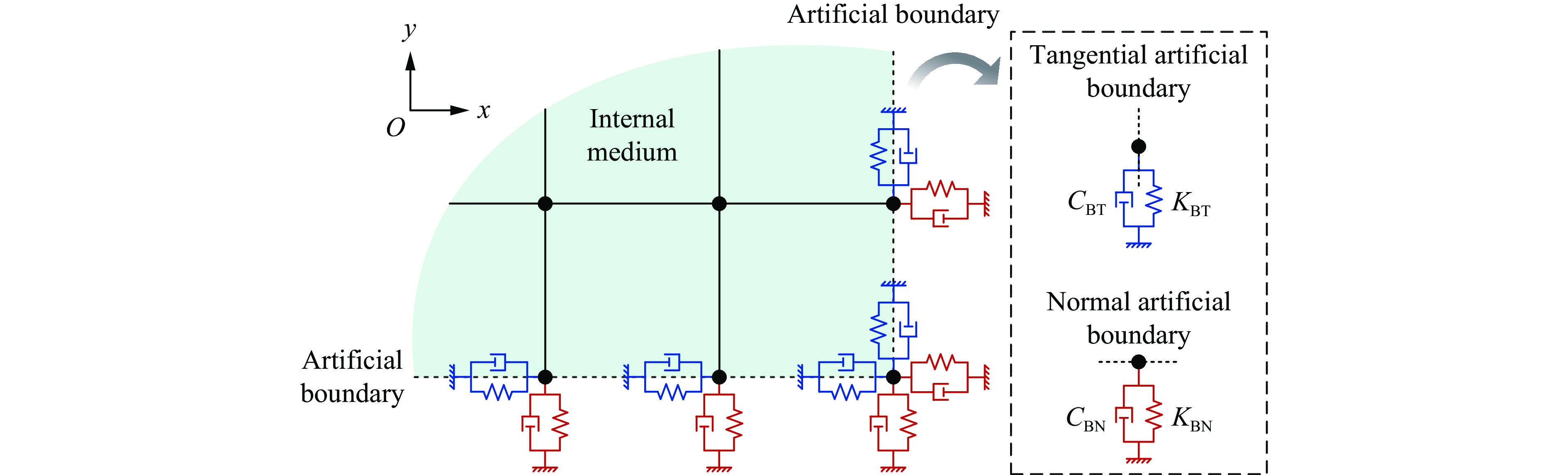
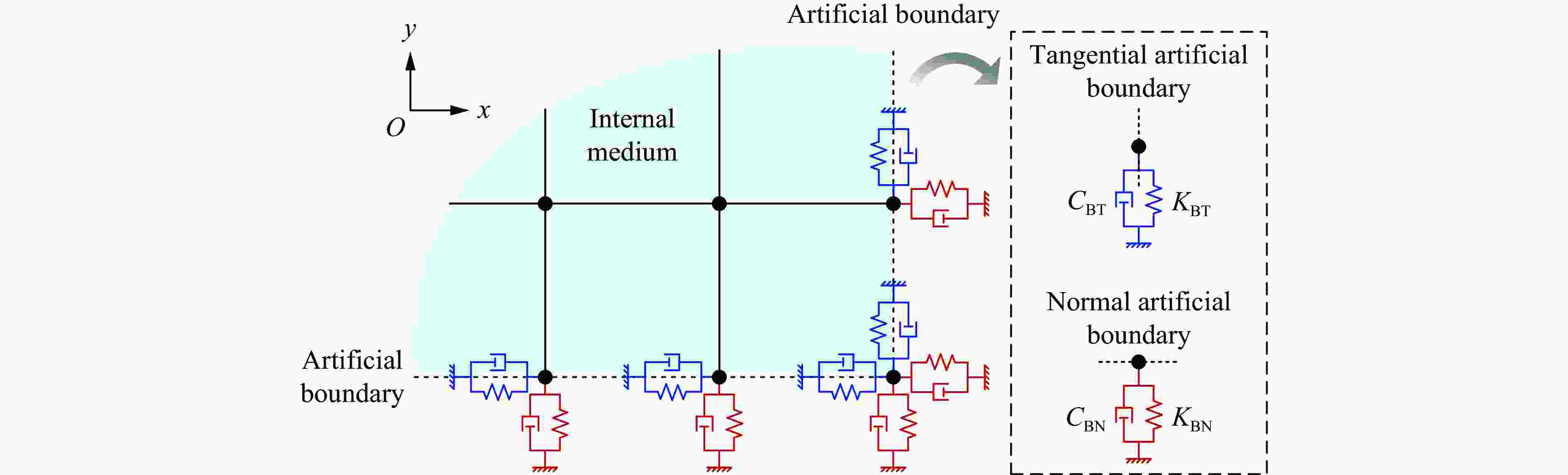
Stability conditions of explicit algorithms when using viscoelastic artificial boundaries
-
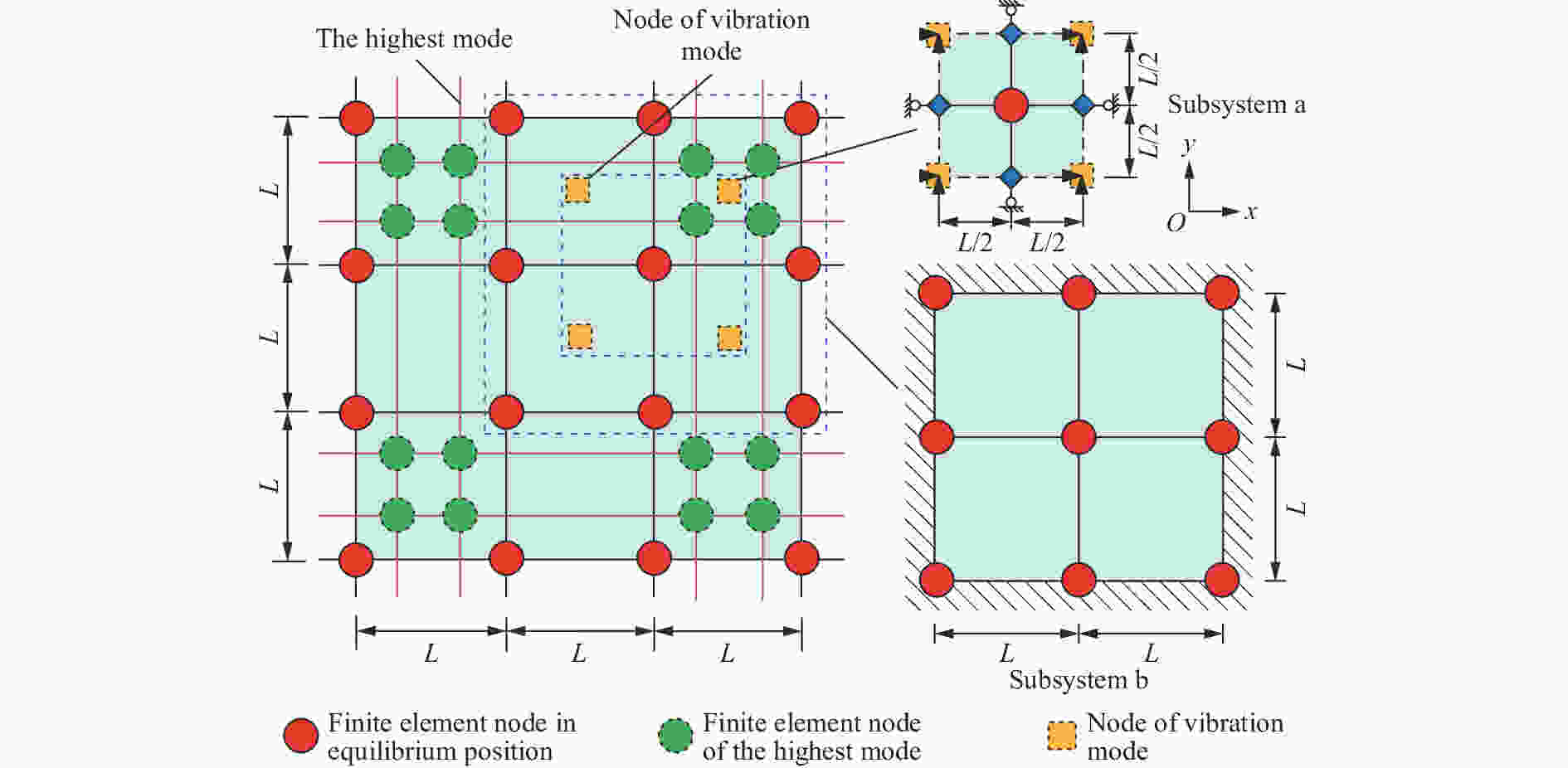
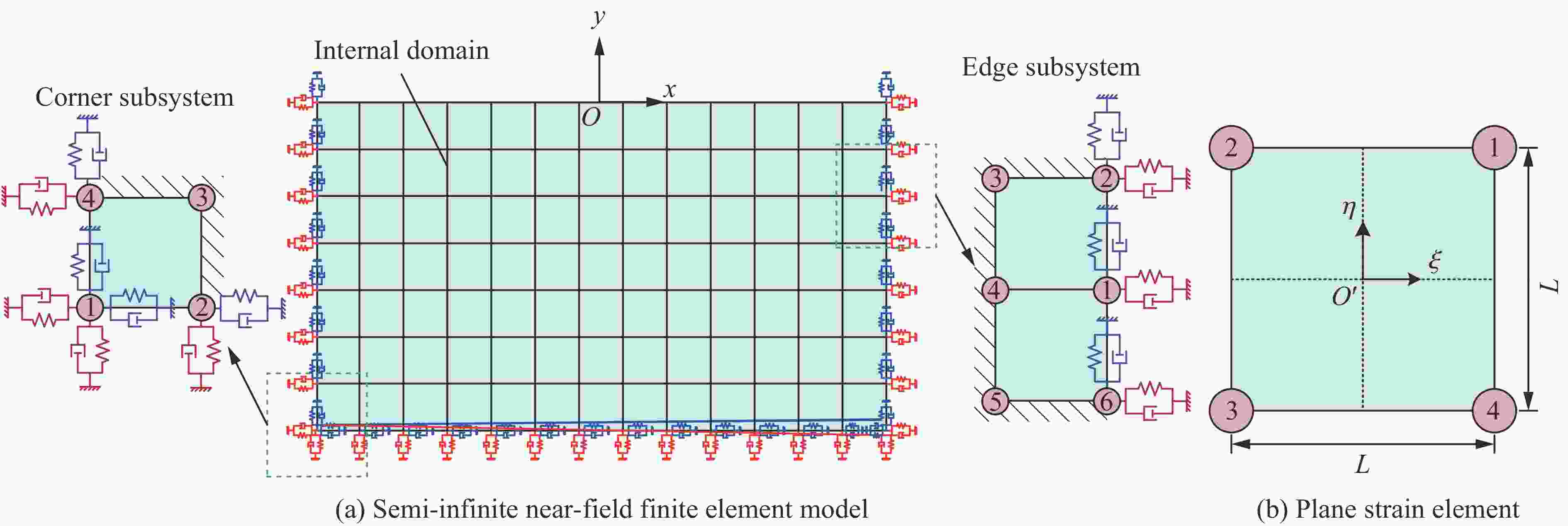
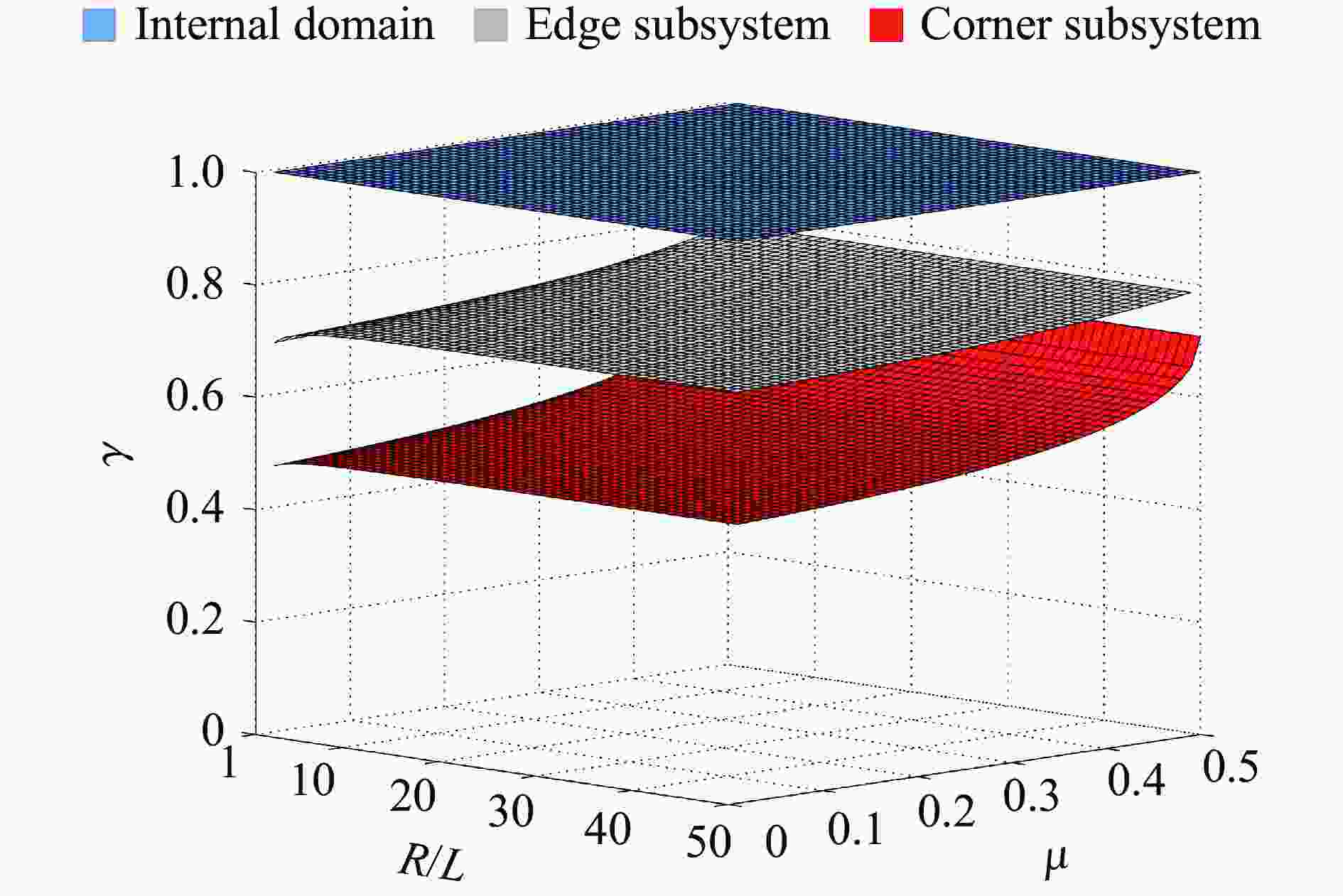
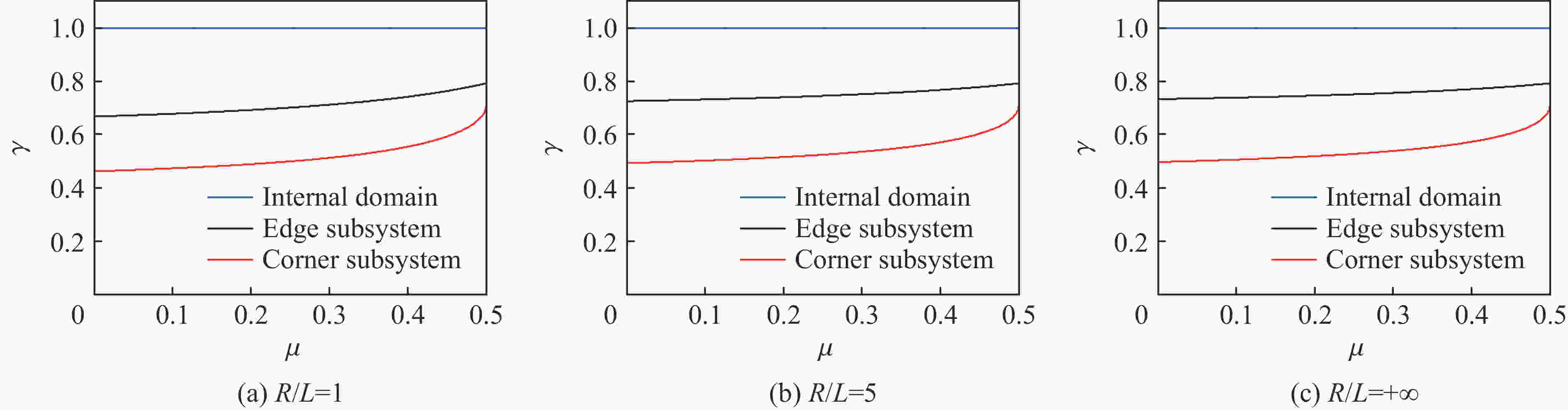
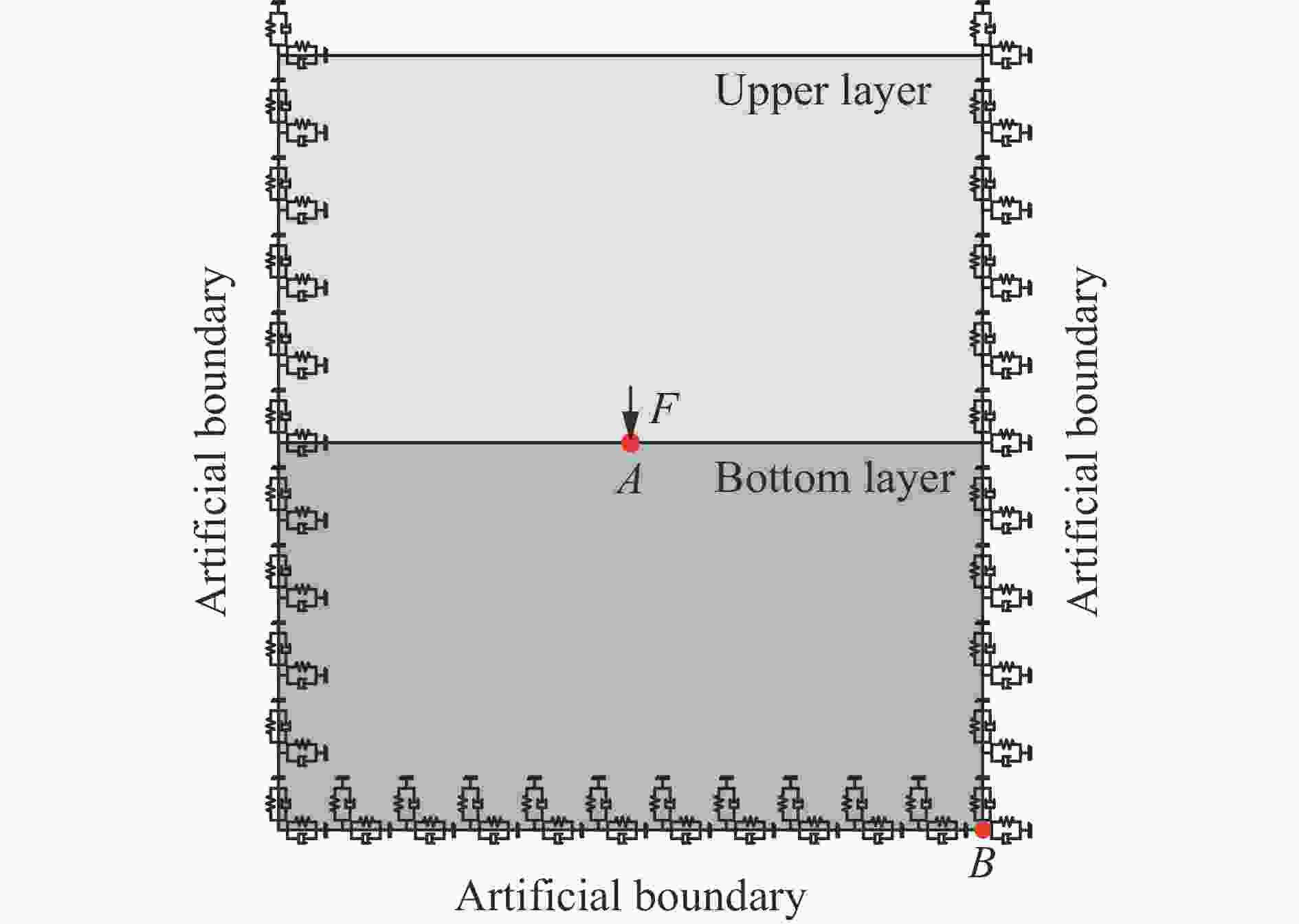
摘要: 黏弹性人工边界是处理无限域波动问题常用的数值模拟方法。采用显式时域逐步积分算法进行计算时,受黏弹性人工边界的阻尼、刚度等影响,人工边界区的稳定性比内部计算域的更严格,尚无明确、实用的稳定性判别准则,这限制了黏弹性人工边界在显式动力分析中的应用。针对二维黏弹性人工边界,利用基于局部子系统的稳定性分析方法和基于传递矩阵谱半径的稳定性判别准则,给出了可代表整体模型局部特征的不同边界子系统的稳定性条件解析解。通过对比分析不同计算区域的稳定性条件及其影响因素,证明了整体模型的稳定性由角点子系统控制。在此基础上,获得了含黏弹性人工边界的整体模型在显示动力计算中的统一稳定性判别准则和简化实用计算方法。在实际应用中,令积分时间步长满足稳定性条件,即可顺利完成整体模型的动力计算。以上研究可为将黏弹性人工边界应用于显式动力计算时积分时间步长的合理选取提供参考。Abstract: Viscoelastic artificial boundary is a commonly used numerical simulation method to deal with the wave propagation problems in an infinite domain. When the explicit time-domain stepwise integration algorithm is adopted for such numerical analysis, the stability conditions of the artificial boundary area are more stringent than those of the internal domain due to the influence of the damping and stiffness of the viscoelastic artificial boundary. However, there is currently no clear and practical stability criterion for this problem, which affects the reasonable selection of the integral time step when using the viscoelastic artificial boundaries, and further restricts the application of viscoelastic artificial boundary in the explicit dynamic analysis. Aiming at the two-dimensional (2D) viscoelastic artificial boundary, two typical types of boundary subsystem that can represent the localized characteristics of the overall numerical model, namely the edge boundary subsystem and the corner boundary subsystem, were established and their motion equations as well as the transfer matrixes were obtained according to the stability analysis method based on the local subsystem. Then through the stability criteria based on the spectral radius of the transfer matrix, the analytical solutions of the stability conditions of different local subsystems were derived. Through the comparative analysis of the stability conditions of different calculation areas and their influencing factors, it is found that the stability of the overall model is controlled by the corner boundary subsystem. On that basis, a uniform stability criterion and a simplified practical calculation method of the stability condition for the overall model with 2D viscoelastic artificial boundary in explicit dynamic calculations were proposed. In practical applications, the dynamic calculation of the overall model can be successfully completed once the integral time step meets the proposed stability condition of the numerical system. This study provides theoretical guidance for the reasonable selection of the integral time step when applying 2D viscoelastic artificial boundaries in explicit dynamic calculations.
-
表 1 二维黏弹性人工边界参数的数据[23]
Table 1. The values of two-dimensional viscoelastic artificial boundary coefficients[23]
参数 范围 建议 αT 0.35~0.65 0.5 αN 0.80~1.20 1.0 表 2 建议的几种常见情况的稳定性系数
Table 2. Recommended stability coefficients for several common cases
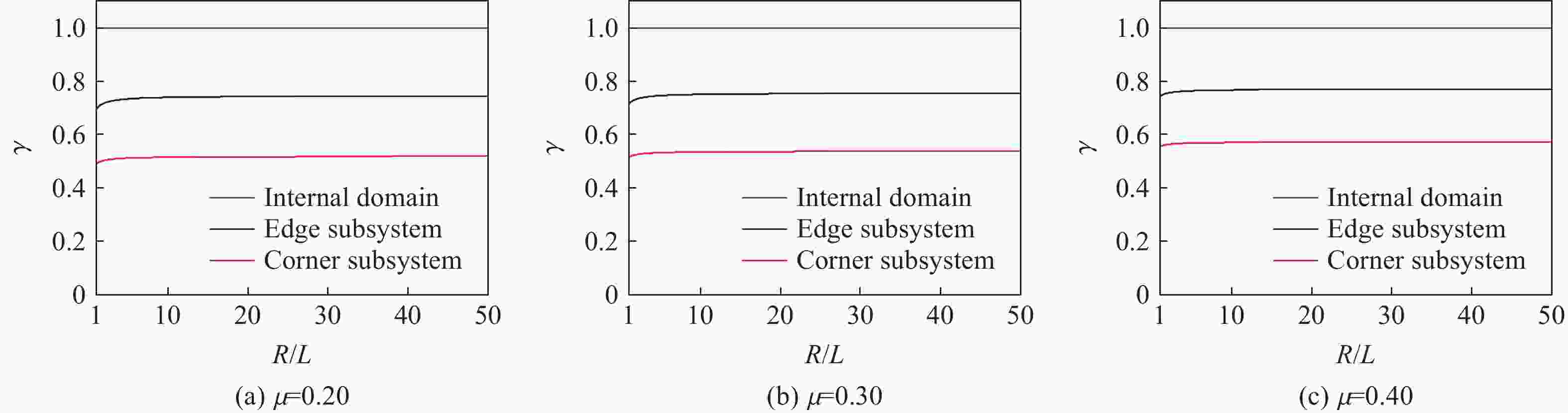
R/L γ μ=0.10 μ=0.15 μ=0.20 μ=0.25 μ=0.30 μ=0.35 μ=0.40 1 0.47 0.48 0.49 0.50 0.51 0.53 0.55 5 0.50 0.50 0.51 0.52 0.53 0.55 0.57 10 0.50 0.51 0.51 0.52 0.53 0.55 0.57 20 0.50 0.51 0.52 0.53 0.54 0.55 0.57 50 0.50 0.51 0.52 0.53 0.54 0.55 0.57 +∞ 0.51 0.51 0.52 0.53 0.54 0.55 0.57 表 3 均匀半空间模型的稳定性系数和最大稳定时间步长
Table 3. Stability coefficients and maximum stable time steps of the homogeneous model
模型分区 稳定性系数γ 最大稳定时间步长Δt/s 计算 建议 计算 建议 内部区域 1.00 0.50 0.002 7 0.001 35 侧边子系统 0.74 0.50 0.002 0 0.001 35 角点子系统 0.52 0.50 0.001 4 0.001 35 表 4 不同固定时间步长时均匀半空间模型的稳定性状态
Table 4. The stability states of the homogeneous model under different fixed time steps
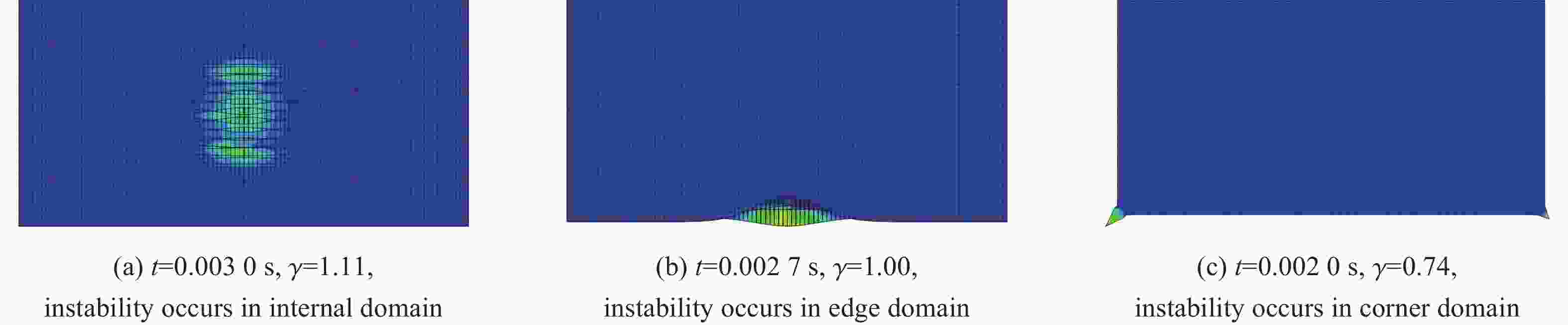
时间步长$ {{\Delta }}t$/s 稳定性系数γ 稳定性状态 0.003 0 1.11 内部首先失稳 0.002 7 1.00 侧边首先失稳 0.002 0 0.74 角点首先失稳 0.001 4 0.52 稳定计算 0.001 35 0.50 稳定计算 表 5 成层半空间模型的稳定性系数与最大稳定时间步长
Table 5. Stability coefficients and maximum stable time steps of the layered model
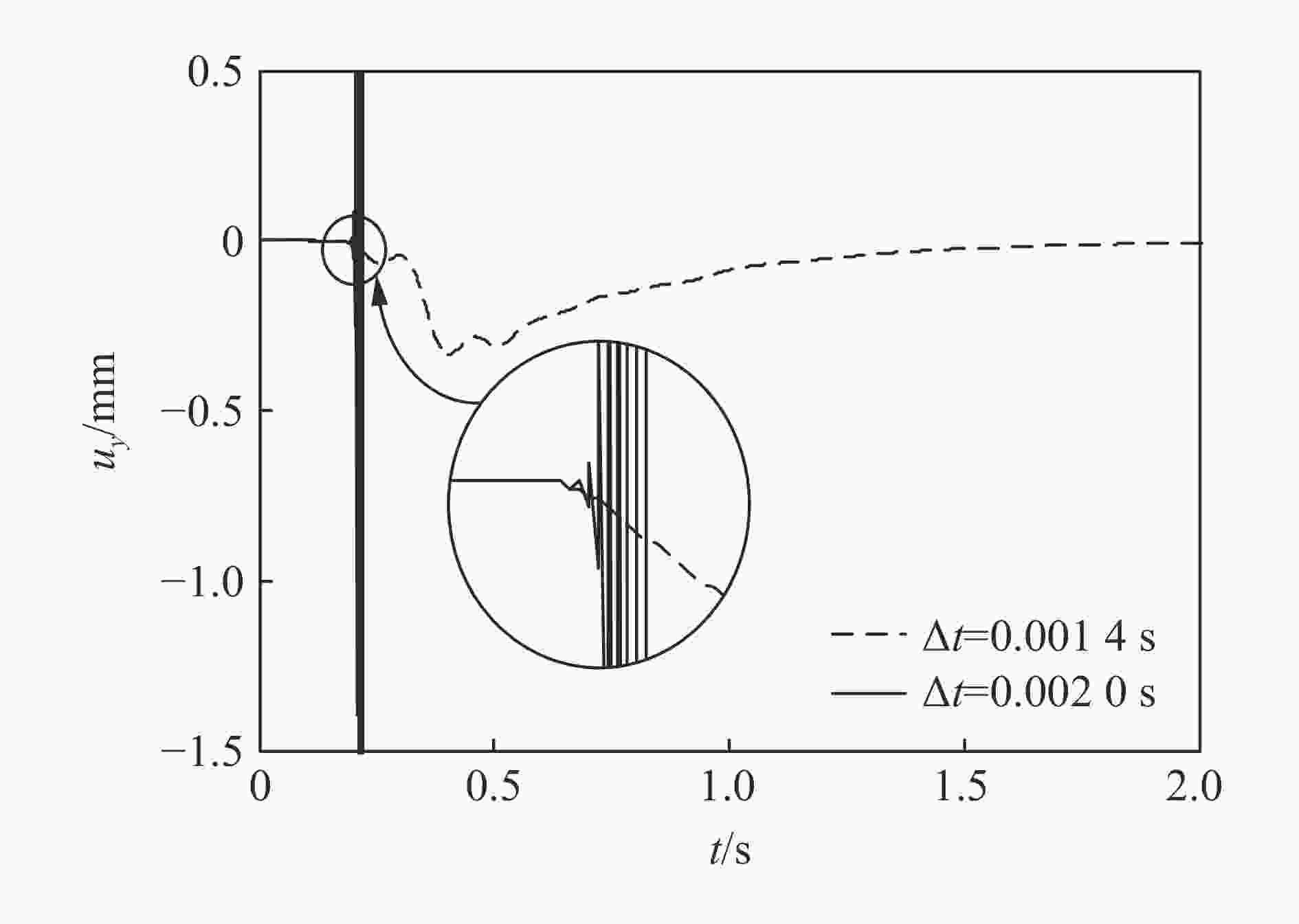
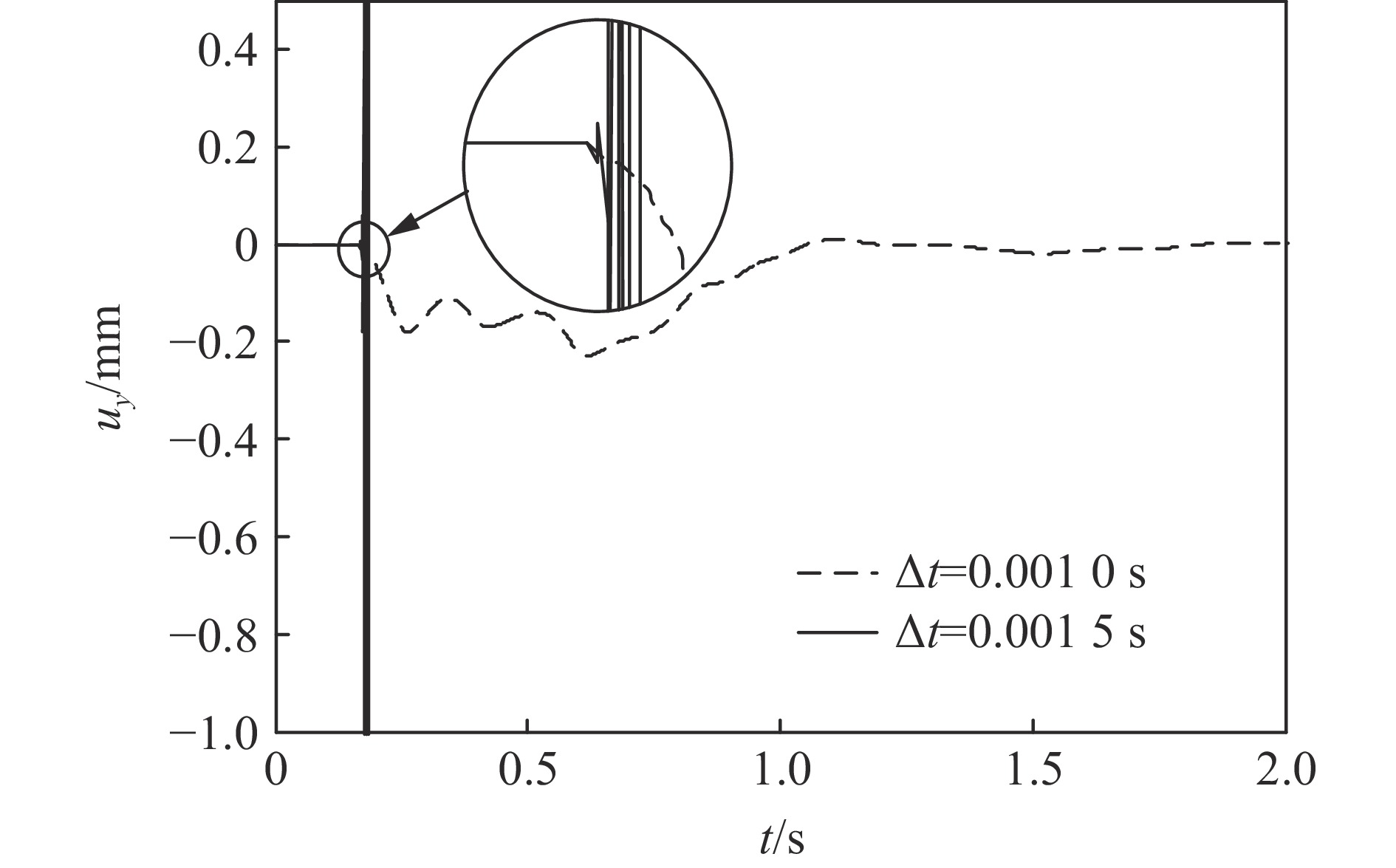
介质 模型分区 稳定性系数γ 最大稳定时间步长Δt/s 计算 建议 计算 建议 上层 内部区域 1.00 0.5 0.003 7 0.000 95 侧边子系统 0.76 0.5 0.002 8 0.000 95 下层 内部区域 1.00 0.5 0.001 9 0.000 95 侧边子系统 0.79 0.5 0.001 5 0.000 95 角点子系统 0.59 0.5 0.001 1 0.000 95 表 6 采用不同固定时间步长时成层半空间模型的稳定性状态
Table 6. The stability state of the layered model under different fixed time steps
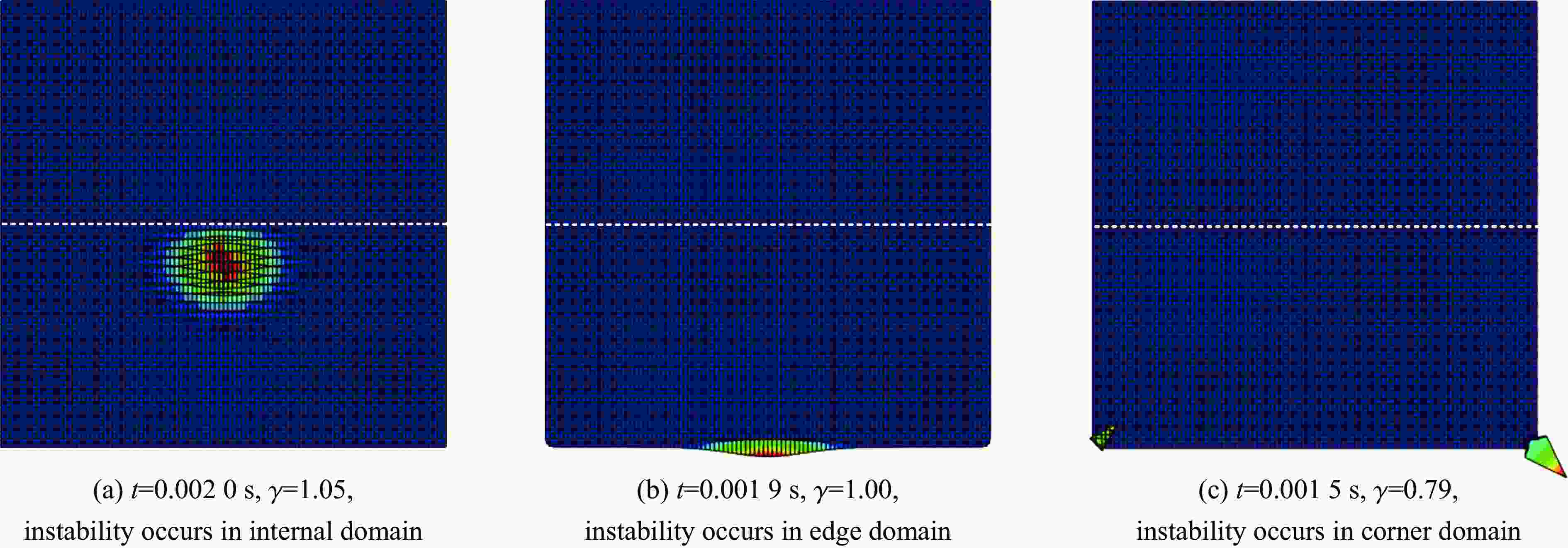
时间步长$ {{\Delta }}t$/s 稳定性系数γ 稳定性状态 0.002 0 1.05 内部首先失稳 0.001 9 1.00 侧边首先失稳 0.001 5 0.79 角点首先失稳 0.001 0 0.53 稳定计算 0.000 95 0.50 稳定计算 -
[1] LIAO Z P, WONG H L. A transmitting boundary for the numerical simulation of elastic wave propagation [J]. International Journal of Soil Dynamics and Earthquake Engineering, 1984, 3(4): 174–183. DOI: 10.1016/0261-7277(84)90033-0. [2] 廖振鹏, 周正华, 张艳红. 波动数值模拟中透射边界的稳定实现 [J]. 地球物理学报, 2002, 45(4): 533–545. DOI: 10.3321/j.issn:0001-5733.2002.04.011.LIAO Z P, ZHOU Z H, ZHANG Y H. Stable implementation of transmitting boundary in numerical simulation of wave motion [J]. Chinese Journal of Geophysics, 2002, 45(4): 533–545. DOI: 10.3321/j.issn:0001-5733.2002.04.011. [3] LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media [J]. Journal of the Engineering Mechanics Division, 1969, 95(4): 859–878. DOI: 10.1061/JMCEA3.0001144. [4] 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界 [J]. 工程力学, 2005, 22(6): 46–51. DOI: 10.3969/j.issn.1000-4750.2005.06.008.LIU J B, WANG Z Y, DU X L, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics, 2005, 22(6): 46–51. DOI: 10.3969/j.issn.1000-4750.2005.06.008. [5] 刘晶波, 李彬. 三维黏弹性静-动力统一人工边界 [J]. 中国科学: E辑, 2005, 35(9): 966–908.LIU J B, LI B. Three-dimensional viscoelastic static-dynamic unified artificial boundary [J]. Science in China: Series E, 2005, 35(9): 966–908. [6] DU X L, ZHAO M. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media [J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 937–946. DOI: 10.1016/j.soildyn.2010.04.004. [7] BREBBIA C A. The boundary element method for engineers [M]. London: Wiley, 1978. [8] 金峰, 王光纶, 贾伟伟. 离散元-边界元动力耦合模型在地下结构动力分析中的应用 [J]. 水利学报, 2001(2): 24–28. DOI: 10.3321/j.issn:0559-9350.2001.02.004.JIN F, WANG G L, JIA W W. Application of distinct element-boundary element coupling model in underground structure dynamic analysis [J]. Journal of Hydraulic Engineering, 2001(2): 24–28. DOI: 10.3321/j.issn:0559-9350.2001.02.004. [9] BERENGER J P. Perfectly matched layer for the FDTD solution of wave-structure interaction problems [J]. IEEE Transactions on Antennas and Propagation, 1996, 44(1): 110–117. DOI: 10.1109/8.477535. [10] KUCUKCOBAN S, KALLIVOKAS L F. A symmetric hybrid formulation for transient wave simulations in PML-truncated heterogeneous media [J]. Wave Motion, 2013, 50(1): 57–79. DOI: 10.1016/j.wavemoti.2012.06.004. [11] 李彬, 刘晶波. 粘弹性人工边界在Marc中的实现 [C] // 第14届全国结构工程学术会议论文集(第一册). 烟台: 中国力学学会工程力学编辑部, 2005: 303−307. [12] 胡汛训, 张燎军, 华慧玲. 粘弹性人工边界在LS-DYNA中的实现 [C] // 首届全国水工抗震防灾学术会议论文集. 南京: 中国水力发电工程学会, 2006: 134−139. [13] 刘晶波, 杜义欣, 闫秋实. 粘弹性人工边界及地震动输入在通用有限元软件中的实现 [C] // 第三届全国防震减灾工程学术研讨会论文集. 南京: 中国土木工程学会, 2007: 43−48. [14] 张燎军, 张慧星, 王大胜, 等. 黏弹性人工边界在ADINA中的应用 [J]. 世界地震工程, 2008, 24(1): 12–16.ZHANG L J, ZHANG H X, WANG D S, et al. The application of artificial viscous-spring boundary in ADINA [J]. World Earthquake Engineering, 2008, 24(1): 12–16. [15] 张焜煌, 钱彦岭, 徐慧峰, 等. 基于Nastran的粘性和粘弹性人工边界的模拟与验证 [J]. 兵工自动化, 2009, 28(3): 29–31. DOI: 10.3969/j.issn.1006-1576.2009.03.011.ZHANG K H, QIAN Y L, XU H F, et al. Simulation and verification of viscous and viscous-spring artificial boundary based on Nastran [J]. Ordnance Industry Automation, 2009, 28(3): 29–31. DOI: 10.3969/j.issn.1006-1576.2009.03.011. [16] HUANG J Q, DU X L, JIN L, et al. Impact of incident angles of P waves on the dynamic responses of long lined tunnels [J]. Earthquake Engineering and Structural Dynamics, 2016, 45(15): 2435–2454. DOI: 10.1002/eqe.2772. [17] WANG J T, ZHANG C H, JIN F. Nonlinear earthquake analysis of high arch dam-water-foundation rock systems [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(7): 1157–1176. DOI: 10.1002/eqe.1178. [18] 郜新军, 赵成刚, 张延. 多源散射黏弹性叠加人工边界探究及在桥梁工程中的应用 [J]. 土木工程学报, 2010, 43(11): 130–138. DOI: 10.15951/j.tmgcxb.2010.11.005.GAO X J, ZHAO C G, ZHANG Y. A study of viscous-spring superposition artificial boundary for multi-source scattering problems and its application in bridge engineering [J]. China Civil Engineering Journal, 2010, 43(11): 130–138. DOI: 10.15951/j.tmgcxb.2010.11.005. [19] 李忠诚, 凡红. 基于粘弹性人工边界的核电工程地基动力阻抗分析 [J]. 核动力工程, 2014, 35(2): 67–70.LI Z C, FAN H. Dynamic impedance analysis based on an artificial viscoelastic boundary technology for nuclear power engineering [J]. Nuclear Power Engineering, 2014, 35(2): 67–70. [20] 王子辉. 饱和两相与单相土互层场地中地铁车站地震反应分析 [D]. 北京: 北京交通大学, 2008: 95−96. [21] 闫秋实. 典型地铁结构内爆炸流场分布及动力反应研究 [D]. 北京: 清华大学, 2011: 100−102. [22] BAO X, LIU J B, LI S T, et al. Seismic response analysis of the reef-seawater system under obliquely incident P and SV waves [J]. Ocean Engineering, 2020, 200: 107021. DOI: 10.1016/j.oceaneng.2020.107021. [23] 刘晶波, 谷音, 杜义欣. 一致粘弹性人工边界及粘弹性边界单元 [J]. 岩土工程学报, 2006, 28(9): 1070–1075. DOI: 10.3321/j.issn:1000-4548.2006.09.004.LIU J B, GU Y, DU Y X. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070–1075. DOI: 10.3321/j.issn:1000-4548.2006.09.004. [24] KAMEL A H. A stability checking procedure for finite-difference schemes with boundary conditions in acoustic media [J]. Bulletin of the Seismological Society of America, 1989, 79(5): 1601–1606. DOI: 10.1785/BSSA0790051601. [25] 关慧敏, 廖振鹏. 局部人工边界稳定性的一种分析方法 [J]. 力学学报, 1996, 28(3): 376–380. DOI: 10.6052/0459-1879-1996-3-1995-344.GUAN H M, LIAO Z P. A method for the stability analysis of local artificial boundaries [J]. Acta Mechanica Sinica, 1996, 28(3): 376–380. DOI: 10.6052/0459-1879-1996-3-1995-344. [26] 李述涛, 刘晶波, 宝鑫, 等. 采用粘弹性人工边界单元时显式算法稳定性分析 [J]. 工程力学, 2020, 37(11): 1–11,46. DOI: 10.6052/j.issn.1000-4750.2019.12.0755.LI S T, LIU J B, BAO X, et al. Stability analysis of explicit algorithms with visco-elastic artificial boundary elements [J]. Engineering Mechanics, 2020, 37(11): 1–11,46. DOI: 10.6052/j.issn.1000-4750.2019.12.0755. [27] Abaqus analysis user’s manual (version 6.14) [Z]. 2013. [28] HUGHES T J R. Analysis of transient algorithms with particular reference to stability behavior [C] // BELYTSCHKO T, HUGHES T J R. Computational methods for transient analysis. Amsterdam: Elsevier, 1983: 67−155. [29] 杜修力. 工程波动理论与方法 [M]. 北京: 科学出版社, 2009: 215−216. [30] 王勖成, 邵敏. 有限单元法基本原理和数值方法 [M]. 北京: 清华大学出版社, 1997: 66−67. -






 下载:
下载: