波阻抗梯度材料加强型Whipple结构撞击极限研究

张品亮; 曹燕; 陈川; 宋光明; 武强; 李宇; 龚自正; 李明

doi:10.11883/bzycj-2021-0230

波阻抗梯度材料加强型Whipple结构撞击极限研究

doi: 10.11883/bzycj-2021-0230

张品亮^1,,
曹燕¹,
陈川¹,
宋光明¹,
武强¹,
李宇¹,
龚自正^1, ,,
李明²

1.
北京卫星环境工程研究所，北京 100094
2.
中国空间技术研究院，北京 100094

基金项目: 国家重点研发计划 (2017YFB0702000)；民用航天预研项目（D020304）；空间碎片科研项目（KJSP2016030301）

详细信息

作者简介:
张品亮（1986－　），男，博士，高级工程师， zhangpinliang620@126.com

通讯作者:
龚自正（1964－　），男，博士，研究员，博士生导师， gongzz@263.net

中图分类号: O389
计量
- 文章访问数: 336
- HTML全文浏览量: 269
- PDF下载量: 107
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-04
- 录用日期: 2021-12-02
- 修回日期: 2021-08-10
- 网络出版日期: 2021-12-06
- 刊出日期: 2022-02-28

Ballistic limit of an impedance-graded-material enhanced Whipple shield

1.
Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China
2.
China Academy of Space Technology, Beijing 100094, China

摘要

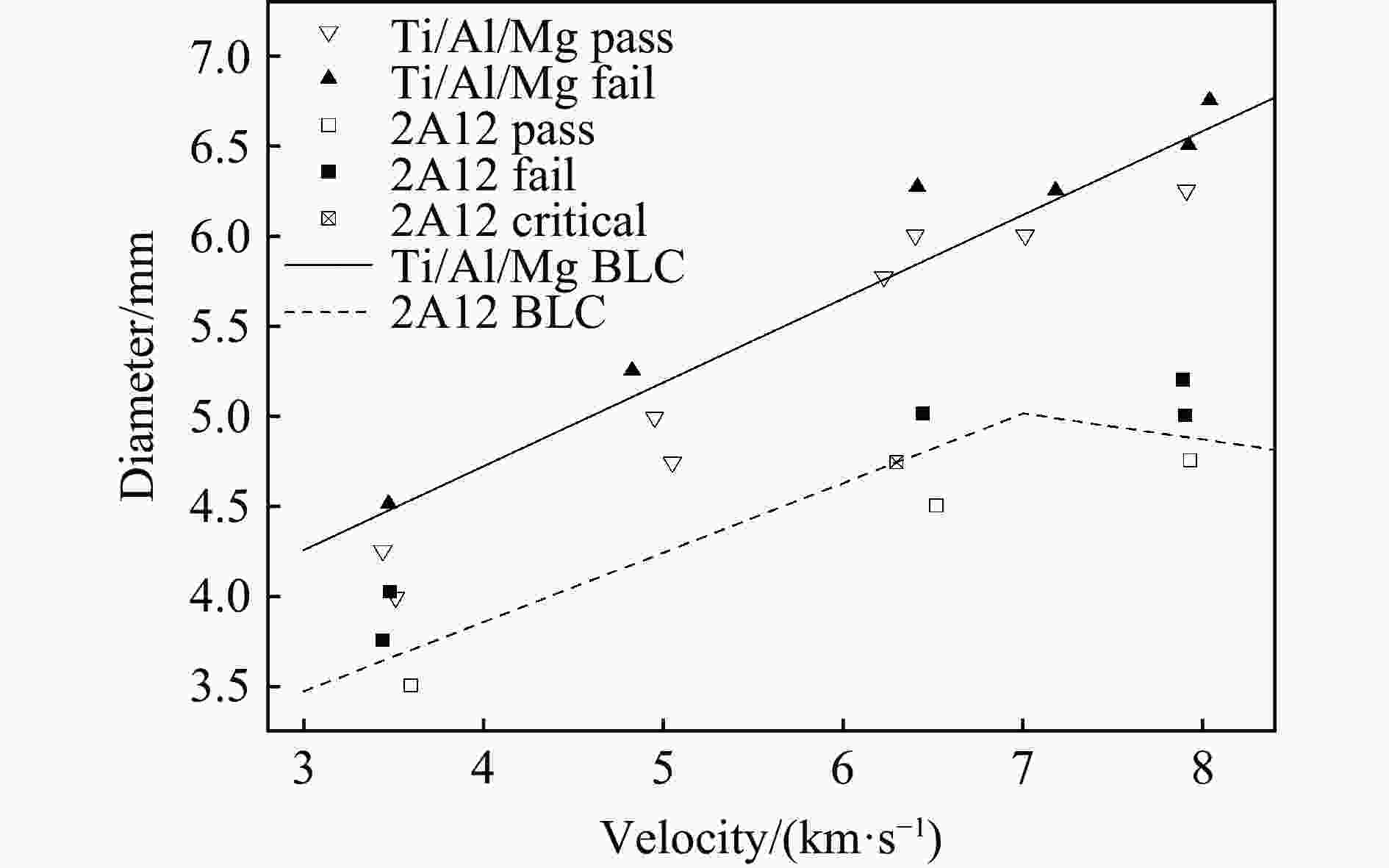
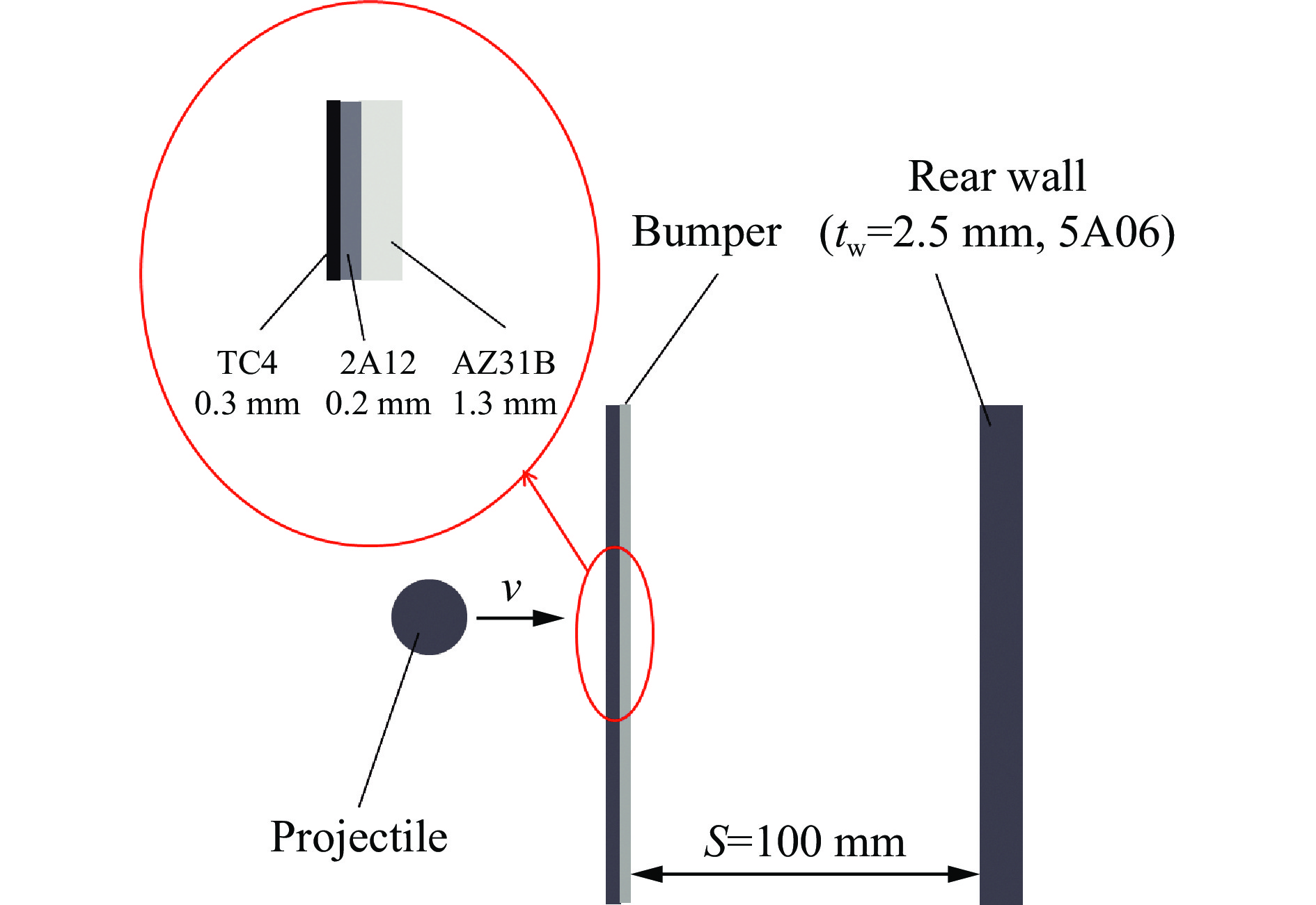
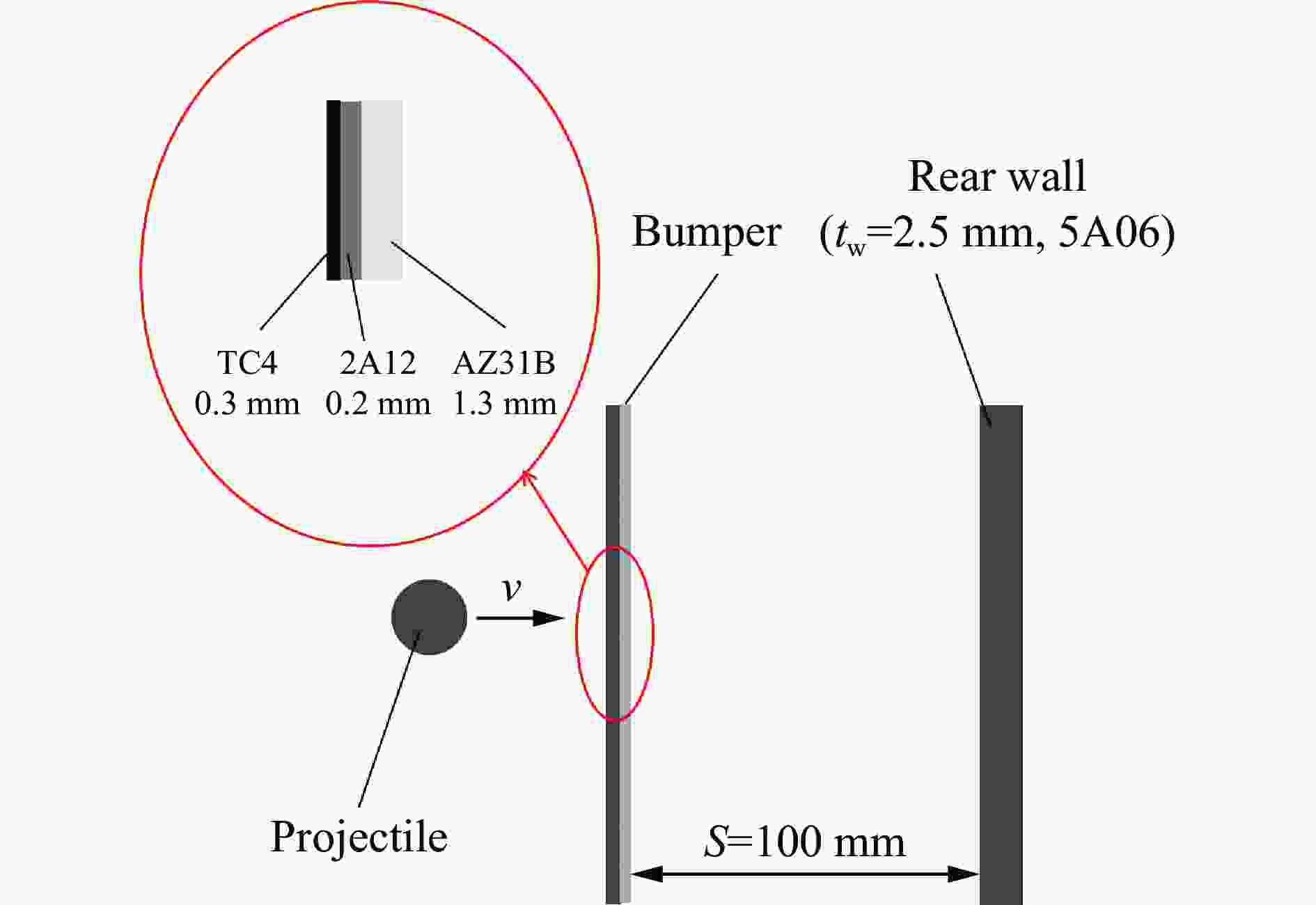
摘要: 为研究一种改进型的波阻抗梯度材料防护结构Ti/Al/Mg结构的撞击极限，采用二级轻气炮以3.0～8.0 km/s的速度对Ti/Al/Mg结构、Al/Mg结构和2A12结构开展了超高速撞击实验，建立了Ti/Al/Mg结构的撞击极限曲线。结果表明：高阻抗的钛合金表层能产生更高的冲击压力和温升，使弹丸充分破碎；在面密度相同的条件下，与Al/Mg结构和2A12结构相比，Ti/Al/Mg结构具有更强的防护性能。通过理论计算得到Ti/Al/Mg结构撞击极限曲线的区间转变速度小于7.0 km/s，但其实验撞击极限曲线上并未出现明显的区间转变，在实验速度范围内，撞击极限随着撞击速度的提升而增大，这与典型Whipple结构撞击极限曲线存在差异。
- 超高速撞击 /
- Whipple 结构 /
- 阻抗梯度材料 /
- 撞击极限 /
- 空间碎片
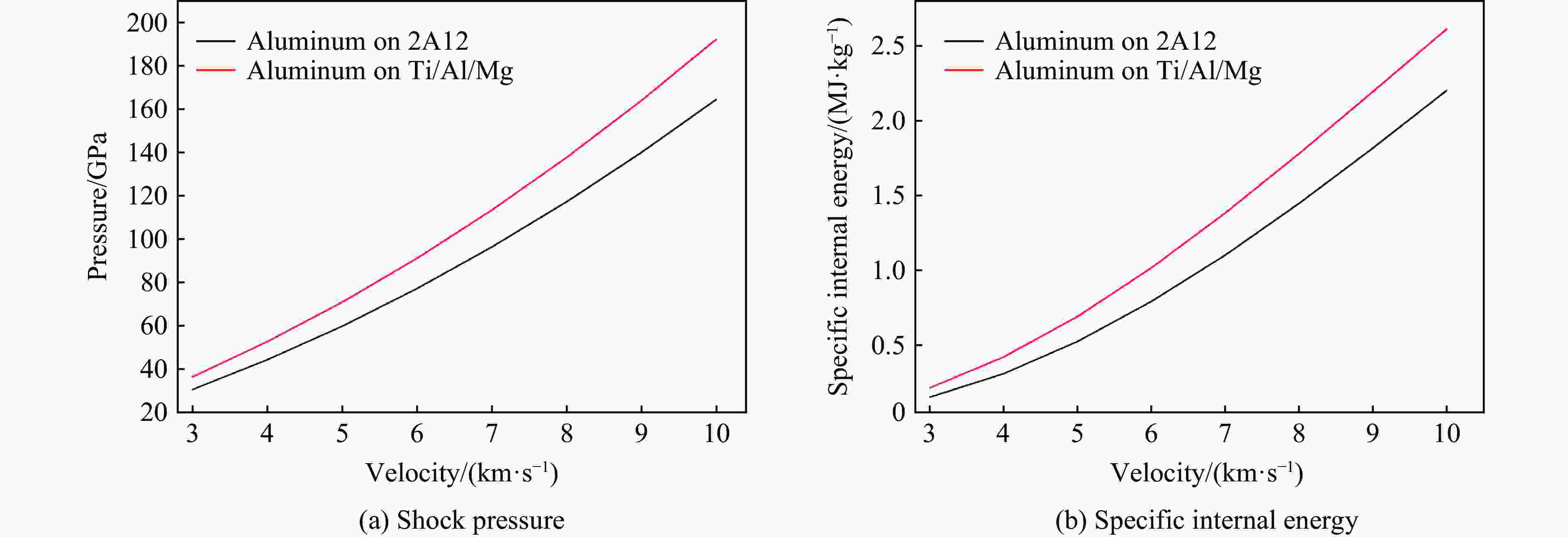
Abstract: Impedance-graded-material enhanced Whipple shields have excellent protective performance. The purpose of this paper is to study the ballistic limit of Ti/Al/Mg shields, which is an improved impedance-graded-material enhanced Whipple shield. Hypervelocity impact experiments on Ti/Al/Mg, Al/Mg and 2A12 shields were performed using a two-stage light-gas gun at impact velocities of 3.0–8.0 km/s. The hypervelocity impact characteristics, the ballistic limit curve and shielding performance of the Ti/Al/Mg shields were studied. The reason of its excellent performance is explained by comparative analysis. As the impact velocity increases, the failure mode of the rear wall showed a detached spall or tearing damage instead of tiny perforations similar to an aluminum shield. The results show that a high-acoustic-impedance titanium alloy layer can generate higher shock pressures and induce a greater temperature increase, which is more effective for fragmenting an impacting projectile. The shock pressure and specific internal energy in the projectile increased by 23.0% and 30.7% compared to the aluminum on aluminum impact event at 8.0 km/s, respectively. The shielding capability of a Ti/Al/Mg shield is significantly greater than that of 2A12 and Al/Mg shields when the bumper has the same areal density. The critical projectile diameter of Ti/Al/Mg shields is 6.58 mm at ~8.0 km/s, which is an improvement of approximately 34.8 % compared to the 4.88 mm of aluminum shields. Finally, to explore the transition velocities of the ballistic limit curve of the Ti/Al/Mg shields, a theoretical analysis was conducted, which suggests that for an aluminum projectile impacting a Ti/Al/Mg bumper, this value might be ＜7.0 km/s. However, a transition point is not apparent in the experimental ballistic limit curve, and the critical projectile diameter increases with increasing velocity in the range of 3.0–8.0 km/s. It is different from the typical Whipple shield. Further hypervelocity impact tests and additional research needs to be conducted to study in detail the ballistic limit of the Ti/Al/Mg shields.
- hypervelocity impact /
- Whipple shield /
- impedance-graded material /
- ballistic limit /
- space debris

HTML全文

图 1 实验原理示意图

Figure 1. Schematic diagram of experimental configuration

下载: 全尺寸图片幻灯片

图 2 在约3.5 km/s速度撞击下后墙前表面和后表面(插图)损伤形貌

Figure 2. Photographs of damage patterns on the front and rear (inset) surfaces of the rear wall produced by an aluminum sphere impacting at about 3.5 km/s

下载: 全尺寸图片幻灯片

图 3 在约6.2 km/s速度撞击下，后墙前表面和后表面的损伤形貌

Figure 3. Photographs of damage patterns on the front and rear (inset) surfaces of the rear wall produced by an aluminum sphere impacting at about 6.2 km/s

下载: 全尺寸图片幻灯片

图 4 冲击压力和比内能与撞击速度的关系

Figure 4. Calculated shock pressure and specific internal energy as a function of the impact velocity

下载: 全尺寸图片幻灯片

图 5 撞击速度约3.5 km/s时Ti/Al/Mg结构后墙后表面损伤形貌

Figure 5. Photographs of damage to the rear surface of Ti/Al/Mg shield’s rear walls when the impact velocity is about 3.5 km/s

下载: 全尺寸图片幻灯片

图 6 撞击速度约5.0 km/s时Ti/Al/Mg结构后墙后表面损伤形貌

Figure 6. Photographs of damage to the rear surface of Ti/Al/Mg shield’s rear walls when the impact velocity is about 5.0 km/s

下载: 全尺寸图片幻灯片

图 7 撞击速度约6.5 km/s时Ti/Al/Mg结构后墙后表面损伤形貌

Figure 7. Photographs of damage to the rear surface of Ti/Al/Mg shield’s rear walls when the impact velocity is about 6.5 km/s

下载: 全尺寸图片幻灯片

图 8 撞击速度约7.0 km/s时Ti/Al/Mg结构后墙后表面损伤形貌

Figure 8. Photographs of damage to the rear surface of Ti/Al/Mg shield’s rear walls when the impact velocity is about 7.0 km/s

下载: 全尺寸图片幻灯片

图 9 撞击速度约8.0 km/s时Ti/Al/Mg结构后墙后表面损伤形貌

Figure 9. Photographs of damage to the rear surface of Ti/Al/Mg shield’s rear walls when the impact velocity is about 8.0 km/s

下载: 全尺寸图片幻灯片

图 10 Ti/Al/Mg结构和2A12结构的撞击极限

Figure 10. Ballistic limit curves and test data for Ti/Al/Mg shields compared to 2A12 shields

下载: 全尺寸图片幻灯片

表 1 超高速撞击实验参数与结果

Table 1. Hypervelocity impact test conditions and results

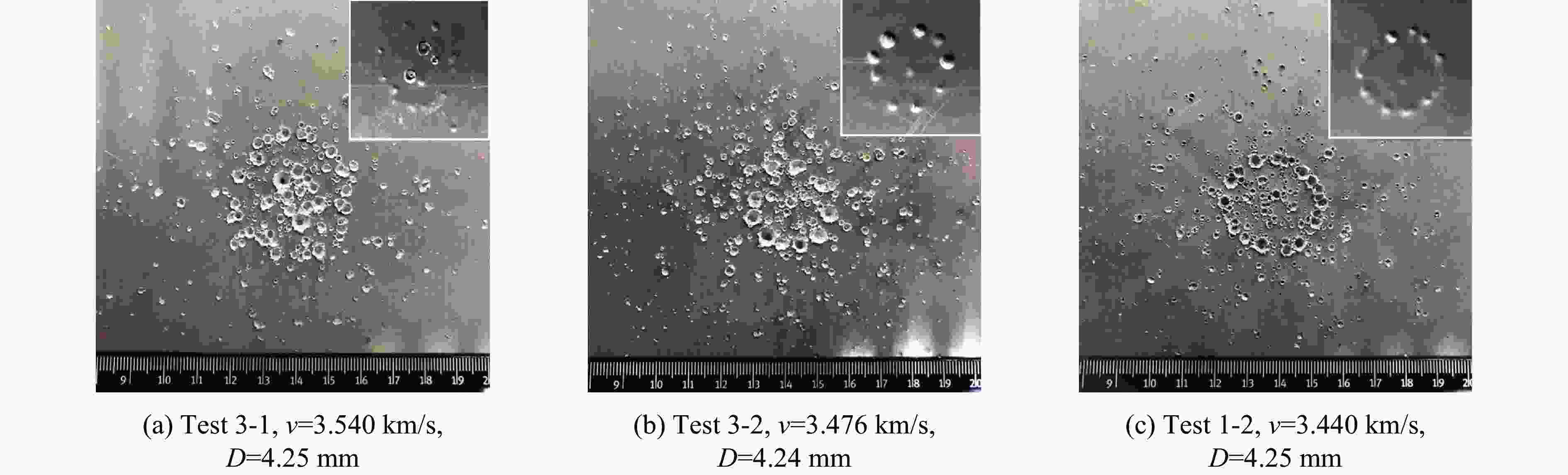
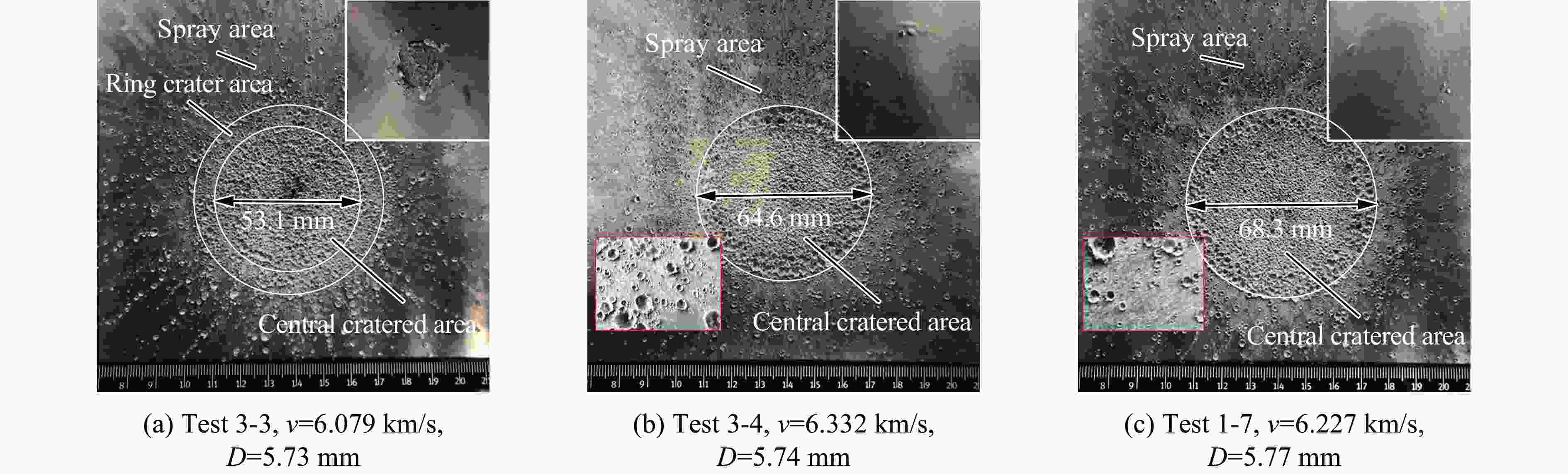
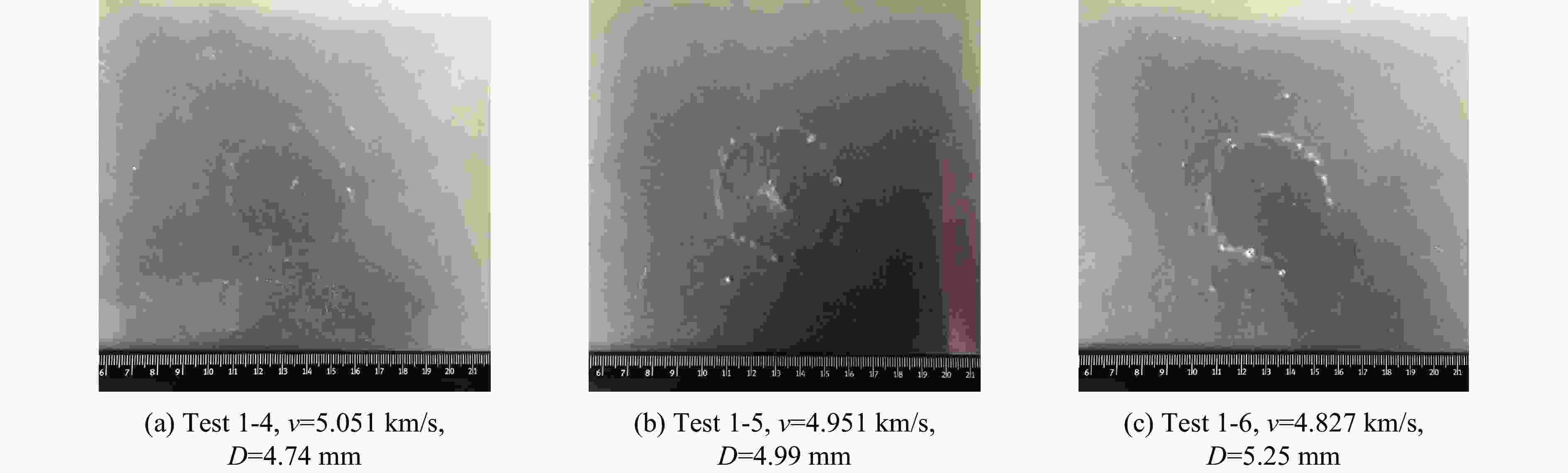
实验	结构类型	撞击速度/（km·s⁻¹）	弹丸直径/mm	失效状态	实验	结构类型	撞击速度/（km·s⁻¹）	弹丸直径/mm	失效状态
1-1	Ti/Al/Mg	3.512	3.99	未失效	2-1	2A12	3.596	3.50	未失效
1-2	Ti/Al/Mg	3.440	4.25	未失效	2-2	2A12	3.440	3.75	失效
1-3	Ti/Al/Mg	3.473	4.51	失效	2-3	2A12	3.480	4.02	失效
1-4	Ti/Al/Mg	5.051	4.74	未失效	2-4	2A12	6.518	4.50	未失效
1-5	Ti/Al/Mg	4.951	4.99	未失效	2-5	2A12	6.296	4.74	临界
1-6	Ti/Al/Mg	4.827	5.25	失效	2-6	2A12	6.442	5.01	失效
1-7	Ti/Al/Mg	6.227	5.77	未失效	2-7	2A12	7.170	5.00	失效
1-8	Ti/Al/Mg	6.400	6.00	未失效	2-8	2A12	7.930	4.75	未失效
1-9	Ti/Al/Mg	6.412	6.27	失效	2-9	2A12	7.900	5.00	失效
1-10	Ti/Al/Mg	7.011	6.00	未失效	3-1	2A12	3.540	4.25	失效
1-11	Ti/Al/Mg	7.181	6.25	失效	3-2	Al/Mg	3.476	4.24	临界
1-12	Ti/Al/Mg	7.907	6.25	未失效	3-3	2A12	6.079	5.73	失效
1-13	Ti/Al/Mg	7.920	6.50	失效	3-4	Al/Mg	6.332	5.74	失效
1-14	Ti/Al/Mg	8.037	6.75	失效

下载: 导出CSV

表 2 材料主要参数^[21-24]

Table 2. Key parameters of materials for shock coupling^[21-24]

材质	ρ₀/（g·cm⁻³）	c₀/（km·s⁻¹）	λ	γ₀
铝合金	2.784	5.370	1.290	2.000
钛合金	4.419	5.130	1.028	1.230
镁合金	1.775	4.516	1.256	1.540

下载: 导出CSV

参考文献(26)

[1]	WHIPPLE F L. Meteorites and space travel [J]. Astronomical Journal, 1947, 52(5): 131. DOI: 10.1086/106009.
[2]	SCHMIDT R M, HOUSEN K R, BJORKMAN M D, et al. Advanced all-metal orbital debris shield performance at 7 to 17 km/s [J]. International Journal of Impact Engineering, 1995, 17(4): 719–730. DOI: 10.1016/0734-743X(95)99894-W.
[3]	郭运佳, 文雪忠, 黄洁, 等. 不同填充层材料的空间碎片防护结构性能试验研究 [J]. 航天器环境工程, 2020, 37(6): 589–595. DOI: 10.12126/see.2020.06.009. GUO Y J, WEN X Z, HUANG J, et al. Experimental study of shielding performance of protecting structures stuffed with different materials [J]. Spacecraft Environment Engineering, 2020, 37(6): 589–595. DOI: 10.12126/see.2020.06.009.
[4]	黄鑫, 凌中, 刘宗德, 等. 梯度复合Whipple防护结构的超高速撞击实验 [J]. 爆炸与冲击, 2013, 33(S1): 92–98. HUANG X, LING Z, LIU Z D, et al. Hypervelocity impact experiments on new gradient Whipple shield structure [J]. Explosion and Shock Waves, 2013, 33(S1): 92–98.
[5]	HOFMANN D C, HAMILL L, CHRISTIANSEN E, et al. Hypervelocity impact testing of a metallic glass-stuffed Whipple shield [J]. Advanced Engineering Materials, 2015, 17(9): 1313–1322. DOI: 10.1002/adem.201400518.
[6]	PUTZAR R, ZHENG S G, AN J, et al. A stuffed Whipple shield for the Chinese space station [J]. International Journal of Impact Engineering, 2019, 132: 103304. DOI: 10.1016/j.ijimpeng.2019.05.018.
[7]	CHRISTIANSEN E L. Meteoroid/debris shielding [R]. Houston, USA: NASA, 2003.
[8]	CHRISTIANSEN E L, NAGY K, LEAR D M, et al. Space station MMOD shielding [J]. Acta Astronautica, 2009, 65(7/8): 921–929. DOI: 10.1016/j.actaastro.2008.01.046.
[9]	ZHANG P L, GONG Z Z, TIAN D B, et al. Comparison of shielding performance of Al/Mg impedance-graded-material-enhanced and aluminum Whipple shields [J]. International Journal of Impact Engineering, 2019, 126: 101–108. DOI: 10.1016/j.ijimpeng.2018.12.007.
[10]	张品亮, 宋光明, 龚自正, 等. Al/Mg波阻抗梯度材料加强型Whipple结构超高速撞击特性研究 [J]. 爆炸与冲击, 2019, 39(12): 125101. DOI: 10.11883/bzycj-2018-0461. ZHANG P L, SONG G M, GONG Z Z, et al. Shielding performances of a Whipple shield enhanced by Al/Mg impedance-graded materials [J]. Explosion and Shock Waves, 2019, 39(12): 125101. DOI: 10.11883/bzycj-2018-0461.
[11]	HUANG X, LING Z, LIU Z D, et al. Amorphous alloy reinforced Whipple shield structure [J]. International Journal of Impact Engineering, 2012, 42: 1–10. DOI: 10.1016/j.ijimpeng.2011.11.001.
[12]	ZHANG P L, XU K B, LI M, et al. Study of the shielding performance of a Whipple shield enhanced by Ti-Al-nylon impedance-graded materials [J]. International Journal of Impact Engineering, 2019, 124: 23–30. DOI: 10.1016/j.ijimpeng.2018.08.005.
[13]	宋光明, 李明, 武强, 等. 超高速撞击下波阻抗梯度防护结构碎片云特性研究 [J]. 爆炸与冲击, 2021, 41(2): 021405. DOI: 10.11883/bzycj-2020-0299. SONG G M, LI M, WU Q, et al. Debris cloud characteristics of graded-impedance shields under hypervelocity impact [J]. Explosion and Shock Waves, 2021, 41(2): 021405. DOI: 10.11883/bzycj-2020-0299.
[14]	LONG L P, PENG Y B, ZHOU W, et al. Study on hypervelocity impact characteristics of Ti/Al/Mg density-graded materials [J]. Metals, 2020, 10(5): 697. DOI: 10.3390/met10050697.
[15]	LONG L P, LIU W S, MA Y Z, et al. Microstructure and diffusion behaviors of the diffusion bonded Mg/Al joint [J]. High Temperature Materials and Processes, 2017, 36(9): 897–903. DOI: 10.1515/htmp-2016-0023.
[16]	PIEKUTOWSKI A J, POORMON K L. Impact of thin aluminum sheets with aluminum spheres up to 9 km/s [J]. International Journal of Impact Engineering, 2008, 35(12): 1716–1722. DOI: 10.1016/j.ijimpeng.2008.07.023.
[17]	GRADY D E, KIPP M E. Experimental measurement of dynamic failure and fragmentation properties of metals [J]. International Journal of Solids and Structures, 1995, 32(17): 2779–2791. DOI: 10.1016/0020-7683(94)00297-A.
[18]	MEYERS M A. 材料的动力学行为 [M]. 张庆明, 刘彦, 黄风雷, 等, 译. 北京: 国防工业出版社, 2006: 83.
[19]	谭华. 实验冲击波物理导引 [M]. 北京: 国防工业出版社, 2007.
[20]	经福谦. 实验物态方程导引 [M]. 2版. 北京: 科学出版社, 1999.
[21]	MARSH S P. LASL shock hugoniot data [M]. California, USA: University of California, 1980.
[22]	ANDERSON C E Jr, TRUCANO T G, MULLIN S A. Debris cloud dynamics [J]. International Journal of Impact Engineering, 1990, 9(1): 89–113. DOI: 10.1016/0734-743X(90)90024-P.
[23]	MCQUEEN R G, MARSH S P. Equation of state for nineteen metallic elements from shock-wave measurements to two megabars [J]. Journal of Applied Physics, 1960, 31(7): 1253–1269. DOI: 10.1063/1.1735815.
[24]	徐锡申, 张万箱. 实用物态方程理论导引 [M]. 北京: 科学出版社, 1986.
[25]	CHRISTIANSEN E L, KERR J H. Ballistic limit equations for spacecraft shielding [J]. International Journal of Impact Engineering, 2001, 26(1−10): 93–104. DOI: 10.1016/S0734-743X(01)00070-7.
[26]	SCHONBERG W P. Using modified ballistic limit equations in spacecraft risk assessments [J]. Acta Astronautica, 2016, 126: 199–204. DOI: 10.1016/j.actaastro.2016.03.038.