Analysis for impact resistance of the high-voltage power module with different fixed modes
-
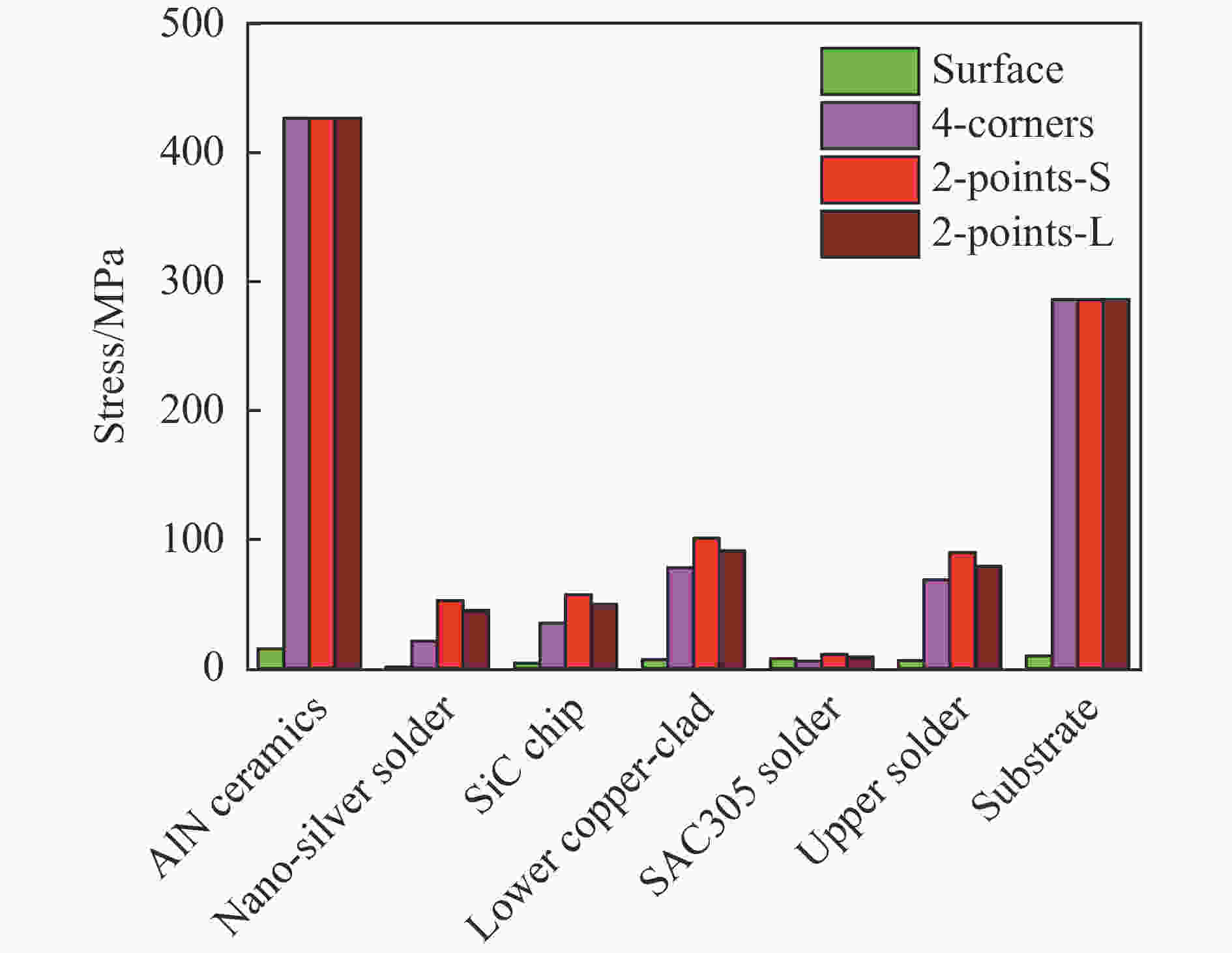
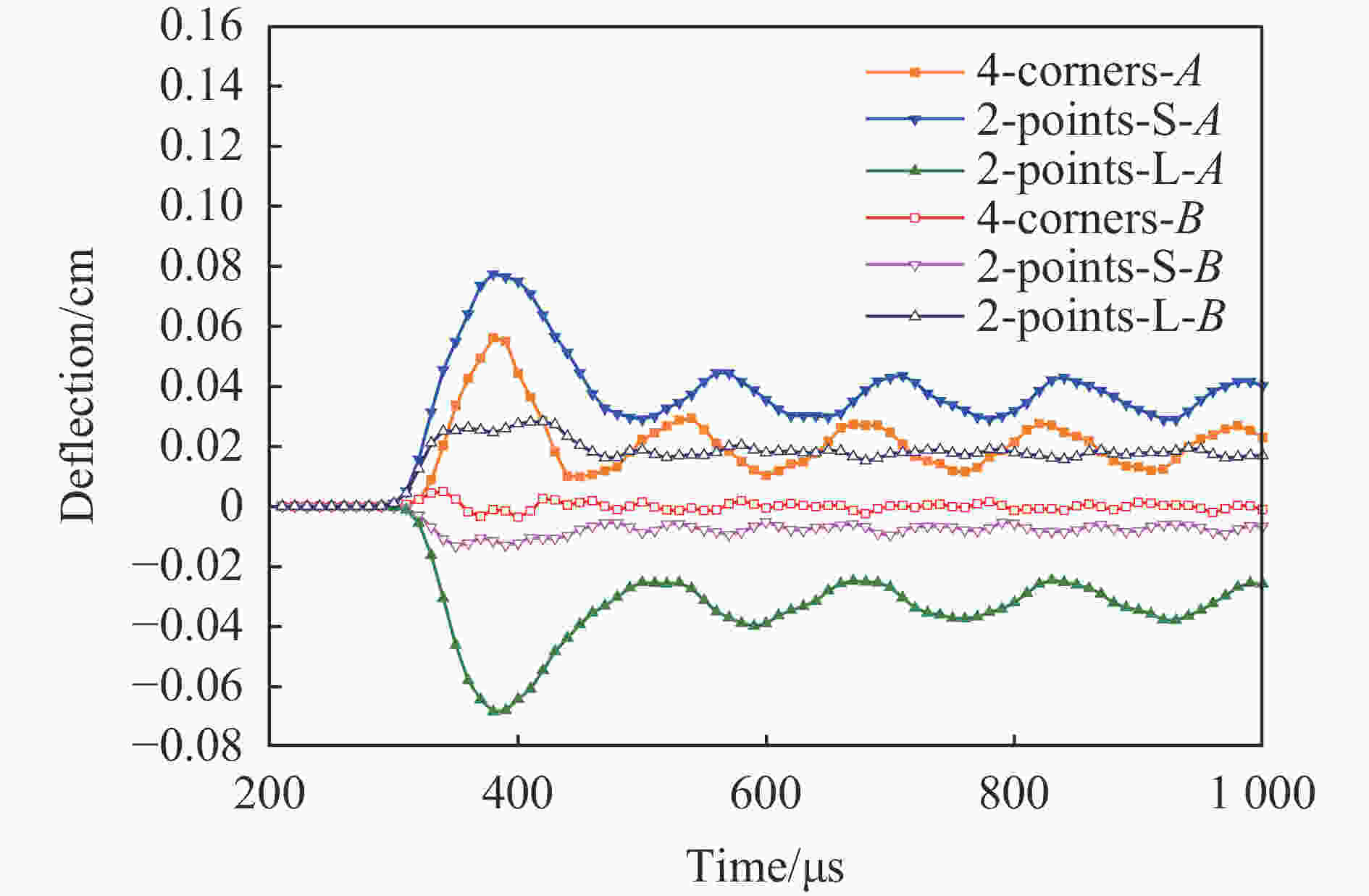
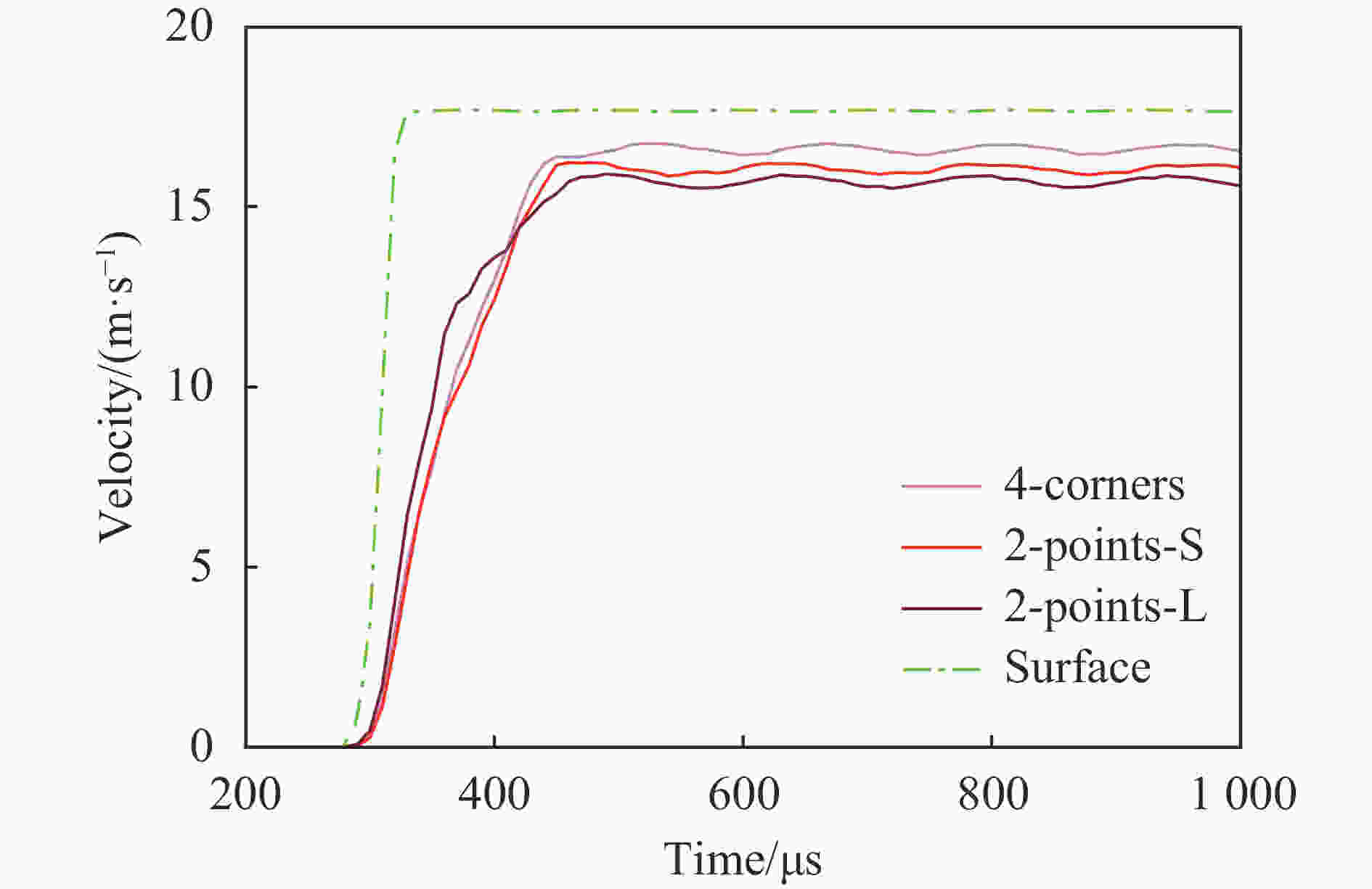
摘要: 为了提升高压功率模块在高速冲击环境中的结构可靠性,研究了高压功率模块采用不同固定方式的抗冲击特性。基于一维应力波条件,针对模块在自由式霍普金森杆系统中的运动响应以及能量转换形式进行理论分析,完成了模块的变形能与动能结果对比。采用有限元方法模拟了20 m/s冲击速度下模块的运动和变形过程,提取关键结构的应力分布、挠度、位移响应速度和加速度响应曲线,其中应力响应最高位置在陶瓷基板层,达到427 MPa,挠度响应最高位置在金属底板层,达到了773.8 μm,模块整体位移速度最高达到17.68 m/s,加速度最高达到51 110.7g。对比4种固定方式的冲击响应结果,模块冲击后底板变形量由小到大分别为面贴装固定、四角点固定、短边两点固定和长边两点固定,面贴装模块的位移动能和加速度峰值最大。结果表明采用面贴装固定的模块在冲击加速度载荷下发生变形失效的可能性最小,面贴装在四种固定方式中是可靠性最高的安装方式,之后的选择优先度分别是四角点固定、短边两点固定和长边两点固定。研究成果为半导体高压功率模块在实际应用中的安装固定方式选择提供了重要理论依据。Abstract: High-voltage power module is a key component to realize stable current output. In order to improve the structural reliability of the high-voltage power module and optimize the fixed modes under high-speed impact, the impact resistance characteristics with different fixed modes are studied. Based on the one-dimensional stress wave theory, the comparison of deformation energy and kinetic energy of the module with different fixed modes are obtained by analyzing the dynamic response and energy conversion form of the module on the free Hopkinson pulse bar (FHPB). The finite element method is used to simulate the processes of motion and deformation under impact velocity of 20 m/s. The stress distributions, the deflection curves, the velocity curves, and the acceleration curves of the module under the same impact are obtained. It is found that the maximum stress (427 MPa) appears at the ceramic layer, while the maximum deflection (773.8 μm) occurs at the metal substrate layer. The magnitude of the maximum displacement speed is up to 17.68 m/s, and the magnitude of the maximum acceleration is up to 51 110.7g. By comparing the impact response results of the four fixed modes, the deformation of bottom substrate from small to large is the surface mounting, four-corner point fixing, two-point fixing on the short side and two-point fixing on the long side. The highest kinetic energy and acceleration are produced on the surface mounting modules. The results indicate that a minimum failure probability exists on surface mounting module under high impact loading. In summary, surface mounting is the most reliable fixed method among the four fixed methods. Then, the selection priorities are as following: the four-corner fixing, two-point fixing on the short side and two-point fixing on the long side. Out study results would provide an important theoretical basis of the mounting and fixing methods for semiconductor high-voltage power modules in practical application.
-
Key words:
- high-voltage power module /
- fixed mode /
- high-speed impact /
- finite element method
-
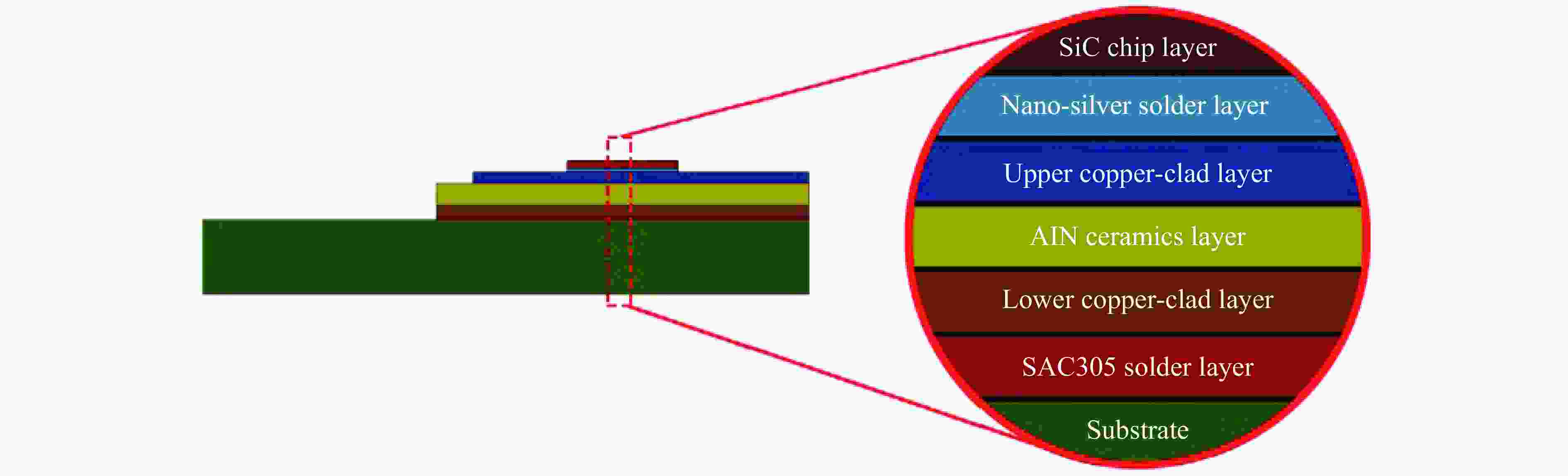
表 1 功率模块内部关键结构材料参数
Table 1. Material parameters of plate-level power module
结构 厚度
/mm密度
/(kg·m−3)弹性模量
/GPa泊松比 屈服强度
/MPaFHPB冲击系统 1500 7800 210 0.30 — 金属细支架 10 7800 210 0.30 — 铜底板 2 8930 117 0.34 286.0 覆铜层 0.3 8930 117 0.34 286.0 氮化铝陶瓷 0.6 3400 320 0.22 427.0 SAC305焊料 0.1 7400 33 0.32 55.3 纳米银焊料 0.1 10500 73.2 0.38 180.0 碳化硅芯片 0.2 3200 330 0.14 73.6 表 2 四种固定方式下的冲击响应
Table 2. Impact response in four fixed modes
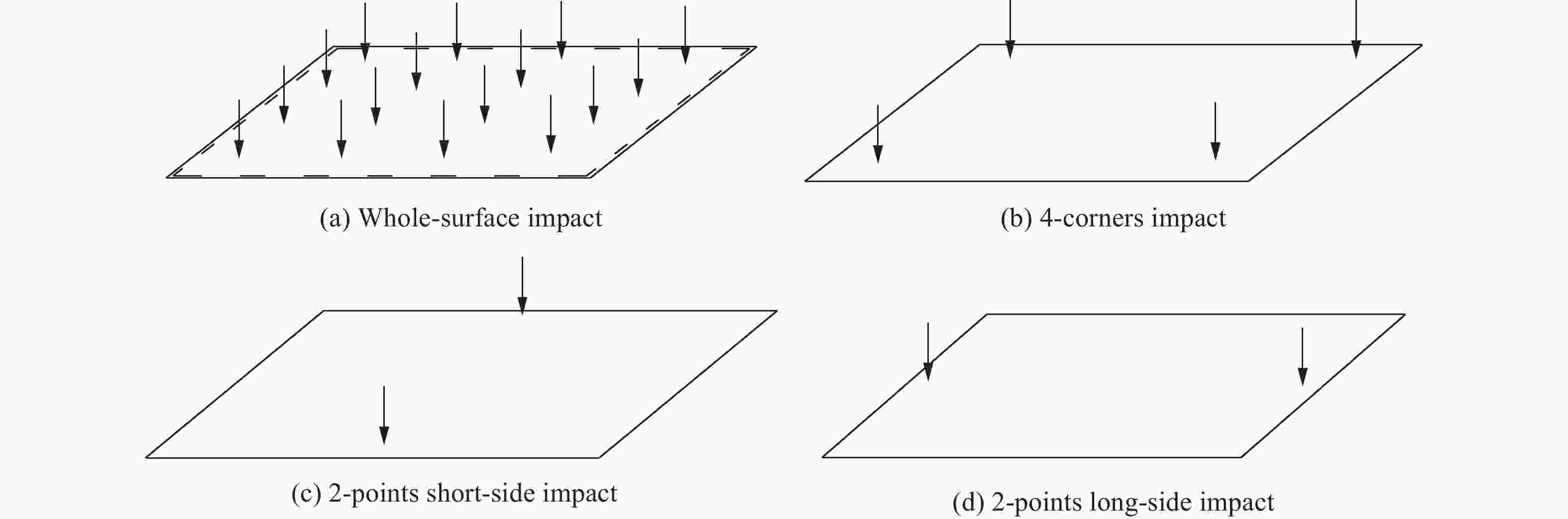
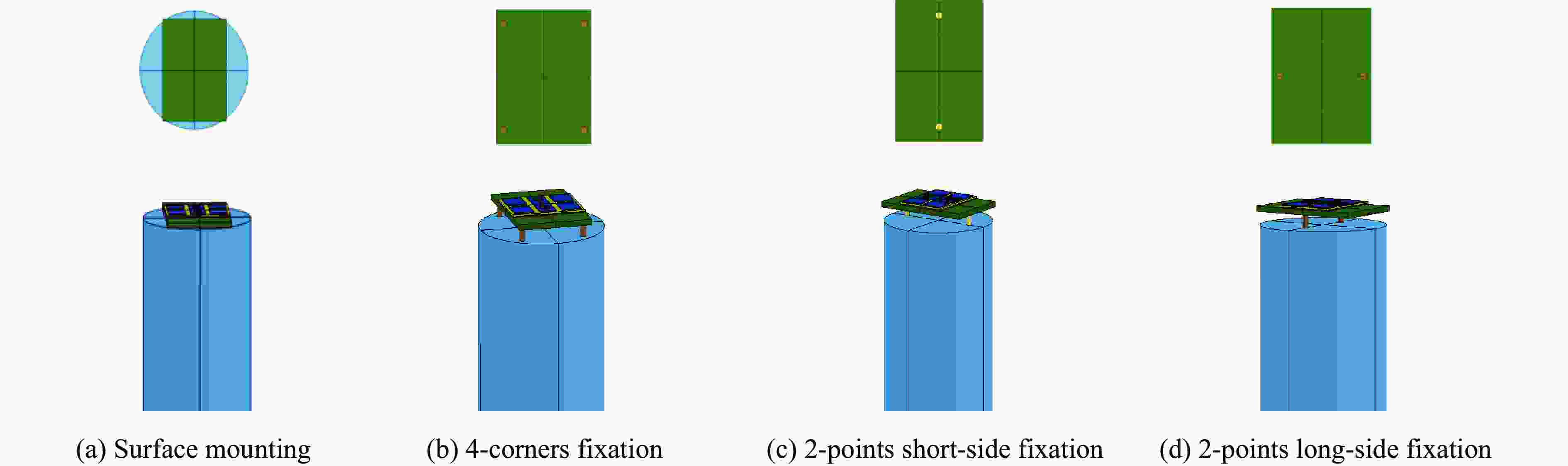
冲击加载方式 底板挠度/cm 最大等效应力/MPa 最大速度/(m·s−1) 底板过载加速度峰值/g Surface 0 15.32 17.68 51 110.7 4-corners-x 0.056 17 427 16.75 21 181.9 4-corners-y 0.004 96 427 16.75 21 181.9 2-points-S-x 0.077 38 427 16.22 19 000.9 2-points-S-y 0.013 15 427 16.22 19 000.9 2-points-L-x 0.068 33 427 15.91 30 339.5 2-points-L-y 0.028 26 427 15.91 30 339.5 -
[1] SAMAVATIAN V, MASOUMIAN A, MAFI M, et al. Influence of directional random vibration on the fatigue life of solder joints in a power module [J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2019, 9(2): 262–268. DOI: 10.1109/TCPMT. 2018.2838148. [2] HUANG C, WU K, WANG Z Y. Mechanical reliability testing of air-gap through-silicon vias [J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2016, 6(5): 712–721. DOI: 10.1109/TCPMT. 2016.2544762. [3] SHAMMAS N Y A. Present problems of power module packaging technology [J]. Microelectronics Reliability, 2003, 43(4): 519–527. DOI: 10.1016/S0026-2714(03)00019-2. [4] YU Q, KIKUCHI H, IKEDA S, et al. Dynamic behavior of electronics package and impact reliability of BGA solder joints[C]//Proceedings of the 8th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems. San Diego: IEEE, 2002: 953–960. DOI : 10.1109/ITHERM.2002.1012559. [5] 周新. 板级无铅焊点跌落冲击载荷下可靠性分析[D]. 上海: 上海交通大学, 2007: 43–46.ZHOU X. Board level lead-free solder joints reliability analysis under drop shock loading[D]. Shanghai: Shanghai Jiaotong university, 2007: 43–46. [6] TEE T Y, LUAN J E, PEK E, et al. Novel numerical and experimental analysis of dynamic responses under board level drop test[C]// Proceedings of the 5th International Conference on Thermal and Mechanical Simulation and Experiments in Microelectronics and Microsystems. Brussels: IEEE, 2004: 133–140. DOI: 10.1109/ESIME.2004.1304032. [7] WONG S F, MALATKAR P, RICK C, et al. Vibration testing and analysis of ball grid array package solder joints[C]// Proceedings of the 57th Electronic Components and Technology Conference. Sparks: IEEE, 2007: 373–380. DOI: 10.1109/ECTC.2007.373825. [8] 姬永强, 李映辉, 聂飞. 弹载数据存储模块抗高过载防护技术研究 [J]. 振动与冲击, 2012, 31(18): 104–106. DOI: 10.13465/j.cnki.jvs.2012.18.018.JI Y Q, LI Y H, NIE F. Protection technology for onboard data storage module against high overload [J]. Journal of Vibration and Shock, 2012, 31(18): 104–106. DOI: 10.13465/j.cnki.jvs.2012.18.018. [9] 陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2007: 115–118. [10] 王礼立. 应力波基础[M]. 北京: 国防工业出版社, 1985: 51–59. [11] 王娜, 沈瑞琪, 叶迎华. 霍普金森杆测量火工品过载情况的研究与数值模拟 [J]. 火工品, 2004, 1: 42–47. DOI: 10.3969/j.issn.1003-1480.2004.01.014.WANG N, SHEN R Q, YIE Y H. Study on the measurement of over-loaded initiator by Hopkinson bar and numerical simulation [J]. Initiators and Pyrotechnics, 2004, 1: 42–47. DOI: 10.3969/j.issn.1003-1480.2004.01.014. [12] 王吉会, 郑俊萍, 刘家臣, 等. 材料力学性能[M]. 天津: 天津大学出版社, 2006: 66–70. -







 下载:
下载: