地面和埋置爆炸土中地冲击作用分区数值模拟及试验研究

刘琦; 翟超辰; 张跃飞; 曲建波; 吴祥云

doi:10.11883/bzycj-2021-0326

地面和埋置爆炸土中地冲击作用分区数值模拟及试验研究

doi: 10.11883/bzycj-2021-0326

1.
湘潭大学土木工程与力学学院，湖南湘潭 411105
2.
军事科学院国防工程研究院工程防护研究所，河南洛阳 471023

基金项目: 湖南省研究生科研创新项目（CX20190495，CX20200648）

详细信息

作者简介:
刘　琦（1993－　），男，博士研究生，hhxylq@126.com

通讯作者:
吴祥云（1964－　），男，博士，研究员，13503882599@139.com

中图分类号: O383
计量
- 文章访问数: 686
- HTML全文浏览量: 218
- PDF下载量: 149
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-30
- 修回日期: 2022-02-21
- 网络出版日期: 2022-04-06
- 刊出日期: 2022-09-09

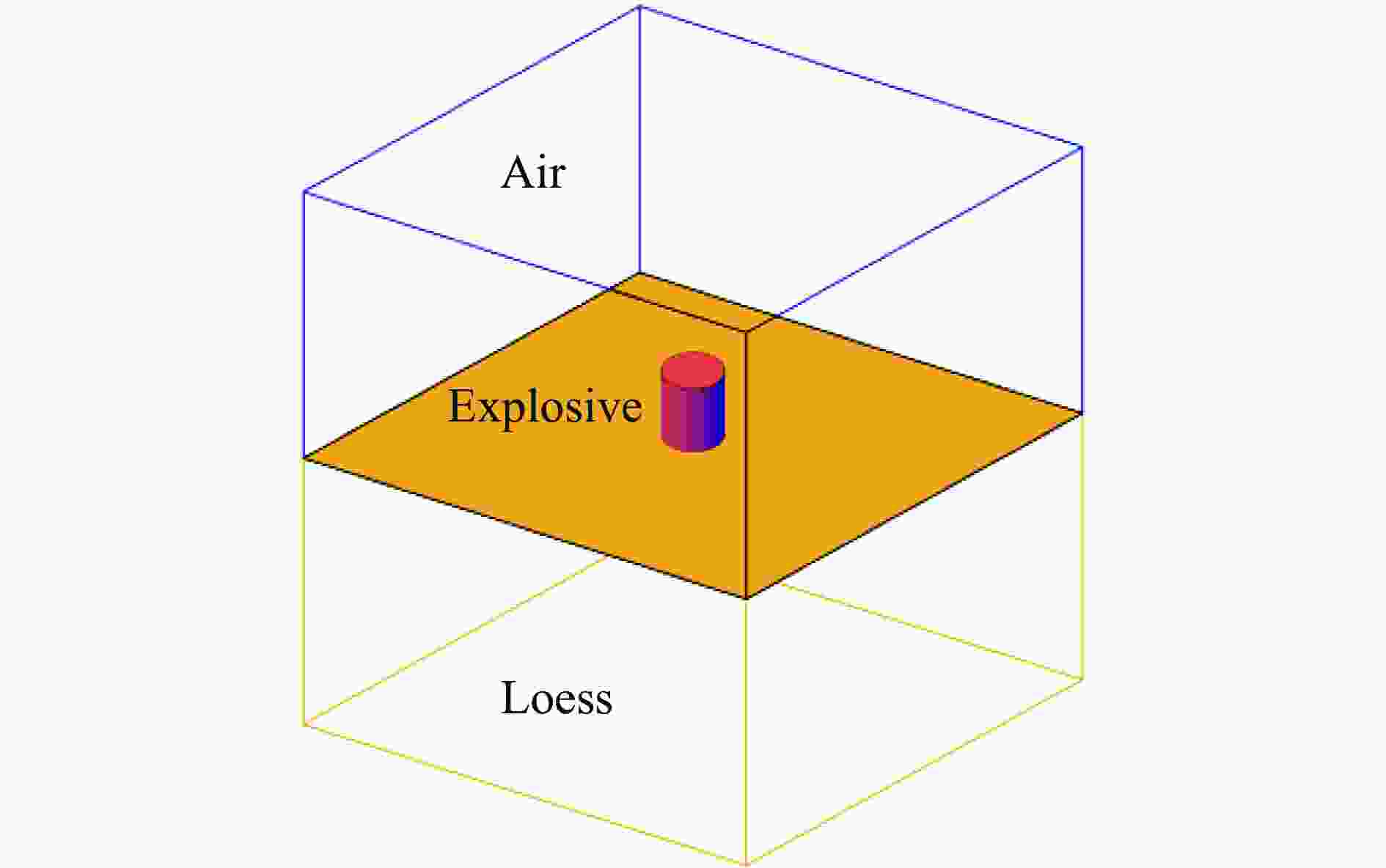
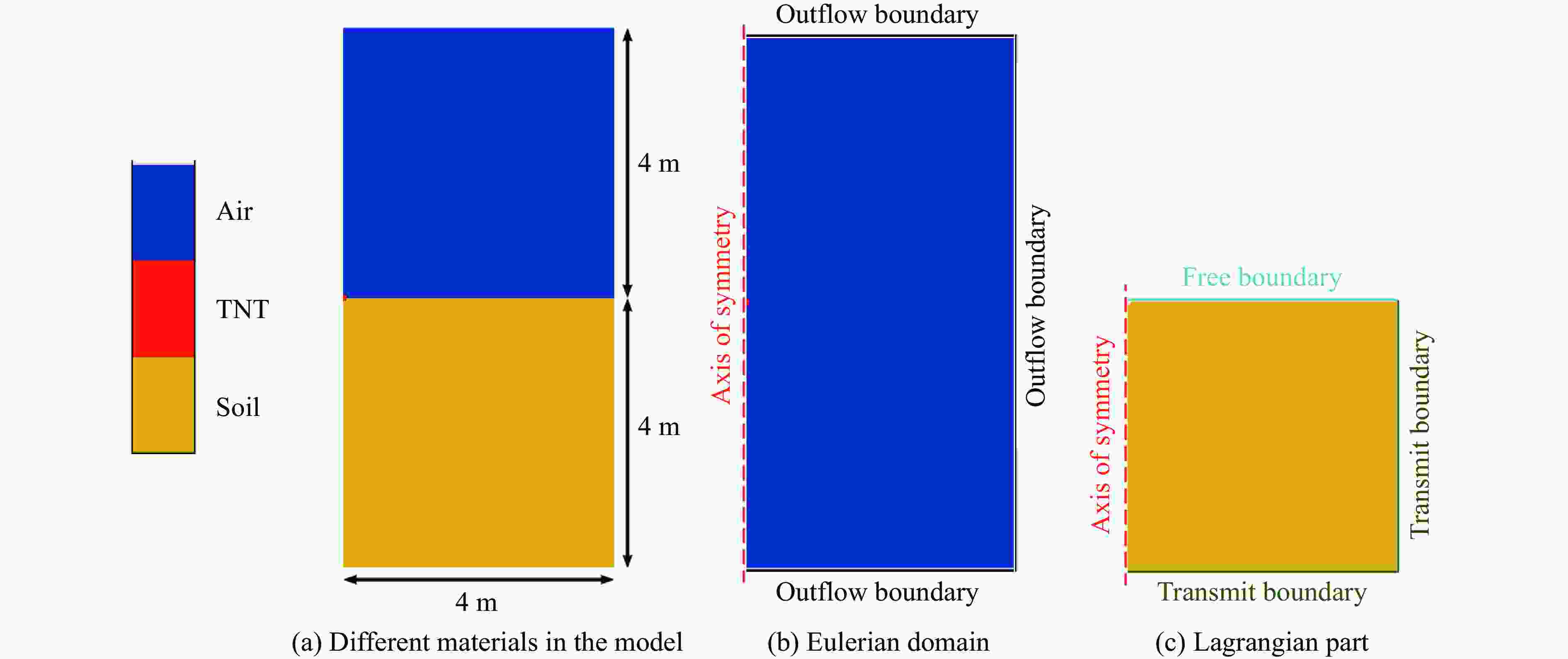
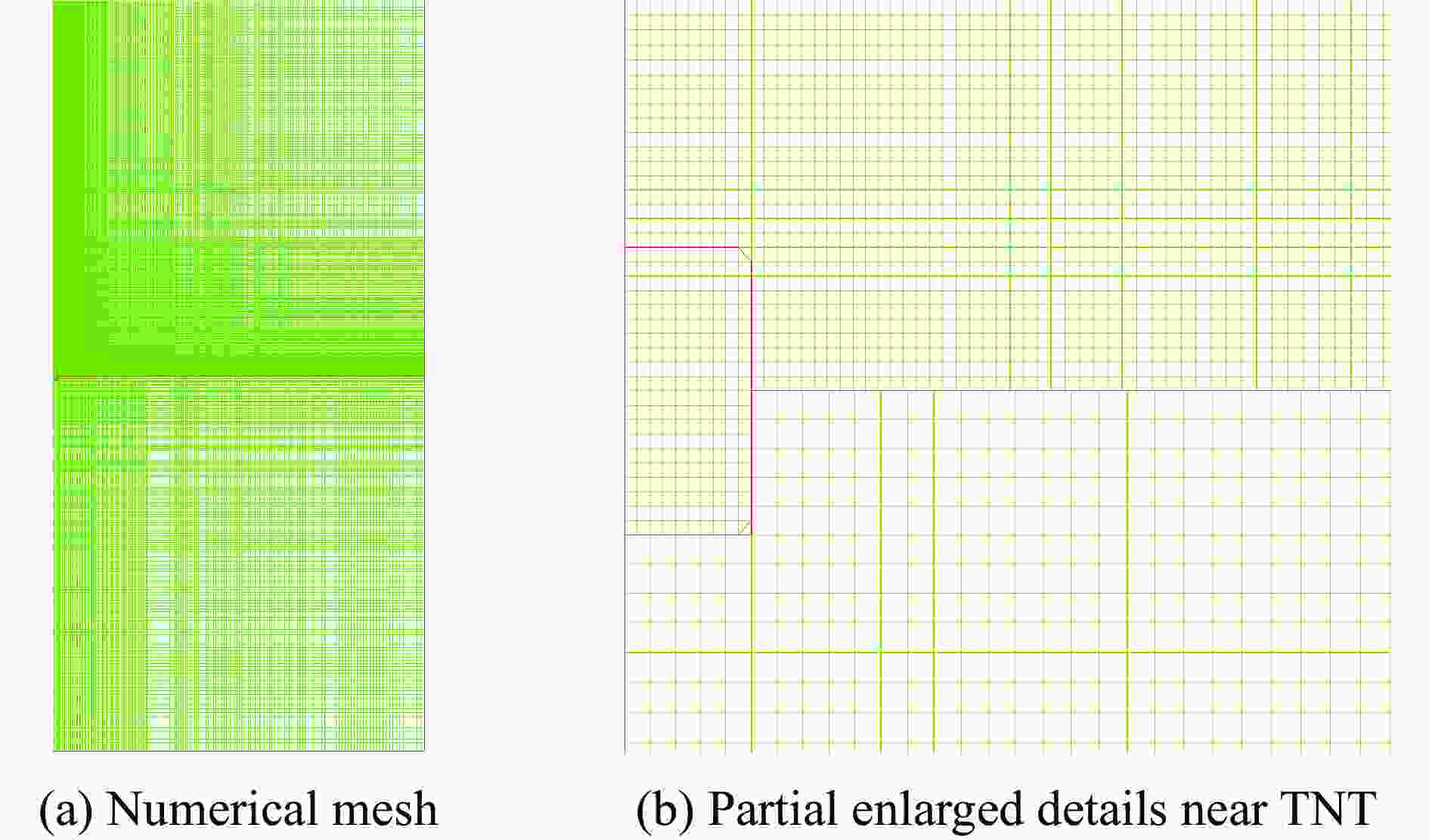
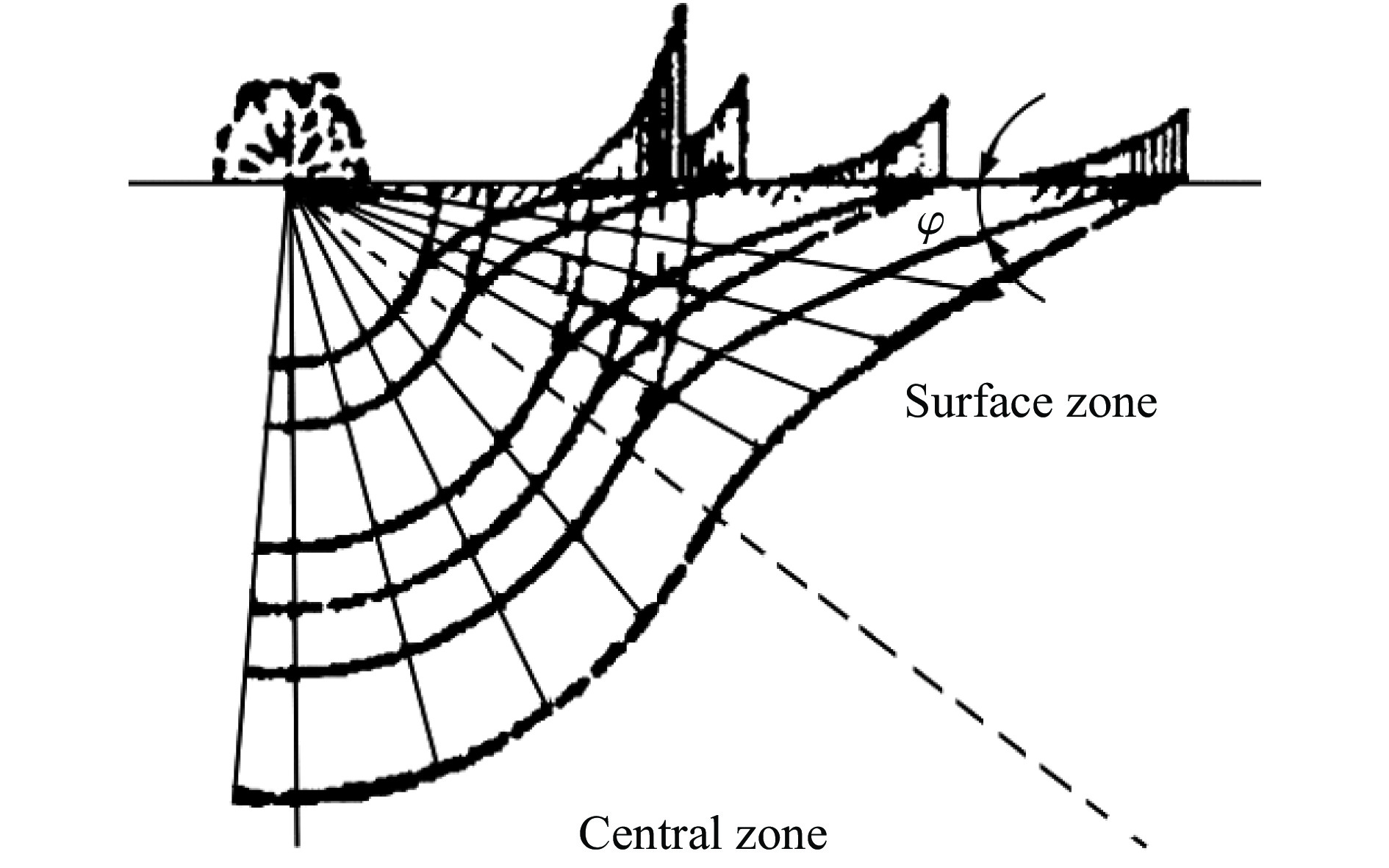
Numerical simulation and test study on ground shock subzones in soil produced by ground and buried explosion

1.
Civil Engineering and Mechanics College, Xiangtan University, Xiangtan 411105, Hunan, China
2.
Institution of Engineering Protection, IDE, AMS, PLA, Luoyang 471023, Henan, China

摘要

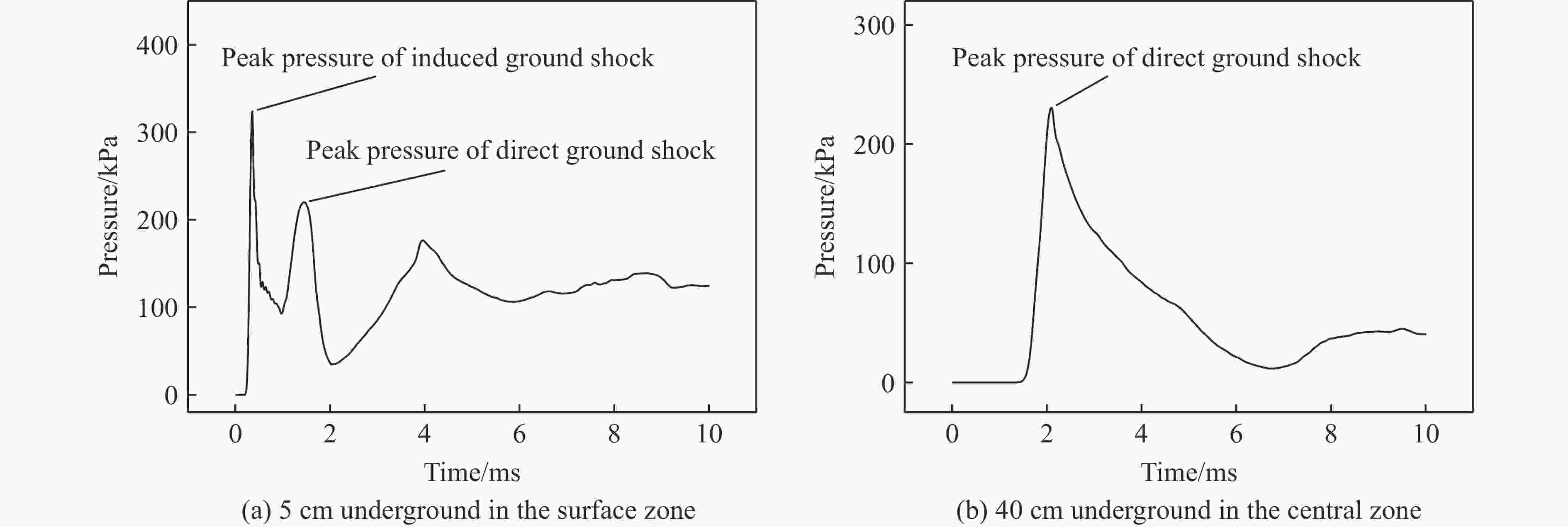
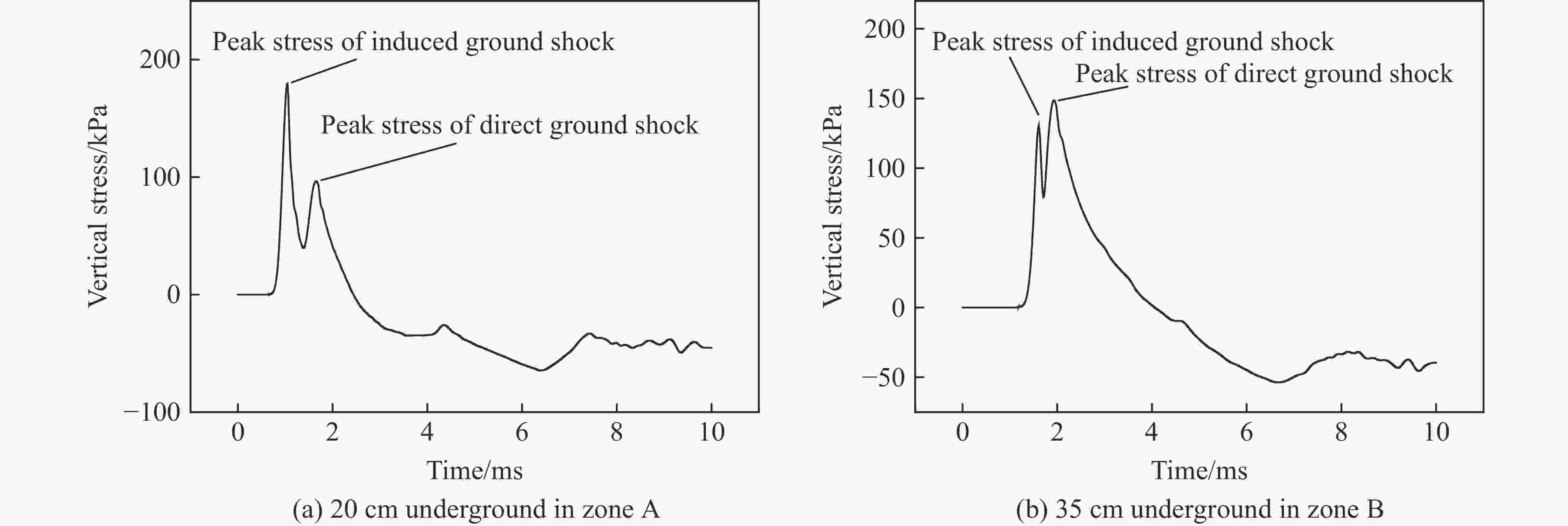
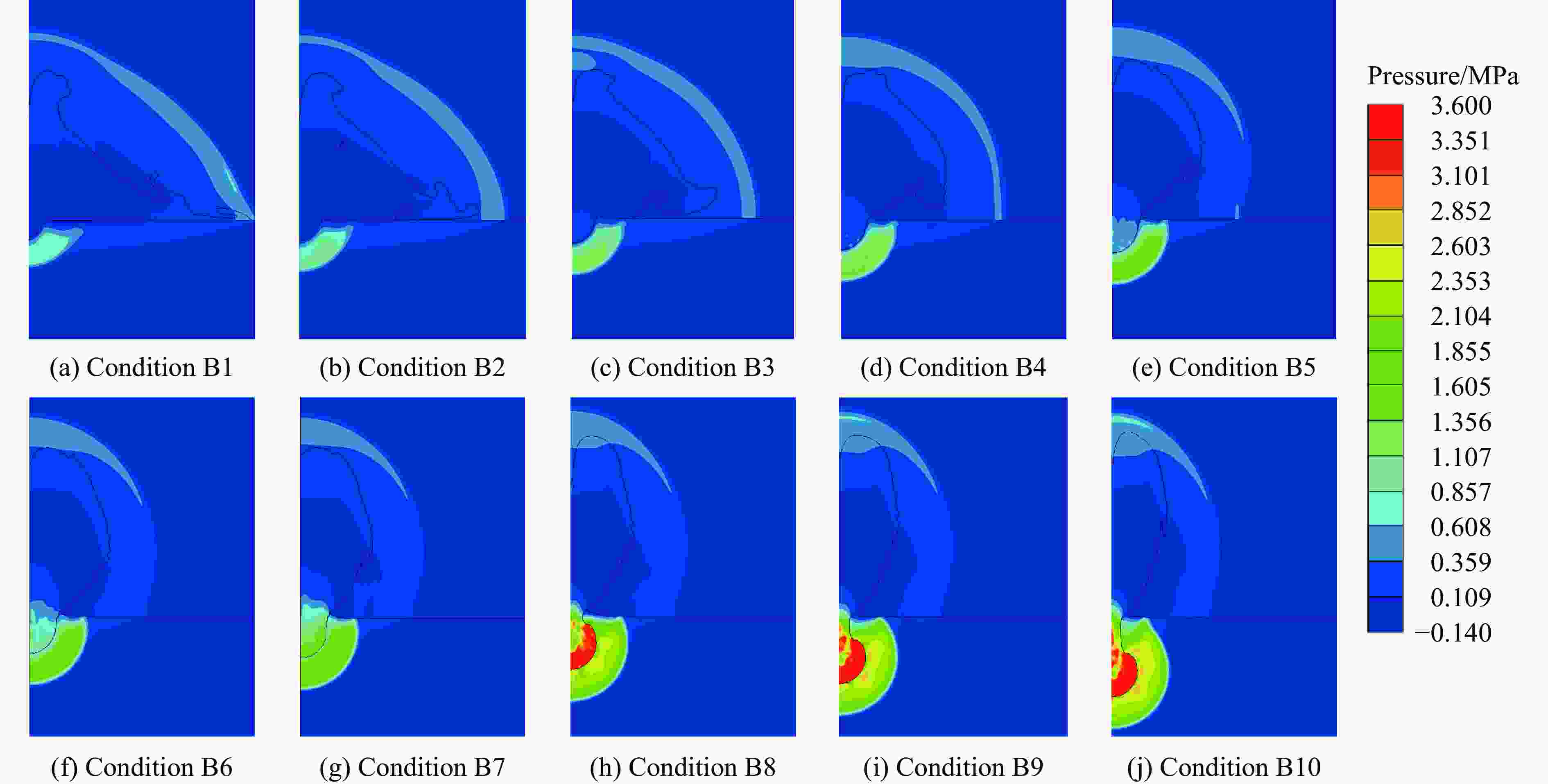
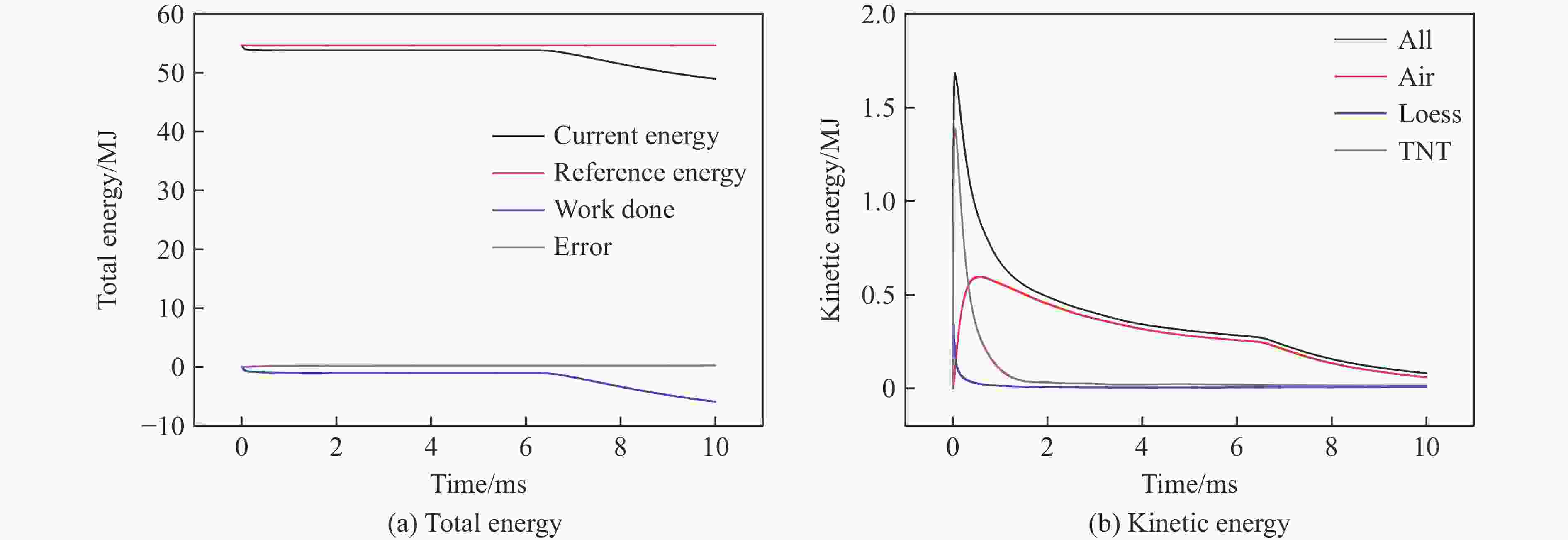
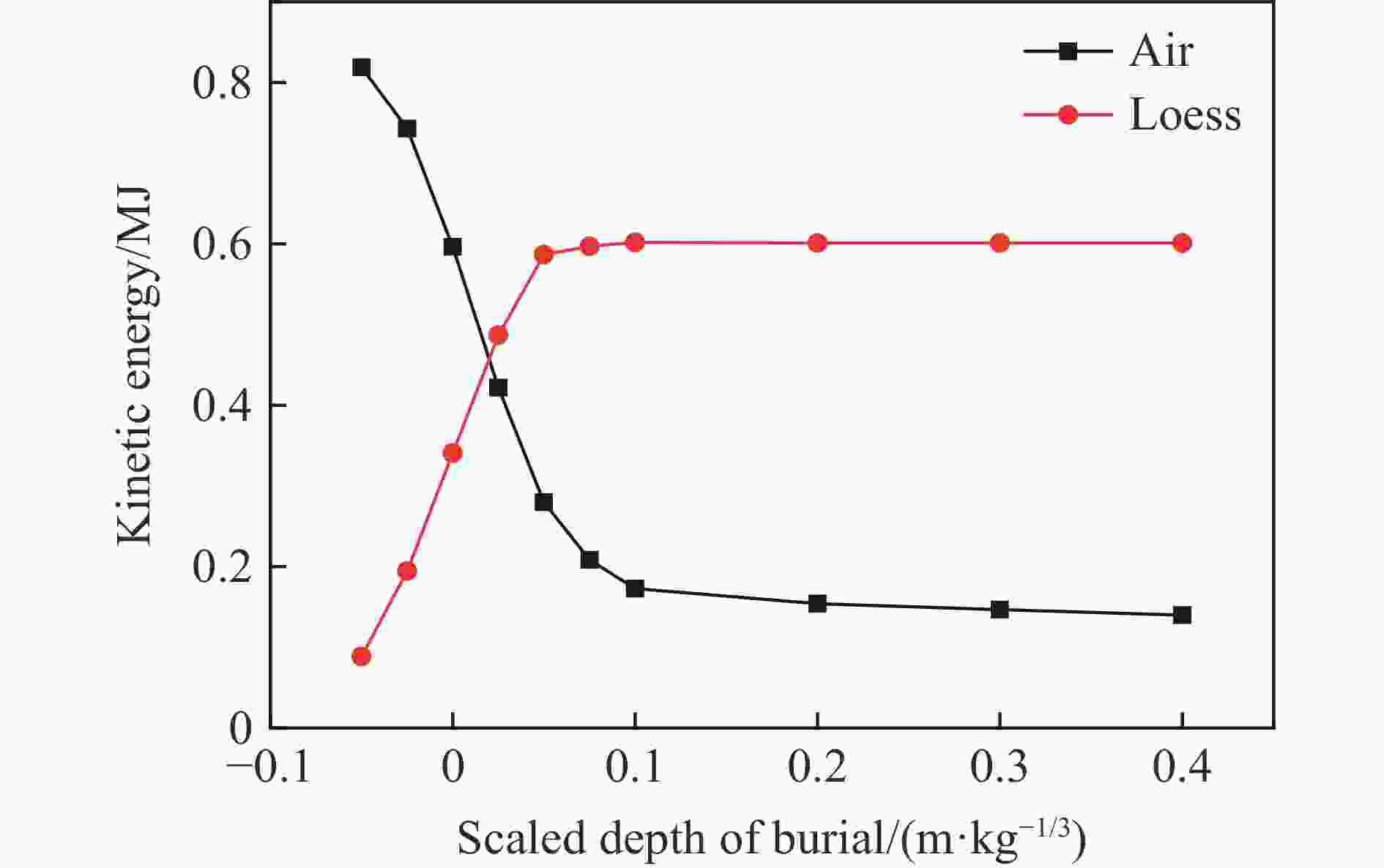
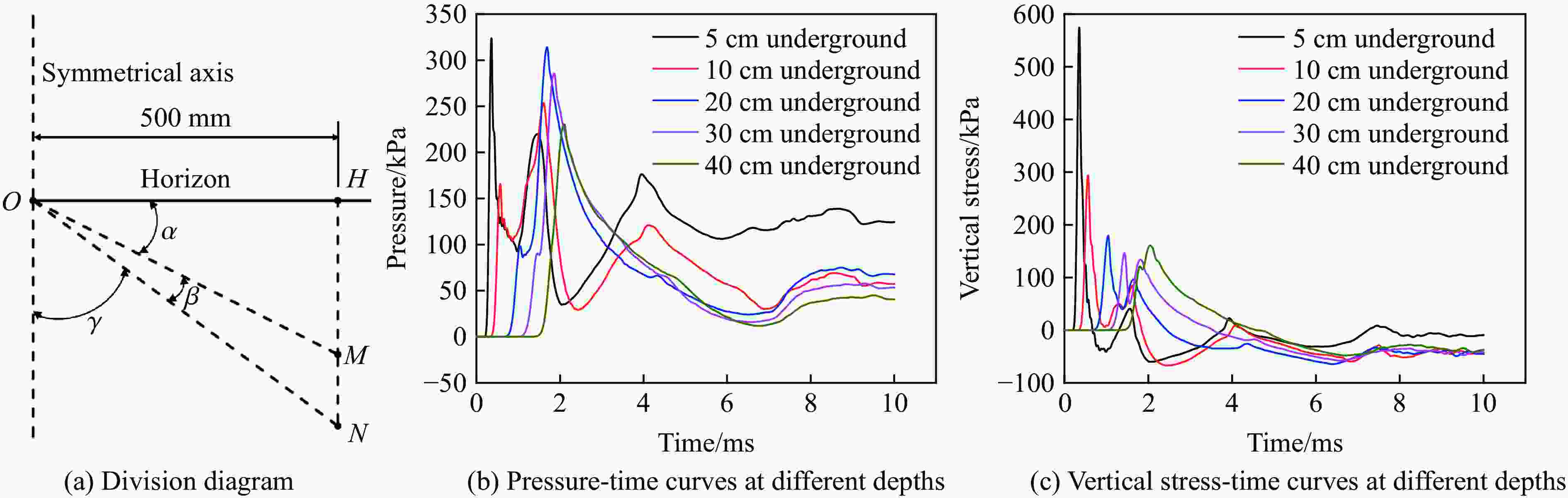
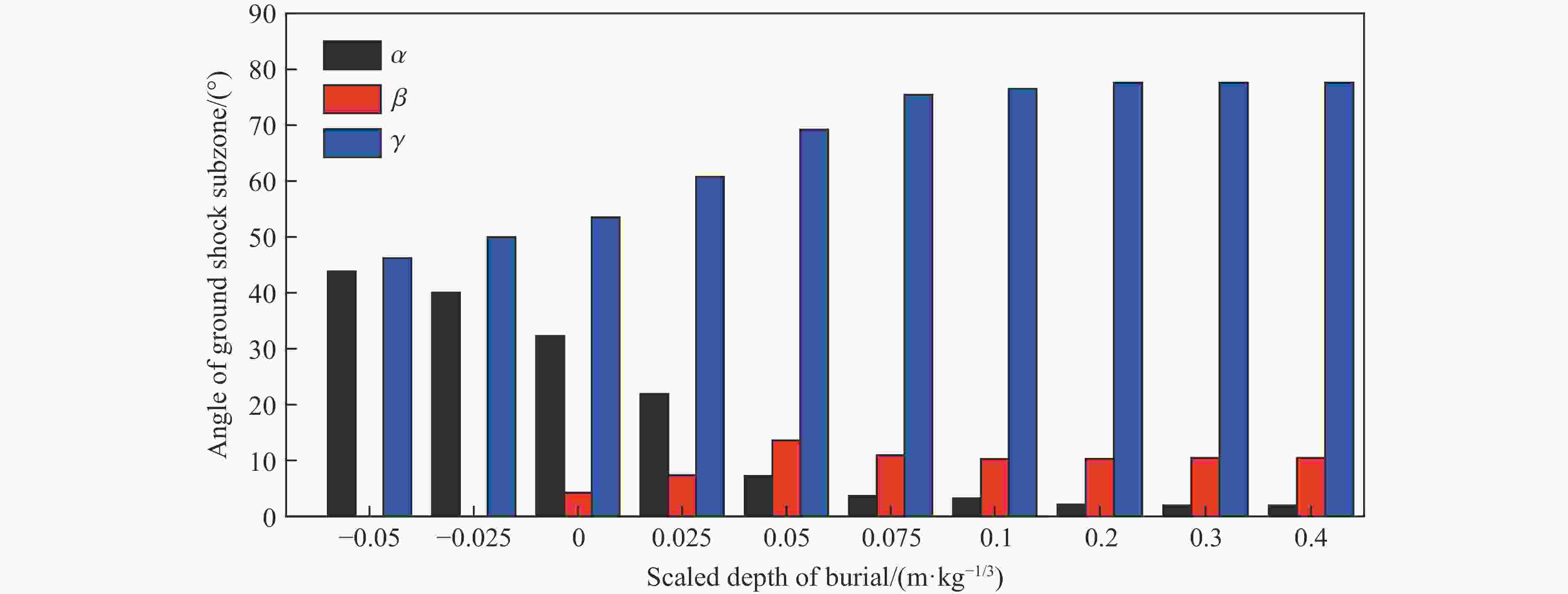
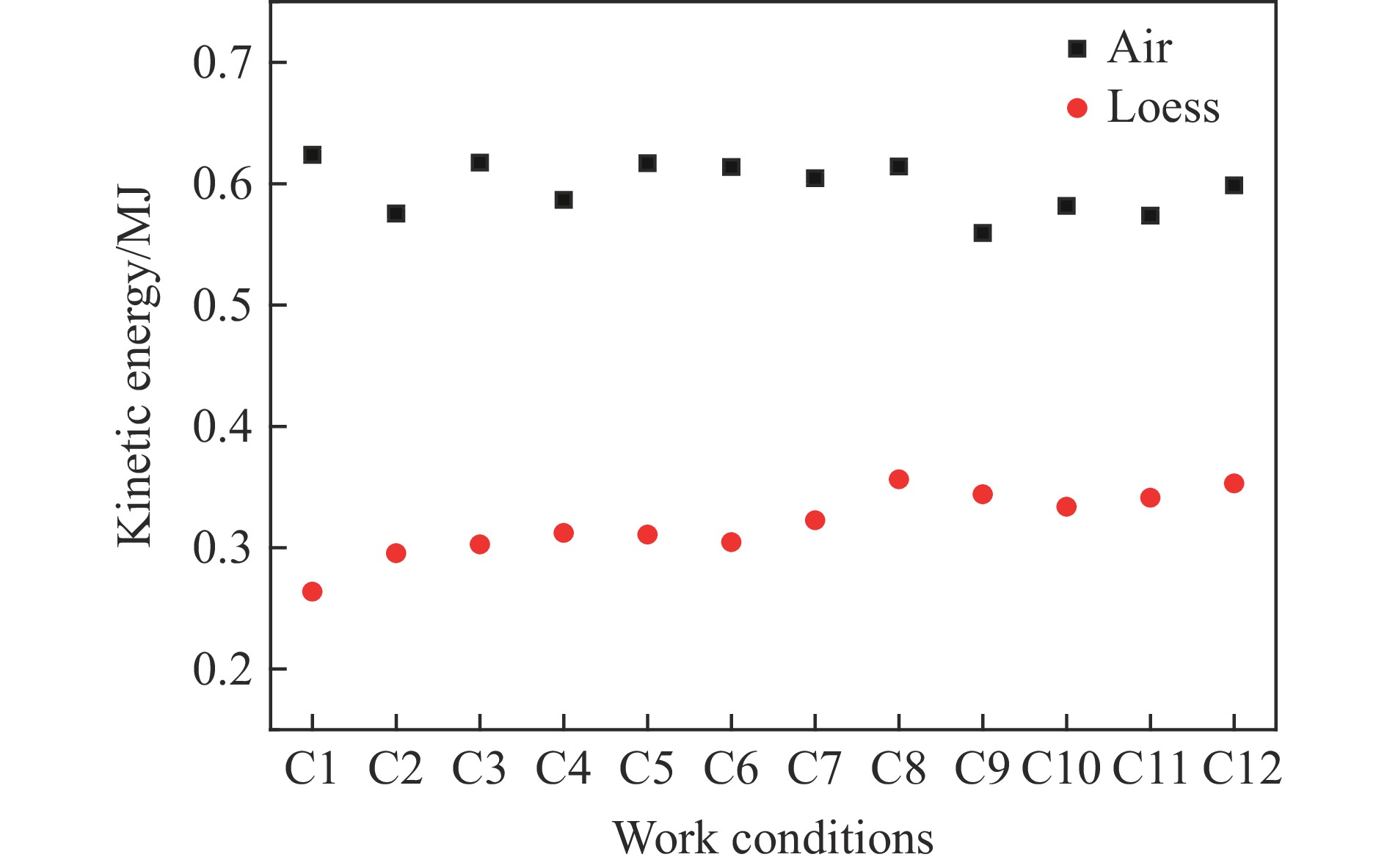
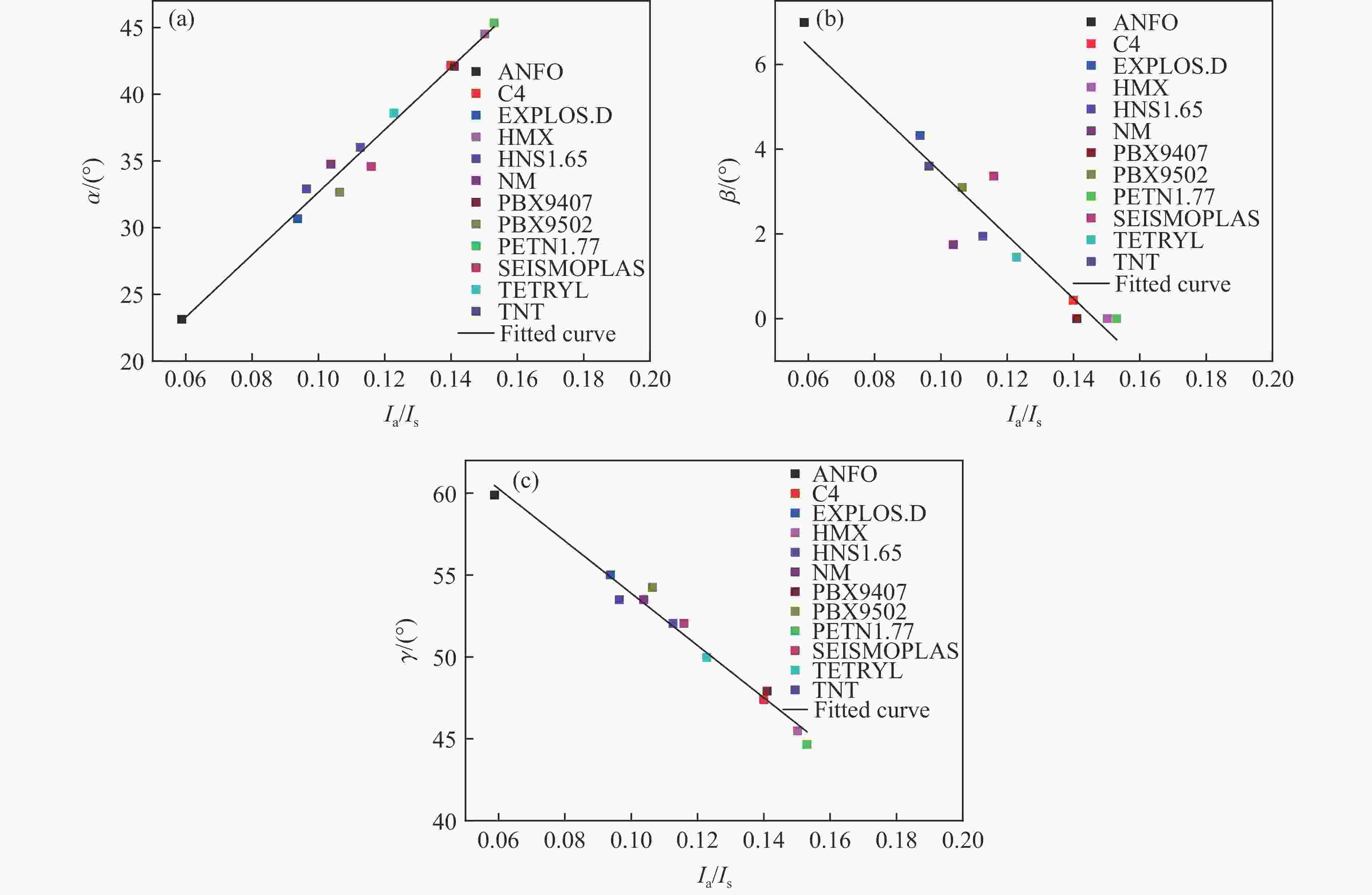
摘要: 为研究爆炸条件下土中应力波的时空分布，基于黄土中接触爆炸和半埋爆炸试验，验证了ANSYS/AUTODYN软件建立的计算模型，并在此基础上开展了土中爆炸地冲击效应研究。结果表明：随着土介质深度的增加，感生地冲击峰值减小，而直接地冲击峰值增大，最终，压力和竖向应力时程曲线中的2个峰值减少为1个峰值，据此特征可将土中应力波场分为3个区域，即地表区、近地表区和中心区；当装药比例埋深为−0.05～0.075 m/kg^1/3时，随着装药比例埋深的增大，中心区迅速扩大，地表区迅速缩小，近地表区逐渐扩大；当装药比例埋深为0.1～0.4 m/kg^1/3时，地冲击作用区的分布趋于稳定；爆炸耦合进入空气和土介质中的动能受炸药类型影响，但在一定范围内，地冲击作用区角度与地面空气冲击波超压冲量和直接地冲击应力冲量之比呈线性相关关系。
- 地面爆炸 /
- 埋置爆炸 /
- 直接地冲击 /
- 感生地冲击 /
- 地冲击作用分区
Abstract: In order to investigate the temporal and spatial distribution of the stress wave in the soil produced by buried explosion, the ANSYS/AUTODYN software was employed for modelling and simulation, and the ground shock effect of explosion in soil was analyzed. Based on the relationship between the pressure and volumetric strain of Luoyang loess obtained by predecessors, the relationship between the pressure and density of the impact compaction in the SAND model was modified. The numerical model was validated by the test data, which were measured from the contact explosion and semi-buried explosion test in loess. Then, a total of 22 numerical simulation conditions were examined to study the influence of the scaled buried depth of the charge and the type of the explosive on the ground shock subzones. The results show that as the depth of the soil medium increases, the peak of induced ground shock decreases, while the peak of direct ground shock increases, until the peak of the pressure-time curve and the peak in the vertical stress-time curve finally merge into a single peak. According to the characteristics of the pressure and vertical stress at various depths, the stress wave field in soil can be divided into three subzones consisting of surface subzone, near-surface subzone and central subzone. With the increase of the scaled buried depth of the charge, the central subzone rapidly increases, the surface subzone rapidly decreases, and the near-surface subzone gradually increases from zero, when the scaled buried depth of the charge ranges from −0.05 m/kg^1/3 to 0.075 m/kg^1/3. The distribution of the ground shock subzones tends to be stable, when the scaled buried depth of the charge ranges from 0.1 m/kg^1/3 to 0.4 m/kg^1/3. The energy of the explosive coupling into the air and soil mediums is affected by the type of the explosive. In certain extent, the angle of the ground shock subzones is linearly related to the ratio of the air-blast overpressure impulse to the impulse of the direct ground shock stress.
- ground explosion /
- buried explosion /
- direct ground shock /
- induced ground shock /
- ground shock subzone

HTML全文

图 1 波阵面的连续位置^[9]

Figure 1. Successive locations of wave fronts^[9]

下载: 全尺寸图片幻灯片

图 2 爆炸模型

Figure 2. The explosion model

下载: 全尺寸图片幻灯片

图 3 有限元模型和边界条件

Figure 3. The finite element model and boundary conditions

下载: 全尺寸图片幻灯片

图 4 工况B1～B10下炸药附近区域的放大

Figure 4. Enlarged details near TNT under conditions B1−B10

下载: 全尺寸图片幻灯片

图 5 数值网格

Figure 5. Numerical mesh

下载: 全尺寸图片幻灯片

图 6 测试布置

Figure 6. Test arrangements

下载: 全尺寸图片幻灯片

图 7 试验中的测量仪器

Figure 7. Measuring instrumentation used in test

下载: 全尺寸图片幻灯片

图 8 试验前现场布置

Figure 8. Site layout before the test

下载: 全尺寸图片幻灯片

图 9 试验后破坏情况

Figure 9. Damages after the tests

下载: 全尺寸图片幻灯片

图 10 地面空气冲击波超压和土中直接地冲击竖向应力时程曲线试验结果

Figure 10. Tested time history curves of air-blast overpressure and vertical stress of direct ground shock

下载: 全尺寸图片幻灯片

图 11 地面空气冲击波超压和土中直接地冲击竖向应力时程曲线数值模拟结果

Figure 11. Numerically-simulated time history curves of air-blast overpressure and vertical stress of direct ground shock

下载: 全尺寸图片幻灯片

图 12 试验与数值模拟数据对比

Figure 12. Comparison of tests and simulations

下载: 全尺寸图片幻灯片

图 13 工况B3下的压力云图

Figure 13. Pressure contours under condition B3

下载: 全尺寸图片幻灯片

图 14 工况B3下爆心水平距离0.5 m处的压力时程曲线

Figure 14. Pressure-time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

下载: 全尺寸图片幻灯片

图 15 工况B3下爆心水平距离0.5 m处竖向应力时程曲线

Figure 15. Vertical stress time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

下载: 全尺寸图片幻灯片

图 16 工况B1～B10下1.0 ms时的压力云图

Figure 16. Pressure contours at 1.0 ms under conditions B1−B10

下载: 全尺寸图片幻灯片

图 17 工况B3下的能量时程曲线

Figure 17. Energy time history curves under condition B3

下载: 全尺寸图片幻灯片

图 18 工况B1～B10下空气和黄土的动能峰值随装药比例埋深的变化

Figure 18. Peak kinetic energy of air and loess varying with charge scaled depth of burial under conditions B1−B10

下载: 全尺寸图片幻灯片

图 19 α、β和γ的取值方法

Figure 19. Determination methods of α, β and γ

下载: 全尺寸图片幻灯片

图 20 工况B1～B10下地冲击作用区的角度随装药比例埋深的变化

Figure 20. Angles of ground shock subzones varying with charge scaled depth of burial under conditions B1−B10

下载: 全尺寸图片幻灯片

图 21 工况C1～C12下1.0 ms时的压力云图

Figure 21. Pressure contours at 1.0 ms under conditions C1−C12

下载: 全尺寸图片幻灯片

图 22 工况C1～C12下空气和黄土的动能峰值

Figure 22. Peak kinetic energy of air and loess under conditions C1−C12

下载: 全尺寸图片幻灯片

图 23 I_a/I_s随炸药爆速和爆压的变化

Figure 23. Variation of I_a/I_s with detonation velocity and detonation pressure of explosive

下载: 全尺寸图片幻灯片

图 24 α、β和γ随I_a/I_s的变化

Figure 24. Variation of α, β and γ with I_a/I_s

下载: 全尺寸图片幻灯片

表 1 计算工况

Table 1. Calculation conditions

工况	炸药类型	装药量/kg	装药比例埋深/(m·kg^−1/3)	装药半径/mm	装药高度/mm
B1	TNT	1	−0.05	44.2	100
B2	TNT	1	−0.025	44.2	100
B3	TNT	1	0	44.2	100
B4	TNT	1	0.025	44.2	100
B5	TNT	1	0.05	44.2	100
B6	TNT	1	0.075	44.2	100
B7	TNT	1	0.1	44.2	100
B8	TNT	1	0.2	44.2	100
B9	TNT	1	0.3	44.2	100
B10	TNT	1	0.4	44.2	100
C1	ANFO	1.380	0	61.8	123.6
C2	C4	0.655	0	40.2	80.4
C3	EXPLOS.D	0.968	0	47.7	95.4
C4	HMX	0.663	0	38.2	76.4
C5	HNS 1.65	0.815	0	42.8	85.6
C6	NM	0.814	0	48.6	97.2
C7	PBX9407	0.685	0	40.8	81.6
C8	PBX9502	0.987	0	43.6	87.2
C9	PETN 1.77	0.645	0	38.7	77.4
C10	SEISMOPLAS	0.835	0	43.7	87.4
C11	TETRYL	0.777	0	41.5	83.0
C12	TNT	1	0	46.0	92.0

下载: 导出CSV

表 2 炸药参数^[23]

Table 2. Explosive parameters^[23]

工况	炸药类型	ρ₀/(g·cm⁻³)	A/GPa	B/GPa	R₁	R₂	ω	D_d/(m·s⁻¹)	p_d/GPa	E₀/(GJ·m⁻³)
C1	ANFO	0.931	49.46	1.891	3.907	1.118	0.333	4160	5.15	2.484
C2	C4	1.601	609.77	12.95	4.5	1.4	0.25	8193	28	9.0
C3	EXPLOS.D	1.42	300.7	3.94	4.3	1.2	0.35	6500	16	5.4
C4	HMX	1.891	778.28	7.0714	4.2	1.0	0.30	9110	42	10.5
C5	HNS 1.65	1.65	463.1	8.873	4.55	1.35	0.35	7030	21.5	7.45
C6	NM	1.128	209.25	5.689	4.4	1.2	0.30	6280	12.5	5.1
C7	PBX9407	1.60	573.2	14.64	4.6	1.4	0.32	7910	26.5	8.6
C8	PBX9502	1.895	460.3	9.544	4.0	1.7	0.48	7710	30.2	7.07
C9	PETN 1.77	1.77	617.05	16.926	4.4	1.2	0.25	8300	33.5	10.1
C10	SEISMOPLAS	1.588	620.60	23.27	5.399	1.651	0.282	7200	20.5	7.0
C11	TETRYL	1.73	586.83	10.671	4.4	1.2	0.275	7910	28.5	8.2
C12	TNT	1.63	373.77	3.7471	4.15	0.9	0.35	6930	21.0	6.0
B1～B10	TNT	1.63	373.77	3.7471	4.15	0.9	0.35	6930	21.0	6.0

下载: 导出CSV

表 3 SAND模型参数^[32-33]

Table 3. Parameters of the SAND model^[32-33]

冲击压实方程（参考密度ρ=2.641 g/cm³）				颗粒强度模型
压力/MPa	密度1/(g·cm⁻³)	声速/(km·s⁻¹)	密度2/(g·cm⁻³)	压力/MPa	强度/MPa	密度/(g·cm⁻³)	剪切模量/GPa
0	1.674	0.2652	1.674	0	0	1.674	0.077
4.577	1.739	0.8521	1.745	3.40	4.23	1.746	0.869
14.98	1.874	1.722	2.086	3.49	44.7	2.086	4.03
29.15	1.997	1.875	2.147	101	124	2.147	4.91
59.17	2.144	2.265	2.300	185	226	2.300	7.77
98.09	2.250	2.956	2.572	500	226	2.572	14.8
179.4	2.380	3.112	2.598			2.598	16.6
289.4	2.485	4.600	2.635	静水拉力极限 p_min= −1.00 kPa		2.635	36.7
450.2	2.585	4.634	2.641			2.641	37.3
650.7	2.670	4.634	2.800			2.800	37.3
注：(1)利用压力与密度1的分段线性函数来描述砂土的塑性压实过程；(2)利用声速与密度2的分段线性函数来描述砂土的弹性加载和卸载过程。

下载: 导出CSV

表 4 线性压实状态方程中压力与密度1的关系（基于式(3)）

Table 4. Relationship between pressure and density 1 in the compaction linear equation of state (based on formula (3))

密度1/(g·cm⁻³)	体应变$ {\varepsilon _i}{\text{ = }}1{{ - {\rho _i}} \mathord{\left/ {\vphantom {{ - {\rho _i}} {{\rho _{i + 1}}}}} \right. } {{\rho _{i + 1}}}} $	累积体应变$\varepsilon $	修正后压力/MPa
1.674	0	0	0
1.739	0.03738	0.03738	1.750
1.874	0.07204	0.10942	6.844
1.997	0.06159	0.17101	21.96
2.144	0.06856	0.23957	80.42
2.250	0.04711	0.28668	196.2
2.380	0.05462	0.34131	551.8
2.485	0.04225	0.38356	1227.8
2.585	0.03868	0.42224	2553.6
2.670	0.03184	0.45408	4665.3

下载: 导出CSV

表 5 试验工况

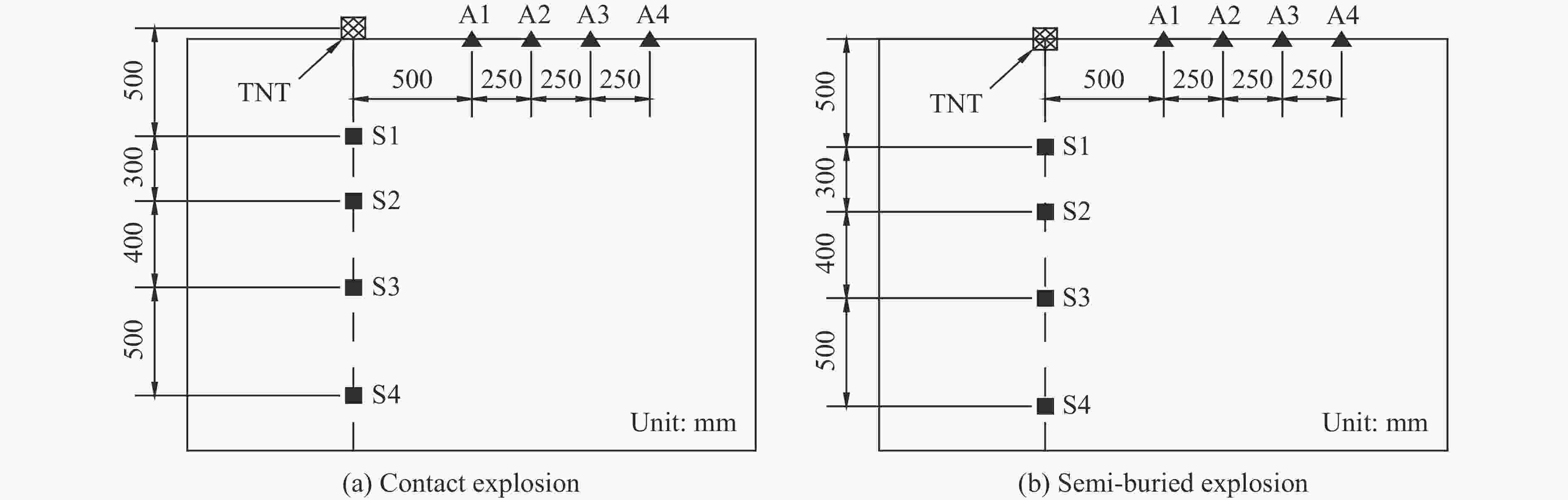
Table 5. Test conditions

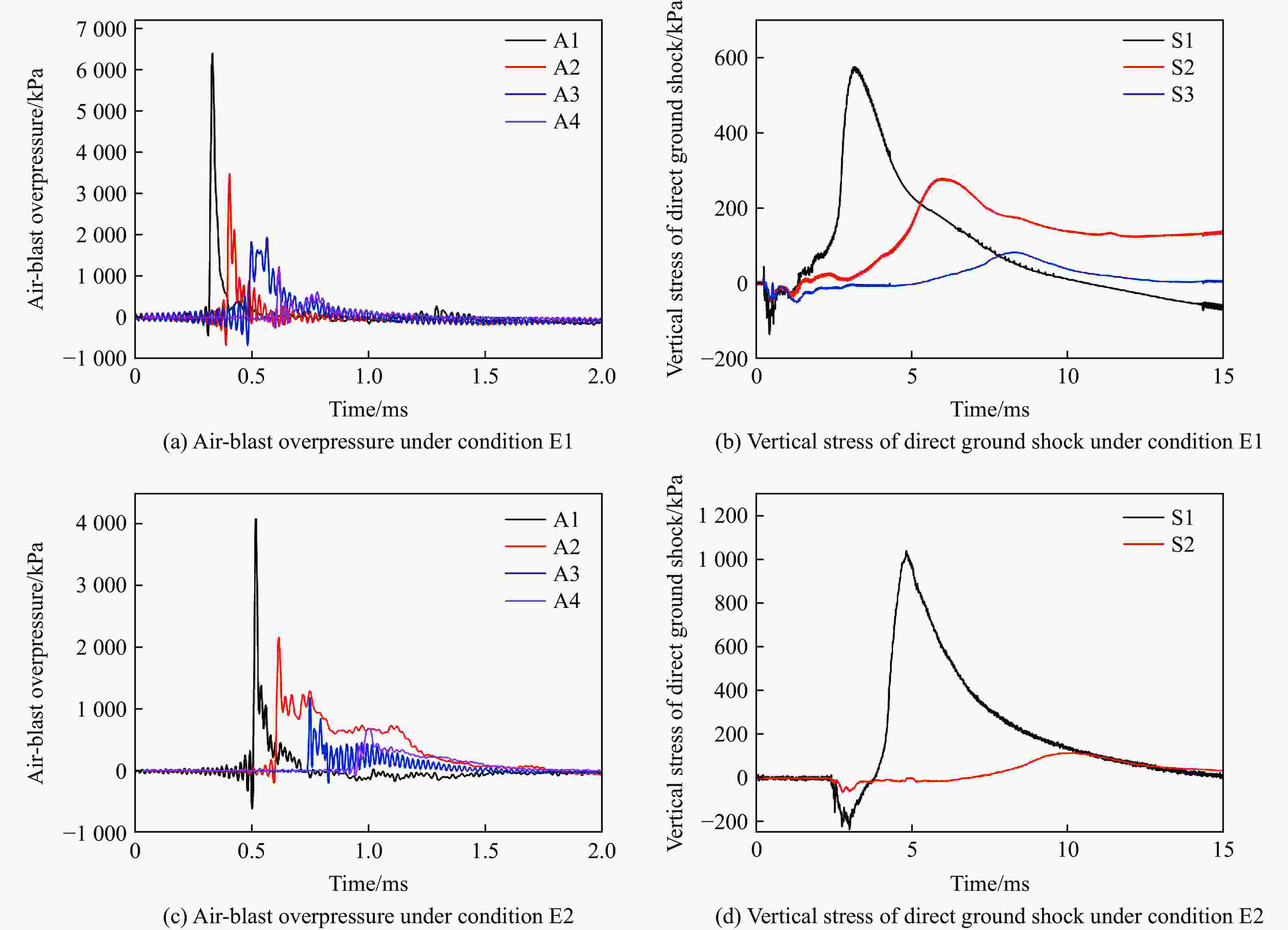
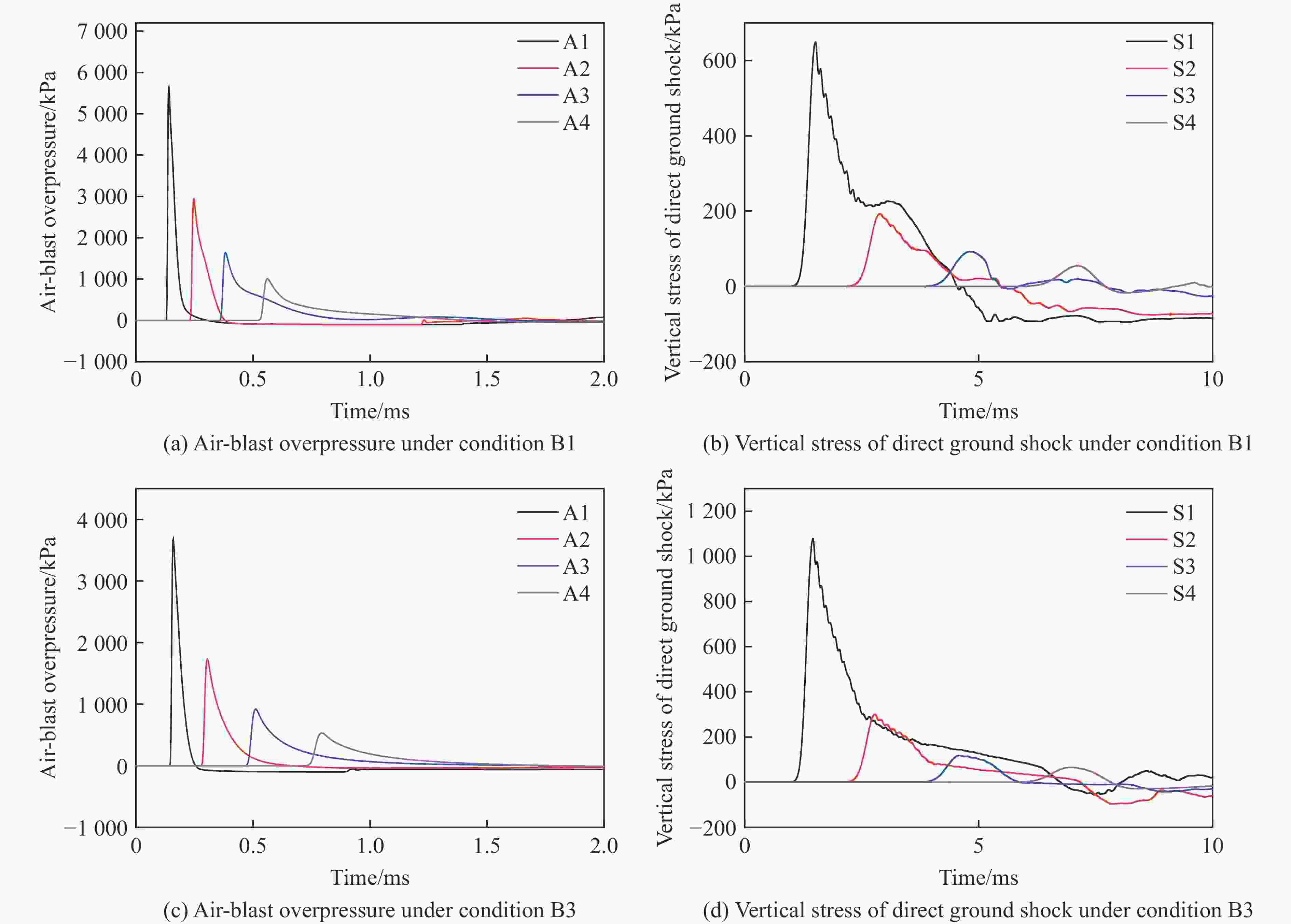
工况	装药量/kg	装药比例埋深/(m·kg^−1/3)	地面空气冲击波超压测点	土中直接地冲击竖向应力测点
E1	1	−0.05	A1～A4	S1～S4
E2	1	0.00	A1～A4	S1～S4

下载: 导出CSV

表 6 试验与数值模拟荷载峰值

Table 6. Peak loads obtained by tests and simulations

工况	测点	荷载峰值			工况	测点	荷载峰值
工况	测点	模拟值/kPa	试验值/kPa	偏差/%	工况	测点	模拟值/kPa	试验值/kPa	偏差/%
E1（B1）	A1	5650	6394	11.6	E2（B3）	A1	3678	4092	10.1
E1（B1）	A2	2943	3470	15.2	E2（B3）	A2	1731	2167	20.1
E1（B1）	A3	1640	1832	10.5	E2（B3）	A3	920	1180	22.0
	A4	1008	1231	18.1		A4	533	686	22.3
	S1	649	575	12.9		S1	1079	1041	3.7
	S2	193	279	30.8		S2	300
	S3	92	82	12.2		S3	118	114	3.5
	S4	55				S4	66

下载: 导出CSV

表 7 工况C1～C12下的数值模拟结果

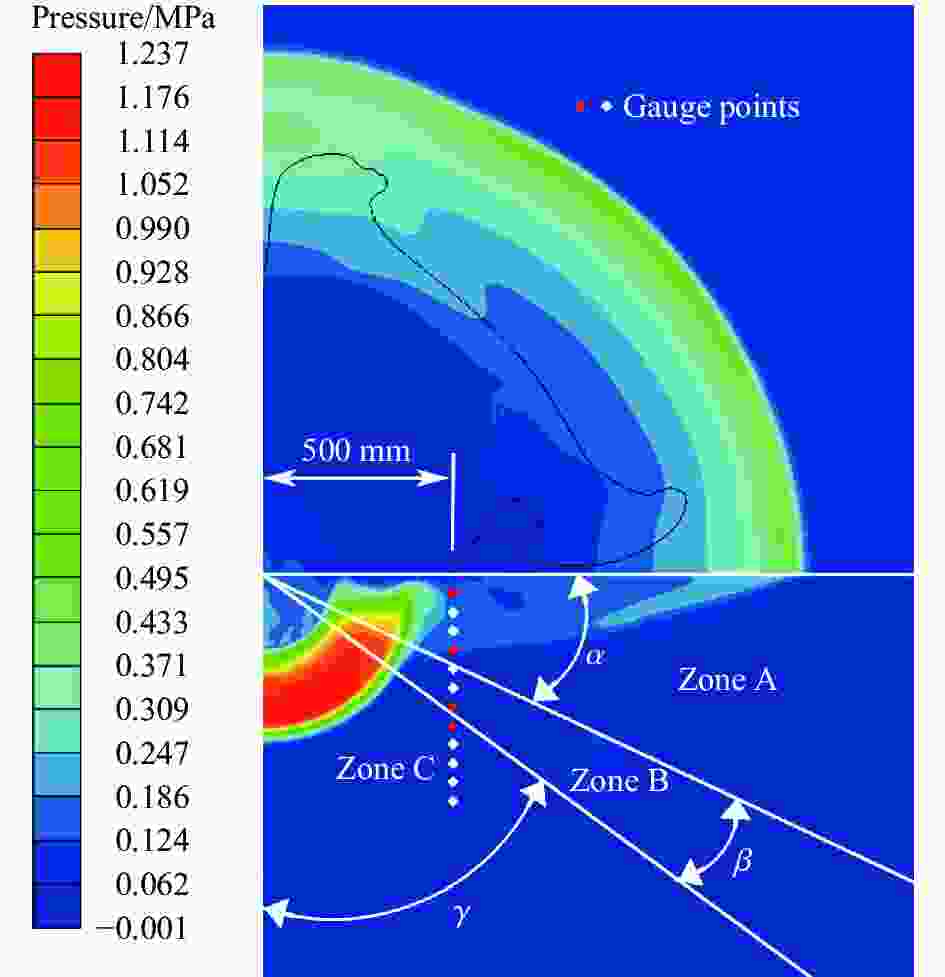
Table 7. Numerically simulated results under conditions C1−C12

工况	炸药类型	α/(°)	β/(°)	γ/(°)	p_0.5/kPa	σ_0.5/kPa	I_a/(kPa·ms)	I_s/(kPa·ms)	I_a/I_s
C1	ANFO	23.12	6.99	59.89	2835.50	1636.93	137.3128	2336.691	0.05876
C2	C4	42.18	0.43	47.39	3733.34	893.77	159.3808	1138.626	0.13998
C3	EXPLOS.D	30.67	4.32	55.01	3451.48	1164.38	147.5805	1575.046	0.09370
C4	HMX	44.51	0.00	45.49	4125.33	849.82	161.8497	1077.647	0.15019
C5	HNS1.65	36.01	1.94	52.05	3794.17	1043.78	153.7076	1364.579	0.11264
C6	NM	34.75	1.75	53.50	3535.13	1121.93	154.8051	1491.994	0.10376
C7	PBX9407	42.09	0.00	47.91	3990.68	894.76	162.5825	1153.090	0.14100
C8	PBX9502	32.66	3.10	54.24	3932.76	1064.81	150.5989	1415.379	0.10640
C9	PETN1.77	45.35	0.00	44.65	3907.44	843.95	162.0005	1058.838	0.15300
C10	SEISMOPLAS	34.59	3.36	52.05	3592.10	983.94	150.9218	1301.707	0.11594
C11	TETRYL	38.58	1.45	49.97	3758.19	963.50	152.3302	1240.691	0.12278
C12	TNT	32.90	3.60	53.50	3562.00	1133.18	146.1541	1515.783	0.09642

下载: 导出CSV

参考文献(38)

[1]	WU C, LU Y, HAO H, et al. Characterisation of underground blast-induced ground motions from large-scale field tests [J]. Shock Waves, 2003, 13(3): 237–252. DOI: 10.1007/s00193-003-0212-3.
[2]	何翔, 吴祥云, 李永池, 等. 石灰岩中爆炸成坑和地冲击传播规律的试验研究 [J]. 岩石力学与工程学报, 2004, 23(5): 725–729. DOI: 10.3321/j.issn:1000-6915.2004.05.004. HE X, WU X Y, LI Y C, et al. Testing study on crater formed by explosion and propagation laws of ground shock in limestone [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 725–729. DOI: 10.3321/j.issn:1000-6915.2004.05.004.
[3]	LEONG E C, ANAND S, CHEONG H K, et al. Re-examination of peak stress and scaled distance due to ground shock [J]. International Journal of Impact Engineering, 2007, 34(9): 1487–1499. DOI: 10.1016/j.ijimpeng.2006.10.009.
[4]	吴祥云, 刘国军, 杨仁华, 等. 常规装药爆炸埋深对自由场直接地冲击参数的影响 [J]. 防护工程, 2009, 31(5): 26–30. WU X Y, LIU G J, YANG R H, et al. The influence of buried depth of conventional charge on free field direct ground shock parameters [J]. Protective Engineering, 2009, 31(5): 26–30.
[5]	叶亚齐, 任辉启, 李永池, 等. 砂质黏土中不同深度爆炸自由场地冲击参数预计方法研究 [J]. 岩石力学与工程学报, 2011, 30(9): 1918–1923. DOI: CNKI:SUN:YSLX.0.2011-09-024. YE Y Q, REN H Q, LI Y C, et al. Study of prediction of ground shock parameters in free field at different depths of burst in sandy clay [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1918–1923. DOI: CNKI:SUN:YSLX.0.2011-09-024.
[6]	YANKELEVSKY D Z, KARINSKI Y S, FELDGUN V R. Re-examination of the shock wave’s peak pressure attenuation in soils [J]. International Journal of Impact Engineering, 2011, 38(11): 864–881. DOI: 10.1016/j.ijimpeng.2011.05.011.
[7]	JAYASINGHE L B, THAMBIRATNAM D P, PERERA N, et al. Blast induced ground shock effects on pile foundations [J]. International Journal of Civil, Environmental, Structural, Construction and Architectural Engineering, 2013, 7(4): 176–180. DOI: 10.5281/zenodo.1073675.
[8]	SONG J, LI S C. Study on numerical simulation of explosion in soil based on fluid-solid coupling arithmetic [J]. Applied Mechanics and Materials, 2014, 580-583: 2916–2919. DOI: 10.4028/www.scientific.net/AMM.580-583.2916.
[9]	ALEKSEYENKO V D, GRIGORYAN S S, KOSHELEV L I, et al. Measurement of stress waves in soft soil [R]. Hanover, NH, USA: U. S. Army Cold Regions Research and Engineering Laboratory, 1970: 12–19.
[10]	BESHARA F B A. Modelling of blast loading on aboveground structures: Ⅱ. internal blast and ground shock [J]. Computers & Structures, 1994, 51(5): 597–606. DOI: 10.1016/0045-7949(94)90067-1.
[11]	WU C Q, HAO H. Modeling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions [J]. International Journal of Impact Engineering, 2005, 31(6): 699–717. DOI: 10.1016/j.ijimpeng.2004.03.002.
[12]	WU C Q, HAO H. Numerical simulation of structural response and damage to simultaneous ground shock and airblast loads [J]. International Journal of Impact Engineering, 2007, 34(3): 556–572. DOI: 10.1016/j.ijimpeng.2005.11.003.
[13]	范俊余, 方秦, 柳锦春. 炸药地面爆炸条件下土中浅埋结构上荷载的作用特点 [J]. 解放军理工大学学报(自然科学版), 2008, 9(6): 676–680. DOI: 10.3969/j.issn.1009-3443.2008.06.026. FAN J Y, FANG Q, LIU J C. Characteristics of loads on shallow-buried structures under the ground explosions [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2008, 9(6): 676–680. DOI: 10.3969/j.issn.1009-3443.2008.06.026.
[14]	柳锦春, 方秦, 还毅, 等. 炸药地面接触爆炸下土中感生地冲击的实用计算方法 [J]. 解放军理工大学学报(自然科学版), 2010, 11(2): 121–124. DOI: 10.3969/j.issn.1009-3443.2010.02.005. LIU J C, FANG Q, HUAN Y, et al. Practicable calculating method of indirect ground shock in soil at surface contact explosion [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2010, 11(2): 121–124. DOI: 10.3969/j.issn.1009-3443.2010.02.005.
[15]	杨仁华, 张新乐, 吴祥云, 等. 间接地冲击在黄土中衰减规律的试验研究 [J]. 防护工程, 2010, 32(5): 6–9. YANG R H, ZHANG X L, WU X Y, et al. Experimental research on attenuation laws of airblast-induced ground shock in loess [J]. Protective Engineering, 2010, 32(5): 6–9.
[16]	吴祥云, 曲建波, 李宝宝, 等. 岩石中装药埋深对地表空气冲击波超压的影响 [J]. 防护工程, 2013, 35(4): 23–26. WU X Y, QU J B, LI B B, et al. The influence of buried depth of a conventional charge on the direct ground shock parameters [J]. Protective Engineering, 2013, 35(4): 23–26.
[17]	KRAUTHAMMER T, BAZEOS N, HOLMQUIST T J. Modified SDOF analysis of RC box-type structures [J]. Journal of Structural Engineering, 1986, 112(4): 726–744. DOI: 10.1061/(ASCE)0733-9445(1986)112:4(726).
[18]	KRAUTHAMMER T, ASTARLIOGLU S. Direct shear resistance models for simulating buried RC roof slabs under airblast-induced ground shock [J]. Engineering Structures, 2017, 140: 308–316. DOI: 10.1016/j.engstruct.2017.02.056.
[19]	CHEE K H. Analysis of shallow buried reinforced concrete box structures subjected to airblast loads [D]. Gainesville, Florida, USA: University of Florida, 2008: 19–53.
[20]	荣吉利, 宋逸博, 王玺, 等. 核爆炸对地冲击作用下土体运动特性等效模拟 [J]. 兵工学报, 2021, 42(1): 56–64. DOI: 10.3969/j.issn.1000-1093.2021.01.006. RONG J L, SONG Y B, WANG X, et al. Equivalent simulation of soil motion characteristics under the action of ground shock induced by nuclear explosion [J]. Acta Armamentarii, 2021, 42(1): 56–64. DOI: 10.3969/j.issn.1000-1093.2021.01.006.
[21]	刘峥, 程怡豪, 邱艳宇, 等. 成层式防护结构抗超高速侵彻的数值分析 [J]. 爆炸与冲击, 2018, 38(6): 1317–1324. DOI: 10.11883/bzycj-2017-0181. LIU Z, CHENG Y H, QIU Y Y, et al. Numerical analysis on hypervelocity penetration into layered protective structure [J]. Explosion and Shock Waves, 2018, 38(6): 1317–1324. DOI: 10.11883/bzycj-2017-0181.
[22]	陈材, 石全, 尤志锋, 等. 圆柱形弹药空气中爆炸相似性规律 [J]. 爆炸与冲击, 2019, 39(9): 092202. DOI: 10.11883/bzycj-2018-0255. CHEN C, SHI Q, YOU Z F, et al. Similarity law of cylindrical ammunition explosions in air [J]. Explosion and Shock Waves, 2019, 39(9): 092202. DOI: 10.11883/bzycj-2018-0255.
[23]	Century Dynamics Inc. Ansys/Autodyn Version 11.0, User Documentation [Z]. Pennsylvania, USA: Century Dynamics Inc, 2007: 89–112.
[24]	LEE E L, TARVER C M. Phenomenological model of shock initiation in heterogeneous explosives [J]. The Physics Fluids, 1980, 23(12): 2362. DOI: 10.1063/1.862940.
[25]	LUCCIONI B, AMBROSINI D, NURICK G, et al. Craters produced by underground explosions [J]. Computers & Structures, 2009, 87(21/22): 1366–1373. DOI: 10.1016/j.compstruc.2009.06.002.
[26]	FISEROVA D. Numerical analysis of buried mine explosions with emphasis on effect of soil properties on loading [D]. Cranfield, England: Cranfield University, 2006: 37–51.
[27]	LAINE L, SANDVIK A. Derivation of mechanical properties for sand [C]//Proceedings of the 4th Asia-Pacific Conference on Shock and Impact Loads on Structures. Singapore: CI-Premier PTE LTD, 2001: 361–368.
[28]	LAINE L. Study of planar ground shock in different soils and its propagation around a rigid block [C]//Proceedings of the 77th Shock and Vibration Symposium. Monterey, CA, USA: Shock and Vibration Information Analysis Center, 2006: 1–10.
[29]	LAINE L, LARSEN O P. Proposal on how to model the unloading in a compaction equation of state based upon tri-axial tests on dry sand [C]//Proceedings of the 80th Shock and Vibration Symposium. San Diego, USA: Shock and Vibration Information Analysis Center, 2009: 1–14.
[30]	LAINE L, LARSEN O P. Implementation of equation of state for dry sand in Autodyn [C]//Proceedings of the 83rd Shock and Vibration Symposium. New Orleans, USA: Shock and Vibration Exchange, 2012: 1–15.
[31]	肖诗云, 林皋, 王哲. Drucker-Prager材料一致率型本构模型 [J]. 工程力学, 2003, 20(4): 147–151. DOI: 10.3969/j.issn.1000-4750.2003.04.026. XIAO S Y, LIN G, WANG Z. A Drucker-Prager consistent rate-dependent model [J]. Engineering Mechanics, 2003, 20(4): 147–151. DOI: 10.3969/j.issn.1000-4750.2003.04.026.
[32]	张坤, 郑全平, 李四伟, 等. 土中爆炸对埋地管线冲击作用的数值模拟分析 [J]. 后勤工程学院学报, 2013, 29(3): 12–17; 23. DOI: 10.3969/j.issn.1672-7843.2013.03.003. ZHANG K, ZHENG Q P, LI S W, et al. Numerical simulation and analysis for impact of explosion under ground on buried pipelines [J]. Journal of Logistical Engineering University, 2013, 29(3): 12–17; 23. DOI: 10.3969/j.issn.1672-7843.2013.03.003.
[33]	金辉, 张庆明, 高春生, 等. 装药水下沉底爆炸压力场特性研究 [J]. 科技导报, 2009, 27(14): 32–37. DOI: 10.3321/j.issn:1000-7857.2009.14.007. JIN H, ZHANG Q M, GAO C S, et al. Characteristics of pressure field in ground explosion [J]. Science & Technology Review, 2009, 27(14): 32–37. DOI: 10.3321/j.issn:1000-7857.2009.14.007.
[34]	扶涛涛. 黄土湿陷和塌陷机理研究 [J]. 河南科技, 2018(23): 104–105. DOI: 10.3969/j.issn.1003-5168.2018.23.058. FU T T. Discussion on collapsibility and collapse mechanism of loess [J]. Henan Science and Technology, 2018(23): 104–105. DOI: 10.3969/j.issn.1003-5168.2018.23.058.
[35]	王志良. 河南郑州-洛阳地区黄土湿陷机理研究 [D]. 北京: 中国地质科学院, 2013: 7–14. WANG Z L. The study on collapsible mechanism of loess between Zhengzhou with Luoyang of Henan region [D]. Beijing, China: Chinese Academy of Geological Sciences, 2013: 7-14.
[36]	申永庆. 洛阳地区黄土湿陷性及其影响因素研究 [D]. 石家庄: 河北地质大学, 2015: 21–23. SHEN Y Q. Research on the collapsibility and influential factors of loess in Luoyang [D]. Shijiazhuang, Hebei, China: Hebei GEO University, 2015: 21–23.
[37]	顾文彬, 叶序双, 詹发民, 等. 球形装药半无限土介质中爆炸动力学分析 [J]. 工程爆破, 1999, 5(1): 5–10. DOI: 10.3969/j.issn.1006-7051.1999.01.002. GU W B, YE X S, ZHAN F M, et al. Dynamic analysis on spherical charges exploding in semi-infinite soil medium [J]. Engineering Blasting, 1999, 5(1): 5–10. DOI: 10.3969/j.issn.1006-7051.1999.01.002.
[38]	陈亚娟, 王利. 土介质中TNT炸药爆炸波传播特性的数值模拟 [J]. 河南理工大学学报(自然科学版), 2010, 29(1): 88–91. DOI: 10.3969/j.issn.1673-9787.2010.01.018. CHEN Y J, WANG L. Numerical study on the propagation and damage behavior of the blasting wave with TNT in soil medium [J]. Journal of Henan Polytechnic University (Natural Science), 2010, 29(1): 88–91. DOI: 10.3969/j.issn.1673-9787.2010.01.018.