Study on mechanical properties of the kinked rebar under high speed dynamic tension
-
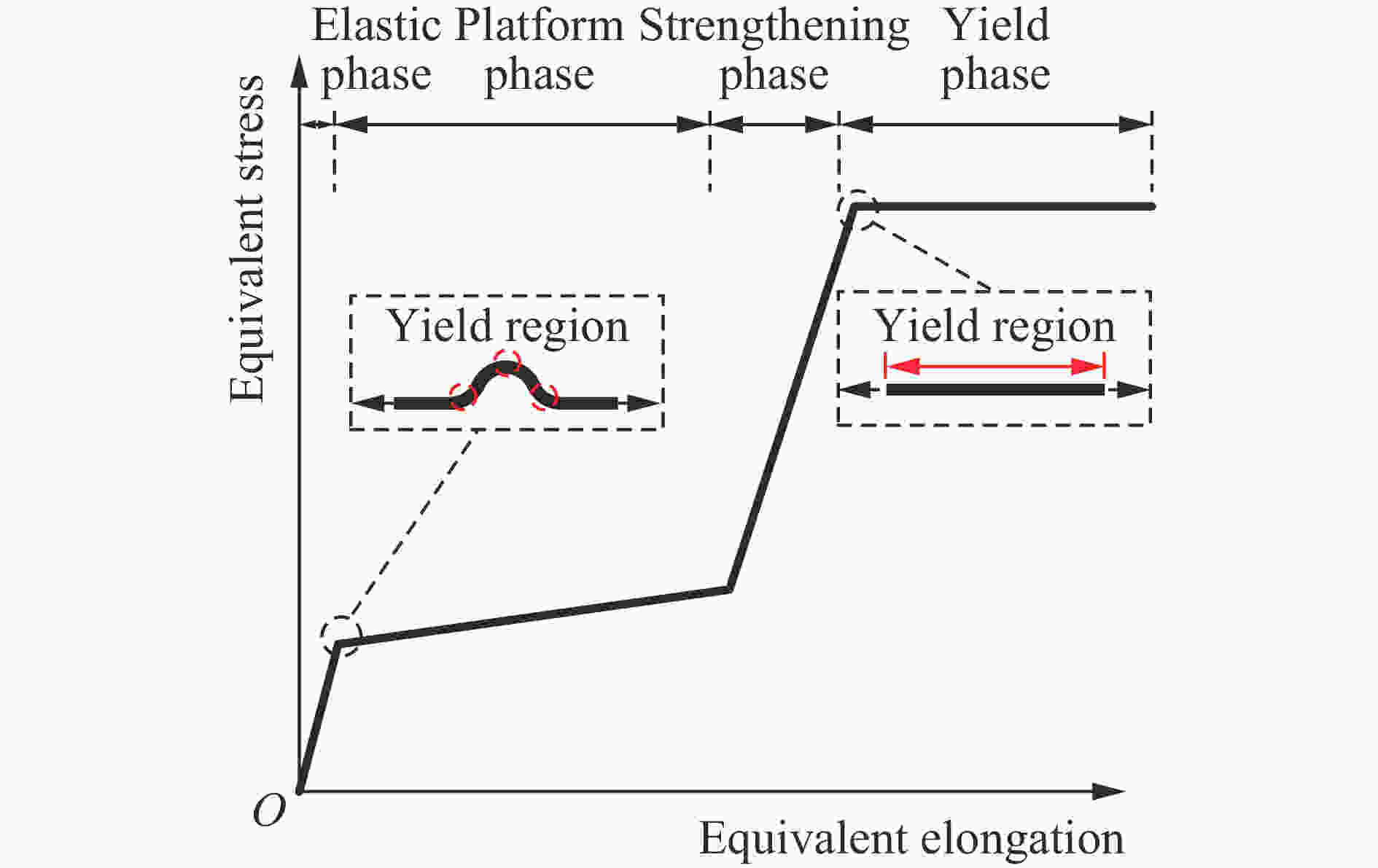
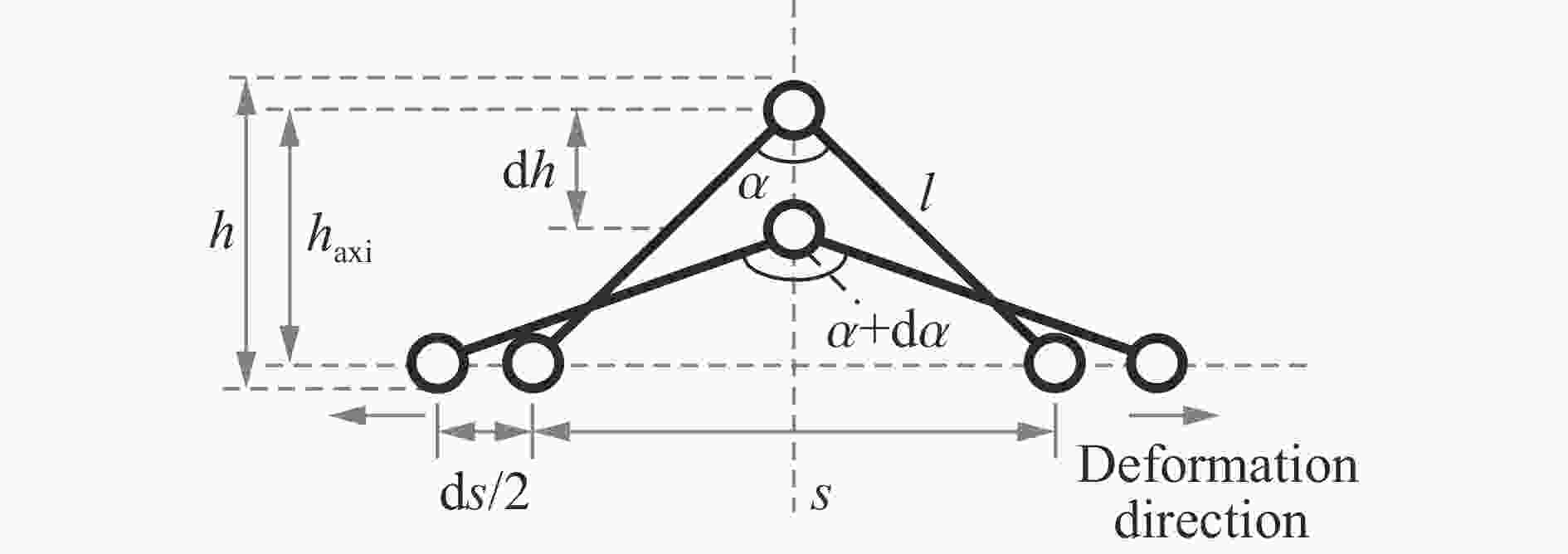
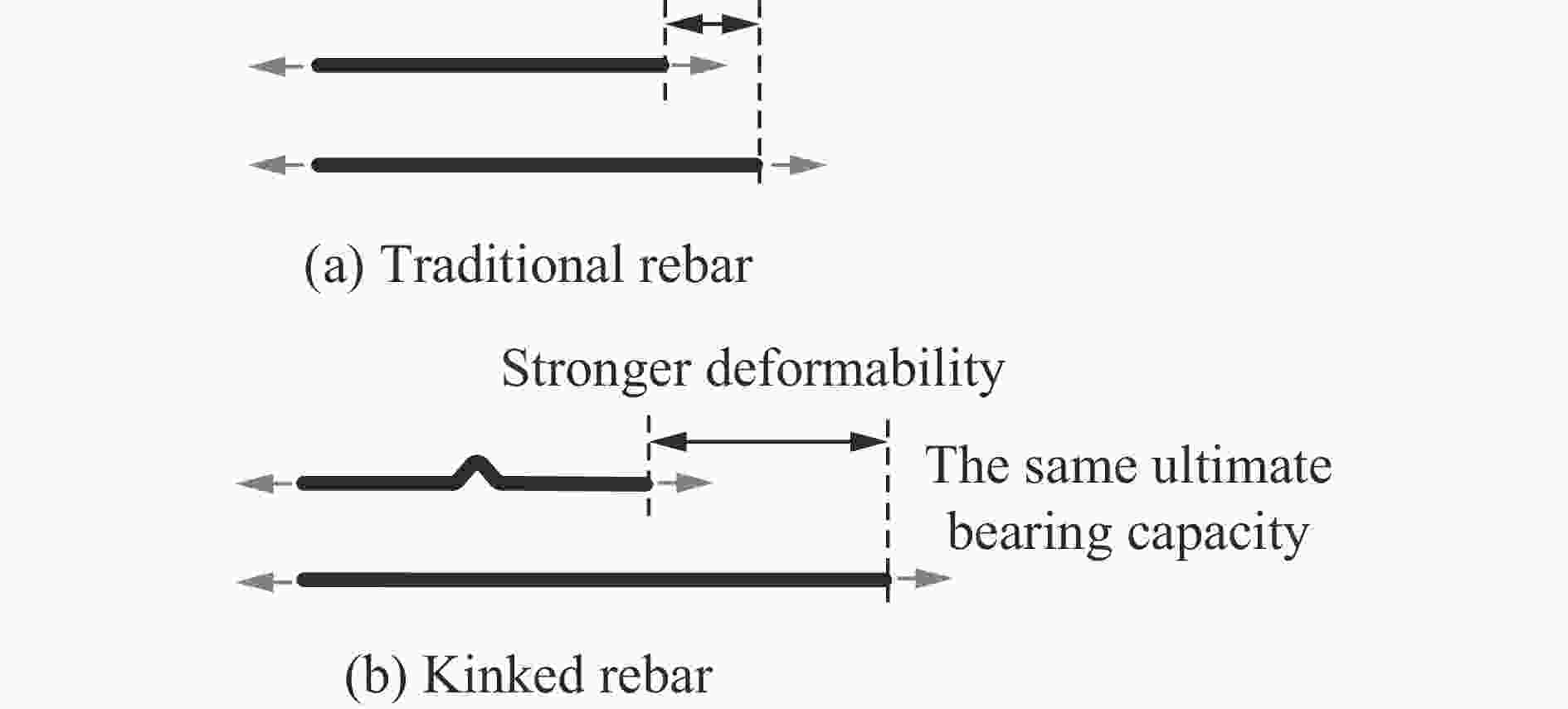
摘要: 针对提高混凝土梁抗冲击爆炸性能的起波配筋新技术,采用理论分析与动态冲击拉伸试验相结合的方法,揭示了起波钢筋的快速拉伸变形作用机理,分析了拉伸速度、起波矢高等因素对起波钢筋抗拉强度的影响规律,确定了起波钢筋静态弹性极限强度计算方法。提出了起波钢筋等效拉伸应变率新概念,建立了弹性极限强度动力放大系数(dynamic increase factors,DIF)计算模型。研究结果表明,预先弯折起波使得钢筋在受力拉直过程中产生截面弯矩,起波钢筋的力学性能存在明显的应变率效应;起波钢筋弹性抗拉极限强度DIF随起波矢高的增高先增大后减小,存在一个最优起波设计矢高,可以使起波钢筋抗拉强度动态放大系数达到最大。研究成果可为进一步推动起波配筋技术在防护工程中的应用提供依据。Abstract: Aiming at new technology of the kinked rebar which can improve the resistance of concrete beams to impact and blast loading, the mechanism of rapid tensile deformation of the kinked rebar was revealed through theoretical analysis combined with dynamic impact tensile tests. The influences of the tensile velocity and the bending height of the kinked rebar on its tensile strength were analyzed. According to the mechanism of tensile deformation, the calculation method of the static elastic ultimate strength of the kinked rebar was determined by using the classical plastic mechanics theory, and the proposed calculation method was modified based on the existing literature data to consider the error caused by the Bauschinger effect. A new concept of equivalent tensile strain rate of the kinked rebar was put forward, the kinked rebar was regarded as an equivalent material, and the average strain rate of the bending part of the rebar was defined as the equivalent tensile strain rate of the kinked rebar. Considering the influence of the tensile velocity and the bending height of the kinked rebar, the calculation model of dynamic increase factors (DIF) of the elastic ultimate strength was established, referring to the form of the Johnson-Cook material constitutive model. The results show that the pre-bending kink results in the section bending moment of the steel bar during force straightening and the mechanical properties of the kinked rebar have an obvious strain rate effect. The tensile yield strength first increases and then decreases with the increase of the bending height of the kinked rebar. There is an optimal bending height for the kinked rebar at high strain rates, which can maximize the dynamic amplification factor of the tensile strength of the kinked rebar. The research results can provide a basis for further promotion of the application of the kinked rebar technology in protection engineering.
-
表 1 试验工况
Table 1. Test parameters
试件 起波矢高 h/mm 起波间距 s/mm 拉伸速度 v/(m·s−1) 试件数量 W1-2.5 40 150 2.5 3 W1-5 40 150 5.0 3 W1-10 40 150 10.0 3 W1-15 40 150 15.0 3 W2-2.5 50 150 2.5 3 W2-5 50 150 5.0 3 W2-10 50 150 10.0 3 W2-15 50 150 15.0 3 W3-2.5 60 150 2.5 3 W3-5 60 150 5.0 3 W3-10 60 150 10.0 3 W3-15 60 150 15.0 3 注:试件编号中W表示起波钢筋,字母后第1个数字表示不同起波矢高的钢筋组号,第2个数字表示拉伸速度值。 表 2 起波钢筋的静态弹性极限强度和抗拉极限
Table 2. Elastic ultimate strength and tensile capacity of the kinked rebar under static loading
钢筋参数 σ/MPa F/KN d=10 mm(直筋) 400.00 31.40 h=40 mm 127.66 32.50 h=50 mm 92.49 23.54 h=60 mm 71.99 18.32 表 3 各组起波钢筋的弹性极限强度
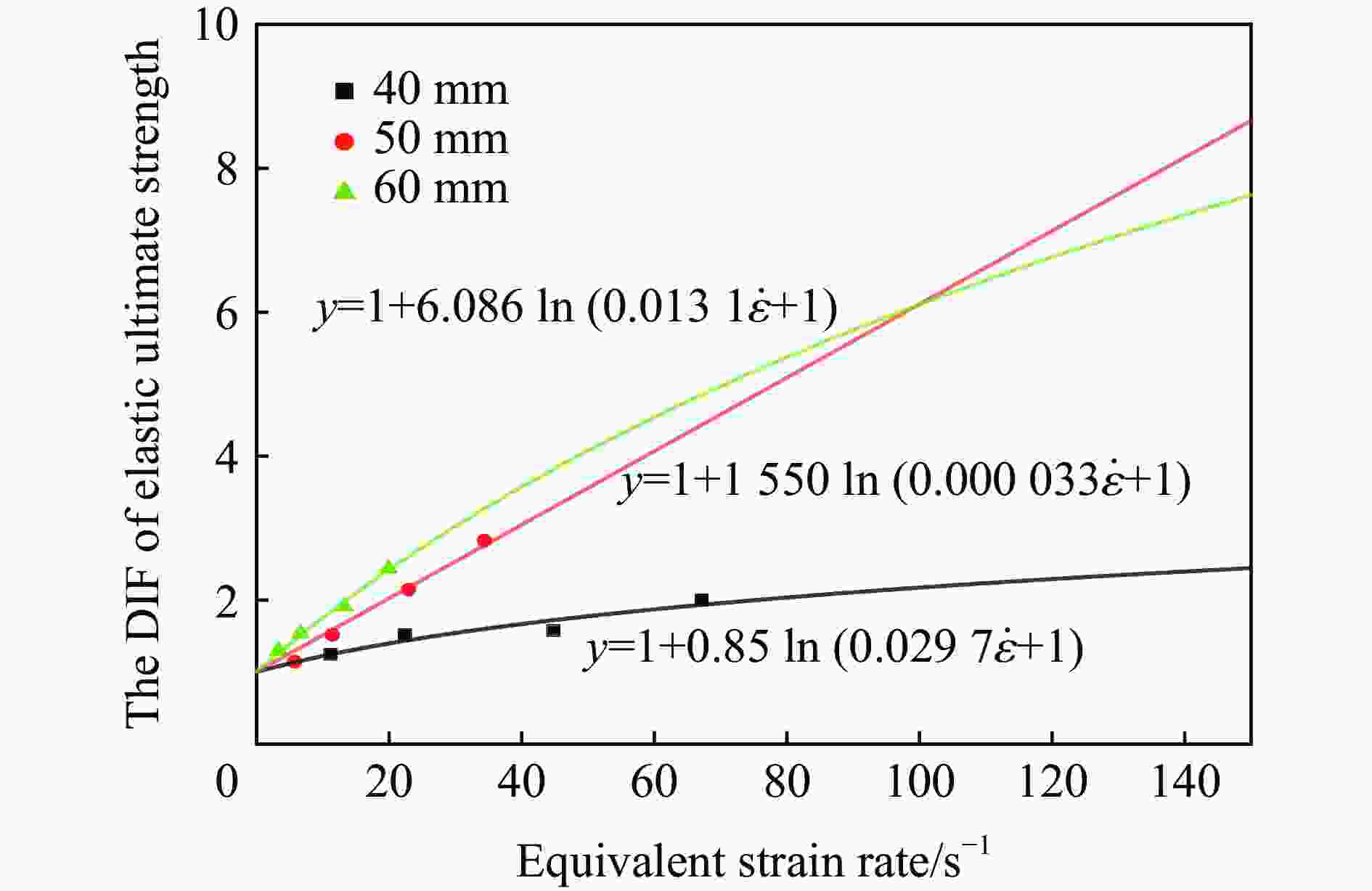
Table 3. Elastic ultimate strengths of the kinked rebars
拉伸速率
v/(m·s−1)弹性极限强度σ/MPa h=40 mm h=50 mm h=60 mm 2.5 159.46 105.78 93.50 5.0 193.99 140.19 111.03 10.0 201.13 198.50 137.56 15.0 255.40 261.14 175.61 表 4 三组DIF拟合公式中的
$a $ 、$b $ 值Table 4. Values of a and b of the three groups of the kinked rebars
起波失高h/mm a b 40 0.85 0.029700 50 1550 0.000033 60 6.086 0.013100 表 5 起波钢筋静态弹性极限强度理论值与试验值对比
Table 5. Comparison between the theoretical and experimental values of the static elastic ultimate strength
试件 极限强度σ/MPa 误差/
%修正后强度
σr/MPa修正后的
误差/%试验[1] 理论 F10-30 81.917 119.260 31.3 95.41 14.1 F10-45 67.486 61.586 9.6 49.27 37.0 F10-60 96.457 46.027 109.6 − − S10-30 34.127 46.167 26.1 36.93 7.6 S10-45 35.903 43.825 18.1 35.06 2.4 S10-60 17.850 24.140 26.1 19.31 7.6 -
[1] FENG P, QIANG H L, QIN W H, et al. A novel kinked rebar configuration for simultaneously improving the seismic performance and progressive collapse resistance of RC frame structures [J]. Engineering Structures, 2017, 147: 752–767. DOI: 10.1016/j.engstruct.2017.06.042. [2] 杨健翔. 起波钢筋RC梁柱子结构抗连续倒塌性能研究 [D]. 南京: 东南大学, 2019: 1−121. DOI: 10.27014/d.cnki.gdnau.2019.001378.YANG J X. Study on progressive collapse behavior of RC beam-column substructure with a kinked rebar configuration [D]. Nanjing: Southeast University, 2019: 1−121. DOI: 10.27014/d.cnki.gdnau.2019.001378. [3] 樊源, 陈力, 任辉启, 等. 起波配筋RC梁抗爆作用机理及抗力动力系数的理论计算方法 [J]. 爆炸与冲击, 2019, 39(3): 035102. DOI: 10.11883/bzycj-2018-0181.FAN Y, CHEN L, REN H Q, et al. Blast-resistant mechanism of RC beam with kinked rebar and calculation method of dynamic resistance coefficient [J]. Explosion and Shock Waves, 2019, 39(3): 035102. DOI: 10.11883/bzycj-2018-0181. [4] 陈力, 任辉启, 樊源, 等. 强动载作用下起波配筋梁抗力性能的试验研究 [J]. 土木工程学报, 2021, 54(10): 1–8;19. DOI: 10.15951/j.tmgcxb.2021.10.001.CHEN L, REN H Q, FAN Y, et al. Experimental study on the resistance of RC beam with kinked rebar under severe dynamic loading [J]. China Civil Engineering Journal, 2021, 54(10): 1–8;19. DOI: 10.15951/j.tmgcxb.2021.10.001. [5] 陈肇元, 王志浩, 方秦. 第十一篇 防护工程 [M] // 中国土木工程指南. 2版. 北京: 科学出版社, 2000: 1528−1529.CHEN Z Y, WANG Z H, FANG Q. Chapter eleven. Protection engineering [M] // Guide to Civil Engineering in China. 2nd ed. Beijing: Science Press, 2000: 1528−1529. [6] 方秦, 柳锦春. 地下防护结构 [M]. 北京: 中国水利水电出版社, 2010: 228−234.FANG Q, LIU J C. Underground protective structure [M]. Beijing: China Water and Power Press, 2010: 228−234. [7] SOROUSHIAN P, CHOI K B. Steel mechanical properties at different strain rates [J]. Journal of Structural Engineering, 1987, 113(4): 663–672. DOI: 10.1061/(ASCE)0733-9445(1987)113:4(663). [8] CEB. Concrete structures under impact and impulsive loading [R]. Lausanne: Comite Euro-International du Beton, 1988. [9] ROHR I, NAHME H, THOMA K. Material characterization and constitutive modelling of ductile high strength steel for a wide range of strain rates [J]. International Journal of Impact Engineering, 2005, 31(4): 401–433. DOI: 10.1016/j.ijimpeng.2004.02.005. [10] 林峰, 顾祥林, 匡昕昕, 等. 高应变率下建筑钢筋的本构模型 [J]. 建筑材料学报, 2008, 11(1): 14–20. DOI: 10.3969/j.issn.1007-9629.2008.01.003.LIN F, GU X L, KUANG X X, et al. Constitutive models for reinforcing steel bars under high strain rates [J]. Journal of Building Materials, 2008, 11(1): 14–20. DOI: 10.3969/j.issn.1007-9629.2008.01.003. [11] 李敏, 李宏男. 建筑钢筋动态试验及本构模型 [J]. 土木工程学报, 2010, 43(4): 70–75. DOI: 10.15951/j.tmgcxb.2010.04.012.LI M, LI H N. Dynamic test and constitutive model for reinforcing steel [J]. China Civil Engineering Journal, 2010, 43(4): 70–75. DOI: 10.15951/j.tmgcxb.2010.04.012. [12] 黄晓莹, 陶俊林. 三种建筑钢筋材料高应变率下拉伸力学性能研究 [J]. 工程力学, 2016, 33(7): 184–189. DOI: 10.6052/j.issn.1000-4750.2014.12.1064.HUANG X Y, TAO J L. Tensile mechanical properties research of three construction steel bars in high strain rate [J]. Engineering Mechanics, 2016, 33(7): 184–189. DOI: 10.6052/j.issn.1000-4750.2014.12.1064. [13] YU T X, JOHNSON W. Influence of axial force on the elastic-plastic bending and springback of a beam [J]. Journal of Mechanical Working Technology, 1982, 6(1): 5–21. DOI: 10.1016/0378-3804(82)90016-X. -






 下载:
下载: