A theoretically-modified method for calculating the volumetric stresses in passive confined pressure SHPB tests of granular materials
-
摘要: SHPB被动围压试验为探究散体介质在爆炸和冲击荷载作用下的力学行为提供了一个行之有效的方法。针对相关试验设计和计算中存在的弊端和不足，借助经典板壳理论将SHPB被动围压试验中用于约束散体介质的刚性套筒简化为受均匀带状内压作用的圆柱形壳体。理论计算了套筒径向位移、环向应变与均匀带状内压及套筒几何、力学参数的关系，得到了套筒径向位移、环向应变沿其轴向的分布规律；分析了套筒长度、厚度、内外径以及均匀带状内压宽度之间等无量纲几何参数对计算结果的影响；将理论计算结果与试验和数值模拟结果进行对比，验证了理论计算结果的正确性。本文中提出的理论修正方法可为指导散体介质SHPB被动围压试验提供参考。Abstract: The passive confined pressure SHPB (split Hopkinson pressure bar) test provides an efficient way to study the mechanical behaviors of granular materials at high strain rates (102 − 104 s−1) under the action of explosion and shock wave. In this study, aiming to overcome the disadvantages and demerits of design and calculations in the original passive confined pressure SHPB tests provided in previous works, which has been widely used to investigate the dynamical behaviors of granular materials, a rigid steel sleeve used to restrict the granular specimen is simplified as a circular cylindrical shell, instead of a thick-walled cylinder, subjected to band inner pressure. By using classical shell theory, the theoretical expressions are formulated for radial displacement and hoop strain of the steel sleeve, which contain the mechanical and geometrical parameters of inner pressure and rigid steel sleeve. The distributions of radial displacement and hoop strain along with the steel sleeve are also obtained, while the effects of dimensionless parameters (such as length, thickness, radius of steel sleeve and the width of inner pressure) on the calculation results are studied. Compared with the thick-walled cylinder theory, a modified coefficient k is proposed for estimating the stress states in granular specimens more accurately. To check the feasibility and validate the proposed modified theoretical method, the results derived from shell theory and hollow cylinder theory are compared with experimental and numerical results. It is noted that the shell theory gives better approximations than hollow cylinder theory, especially when d/L is much smaller than one; when the value of d/L approaches to one, the accuracy of two theories is both high, which could be accepted in engineering practices. Therefore, it is concluded that the modified theoretical method proposed in this study for estimating the stress state of specimen can serve as a reference in the passive confined pressure SHPB tests for granular materials.
-
Key words:
- granular materials /
- SHPB tests /
- circular cylindrical shell /
- correction factor
-
图 3 套筒环向应变沿轴线的分布
Figure 3. Distribution of hoop strain on the outer surface along with the steel sleeve
图 4 理论计算得到的修正系数与数值模拟结果的比较
Figure 4. Comparison of theoretical correction factors with numerical results
图 6 理论计算得到的修正系数与数值模拟结果的比较（算例1）
Figure 6. Comparison of theoretical correction factors with numerical results (case 1)
图 7 理论计算得到的修正系数与数值模拟结果的比较（算例2）
Figure 7. Comparison of theoretical correction factors with numerical results (case 2)
-
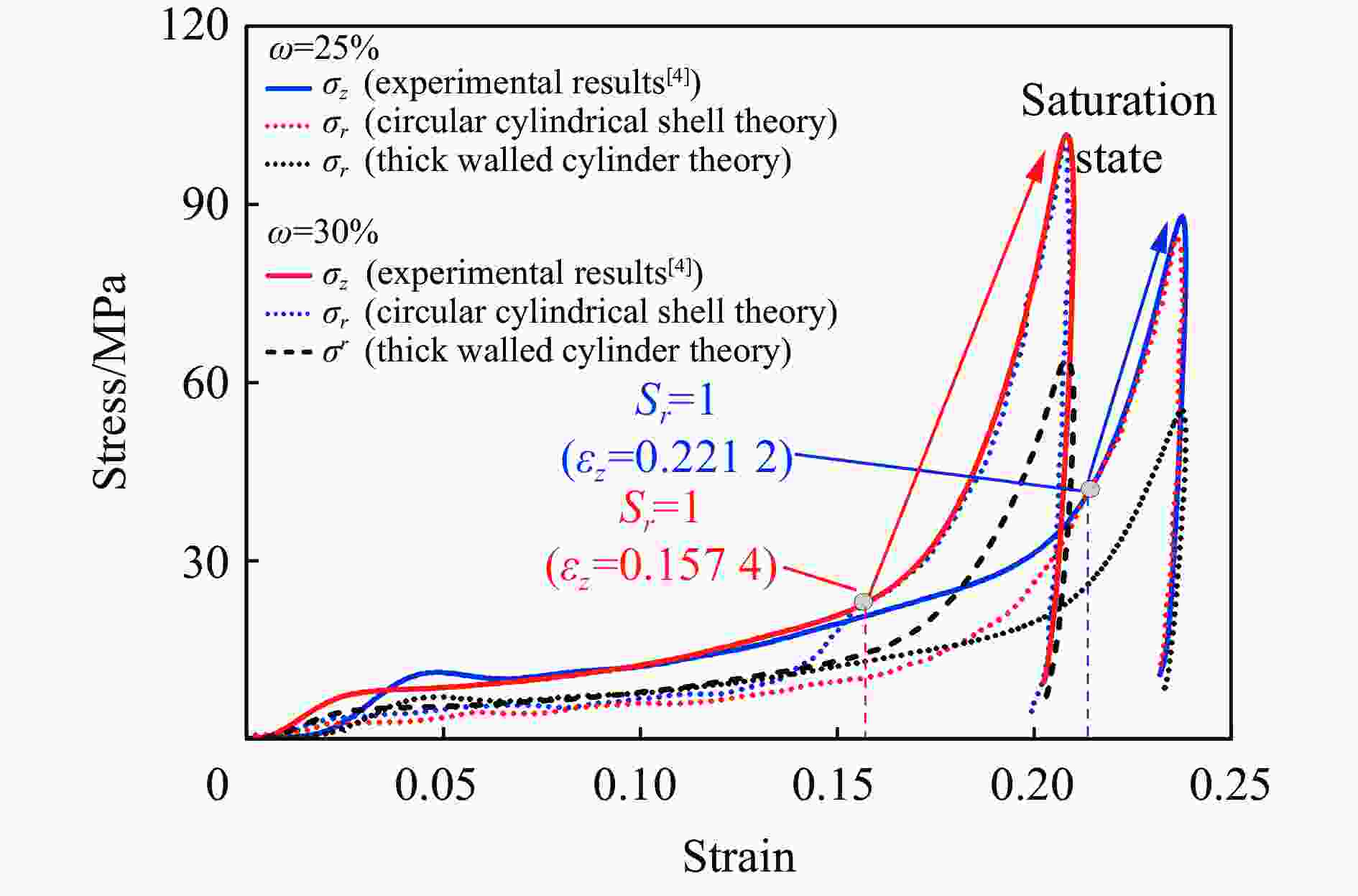
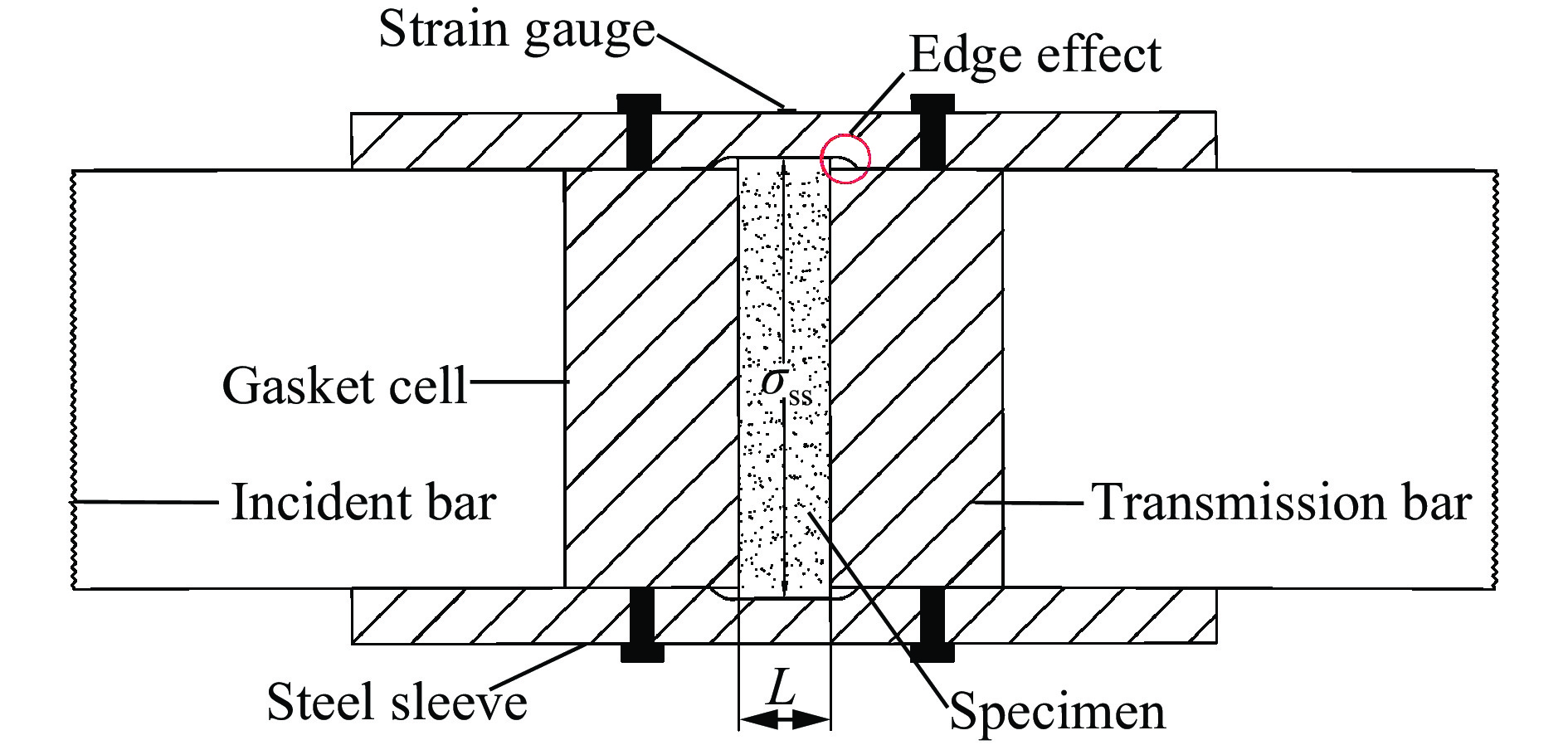
[1] YAMAMURO J A, ABRANTES A E, LADE P V. Effect of strain rate on the stress-strain behavior of sand [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(12): 1169–1178. DOI: 10.1061/(ASCE)GT.1943-5606.0000542. [2] LUO H, LU H, COOPER W L, et al. Effect of mass density on the compressive behavior of dry sand under confinement at high strain rates [J]. Experimental Mechanics, 2011, 51(9): 1499–1510. DOI: 10.1007/s11340-011-9475-2. [3] LUO H Y, COOPER W L, LU H B. Effects of particle size and moisture on the compressive behavior of dense Eglin sand under confinement at high strain rates [J]. International Journal of Impact Engineering, 2014, 65: 40–55. DOI: 10.1016/j.ijimpeng.2013.11.001. [4] 魏久淇, 张春晓, 曹少华, 等. 一种散体材料SHPB被动围压试验体应力修正方法 [J]. 爆炸与冲击, 2020, 40(12): 124201. DOI: 10.11883/bzycj-2019-0411.WEI J Q, ZHANG C X, CAO S H, et al. A volume stress correction method for SHPB passive confined pressure of granular materials [J]. Explosion and Shock Waves, 2020, 40(12): 124201. DOI: 10.11883/bzycj-2019-0411. [5] 赵章泳, 邱艳宇, 紫民, 等. 含水率对非饱和钙质砂动力特性影响的试验研究 [J]. 爆炸与冲击, 2020, 40(2): 023102. DOI: 10.11883/bzycj-2019-0066.ZHAO Z Y, QIU Y Y, ZI M, et al. Experimental study on dynamic compression of unsaturated calcareous sand [J]. Explosion and Shock Waves, 2020, 40(2): 023102. DOI: 10.11883/bzycj-2019-0066. [6] 文祝, 邱艳宇, 紫民, 等. 钙质砂的准一维应变压缩试验研究 [J]. 爆炸与冲击, 2019, 39(3): 033101. DOI: 10.11883/bzycj-2018-0015.WEN Z, QIU Y Y, ZI M, et al. Experimental study on quasi-one-dimensional strain compression of calcareous sand [J]. Explosion and Shock Waves, 2019, 39(3): 033101. DOI: 10.11883/bzycj-2018-0015. [7] HOPKINSON B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets [J]. Proceedings of the Royal Society of London: Series A, 1914, 89(612): 411–413. DOI: 10.1098/rspa.1914.0008. [8] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society: Section B, 1949, 62(11): 676–700. DOI: 10.1088/0370-1301/62/11/302. [9] BRAGOV A M, LOMUNOV A K, SERGEICHEV I V, et al. Determination of physicomechanical properties of soft soils from medium to high strain rates [J]. International Journal of Impact Engineering, 2008, 35(9): 967–976. DOI: 10.1016/j.ijimpeng.2007.07.004. [10] MA Z, RAVI-CHANDAR K. Confined compression: a stable homogeneous deformation for constitutive characterization [J]. Experimental Mechanics, 2000, 40(1): 38–45. DOI: 10.1007/BF02327546. [11] SONG B, CHEN W N, LUK V. Impact compressive response of dry sand [J]. Mechanics of Materials, 2009, 41(6): 777–785. DOI: 10.1016/j.mechmat.2009.01.003. [12] 曹志远. 板壳振动理论 [M]. 北京: 中国铁道出版社, 1989: 304–305. [13] 王敏中, 王炜, 武际可. 弹性力学教程 [M]. 北京: 北京大学出版社, 2011: 264–266. -
下载:
点击查看大图
图(8)
计量
- 文章访问数: 319
- HTML全文浏览量: 160
- PDF下载量: 50
- 被引次数: 0