On penetration depth of typical earth-penetrating projectilesinto concrete targets considering the scaling effect
-
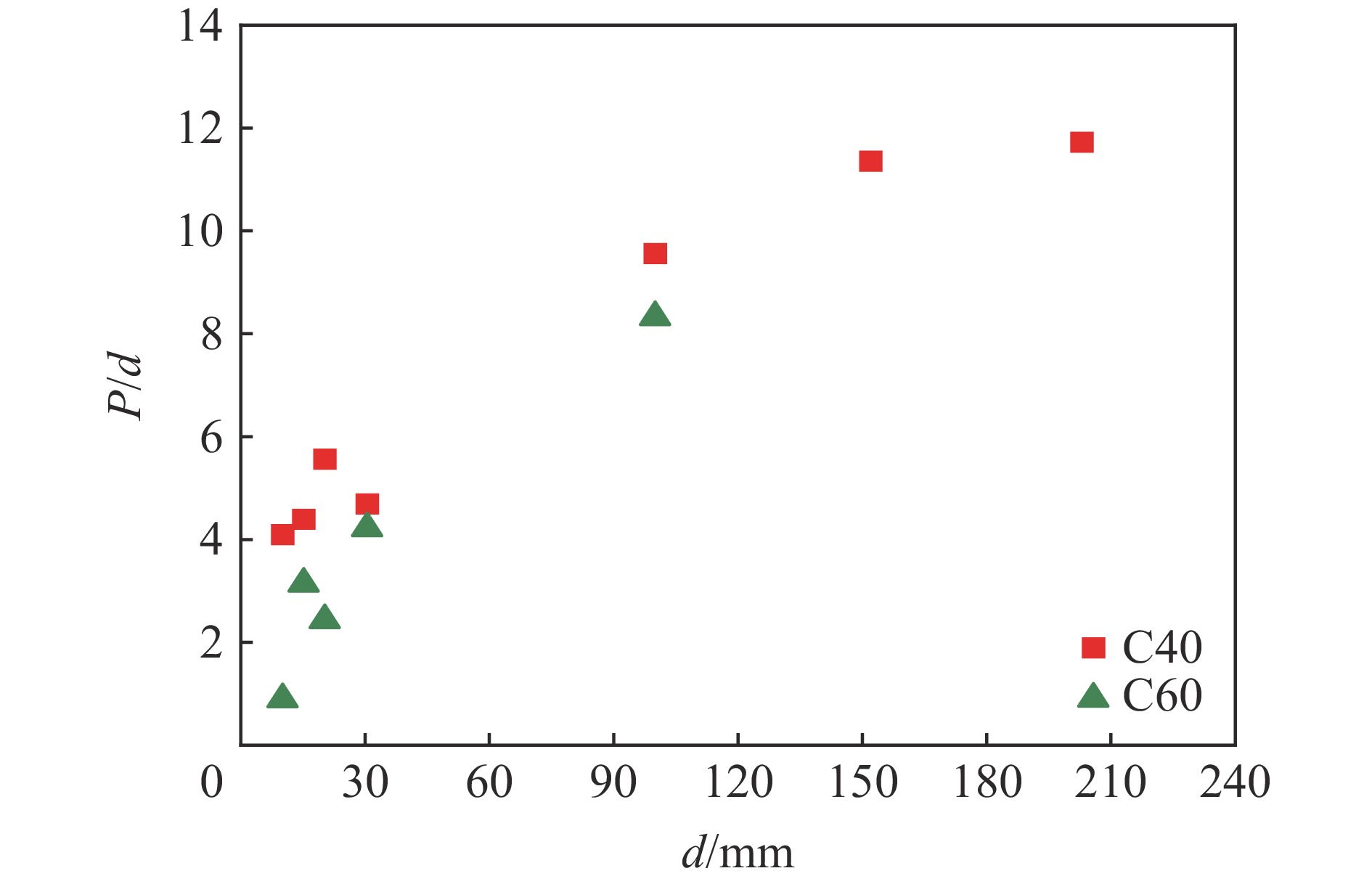
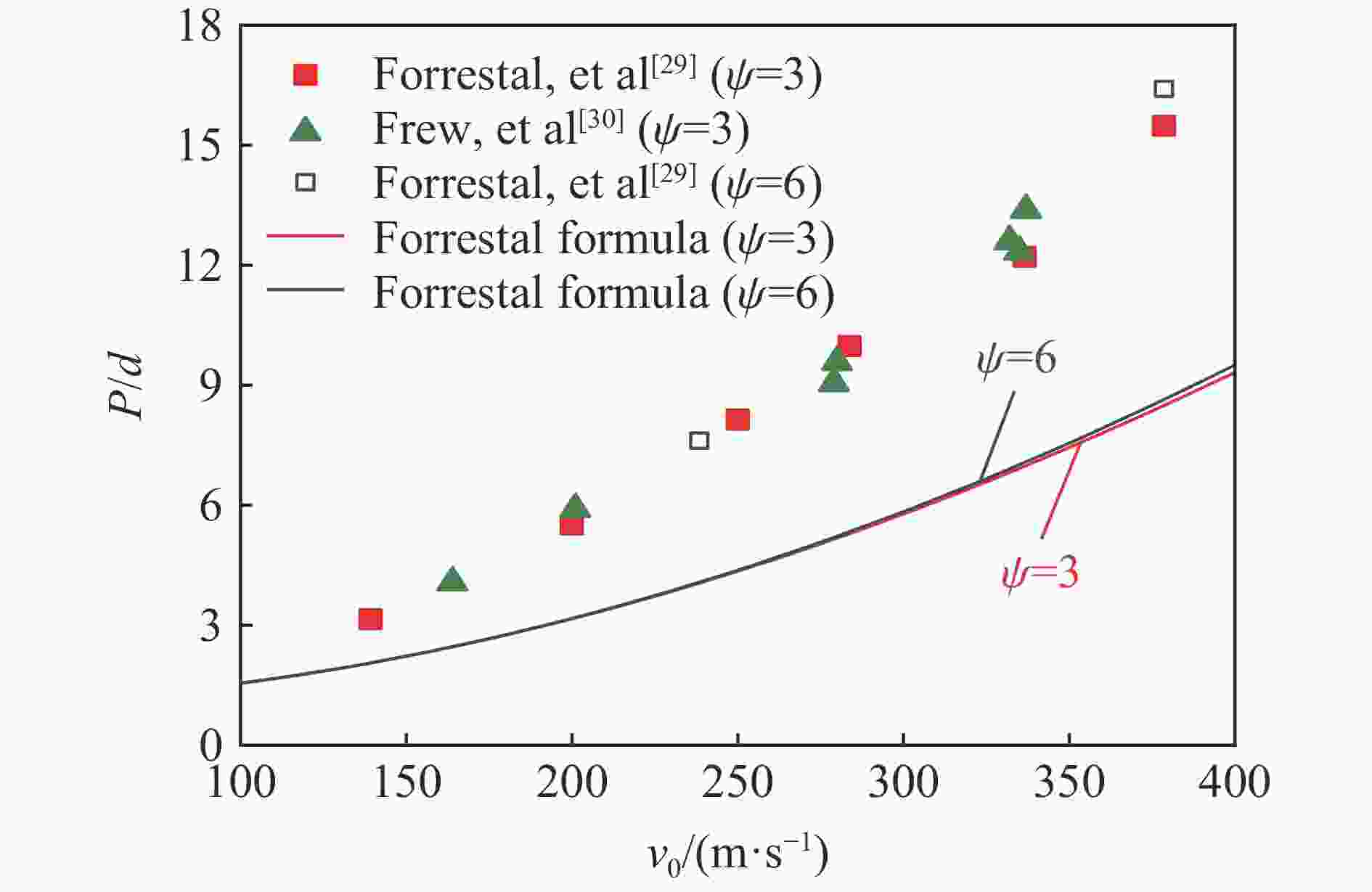
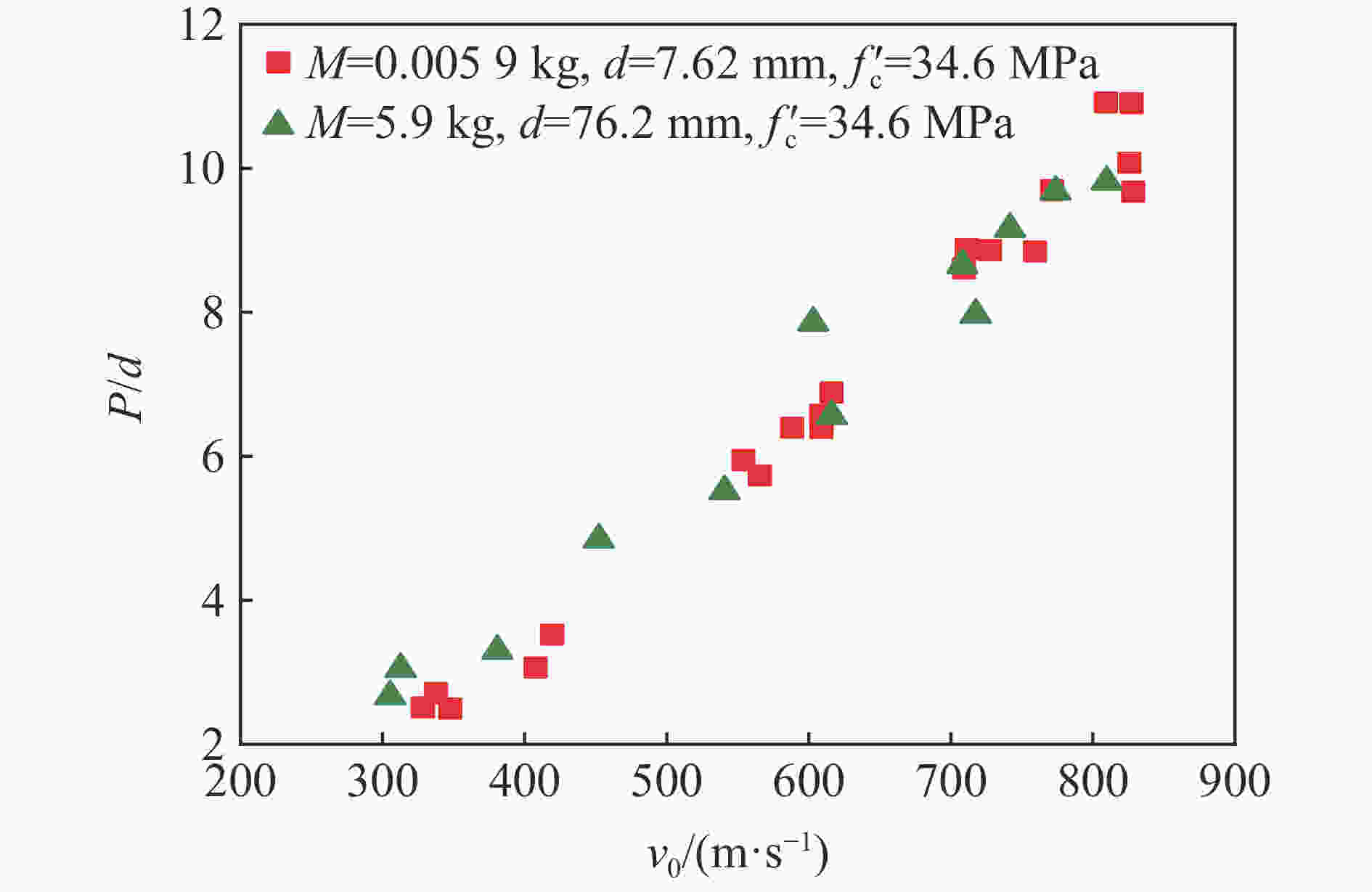
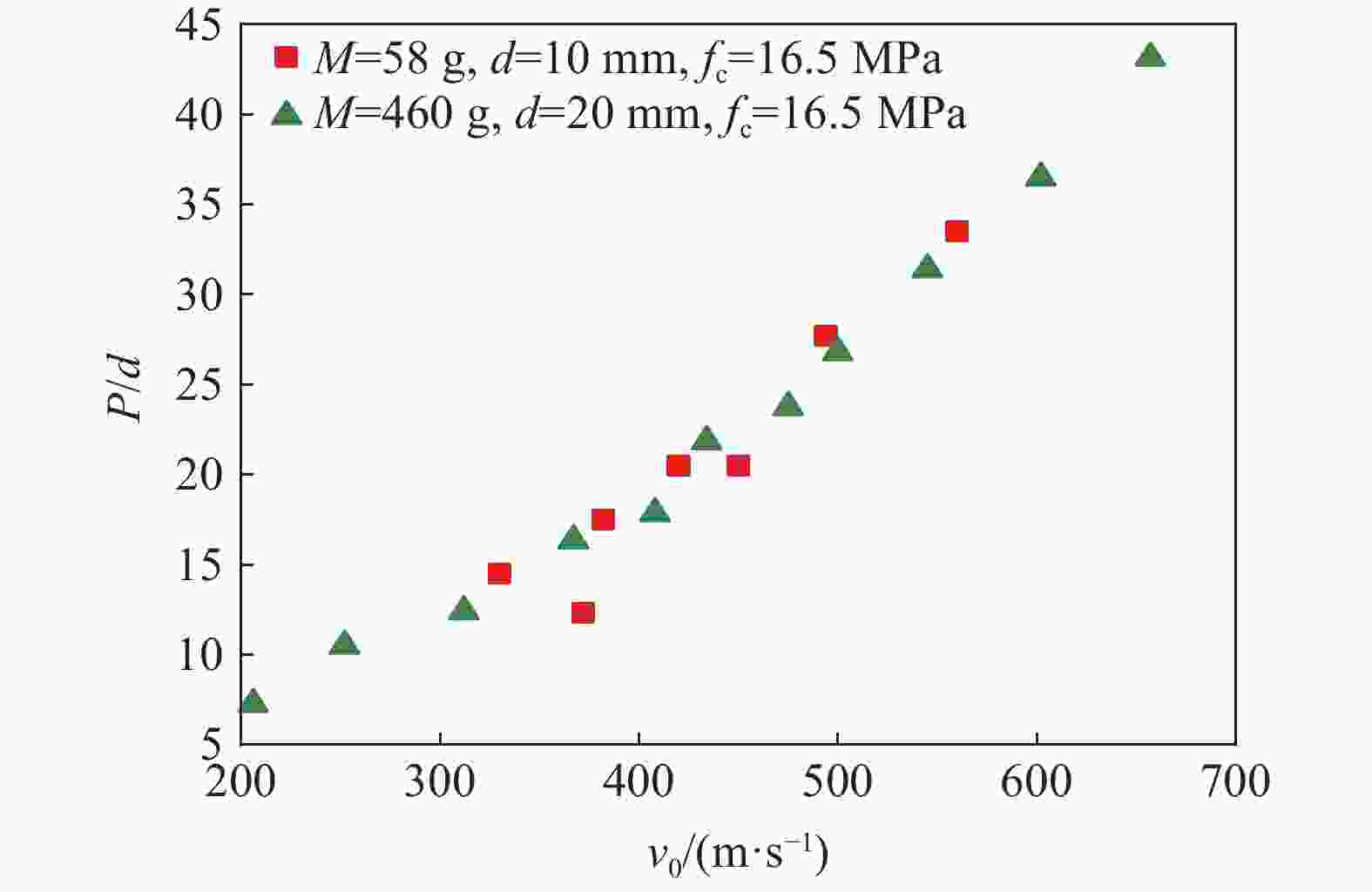
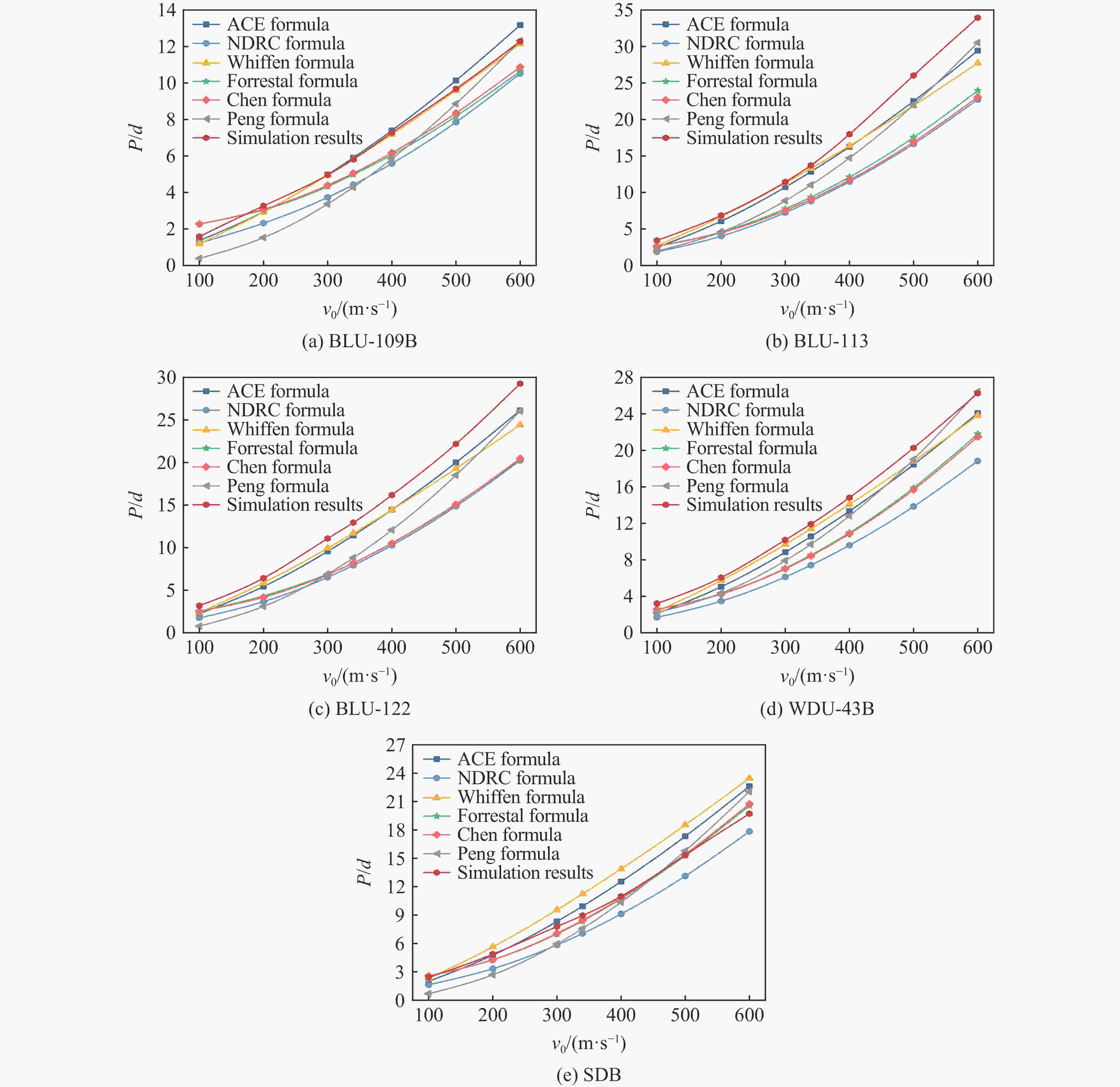
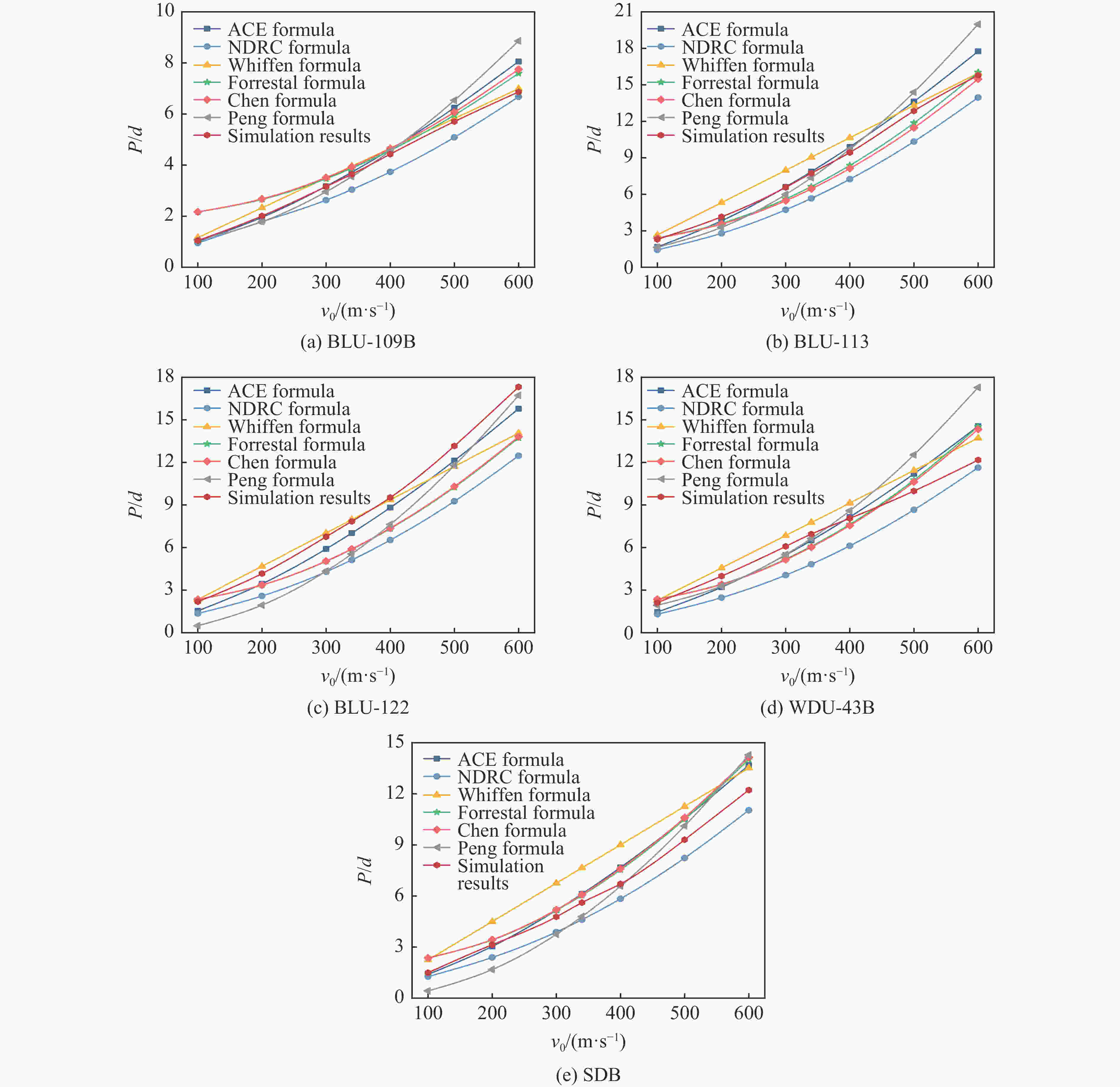
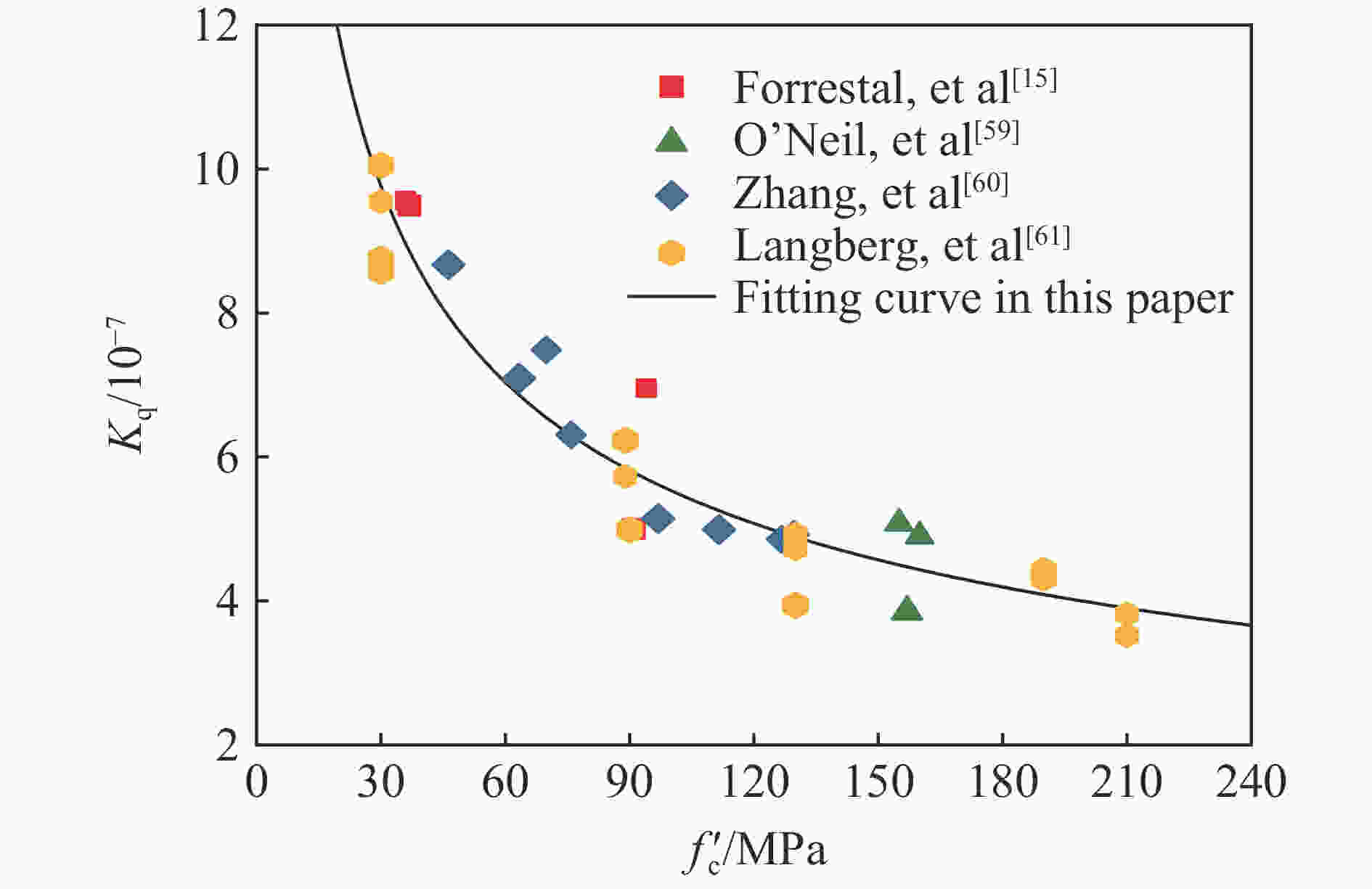
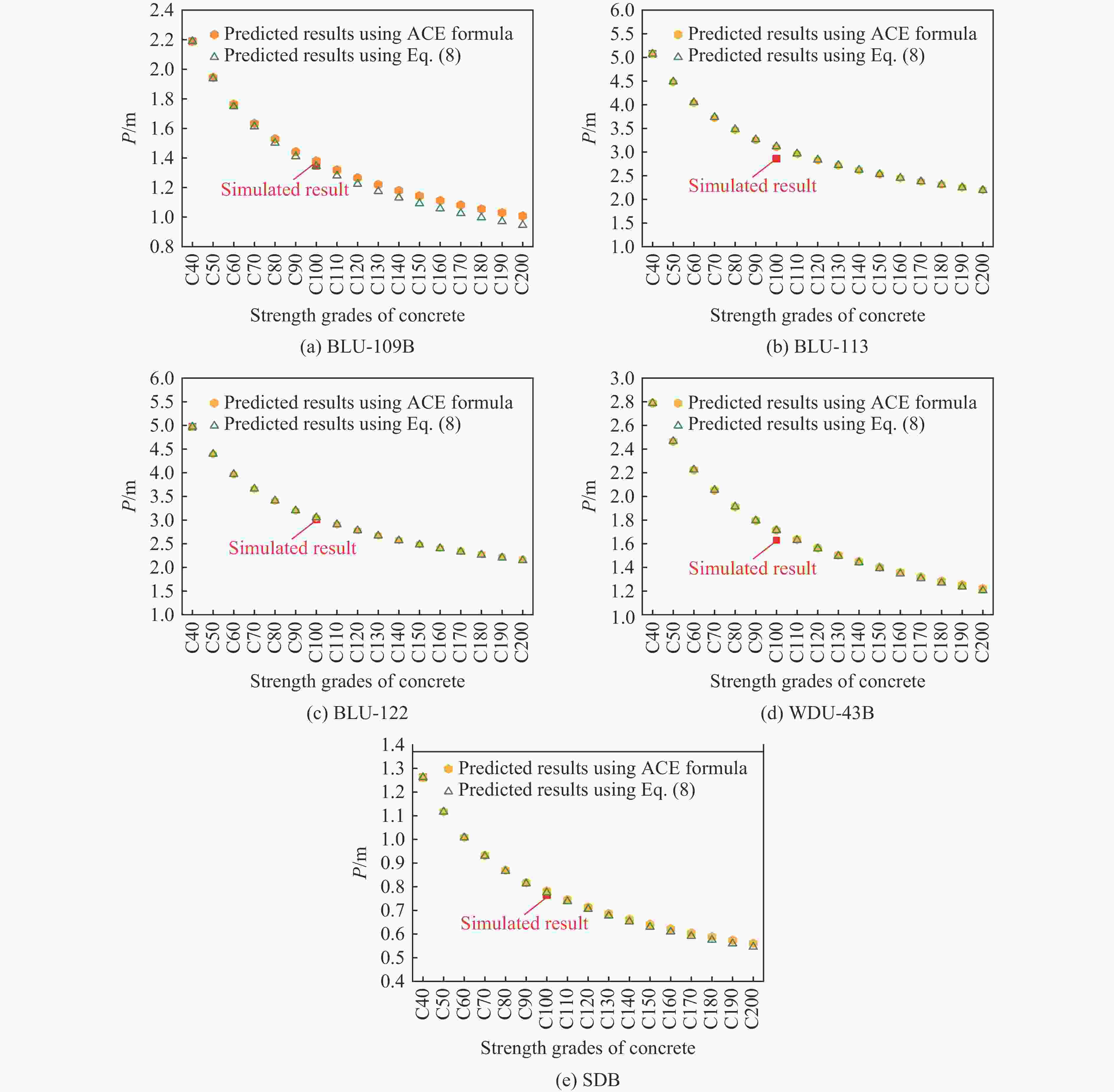
摘要: 准确评估精确制导武器的侵彻深度可为防护工程设计提供重要参考。已有研究工作大多集中于中、小口径弹体和普通强度混凝土靶体,且由于尺寸效应的影响使得现有计算方法对预测大口径典型钻地弹侵彻深度的适用性值得商榷。首先,综合分析了已有弹体侵彻试验数据,发现引起侵彻深度尺寸效应的主要原因是混凝土粗骨料粒径未随弹体尺寸进行同比缩放;其次,开展了5发100.0和203.0 mm口径缩比钻地弹侵彻C40和C100混凝土的试验和数值模拟分析,提出并验证了大口径弹体侵彻混凝土深度的实用化有限元计算方法;然后,确定了美军5种典型钻地弹在不同侵彻速度(100~600 m/s)下对上述2种强度混凝土靶体的侵彻深度,并对现有7种计算公式的适用性进行了评估;最后,基于已有大量试验数据拟合确定了侵彻深度随混凝土强度的衰减规律,并计算得到340 m/s侵彻速度下5种典型钻地弹对C40~C200混凝土的侵彻深度。Abstract: Accurately evaluating the penetration depth of precision-guided weapons can provide an important reference for the design of protective engineering. The existing work mainly focuses on small or medium caliber projectiles and normal strength concrete targets. Besides, the applicability of existing calculation methods to predict the penetration depth of typical large-caliber earth-penetrating projectiles is worthy of discussion due to the scaling effect. Firstly, by analyzing the existing penetration test data, the main cause of the size effect of penetration depth is that the particle size of the coarse aggregate is not scaled with the projectile size accordingly. Then, five tests were carried out with 100.0-mm and 203.0-mm caliber scaled earth-penetrating projectiles penetrating into C40 and C100 concrete targets. The corresponding two-dimensional axisymmetric finite element model was established. By adjusting the predefined value of the eroding plastic strain to make the numerical penetration depth close to the test data, the constitutive model parameters, as well as the matched mesh size and the erosion criterion, were determined. Thus, a practical finite element analyses method for the penetration depth of large-caliber projectiles into concrete was proposed and verified. Furthermore, for the above two concrete strength grades, the penetration depths of the five typical earth-penetrating projectiles of the U.S. military into concrete at different impact velocities (100-600 m/s) were determined, and the applicability of the existing seven empirical or semi-empirical formulas was evaluated. The comparison results show that the ACE formula can obtain a better prediction of the penetration depth. Finally, the attenuation law of the penetration depth with the compressive strength of concrete was confirmed by fitting the existing penetration test data. The corresponding penetration depths of the five typical earth-penetrating projectiles into the C40-C200 concrete targets at the velocity of 340 m/s were determined. The present work and conclusions can be directly used in the protective engineering design.
-
Key words:
- concrete target /
- penetration depth /
- earth-penetrating projectile /
- scaling effect
-
表 1 试验结果
Table 1. Test results
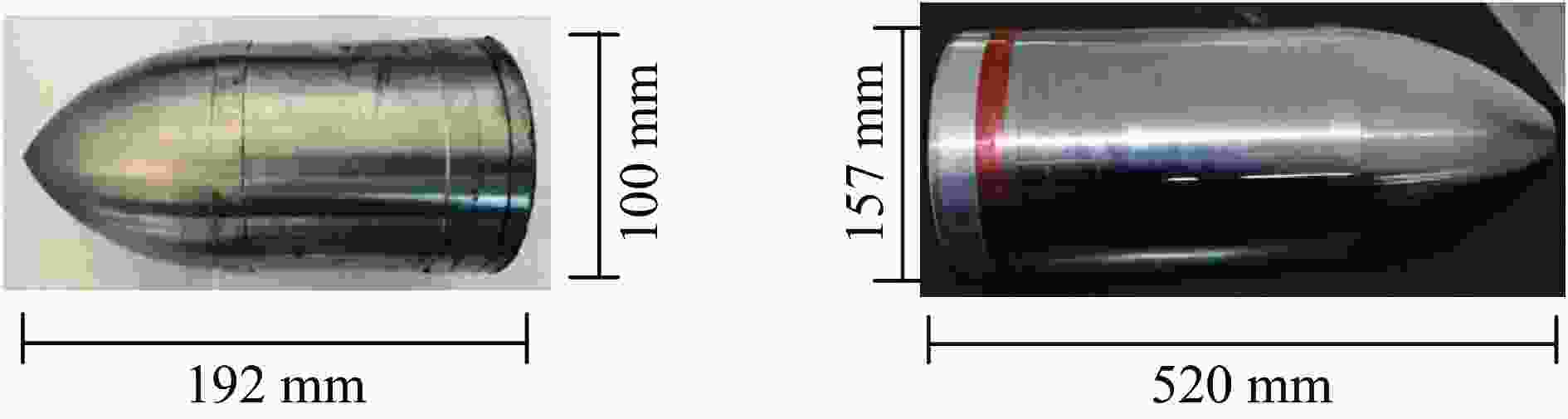
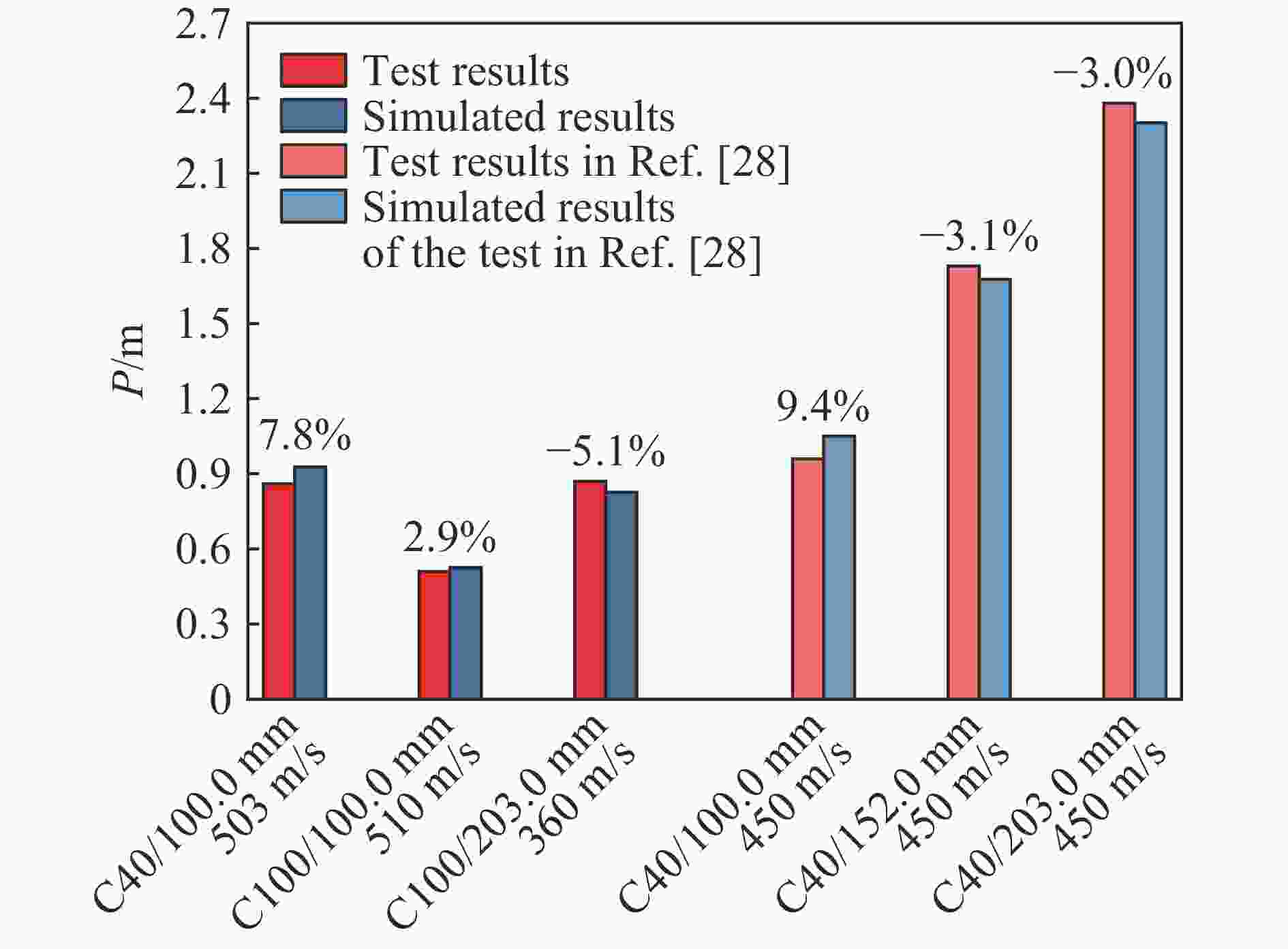
试验编号 f/MPa d/mm M/kg v0/(m·s−1) P/m 1 40 100.0 17.3 503 0.86 2 40 105.0 20.1 325 0.52 3 100 100.0 17.3 357 0.35 4 100 100.0 17.3 510 0.51 5 100 203.0 145.0 360 0.87 表 2 5种战斗部参数
Table 2. Parameters of five warheads
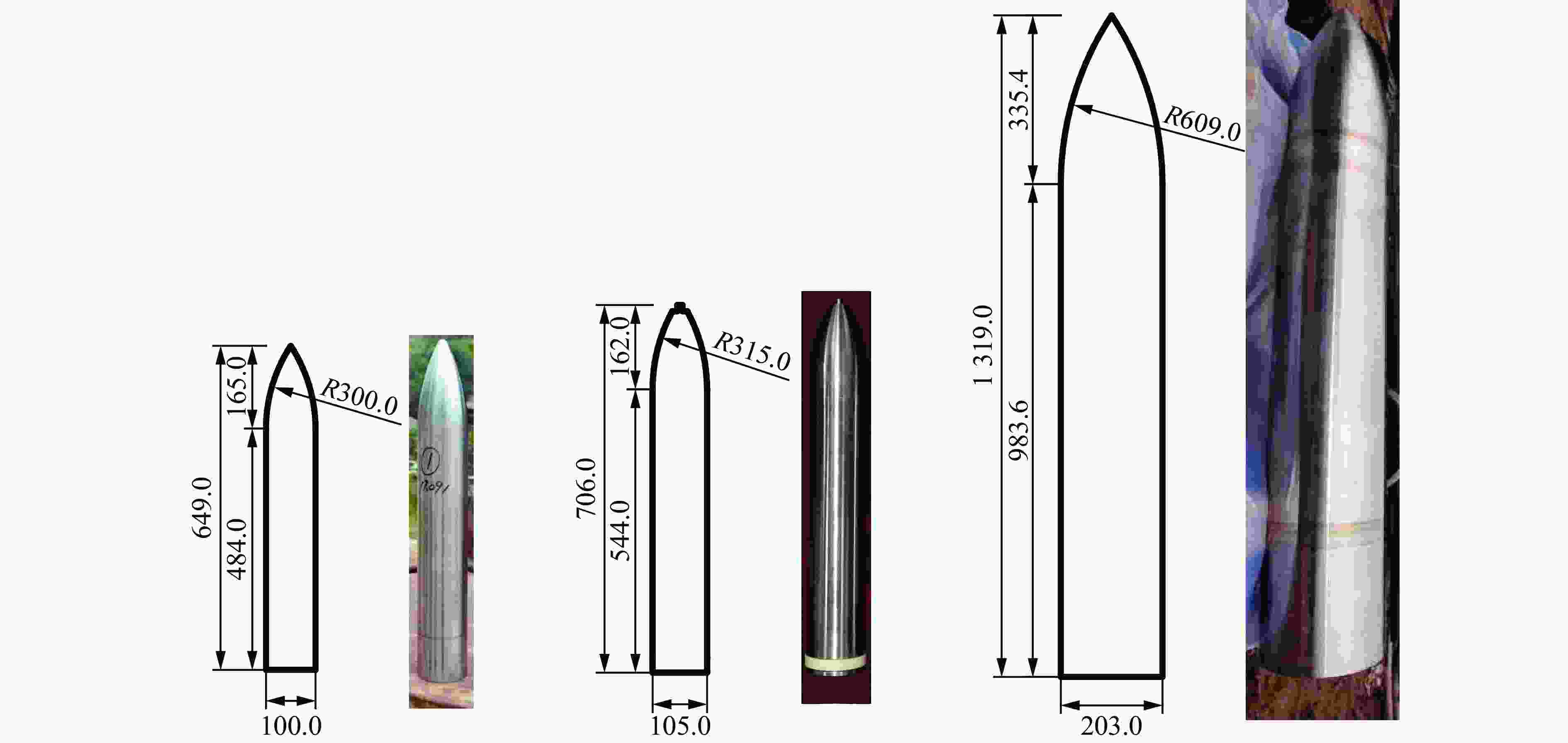
战斗部 d/mm M/kg L/mm w/mm ψ BLU-109B 368.3 874 2 400 25.4 3 BLU-113 368.3 1 996 3 886 58.0 3 BLU-122 389.0 2 018 4 038 44.5 WDU-43B 234.0 454 2 400 41.5 9 SDB 150.0 129 1 800 10.8 3 -
[1] PETRY L. Monographies de systemes d’Artillerie [M]. Brussels, Belgium: Cans et Compagnie, 1910. [2] GWALTNEY R C. Missile generation and protection in light-water-cooled power reactor plants: ORNL-NSIC-22 [R]. Oak Ridge, USA: Oak Ridge National Laboratory, 1968. [3] Army Corps of Engineers. Fundamentals of protective design: AT1207821 [R]. Pennsylvania, USA: Office of the Chief of Engineers, 1946. [4] National Defense Research Committee. Effects of impact and explosion: summary technical report of division 2, vol. 1 [R]. Washington, USA: National Defense Research Committee, 1946. [5] KENNEDY R P. A review of procedures for the analysis and design of concrete structures to resist missile impact effects [J]. Nuclear Engineering and Design, 1976, 37(2): 183–203. DOI: 10.1016/0029-5493(76)90015-7. [6] WHIFFEN P. UK road research laboratory: MOS/311 [R]. 1943. [7] KAR A K. Local effects of tornado-generated missiles [J]. Journal of the Structural Division, 1978, 104(5): 809–816. DOI: 10.1061/JSDEAG.0004915. [8] BARR P. Guidelines for the design and assessment of concrete structures subjected to impact [R]. London, UK: UK Atomic Energy Authority, Safety and Reliability Directorate, 1990. [9] HALDAR A, HAMIEH H A. Local effect of solid missiles on concrete structures [J]. Journal of Structural Engineering, 1984, 110(5): 948–960. DOI: 10.1061/(ASCE)0733-9445(1984)110:5(948). [10] ADELI H, AMIN A M. Local effects of impactors on concrete structures [J]. Nuclear Engineering and Design, 1985, 88(3): 301–317. DOI: 10.1016/0029-5493(85)90165-7. [11] HUGHES G. Hard missile impact on reinforced concrete [J]. Nuclear Engineering and Design, 1984, 77(1): 23–35. DOI: 10.1016/0029-5493(84)90058-X. [12] BANGASH M Y H. Concrete and concrete structures: numerical modelling and application [M]. London, UK: Elsevier Applied Science, 1989. [13] BANGASH M Y H. Impact and explosion: structural analysis and design [R]. Boca Raton, USA: CRC Press, 1993. [14] CHANG W S. Impact of solid missiles on concrete barriers [J]. Journal of the Structural Division, 1981, 107(2): 257–271. DOI: 10.1061/JSDEAG.0005640. [15] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743x(94)80024-4. [16] FREW D J, HANCHAK S J, GREEN M L, et al. Penetration of concrete targets with ogive-nose steel rods [J]. International Journal of Impact Engineering, 1998, 21(6): 489–497. DOI: 10.1016/S0734-743X(98)00008-6. [17] CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2. [18] ROSENBERG Z, DEKEL E. The deep penetration of concrete targets by rigid rods-revisited [J]. International Journal of Protective Structures, 2010, 1(1): 125–144. DOI: 10.1260/2041-4196.1.1.125. [19] ROSENBERG Z, KOSITSKI R. Modeling the penetration and perforation of concrete targets by rigid projectiles [J]. International Journal of Protective Structures, 2016, 7(2): 157–178. DOI: 10.1177/2041419616632422. [20] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures [C]//Proceedings of the 14th International Symposium on Ballistic. Quebec, Canada: American Defense Preparedness Association, 1993: 591−600. [21] TAYLOR L M, CHEN E P, KUSZMAUL J S. Microcrack-induced damage accumulation in brittle rock under dynamic loading [J]. Computer Methods in Applied Mechanics and Engineering, 1986, 55(3): 301–320. DOI: 10.1016/0045-7825(86)90057-5. [22] REIDEL W, THORMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500, numerical analysis using a new macroscopic concrete model for hydrocodes [C]//Proceedings of the 9th International Symposium on Interaction of the Effects of Munitions with Structures. Berlin-Strausberg, Germany, 1999: 315−322. [23] KONG X Z, FANG Q, WU H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61–71. DOI: 10.1016/j.ijimpeng.2016.04.014. [24] KONG X Z, FANG Q, LI Q M, et al. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact [J]. International Journal of Impact Engineering, 2017, 108: 217–228. DOI: 10.1016/j.ijimpeng.2017.02.016. [25] KONG X Z, FANG Q, CHEN L, et al. A new material model for concrete subjected to intense dynamic loadings [J]. International Journal of Impact Engineering, 2018, 120: 60–78. DOI: 10.1016/j.ijimpeng.2018.05.006. [26] 邓勇军, 陈小伟, 钟卫洲, 等. 弹体正侵彻钢筋混凝土靶的试验及数值模拟研究 [J]. 爆炸与冲击, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001.DENG Y J, CHEN X W, ZHONG W Z, et al. Experimental and numerical study on normal penetration of a projectile into a reinforced concrete target [J]. Explosion and Shock Waves, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001. [27] 马天宝, 武珺, 宁建国. 弹体高速侵彻钢筋混凝土的实验与数值模拟研究 [J]. 爆炸与冲击, 2019, 39(10): 103301. DOI: 10.11883/bzycj-2018-0275.MA T B, WU J, NING J G. Experimental and numerical study on projectiles’ high-velocity penetration into reinforced concrete [J]. Explosion and Shock Waves, 2019, 39(10): 103301. DOI: 10.11883/bzycj-2018-0275. [28] 吴飚, 任辉启, 陈力, 等. 弹体侵彻混凝土尺度效应试验研究与理论分析 [J]. 防护工程, 2020, 42(2): 1–10. DOI: 10.3969/j.issn.1674-1854.2020.02.001.WU B, REN H Q, CHEN L, et al. Experimental study and theoretical analysis of size effect on projectile penetrating concrete [J]. Protective Engineering, 2020, 42(2): 1–10. DOI: 10.3969/j.issn.1674-1854.2020.02.001. [29] FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements [J]. International Journal of Impact Engineering, 2003, 28(5): 479–497. DOI: 10.1016/S0734-743X(02)00108-2. [30] FREW D J, FORRESTAL M J, CARGILE J D. The effect of concrete target diameter on projectile deceleration and penetration depth [J]. International Journal of Impact Engineering, 2006, 32(10): 1584–1594. DOI: 10.1016/j.ijimpeng.2005.01.012. [31] CANFIELD J A, CLATOR I G. Development of a scaling law and techniques to investigate penetration in concrete: NWL Report No. 2057 [R]. Dahlgren, VA, USA: US Naval Weapons Laboratory, 1966. [32] 徐建波. 长杆射弹对混凝土的侵彻特性研究 [D]. 长沙: 国防科学技术大学, 2001.XU J B. Investigations on long projectiles penetrating into concrete targets [D]. Changsha, Hunan, China: National University of Defense Technology, 2001. [33] WU H, LI Y C, FANG Q, et al. Scaling effect of rigid projectile penetration into concrete target: 3D mesoscopic analyses [J]. Construction and Building Materials, 2019, 208: 506–524. DOI: 10.1016/j.conbuildmat.2019.03.040. [34] 彭永, 卢芳云, 方秦, 等. 弹体侵彻混凝土靶体的尺寸效应分析 [J]. 爆炸与冲击, 2019, 39(11): 113301. DOI: 10.11883/bzycj-2018-0402.PENG Y, LU F Y, FANG Q, et al. Analyses of the size effect for projectile penetrations into concrete targets [J]. Explosion and Shock Waves, 2019, 39(11): 113301. DOI: 10.11883/bzycj-2018-0402. [35] FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. DOI: 10.1016/0734-743X(95)00048-F. [36] 黄蒙, 欧卓成, 段卓平, 等. 刚性弹体侵彻混凝土的相似性研究 [J]. 兵工学报, 2016, 37(S2): 176–180.HUANG M, OU Z C, DUAN Z P, et al. A study of similarity analysis of hard projectile penetrating into concrete [J]. Acta Armamentarii, 2016, 37(S2): 176–180. [37] GOMEZ J T, SHUKLA A. Multiple impact penetration of semi-infinite concrete [J]. International Journal of Impact Engineering, 2001, 25(10): 965–979. DOI: 10.1016/S0734-743X(01)00029-X. [38] 石志勇. 长杆射弹侵彻两种混凝土靶的特性研究 [D]. 长沙: 国防科学技术大学, 2002.SHI Z Y. Study on the characteristics of long-rod projectile penetrating two kinds of concrete targets [D]. Changsha, Hunan, China: National University of Defense Technology, 2002. [39] 蒋荣峰. 动能侵彻弹侵彻混凝土技术研究 [D]. 成都: 四川大学, 2003.JIANG R F. Techniques of kinetic energy projectile penetrating into the concrete [D]. Chengdu, Sichuan, China: Sichuan University, 2003. [40] 顾晓辉, 王晓鸣, 陈惠武, 等. 动能弹低速垂直侵彻钢筋混凝土的试验研究 [J]. 南京理工大学学报, 2006, 30(1): 1–4. DOI: 10.14177/j.cnki.32-1397n.2006.01.001.GU X H, WANG X M, CHEN H W, et al. Experimental studies on kinetic projectile’s direct penetrations with low-speed against reinforced concrete targets [J]. Journal of Nanjing University of Science and Technology, 2006, 30(1): 1–4. DOI: 10.14177/j.cnki.32-1397n.2006.01.001. [41] 孙传杰, 卢永刚, 张方举, 等. 新型头形弹体对混凝土的侵彻 [J]. 爆炸与冲击, 2010, 30(3): 269–275. DOI: 10.11883/1001-1455(2010)03-0269-07.SUN C J, LU Y G, ZHANG F J, et al. Penetration of cylindrical-nose-tip projectiles into concrete targets [J]. Explosion and Shock Waves, 2010, 30(3): 269–275. DOI: 10.11883/1001-1455(2010)03-0269-07. [42] 邓云飞, 崔亚男, 慕忠成, 等. 卵形头弹体对素混凝土高速侵彻的实验研究 [J]. 应用力学学报, 2019, 36(5): 1144–1151.DENG Y F, CUI Y N, MU Z C, et al. An experimental investigation of ogive-nosed projectiles penetration into plain concrete at high velocities [J]. Chinese Journal of Applied Mechanics, 2019, 36(5): 1144–1151. [43] 林圣灵. 弹丸侵彻混凝土靶实验及仿真 [D]. 北京: 北京理工大学, 2016.LIN S L. Experiment and simulation of projectile penetrating concrete target [D]. Beijing, China: Beijing Institute of Technology, 2016. [44] 梁斌. 动能攻坚战斗部对混凝土靶侵爆效应研究 [D]. 四川绵阳: 中国工程物理研究院, 2009.LIANG B. Study on the penetration and blasting damage of concrete for anti-hard-target warhead [D]. Mianyang, Sichuan, China: China Academy of Engineering Physics, 2009. [45] 张广乐. 高速杆弹侵彻混凝土效应研究 [D]. 南京: 南京理工大学, 2011.ZHANG G L. Study on the effects of high-speed long rod projectile penetrating concrete [D]. Nanjing, Jiangsu, China: Nanjing Institute of Technology, 2011. [46] 武海军, 黄风雷, 王一楠, 等. 高速侵彻混凝土弹体头部侵蚀终点效应实验研究 [J]. 兵工学报, 2012, 33(1): 48–55.WU H J, HUANG F L, WANG Y N, et al. Experimental investigation on projectile nose eroding effect of high-velocity penetration into concrete [J]. Acta Armamentarii, 2012, 33(1): 48–55. [47] 庞春旭, 何勇, 沈晓军, 等. 刻槽弹体旋转侵彻混凝土效应试验研究 [J]. 兵工学报, 2015, 36(1): 46–52. DOI: 10.3969/j.issn.1000-1093.2015.01.007.PANG C X, HE Y, SHEN X J, et al. Experimental investigation on penetration of grooved projectiles into concrete targets [J]. Acta Armamentarii, 2015, 36(1): 46–52. DOI: 10.3969/j.issn.1000-1093.2015.01.007. [48] 胡玉涛, 柯明, 杨慧, 等. 弹体侵彻混凝土靶侵蚀实验研究 [C]//中国力学大会论文集(CCTAM 2019). 杭州: 中国力学学会, 2019. [49] 赵晓宁. 高速弹体对混凝土侵彻效应研究 [D]. 南京: 南京理工大学, 2011.ZHAO X N. Study on the effect of projectiles high-velocity normal penetrating into concrete targets [D]. Nanjing, Jiangsu, China: Nanjing Institute of Technology, 2011. [50] 柴传国. 异形头部弹体对混凝土靶的侵彻效应研究 [D]. 北京: 北京理工大学, 2014.CHAI C G. Study on the mechanism of penetration into concrete of nose headed projectile [D]. Beijing, China: Beijing Institute of Technology, 2014. [51] 郭磊, 何勇, 潘绪超, 等. 高速侵彻混凝土弹体侵蚀效应试验研究 [J]. 实验力学, 2020, 35(1): 82–90. DOI: 10.7520/1001-4888-18-182.GUO L, HE Y, PAN X C, et al. Experimental study on mass loss of projectile subjected to high-velocity penetration into concrete target [J]. Journal of Experimental Mechanics, 2020, 35(1): 82–90. DOI: 10.7520/1001-4888-18-182. [52] 陈小伟, 张方举, 杨世全, 等. 动能深侵彻弹的力学设计(Ⅲ):缩比实验分析 [J]. 爆炸与冲击, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-10.CHEN X W, ZHANG F J, YANG S Q, et al. Mechanics of structural design of EPW (Ⅲ): investigations on the reduced-scale tests [J]. Explosion and Shock Waves, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-10. [53] 黄民荣. 刚性弹体对混凝土靶的侵彻与贯穿机理研究 [D]. 南京: 南京理工大学, 2011.HUANG M R. Penetration and perforation mechanism of rigid projectile into the concrete target [D]. Nanjing, Jiangsu, China: Nanjing Institute of Technology, 2011. [54] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual volume Ⅱ: material models [M]. Livermore, USA: Livermore Software Technology Corporation, 2012. [55] BORRVALL T, RIEDEL W. The RHT concrete model in LS-DYNA [C]//Proceedings of the 8th European LS-DYNA Users Conference. Strasbourg, France: Springer, 2011. [56] 甄建伟, 曹凌宇, 孙福. 弹药毁伤效应数值仿真技术 [M]. 北京: 北京理工大学出版社, 2018.ZHEN J W, CAO L Y, SUN F. Numerical simulation of ammunition damage effect [M]. Beijing, China: Beijing Institute of Technology Press, 2018. [57] 严平, 谭波, 苗润, 等. 战斗部及其毁伤原理 [M]. 北京: 国防工业出版社, 2020.YAN P, TAN B, MIAO R, et al. Warhead and its damage principle [M]. Beijing, China: National Defense Industry Press, 2020. [58] PENG Y, WU H, FANG Q, et al. Geometrical scaling effect for penetration depth of hard projectiles into concrete targets [J]. International Journal of Impact Engineering, 2018, 120: 46–59. DOI: 10.1016/j.ijimpeng.2018.05.010. [59] O’NEIL E F, NEELEY B D, CARGILE J D. Tensile properties of very-high-strength concrete for penetration-resistant structures [J]. Shock and Vibration, 1999, 6(5/6): 237–245. DOI: 10.1155/1999/415360. [60] ZHANG M H, SHARIF M S H, LU G. Impact resistance of high-strength fibre-reinforced concrete [J]. Magazine of Concrete Research, 2007, 59(3): 199–210. DOI: 10.1680/macr.2007.59.3.199. [61] LANGBERG H, MARKESET G. High performance concrete penetration resistance and material development [C]//Proceedings of the 9th International Symposium on Interaction of the Effects of Munitions with Structures. Norway: Norwegian Defense Construction Service, 1999. -







 下载:
下载: