Failure law of surrounding rock under underground explosion based on a new damage-virtual tensile crack model
-
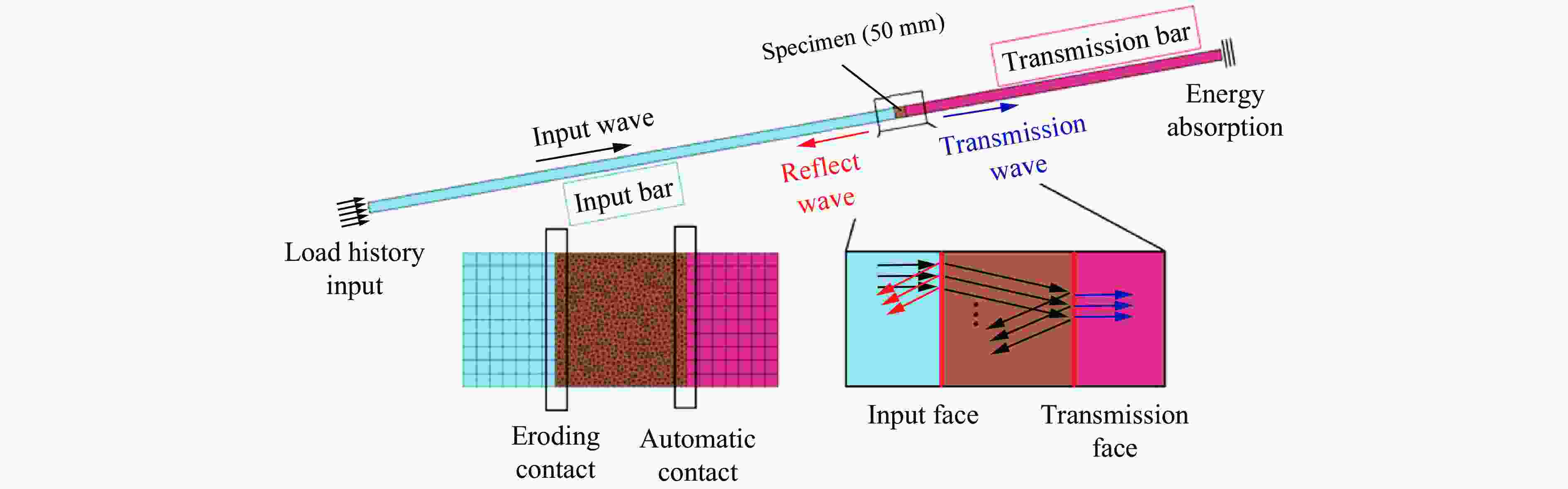
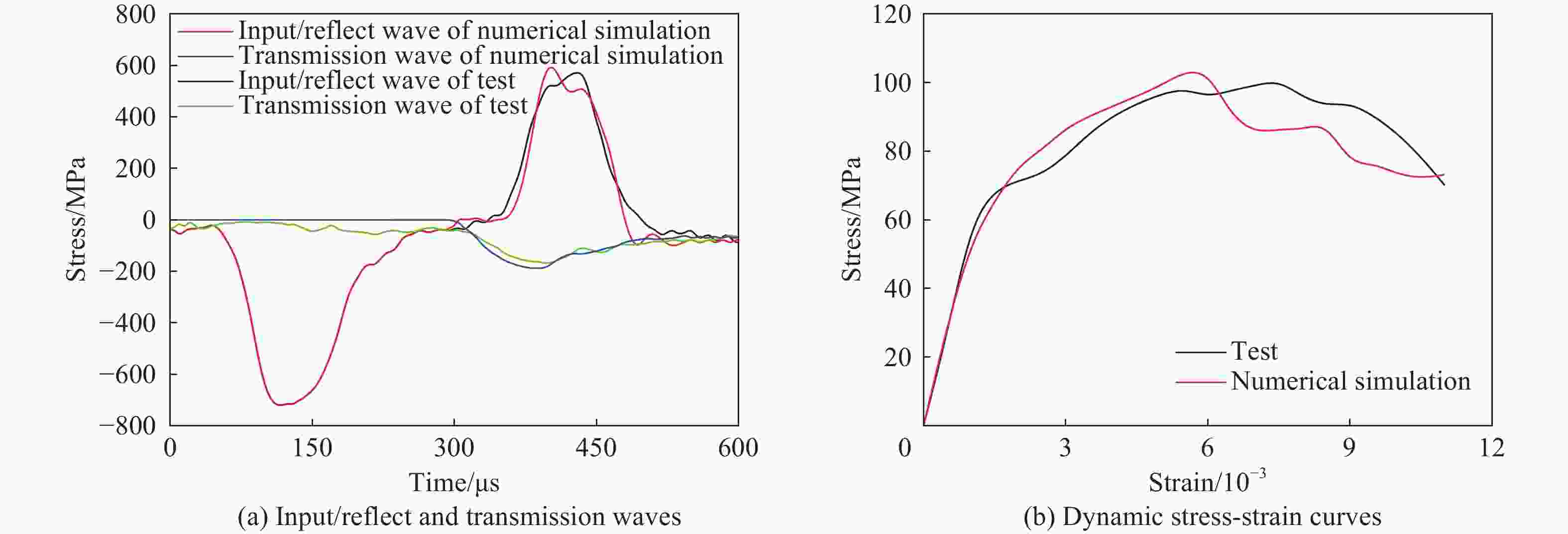
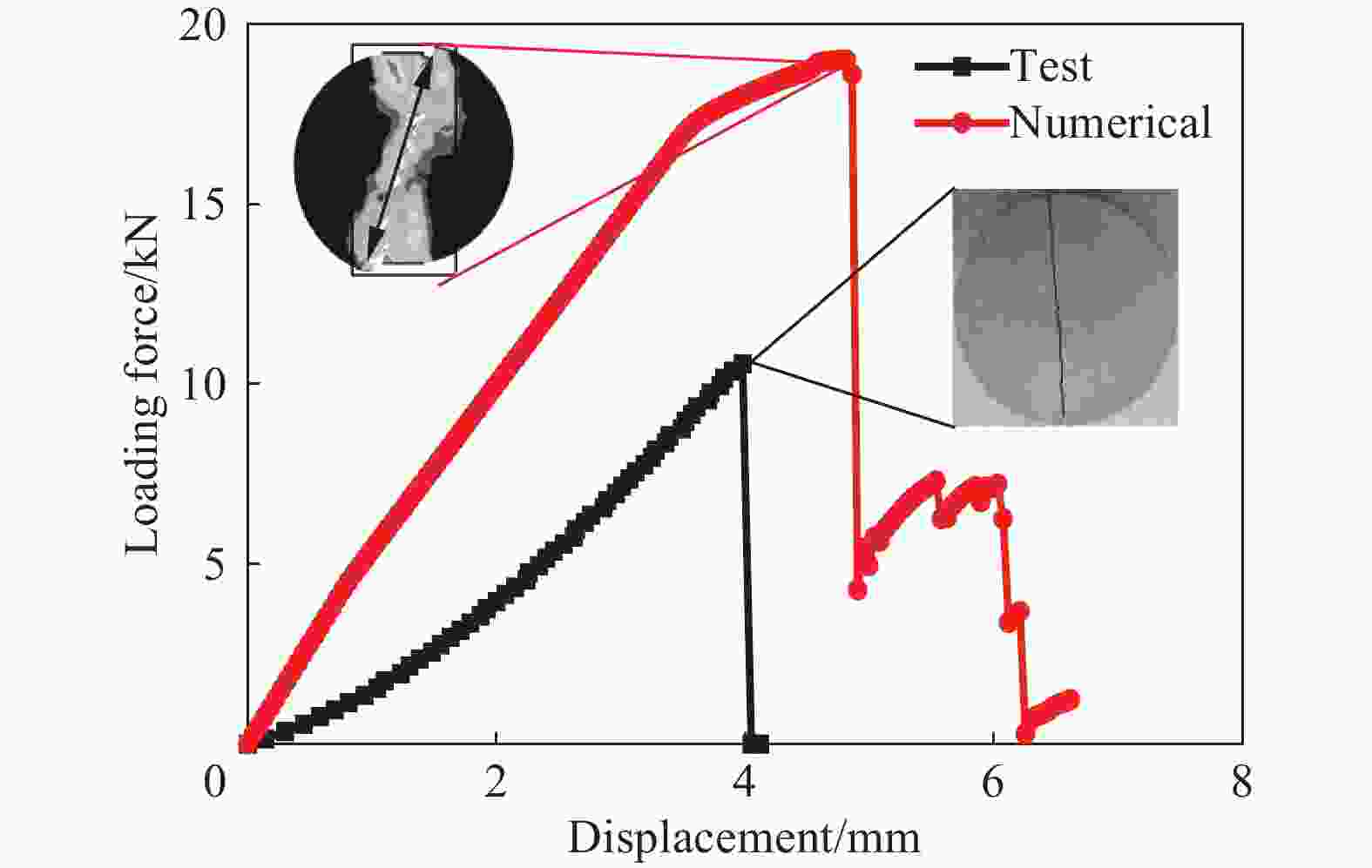
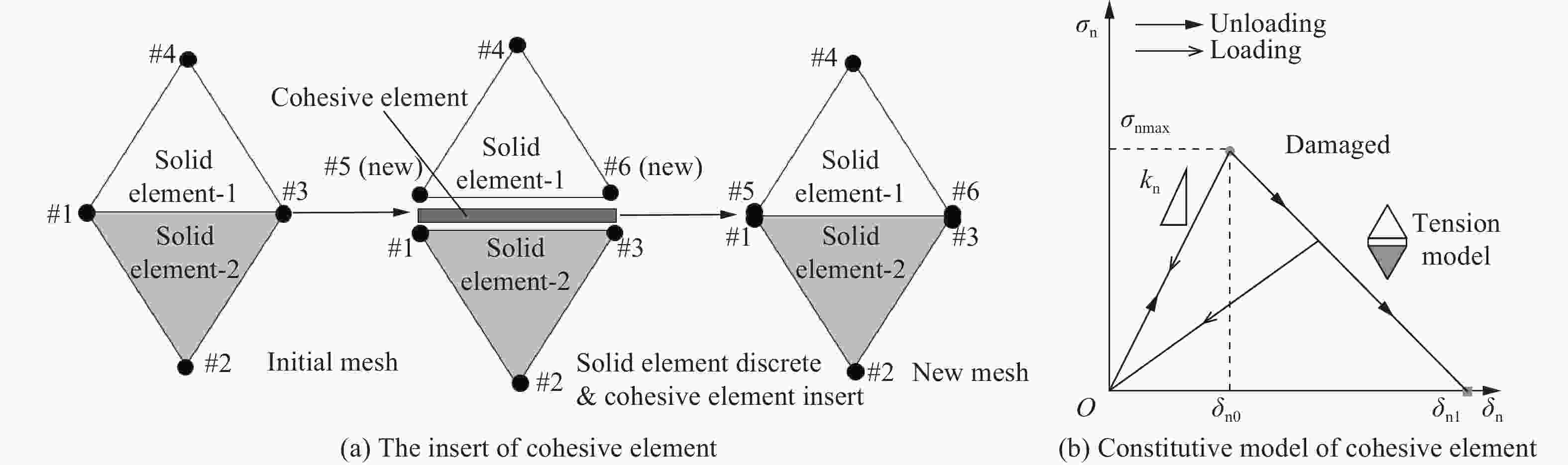
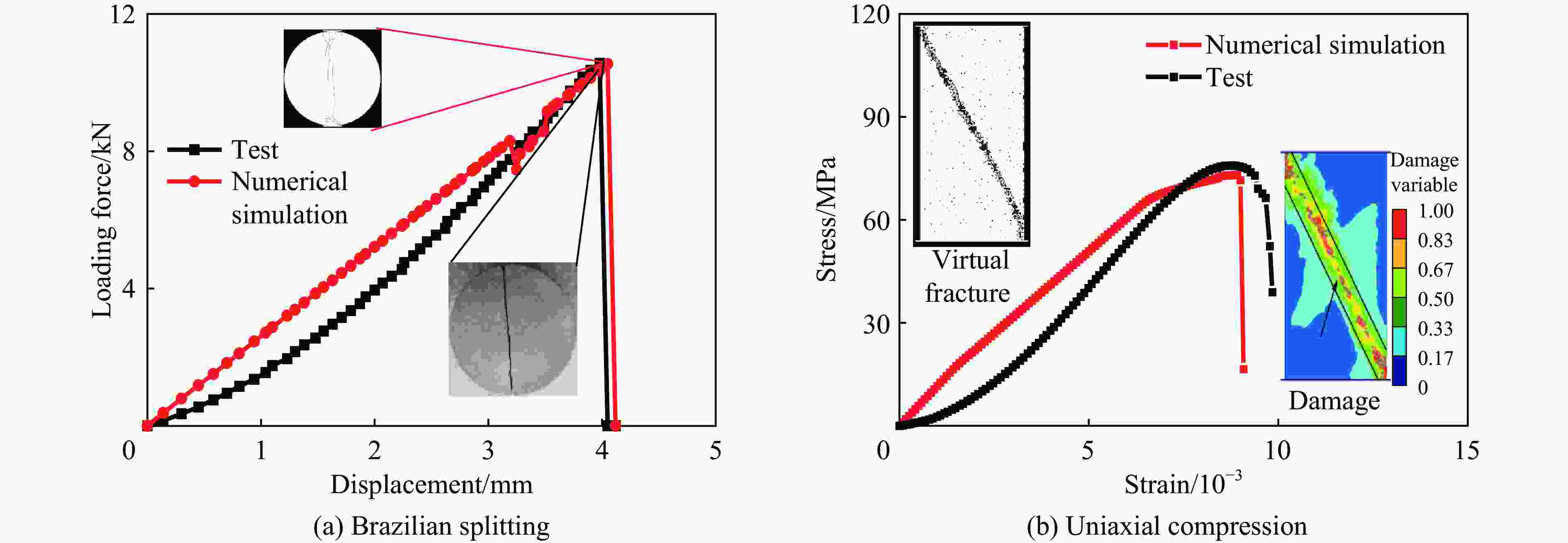
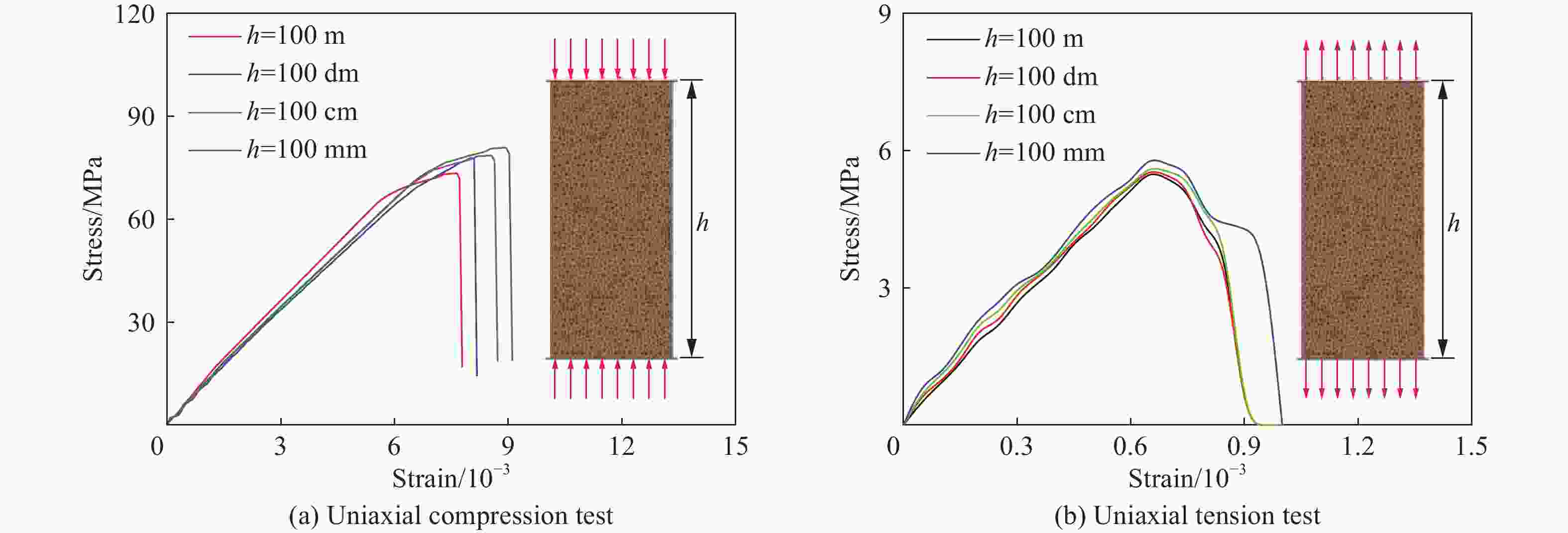
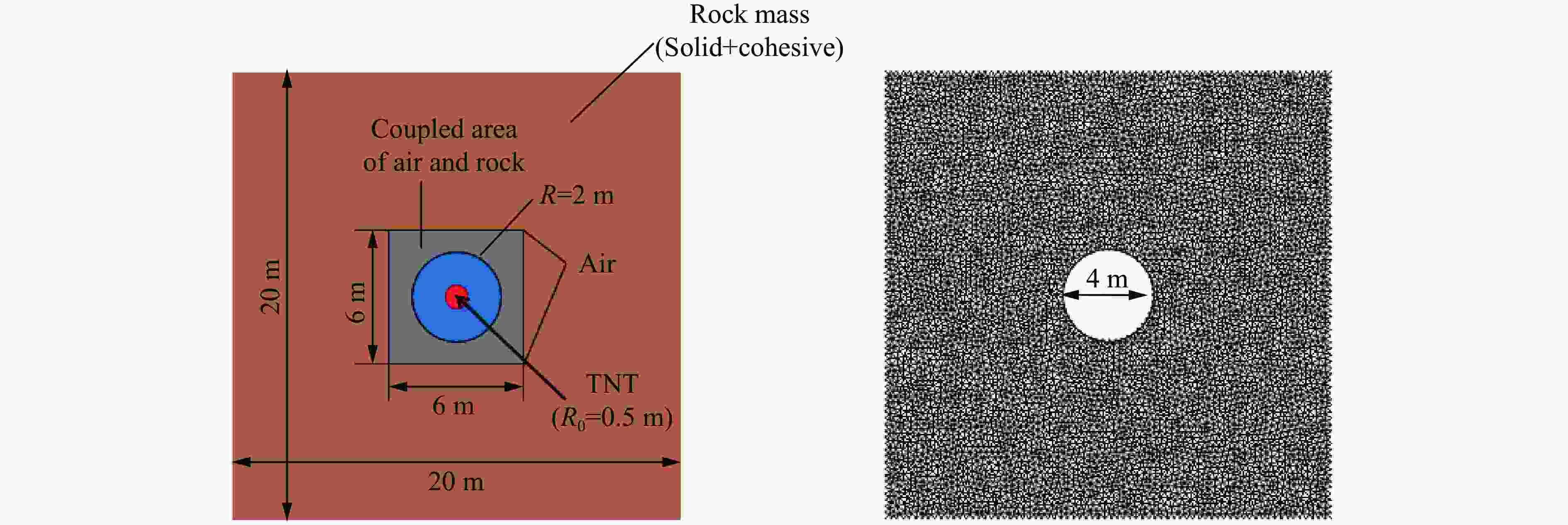
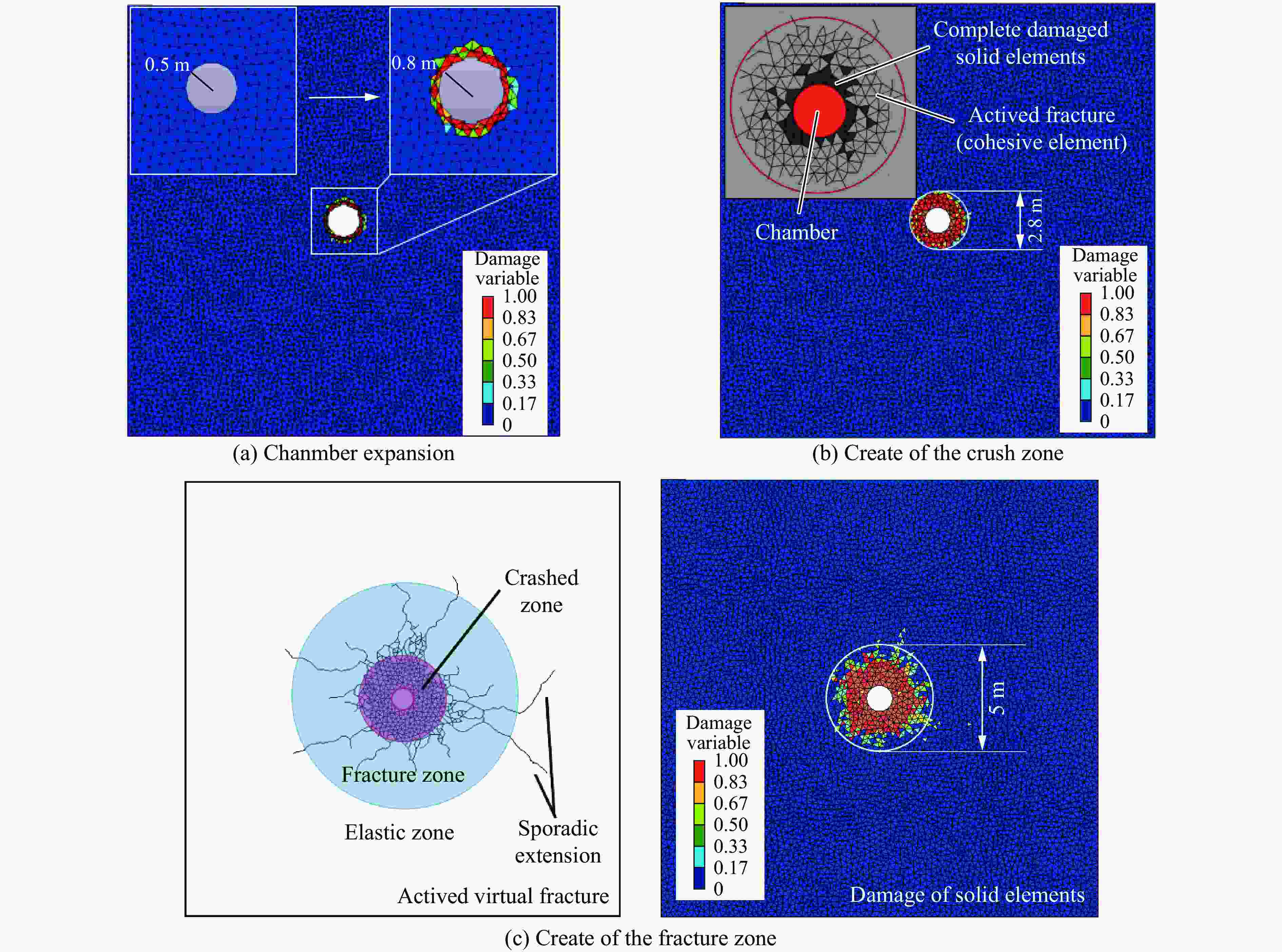
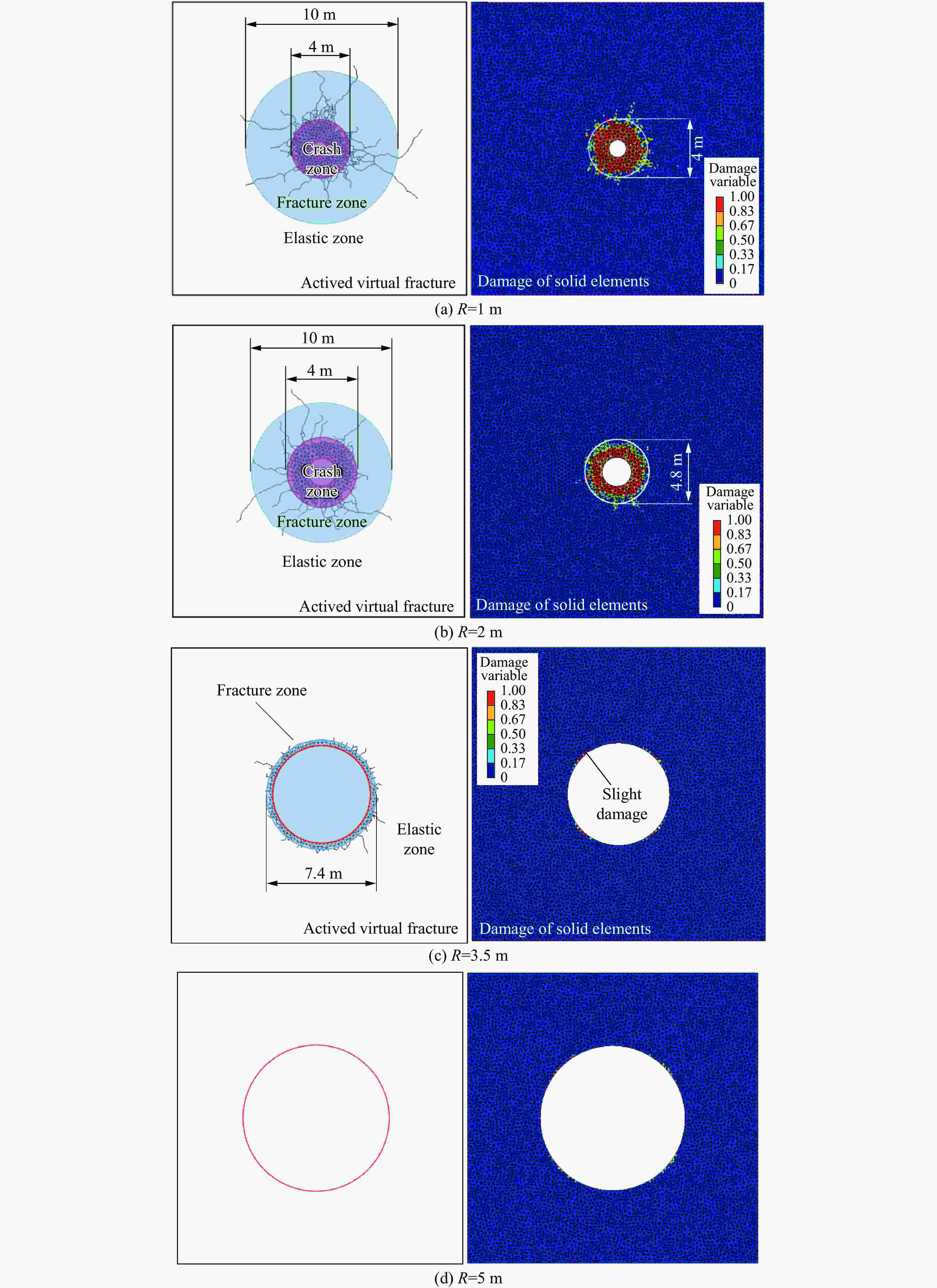
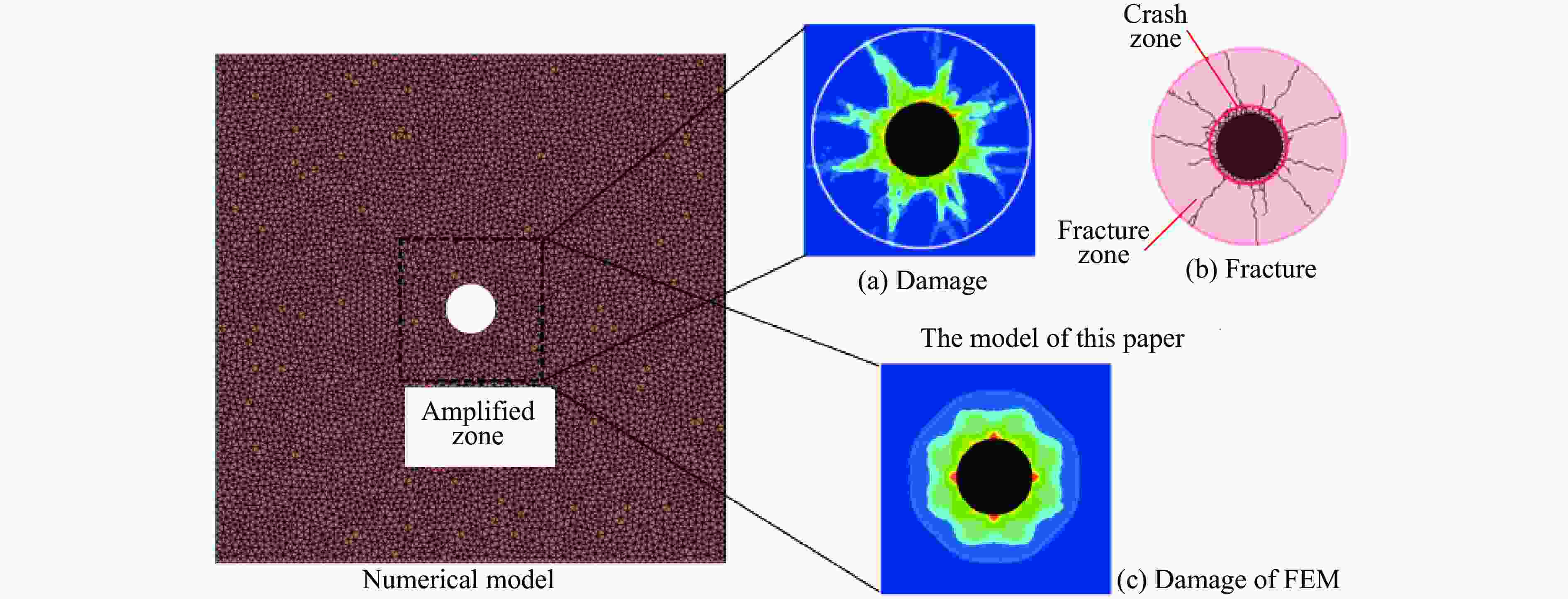
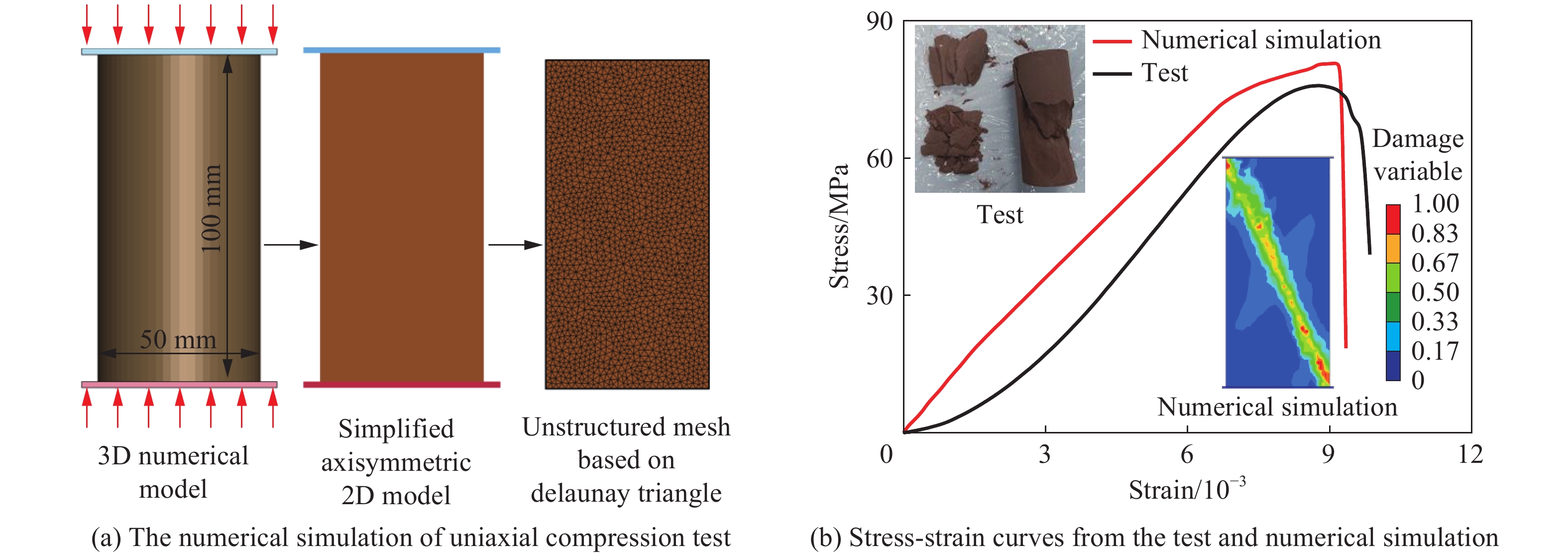
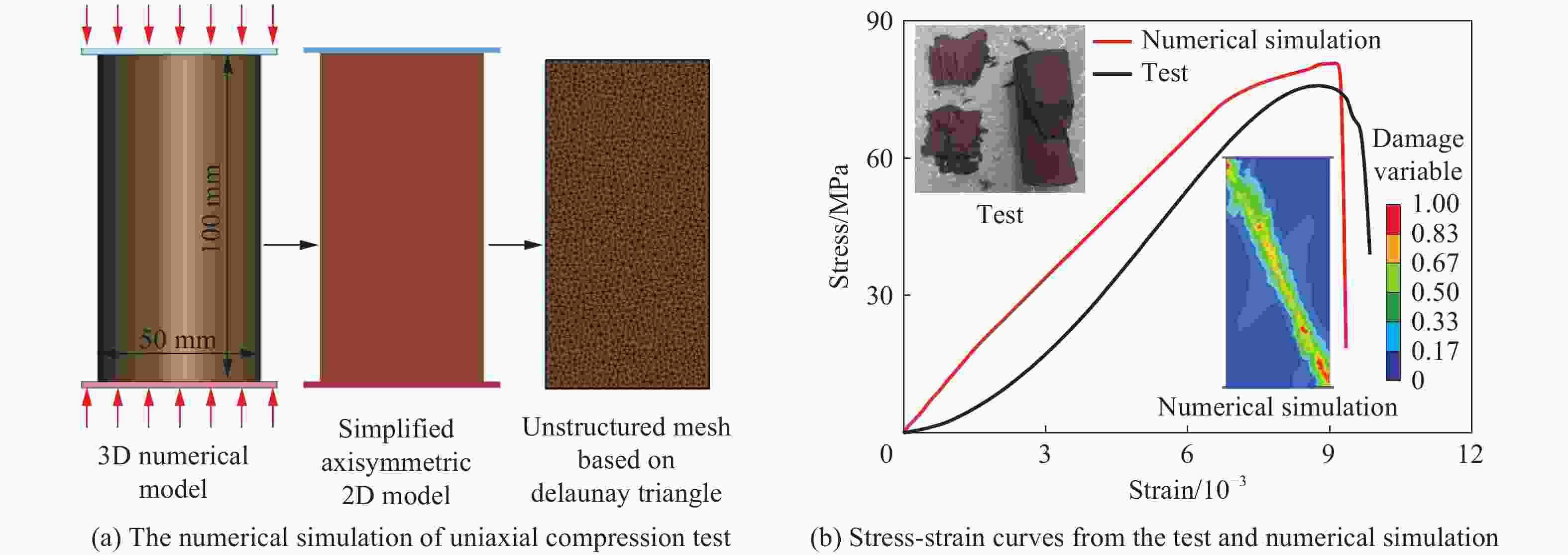
摘要: 地下硐室作为爆炸危险物的隐蔽贮藏空间，有潜在的内爆炸风险。为研究内爆炸作用下硐室围岩的动态响应机制，提出了一种基于岩石HJC (Holmquist-Johnson-Cook)模型和节理内聚力单元的损伤-虚拟裂纹模型。分析了模拟方法的可靠性，并在此基础上，通过多物质ALE算法对球形硐室内爆炸过程进行数值模拟，分析了围岩损伤范围和分区破坏规律。研究表明：插入内聚力单元弥补了HJC模型无法模拟低静水压力下张拉破坏的不足，且尺寸效应易于处理。模拟方法同时考虑了岩体内张拉裂纹的扩展和岩石材料的塑性损伤，能够真实地反映岩石破坏的全过程。以红砂岩为例，根据数值模拟结果，填实（耦合装药）爆炸时围岩分区破坏规律明显，破碎区比例半径为0.26 m/kg1/3、裂隙区比例半径为0.47 m/kg1/3。随着硐室尺寸的增大，空气的间隔作用可以减小爆炸荷载对围岩的损伤作用，比例半径达到0.52 m/kg1/3时，可以实现爆炸荷载的完全解耦。Abstract: As a hidden storage space for explosive hazards, the underground cavern has a potential risk of an internal explosion. To study the mechanism of the dynamic response of the surrounding rock under an internal explosion load, a new coupled damage and virtual crack model based on the HJC (Holmquist-Johnson-Cook) constitutive model of rock and the tensile failure cohesion element of the joint is proposed. And the quasi-static uniaxial compression, Brazilian splitting experiments, and dynamic SHPB experiments were calibrated. Therefore, this model is available for the simulation of middle-high strain rate problems, such as an underground explosion. Based on the new method, a series of underground explosions in spherical caverns is simulated by the multi-material ALE algorithm. The damage range and zoning failure law of the surrounding rock are analyzed. The research shows that the insertion of cohesive elements compensates for the deficiency of the HJC materials which cannot simulate tensile failure at low hydrostatic pressure. And the size effect of the model proposed in the paper is easy to deal with. The new method in this paper considers both the propagation of tensile crack by cohesive elements and the plastic damage by the HJC model, which can reflect the failure process of rock more accurately and completely. According to the numerical simulation results, the failure law of red sandstone during filling (coupling charge) explosion shows zonal characteristics with crashed zone and fracture zone from inside to outside. The proportional radius of the crashed zone is about 0.26 m/kg1/3, and that of the fracture zone is 0.47 m/kg1/3. The existence of the air chamber changes the loading form and reduces the load intensity acting on the cavern. Therefore, with the increase of the chamber size, the interval effect of air can reduce the damage of the surrounding rock during the explosion. Taking the red sandstone as an example, when the proportional radius reaches 0.52 m/kg1/3, there was no damage and no fracture generated by the explosion load. The conclusions above can be used as guidance for the anti-explosion design and protection of underground works.
-
图 4 采用有限元方法进行的巴西劈裂数值模拟
Figure 4. Numerical test of Brazilian splitting test based on FEM
图 6 巴西劈裂及单轴压缩数值模拟
Figure 6. Numerical simulation of the Brazilian splitting and uniaxial compression based on the proposed method
图 7 不同尺度的单轴压缩和单轴拉伸应力-应变曲线
Figure 7. Stress-strain curves of uniaxial compression and uniaxial tension at different scales
图 10 空腔爆炸模型最终的破坏形态
Figure 10. Final failure characteristics of the cavity explosion models
图 11 本文模拟方法与有限元方法的对比
Figure 11. Comparison between the method in this paper and the FEM
表 1 红砂岩的基本力学参数
Table 1. Basic mechanical parameters of red sandstone
单轴抗压强度
fc/MPa弹性模量
E/GPa单轴抗拉强度
T/MPa天然密度
ρ/(kg·m−3）泊松比
υ黏聚力
c/MPa内摩擦角
ϕ/(°)75.86 11.05 5.4 2956 0.27 2.6 35 
下载: 导出CSV
表 2 红砂岩HJC模型参数
Table 2. Parameters of the HJC model of red sandstone
极限面参数 基础力学参数 应变率参数 A B N Smax ρ/(kg∙m−3) fc/MPa G/GPa T/MPa C 0.034 1.801 0.795 4 2956 75.86 4.72 2.70 0.0023
下载: 导出CSV
损伤参数 压力参数 εf D1 D2 pc/MPa μc pl/GPa μl K1/GPa K2/GPa K3/GPa 0.012 0.059 1.0 25.29 0.00453 1.42 0.102 43.18 −90.61 171.50
下载: 导出CSV
表 3 TNT炸药爆轰产物JWL参数
Table 3. JWL EOS parameters of the TNT detonation product
A/GPa B/GPa ω R1 R2 E0/(GJ·m−3) 371.2 3.231 0.3 4.15 0.95 6.6
下载: 导出CSV
-
[1] 周小平, 钱七虎, 张伯虎, 等. 深埋球形洞室围岩分区破裂化机理 [J]. 工程力学, 2010, 27(1): 69–75, 90.ZHOU X P, QIAN Q H, ZHANG B H, et al. The mechanism of the zonal disintegration phenomenon around deep spherical tunnels [J]. Engineering Mechanics, 2010, 27(1): 69–75, 90. [2] LATTER A L, LELEVIER R E, MARTINELLI E A, et al. A method of concealing underground nuclear explosions [J]. Journal of Geophysical Research, 1961, 66(3): 943–946. DOI: 10.1029/JZ066i003p00943. [3] 朱号锋, 靳平, 肖卫国. 地下爆炸地震耦合效应的静态分析 [J]. 地震学报, 2010, 32(2): 234–241.ZHU H F, JIN P, XIAO W G. Static analysis on seismic coupling of underground explosions [J]. Acta Seismologica Sinica, 2010, 32(2): 234–241. [4] 李孝兰. 空腔解耦爆炸实验研究的基础理论(Ⅰ) [J]. 爆炸与冲击, 2000, 20(2): 186–192.LI X L. Basic theory of decoupled explosions in cavities (Ⅰ) [J]. Explosion and Shock Waves, 2000, 20(2): 186–192. [5] 李孝兰. 空腔解耦爆炸实验研究的基础理论(Ⅱ) [J]. 爆炸与冲击, 2000, 20(3): 283–288.LI X L. Basic theory of decoupled explosions in cavities (Ⅱ) [J]. Explosion and Shock Waves, 2000, 20(3): 283–288. [6] 楼沩涛, 张海波, 肖卫国. 岩体中非填实爆炸空腔壁振动状态分析 [J]. 爆炸与冲击, 2001, 21(3): 237–240.LOU W T, ZHANG H B, XIAO W G. Study on vibration behaviors of rock-wall in decoupling explosion [J]. Explosion and Shock Waves, 2001, 21(3): 237–240. [7] 王占江. 岩土中填实与空腔解耦爆炸的化爆模拟实验研究 [D]. 长沙: 国防科学技术大学, 2003.WANG Z J. Experimental investigation on tamped and cavity decoupled explosion in rock-soil by mili-explosive charge [D]. Changsha: National University of Defense Technology, 2003. [8] WANG G Y, CAO A S, WANG X Y, et al. Numerical simulation of the dynamic responses and damage of underground cavern under multiple explosion sources [J]. Engineering Failure Analysis, 2021, 120: 105085. DOI: 10.1016/j.engfailanal.2020.105085. [9] 熊益波, 钟方平, 王万鹏, 等. 硬岩中的可重复使用抗爆洞室结构设计技术 [J]. 岩土工程学报, 2019, 41(9): 1759–1766. DOI: 10.11779/CJGE201909022.XIONG Y B, ZHONG F P, WANG W P, et al. Structural design technology of reusable blast-resistant caverns in hard rock mass [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1759–1766. DOI: 10.11779/CJGE201909022. [10] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures [C] // Proceedings of the 14th International Symposium on Ballistics. Quebec, Canada: American Defense Preparedness Association, 1993: 591−600. [11] TAYLOR L M, CHEN E P, KUSZMAUL J S. Microcrack-induced damage accumulation in brittle rock under dynamic loading [J]. Computer Methods in Applied Mechanics and Engineering, 1986, 55(3): 301–320. DOI: 10.1016/0045-7825(86)90057-5. [12] RIEDEL W, THOMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500 - numerical analysis using a new macroscopic concrete model for hydrocodes [C] // Proceeding of the 9th International Symposium on Interaction of the Effects of Munitions with Structures. Berlin, German: ISIEMS, 1999: 315−322. [13] 刘文韬, 刘永, 桂荣, 等. 裂纹长度对裂隙岩体力学特性及破坏模式的影响 [J]. 南华大学学报(自然科学版), 2017, 31(4): 53–58, 63. DOI: 10.19431/j.cnki.1673-0062.2017.04.011.LIU W T, LIU Y, GUI R, et al. Influence of crack length on mechanics characteristic and damage mode of fractured rock-mass [J]. Journal of University of South China (Science and Technology), 2017, 31(4): 53–58, 63. DOI: 10.19431/j.cnki.1673-0062.2017.04.011. [14] YE Y, ZENG Y W, CHENG S F, et al. Numerical investigation of rock sphere breakage upon oblique impact: effect of the contact friction coefficient and impact angle [J]. Computers and Geotechnics, 2021, 136: 104207. DOI: 10.1016/j.compgeo.2021.104207. [15] 张嘉凡, 高壮, 程树范, 等. 煤岩HJC模型参数确定及液态CO2爆破特性研究 [J]. 岩石力学与工程学报, 2021, 40(S1): 2633–2642. DOI: 10.13722/j.cnki.jrme.2020.0267.ZHANG J F, GAO Z, CHENG S F, et al. Parameters determination of coal-rock HJC model and research on blasting characteristics by liquid CO2 [J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S1): 2633–2642. DOI: 10.13722/j.cnki.jrme.2020.0267. [16] WU Z J, ZHANG P L, FAN L F, et al. Debris characteristics and scattering pattern analysis of reinforced concrete slabs subjected to internal blast loads–a numerical study [J]. International Journal of Impact Engineering, 2019, 131: 1–16. DOI: 10.1016/j.ijimpeng.2019.04.024. [17] KUCEWICZ M, BARANOWSKI P, MAŁACHOWSKI J. Dolomite fracture modeling using the Johnson-Holmquist concrete material model: parameter determination and validation [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(2): 335–350. DOI: 10.1016/j.jrmge.2020.09.007. [18] 方秦, 孔祥振, 吴昊, 等. 岩石Holmquist-Johnson-Cook模型参数的确定方法 [J]. 工程力学, 2014, 31(3): 197–204. DOI: 10.6052/j.issn.1000-4750.2012.10.0780.FANG Q, KONG X Z, WU H, et al. Determination of Holmquist-Johnson-Cook consitiutive model parameters of rock [J]. Engineering Mechanics, 2014, 31(3): 197–204. DOI: 10.6052/j.issn.1000-4750.2012.10.0780. [19] 闻磊, 李夕兵, 吴秋红, 等. 花岗斑岩Holmquist-Johnson-Cook本构模型参数研究 [J]. 计算力学学报, 2016, 33(5): 725–731. DOI: 10.7511/jslx201605011.WEN L, LI X B, WU Q H, et al. Study on parameters of Holmquist-Johnson-Cook model for granite porphyry [J]. Chinese Journal of Computational Mechanics, 2016, 33(5): 725–731. DOI: 10.7511/jslx201605011. [20] 孙其然, 李芮宇, 赵亚运, 等. HJC模型模拟钢筋混凝土侵彻实验的参数研究 [J]. 工程力学, 2016, 33(8): 248–256. DOI: 10.6052/j.issn.1000-4750.2014.12.1094.SUN Q R, LI R Y, ZHAO Y Y, et al. Investigation on parameters of HJC model applied to simulate perforation experiments of reinforced concrete [J]. Engineering Mechanics, 2016, 33(8): 248–256. DOI: 10.6052/j.issn.1000-4750.2014.12.1094. [21] WU Z J, ZHANG P L, FAN L F, et al. Numerical study of the effect of confining pressure on the rock breakage efficiency and fragment size distribution of a TBM cutter using a coupled FEM-DEM method [J]. Tunnelling and Underground Space Technology, 2019, 88: 260–275. DOI: 10.1016/j.tust.2019.03.012. [22] 宋力, 胡时胜. SHPB数据处理中的二波法与三波法 [J]. 爆炸与冲击, 2005, 25(4): 368–373. DOI: 10.11883/1001-1455(2005)04-0368-06.SONG L, HU S S. Two-wave and three-wave method in SHPB data processing [J]. Explosion and Shock Waves, 2005, 25(4): 368–373. DOI: 10.11883/1001-1455(2005)04-0368-06. [23] KAZERANI T. Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 64: 44–55. DOI: 10.1016/j.ijrmms.2013.08.016. [24] KONG X X, LIU Q S, ZHANG Q B, et al. A method to estimate the pressure arch formation above underground excavation in rock mass [J]. Tunnelling and Underground Space Technology, 2018, 71: 382–390. DOI: 10.1016/j.tust.2017.09.004. [25] LIU Q S, DENG P H. A numerical investigation of element size and loading/unloading rate for intact rock in laboratory-scale and field-scale based on the combined finite-discrete element method [J]. Engineering Fracture Mechanics, 2019, 211: 442–462. DOI: 10.1016/j.engfracmech.2019.02.007. [26] WU Z J, MA L L, FAN L F. Investigation of the characteristics of rock fracture process zone using coupled FEM/DEM method [J]. Engineering Fracture Mechanics, 2018, 200: 355–374. DOI: 10.1016/j.engfracmech.2018.08.015. [27] LS-DYNA keyword user’s manual, version 971-R11.1 [Z]. Livermore, California: Livermore Software Technology Corporation, 2020. [28] WESCOTT B L, STEWART D S, DAVIS W C. Equation of state and reaction rate for condensed-phase explosives [J]. Journal of Applied Physics, 2005, 98(5): 053514. DOI: 10.1063/1.2035310. [29] 吴志军, 张鹏林, 刘泉声, 等. 基于零厚度粘聚力单元的钢筋混凝土板在爆炸荷载下的动态破坏过程分析 [J]. 工程力学, 2018, 35(8): 79–90, 110. DOI: 10.6052/j.issn.1000-4750.2017.04.0270.WU Z J, ZHANG P L, LIU Q S, et al. Dynamic failure analysis of reinforced concrete slab based on cohesive element under explosive load [J]. Engineering Mechanics, 2018, 35(8): 79–90, 110. DOI: 10.6052/j.issn.1000-4750.2017.04.0270. [30] 亨利奇 J. 爆炸动力学及其应用 [M]. 熊建国, 译. 北京: 科学出版社, 1987. [31] 吴亮, 卢文波, 钟冬望, 等. 混凝土介质中空气间隔装药的爆破机理 [J]. 爆炸与冲击, 2010, 30(1): 58–64. DOI: 10.11883/1001-1455(2010)01-0058-07.WU L, LU W B, ZHONG D W, et al. Blasting mechanism of air-decked charge in concrete medium [J]. Explosion and Shock Waves, 2010, 30(1): 58–64. DOI: 10.11883/1001-1455(2010)01-0058-07. -
图(11) / 表(4)
计量
- 文章访问数: 347
- HTML全文浏览量: 192
- PDF下载量: 83
- 被引次数: 0