混凝土冲击破坏动态力学及能量特性分析

党发宁; 李玉涛; 任劼; 周玫

doi:10.11883/bzycj-2021-0444

混凝土冲击破坏动态力学及能量特性分析

doi: 10.11883/bzycj-2021-0444

西安理工大学岩土工程研究所，陕西西安 710048

基金项目: 国家自然科学基金（51979225，51679199）

详细信息

作者简介:
党发宁（1962－　），男，博士，教授，dangfn@mail.xaut.edu.cn

通讯作者:
李玉涛（1992－　），男，博士研究生，1200710003@stu.xaut.edu.cn

中图分类号: O383; TU502
计量
- 文章访问数: 296
- HTML全文浏览量: 106
- PDF下载量: 95
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-28
- 修回日期: 2022-01-25
- 网络出版日期: 2022-08-10
- 刊出日期: 2022-09-09

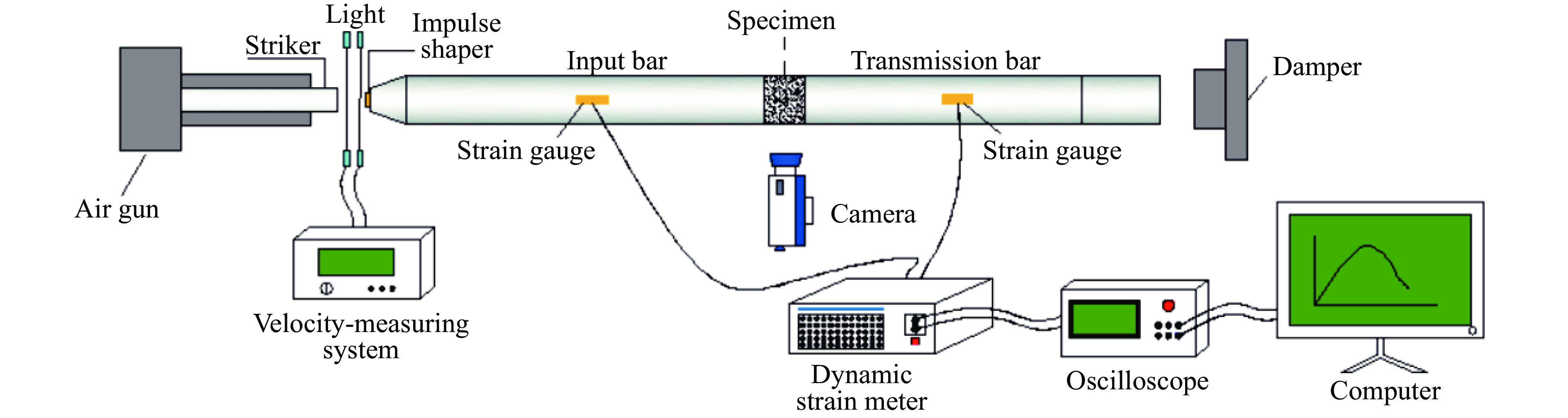
Analysis of dynamic mechanics and energy characteristics of concrete impact failure

Institute of Geotechnical Engineering, Xi’an University of Technology, Xi’an 710048, Shaanxi, China

摘要

摘要: 动强度和能量耗散规律是研究混凝土动力特性的主要内容。为探究混凝土在冲击荷载作用下的动态力学、变形以及能量演化特征，利用直径为100 mm的霍普金森杆装置对骨料率为0、32%、37%和42%的混凝土试样，分别进行了冲击速度为5、6、7 m/s的冲击压缩试验。探讨了冲击速度和骨料率对试样变形、动强度以及分形维数的影响，建立了动强度关于冲击速度和骨料率的表达式，并对试样吸收能和裂纹表面能之间的关系进行了对比分析。结果表明：混凝土试样破坏时出现了变形滞后现象，破坏形式主要以劈裂拉伸破坏为主；动强度随冲击速度、骨料率的增大而增大，用所建动强度公式可以较好地预估混凝土动强度；混凝土破坏碎块分形维数、吸收能和裂纹表面能均随冲击速度的增大而增大，随骨料率的增大而减小，且吸收能始终高于裂纹表面能，当骨料率为37%时，吸收能转化率最高，约91%转化为裂纹表面能。
- 混凝土 /
- 动强度 /
- 骨料率 /
- 冲击速度 /
- 裂纹表面能
Abstract: To investigate the mechanics, deformation, and energy evolution characteristics of concrete under dynamic loading, impact compression tests at impact velocities of 5, 6, and 7 m/s, and splitting tensile tests at 4 m/s were carried out on concrete specimens with aggregate volume rates of 0, 32%, 37%, and 42% using a 100 mm diameter split Hopkinson pressure bar (SHPB) device. The failure process of concrete specimens was acquired by a high-speed camera, and the damaged concrete fragments were collected and sorted. Furthermore, the fractal dimension of fragments was calculated by dividing the fragments into different grades. The stress and strain of the concrete specimen were obtained through the corresponding calculation formulas. The relationships between specimen deformation, dynamic strength, and fractal dimension with impact velocity and aggregate rate were studied, and the expression for dynamic strength with respect to impact velocity and aggregate rate was developed. In addition, the fractal dimension was used to characterize the surface roughness of the concrete fragments, and the function expression between crack surface energy and fractal dimension was established. The relationship between sample absorption energy and crack surface energy was analyzed and compared. The results show that deformation hysteresis occurs when concrete specimens are destroyed and the failure is mainly in the form of splitting tensile damage. The dynamic strength increases with the increase of impact velocity and aggregate ratio, the dynamic strength of concrete can be better predicted by using the proposed dynamic strength formula. The fractal dimension of concrete breaking fragments, absorbed energy and crack surface energy all increase with the increase of impact velocity and decrease with the increase of aggregate rate, and the absorbed energy is always higher than the crack surface energy. The highest conversion rate of absorbed energy is achieved when the aggregate rate is 37%, with approximately 91% converts to crack surface energy.
- concrete /
- dynamic strength /
- aggregate rate /
- impact velocity /
- crack surface energy

HTML全文

图 1 SHPB试验装置

Figure 1. SHPB test device

下载: 全尺寸图片幻灯片

图 2 SHPB试验原始波形图

Figure 2. Primitive waveform in SHPB test

下载: 全尺寸图片幻灯片

图 3 冲击速度不变时不同骨料率混凝土试样开裂状态

Figure 3. Cracking states of concrete specimens with different aggregate ratios at a certain impact velocity

下载: 全尺寸图片幻灯片

图 4 骨料率不变时不同冲击速度下混凝土试样开裂状态

Figure 4. Cracking states of concrete specimens with a fixed aggregate ratio at different impact velocities

下载: 全尺寸图片幻灯片

图 5 冲击速度为6 m/s时混凝土应力-应变时程曲线

Figure 5. Stress and strain history curves for concrete at an impact velocity of 6 m/s

下载: 全尺寸图片幻灯片

图 6 骨料率为32%时混凝土应力、应变时程曲线

Figure 6. Stress- and strain- time curves for concrete at the aggregate ratio of 32%

下载: 全尺寸图片幻灯片

图 7 混凝土应力-应变曲线

Figure 7. Stress-strain curves of concrete

下载: 全尺寸图片幻灯片

图 8 混凝土动强度与冲击速度拟合关系

Figure 8. Fitting relationships between concrete dynamic strength and impact velocity

下载: 全尺寸图片幻灯片

图 9 骨料率与材料参数的拟合关系

Figure 9. Fitting relationships between aggregate rates and material parameters

下载: 全尺寸图片幻灯片

图 10 混凝土动强度与冲击速度关系

Figure 10. Relationship between concrete dynamic strength and impact velocity

下载: 全尺寸图片幻灯片

图 11 分形维数双对数曲线

Figure 11. Double logarithmic curves of fractal dimension

下载: 全尺寸图片幻灯片

图 12 冲击速度、骨料率与分形维数关系

Figure 12. Relationships between impact velocity, aggregate ratio and fractal dimension

下载: 全尺寸图片幻灯片

图 13 不同冲击速度以及分形维数下的混凝土破坏形态

Figure 13. Concrete failure morphology at different impact speeds and fractal dimensions

下载: 全尺寸图片幻灯片

图 14 试样吸收能、裂纹表面能与骨料率关系

Figure 14. Relationships of absorbed energy and crack surface energy of the specimens with aggregate ratio

下载: 全尺寸图片幻灯片

图 15 试样吸收能、裂纹表面能与冲击速度关系

Figure 15. Relationships of absorbed energy and crack surface energy of the specimens with impact velocity

下载: 全尺寸图片幻灯片

图 16 冲击速度与α关系

Figure 16. Relationship between impact velocity and α

下载: 全尺寸图片幻灯片

表 1 混凝土配合比

Table 1. Concrete mix proportions

骨料率/ %	水泥/ （kg·m⁻³）	水/ （kg·m⁻³）	砂/ （kg·m⁻³）	碎石/ （kg·m⁻³）	减水剂/ （kg·m⁻³）
0	321	135	1944	0	3.2
32	321	135	1073	870	3.2
37	321	135	937	1006	3.2
42	321	135	801	1142	3.2

下载: 导出CSV

表 2 动强度与冲击速度拟合关系

Table 2. Fitting relationship between dynamic strength and impact velocity

骨料/%	拟合关系	R²
0	$\sigma =84.36\;\text{ln}(v-3.38）$	0.967
32	$\sigma =73.57\;\text{ln}(v-2.77）$	0.960
37	$\sigma =71.19\;\text{ln}(v-2.31）$	0.989
42	$\sigma =68.34\;\text{ln}(v-1.66）$	0.980

下载: 导出CSV

表 3 单位表面能计算结果

Table 3. Calculation results of specific surface energy

试样编号	冲击速度/ （m·s⁻¹）	碎块新增面积/cm²	吸收能量/J	单位表面能/ （J·cm⁻²）
T-0-1	4	3019.11	41.78	0.014
T-0-2	4	2805.35	48.07	0.017
T-32%-1	4	1647.82	38.05	0.023
T-32%-2	4	1706.49	47.33	0.028
T-37%-1	4	1101.38	36.09	0.033
T-37%-2	4	1350.77	42.80	0.032
T-42%-1	4	872.50	36.17	0.041
T-42%-2	4	792.77	33.17	0.043

下载: 导出CSV

参考文献(30)

[1]	FALLON C, MCSHANE G J. Impact mitigating capabilities of a spray-on elastomer coating applied to concrete [J]. International Journal of Impact Engineering, 2019, 128: 72–85. DOI: 10.1016/j.ijimpeng.2019.02.003.
[2]	KOLCHUNOV V I, ANDROSO N B. Influence of the structure of the cross-section of load-bearing structures on their deformation during emergency actions [J]. IOP Conference Series: Materials Science and Engineering, 2018, 463(3). DOI: 10.1088/1757-899X/463/3/032067.
[3]	高光发, 郭扬波. 高强混凝土动态压缩试验分析 [J]. 爆炸与冲击, 2019, 39(3): 63–72. DOI: 10.11883/bzycj-2017-0405. GAO G F, GUO Y B. Analysis of the dynamic compressive test of high strength concrete [J]. Explosion and Shock Waves, 2019, 39(3): 63–72. DOI: 10.11883/bzycj-2017-0405.
[4]	刘传雄, 李玉龙, 吴子燕, 等. 混凝土材料的动态压缩破坏机理及本构关系 [J]. 振动与冲击, 2011, 30(5): 1–5. DOI: 10.13465/j.cnki.jvs.2011.05.015. LIU C X, LI Y L, WU Z Y, et al. Failure mechanism and constitutive model of a concrete material under dynamic compressive loads [J]. Journal of Vibration and Shock, 2011, 30(5): 1–5. DOI: 10.13465/j.cnki.jvs.2011.05.015.
[5]	李庆斌, 郑丹. 混凝土动力强度提高的机理探讨 [J]. 工程力学, 2005, 22(S1): 188–193. LI Q B, ZHENG D. Micro-mechanism on the enhancement of dynamic strength for concrete [J]. Engineering Mechanics, 2005, 22(S1): 188–193.
[6]	EIBL J, CURBACH M. An attempt to explain strength increase due to high loading rates [J]. Nuclear Engineering & Design, 1989, 112: 45–50.
[7]	WEERHEIJM J, REINHARDT H W. Device for testing concrete under impact tensile loading and lateral compression [J]. Nuclear Engineering & Design, 1991, 126(3): 395–401. DOI: 10.1016/0029-5493(91)90028-G.
[8]	ROSSI P. Coupling between the crack propagation velocity and the vapour diffusion in concrete [J]. Materials and Structures, 1989, 22(2): 91–97. DOI: 10.1007/BF02472279.
[9]	ROSSI P. Influence of cracking in the presence of free water on the mechanical behaviour of concrete [J]. Magazine of Concrete Research, 2015, 43(154): 53–57. DOI: 10.1680/macr.1991.43.154.53.
[10]	GURUSIDESWAR S, SHUKLA A, JONNALAGADDA K N, et al. Tensile strength and failure of ultra-high performance concrete (UHPC) composition over a wide range of strain rates [J]. Construction and Building Materials, 2020, 258: 119642. DOI: 10.1016/j.conbuildmat.2020.119642.
[11]	马怀发, 王立涛, 陈厚群, 等. 混凝土动态损伤的滞后特性 [J]. 水利学报, 2010, 41(6): 659–664. DOI: 10.13243/j.cnki.slxb.2010.06.013. MA H F, WANG L T, CHEN H Q, et al. Mechanism of dynamic damage delay characteristic of concrete [J]. Journal of Hydraulic Engineering, 2010, 41(6): 659–664. DOI: 10.13243/j.cnki.slxb.2010.06.013.
[12]	秦川, 武明鑫, 张楚汉. 混凝土冲击劈拉实验与细观离散元数值仿真 [J]. 水利发电学报, 2013, 32(1): 196–205. QIN C, WU M X, ZHANG C H. Impact splitting tensile experiments of concrete and numerical modeling by meso-scale discrete elements [J]. Journal of Hydroelectric Engineering, 2013, 32(1): 196–205.
[13]	党发宁, 焦凯, 潘峰. 混凝土抗折动强度及其极值研究 [J]. 爆炸与冲击, 2016, 36(3): 422–428. DOI: 10.11883/1001-1455(2016)03-0422-07. DANG F N, JIAO K, PAN F. Investigation on concrete dynamic bending intensity and limit flexural intensity [J]. Explosion and Shock Waves, 2016, 36(3): 422–428. DOI: 10.11883/1001-1455(2016)03-0422-07.
[14]	谢和平, 彭瑞东, 鞠杨, 等. 岩石破坏的能量分析初探 [J]. 岩石力学与工程学报, 2005, 24(15): 2604–2608. DOI: 10.3321/j.issn:1000-6915.2005.15.001. XIE H P, PENG R D, JU Y, et al. On energy analysis of rock failure [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2604–2608. DOI: 10.3321/j.issn:1000-6915.2005.15.001.
[15]	李庆华, 赵昕, 徐世烺. 纳米二氧化硅改性超高韧性水泥基复合材料冲击压缩试验研究 [J]. 工程力学, 2017, 34(2): 85–93. DOI: 10.6052/j.issn.1000-4750.2015.06.0477. LI Q H, ZHAO X, XU S L. Impact compression properties of nano-sio₂ modified ultrahigh toughness cementitious composites using a split Hopkinson pressure bar [J]. Engineering Mechanics, 2017, 34(2): 85–93. DOI: 10.6052/j.issn.1000-4750.2015.06.0477.
[16]	巫绪涛, 代仁强, 陈德兴, 等. 钢纤维混凝土动态劈裂试验的能量耗散分析 [J]. 应用力学学报, 2009, 26(1): 151–154+218. WU X T, DAI R Q, CHEN D X, et al. Energy dissipation analysis on dynamic splitting-tensile test of steel fiber reinforced concrete [J]. Chinese Journal of Applied Mechanics, 2009, 26(1): 151–154+218.
[17]	LI Y, ZHAI Y, LIU X Y, et al. Research on fractal characteristics and energy dissipation of concrete suffered freeze-thaw cycle action and impact loading [J]. Materials, 2019, 12(16): 2585. DOI: 10.3390/ma12162585.
[18]	TAN Y, CHENG Y, LIU J, et al. Experimental study of the dynamic mechanical properties of high-performance equal-sized–aggregate concrete [J]. Journal of Materials in Civil Engineering, 2021, 33(2): 04020463. DOI: 10.1061/(ASCE)MT.1943-5533.0003474.
[19]	ZHANG Z X, KOU S Q, JIANG L G, et al. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745–762. DOI: 10.1016/S1365-1609(0)00008-3.
[20]	翟越, 马国伟, 赵均海, 等. 花岗岩和混凝土在单轴冲击压缩荷载下的动态性能比较 [J]. 岩石力学与工程学报, 2007, 26(4): 762–768. DOI: 10.3321/j.issn:1000-6915.2007.04.015. ZHAI Y, MA G W, ZHAO J H, et al. Comparison of dynamic capabilities of granite and concrete under uniaxial impact compressive loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 762–768. DOI: 10.3321/j.issn:1000-6915.2007.04.015.
[21]	李淼, 乔兰, 李庆文. 高应变率下预制单节理岩石SHPB劈裂试验能量耗散分析 [J]. 岩土工程学报, 2017, 39(7): 1336–1343. DOI: 10.11779/CJGE201707021. LI M, QIAO L, LI Q W. Energy dissipation of rock specimens under high strain rate with single joint in SHPB tensile tests [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1336–1343. DOI: 10.11779/CJGE201707021.
[22]	吕太洪, 陈小伟, 陈刚. 基于混凝土试样SHPB实验的波形特征分析 [J]. 解放军理工大学学报(自然科学版), 2016, 17(4): 345–349. DOI: 10.12018/j.issn.1009-3443.20160519005. LV T H, CHEN X W, CHEN G. Waveform features of split Hopkinson pressure bar tests of concrete specimen [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2016, 17(4): 345–349. DOI: 10.12018/j.issn.1009-3443.20160519005.
[23]	马芹永, 高常辉. 冲击荷载下玄武岩纤维水泥土吸能及分形特征 [J]. 岩土力学, 2018, 39(11): 3921–3928;3968. DOI: 10.16285/j.rsm.2017.0666. MA Q Y, GAO C H. Energy absorption and fractal characteristics of basalt fiber-reinforced cement-soil under impact loads [J]. Rock and Soil Mechanics, 2018, 39(11): 3921–3928;3968. DOI: 10.16285/j.rsm.2017.0666.
[24]	胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.
[25]	马菊荣, 刘海峰, 杨维武. 沙漠砂混凝土动态力学性能实验研究 [J]. 实验力学, 2015, 30(4): 491–498. DOI: 10.7520/1001-4888-14-171. MA J R, LIU H F, YANG W W. Experimrntal study of dynamic mechanical properties of desert sand concrete [J]. Journal of Experimental Mechanics, 2015, 30(4): 491–498. DOI: 10.7520/1001-4888-14-171.
[26]	白二雷, 许金余, 高志刚. 冲击荷载作用下EPS混凝土动态性能研究 [J]. 振动与冲击, 2012, 31(13): 53–57. DOI: 10.3969/j.issn.1000-3835.2012.13.011. BAI E L, XU J Y, GAO Z G. Dynamic mechanical property of expanded polystyrene concrete under impact loading [J]. Journal of Vibration and Shock, 2012, 31(13): 53–57. DOI: 10.3969/j.issn.1000-3835.2012.13.011.
[27]	IBRAHIM S M, ALMUSALLAM T H. , AL-SALLOUM Y A, et al. Strain rate dependent behavior and modeling for compression response of hybrid fiber reinforced concrete[J]. Latin American Journal of Solids and Structures, 2019, 13(9). DOI: 10.1590/1679-78252717.
[28]	李占金, 郝家旺, 甘德清, 等. 动载作用下磁铁矿石破坏特性实验研究 [J]. 振动与冲击, 2019, 38(12): 231–238; 245. DOI: 10.13465/j.cnki.jvs.2019.12.033. LI Z J, HAO J W, GAN D Q, et al. An experimental study on the failure characteristics of magnetite ore based on dynamic load [J]. Journal of Vibration and Shock, 2019, 38(12): 231–238; 245. DOI: 10.13465/j.cnki.jvs.2019.12.033.
[29]	赵昕, 徐世烺, 李庆华. 高温后超高韧性水泥基复合材料冲击破碎分形特征分析 [J]. 土木工程学报, 2019, 52(2): 44–55. DOI: 10.15951/j.tmgcxb.2019.02.005. ZHAO X, XU S L, LI Q H. Fractal characteristics of fire-damaged ultrahigh toughness cementitious composite after impact loading [J]. China Civil Engineering Journal, 2019, 52(2): 44–55. DOI: 10.15951/j.tmgcxb.2019.02.005.
[30]	平琦, 马芹永, 袁璞. 岩石试样SHPB劈裂拉伸试验中能量耗散分析 [J]. 采矿与安全工程学报, 2013, 30(3): 401–407. PING Q, MA Q Y, YUAN P. Energy dissipation analysis of stone specimens in SHPB tensile test [J]. Journal of Mining & Safety Engineering, 2013, 30(3): 401–407.