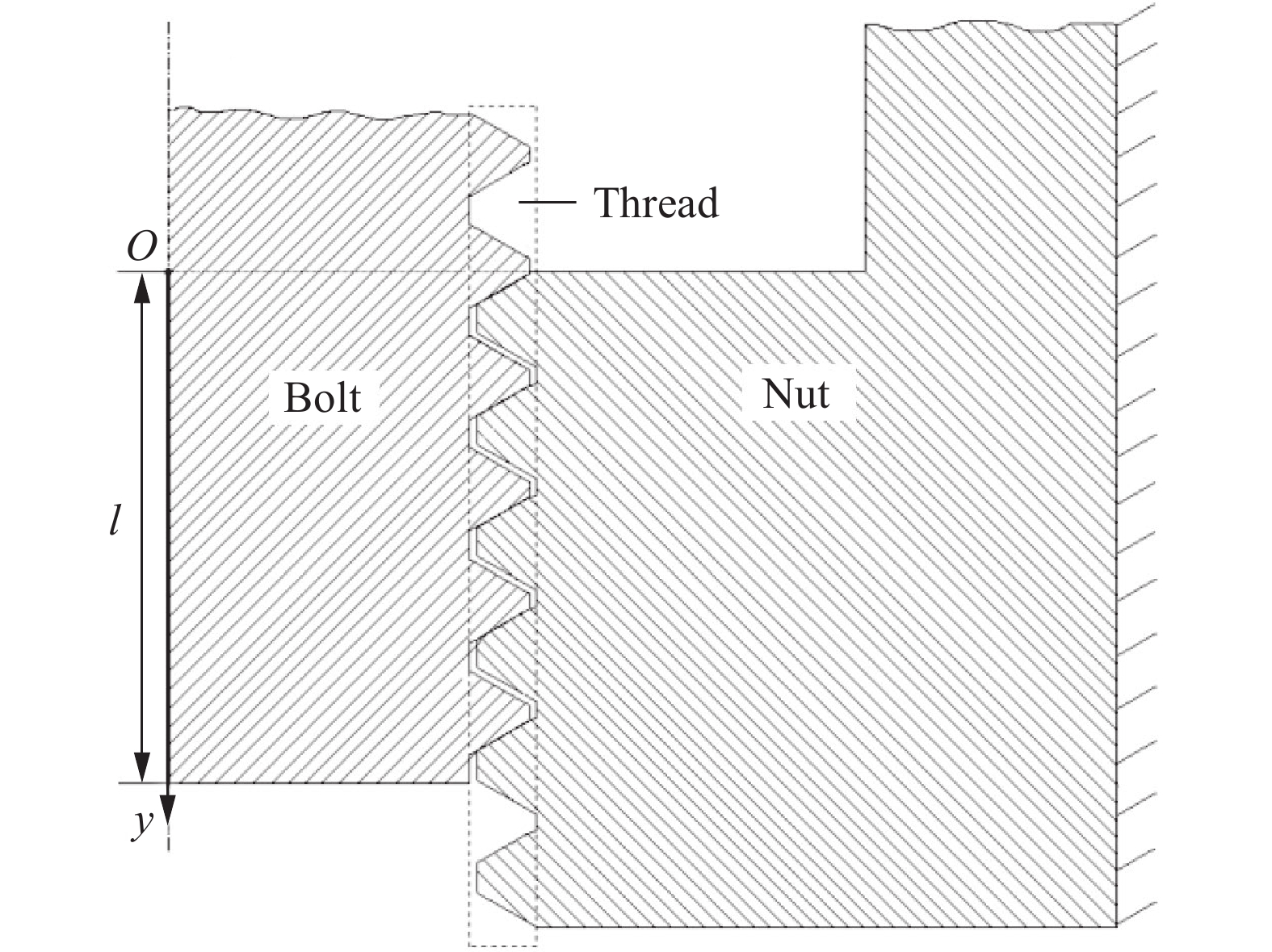
Vibration characteristics of the threaded connection between a projectile and a fuze during penetration
-
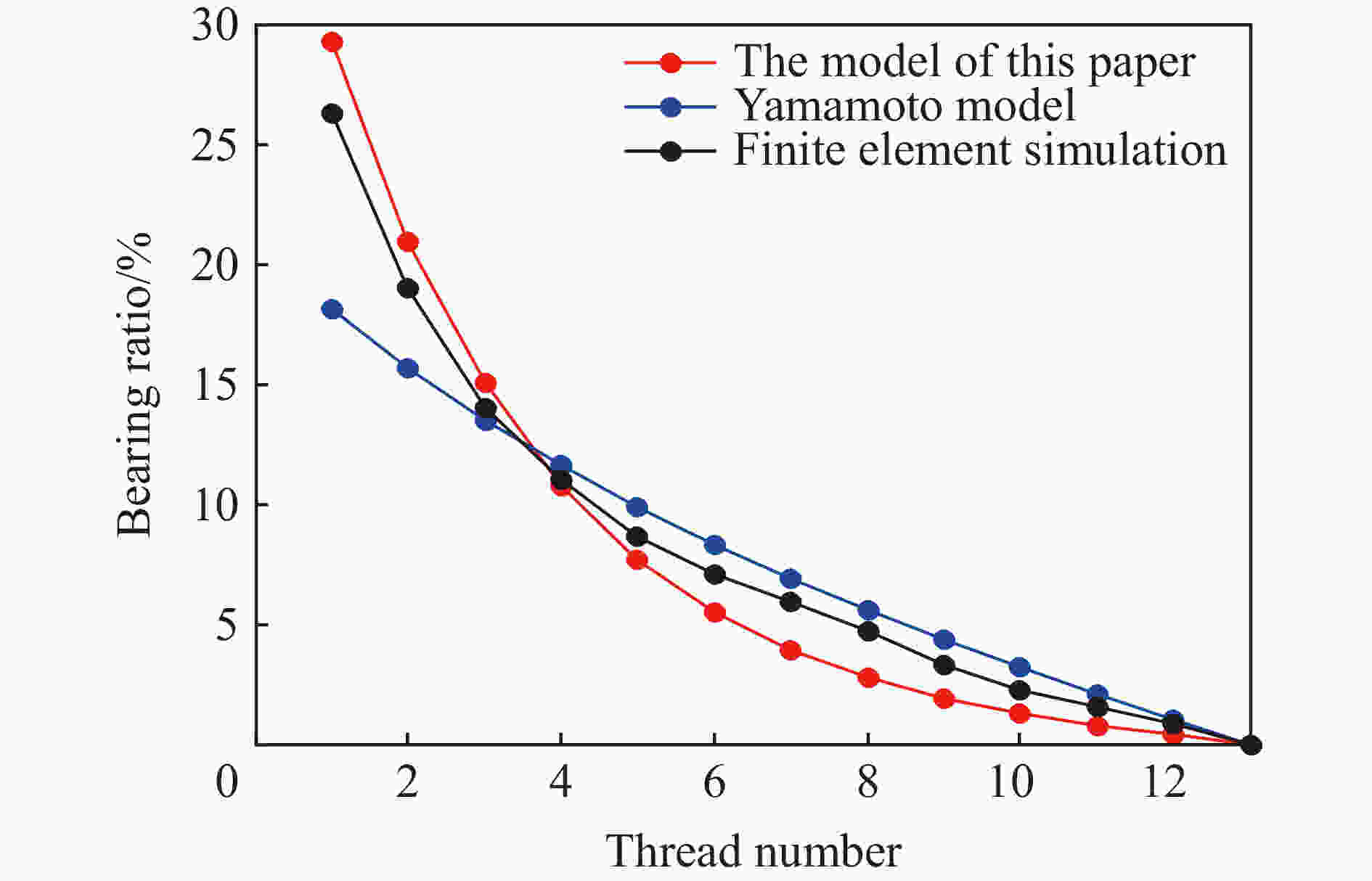
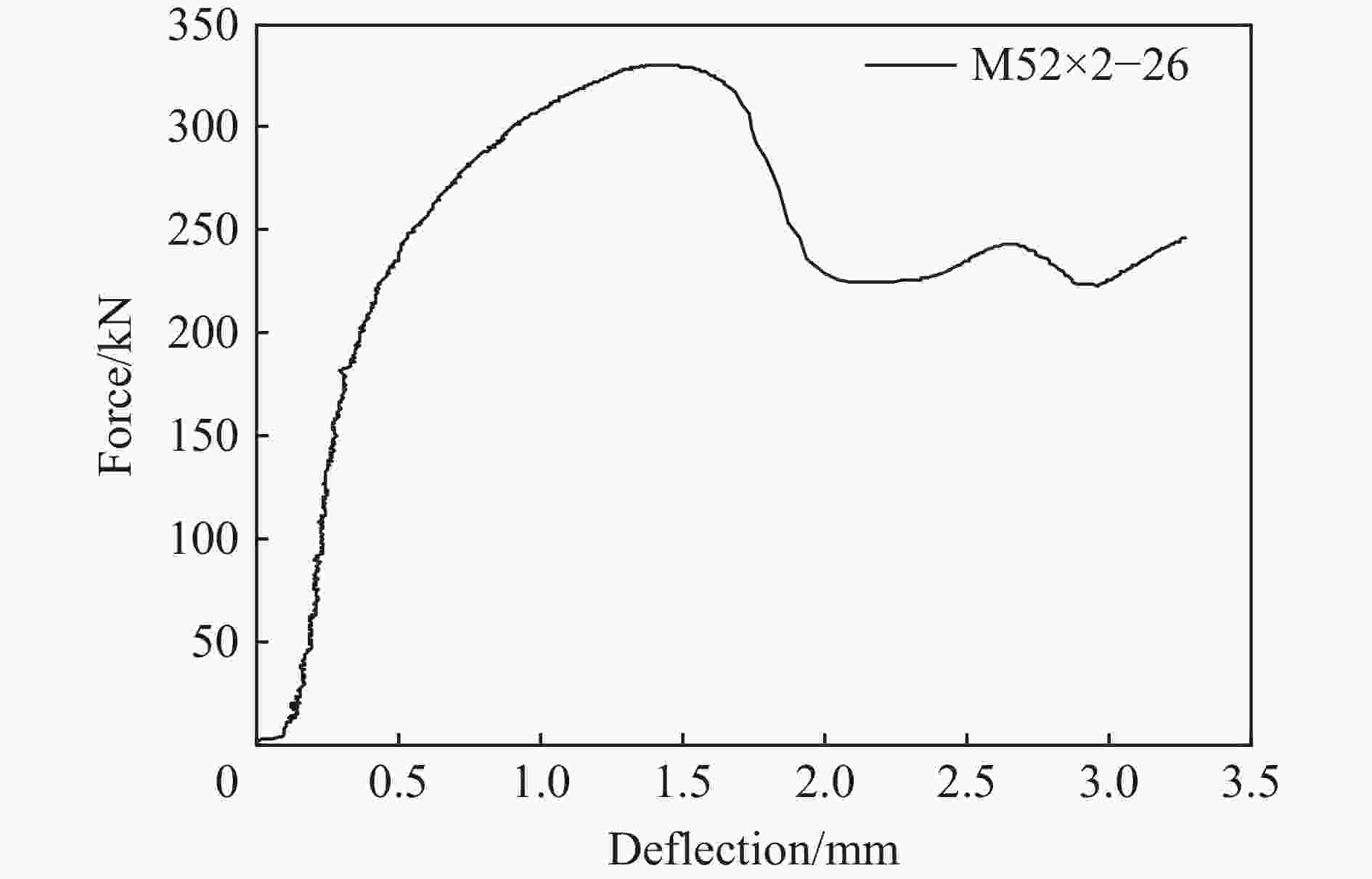
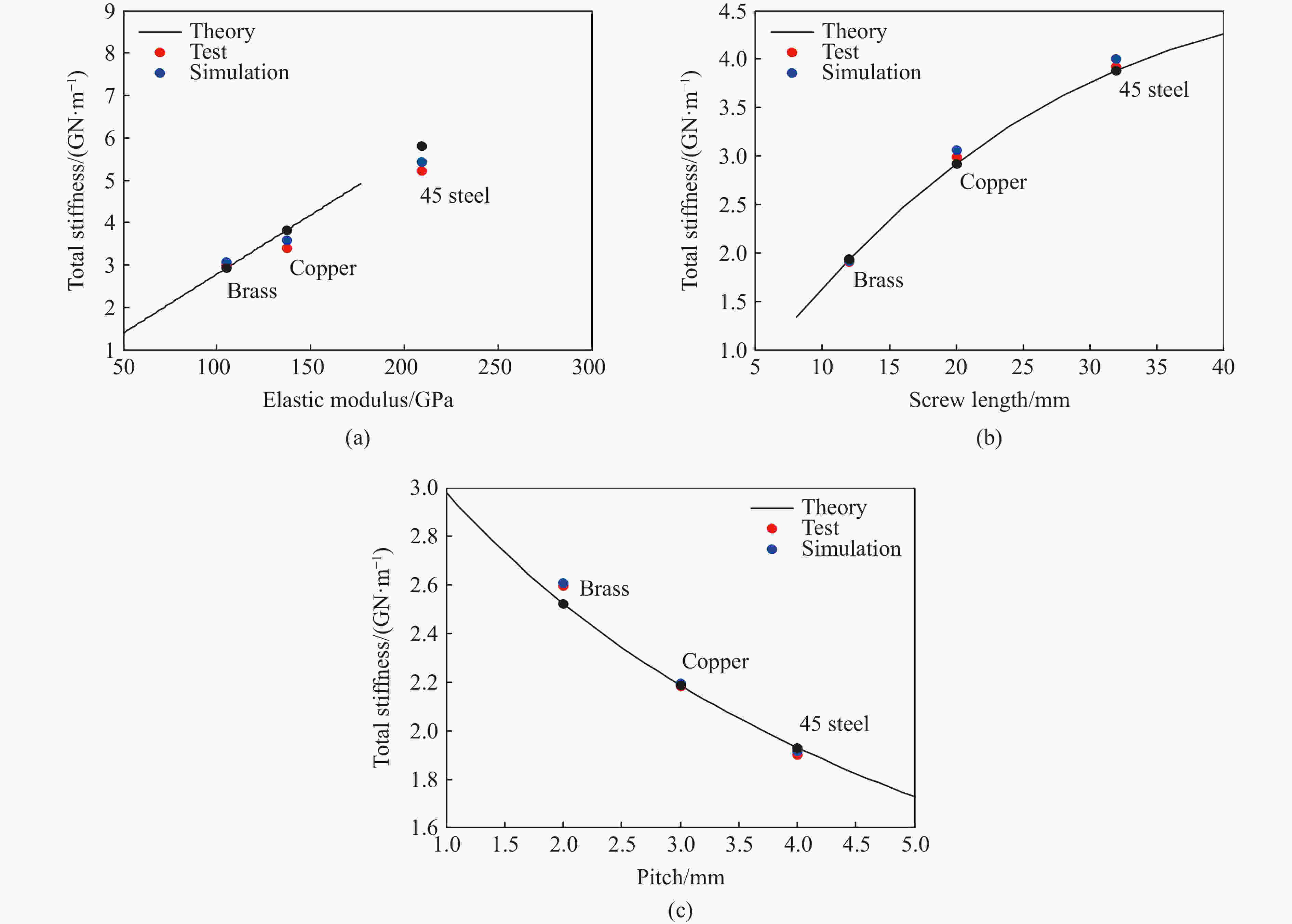
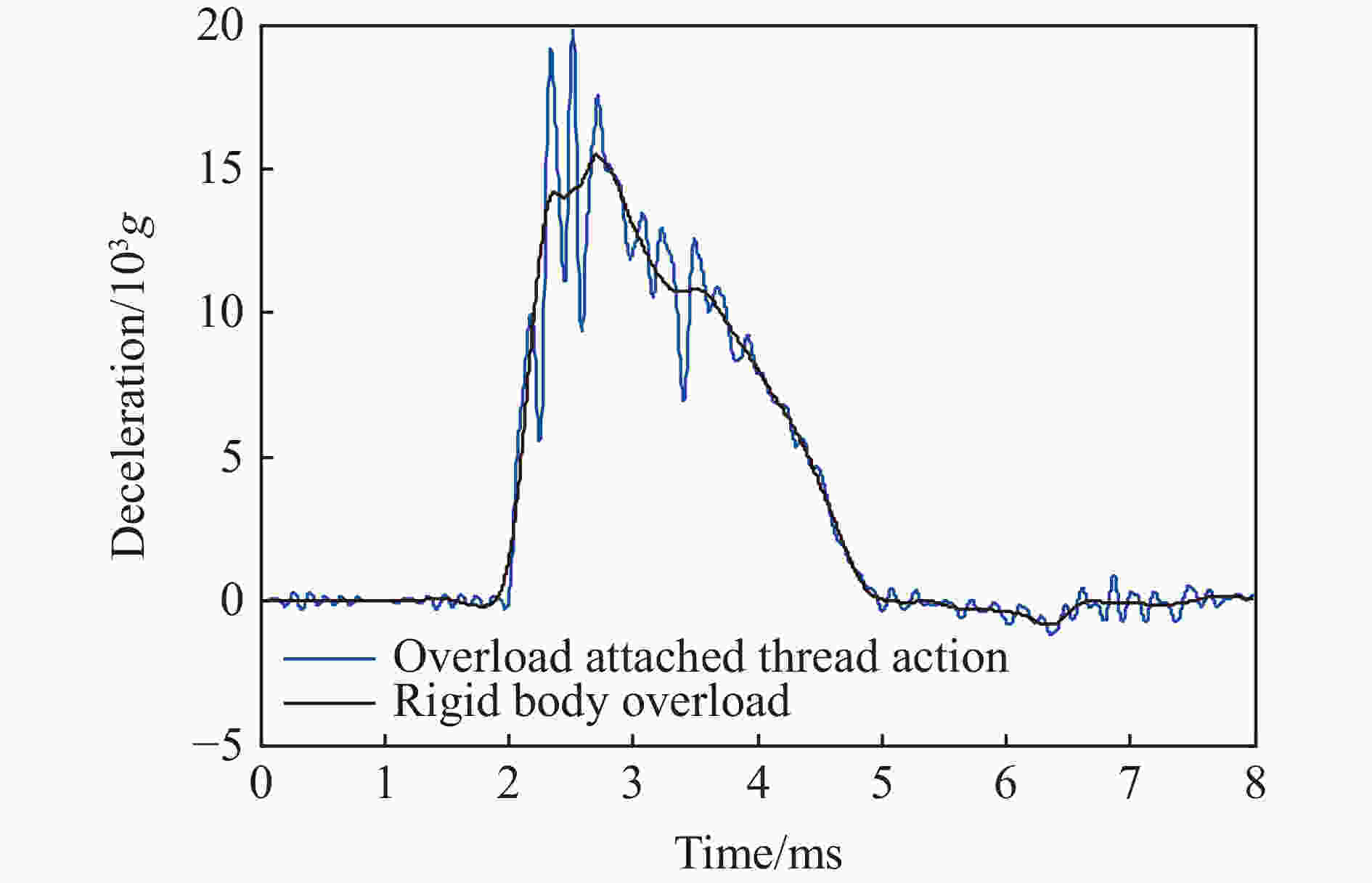
摘要: 针对侵彻过程中的弹引系统,对弹引螺纹连接结构振动特性进行了研究,建立了弹引螺纹连接结构弹性模型。在模型中,充分考虑了螺纹载荷分布不均匀的特性,不但给出了螺纹载荷分布规律,还给出了螺纹连接结构的等效刚度和振动频率;同时,为了验证模型的正确性,对弹引螺纹连接结构的拉伸和冲击过程进行了有限元仿真和试验,分别通过对弹引系统各结构振动特性的计算和对实测过载信号进行时频分析得到了系统的频率特性;将弹引系统的振动频率与实测过载信号的时频分析结果进行了对比。分析计算和试验结果发现:与静载荷时相比,冲击载荷作用下第一扣螺纹承受的载荷更大;螺纹连接结构的刚度明显小于固连结构;增加螺纹材料刚度、增加螺纹旋合长度、减小螺距能够有效增加螺纹连接结构固有频率;在侵彻过载测试信号的时频分析结果中明显存在与螺纹连接结构的振动频率一致的振动信号,并且该频率成分的信号幅值很高,对过载信号影响很大。Abstract: In view of the projectile fuze system in the process of penetration, the vibration characteristics of the threaded connection between a projectile and a fuze were studied. An elastic model for the missile fuze threaded connection between projectile and fuze was established. This model took the uneven distribution characteristics of the thread load into consideration. Not only the distribution law of the thread load was given, but also the equivalent stiffness and vibration frequency of the threaded connection structure were given. At the same time, in order to verify the correctness of the model, the finite element simulation and the static tensile and impact tests of the spring thread connection structure were carried out. The frequency characteristics of the system were obtained by calculating the vibration characteristics of each structure and analyzing the measured overload signals. Finally, the vibration frequency of the projectile-fuze system was compared with the time-frequency analysis results of the measured overload signal. For impact load and static load, the results of calculation and test show that the load on the first thread close to the force action point is the largest, and the load on the threads far away from the action point decreases gradually. Compared with the static load, the first thread supports more load under the impact load. The stiffness of the screw connection structure is obviously lower than that of the fixed connection structure. By increasing the stiffness of the thread material, increasing the screw length and reducing the pitch, the natural frequency of the threaded connection structure can be effectively increased. Based on the time-frequency analysis of the penetration overload test signals, it is found that there is a signal having the same vibration frequency with that of the threaded connection structure. Moreover, the amplitude of this signal is very high and it has a great impact on the overload signal.
-
表 1 弹体和引信体一~六阶振动频率
Table 1. The first to sixth order vibration frequencies of the projectile and fuze
阶次 振动频率/kHz 弹体轴向 引信体轴向 弹体横向 引信体横向 1 3.23 14.35 2.28 28.93 2 9.69 43.06 14.29 181.35 3 16.15 71.77 40.03 50.77 4 22.10 100.49 78.45 99.50 5 29.07 129.20 109.66 139.09 6 35.68 164.09 146.00 185.18 表 2 小波分解信号的频率范围
Table 2. Frequency range of wavelet decomposition signals
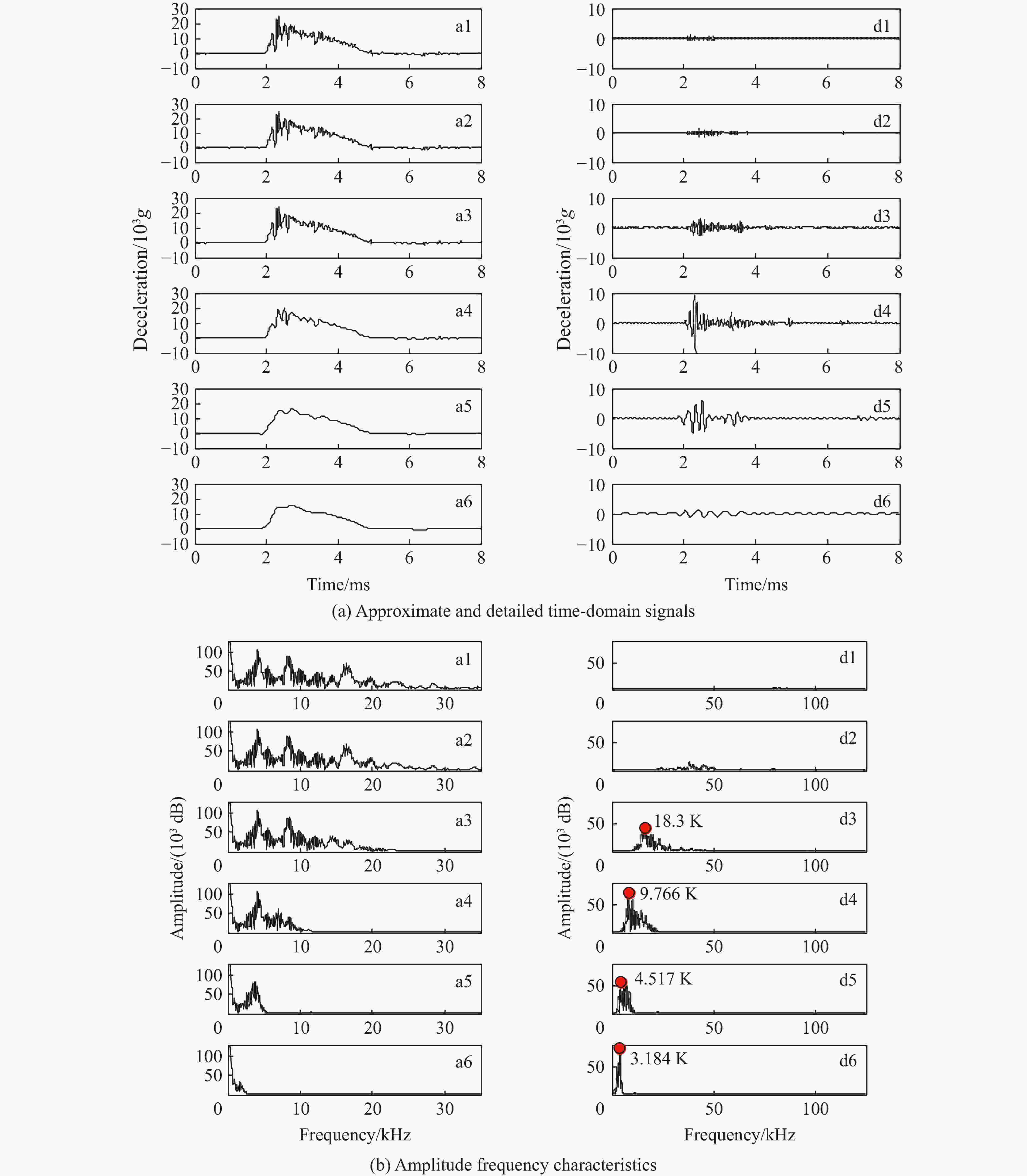
分解层数n 频率范围/kHz 近似信号a 细节信号d 1 0~62.5 62.5~125 2 0~31.25 31.25~62.5 3 0~15.625 15.625~31.25 4 0~7.8125 7.8125~15.625 5 0~0.390625 3.90625~7.8125 6 0~1.95312525 1.95312525~3.90625 表 3 计算结果对照
Table 3. Comparison of calculation results
螺纹型号 材料 强度极限/MPa 螺纹刚度/(GN·m−1) 材料 螺纹 试验 数值模拟 本文模型 Yamamoto模型 M52×2−26 45钢 845 236 5.3104 5.5527 5.6835 8.0321 -
[1] DEN HARTOG J P. The mechanics of plate rotors for turbo-generators [J]. IEEE/ASME Transactions on Mechatronics, 1929, 51: 1–10. [2] SOPWITH D G. The distribution of load in screw threads [J]. Proceedings of the Institution of Mechanical Engineers, 1948, 159: 373–383. DOI: 10.1243/PIME_PROC_1948_159_030_02. [3] YAMATOTO A. The theory and computation of threads connection [M]. Tokoy: Yokendo, 1980. [4] ERAMO M D, CAPPA P. An experimental validation of load distribution in screw threads [J]. Experimental Mechanics, 1991, 31(1): 70–75. DOI: 10.1007/bf02325727. [5] ZHAO H. A numerical method for load distribution in threaded connections [J]. Journal of Mechanical Design, 1996, 118(2): 274–279. DOI: 10.1115/1.2826880. [6] CHAABAN A, JUTRAS M. Static analysis of buttress threads using the finite element method [J]. Journal of Pressure Vessel Technology, 1990, 114: 209–212. DOI: 10.1115/1.2929031. [7] DRAGONI E. Effect of nut compliance on screw thread load distribution [J]. The Journal of Strain Analysis for Engineering Design, 1990, 25(3): 147–150. DOI: 10.1243/03093247v253147. [8] KENNY B, PATTERSON E A. Load and stress distribution in screw threads [J]. Experimental Mechanics, 1985, 51: 1–10. DOI: 10.1007/BF02325089. [9] MILLER D L, MARSHEK K M, NAJI M R. Determination of load distribution in a threaded connection [J]. Mechanism & Machine Theory, 1983, 18(6): 421–430. DOI: 10.1016/0094-114X(83)90057-5. [10] CHEN J J, SHIH Y S. A study of the helical effect on the thread connection by three dimensional finite element analysis [J]. Nuclear Engineering and Design, 1999, 191(2): 109–116. DOI: 10.1016/S0029-5493(99)00134-X. [11] SUN F. Analysis of the screw thread connection strength based on nonlinear finite element method [J]. Applied Mechanics and Materials, 2013, 301–403: 55–58.DOI. DOI: 10.4028/www.scientific.net/AMM.401-403.55. [12] CHAABAN A, MUZZO U. Finite element analysis of residual stresses in threaded end closures [J]. Journal of pressure vessel technology, 1991, 113(3): 398–401. DOI: 10.1115/1.2928773. [13] BRETI J L, COOK R D. Modeling the load transfer in threaded connections by the finite element method [J]. International Journal for Numerical Methods in Engineering, 1979, 14(9): l359–1377. DOI: 10.1002/nme.1620140909. [14] 张冬梅, 高世桥, 牛少华. 侵彻过程中螺纹连接结构的应力传递仿真分析 [J]. 兵工学报, 2014, 36: 284–288.ZHANG D M, GAO S Q, NIU S H. Simulation analysis of stress transmission of screw joint structures during projectile penetration [J]. Acta Armamentarii, 2014, 36: 284–288. [15] ZHANG D M, GAO S Q, XU X. A new computational method for bolted-joint stiffness [J]. Advances in Mechanical Engineering, 2016, 8(11): 1–9. DOI: 10.1177/1687814016682653. -







 下载:
下载: