基于动力放大系数与等效单自由度体系的圆中空夹层钢管混凝土抗撞设计方法

王帅峰; 王蕊; 赵晖; 郭志辉

doi:10.11883/bzycj-2021-0467

基于动力放大系数与等效单自由度体系的圆中空夹层钢管混凝土抗撞设计方法

doi: 10.11883/bzycj-2021-0467

王帅峰^1,,
王蕊¹,
赵晖^{1, 2, ,},
郭志辉¹

1.
太原理工大学土木工程学院，山西太原 030024
2.
天津大学建筑工程学院，天津 300350

基金项目: 国家自然科学基金（52108162）；山西省自然科学研究面上项目（20210302123119）；哈尔滨工业大学结构工程灾变与控制教育部重点实验室开放基金（HITCE201906）

详细信息

作者简介:
王帅峰（1997－　），男，硕士，wangshuaifeng1119@163.com

通讯作者:
赵　晖（1988－　），男，博士，副教授，zhaohui01@tyut.edu.cn

中图分类号: O347; TU398.9
计量
- 文章访问数: 472
- HTML全文浏览量: 127
- PDF下载量: 66
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-10
- 修回日期: 2022-03-14
- 网络出版日期: 2022-03-29
- 刊出日期: 2022-10-31

Design method for impact resistance of circular concrete-filled double-skin steel tubular members based on dynamic increase factor and equivalent single DoF system

WANG Shuaifeng^1
,,
WANG Rui¹,
ZHAO Hui^{1, 2
, ,},
GUO Zhihui¹

1.
College of Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China
2.
School of Civil Engineering and Architecture, Tianjin University, Tianjin 300350, China

摘要

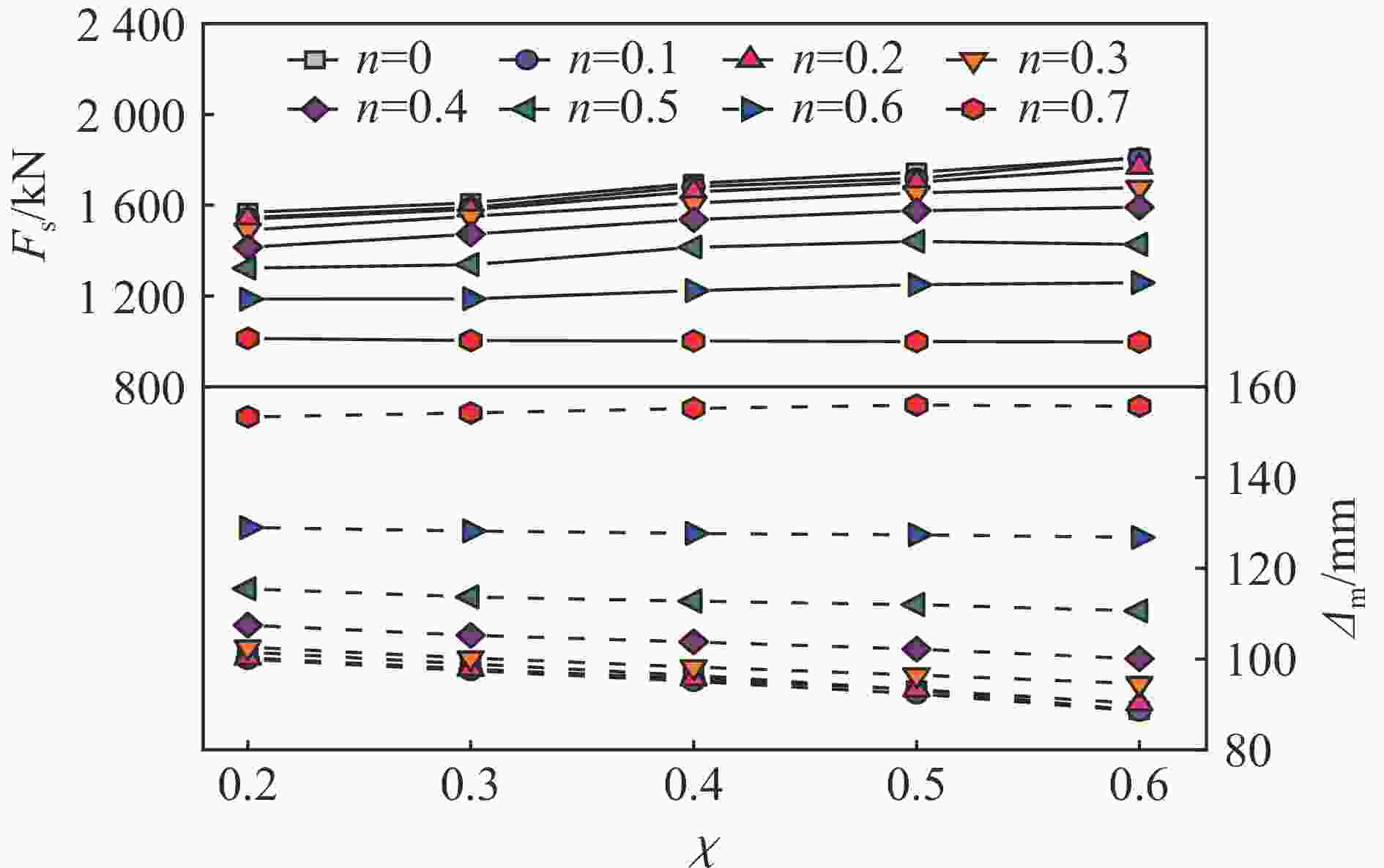
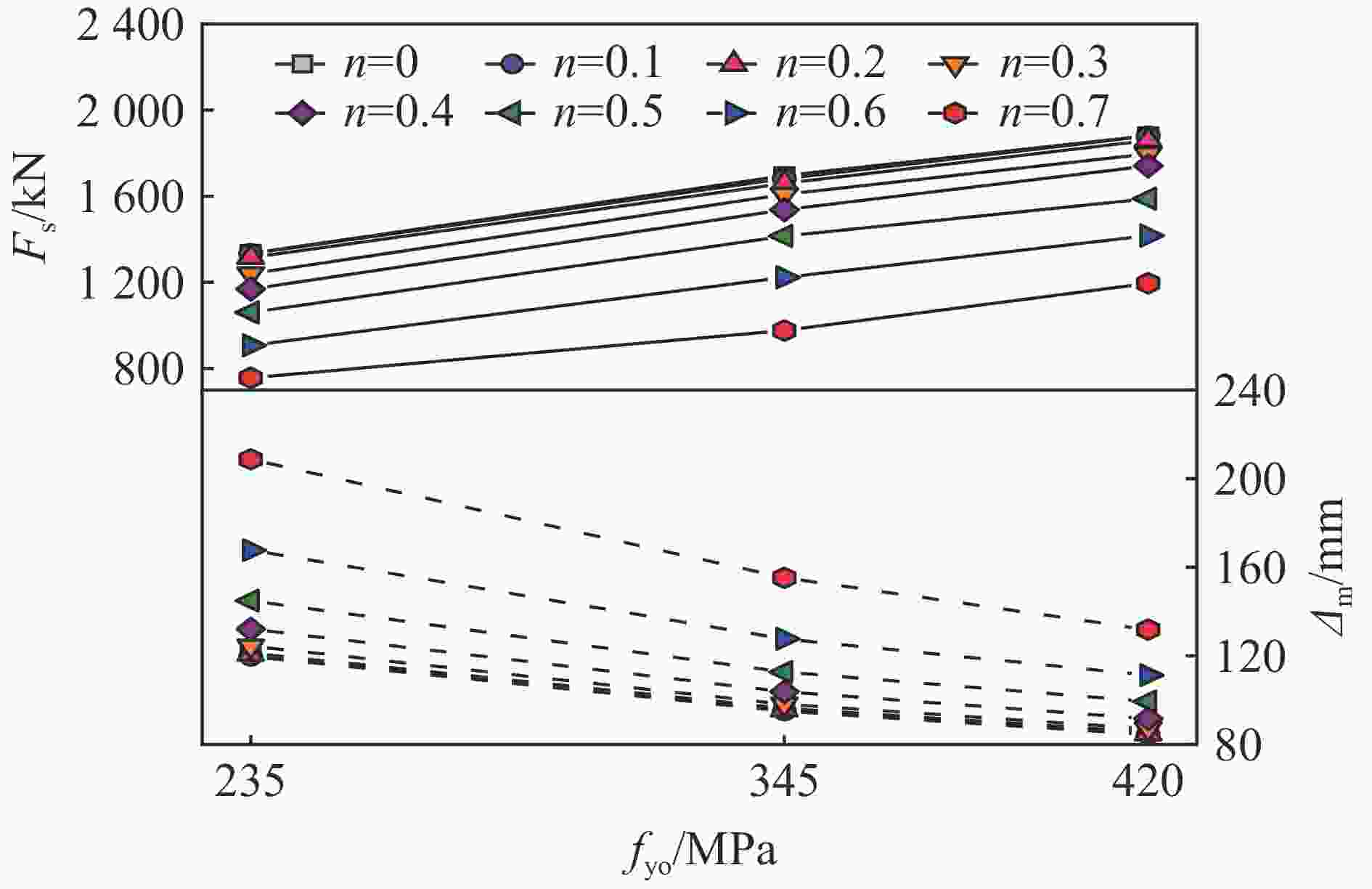
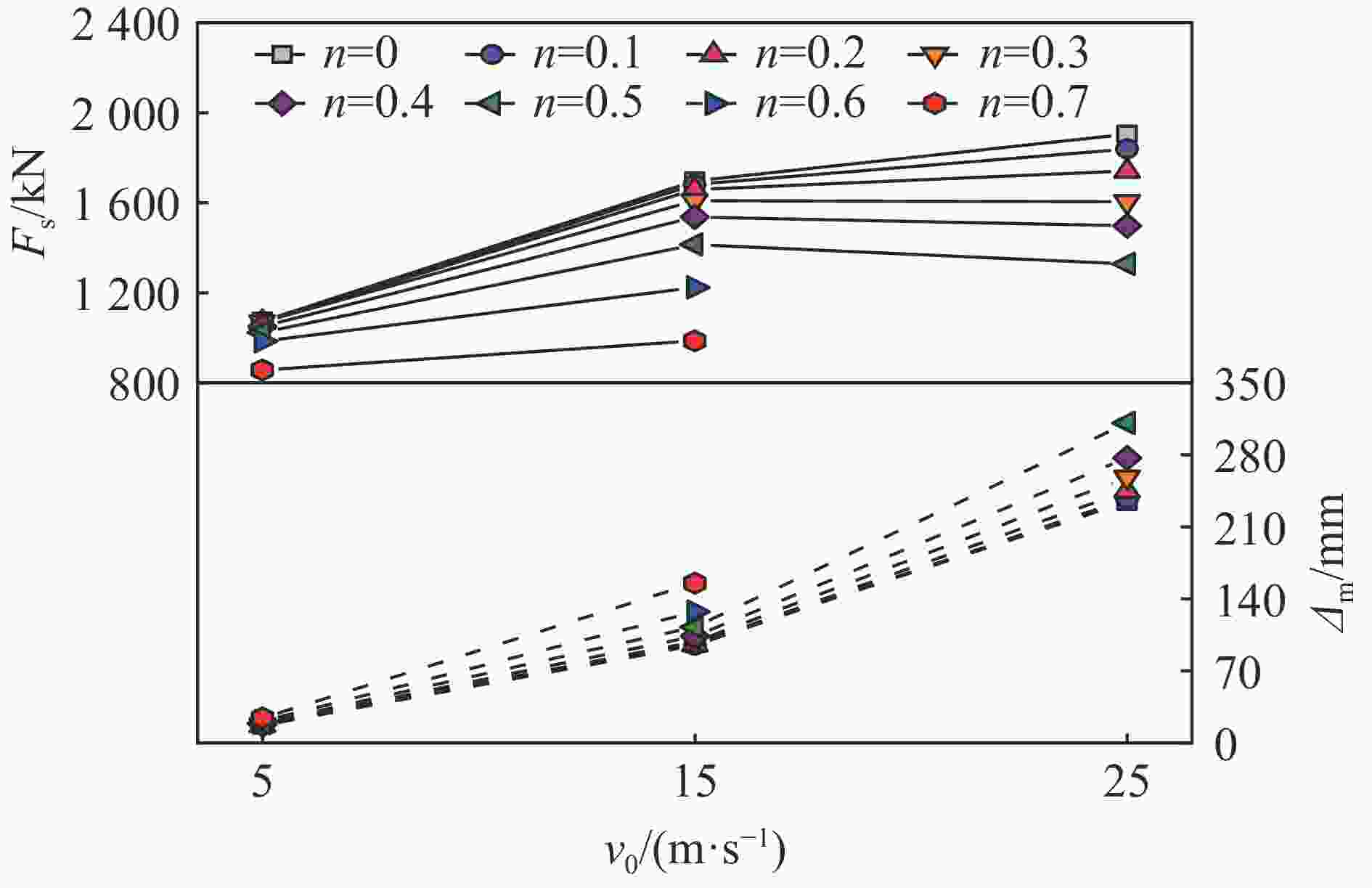
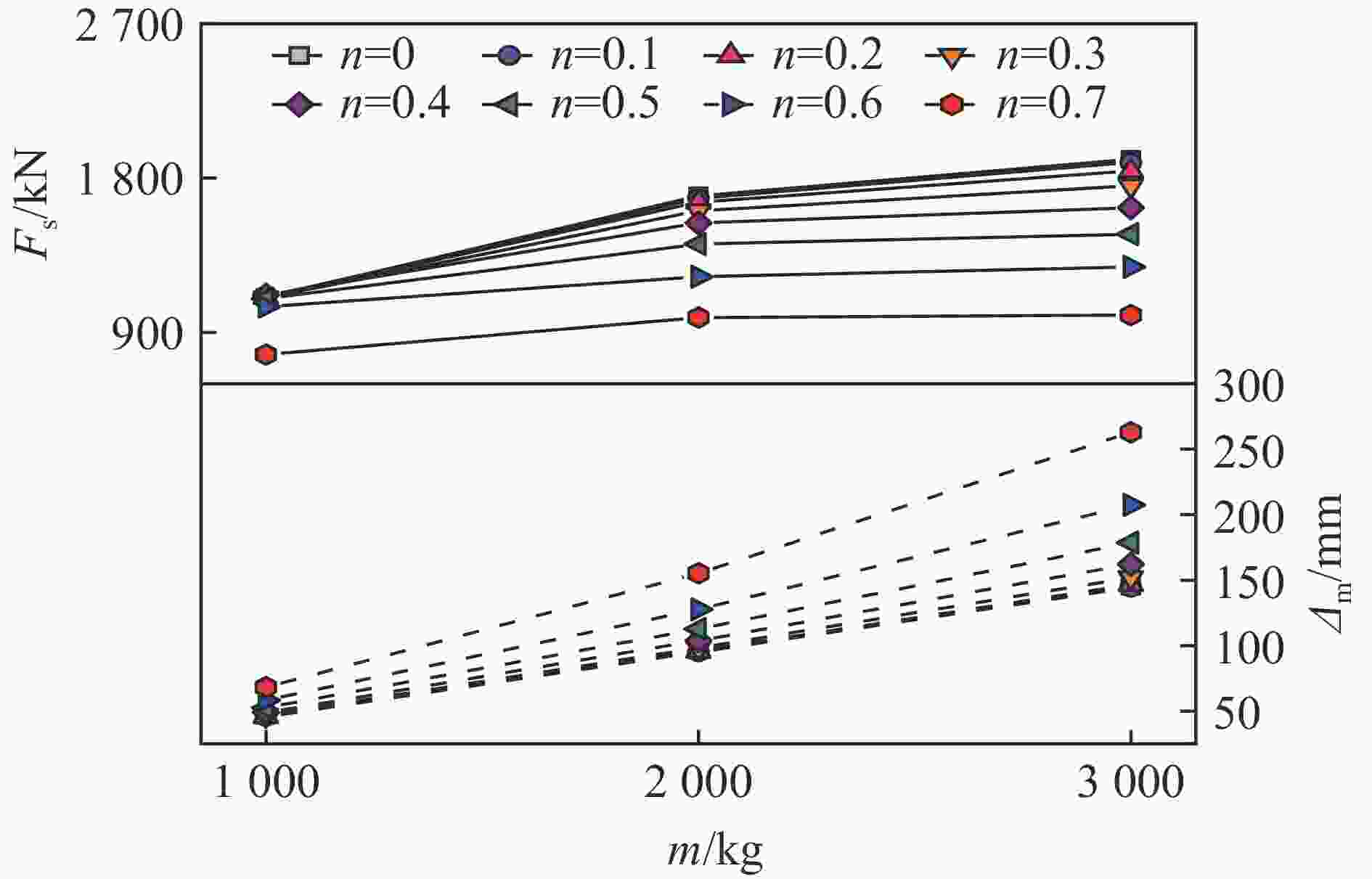
摘要: 中空夹层钢管混凝土（concrete-filled double-skin steel tubular，CFDST）构件作为超高输电塔、海上平台等重要结构的承重构件，其抗撞性能是设计阶段需考虑的关键问题。因此，在前期试验研究的基础上，采用ABAQUS有限元软件建立了200个圆CFDST柱力学模型，并进行了轴力与撞击耦合作用下的抗撞机理分析，研究了在0~0.7轴压比下不同名义含钢率、空心率、截面直径、材料强度对构件抗撞性能的影响规律；基于动力放大系数和等效单自由度方法提出了构件抗撞承载力计算公式，并预测了撞击作用下构件的跨中动力响应。结果表明：在0~0.7轴压比下，名义含钢率、外径、外钢管强度、撞击速度与撞击质量对构件跨中挠度峰值和撞击力平台值影响显著，空心率与混凝土强度影响较小；提出的简化计算方法能较好地预测圆CFDST构件的抗撞承载力和跨中位移响应。
- 圆中空夹层钢管混凝土 /
- 抗撞性能 /
- 空心率 /
- 动力放大系数 /
- 等效单自由度法
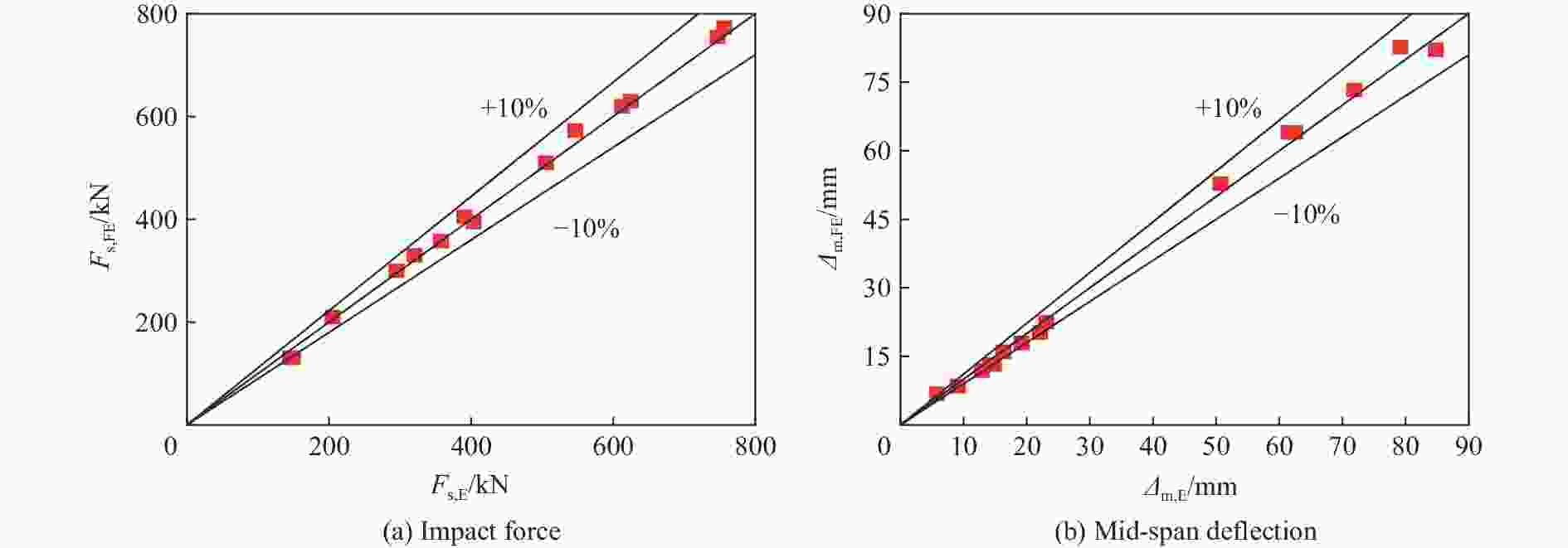
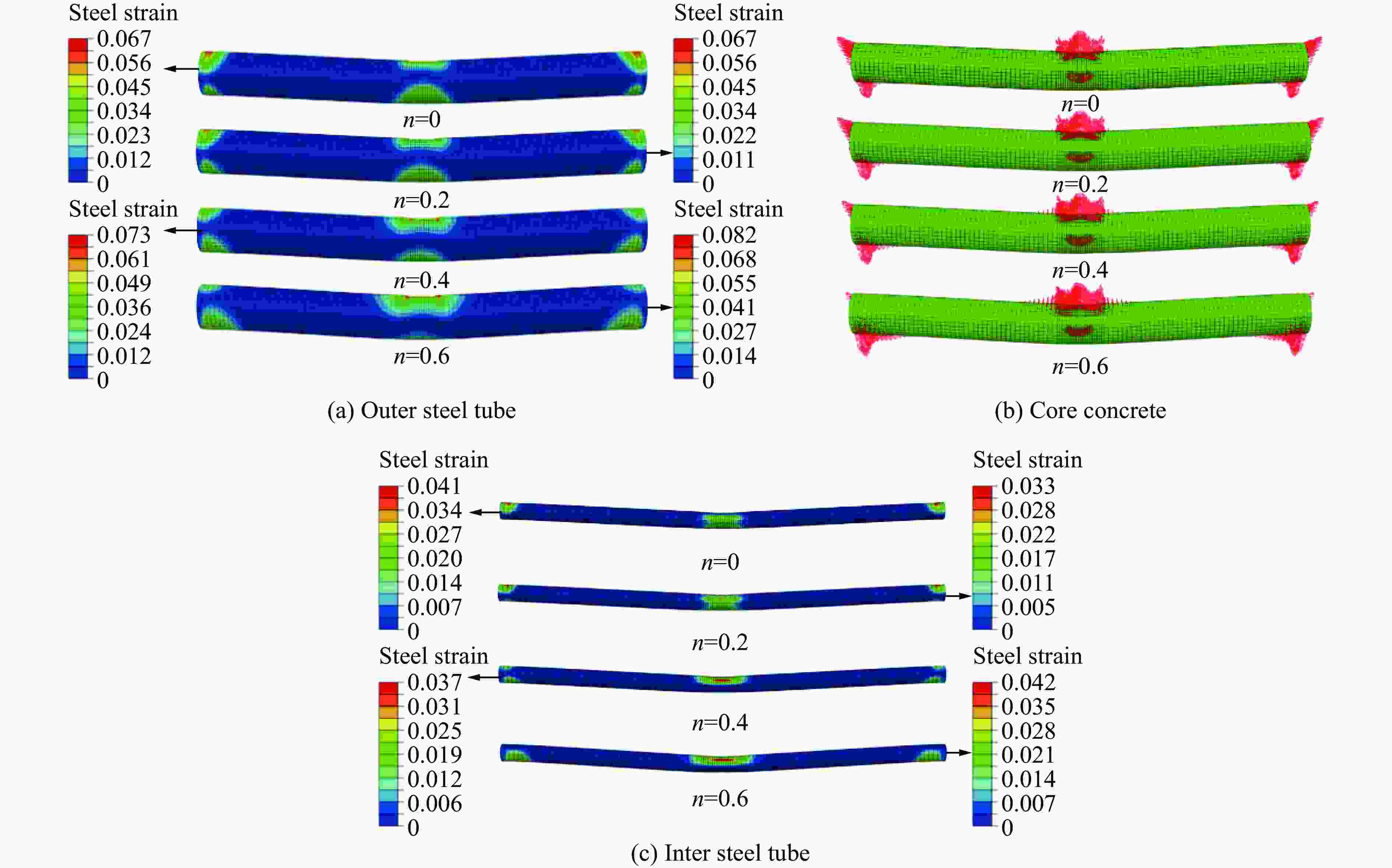
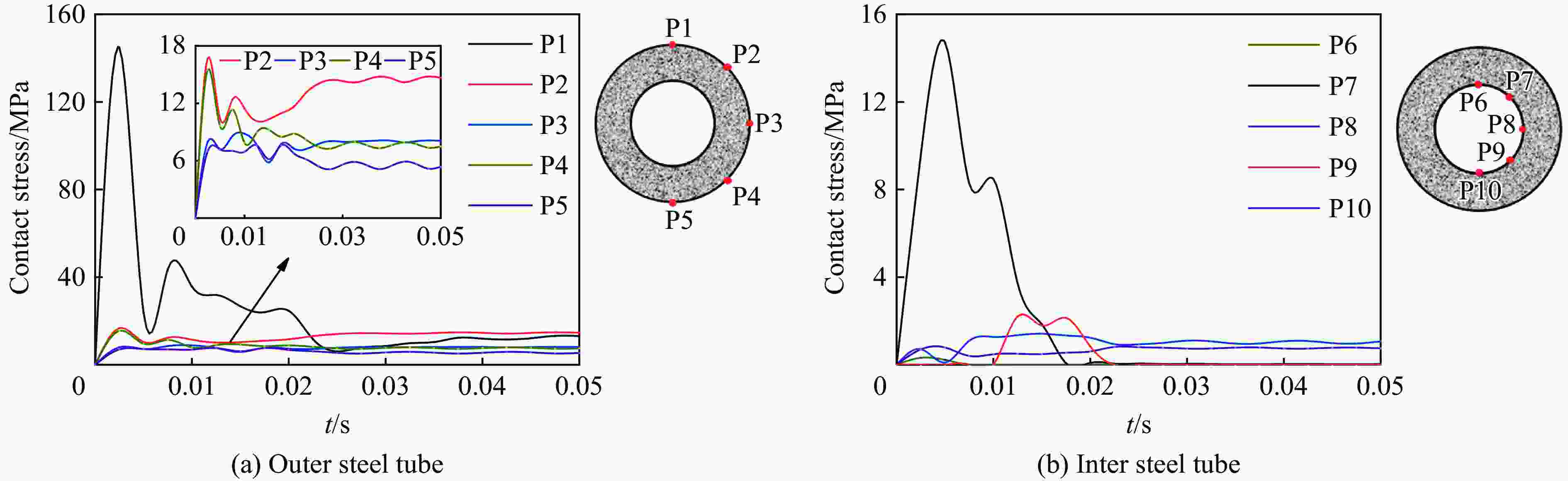
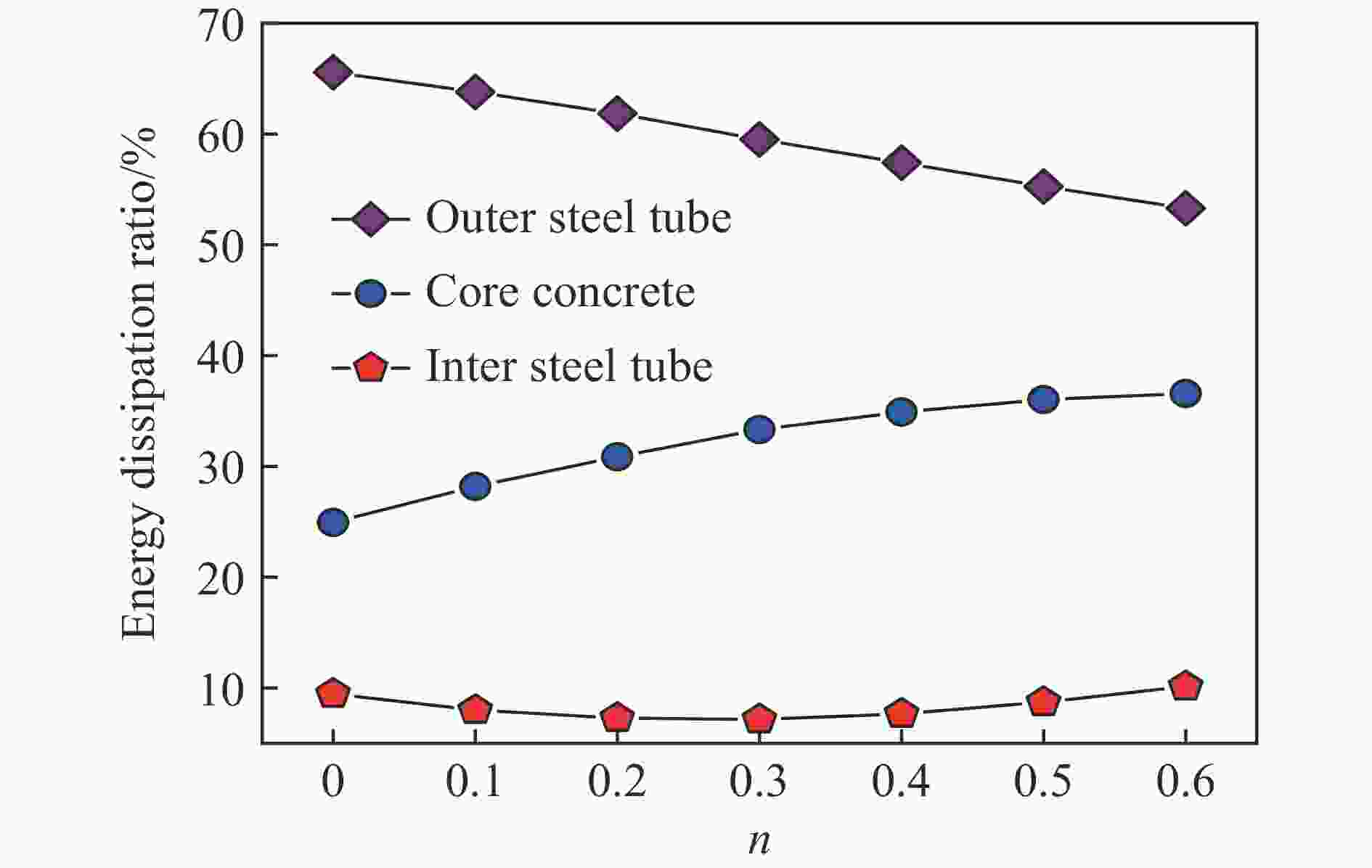
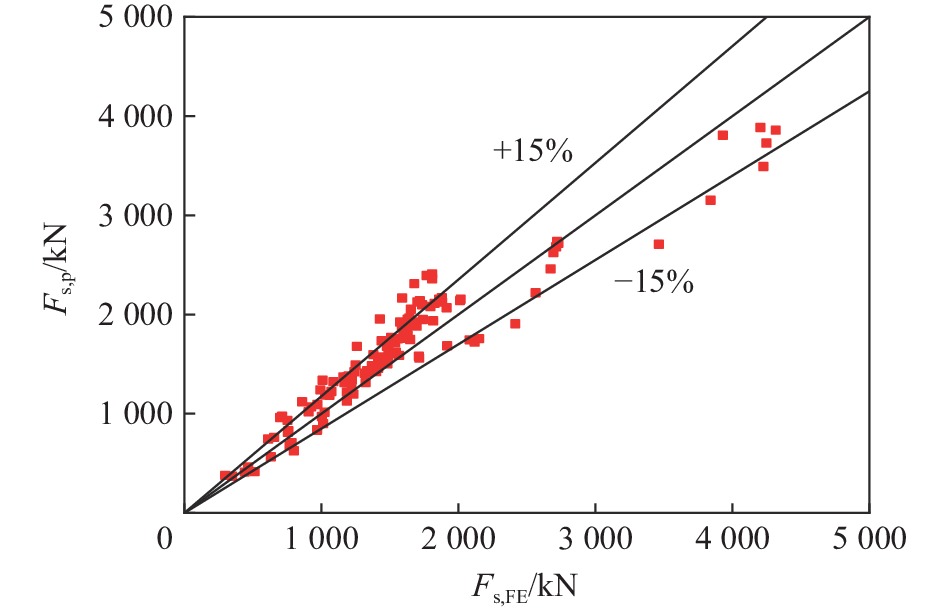
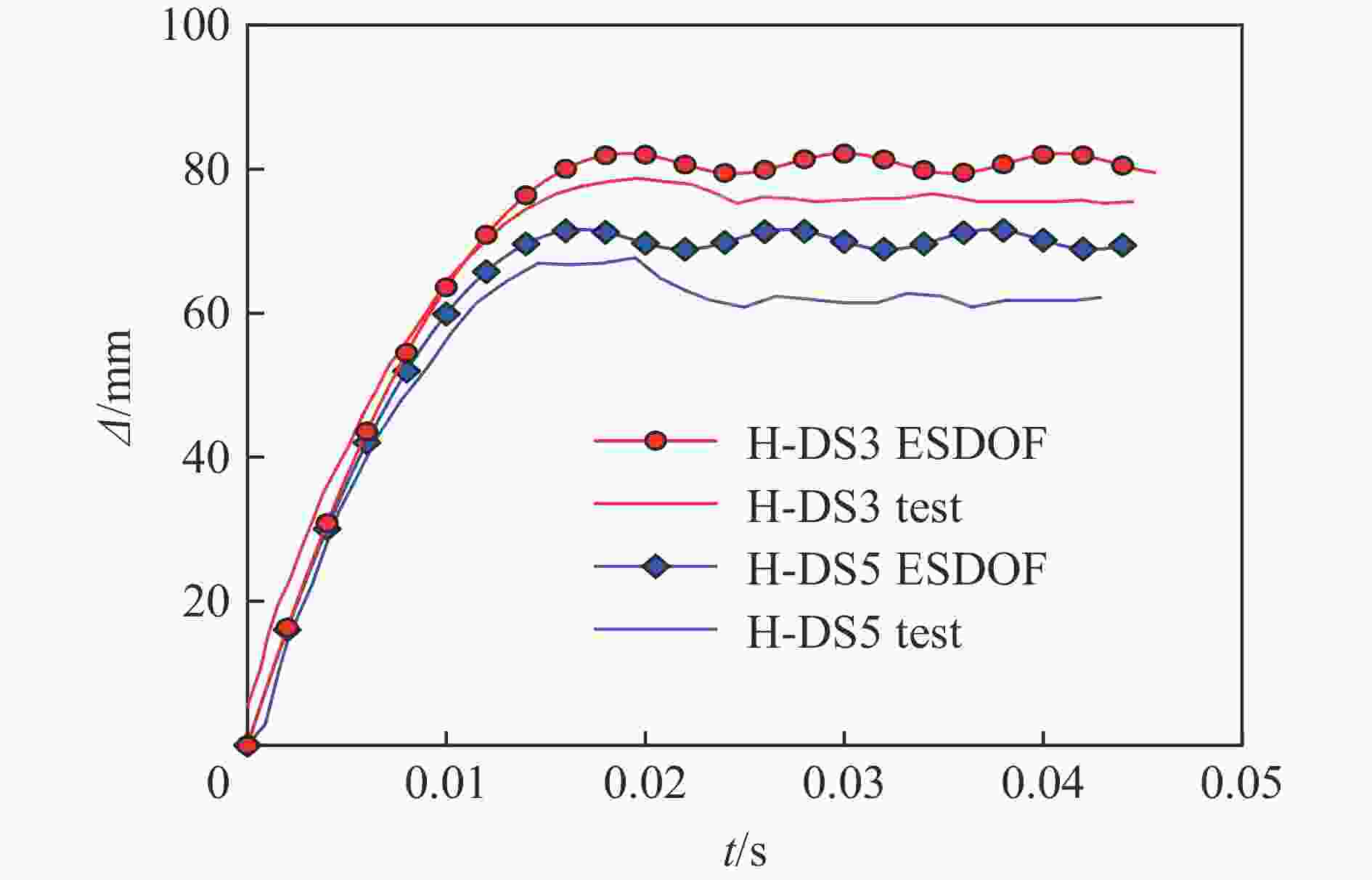
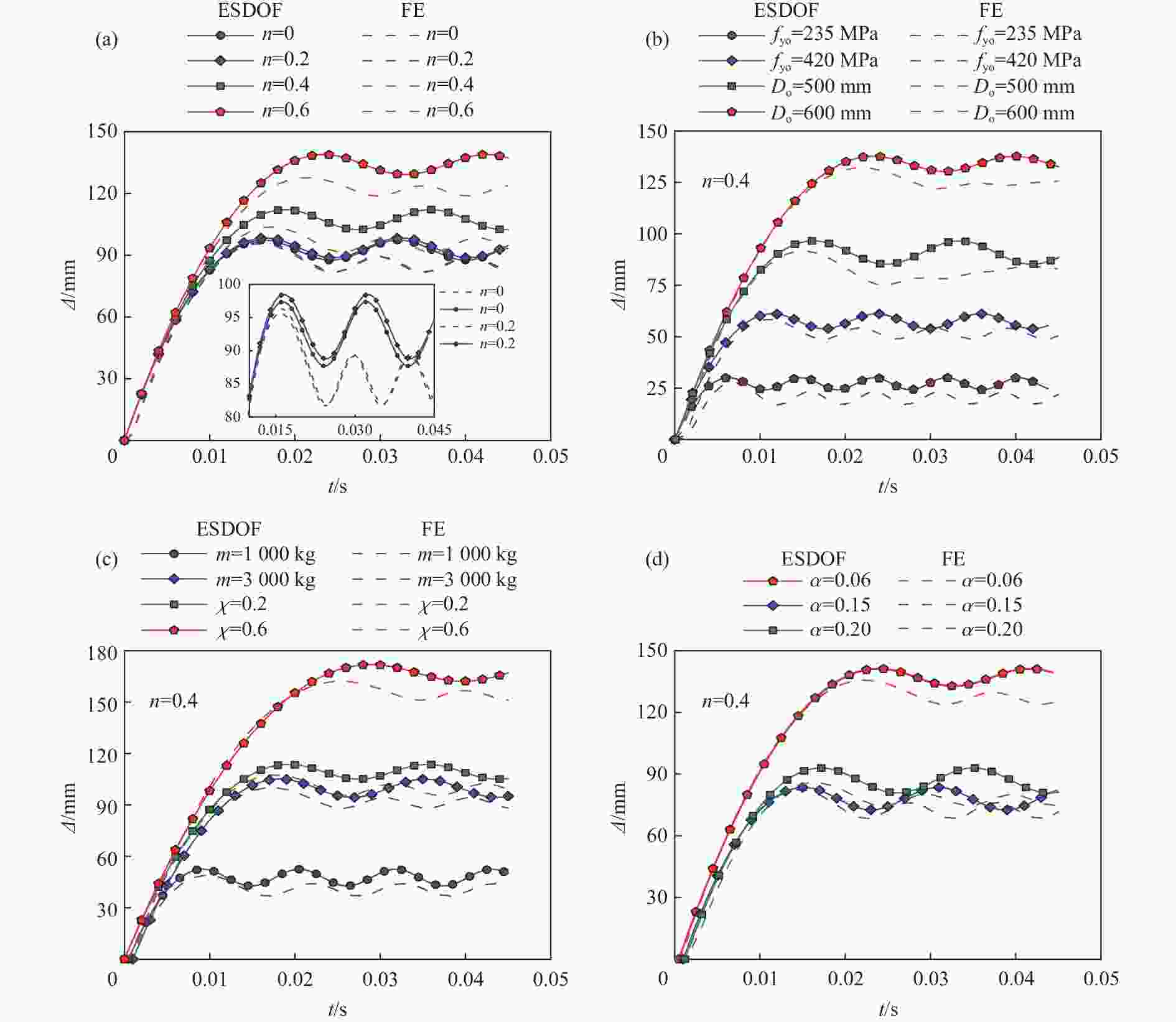
Abstract: Concrete-filled double-skin steel tubular (CFDST) members are widely employed as load-bearing members in the ultra-high power transmission tower and offshore platform. The impact resistance of this type of members should be considered in the design stage. Based on the previous test results, in total 200 finite element (FE) models considering the coupling of axial and lateral impact loads were established with the ABAQUS software, and the damage mechanism of impact resistance was analyzed. Then, the parametrical studies were carried out to investigate the influences of key factors, including the nominal steel ratio, hollow ratio, cross-sectional diameter and material strength on the impact resistance of the members for the axial load ratio ranging from 0 to 0.7. Finally, the calculation formula for the impact bearing capacity is proposed and the dynamic response at the mid-span was predicted based on the methods of dynamic increase factor and an equivalent single degree-of-freedom model. In this work, the deflection at the mid-span and the plateau impact force were taken as the key indexes to evaluate the impact resistance. Results indicate that the impact resistance of the circular CFDST columns decreases with the increasing of axial load ratio. Under lateral impact, the CFDST members with the hollow ratio lower than 0.7 exhibit flexural failure. The interaction between the external steel tube and the inner concrete is stronger than that between the inner steel tube and the outer concrete. In addition, the nominal steel ratio, outer diameter of the cross-section, yield strength of the outer tube, impact velocity and impact mass all play significant roles on the maximum deflection at the mid-span and the plateau impact force when the axial load ratio ranges from 0 to 0.7. Effects of hollow ratio and concrete strength are marginal. The proposed calculation methods can reasonably predict the impact bearing capacity and mid-span displacement response of the CFDST members subjected to an impact.
- circular concrete filled double-skin steel tube /
- impact resistance /
- hollow ratio /
- dynamic increase factor /
- equivalent single degree-of-freedom system

HTML全文

图 1 试验结果与有限元模型的破坏模式对比

Figure 1. Comparison of failure patterns between the test result and the FE model

下载: 全尺寸图片幻灯片

图 2 撞击力和跨中挠度时程曲线的试验结果与有限元结果对比

Figure 2. Comparison of test and FE results for impact force and the time history curve of mid-span deflection

下载: 全尺寸图片幻灯片

图 3 撞击力平台值和跨中挠度峰值的有限元与试验值的对比

Figure 3. Comparison of FE and test values for the plateau impact force and the maximum deflection in mid-span

下载: 全尺寸图片幻灯片

图 4 内外钢管与核心混凝土等效塑性应变云图

Figure 4. Equivalent plastic strain diagrams of inner and outer steel tubes and core concrete

下载: 全尺寸图片幻灯片

图 5 混凝土与钢管之间的接触应力

Figure 5. Contact stress between concrete and steel tube

下载: 全尺寸图片幻灯片

图 6 不同轴压比下各部件塑性应变能分配

Figure 6. Distribution of plastic strain energy of each component under different axial-load ratio

下载: 全尺寸图片幻灯片

图 7 轴压比对跨中挠度峰值和撞击力平台值的影响

Figure 7. Influences of axial-load ratios on the maximum deflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 8 名义含钢率对跨中挠度峰值和平台撞击力的影响

Figure 8. Influences of nominal steel ratios on the maximum deflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 9 空心率对跨中挠度峰值和平台撞击力的影响

Figure 9. Influences of hollow ratios on the maximum deflectionin mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 10 外钢管屈服强度对跨中挠度峰值和撞击力平台值的影响

Figure 10. Influences of yield strength of outer steel tube on the maximum deflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 11 混凝土强度对跨中挠度峰值和撞击力平台值的影响

Figure 11. Influences of concrete strength on the maximum deflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 12 撞击速度对跨中挠度峰值和撞击力平台值的影响

Figure 12. Influences of impact velocity on the maximumdeflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 13 撞击质量对跨中挠度峰值和撞击力平台值的影响

Figure 13. Influences of impact mass on the maximum deflectionin mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 14 截面外径对跨中挠度峰值和撞击力平台值的影响

Figure 14. Influence of cross-sectional diameter on the maximum deflection in mid-span and the plateau impact force

下载: 全尺寸图片幻灯片

图 15 有限元和简化计算对比

Figure 15. Comparison between FE and simplified calculation results

下载: 全尺寸图片幻灯片

图 16 等效单自由度计算流程图

Figure 16. Flow chart of ESDOF calculation

下载: 全尺寸图片幻灯片

图 17 ESDOF体系简化示意图

Figure 17. Simplified diagram of ESDOF system

下载: 全尺寸图片幻灯片

图 18 轴力对抗力函数的影响

Figure 18. Influence of axial force on the resistance function

下载: 全尺寸图片幻灯片

图 19 ESDOF方法预测结果与试验结果的对比

Figure 19. Comparison between ESDOF predictions and test results

下载: 全尺寸图片幻灯片

图 20 ESDOF方法预测结果与有限元结果的对比

Figure 20. Comparison between results from ESDOF predictions and FE model

下载: 全尺寸图片幻灯片

表 1 试件参数

Table 1. Specimen parameters

D_o/mm	t_o/mm	D_i/mm	t_i/mm	α_n	χ	f_yo/MPa	f_cu/MPa	v₀/(m·s⁻¹)
300	7.5	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	15
500	12.5	152	10	0.10	0.4	345	50	15
600	15	152	10	0.10	0.4	345	50	15
400	10	76	10	0.10	0.2	345	50	15
400	10	114	10	0.10	0.3	345	50	15
400	10	152	10	0.10	0.4	345	50	15
400	10	190	10	0.10	0.5	345	50	15
400	10	228	10	0.10	0.6	345	50	15
400	6	152	10	0.06	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	15
400	14	152	10	0.15	0.4	345	50	15
400	18	152	10	0.20	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	5
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	50	25
400	10	152	10	0.10	0.4	235	50	15
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	420	50	15
400	10	152	10	0.10	0.4	345	40	15
400	10	152	10	0.10	0.4	345	50	15
400	10	152	10	0.10	0.4	345	60	15

下载: 导出CSV

表 2 DIF公式的适用范围

Table 2. Parameter range of DIF formula

撞击位置	t_o/mm	D_o/mm	内钢管径厚比	χ	n	α_n	L/m	m/kg	v₀/(m·s⁻¹)
跨中	6～18	300～600	76～228	0～0.6	0～0.7	0.06～0.20	4	1 000～3 000	5～25

下载: 导出CSV

参考文献(25)

[1]	韩林海. 钢管混凝土结构: 理论与实践 [M]. 北京: 科学出版社, 2007.
[2]	陶忠, 于清. 新型组合结构柱: 试验, 理论与方法 [M]. 北京: 科学出版社, 2006.
[3]	MARIA G, IGNACIO P Z, VENKATESH K, et al. Fire hazard in bridges: review, assessment and repair strategies [J]. Engineering Structures, 2012, 35: 89–98. DOI: 10.1016/j.engstruct.2011.11.002.
[4]	王丙斌, 王蕊. 空心率对中空夹层钢管混凝土组合柱耐撞性能影响 [J]. 爆炸与冲击, 2018, 38(1): 204–211. DOI: 10.11883/bzycj-2016-0143. WANG B B, WANG R. Effect of hollow ratio on crashworthiness of stainless steel-concrete-steel double-skin tubular columns [J]. Explosion and Shock Waves, 2018, 38(1): 204–211. DOI: 10.11883/bzycj-2016-0143.
[5]	史艳莉, 鲜威, 王蕊等. 方套圆中空夹层钢管混凝土组合构件横向撞击试验研究 [J]. 土木工程学报, 2019, 52(12): 11–21. DOI: 10.15951/j.tmgcxb.2019.12.002. SHI Y L, XIAN W, WANG R, et al. Experimental study on circular-in-square concrete filled double-skin steel tubular (CFDST) composite components under lateral impact [J]. China Civil Engineering Journal, 2019, 52(12): 11–21. DOI: 10.15951/j.tmgcxb.2019.12.002.
[6]	LI W, GU Y Z, HAN L H, et al. Behaviour of ultra-high strength steel hollow tubes subjected to low velocity lateral impact: experiment and finite element analysis [J]. Thin-Wall Structures, 2019, 134: 524–536. DOI: 10.1016/j.tws.2018.10.026.
[7]	WANG R, HAN L H, ZHAO X L, et al. Experimental behavior of concrete filled double steel tubular (CFDST) members under low velocity drop weight impact [J]. Thin-Walled Structures, 2015, 97: 279–295. DOI: 10.1016/j.tws.2015.09.009.
[8]	WANG R, HAN L H, ZHAO X L, et al. Analytical behavior of concrete filled double steel tubular (CFDST) members under lateral impact [J]. Thin-Walled Structures, 2016, 101: 129–140. DOI: 10.1016/j.tws.2015.12.006.
[9]	ZHAO H, WANG R, H C C, et al. Performance of circular CFDST members with external stainless steel tube under transverse impact loading [J]. Thin-Walled Structures, 2019, 145: 106380. DOI: 10.1016/j.tws.2019.106380.
[10]	ZHU X, ZHAO P J, TIAN Y, et al. Experimental study of RC columns and composite columns under low-velocity impact [J]. Thin-Walled Structures, 2021, 160: 107374. DOI: 10.1016/j.tws.2020.107374.
[11]	AGHDAMY S, THAMBIRATNAM D P, DHANASEKAR M, et al. Effects of structure-related parameters on the response of concrete-filled double-skin steel tube columns to lateral impact [J]. Thin-Walled Structures, 2016, 108: 351–368. DOI: 10.1016/j.tws.2016.08.009.
[12]	ZHANG J X, YE Y, YUAN H, et al. A theoretical study of low-velocity impact of metal foam-filled circular tubes [J]. Thin-Walled Structures, 2020, 148: 106525. DOI: 10.1016/j.tws.2019.106525.
[13]	ZHANG J X, YE Y, ZHU Y Q, et al. On axial splitting and curling behavior of circular sandwich metal tubes with mental foam core [J]. International Journal of Solids and Structures, 2020, 202: 111–125. DOI: 10.1016/j.ijsolstr.2020.06.021.
[14]	ZHANG J X, YE Y, LI J F, et al. Dynamic collapse of circular metal foam core sandwich tubes in splitting and curling mode [J]. Thin-Wall Structures, 2021, 161: 107464. DOI: 10.1016/j.tws.2021.107464.
[15]	中国土木工程学会, 中空夹层钢管混凝土结构技术规程: T/CCES 7—2020 [S]. 北京: 中国建筑工业出版社, 2020. China Civil Engineering Society. Technical specification for concrete-filled double skin steel tubular structure: T/CCES 7—2020 [S]. Beijing: China Building Industry Press, 2020.
[16]	WANG R, HAN L H, TAO Z. Behavior of FRP-concrete-steel double skin tubular members under lateral impact: experimental study [J]. Thin-Walled Structures, 2015, 95: 363–373. DOI: 10.1016/j.tws.2015.06.022.
[17]	LI W, GU Y Z, HAN L H, et al. Behaviour of grout-filled double-skin steel tubular T-joint subjected to low-velocity impact [J]. Thin-Walled Structures, 2019, 144: 106270. DOI: 10.1016/j.tws.2019.106270.
[18]	安国青, 赵晖, 王蕊等. 外包不锈钢圆中空夹层钢管混凝土柱抗撞计算方法研究 [J]. 工程力学, 2021, 38(6): 227–236. DOI: 10.6052/j.issn.1000-4750.2020.11.08.023. AN G Q, ZHAO H, WANG R, et al. Calculation method for impact resistance of circular concrete-filled double-skin tubular columns with external stainless steel tube [J]. Engineering Mechanics, 2021, 38(6): 227–236. DOI: 10.6052/j.issn.1000-4750.2020.11.08.023.
[19]	GUO Q Q, ZHAO W Y. Displacement response analysis of steel-concrete composite panels subjected to impact loadings [J]. International Journal of Impact Engineering, 2019, 131: 272–281. DOI: 10.1016/j.ijimpeng.2019.05.022.
[20]	师燕超, 张浩, 李忠献. 钢筋混凝土梁式构件抗爆分析的改进等效单自由度方法 [J]. 建筑结构学报, 2019, 40(10): 8–16. DOI: 10.14006/j.jzjgxb.2019.0096. SHI Y C, ZHANG H, LI Z X. Improved equivalent single degree of freedom method for blast analysis of RC beams [J]. Journal of Building Structures, 2019, 40(10): 8–16. DOI: 10.14006/j.jzjgxb.2019.0096.
[21]	WANG Y H, SAH T P, LU J Y, et al. Behavior of steel-concrete-steel sandwich beams with blot connectors under off-center impact load [J]. Journal of Constructional Steel Research, 2021, 186: 106889. DOI: 10.1016/j.jcsr.2021.106889.
[22]	CLOUGH R W, PENZIEN J. 结构动力学 [M]. 2版. 王光远, 译. 北京: 高等教育出版社, 2007.
[23]	汤福静. 钢筋混凝土梁抗力函数的落锤实验研究 [D]. 长沙: 国防科学技术大学, 2011. TANG F J. Study on resistance function of reinforced concrete beam by drop hammer [D]. Changsha: National University of Defense Technology, 2011.
[24]	FUJIKAKE K, LI B, SOEUN S. Impact response of reinforced concrete beam and its analytical evaluation [J]. Journal of Structural Engineering, 2009, 135(8): 938–950. DOI: 10.1061/(ASCE)ST.1943-541X.0000039.
[25]	PHAM T M, HAO H. Influence of global stiffness and equivalent model on prediction of impact response of RC beams [J]. International Journal of Impact Engineering, 2018, 113: 88–97. DOI: 10.1016/j.ijimpeng.2017.11.014.