Numerical study on the flow field and load characteristics of a head-ventilated revolving body during water entry
-
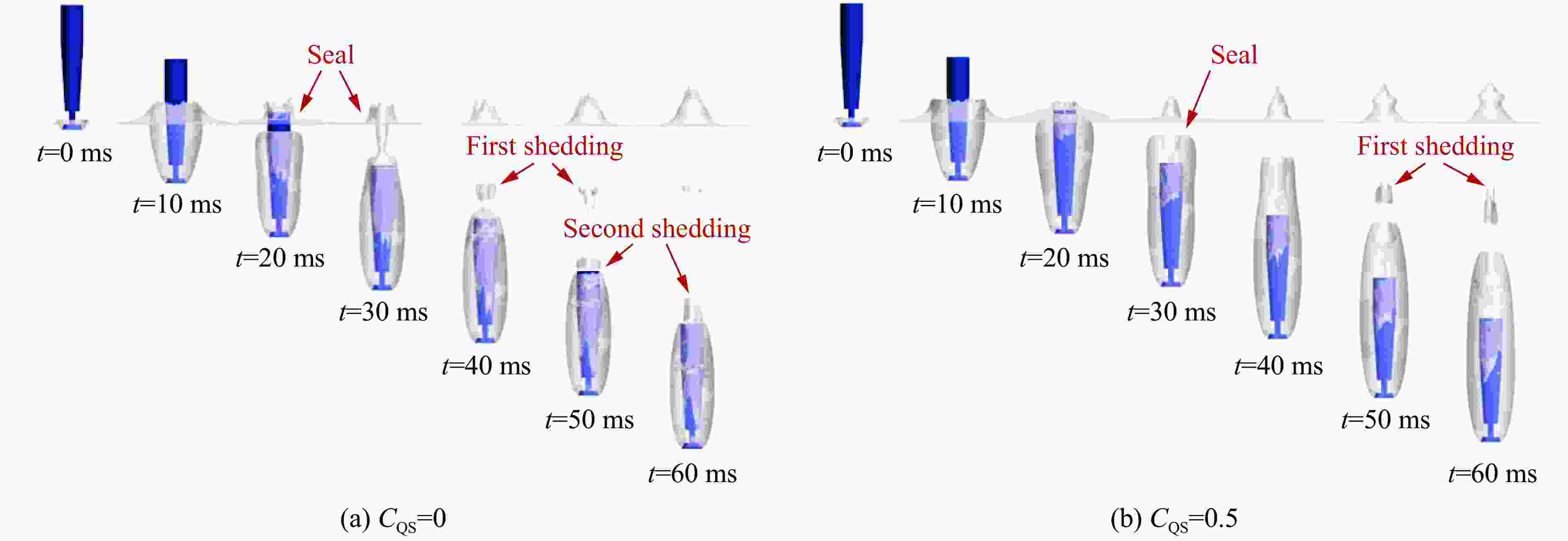
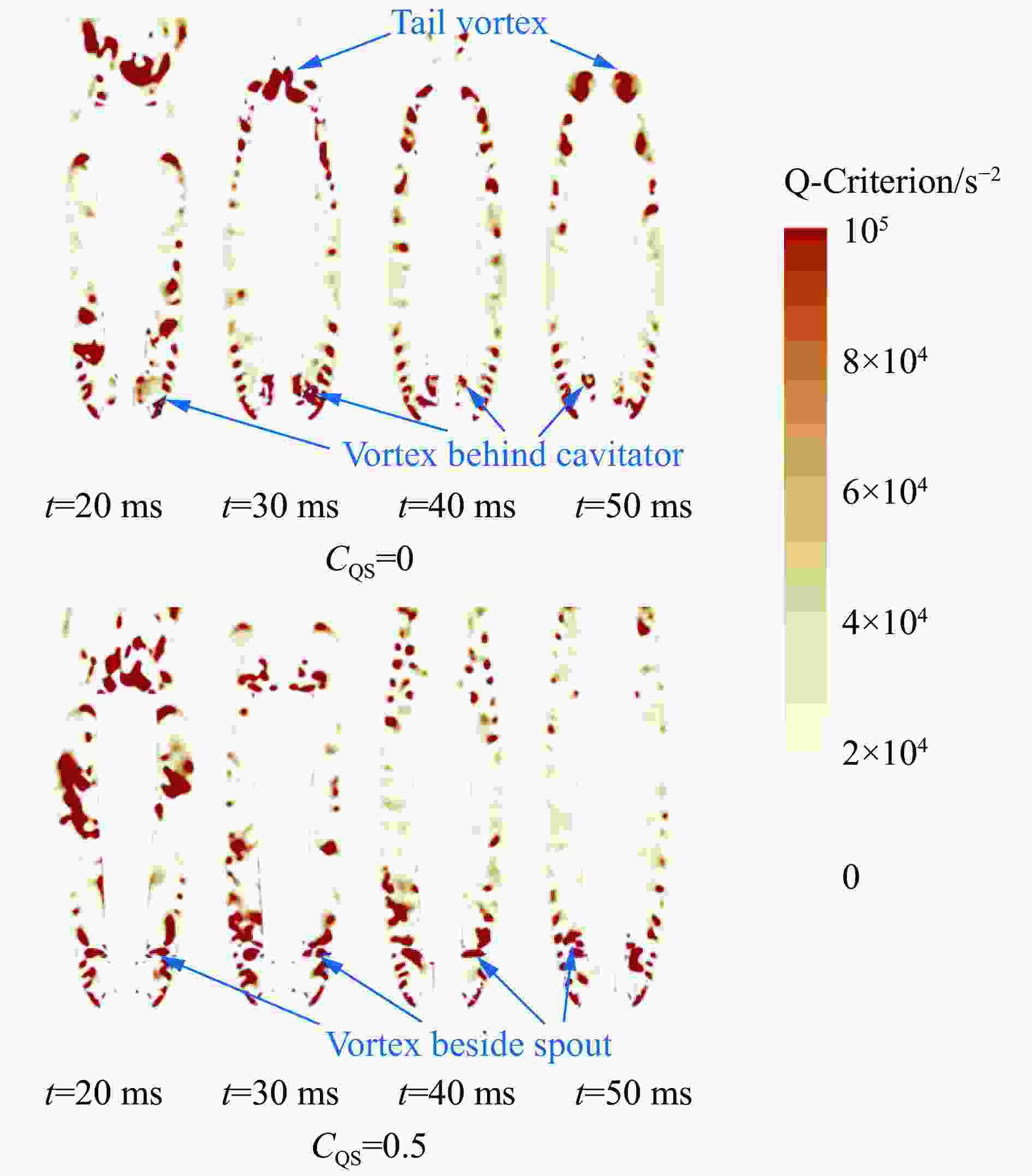
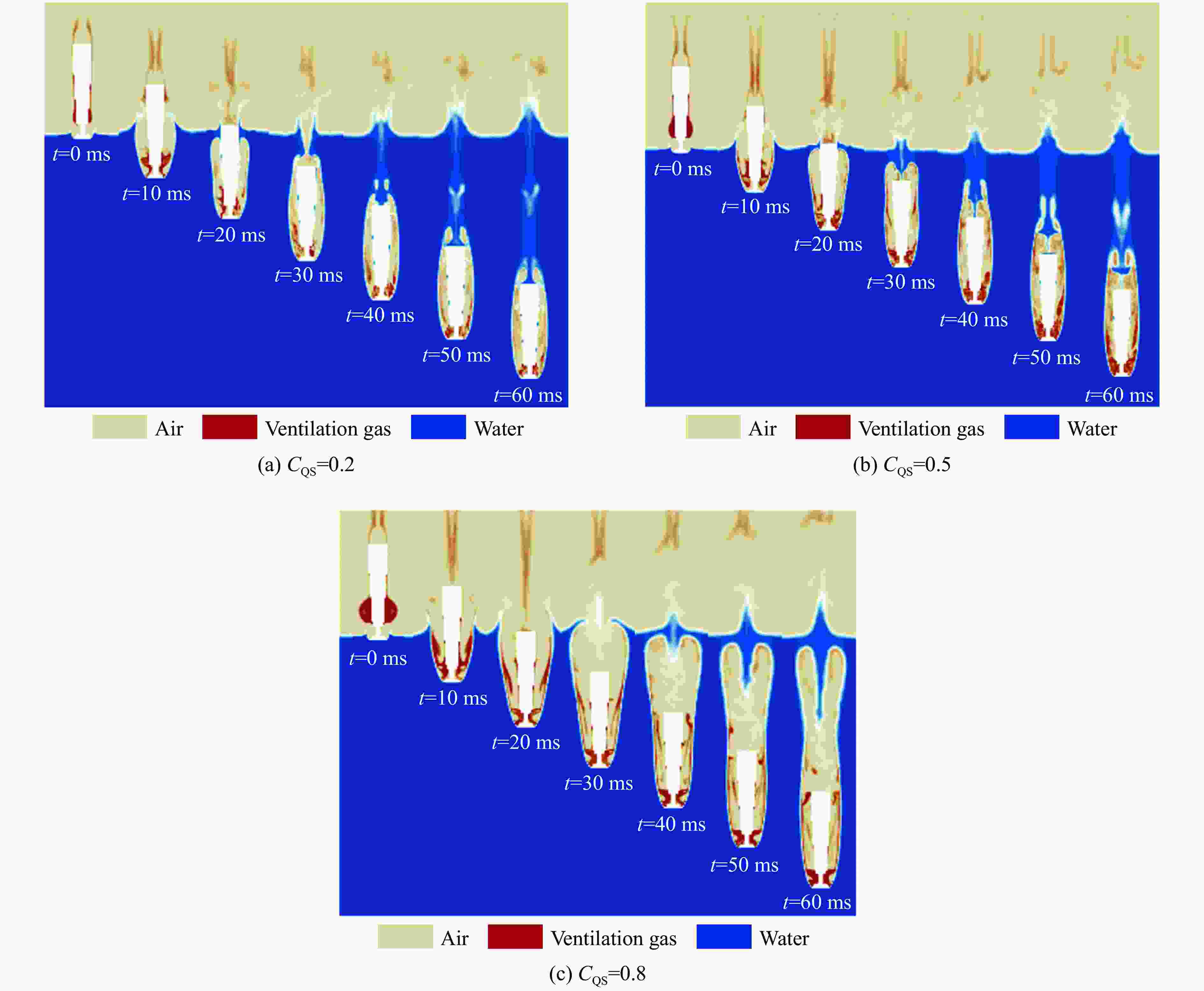
摘要: 为探究周向通气对回转体入水表面载荷的影响，基于VOF(volume of fluid)模型和Realizable k-ε两层湍流模型，开展了周向通气回转体低速入水流场演化数值预报和表面载荷特性分析。通过将数值预报的空泡形态与试验结果相对比，验证了所采用的数值方法的有效性，并分析了不同通气率对空泡形态、流场特性和表面载荷特性的影响。结果表明，通气会改变回转体入水空泡演化过程以及侧壁表面压力，在通气作用下空泡第一次脱落时间延缓，并且通气气体流向空化器后方负压区，改善了空化器后方的负压情况；其次，通气气体在通气口附近形成了明显的涡结构，之后与壁面处由空化器形成的涡融合，增强了空泡中部的涡流强度；最后，通气率越大，空泡闭合时间越晚，空泡体积越大，尾部空泡越不容易发生脱落，同时通气会减缓回转体表面的压力波动，通气率越大压力波动越小。综合分析可以认为，侧向通气对于回转体低速入水流场及表面载荷特性有一定的改善作用。Abstract: To study the influence of side-direction ventilation on the surface loads of a revolving body during water entry, based on the VOF (volume of fluid) model and the Realizable k-ε two-layer turbulence model, the numerical prediction of the flow field evolution and analysis of the surface load characteristics when a side-direction ventilated revolving body into the water at a low-speed are carried out. By comparing the cavity shape between the numerical predictions and the experimental results, the validity of the numerical method is verified. The effects of different ventilation rates on the cavity shape, the flow field evolution, and the surface load characteristics are then analyzed. The results show that ventilation changes the process of the cavity evolution and the pressure on the sidewall surface of the revolving body. With the effect of ventilation, the time when the first cavity falls off is delayed, and the ventilation gas flows to the area behind the cavitator, which improves the negative pressure situation behind the cavitator. The ventilation gas forms an obvious vortex structure near the spout, which then merges with another vortex formed by the cavitator at the cavity wall, leading to an increase in the vortex intensity in the middle of the cavity. With the increase of the ventilation rate, the closure time of the cavity becomes later, the volume of the cavity gets bigger, and the cavity near the tail of the revolving body is less likely to fall off. Compared to the non-ventilation situation, the ventilation will reduce the fluctuations of the surface loads. The greater the ventilation rate, the less the surface load fluctuations are. In general, the side-direction ventilation improves the flow field and the surface load characteristics of the revolving body during low-speed water entry.
-
Key words:
- revolving body /
- head-ventilation /
- water entry /
- flow field evolution /
- surface load
-
图 3 数值模拟得到的空泡形态与试验结果的对比
Figure 3. Comparison of cavity shape between numerical simulation and experiment
图 5 t=10～40 ms时回转体侧壁表面相对压力
Figure 5. Relative pressure of revolving body at t=10～40 ms
图 9 监测点P1、P2在不同通气率条件下的压力时间曲线
Figure 9. Pressure-time curves at point P1 and P2 at different ventilation rates
表 1 空泡最大直径及长度
Table 1. Maximum diameter and length of cavity
时间/ms 空泡最大直径/mm 空泡长度/mm CQS=0 CQS=0.5 CQS=0 CQS=0.5 10 51.2 52.0 78.5 79.0 20 46.8 56.8 102.3 115.8 30 44.7 49.6 129.0 147.7 40 43.0 48.0 130.0 176.9 50 43.1 48.0 118.3 177.1 60 43.0 48.0 121.3 184.2 
下载: 导出CSV
-
[1] 张岳青, 蔡卫军, 李建辰. 鱼雷斜入水过程非定常运动仿真研究 [J]. 船舶力学, 2019, 23(1): 20–28. DOI: 10.3969/j.issn.1007-7294.2019.01.003.ZHANG Y Q, CAI W J, LI J C. Study of unsteady motion simulation for the torpedo oblique water entry problem [J]. Journal of Ship Mechanics, 2019, 23(1): 20–28. DOI: 10.3969/j.issn.1007-7294.2019.01.003. [2] SHI Y, GAO X F, PAN G. Experimental and numerical investigation of the frequency-domain characteristics of impact load for AUV during water entry [J]. Ocean Engineering, 2020, 202: 107203. DOI: 10.1016/j.oceaneng.2020.107203. [3] 杨晓彬, 许国冬. 基于重叠网格法的飞机水上降落水动力砰击载荷研究 [J]. 振动与冲击, 2020, 39(2): 57–63. DOI: 10.13465/j.cnki.jvs.2020.02.009.YANG X B, XU G D. Identification of hydrodynamic impact loads during the airplane ditching based on overset grid method [J]. Journal of Vibration and Shock, 2020, 39(2): 57–63. DOI: 10.13465/j.cnki.jvs.2020.02.009. [4] 秦洪德, 赵林岳, 申静. 入水冲击问题综述 [J]. 哈尔滨工业大学学报, 2011, 43(S1): 152–157.QIN H D, ZHAO L Y, SHEN J. Review of water entry problem [J]. Journal of Harbin Institute of Technology, 2011, 43(S1): 152–157. [5] WORTHINGTON A M. On impact with a liquid surface [J]. Proceedings of the Royal Society of London, 1883, 34(220/221/222/223): 217–230. DOI: 10.1098/rspl.1882.0035. [6] VON KARMAN T. The impact on seaplane floats during landing: NACA-TN-321[R]. Washington: NACA, 1929. [7] 陈学农, 何友声. 平头物体三维带空泡入水的数值模拟 [J]. 力学学报, 1990, 22(2): 129–138.CHEN X N, HE Y S. Numerical simulation of 3-D water entry of blunt cylinder with a ventilatedcavity [J]. Chinese Journal of Theoretical and Applied Mechanics, 1990, 22(2): 129–138. [8] ZHAO R, FALTINSEN O. Water entry of two-dimensional bodies [J]. Journal of Fluid Mechanics, 1993, 246: 593–612. DOI: 10.1017/S002211209300028X. [9] 王永虎, 魏照宇. 楔形体入水时域解的复边界元数值分析 [J]. 爆炸与冲击, 2012, 32(1): 55–60. DOI: 10.11883/1001-1455(2012)01-0055-06.WANG Y H, WEI Z Y. Numerical analysis for water entry of wedges based on a complex variable boundary element method [J]. Explosion and Shock Waves, 2012, 32(1): 55–60. DOI: 10.11883/1001-1455(2012)01-0055-06. [10] 马庆鹏, 魏英杰, 王聪, 等. 不同头型运动体高速入水空泡数值模拟 [J]. 哈尔滨工业大学学报, 2014, 46(11): 24–29. DOI: 10.11918/j.issn.0367-6234.2014.11.004.MA Q P, WEI Y J, WANG C, et al. Numerical simulation of high-speed water entry cavity of cylinders [J]. Journal of Harbin Institute of Technology, 2014, 46(11): 24–29. DOI: 10.11918/j.issn.0367-6234.2014.11.004. [11] 宋武超, 王聪, 魏英杰, 等. 不同头型回转体低速倾斜入水过程流场特性数值模拟 [J]. 北京理工大学学报, 2017, 37(7): 661–666. DOI: 10.15918/j.tbit1001-0645.2017.07.001.SONG W C, WANG C, WEI Y J, et al. Numerical simulation of the flow field characteristics of low speed oblique water entry of revolution body [J]. Transactions of Beijing Institute of Technology, 2017, 37(7): 661–666. DOI: 10.15918/j.tbit1001-0645.2017.07.001. [12] HOU Z, SUN T Z, QUAN X B, et al. Large eddy simulation and experimental investigation on the cavity dynamics and vortex evolution for oblique water entry of a cylinder [J]. Applied Ocean Research, 2018, 81: 76–92. DOI: 10.1016/j.apor.2018.10.008. [13] 张佳悦, 李达钦, 吴钦, 等. 航行体回收垂直入水空泡流场及水动力特性研究 [J]. 力学学报, 2019, 51(3): 803–812. DOI: 10.6052/0459-1879-18-364.ZHANG J Y, LI D Q, WU Q, et al. Numerical investigation on cavity structures and hyrodynamics of the vehicle during vertical water-entry [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 803–812. DOI: 10.6052/0459-1879-18-364. [14] SONG Z J, DUAN W Y, XU G D, et al. Experimental and numerical study of the water entry of projectiles at high oblique entry speed [J]. Ocean Engineering, 2020, 211: 107574. DOI: 10.1016/j.oceaneng.2020.107574. [15] 魏海鹏, 史崇镔, 孙铁志, 等. 基于ALE方法的航行体高速入水缓冲降载性能数值研究 [J]. 爆炸与冲击, 2021, 41(10): 112–123. DOI: 10.11883/bzycj-2020-0461.WEI H P, SHI C B, SUN T Z, et al. Numerical study on load-shedding performance of a high-speed water-entry vehicle based on an ALE method [J]. Explosion and Shock Waves, 2021, 41(10): 112–123. DOI: 10.11883/bzycj-2020-0461. [16] ZHENG K Y, ZHAO X Z, YAN D M. Numerical simulation of water entry of two-dimensional structures with complex geometry using a CIP-based model [J]. Applied Ocean Research, 2021, 106: 102379. DOI: 10.1016/j.apor.2020.102379. [17] HOWARD E A. Protective nose cap for torpedoes: US2889772 [P]. 1959-06-09. [18] LI Y, ZONG Z, SUN T Z. Crushing behavior and load-reducing performance of a composite structural buffer during water entry at high vertical velocity [J]. Composite Structures, 2021, 255: 112883. DOI: 10.1016/j.compstruct.2020.112883. [19] SHI Y, PAN G, YIM S C, et al. Numerical investigation of hydroelastic water-entry impact dynamics of AUVs [J]. Journal of Fluids and Structures, 2019, 91: 102760. DOI: 10.1016/j.jfluidstructs.2019.102760. [20] CHUANG S L. Experiments on flat-bottom slamming [J]. Journal of Ship Research, 1966, 10(1): 10–17. DOI: 10.5957/jsr.1966.10.1.10. [21] 陈震, 肖熙. 空气垫在平底结构入水砰击中作用的仿真分析 [J]. 上海交通大学学报, 2005, 39(5): 670–673. DOI: 10.3321/j.issn:1006-2467.2005.05.002.CHEN Z, XIAO X. Simulation analysis on the role of air cushion in the slamming of a flat-bottom structure [J]. Journal of Shanghai Jiaotong University, 2005, 39(5): 670–673. DOI: 10.3321/j.issn:1006-2467.2005.05.002. [22] 潘龙, 王焕然, 姚尔人, 等. 头部喷气平头圆柱体人水缓冲机制研究 [J]. 工程热物理学报, 2015, 36(8): 1691–1695.PAN L, WANG H R, YAO E R, et al. Mechanism research on the water-entry impact of the head-jetting flat cylinder [J]. Journal of Engineering Thermophysics, 2015, 36(8): 1691–1695. [23] 刘华坪, 余飞鹏, 韩冰, 等. 头部喷气影响航行体入水载荷的数值模拟 [J]. 工程热物理学报, 2019, 40(2): 300–305.LIU H P, YU F P, HAN B, et al. Numerical simulation study on influence of top jet in object water entering impact [J]. Journal of Engineering Thermophysics, 2019, 40(2): 300–305. [24] JIANG Y H, BAI T, GAO Y, et al. Water entry of a constraint posture body under different entry angles and ventilation rates [J]. Ocean Engineering, 2018, 153: 53–59. DOI: 10.1016/j.oceaneng.2018.01.091. [25] 赵海瑞, 施瑶, 潘光. 头部喷气航行器高速入水空泡特性数值分析 [J]. 西北工业大学学报, 2021, 39(4): 810–817. DOI: 10.1051/jnwpu/20213940810.ZHAO H R, SHI Y, PAN G. Numerical simulation of cavitation characteristics in high speed water entry of head-jetting underwater vehicle [J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 810–817. DOI: 10.1051/jnwpu/20213940810. [26] SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ε eddy viscosity model for high reynolds number turbulent flows [J]. Computers & Fluids, 1995, 24(3): 227–238. DOI: 10.1016/0045-7930(94)00032-T. [27] RODI W. Experience with two-layer models combining the k-ε model with a one-equation model near the wall [C] // 29th Aerospace Sciences Meeting. Reno, USA: AIAA, 1991: 216. DOI: 10.2514/6.1991-216. [28] HALLER G. An objective definition of a vortex [J]. Journal of Fluid Mechanics, 2005, 525: 1–26. DOI: 10.1017/S0022112004002526. 期刊类型引用(7)
1. 刘平，苏雨萌，陈庞. 钢纤维增韧混凝土抗冲击性能研究综述. 混凝土. 2024(04): 47-51 . 
百度学术2. 余一松，李地元，蒋京泰，马金银，刘家明. 钢纤维混凝土动态力学特性及损伤规律研究. 工程科学学报. 2024(12): 2181-2190 . 百度学术3. 杜闯，刘晓彤，李艳艳，宋帅，高启辉. 冲击爆炸荷载下UHPC动态本构模型研究现状. 混凝土. 2024(11): 51-54+60 . 百度学术4. 谢开仲，刘振威，盖炳州，新赢，朱茂金. 不同岩性的机制砂混凝土本构关系及力学性能. 建筑科学与工程学报. 2021(01): 99-106 . 百度学术5. 陈猛，王浩，齐迈，李艺，王述红，王二磊. 岩石–钢纤维混凝土复合层动态压缩 性能试验研究. 岩石力学与工程学报. 2020(06): 1222-1230 . 百度学术6. 李艳，张文彬，刘泽军. PVA-ECC动态压缩性能研究. 建筑材料学报. 2020(03): 513-520 . 百度学术7. 钟晨，叶中豹，王颖. 一种新形式非线性钢纤维混凝土本构关系. 硅酸盐通报. 2018(05): 1583-1588 . 百度学术其他类型引用(14)
-
百度学术推荐阅读
高速冲击下混凝土动力学性质和动态温度研究
黄晨瑞 等, 爆炸与冲击, 2025
考虑微结构特征的陶瓷材料含损伤本构模型
刘慕皓 等, 爆炸与冲击, 2024
Zl114a铝合金本构关系与失效准则参数的确定
谭毅 等, 爆炸与冲击, 2024
基于3d细观模型的混凝土动态压缩行为分析
张湘茹 等, 爆炸与冲击, 2024
考虑itz厚度的钢纤维混凝土损伤破坏数值分析
万克诚 等, 西安工业大学学报, 2024
钢-混凝土组合框架结构倒塌动力响应特征及参数分析
彭修宁 等, 桂林理工大学学报, 2024
基于构型力断裂准则的骨料干涉作用分析
杜健欢 等, 西南交通大学学报, 2023
Fungal infection of insects: molecular insights and prospects
Hong, Song et al., TRENDS IN MICROBIOLOGY, 2024
Property assessment of high-performance concrete containing three types of fibers
INTERNATIONAL JOURNAL OF CONCRETE STRUCTURES AND MATERIALS
Influence of longitudinal air gaps within charge structure on the detonation performance of explosives
GUO Wencan et al., EXPLOSION AND SHOCK WAVES, 2025
Powered by 
图(9) / 表(1)
计量
- 文章访问数: 489
- HTML全文浏览量: 246
- PDF下载量: 52
- 被引次数: 21