钢框架结构具有构造简单、自重轻和抗震性能好等优点，在中高层建筑和大跨度结构中应用十分广泛。由于各类爆炸事件频发，不仅造成建筑物毁伤，而且严重威胁人身安全，因此爆炸荷载作用下钢框架的动态响应和毁伤效应成为研究的焦点。Al-Thairy^[1]提出横向爆炸荷载作用下轴压钢柱的单自由度（single degree of freedom, SDOF）分析方法；李忠献等^[2]采用数值模拟方法研究了爆炸荷载作用下钢柱和平面钢框架的动态响应和破坏模式；丁阳等^[3]分析了爆炸荷载作用下钢框架结构的动态响应，对比了不同炸药当量下结构的抗倒塌性能；陈烨^[4]研究了爆炸与火灾联合作用下钢框架的抗倒塌机制，并基于损伤评估曲线提出了结构倒塌的预测方法；张秀华等^[5-6]、Jama等^[7]、Nassr等^[8]对爆炸荷载作用下钢梁、钢柱的动态响应进行了数值模拟和实验研究，得到了钢梁、钢柱的动态响应规律。

由于原尺模型爆炸实验限存在模型制作成本高、实验设备难以匹配大尺寸试件等，因此通常选取缩比模型结构进行实验。但缩比模型能否准确反映原尺模型的动态响应特征十分关键。钟渝楷等^[9]研究了冲击作用下单层网壳的相似律，研究中计及几何偏差及重力的影响，结果表明缩比模型能较好地预测原型的动态响应。Fu等^[10]研究了内爆作用下单层柱面网壳的相似律，并给出了合理的模型缩尺比系数。

目前，对远距离爆炸荷载作用下钢框架结构的相似律研究很少，迫切需要开展相应的研究工作。为此，本文中将针对远距离爆炸荷载作用下的钢框架结构开展相似律研究。基于量纲分析方法，推导原型与缩比模型的相似关系。首先，基于已有的钢框架子结构爆炸实验，采用非线性有限元软件AUTODYN验证该数值模型及流固耦合方法的可靠性；然后，将解析爆炸边界方法在钢框架远距离爆炸数值模拟中的准确性和计算效率与流固耦合方法进行对比，以验证解析爆炸边界方法对于钢框架远距离爆炸响应模拟的可靠性；最后，对不同相似比两层三跨钢框架结构在远距离爆炸荷载作用下的动态响应及毁伤效应进行分析，验证相似律的可行性和正确性。

1.   钢框架相似理论

谈庆明^[11] 开展了爆炸成形实验研究，发现不同尺寸构件变形符合几何相似律。本文中将基于量纲分析方法，对钢框架结构在远距离爆炸荷载作用下的相似律进行推导。

若模型与原型的爆炸冲击和边界条件相同，认为构件变形量W与构件尺寸、材料参数以及爆炸荷载相关，可以表示为：

式中：l为结构跨度，l₁、l₂、l₃分别为框架梁上下翼板和腹板的长度，H_c为框架柱的长度，h为框架柱方形截面边长，如图1所示；模拟计算中框架梁的上下翼板、腹板和框架柱外板均采用壳单元， M_b和M_c分别为框架梁和框架柱各个板壳部件的塑性极限弯矩，N_b和N_c分别为框架梁和框架柱各个板壳部件的塑性极限中面力；ρ、E、ν和σ_y分别为钢框架钢材密度、弹性模量、泊松比和屈服应力；p和t分别为爆炸荷载的超压峰值和正压持续时间。

图  1  几何特征量示意图

Figure  1.  Schematic diagram of the geometric characteristic quantity

下载: 全尺寸图片 幻灯片

在仅考虑冲击波作用下结构的动态响应和毁伤效应的前提下，此物理问题中仅有3个基本量纲：M、L和T。而本问题中相关物理量的量纲幂次指数如表1所示。

表  1  爆炸毁伤问题中变量的量纲幂次指数

Table  1.  Dimensional power coefficients of variables in explosion damage problems

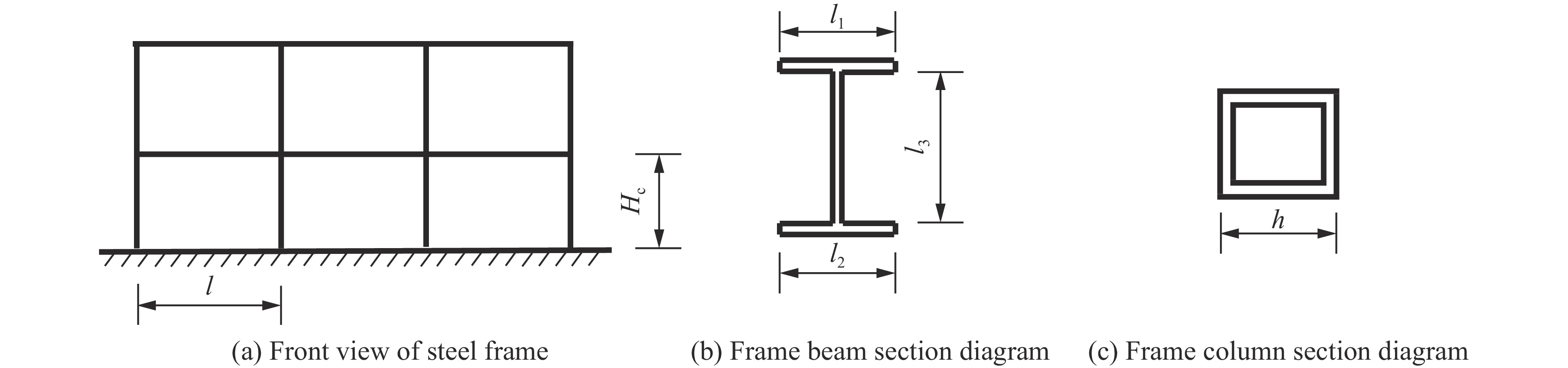
物理量	M	L	T
$l,{l_1},{l_2},{l_3},{H_{\text{c}}},h$	0	1	0
${M_{\text{b}}},{M_{\text{c}}}$	1	2	-2
${N_{\text{b}}},{N_{\text{c}}}$	1	1	-2
ρ	1	-3	0
E	1	1	-2
ν	0	0	0
σy	1	-1	-2
p	1	-1	-2
t	0	0	1

下载: 导出CSV 

| 显示表格

选取钢框架结构跨度l、钢框架构件密度ρ和钢框架构件屈服应力σ_y为基本物理量，则基本量纲M、L和T对应的物理量为$\ \rho {l^3}$、$l$、$\sqrt {\dfrac{{\rho {l^2}}}{{{\sigma _{\text{y}}}}}}$。

根据Π定理，结合表1和量纲对应的物理量对该物理问题表达式进行量纲分析，可将表达式简化为无量纲表达式：

式（2）右边各项为自变量相似准数，如表2所示。从表2可以看出，各相似准数具有明确的物理意义，其中${\varPi _1}$～${\varPi _5}$表征结构几何特性，${\varPi _6}$～${\varPi _9}$表征结构内部广义力。

表  2  爆炸毁伤问题中自变量相似准数

Table  2.  Similar parameters of independent variables in explosion damage problems

${\varPi _1}$	${\varPi _2}$	${\varPi _3}$	${\varPi _4}$	${\varPi _5}$	${\varPi _6}$	${\varPi _7}$	${\varPi _8}$	${\varPi _9}$
$\dfrac{{{l_1}}}{l}$	$\dfrac{{{l_2}}}{l}$	$\dfrac{{{l_3}}}{l}$	$\dfrac{{{H_{\text{c}}}}}{l}$	$\dfrac{h}{l}$	$\dfrac{{{M_{\text{b}}}}}{{{\sigma _{\text{y}}}{l^3}}}$	$\dfrac{{{N_{\text{b}}}}}{{{\sigma _{\text{y}}}{l^2}}}$	$\dfrac{{{M_{\text{c}}}}}{{{\sigma _{\text{y}}}{l^3}}}$	$\dfrac{{{N_{\text{c}}}}}{{{\sigma _{\text{y}}}{l^2}}}$

下载: 导出CSV 

| 显示表格

根据Π定理可知，若要使缩比模型m与原型p满足相似关系，则缩比模型和原型应满足${\varPi _{\text{m}}}/{\varPi _{\text{p}}} = 1$。由于缩比模型和原型按照几何相似比进行缩放，且采用相同材料，因此可得到：

结合式（3），可将式（2）进一步简化为：

考虑到模型和原型材料相同，则式（4）可进一步简化为：

对式（5）应用Π定理，令${\varPi _{10}} = p/{\sigma _{\text{y}}}$，${\varPi _{11}} = t{({\sigma _{\text{y}}}/\rho {l^2})^{1/2}}$，采用${K_X} = {X_{\text{m}}}/{X_{\text{p}}}$表示模型和原型相关物理量的比值，其中X为变量，可得：

进一步分析简化可得：

式（7）、（9）表示当钢框架结构原型与缩比模型满足几何相似，爆炸荷载超压不变、正压持时按照几何相似比进行缩放时，可使钢框架结构原型与缩比模型的变形量满足几何相似关系。

根据Kinney等^[12]的化爆经验公式可计算爆炸荷载的超压峰值p和正压持续时间t：

式中：p₀为标准大气压；Z为比例距离， Z=R/W₀^1/3，其中R为爆炸中心与测点的距离，W₀为TNT炸药当量。

当缩比模型与原型炸药的几何尺寸比、炸药爆炸中心与钢框架测点的几何距离比均等于缩比模型与原型的几何相似比时，即缩比模型与原型的比例距离Z相等时，可得爆炸荷载超压峰值p不变和正压持续时间t按照几何相似比缩放，在远距离爆炸荷载作用下，钢框架结构原型与缩比模型构件变形量W满足几何相似律。因此，当钢框架结构原型与缩比模型满足几何相似时，可得到远距离爆炸荷载作用下钢框架结构原型与缩比模型的位移动态响应相似，基于层间位移角评估指标的钢框架结构原型与缩比模型的毁伤程度相似。

2.   数值方法验证

2.1   爆炸流固耦合方法验证

Dinu等^[13]对装药仓内钢框架子结构试件进行了近距离爆炸实验研究。实验中，钢框架子结构的横梁长度为1400 mm，截面为H220 mm×110 mm×5.9 mm×9.2 mm，立柱高1990 mm，截面为H260 mm×260 mm×10 mm×17.5 mm；圆柱形TNT炸药质量为1.815 kg，放置在距柱腹板表面200 mm、距柱基1250 mm和梁底翼缘300 mm处，梁柱端受横向约束。采用非线性有限元分析软件AUTODYN中的流固耦合方法对该实验进行分析，以验证该方法在结构爆炸响应模拟中的可靠性，建立的钢框架子结构流固耦合数值模型如图2所示。

图  2  钢框架子结构流固耦合数值模型

Figure  2.  Numerical model of a steel frame substructure with fluid-structure interaction

下载: 全尺寸图片 幻灯片

在该数值模型中，钢框架子结构梁、板、柱均采用实体单元建模，构件间采用共节点连接，空气域除底面外均施加无反射边界。空气采用理想气体状态方程，气体绝热指数为1.4，初始密度为1.225 kg/m³。炸药采用JWL状态方程描述：

式中：A、B、R₁、R₂和$\omega$均为材料参数；V为爆轰产物的相对体积；E₀为爆轰产物的初始化内能；参数如表3所示，表中ρ_t为炸药的密度。

表  3  炸药的材料参数

Table  3.  Material parameters of explosive

ρt / (kg∙m−3)	A / GPa	B / GPa	R1	R2	$\omega$	DCJ / (m∙s−1)	PCJ / GPa	E0 / (kJ∙m−3)
1630	373.77	3.7471	4.15	0.9	0.35	6930	21	6×106

下载: 导出CSV 

| 显示表格

钢材材料模型采用Johnson-Cook本构模型^[14-15]，具体方程为：

式中：A、B、C、n和m均为材料参数；${\varepsilon _{\text{p}}}$为等效塑性应变；$\dot \varepsilon_{\rm{p}}$为等效塑性应变率；${\dot \varepsilon _0}$为参考塑性应变率；${T_{\text{H}}}$为无量纲的温度，具体参数如表4所示。实验中，钢框架梁柱腹板及翼缘采用不同屈服强度的钢板，相应材料属性见表5，其中${f_{\text{y}}}$为屈服强度，${f_{\text{u}}}$为极限强度。对于不同钢板，除屈服强度以外，均采用相同J-C本构参数。为模拟材料开裂，采用塑性应变失效准则，失效塑性应变为0.15。

表  4  钢材J-C模型参数

Table  4.  The J-C model parameters of steel

ρ / (kg∙m−3)	E / GPa	ν	B / MPa	C	n	m	${\dot \varepsilon _0}/{{\text{s}}^{ - 1}}$
7850	210	0.3	280	0.022	0.4	1.03	1

下载: 导出CSV 

| 显示表格

表  5  钢框架材料属性

Table  5.  Material properties of steel frame

子结构试件	${f_{\text{y}}}$/ MPa	${f_{\text{u}}}$/ MPa
梁翼缘	345	464
梁腹板	353	463
柱翼缘	420	529
柱腹板	407	539
端板	305	417

下载: 导出CSV 

| 显示表格

数值模拟结果对网格有较高依赖性，首先对实验模型进行网格收敛性分析，建立网格尺寸分别为40、20、15、10和5 mm的数值模型。由图3的柱腹板特征点（应变片1）的位移时程曲线可知，随着网格尺寸的细化，数值结果趋于稳定。当网格尺寸分别为10和5 mm时，测点位移差异较小，最大位移相对误差仅2.91%，因此可认为网格尺寸为10 mm时，数值结果已收敛。考虑计算规模和效率，钢框架子结构模型网格尺寸确定为10 mm。子结构失效模式对比如图4所示，数值结果表明，柱腹板的破坏长度约为627 mm，与实测值600 mm极为接近，误差为4.5%。因此，可认为采用该流固耦合分析方法进行结构爆炸响应分析是可靠的。

图  3  不同网格尺寸得到的特征点（应变片1）位移时程曲线比较

Figure  3.  Comparison of displacement-time curves at the feature point (gauge 1) obtained by different mesh sizes

下载: 全尺寸图片 幻灯片

图  4  失效模式对比

Figure  4.  Comparison of the failure modes

下载: 全尺寸图片 幻灯片

2.2   解析爆炸边界方法验证

根据前文分析，流固耦合方法能够合理模拟结构的爆炸响应，但由于该方法需要建立足够的空气域，对于远距离爆炸，则造成空气域过大，使计算效率极其低下。解析爆炸边界依据美国陆军技术手册TM 5-855-1^[16]提供的经验公式以及荷载曲线，可将压力荷载直接施加到受爆面上，无需建立空气域，使计算效率相对较高。该边界考虑了爆炸距离、爆炸波的入射角、入射超压和反射超压，在无遮挡情况下的结构爆炸荷载毁伤研究中，数值模拟结果与实验结果吻合度较好^[17]，施加的压力载荷计算公式为：

式中：$p(t)$为施加到结构上的压力值；${p_{{\text{0r}}}}$为反射压力峰值，根据入射角和入射超压计算；${t_{{\text{arr}}}}$为冲击波到达时间，${t_0}$为正压持续时间；${\lambda _{\text{R}}}$为衰减参数，按式$\displaystyle\int_{{t_{arr}}}^{{t_{arr}} + {t_0}} {p(t)} {\text{d}}t = I$计算，其中$I$为正压冲量。

因此，采用流固耦合方法和解析爆炸边界方法进行钢框架结构远距离爆炸响应分析，以验证解析爆炸边界方法对于钢框架远距离爆炸响应模拟的可靠性。

选取某钢框架结构的底2层子结构模型作为原型计算模型，子结构原型层高为2层、纵向为3跨、横向为两跨。梁截面为H型钢，柱为方钢管，梁柱材料均使用Q345钢。图5为原型结构示意图。钢框架缩比模型选取30 kg TNT炸药当量进行数值模拟，其中缩比模型几何比为1∶5，炸药置于距横向跨1层中柱一定距离处，其中爆高为0.96 m，爆距为5 m，比例距离Z为1.61 m/kg^1/3；原型爆高为4.8 m，爆距为25 m，比例距离Z为1.61 m/kg^1/3。甘露等^[18]将比例距离Z大于1.2 m/kg^1/3定义为远距离爆炸，本研究工况符合远距离爆炸条件。选择几何比为1∶5的缩比模型，因图纸原型梁柱截面尺寸缩放5倍后厚度等不满足工厂生产加工、结构稳定性要求，因此根据文献[19]选择缩比钢框架模型最小梁柱截面尺寸，分别为梁H100 mm×50 mm×5 mm×7 mm、柱H120 mm×120 mm×5 mm×5 mm，则原型结构截面尺寸为梁H500 mm×250 mm×25 mm×35 mm、柱H600 mm×600 mm×25 mm×25 mm。

图  5  结构示意图

Figure  5.  Schematic diagram of a steel structure

下载: 全尺寸图片 幻灯片

利用AUTODYN软件建立有限元模型。梁柱均采用壳单元，原型网格尺寸为100 mm；梁柱连接处采用共节点建模，所有立柱底部设为固定约束；使用解析爆炸边界方法将压力载荷施加到结构4个短跨方向梁柱表面上，如图5中短跨梁柱阴影表面处。由于本文中拟通过钢框架结构的缩比数值模拟实现对原型结构爆炸响应和毁伤效应的研究，以指导后续缩比实验的开展，因此，依据实际场景中存在的重力场，针对不同尺度钢框架结构模型，均考虑相同的重力场，即重力加速度为9.8 m/s²。由于结构按照几何相似比进行缩放，根据量纲分析，缩比模型重力以几何相似比K_l的3次方得到缩放。模型中，Q345钢屈服强度为345 MPa，采用Johnson-Cook本构模型，参数见表4。损伤模型采用塑性应变失效准则，失效塑性应变为0.15。在远距离爆炸工况下钢框架结构距离炸药较远，因此忽略温度效应。

图6为原型结构分别采用流固耦合和解析爆炸边界计算得到的迎爆面中柱位移对比。由图6可知，对于迎爆面1层中柱测点位移（图6中应变片1所示）、2层中柱测点位移（图6中应变片2所示）整体趋势一致，仅峰值存在较小差异。这可能是由于流固耦合计算中爆炸冲击波发生一定反射、绕射所导致。但总体而言，使用解析爆炸边界方法满足计算精度要求并能显著提高计算效率，因此本文中选用该方法进行分析研究。

图  6  中柱侧移对比

Figure  6.  Comparison of the lateral displacement of the middle column

下载: 全尺寸图片 幻灯片

3.   数值结果分析

3.1   应变率分析

以图5中的钢框架子结构为原型，缩比模型几何比为1∶5，并对30 kg TNT炸药当量工况开展远距离爆炸缩比钢框架数值模拟。缩比模型梁截面尺寸为H100 mm×50 mm×5 mm×7 mm，柱为120 mm×120 mm×5 mm×5 mm；原型梁截面尺寸为H500 mm×250 mm×25 mm×35 mm，柱为600 mm×600 mm×25 mm×25 mm。缩比钢框架数值模拟中爆距分别为5、6 m，比例距离Z分别为1.61、1.93 m/kg^1/3，对结构迎爆面1层中柱柱顶测点（图6中应变片1所示）进行应变率分析。图7为钢框架不同工况下测点的应变时程曲线，表6为由图7计算得到的钢框架在远距离爆炸时不同距离下测点的应变率结果。

图  7  钢框架在不同工况下的应变时程曲线

Figure  7.  Strain history curves of the steel frame under different conditions

下载: 全尺寸图片 幻灯片

表  6  钢框架不同工况下应变率计算

Table  6.  Strain rate of the steel frame under different conditions

工况1	比例1/5	应变率计算值/s−1		工况2	比例1/5	应变率计算值/s−1
30 kg，5 m	m	0.5590		30 kg，6 m	m	0.3475
3750 kg，25 m	p	0.1038		3750 kg，30 m	p	0.0711

下载: 导出CSV 

| 显示表格

由表6可知：两层三跨钢框架结构原型和缩比模型在远距离爆炸工况下，原型和缩比模型的1层中柱迎爆面测点应变率并未出现量级差异。文献[20]中给出了远距离爆炸下的参考应变率范围：0.02～0.30 s⁻¹。本文中计算应变率与文献[20]的结果一致。参考金属材料强度在不同应变率下的实验数据^[20-21]，发现当应变率小于1 s⁻¹时，材料的应变率效应不显著。在本文研究中，钢材本构模型考虑了应变率，但原型和缩比模型得到的应变率差异未达到量级变化且应变率均小于1 s⁻¹，因此，原型和缩比模型中材料受应变率的影响程度几乎相同。综上分析，针对钢框架在远距离爆炸荷载作用下的相似律研究，无需考虑材料应变率效应的缩放。

3.2   钢框架结构相似律验证

以图5中钢框架子结构为原型，其中爆高为4.8 m，爆距为25 m，比例距离Z为1.61 m/kg^1/3。原型梁截面尺寸为H500 mm×250 mm×25 mm×35 mm，柱为H600 mm×600 mm×25 mm×25 mm。根据完全几何相似，缩比模型按几何缩比尺等比完全缩放。表7为模型具体相似比。以结构位移历程一个周期时间为参考，并选取结构迎爆面1层中柱柱顶测点（图6中应变片1所示），得到各相似比动态响应的时间历程曲线并对其按相似比进行相似处理，分析爆炸冲击动态响应随时间历程变化的相似性。图8为各响应的时间历程曲线。

表  7  钢框架缩比模型相似比

Table  7.  The similarity ratios of the scaled steel-frame models

模型	原型	比例1/2	比例1/5	比例1/10	比例1/20
相似比	1	1/2	1/5	1/10	1/20

下载: 导出CSV 

| 显示表格

图  8  钢框架各响应时程曲线

Figure  8.  Response history curves of the steel frame

下载: 全尺寸图片 幻灯片

从响应时间历程曲线看，相似处理之后模型与原型的位移、速度响应时间历程基本一致，应力-应变时程曲线在第1个峰值到达前相似度较高，随后出现较小差异，在远距离爆炸荷载作用下结构的动态响应基本符合几何相似关系。因此，数值模拟表明：两层三跨钢框架模型按几何相似比完全等比缩放时，在远距离爆炸荷载作用下结构的位移动态响应可以通过缩比模型预报。

3.3   钢框架毁伤分析

基于典型建筑结构抗爆标准和损伤评估标准^[22-25]，发现钢框架梁主要采用支座转角及延性比指标进行毁伤评估，对于框架柱则主要采用转角及层间侧向位移指标，并且以上损伤评估指标主要用于单构件评估，缺乏整体框架的爆炸毁伤评估指标。为分析爆炸荷载作用下框架结构的整体损伤，肖绍添^[26]参照建筑抗震设计规范（GB 50011-2010）^[27]中分析结构整体的方法，通过计算层间位移来判断爆炸荷载作用下框架结构的整体损伤，结果表明该方法具有一定适用性。因此，本文中参考文献[26]和建筑结构抗震规范^[27-28]，得到钢框架结构在不同性能要求下的层间位移角限值，文献[29]中定义了与结构损伤状况相对应的层间位移角限制，如表8所示。采用K_δ=δ_m/δ_p表示模型和原型层间位移角的比值，δ=Δu/H，其中Δu为楼层层间位移，H为楼层层高。若模型和原型满足几何相似关系，则K_δ=1，表明钢框架缩比模型与原型结构的毁伤满足几何相似规律。图9为不同缩尺比下钢框架结构模型的应力云图。根据图8的结构位移响应和图9的应力云图数值计算结果，对原型和缩比模型的损伤情况进行分析，可得在远距离爆炸荷载作用下，基于层间位移角评估指标钢框架结构原型与缩比模型的毁伤程度相似。

表  8  与结构损伤状况相对应的层间位移角限制

Table  8.  Interlayer displacement angle limit corresponding to structural damage

性能水平	损伤状态	层间位移角 / %
Ⅰ	完好	δ ≤ 0.2
Ⅱ	很轻微破坏	0.2 < δ ≤ 0.5
Ⅲ	轻微破坏	0.5 < δ ≤ 0.7
Ⅳ	中等破坏	0.7 < δ ≤ 1.5
Ⅴ	严重破坏	1.5 < δ ≤ 2.5
Ⅵ	很严重破坏	2.5 < δ ≤ 5.0
Ⅶ	倒塌	δ > 5.0

下载: 导出CSV 

| 显示表格

图  9  钢框架结构模型应力云图

Figure  9.  Stress contours of the steel frame models

下载: 全尺寸图片 幻灯片

4.   结　论

针对钢框架结构在远距离爆炸荷载作用下的相似律进行研究，基于量纲分析方法，推导了远距离爆炸荷载作用下钢框架原型与缩比模型的几何相似律表达式。首先，基于已有的钢框架子结构爆炸实验，采用AUTODYN建立钢框架子结构数值模型，验证了流固耦合方法在结构爆炸响应分析中的可靠性。在此基础上，将解析爆炸边界方法在钢框架远距离爆炸数值模拟中的准确性和计算效率与流固耦合方法进行对比，结果表明解析爆炸边界方法可以合理模拟钢框架子结构的远距离爆炸响应，且计算效率较高，因此采用该方法对钢框架几何相似律进行验证。通过分析不同相似比两层三跨钢框架结构在远距离爆炸荷载作用下动态响应及毁伤效应，证明了远距离爆炸荷载作用下钢框架几何相似律的合理性。研究结果表明：两层三跨钢框架模型按几何相似比完全等比缩放时，在远距离爆炸荷载作用下钢框架结构原型与缩比模型的位移动态响应相似，基于层间位移角评估指标钢框架结构原型与缩比模型的毁伤程度相似。本文结论可为远距离爆炸荷载作用下钢框架结构的缩比实验提供参考。