A theoretical model of PBXs’ tensile strength based on meso-structure parameters
-
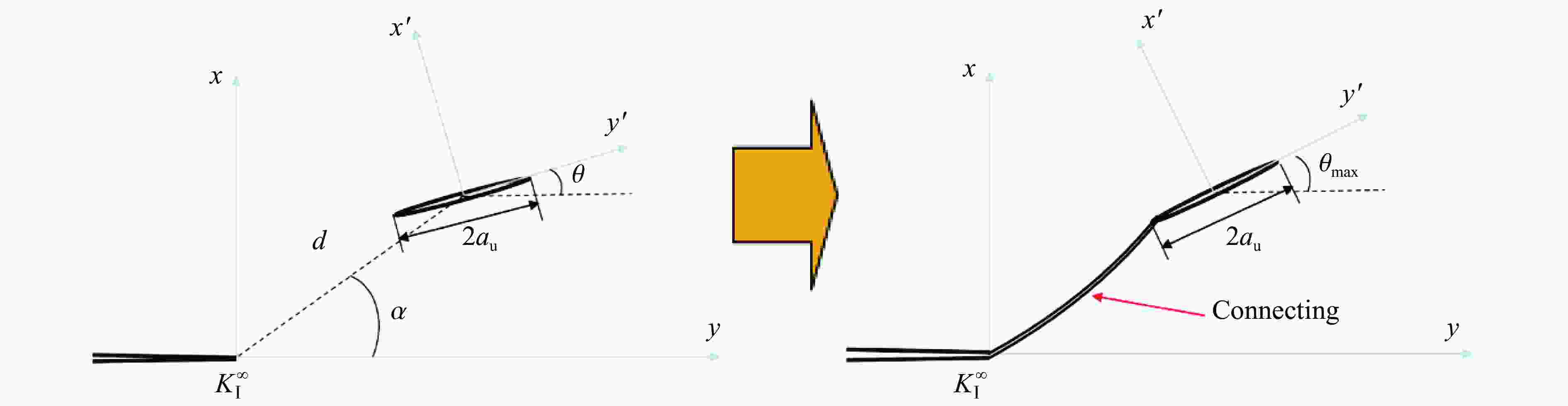
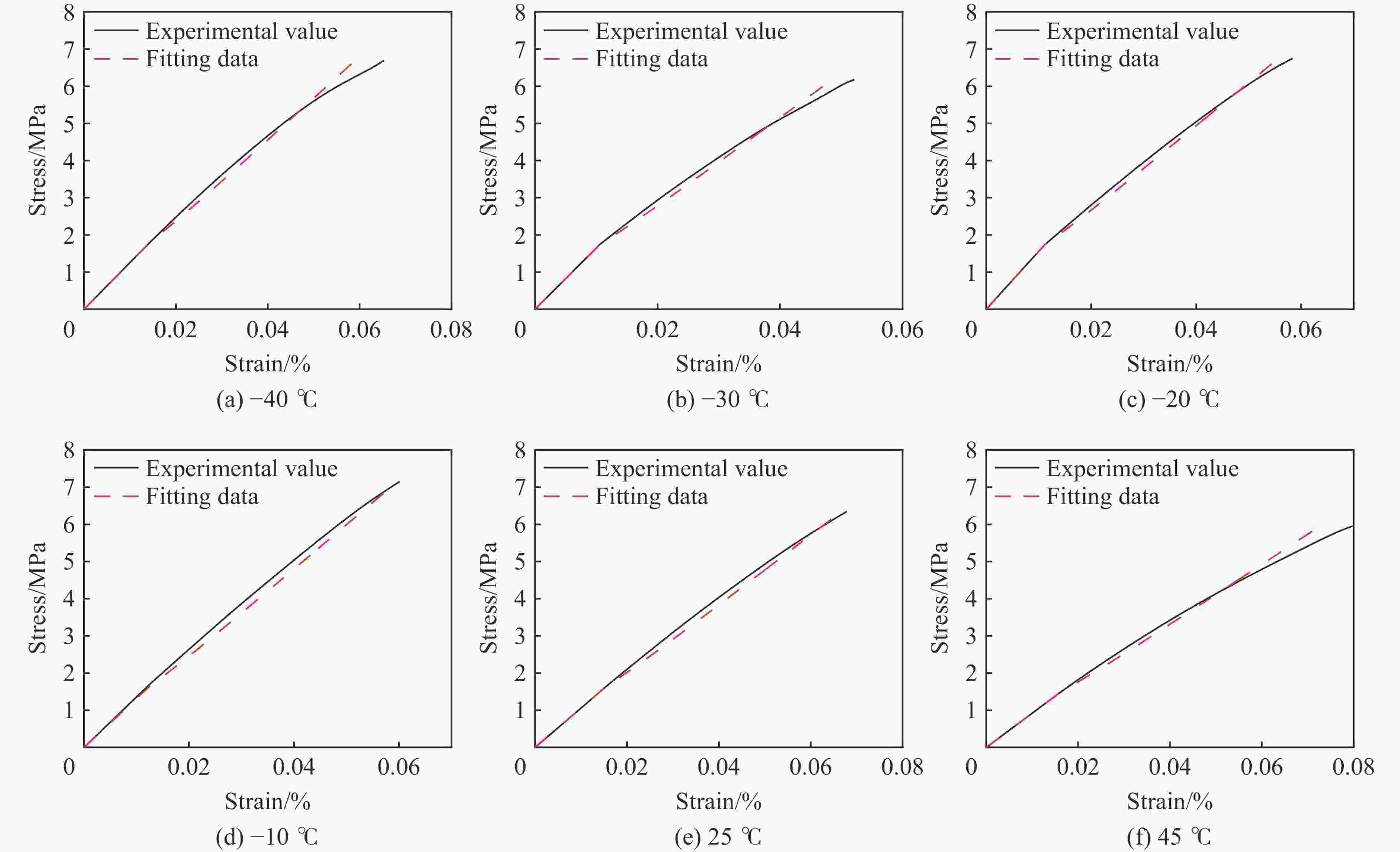
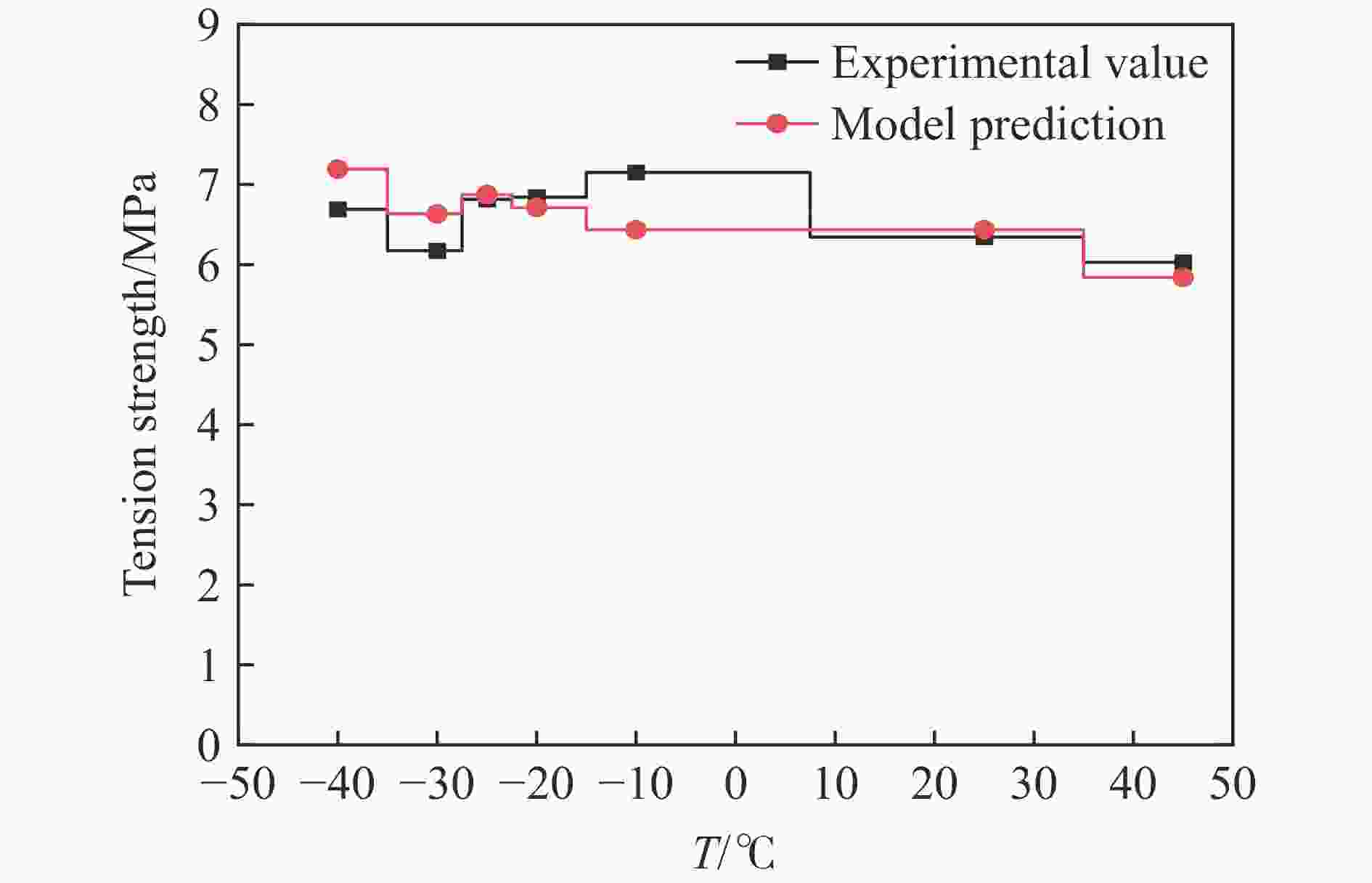
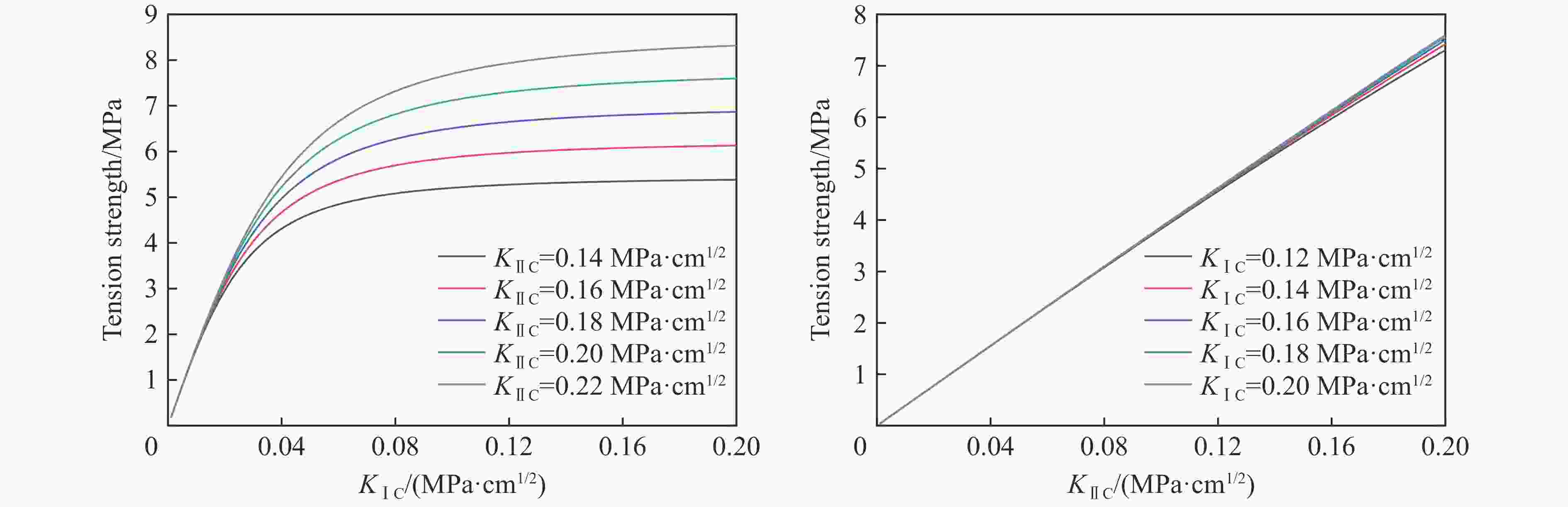
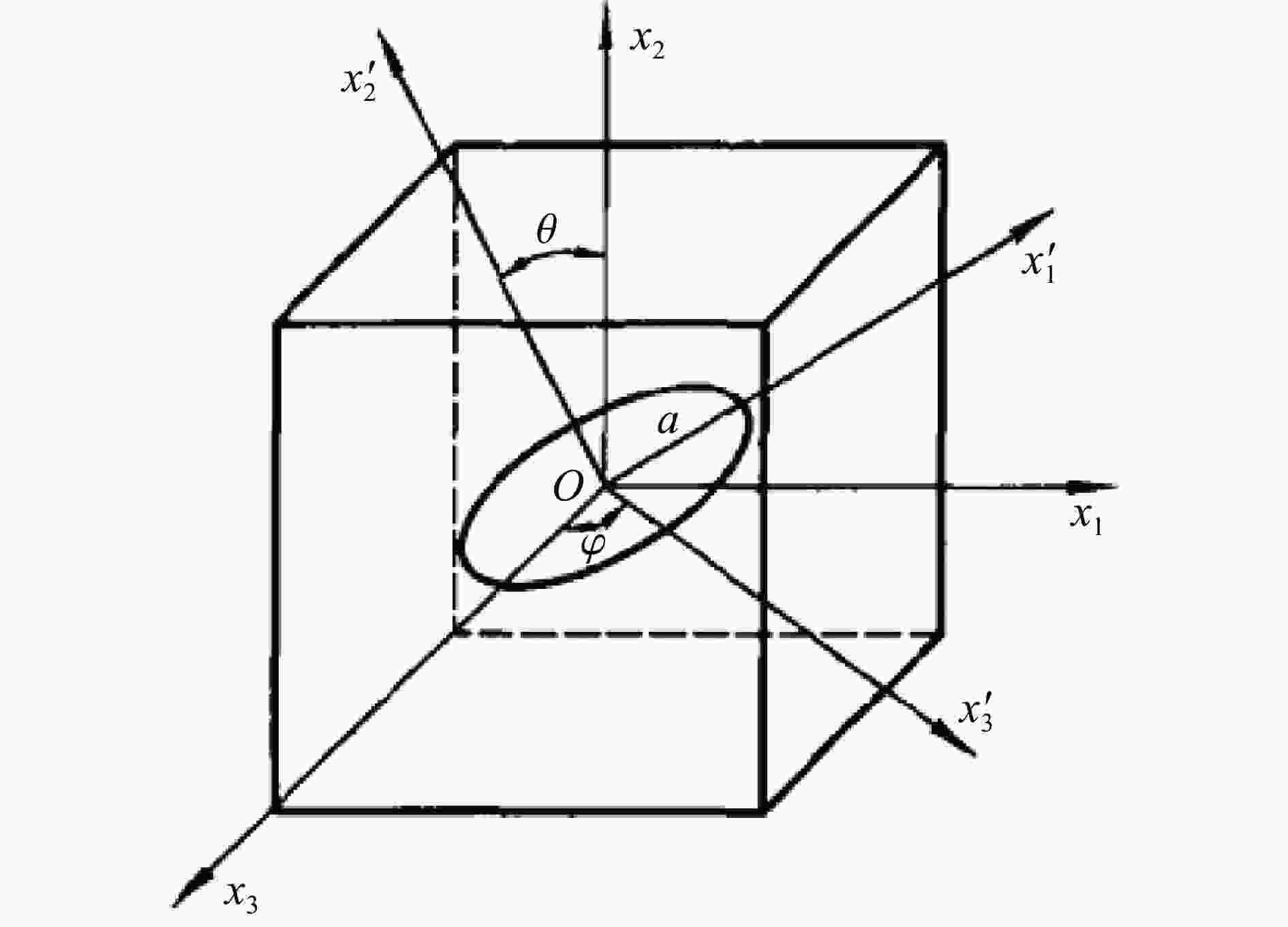
摘要: 为给塑性黏结炸药（PBX）的力学强度设计提供支撑、探索材料细观特征量与材料强度之间的定量规律，应用微裂纹扩展区理论，将PBX炸药的单轴拉伸过程中力学响应特征的变化归结为扩展裂纹取向角度的增加，将扩展裂纹最大取向角与拉伸强度相关联，构建了基于材料细观特征量的拉伸强度理论模型，并采用不同温度的单轴拉伸实验验证了该理论模型的有效性。研究表明：该拉伸强度理论模型可以实现对PBX炸药拉伸强度与炸药微裂纹密度、颗粒/黏结剂界面性能以及颗粒/黏结剂体系的表观杨氏模量、泊松比等细观特征量之间关系的定量描述。Abstract: In practical applications, plastic bonded explosive (PBX) explosives are often used as load bearing structural components. Hence, the mechanical strength is an important parameter in PBXs’ design. It is of great interest how to adjust the microscopic characteristics of the material in the manufacturing process to obtain an PBX with the required strength. PBX consists of a large portion of energetic particles with a small portion of binder. Therefore, a large number of randomly distributed microcracks exist inside. Inspired by the successful application of microcrack extension mechanism in the PBXs’ mechanical response simulation in recent years, the theory related to microcrack extension was applied to the strength modeling study. The domain of microcrack growth (DMG) theory was applied to analyze PBXs’ uniaxial tension. The results shows that the increase in tensile load resulted in microcrack extension at different orientation angles, as well as a decrease in the crack interval. Meanwhile, recent studies on the cascading behavior of randomly distributed microcracks show that the crack cascading behavior with each other is controlled by the orientation angle and crack interval of adjacent cracks. The PBX tensile fracture comes from the instable extension of macroscopic cracks, and the macroscopic crack formation and extension both come from the cascading of microcracks. By treating the strength as the minimum load required for catastrophic crack cascade extension, there is a one-to-one correspondence between the strength and the maximum orientation angle of extended crack. Based on the DMG theory, this one-to-one correspondence is expressed as the theoretical model of tensile strength. This theoretical model establishes the connection between the tensile strength and the meso-structure parameters such as stress intensity factor, microcrack diameter and microcrack density. Comparison of tensile strength model predictions with wide temperature range (from –40 ℃ to 45 ℃) experimental data, indicated that this model is capable to describe the PBXs’ tensile strength. Suggestions for the design of strength enhancement of PBXs can be provided by this theoretical model.
-
Key words:
- PBX /
- tensile strength /
- theoretical model /
- meso damage /
- DMG theory
-
随着航天事业的发展，将会有越来越多的卫星等航天器在轨运行，这些卫星的运行区域大都在空间碎片密集区域，受空间碎片撞击损伤的威胁很高。载人航天器的运行轨道也处于空间碎片密集区域，而空间碎片撞击将直接影响到航天员的安全，决定载人航天任务的成败。为了保障在轨的安全，航天器必须具备一定的防护能力。目前，在航天器空间碎片防护结构上采用了Whipple防护结构、多层冲击防护结构、网格双防护屏结构及填充防护结构等[1-4]，这些防护结构普遍采用了高性能纤维材料，如Nextel、Kevlar，且Nextel/Kevlar填充防护结构几乎覆盖了国际空间站的全部高风险区域。尽管对玄武岩及Kevlar纤维布填充防护结构超高速撞击损伤和防护性能已进行了大量研究，但是由于实验中填充材料及填充层的面密度各不相同，且实验条件不统一，因此所得结论也大相径庭[5-7]。同时，实验中所采用的弹丸直径过于单一，没有准确地给出玄武岩/Kevlar纤维布填充防护结构相对于Nextel/Kevlar填充防护结构及三层铝防护结构的防护性能的优劣。此外，现有文献中仅对玄武岩/Kevlar纤维布填充防护结构的损伤有一些零星的报道，并没有给出造成其不同损伤形貌的具体原因[6]。
本文中，针对玄武岩/Kevlar纤维布填充防护结构进行不同直径弹丸的超高速撞击实验，拟合撞击极限曲线，并与Nextel/Kevlar填充防护结构及三层铝防护结构的撞击极限曲线进行对比，分析玄武岩/Kevlar纤维布填充防护结构的防护性能；研究防护屏、填充层及舱壁的损伤形式，分析造成防护屏、填充层与舱壁不同损伤形貌的原因，探索玄武岩/Kevlar纤维布填充防护结构的防护机理。
1. 实验方案及结果
超高速撞击实验采用二级轻气炮发射装置，其中二级轻气炮一级高压泵管口径为57 mm，二级发射管口径为10 mm。一级驱动气体为氮气，二级驱动气体为氢气。速度测量采用磁感应方法，测量精度高于2%。
玄武岩/Kevlar纤维布填充防护结构形式如图 1所示，第1层防护屏为1 mm厚的6061-T6铝合金板，填充层由3层玄武岩纤维布和3层Kevlar纤维布组成，相对于弹丸撞击方向而言，玄武岩纤维布在前，Kevlar纤维布在后，填充层的面密度为0.168 g/cm2，舱壁为2.5 mm厚的5A06铝合金板，防护结构总的面密度为1.106 g/cm2。防护结构总防护间距(即舱壁前表面到最外层防护屏背面的距离)为100 mm, 填充层位于最外层铝合金防护屏和舱壁中间，即处于总防护间距一半的位置。实验中使用3.97、4.76、6.35和7.94 mm等4种不同直径的2017铝合金弹丸撞击玄武岩/Kevlar纤维布填充防护结构，撞击速度为0.6~5.0 km/s，撞击角为0°。
图 1 玄武岩/Kevlar纤维布填充防护结构示意图Figure 1. Experimental configuration of basalt/Kevlar stuffed Whipple shield玄武岩/Kevlar布填充防护结构超高速撞击实验结果见表 1，表中dp、v和Dh分别为弹丸直径、撞击速度和防护屏穿孔直径。实验过程中，玄武岩/Kevlar纤维布填充防护结构防护效果的判定以铝合金舱壁是否穿孔、剥落为评价依据：舱壁无穿孔、无剥落，防护有效；有穿孔、剥落，防护失效。如果舱壁出现微裂纹损伤形式，则认为防护失效。
表 1 玄武岩/Kevlar纤维填充防护结构超高速撞击实验结果Table 1. Results of hypervelocity impact tests for basalt/Kevlar stuffed shields实验
编号dp/mm v/(km·s-1) Dh/mm 舱壁
损伤防护
效果SW-33 7.94 0.650 8.15 鼓包 有效 SW-22 7.94 0.680 8.26 鼓包 有效 SW-32 7.94 0.750 8.42 穿孔 失效 SW-34 7.94 0.868 8.61 穿孔 失效 SW-26 7.94 0.977 8.73 穿孔 失效 SW-24 7.94 1.076 8.41 穿孔 失效 SW-23 7.94 1.097 8.65 穿孔 失效 SW-01 6.35 0.818 6.81 鼓包 有效 SW-02 6.35 0.940 7.74 微裂纹 失效 SW-04 6.35 0.974 7.01 微裂纹 失效 SW-05 6.35 1.112 7.30 微裂纹 失效 SW-03 6.35 1.149 7.09 穿孔 失效 SW-25 6.35 1.259 7.66 穿孔 失效 SW-13 4.76 1.374 6.04 鼓包 有效 SW-12 4.76 1.525 6.06 开裂 失效 SW-11 4.76 1.595 6.06 穿孔 失效 SW-08 3.97 1.211 5.58 鼓包 有效 SW-09 3.97 1.776 5.62 开裂 失效 SW-07 3.97 1.972 5.74 穿孔 失效 SW-06 3.97 2.242 6.05 穿孔 失效 SW-10 6.35 4.438 10.51 穿孔 失效 SW-47 6.35 4.443 10.34 穿孔 失效 SW-49 6.35 4.450 10.55 微裂 失效 SW-48 6.35 4.700 10.63 鼓包 有效 SW-18 4.76 3.205 7.76 穿孔 失效 SW-40 4.76 3.550 7.56 穿孔 失效 SW-19 4.76 3.572 7.51 穿孔 失效 SW-20 4.76 3.572 7.92 双鼓包 有效 SW-45 4.76 3.660 8.05 微鼓包 有效 SW-36 4.76 3.910 8.31 微鼓包 有效 SW-42 3.97 2.660 6.32 穿孔 失效 SW-43 3.97 2.660 6.55 微裂纹 失效 SW-16 3.97 2.809 6.44 穿孔 失效 SW-46 3.97 2.860 6.71 微裂纹 失效 SW-17 3.97 2.907 6.60 微裂纹 失效 SW-15 3.97 3.379 6.90 微鼓包 有效 SW-14 3.97 3.572 7.09 鼓包 有效 2. 分析
2.1 撞击极限特性
撞击极限曲线是基于撞击极限方程得到的描述防护结构的临界弹丸直径dcr与撞击参数、结构参数之间关系的曲线，其是评价防护结构防护性能的重要手段，同样也是航天器防护结构设计的重要依据。由于弹丸超高速撞击填充防护结构，在不同速度区段呈现不同的动力学特性，因此撞击极限方程分为3段函数来表达。填充防护结构撞击极限方程可表示为：
弹道区(v≤vL):
dcr=CLF∗ρk1pvk2cosk3θ 对于Nextel/Kevlar填充防护结构而言，几何模型函数:
F∗=tw(σ/275.8)0.5+cbmb 液化/气化区(v≥vH):
dcr=CH(twρw)k4Sk5(σ/σ0)k6ρk7bρk8pvk9cosk10θ 破碎区(vL＜v＜vH):
dcr=dcr,vHvH−vvH−vL+dcr,vLv−vLvH−vL 上述方程中：CL、CH、cb、α、k1~k10为撞击极限方程参数; vL、vH为弹道区、破碎区、熔化/气化区3区的临界速度(km/s)，分别称为第1速度阈值和第2速度阈值; ρp、ρb、ρw分别为弹丸、防护屏和舱壁密度(g/cm3); S为防护屏间距(cm); σ为舱壁材料极限屈服强度(MPa); tw为舱壁厚度(cm); θ为撞击角(°)。
对于特定材料弹丸超高速撞击某一填充防护结构，当撞击角为0°时，几何模型函数、弹丸密度、防护屏密度、舱壁密度、舱壁厚度及防护间距等参数均为常数，因此，撞击极限方程简化为：弹道区，dcr=C′Lvk2；液化/汽化区，dcr=C′Hvk2；破碎区, dcr=CMvk2; 其中C′L,C′H,CM为待定系数。
对于本文玄武岩/Kevlar纤维布填充防护结构，根据表 1实验结果，拟合得到预测撞击极限方程为：弹道区(v≤2.528 km/s), dcr=0.605v-0.735; 破碎区, dcr=0.16v-0.105。
图 2给出了玄武岩/Kevlar纤维布填充防护结构的预测撞击极限曲线和同等面密度的Nextel/Kevlar填充防护结构的撞击极限曲线[8-9]及三层铝防护屏的撞击极限曲线[10]。由图 2可知，玄武岩/Kevlar纤维布填充防护结构的撞击极限曲线与Nextel/Kevlar填充防护结构和三层铝防护结构的撞击极限曲线整体趋势基本相同。弹道区时，3种防护结构的撞击极限曲线几乎重合，表明在该碰撞速度范围内，在防护结构面密度相等的条件下，3种防护构型的防护性能相当。破碎区时，玄武岩/Kevlar纤维布填充防护结构的撞击极限曲线始终处于最上端，Nextel/Kevlar填充防护结构的撞击极限曲线位于中间，三层铝防护屏的撞击极限曲线则处于最下端。这表明，在防护结构面密度相等的条件下，三层铝防护屏的防护性能最差，玄武岩/Kevlar纤维布填充防护结构的防护性能最好。总体而言，纤维织物填充防护结构的防护性能优于三层铝防护屏的防护性能，玄武岩/Kevlar纤维布填充防护结构的防护性能已经达到了Nextel/Kevlar填充防护结构的防护水平，可以作为一种新的用于空间碎片防护的填充防护结构。
图 2 玄武岩/Kevlar纤维布填充防护结构撞击极限曲线Figure 2. Ballistic limit curves of basalt/Kevlar stuffed shield2.2 损伤特性
2.2.1 防护屏穿孔特性
最外层防护屏穿孔损伤形貌如图 3所示，其均为圆形穿孔损伤。当撞击速度较低时，防护屏正面孔口边缘有瓣形突缘(堆积突起)；防护屏背面也存在突缘，并有明显的后翘拉伸变形，其为充塞边缘端口。随着撞击速度的升高，处于破碎区段时，防护屏正面瓣形突起产生飞散，并减少；背面孔边缘也产生同正面一样的堆积飞散。其主要原因是弹丸撞击铝合金防护屏，在撞击界面产生巨大的冲击压力，防护屏材料在冲击压缩波的扰动下产生大量能量(热量)，发生熔化，体积迅速增大，并在剪切流动的作用下，以很高的速度飞溅出去，未飞溅出去的材料粘附于圆孔周边，形成了防护屏正面的瓣形突缘。撞击速度愈高，剪切流动力愈大，防护屏熔化材料飞溅速度也愈高，使得残留粘附于孔周边的材料减少。撞击速度较低时，防护屏在拉伸波的扰动下产生整体变形，形成鼓包，并由高速弹丸充塞出一块防护屏材料，形成拉伸形突缘断口；随着撞击速度的增加，弹丸贯穿防护屏的速度大于拉伸波扰动防护屏产生整体变形的速度，使得防护屏未产生整体变形(鼓包)前便被充塞出一块，由于应力做功产生大量能量，防护屏材料熔化，熔化材料在剪切力的作用下沿弹丸飞行方向飞溅。
图 3 防护屏超高速撞击穿孔损伤Figure 3. Perforation damage in the first bumper by hypervelocity impact图 4给出了防护屏穿孔直径随撞击速度的变化曲线。弹丸直径一定时，穿孔直径随撞击速度的升高而增大，呈非线性变化。目前，预测穿孔直径的经验公式主要有Maiden[11]、Nysmith[12]、Sawle[13]、Guan[14]等经验公式。由图 4可知，对于直径为3.97 mm的铝球撞击铝合金防护屏，上述穿孔直径方程并不适用于本文实验结果。其中，Swale[13]公式高估了防护屏穿孔直径，Maiden[11]、Nysmith[12]与Guan[14]3个公式则低估了防护屏穿孔直径，且4个方程预测结果与本文实验结果之间误差均大于20%，最大误差超过50%。综上所述，由于实验和预测公式间选用的材料在性能方面存在差异，预测结果也会带来较大的误差，因此，有必要针对本文材料进行超高速撞击特性研究。
2.2.2 填充层损伤特性
弹丸击穿防护屏后，会产生飞散碎片，飞散碎片会对填充层造成不同形式的损伤。图 5(a)表明，当撞击速度处于低速区时，填充层前面的玄武岩纤维面层上有较规则的方孔，方孔四边分别平行于玄武岩纤维布的经纱和纬纱，且纤维断裂面平滑，纱线断口附近没有出现明显的弯曲变形；背面Kevlar面层也产生了穿孔，但其断裂纱线产生了较大的拉伸变形，形成球冠状突起，遮住贯穿孔，孔周边纱线被弹丸推开，形成倒圆锥式凹陷，并伴有少量抽纱。随着撞击速度接近第1速度阈值时，玄武岩纤维面层上出现许多孔，如图 5(b)和(c)所示，其中弹丸主体在填充层上形成一个方形大孔，而小碎片则在周围形成一些小孔，大小沿径向向外逐渐减小。大孔断面纤维整齐光滑，周围小孔断面不一。Kevlar填充层背面为一个方孔，四边也平行于Kevlar面层的经、纬纱，但断口不是很平滑，纱线拉伸变形较大，且有些纱线明显被拉长但没有断裂，产生推移变形，形成倒圆锥式突起，并伴有少量抽纱。
当撞击速度为破碎区时，填充层正面损伤为圆形大孔，周围有许多小孔呈散射分布；玄武岩和Kevlar断裂的纱线向弹丸飞行的反向翻转，断口不整齐，有毛边。填充层背面为近似方形孔，伴有撕裂，断口不整齐，Kevlar纤维布有明显抽纱现象，如图 5(d)所示。
玄武岩布和Kevlar布的细观损伤形态如图 6所示。玄武岩纤维作为一种陶瓷纤维材料，脆性很强，破坏时发生脆性断裂，随着撞击速度的增高，其纤维断裂截面趋于规整；而Kevlar作为一个高分子聚合物，具有较大韧性，随着撞击速度的提高，应变率升高，Kevlar纤维丝强度增高，韧性减小，侧向劈裂和原纤化加剧。此外，Kevlar纤维材料具有较低的玻璃化温度，撞击过程中Kevlar纤维发生明显的热塑性变形。
以上分析表明，玄武岩/Kevlar纤维布填充层通过纤维丝的断裂和拉伸变形吸收弹丸撞击能量。另外，根据文献[5]可知，玄武岩纤维布具有切割、破碎弹丸的能力，使大碎片或弹丸进一步破碎，且不产生新的大碎片，这也正是玄武岩/Kevlar纤维布填充防护结构防护性能优于Nextel/Kevlar填充防护结构和三层铝防护屏的重要原因。
2.2.3 舱壁损伤特性
图 7给出了不同速度区段舱壁的超高速撞击损伤形貌。弹丸撞击速度低于第1速度阈值时，弹丸仅产生塑性变形，以完整的形态撞击舱壁，造成舱壁穿孔或撞击坑损伤；随着撞击速度的提高，弹丸发生少量破碎，造成舱壁贯穿孔或大撞击坑周围形成小撞击坑。随着弹丸撞击速度的继续提高，当其超过第1速度阈值后，舱壁中心区域损伤最严重，并沿着径向向外损伤程度逐渐减轻。
此外，击穿防护屏后，弹丸形成碎片云，并发生熔化或气化，熔化/气化的碎片云具有较高的温度和速度，当撞击到面层纤维丝时，产生较高的冲击压力，并伴有多种冲击现象，包括弹性波、塑性波和流动波。而纤维丝在横波和纵波的作用下发生解体，以短纤维、纤维团或纤维束的形式喷向舱壁，使舱壁损伤区有黑色喷溅物和丝状物，如图 7(c)所示，其中黑色喷溅物为金属铝液化或气化喷射物和填充层纤维丝烧蚀后的喷射物；丝状物为Kevlar纤维丝，其都以束状或团状出现，一般位于黑色喷溅区边界处。随着撞击速度的提高，这些丝状物逐渐被烧蚀碳化，由于碳化粉末仍有较高的温度，其可以造成舱壁正面烧蚀损伤，如图 7(d)所示。
2.3 防护机理
玄武岩/Kevlar纤维布填充防护结构的防护机理如图 8所示，弹丸撞击铝合金防护屏，在撞击界面产生巨大的冲击压力。
图 8 玄武岩/Kevlar纤维布填充防护结构防护机理Figure 8. Protection mechanism of basalt/Kevlar stuffed shields如撞击速度较低时，冲击压力不足以使弹丸破碎，弹丸贯穿防护屏，头部产生塑性变形，飞行速度降低，其继续撞击纤维布填充层，纤维面层主要通过玄武岩纤维丝的剪切断裂和Kevlar纤维丝拉伸变形消耗弹丸动能，使弹丸剩余能量造成的舱壁损伤减轻。
如果撞击速度较高，弹丸和防护屏在冲击压缩波扰动下破碎，并使弹丸和防护屏材料产生液化或者气化，形成高温碎片云，高温碎片云撞击纤维布填充层，根据2.2.2和2.2.3节可知，玄武岩纤维丝切割碎片，使碎片进一步细化，Kevlar纤维丝对细化碎片进行拦截。
此外，高温高速碎片云使纤维丝体解，烧蚀并粉末化，在舱壁正面形成较大喷溅区，喷溅区面积较大，使得作用在舱壁单位面积上的能量较小，从而减小了对舱壁的损伤。
综上所述，玄武岩/Kevlar纤维布填充防护结构通过填充层消耗、吸收和分散弹丸或碎片云的能量，以起到更好的防护效果。
3. 结论
(1) 通过超高速撞击实验研究了玄武岩/Kevlar纤维布填充防护结构的撞击极限，与同等面密度的Nextel/Kevlar填充防护结构和三层铝防护屏进行比较，得出玄武岩/Kevlar纤维布填充防护结构的防护性能优于三层铝防护屏的防护性能，且也已经达到Nextel/Kevlar填充防护结构的防护水平，完全可以作为一种新的用于空间碎片防护的填充防护结构。
(2) 研究了防护屏、填充层和舱壁的超高速撞击损伤特性，分析了造成防护屏、填充层与舱壁不同损伤形貌的原因，初步探索了玄武岩/Kevlar填充防护结构的防护机理。玄武岩纤维布破碎弹丸，使弹丸或碎片破碎，同时连同Kevlar纤维布一起消耗、吸收弹丸的撞击能量，使玄武岩/Kevlar纤维布填充防护结构具有和Nextel/Kevlar填充防护结构类似的防护效果，优于三层铝防护屏的防护性能。
下一步工作重点是，进一步扩大超高速撞击实验的速度范围，深入分析撞击极限的弹丸形状效应。
-
图 5 两种应力强度因子（KⅠC和KⅡC）对材料强度的影响
Figure 5. Curves of tensile strength with two stress intensity factors (KⅠC and KⅡC)
表 1 与温度无关的PBX-3细观特征量
Table 1. Temperature independent mesoscopic characteristics of PBX-3
n/cm−3 a0/cm au/cm v 1372 0.006352 0.03703 0.3 
下载: 导出CSV
表 2 与温度相关的PBX-3细观特征量
Table 2. Temperature dependent mesoscopic characteristics of PBX-3
T/℃ KⅠC/（MPa·cm1/2） KⅡC/（MPa·cm1/2） −40 0.1628 0.1911 −30 0.1502 0.1763 −25 0.1556 0.1827 −20 0.1520 0.1784 −10 0.1457 0.1711 25 0.1457 0.1711 45 0.1322 0.1552
下载: 导出CSV
-
[1] STEVENS R. A strength model and service envelope for PBX 9501: LA-UR-14-20696 [R]. Los Alamos: Los Alamos National Laboratory, 2014. [2] 肖磊, 刘杰, 郝嘎子, 等. 微纳米RDX颗粒级配对压装PBX性能影响 [J]. 含能材料, 2016, 24(12): 1193–1197. DOI: 10.11943/j.issn.1006-9941.2016.12.011.XIAO L, LIU J, HAO G Z, et al. Effects of nano-/micrometer RDX particle gradation on the property of PBX [J]. Chinese Journal of Energetic Materials, 2016, 24(12): 1193–1197. DOI: 10.11943/j.issn.1006-9941.2016.12.011. [3] 黄辉. 颗粒级配技术及其在含能材料中的应用 [J]. 含能材料, 2001, 9(4): 161–164. DOI: 10.3969/j.issn.1006-9941.2001.04.005.HUANG H. Particle grade technique and application on energetic materials [J]. Energetic Materials, 2001, 9(4): 161–164. DOI: 10.3969/j.issn.1006-9941.2001.04.005. [4] LV K Z, YANG K, ZHOU B, et al. The densification and mechanical behaviors of large-diameter polymer-bonded explosives processed by ultrasonic-assisted powder compaction [J]. Materials & Design, 2021, 207: 109872. DOI: 10.1016/j.matdes.2021.109872. [5] 黄辉, 王晓川. 偶联剂在HMX基浇注固化炸药中的作用 [J]. 含能材料, 2000, 8(1): 13–17. DOI: 10.3969/j.issn.1006-9941.2000.01.004.HUANG H, WANG X C. Behavior of coupling agent in HMX-based extrudable cast explosive [J]. Energetic Materials, 2000, 8(1): 13–17. DOI: 10.3969/j.issn.1006-9941.2000.01.004. [6] LI F, YE L, NIE F D, et al. Synthesis of boron-containing coupling agents and its effect on the interfacial bonding of fluoropolymer/TATB composite [J]. Journal of Applied Polymer Science, 2007, 105(2): 777–782. DOI: 10.1002/app.26117. [7] YANG X L, GONG F Y, ZHANG K, et al. Enhanced creep resistance and mechanical properties for CL-20 and FOX-7 based PBXs by crystal surface modification [J]. Propellants, Explosives, Pyrotechnics, 2021, 46(4): 572–578. DOI: 10.1002/prep.202000277. [8] 冯西桥, 余寿文. 准脆性材料细观损伤力学 [M]. 北京: 高等教育出版社, 2002: 20–41.FENG X Q, YU S W. Damage micromechanics of quasi-brittle materials [M]. Beijing: Higher Education Press, 2002: 20–41. [9] YANG Y Z, LI J L, CHEN J K. Experimental and numerical analysis of shear process of a high particle content bonding material [J]. Journal of Applied Mechanics, 2021, 88(6): 061003. DOI: 10.1115/1.4050277. [10] LIU C, THOMPSON D G. Crack initiation and growth in PBX 9502 high explosive subject to compression [J]. Journal of Applied Mechanics, 2014, 81(10): 101004. DOI: 10.1115/1.4028087. [11] LIU M, HUANG X C, WU Y Q, et al. Numerical simulations of the damage evolution for plastic-bonded explosives subjected to complex stress states [J]. Mechanics of Materials, 2019, 139: 103179. DOI: 10.1016/j.mechmat.2019.103179. [12] CURRAN D R, SEAMAN L, SHOCKEY D A. Dynamic failure of solids [J]. Physics Reports, 1987, 147(5/6): 253–388. DOI: 10.1016/0370-1573(87)90049-4. [13] BENNETT J G, HABERMAN K S, JOHNSON J N, et al. A constitutive model for the non-shock ignition and mechanical response of high explosives [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(12): 2303–2322. DOI: 10.1016/s0022-5096(98)00011-8. [14] ZUO Q H, ADDESSIO F L, DIENES J K, et al. A rate-dependent damage model for brittle materials based on the dominant crack [J]. International Journal of Solids and Structures, 2006, 43(11/12): 3350–3380. DOI: 10.1016/j.ijsolstr.2005.06.083. [15] RAGASWAMY P, LEWIS M W, LIU C, et al. Modeling the mechanical response of PBX 9501: LA-UR-10-01416 [R]. Los Alamos: Los Alamos National Laboratory, 2010. [16] PIJAUDIER-CABOT G, BAŽANT Z P. Nonlocal damage theory [J]. Journal of Engineering Mechanics, 1987, 113(10): 1512–1533. DOI: 10.1061/(asce)0733-9399(1987)113:10(1512. [17] LIU C. Damage and fracture in high explosive materials: LA-UR-11-05618 [R]. Los Alamos: Los Alamos National Laboratory, 2011. [18] ZHANG S L, YANG W. Macrocrack extension by connecting statistically distributed microcracks [J]. International Journal of Fracture, 1998, 90(4): 341–353. DOI: 10.1023/A:1007440012284. 期刊类型引用(8)
1. 武江凯，迟润强，韩增尧，庞宝君，郑世贵. 载人航天器密封舱结构超高速撞击易损性. 哈尔滨工业大学学报. 2023(08): 25-31 . 
百度学术2. 徐铧东，于东，刘文翔，石景富，苗常青. 屏间充气展开式多屏防护结构及其防护性能分析. 载人航天. 2022(01): 75-80 . 百度学术3. 崔俊杰，郭章新，朱明，李永存，栾云博，杨强. 表面带金属层的复合材料层合板低速冲击数值模拟. 材料导报. 2021(04): 4150-4158 . 百度学术4. 武强，张庆明，龚自正，任思远，刘海. 活性Whipple结构超高速撞击防护性能实验研究. 爆炸与冲击. 2021(02): 84-92 . 
本站查看5. 武强，龚自正，张庆明，任思远. 含能活性材料防护结构超高速撞击特性数值模拟研究. 振动与冲击. 2021(11): 202-210 . 百度学术6. 屈雪蕊. Comp.B含能材料落锤冲击应力特性分析. 西安航空学院学报. 2021(03): 70-74+96 . 百度学术7. 古青波，从强，常洁，王巍. 空间柔性充气密封舱用新型填充防护结构碎片撞击计算分析与实验研究. 航天器环境工程. 2020(02): 125-130 . 百度学术8. 贾光辉，姚光乐，张帅. 填充式防护结构弹道极限方程的差异演化优化. 北京航空航天大学学报. 2018(07): 1489-1495 . 百度学术其他类型引用(7)
-
下载:
百度学术
计量
- 文章访问数: 525
- HTML全文浏览量: 169
- PDF下载量: 70
- 被引次数: 15