空孔对直眼掏槽参数及爆破效果的影响研究

张召冉; 王岩; 刘国庆

doi:10.11883/bzycj-2021-0519

空孔对直眼掏槽参数及爆破效果的影响研究

doi: 10.11883/bzycj-2021-0519

张召冉^1,,
王岩^2, ,,
刘国庆³

1.
北方工业大学土木工程学院，北京 100144
2.
北京住总集团有限责任公司，北京 100101
3.
北方爆破科技有限公司，北京 100089

基金项目: 北京市教育委员会科学研究计划（KM202110009008）；国家自然科学基金（51774287）

详细信息

作者简介:
张召冉（1981－　），男，博士，副教授，zhaoran2011@foxmail.com

通讯作者:
王　岩（1982－　），男，硕士，高级工程师，4500820@qq.com

中图分类号: O389；TU45
计量
- 文章访问数: 491
- HTML全文浏览量: 137
- PDF下载量: 139
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-20
- 修回日期: 2022-05-05
- 网络出版日期: 2022-09-08
- 刊出日期: 2023-01-05

Theoretical study of the influence of empty-hole on both the blasting parameters and the blasting effect of straight-hole cutting

1.
School of Civil Engineering, North China University of Technology, Beijing 100144, China
2.
Beijing Residential Group Co., Ltd, Beijing 100101, China
3.
China North Blasting Technology Co., Ltd., Beijing 100089, China

摘要

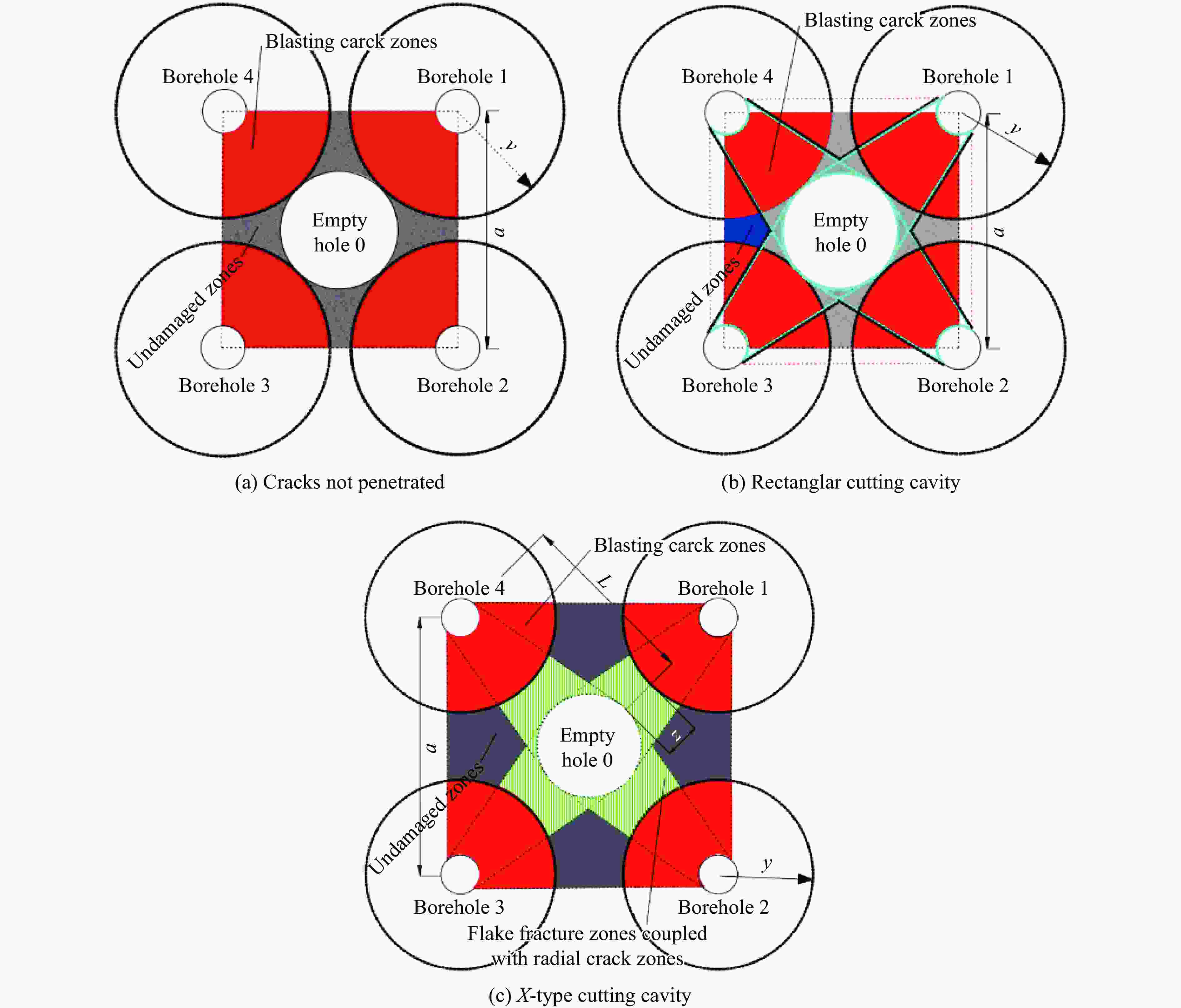
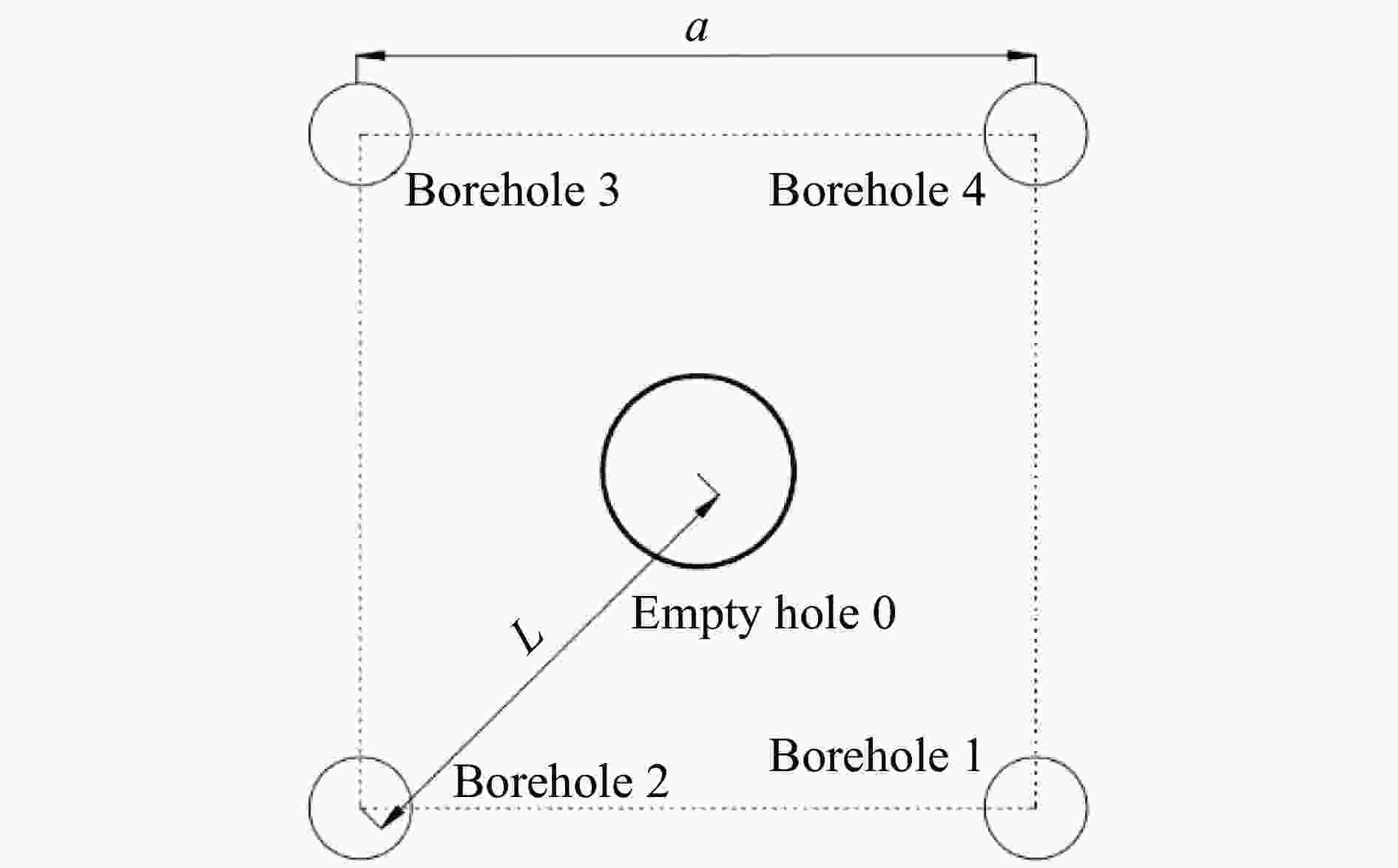
摘要: 为解决含空孔直眼掏槽中炮孔间距、炮孔与空孔距离的确定问题，首先，从爆生气体膨胀做功致裂岩体和空孔效应入手，推导了爆生裂纹的长度计算公式，确定了掏槽炮孔间距a和炮孔与空孔距离L的计算公式，得到了大空孔直眼掏槽空孔处片裂区长度公式，确立了应力集中作用下空孔迎爆侧径向裂纹产生的判据；然后，以灰岩（硬岩）和泥岩（软岩）对比分析了不同设计思想下的爆破参数和掏槽效果；最后，结合工程实践验证了理论分析的可靠性。结果表明：不同设计思想下，含空孔直眼掏槽的爆破破岩机理不同，以a为主时，相邻炮孔间裂纹的贯通是形成槽腔的关键，而以L为主且考虑空孔效应时，炮孔与空孔优先贯通形成槽腔。硬、软岩中应力波（动作用）与爆生气体（静作用）对爆生裂纹长度的贡献率约为4∶1和9∶1，空孔效应导致的软岩的片裂区大于硬岩的，爆破参数设计时应重点考虑；而空孔处产生径向裂纹的临界距离均小于炮孔爆生裂纹长度与空孔半径之和，因此不会产生径向裂纹，爆破参数设计时可不予考虑。以上结果说明，不同设计思想对槽腔掏槽爆破参数和槽腔爆破效果影响较大，基于爆生气体致裂的爆生裂纹长度计算模型可为爆破参数设计提供参考。
- 巷道掘进 /
- 掏槽爆破 /
- 大直径空孔 /
- 爆破参数 /
- 破裂形态
Abstract: The paper is aimed to determine the distance between blast holes (a) and the distance between boreholes and the empty holes (L) in the straight-hole cutting with empty holes. Firstly, by considering the crack mainly being fractured during the quasi-static expansion of explosion gas and the effect of empty hole, the calculation formula of the crack length is derived; and then, the calculation formulas of the distance between boreholes and the distance between blast holes and the empty hole are determined. Moreover, the formula of the length of the crack zone around the empty hole in the straight-hole cutting with large empty holes is obtained, and the criterion of the radial crack at the blasting side of the empty hole is established based on the effect of stress concentration around empty hole. Secondly, by considering two different design ideas, the blasting parameters and cut blasting effect are compared and analyzed for the blasting in both limestone (hard rock) and mudstone (soft rock),while the reliability of the theoretical analysis is verified by engineering practice. The results show that the rock breaking mechanism of straight-hole cut blasting with empty hole is different under the two design ideas. Namely, if a is taken as the main factor, then the coalescence of cracks between adjacent boreholes is the key factor to the formation of the cavity, whilst if L is taken as the main factor, the bore holes and empty holes are preferentially penetrated to form the cavity based on the empty hole effect. In addition, the contributions of stress wave (dynamic action) and detonation gas (static action) to the crack length in both hard rock and soft rock are about 4∶1 and 9∶1, respectively. Considering the empty hole effect, the flake fracture zone in soft rock is larger than that in hard rock, to which more attention should be paid in the design of blasting parameters. Whereas, the critical length of radial crack initiated from the empty hole is less than the sum of the blasting crack length from cutting hole and the radius of empty hole, so that the radial cracks initiated from the empty hole will not be generated, which can be ignored in the blasting parameter design. The results indicate that the two different design ideas have great influence on cutting blasting parameters and blasting effect, and the calculation model of blasting crack length based on the driven of detonation gas can provide a good reference for the design of blasting parameters.
- rock roadway excavation /
- cut blasting /
- empty-hole with large diameter /
- blasting parameters /
- fracture shape

HTML全文

图 1 大空孔直眼掏槽炮孔布置示意图

Figure 1. The layout of cut blasting with empty-hole

下载: 全尺寸图片幻灯片

图 2 空孔附近岩石破坏形式

Figure 2. Rock failure around empty hole during blasting

下载: 全尺寸图片幻灯片

图 3 以a为主时掏槽参数及掏槽区破坏示意图

Figure 3. Cutting parameters and destruction of cutting area when a is taken as the main factor

下载: 全尺寸图片幻灯片

图 4 以L为主时掏槽参数及掏槽区破坏示意图

Figure 4. Cutting parameters and destruction of cutting area when L is taken as the main factor

下载: 全尺寸图片幻灯片

图 5 不同设计思想下灰岩掏槽爆破参数

Figure 5. Cut blasting parameters of limestone under different design ideas

下载: 全尺寸图片幻灯片

图 6 不同设计思想下泥岩掏槽爆破参数

Figure 6. Cut blasting parameters of mudstone under different design ideas

下载: 全尺寸图片幻灯片

图 7 掏槽孔布置

Figure 7. Cutting blasthole layout

下载: 全尺寸图片幻灯片

图 8 掏槽孔现场布置

Figure 8. Cutting borehole arrangement

下载: 全尺寸图片幻灯片

图 9 掏槽爆破效果

Figure 9. Cutting blast effect

下载: 全尺寸图片幻灯片

表 1 掏槽爆破参数

Table 1. Parameters of cut blasting

掏槽区岩体破坏判据	a/mm	L/mm
相邻炮孔间裂隙贯通	$ \bar{y}{\text{≤}} a{\text{≤}} 2\bar{y} $	$ L=\sqrt{2}a/2 $
炮孔与空孔贯通	$ a=\sqrt{2}L $	$ L=({L}_{2\mathrm{m}\mathrm{a}\mathrm{x}}+y+{r}_{1})/2\mathrm{或}L=y+{{\textit{z}}}_{1\mathrm{m}\mathrm{a}\mathrm{x}}+{r}_{1} $

下载: 导出CSV

表 2 岩体物理力学参数

Table 2. Physical and mechanical parameters of rock

岩性	密度/（kg·m⁻³）	静态泊松比	动态泊松比	动态抗压强度/MPa	动态抗拉强度/MPa
灰岩	3 000	0.24	0.192	120.2	13.0
泥岩	2 430	0.26	0.208	50.8	6.1

下载: 导出CSV

表 3 炸药参数

Table 3. Explosive parameters

密度/（kg·m⁻³）	直径/mm	长度/mm	每卷质量/kg	爆容/（m³·kg⁻¹）	爆温/K	余容/（m³·kg⁻¹）	爆速/（m·s⁻¹）
1000	32	200	0.2	0.8	2300	6×10⁻⁴	3200

下载: 导出CSV

表 4 灰岩不同设计思想下$a $与$L $

Table 4. a and L of limestoneunder different design ideas

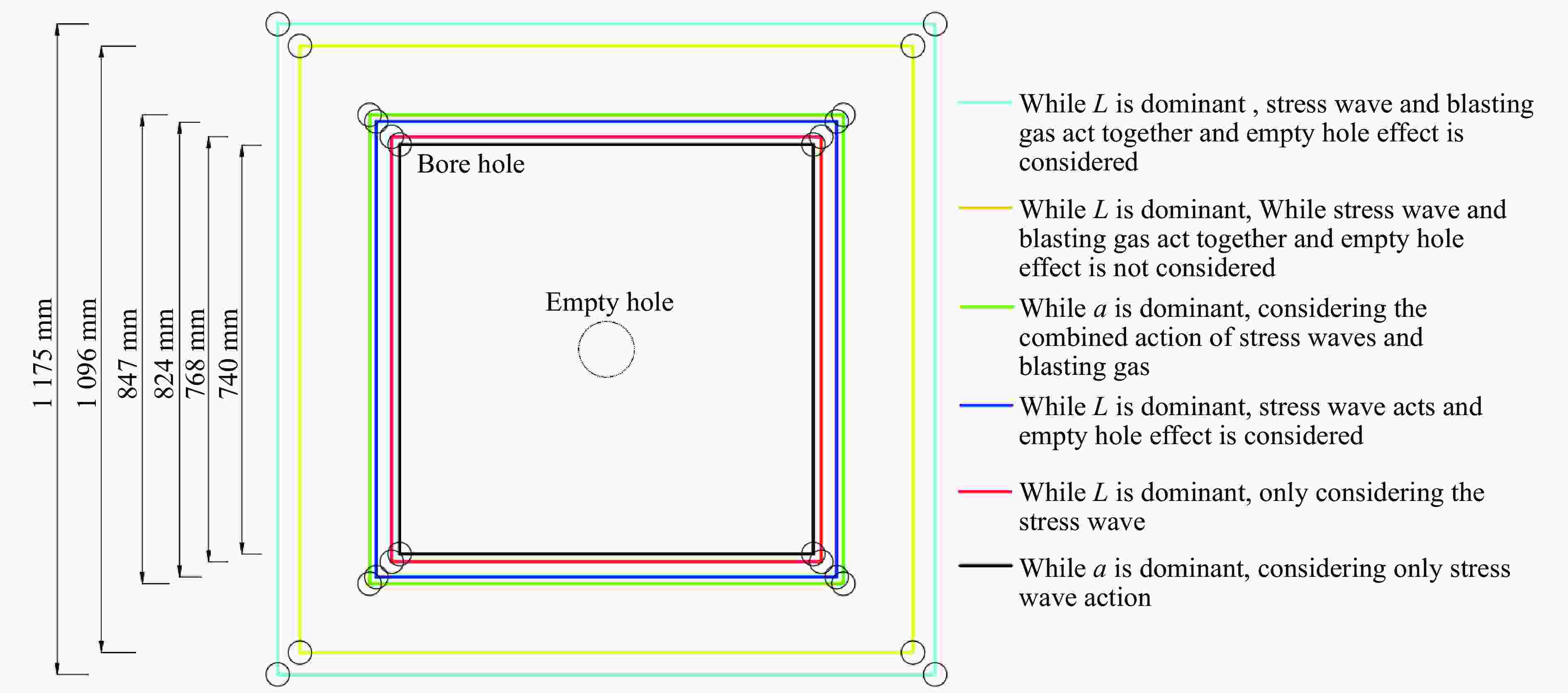
序号	取值依据	L/mm	a/mm	爆生裂纹半径/mm	裂隙与空孔关系	掏槽孔之间关系
1	以L为主	508	718	429	贯通	贯通
2		479	677	429	贯通	贯通
3		405	573	355	贯通	贯通
4		434	614	355	贯通	贯通
5	以a为主	455	644	429	贯通	贯通
6	以a为主	376	533	355	贯通	贯通

下载: 导出CSV

表 5 不同设计思想下泥岩的掏槽爆破参数

Table 5. Cut blasting parameters of mudstone under different design ideas

序号	取值依据	L/mm	a/mm	爆生裂纹半径/mm	裂隙与空孔关系	掏槽孔之间关系
1	以L为主	831	1175	549	贯通	未贯通
2		599	847	549	贯通	贯通
3		543	768	493	贯通	贯通
4		775	1096	493	贯通	未贯通
5	以a为主	582	824	549	贯通	贯通
6	以a为主	523	740	493	贯通	贯通

下载: 导出CSV

表 6 不同岩性下爆破后参数

Table 6. Parameters after blasting in different rocks

指标	应力波与爆生气体共同作用爆生裂纹半径/mm	应力波单独作用爆生裂纹半径/mm	爆生气体作用爆生裂纹扩展长度/mm	爆生气体对爆生裂纹长度贡献率/%	片裂区范围/ mm	空孔处径向裂纹产生条件L_2max/mm
灰岩	429	355	74	17	29	423
泥岩	549	493	56	11	232	527

下载: 导出CSV

表 7 爆破参数

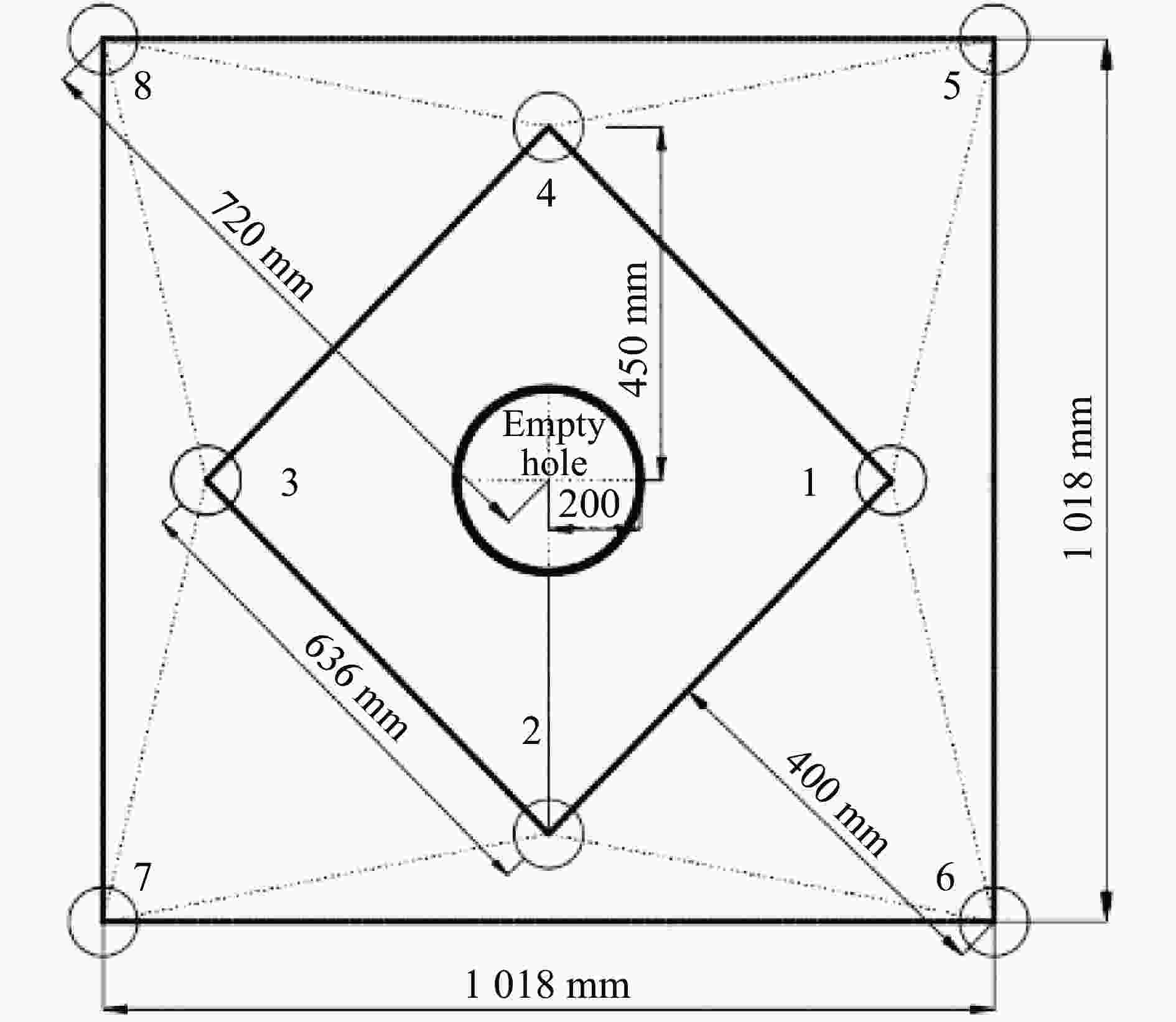
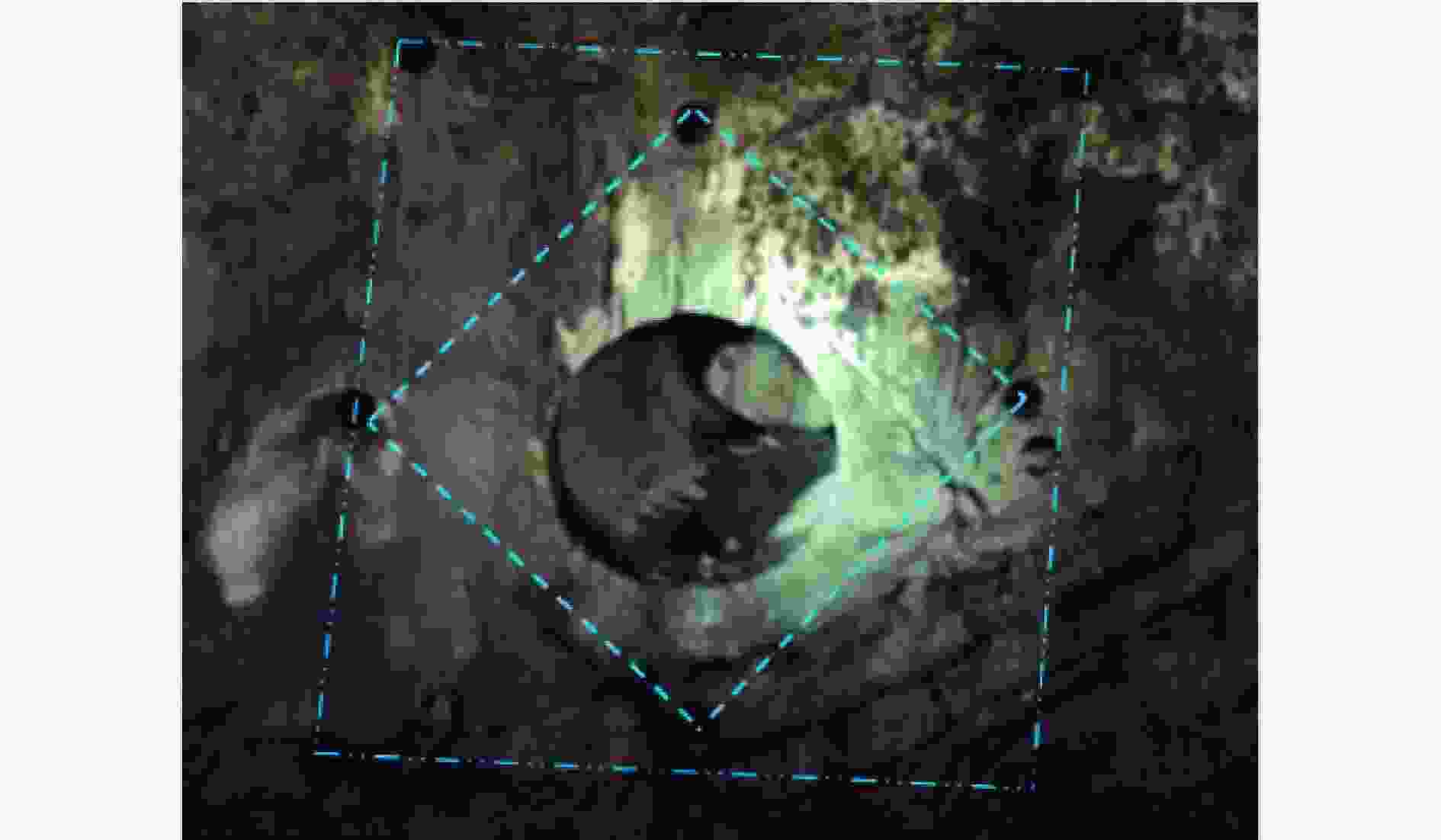
Table 7. Parameters of blasting

炮孔名称	深度/m	a/mm	L/mm	装药量/kg	雷管段别
掏槽孔	3.0	636	450	2.0	Ⅰ
辅助掏槽孔	3.0	1 018	720	1.8	Ⅱ

下载: 导出CSV

参考文献(20)

[1]	戴俊, 杨永琦. 三角柱直眼掏槽爆破参数研究 [J]. 爆炸与冲击, 2000, 20(4): 364–368. DAI J, YANG Y Q. Researches on blasting parameters of triangle burn cut [J]. Explosion and Shock Waves, 2000, 20(4): 364–368.
[2]	周少颖, 汪海波, 宗琦. 直眼掏槽爆破中大直径中空孔作用机理研究 [J]. 煤矿爆破, 2014(1): 23–25. DOI: 10.3969/j.issn.1674-3970.2014.01.007. ZHOU S Y, WANG H B, ZONG Q. Mechanism research of the effects of empty hole in parallel cut blasting [J]. Coal Mine Blasting, 2014(1): 23–25. DOI: 10.3969/j.issn.1674-3970.2014.01.007.
[3]	林大能. 平巷掏槽爆破空孔尺寸效应及围岩频繁震动损伤累积特性研究 [D]. 长沙: 中南大学, 2006: 21–38. DOI: 10.7666/d.y1190361. LIN D N. Research on size effect of empty hole in horizontal roadway cut blasting & accumulating characteristic of surrounding rock damage caused by frequently blasting vibration [D]. Changsha: Central South University, 2006: 21–38. DOI: 10.7666/d.y1190361.
[4]	王从银. 直眼掏槽的破岩机理及掏槽设计 [J]. 爆破, 1995(2): 51–55. WANG C Y. Rock-breaking mechanism and cutting design of straight-hole cutting [J]. Blasting, 1995(2): 51–55.
[5]	刘圣贤, 胡清祥, 张勇. 爆生裂缝扩展长度的理论研究 [J]. 煤矿爆破, 1998(2): 17–19. LIU S X, HU Q X, ZHANG Y. Theoretical study on the propagation length of blasting cracks [J]. Coal Mine Blasting, 1998(2): 17–19.
[6]	宗琦. 爆生气体的准静态破岩特性 [J]. 岩土力学, 1997, 18(2): 73–78. DOI: 10.16285/j.rsm.1997.02.014. ZONG Q. Investigation on features of rock quasi-static fragmentation by gaseous explosion product [J]. Rock and Soil Mechanics, 1997, 18(2): 73–78. DOI: 10.16285/j.rsm.1997.02.014.
[7]	赵新涛, 刘东燕, 程贵海, 等. 爆生气体作用机理及岩体裂纹扩展分析 [J]. 重庆大学学报, 2011, 34(6): 75–80. DOI: 10.11835/j.issn.1000-582x.2011.06.014. ZHAO X T, LIU D Y, CHENG G H, et al. Analysis of blasting gas mechanism and rock crack growth [J]. Journal of Chongqing University, 2011, 34(6): 75–80. DOI: 10.11835/j.issn.1000-582x.2011.06.014.
[8]	杨小林, 王梦恕. 爆生气体作用下岩石裂纹的扩展机理 [J]. 爆炸与冲击, 2001, 21(2): 111–116. DOI: 10.3321/j.issn:1001-1455.2001.02.005. YANG X L, WANG M S. Mechanism of rock crack growth under detonation gas loading [J]. Explosion and Shock Waves, 2001, 21(2): 111–116. DOI: 10.3321/j.issn:1001-1455.2001.02.005.
[9]	严成增, 孙冠华, 郑宏, 等. 爆炸气体驱动下岩体破裂的有限元-离散元模拟 [J]. 岩土力学, 2015, 36(8): 2419–2425. DOI: 10.16285/j.rsm.2015.08.039. YAN C Z, SUN G H, ZHENG H, et al. Simulation of explosive gas-driven rock fracture by FEM/DEM [J]. Rock and Soil Mechanics, 2015, 36(8): 2419–2425. DOI: 10.16285/j.rsm.2015.08.039.
[10]	戴俊, 杜晓丽. 岩石巷道楔形掏槽爆破参数研究 [J]. 矿业研究与开发, 2011, 31(2): 90–93,104. DOI: 10.13827/j.cnki.kyyk.2011.02.009. DAI J, DU X L. Research on blasting parameters of wedge-shaped cutting for rock tunnel driving [J]. Mining Research and Development, 2011, 31(2): 90–93,104. DOI: 10.13827/j.cnki.kyyk.2011.02.009.
[11]	单仁亮, 黄宝龙, 高文蛟, 等. 岩巷掘进准直眼掏槽爆破新技术应用实例分析 [J]. 岩石力学与工程学报, 2011, 30(2): 224–232. SHAN R L, HUANG B L, GAO W J, et al. Case studies of new technology application of quasi-parallel cut blasting in rock roadway drivage [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 224–232.
[12]	张召冉, 杨仁树. 岩石巷道“多阶段”掏槽技术及应用研究 [J]. 岩石力学与工程学报, 2019, 38(3): 551–559. DOI: 10.13722/j.cnki.jrme.2018.0460. ZHANG Z R, YANG R S. Multi-step cutting technology and its application in rock roadways [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(3): 551–559. DOI: 10.13722/j.cnki.jrme.2018.0460.
[13]	费鸿禄, 洪陈超. 应力波和爆生气体共同作用下裂隙区范围研究 [J]. 爆破, 2017, 34(1): 33–36,107. DOI: 10.3963/j.issn.1001-487X.2017.01.006. FEI H L, HONG C C. Study on crushed and fracture zone range under combined action of stress and detonation gas [J]. Blasting, 2017, 34(1): 33–36,107. DOI: 10.3963/j.issn.1001-487X.2017.01.006.
[14]	王文龙. 钻眼爆破 [M]. 北京: 煤炭工业出版社, 1984: 92–93.
[15]	戴俊. 岩石动力学特性与爆破理论 [M]. 2版. 北京: 冶金工业出版社, 2013: 234–238.
[16]	张召冉, 陈华义, 矫伟刚, 等. 含空孔直眼掏槽空孔效应及爆破参数研究 [J]. 煤炭学报, 2020, 45(S2): 791–800. DOI: 10.13225/j.cnki.jccs.2019.1591. ZHANG Z R, CHEN H Y, JIAO W G, et al. Rock breaking mechanism and blasting parameters of straight hole cutting with empty-hole [J]. Journal of China Coal Society, 2020, 45(S2): 791–800. DOI: 10.13225/j.cnki.jccs.2019.1591.
[17]	梁瑞, 吕亚茹, 周文海, 等. 地下采场爆破炮孔堵塞效应及长度研究 [J]. 地下空间与工程学报, 2020, 16(5): 1546–1554. LIANG R, LV Y R, ZHOU W H, et al. Study on blockage effect and the stem length in underground stope blasting [J]. Chinese Journal of Underground Space and Engineering, 2020, 16(5): 1546–1554.
[18]	肖思友, 姜元俊, 刘志祥, 等. 高地应力下硬岩爆破破岩特性及能量分布研究 [J]. 振动与冲击, 2018, 37(15): 143–149. DOI: 10.13465/j.cnki.jvs.2018.15.020. XIAO S Y, JIANG Y J, LIU Z X, et al. Hard rock blasting energy distribution and fragmentation characteristics under high earth stress [J]. Journal of Vibration and Shock, 2018, 37(15): 143–149. DOI: 10.13465/j.cnki.jvs.2018.15.020.
[19]	孙可明, 王金彧, 辛利伟. 不同应力差条件下超临界CO₂气爆煤岩体气楔作用次生裂纹扩展规律研究 [J]. 应用力学学报, 2019, 36(2): 466–472. DOI: 10.11776/cjam.36.02.B130. SUN K M, WANG J Y, XIN L W. Research on the law of secondary cracks propagation in coal and rock caused by gas wedging during supercritical CO₂ explosion under different stress differences [J]. Chinese Journal of Applied Mechanics, 2019, 36(2): 466–472. DOI: 10.11776/cjam.36.02.B130.
[20]	郭东明, 李旭鹏, 王汉军, 等. 益新煤矿中心大空孔掏槽爆破现场试验研究 [J]. 中国矿业, 2016, 25(4): 82–86. DOI: 10.3969/j.issn.1004-4051.2016.04.017. GUO D M, LI X P, WANG H J, et al. Field test on center big empty hole in cut blasting in Yixin coal mine [J]. China Mining Magazine, 2016, 25(4): 82–86. DOI: 10.3969/j.issn.1004-4051.2016.04.017.