基于双折线抗力模型的空爆荷载梁式构件振动位移研究

耿少波; 陈佳龙; 赵洲; 牛艳伟

doi:10.11883/bzycj-2021-0524

基于双折线抗力模型的空爆荷载梁式构件振动位移研究

doi: 10.11883/bzycj-2021-0524

耿少波^{1, 2,},
陈佳龙¹,
赵洲¹,
牛艳伟^2, ,

1.
中北大学理学院土木工程学科部，山西太原 030051
2.
长安大学公路大型结构安全教育部工程研究中心，陕西西安 710064

基金项目: 国家自然科学基金（51408558）；旧桥检测与加固技术交通运输行业重点实验室（长安大学）开放基金(300102212516)

详细信息

作者简介:
耿少波（1982－　），男，博士，副教授，gengshaobo@nuc.edu.cn

通讯作者:
牛艳伟（1981－　），男，博士，副教授，niuyanwei@chd.edu.cn

中图分类号: O383.2
计量
- 文章访问数: 505
- HTML全文浏览量: 228
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-21
- 修回日期: 2022-07-08
- 网络出版日期: 2022-08-10
- 刊出日期: 2022-10-31

A study on vibration displacements of beam members under air blast loading based on the bilinear resistance model

GENG Shaobo^{1, 2
,},
CHEN Jialong¹,
ZHAO Zhou¹,
NIU Yanwei^{2
, ,}

1.
Department of Civil Engineering, School of Science, North University of China, Taiyuan 030051, Shanxi, China
2.
Research Center of Highway Large Structure Engineering on Safety, Ministry of Education, Chang’an University, Xi’an 710064, Shaanxi, China

摘要

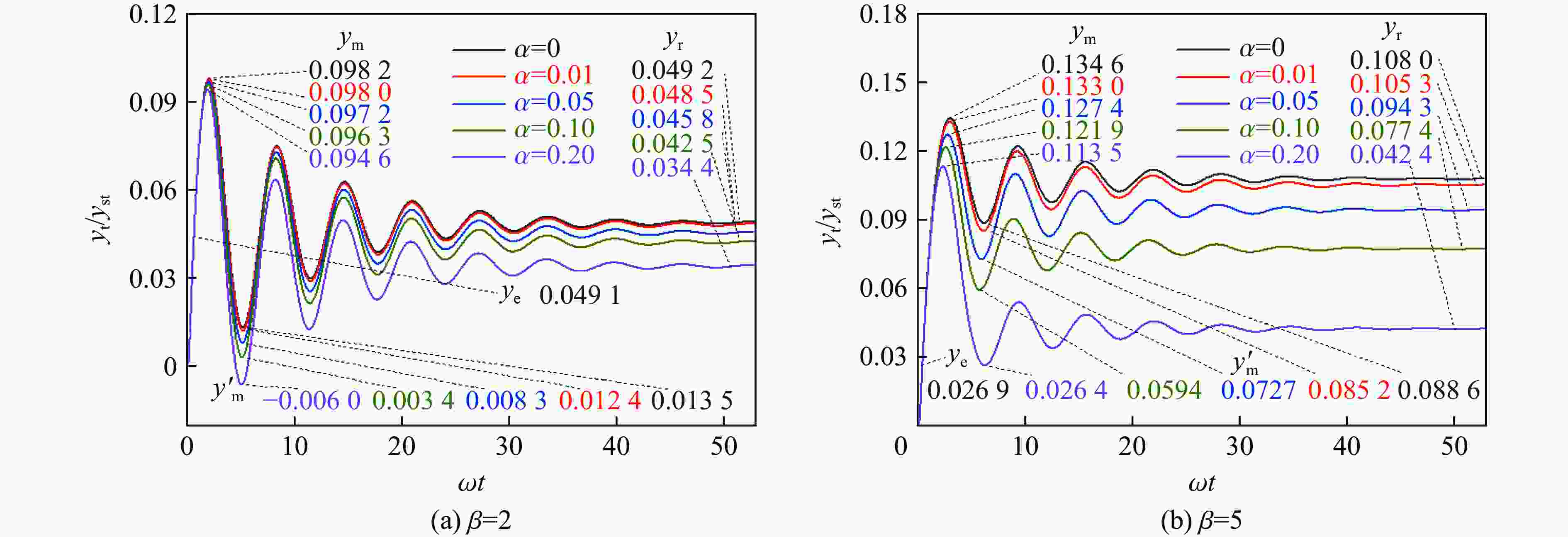
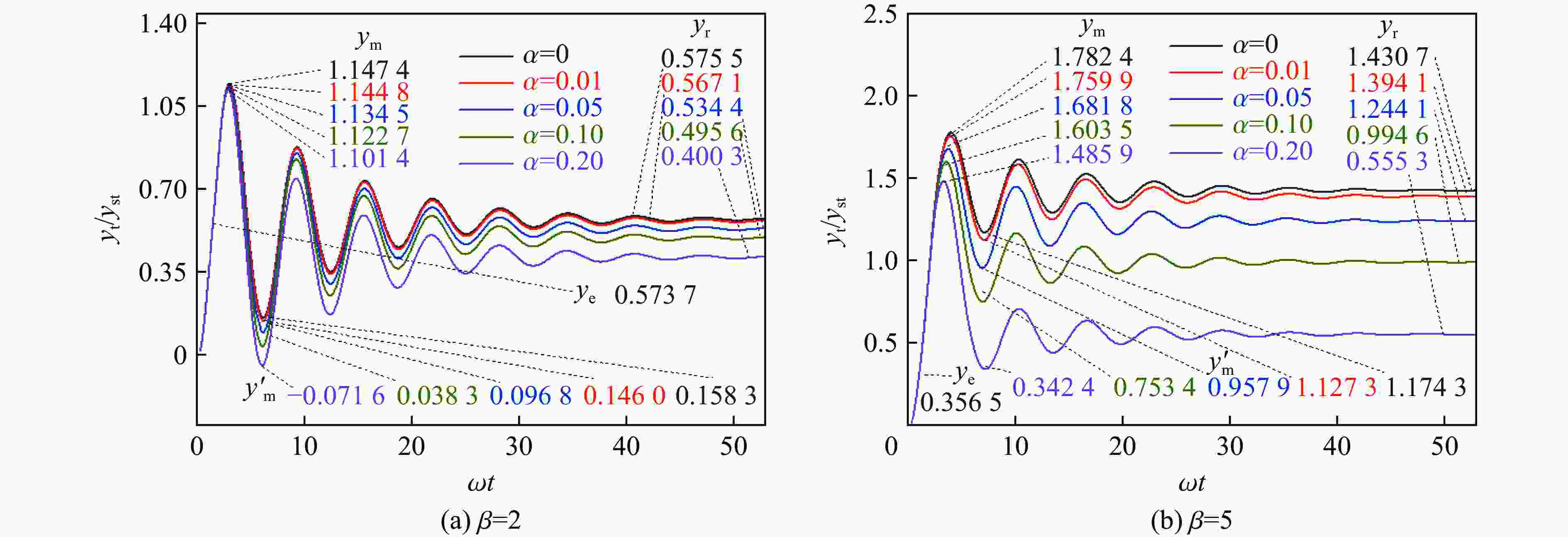
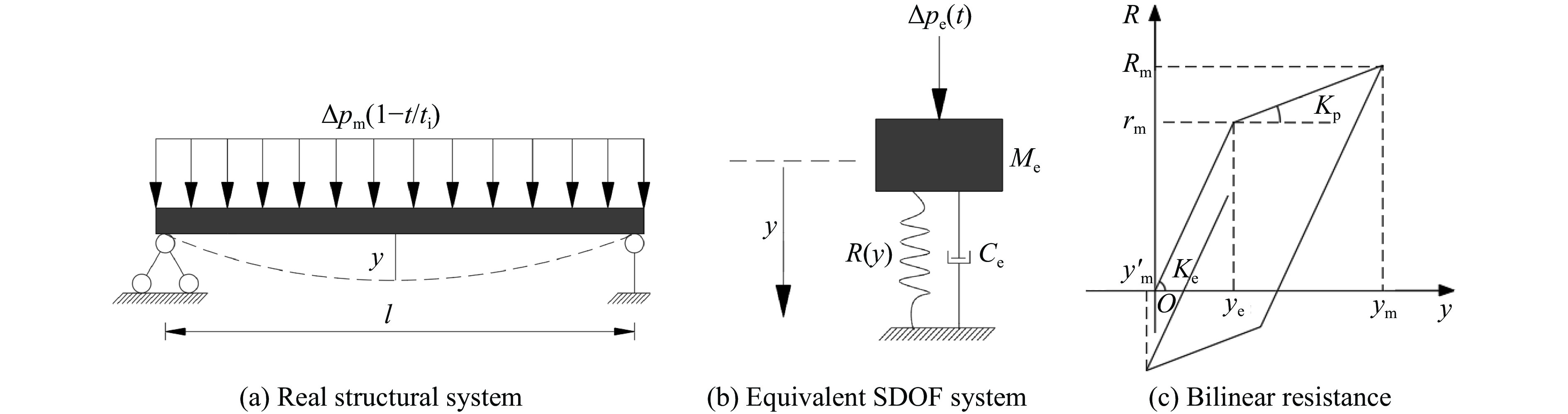
摘要: 为研究双折线抗力模型对空爆荷载梁式构件振动位移的影响，提出了柔性、刚性两类梁式构件正向弹塑性振动及回弹阶段弹塑性振动的分析法。应用等效单自由度法建立了各阶段振动方程并依据不同的初始条件推导出了各阶段的理论解。采用此理论解和代表性塑性强化系数，开展了双折线抗力模型中不同塑性强化程度对两类梁式构件正向弹塑性振动及回弹阶段弹塑性振动位移的典型工况验证。研究结果表明：基于双折线抗力模型位移理论解的适用范围更广；随着双折线抗力模型塑性强化系数的增大，两类梁式构件的最大弹塑性位移、残余变形均逐渐减小，且残余变形降低程度高于最大弹塑性位移；塑性强化系数增大到一定程度，梁式构件回弹阶段将出现塑性振动位移，进一步降低残余变形，无塑性回弹位移的理想弹塑性抗力模型会高估空爆荷载下梁式构件的残余变形。
- 双折线抗力模型 /
- 空爆荷载 /
- 弹塑性位移 /
- 残余变形
Abstract: In order to study the influence of bilinear resistance model on the vibration displacement of beam members under air blast loading, both the theoretical elast-plastic displacement solutions of the flexible and rigid members in forward and rebound stages were deduced, respectively. According to the relationship between blast duration and elastic duration from static position to maximum elastic displacement for members, the vibration situations could be divided into elastic forced vibration, elastic free vibration, plastic forced vibration, plastic free vibration, elastic rebound and plastic rebound. The equivalent single degree of freedom method was used to establish the vibration equations of each stage and the theoretical solutions of each stage were derived for different initial conditions. The method of the general solution plus the special solution was applied to solve each differential equation. Based on the theoretical solutions and the representative plastic strengthening coefficient, the elastoplastic vibration displacements of two types of beam members under different plastic strengthening degrees in the bilinear resistance model were verified under typical calculation cases. The corresponding complete vibration curves were finished for comparative analysis. The influence of the degree of plastic strengthening on the vibration representative value was analyzed. The results show that the displacement theoretical solution based on the bilinear resistance model has a wider range of application. With the increase of plastic strengthening coefficient of the bilinear resistance model, the maximum elastic-plastic displacement and residual deformation of the two types of beam members decrease gradually, and the reduction degree of residual deformation is higher than that of the maximum elastic-plastic displacement. When the plastic strengthening coefficient increases to a certain extent, the plastic vibration displacement will appear in the rebound stage of the beam members, further reducing the residual deformation. Compared with the bilinear resistance model, the elastic-perfectly plastic resistance overestimates the residual deformation of beam members under air blast loading.
- bilinear resistance model /
- air blast loading /
- elastic-plastic displacement /
- residual deformation

HTML全文

图 1 双折线抗力模型等效单自由度体系

Figure 1. Equivalent single-degree-of-freedom system of the bilinear resistance model

下载: 全尺寸图片幻灯片

图 2 柔性构件（ωt_i=0.2）弹塑性振动时程曲线

Figure 2. Time history curves of elastoplastic vibration for flexible members (ωt_i=0.2)

下载: 全尺寸图片幻灯片

图 3 刚性构件（ωt_i=2.0）弹塑性振动时程曲线

Figure 3. Time history curves of elastoplastic vibration for rigid members (ωt_i=2.0)

下载: 全尺寸图片幻灯片

图 4 塑性回弹状态与塑性强化系数的关系

Figure 4. Relationship between plastic rebound state and plastic hardening coefficient

下载: 全尺寸图片幻灯片

表 1 相对于理想弹塑性抗力模型的差异性结果

Table 1. Difference results relative to ideal elastoplastic resistance model

α	柔性构件				刚性构件
	β=2		β=5		β=2		β=5
	γ_β/%	γ_r/%	γ_β/%	γ_r/%	γ_β/%	γ_r/%	γ_β/%	γ_r/%
0.01	−0.5	−1.4	−1.2	−2.5	−0.5	−1.5	−1.2	−2.6
0.05	−1.0	−6.9	−5.2	−12.7	−1.5	−7.1	−5.6	−13.0
0.10	−2.0	−13.6	−9.4	−31.1	−2.5	−13.9	−10.0	−30.5
0.20	−3.5	−30.1	−15.6	−60.7	−4.0	−30.4	−16.6	−61.2

下载: 导出CSV

参考文献(23)

[1]	中华人民共和国建设部, 中华人民共和国国家质量监督检验检疫总局. 人民防空地下室设计规范: GB 50038—2005 [S]. 北京: 中国标准出版社, 2006.
[2]	US Army Corps of Engineers. Structures to resist the effects of accidental explosions: TM 5-1300 [S]. Washington, USA: US Department of the Army, 1990.
[3]	Canadian Standards Association. Design and assessment of buildings subjected to blast loads: CSA S850-12 [S]. Toronto, Canada: Canadian Standards Association, 2012.
[4]	中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012 [S]. 北京: 中国建筑工业出版社, 2012.
[5]	NASSR A A, YAGI T, MARUYAMA T, et al. Damage and wave propagation characteristics in thin GFRP panels subjected to impact by steel balls at relatively low-velocities [J]. International Journal of Impact Engineering, 2018, 111: 21–33. DOI: 10.1016/j.ijimpeng.2017.08.007.
[6]	NAGATA M, BEPPU M, ICHINO H, et al. Method for evaluating the displacement response of RC beams subjected to close-in explosion using modified SDOF model [J]. Engineering Structures, 2018, 157: 105–118. DOI: 10.1016/j.engstruct.2017.11.067.
[7]	RITCHIE C B, PACKER J A, SEICA M V, et al. Behaviour and analysis of concrete-filled rectangular hollow sections subject to blast loading [J]. Journal of Constructional Steel Research, 2018, 147: 340–359. DOI: 10.1016/j.jcsr.2018.04.027.
[8]	RIEDEL W, FISCHER K, KRANZER C, et al. Modeling and validation of a wall-window retrofit system under blast loading [J]. Engineering Structures, 2012, 37: 235–245. DOI: 10.1016/j.engstruct.2011.12.015.
[9]	SYED Z I, RAMAN S N, NGO T, et al. The failure behaviour of reinforced concrete panels under far-field and near-field blast effects [J]. Structures, 2018, 14: 220–229. DOI: 10.1016/j.istruc.2018.03.009.
[10]	陈万祥, 郭志昆, 罗立胜, 等. 考虑面力效应的HFR-LWC梁抗爆理论模型与试验验证 [J]. 工程力学, 2021, 38(2): 77–91. DOI: 10.6052/j.issn.1000-4750.2020.03.0200. CHEN W X, GUO Z K, LUO L S, et al. Theoretical model for HFR-LWC beam under blast loading accompanying membrane action and its experimental validation [J]. Engineering Mechanics, 2021, 38(2): 77–91. DOI: 10.6052/j.issn.1000-4750.2020.03.0200.
[11]	LI Z X, ZHONG B, SHI Y C. An effective model for analysis of reinforced concrete members and structures under blast loading [J]. Advances in Structural Engineering, 2016, 19(12): 1815–1831. DOI: 10.1177/1369433216649393.
[12]	STOCHINO F, TABANDEH A, GARDONI P, et al. Physics-based probabilistic demand model and reliability analysis for reinforced concrete beams under blast loads [J]. Engineering Structures, 2021, 248: 112932. DOI: 10.1016/J.engstruct.2021.112932.
[13]	ZHANG D, YAO S J, LU F Y. Experimental study on scaling of RC beams under close-in blast loading [J]. Engineering Failure Analysis, 2013, 33: 497–504. DOI: 10.1016/j.engfailanal.2013.06.020.
[14]	ROKAYA A, KIM J. An accurate analysis for sandwich steel beams with graded corrugated core under dynamic impulse [J]. International Journal of Steel Structures, 2018, 18(5): 1541–1559. DOI: 10.1007/s13296-018-0062-6.
[15]	BRUHL J C, VARMA A H. Analysis and design of one-way steel-plate composite walls for far-field blast effects [J]. Journal of Structural Engineering, 2021, 147(1): 04020288. DOI: 10.1061/(ASCE)ST.1943-541X.0002868.
[16]	FALLAH A S, LOUCA L A. Pressure-impulse diagrams for elastic-plastic-hardening and softening single-degree-of-freedom models subjected to blast loading [J]. International Journal of Impact Engineering, 2007, 34(4): 823–842. DOI: 10.1016/j.ijimpeng.2006.01.007.
[17]	方秦, 杜茂林. 爆炸荷载作用下弹性与阻尼支承梁的动力响应 [J]. 力学与实践, 2006, 28(2): 53–56. DOI: 10.3969/j.issn.1000-0879.2006.02.012. FANG Q, DU M L. Dynamic responses of an elastically supported beams with damping subjected to blast loads [J]. Mechanics in Engineering, 2006, 28(2): 53–56. DOI: 10.3969/j.issn.1000-0879.2006.02.012.
[18]	方秦, 陈力, 杜茂林. 端部设置弹簧和阻尼器提高防护门抗力的理论与数值分析 [J]. 工程力学, 2008, 25(3): 194-199, 221. FANG Q, CHEN L, DU M L. Theoretical and numerical investigations in effects of end-supported springs and dampers on increasing resistance of blast doors [J]. Engineering Mechanics, 2008, 25(3): 194-199; 221.
[19]	耿少波, 李洪, 葛培杰. 考虑跃迁的指数型炸药空爆荷载等效静载动力系数 [J]. 爆炸与冲击, 2019, 39(3): 032201. DOI: 10.11883/bzycj-2018-0048. GENG S B, LI H, GE P J. Equivalent static load dynamical coefficient for exponential air blast loading with transition [J]. Explosion and Shock Waves, 2019, 39(3): 032201. DOI: 10.11883/bzycj-2018-0048.
[20]	耿少波, 罗干, 陈佳龙, 等. 阻尼对空爆荷载等效静载动力系数的影响 [J]. 爆炸与冲击, 2022, 42(2): 023201. DOI: 10.11883/bzycj-2021-0036. GENG S B, LUO G, CHEN J L, et al. Effect of damping on equivalent static load dynamic factor of air blast load [J]. Explosion and Shock Waves, 2022, 42(2): 023201. DOI: 10.11883/bzycj-2021-0036.
[21]	郭东, 刘晶波, 闫秋实. 爆炸荷载作用下梁板结构反弹机理分析 [J]. 建筑结构学报, 2012, 33(2): 64–71. DOI: 10.14006/j.jzjgxb.2012.02.009. GUO D, LIU J B, YAN Q S. Rebound mechanism analysis in beams and slabs subjected to blast loading [J]. Journal of Building Structures, 2012, 33(2): 64–71. DOI: 10.14006/j.jzjgxb.2012.02.009.
[22]	陈万祥, 郭志昆, 叶均华. 爆炸荷载作用下柔性边界钢筋混凝土梁的动力响应与破坏模式分析 [J]. 兵工学报, 2011, 32(10): 1271–1277. CHEN W X, GUO Z K, YE J H. Dynamic responses and failure modes of reinforced concrete beams with flexible supports under blast loading [J]. Acta Armamentarii, 2011, 32(10): 1271–1277.
[23]	BIGGS J M. Introduction to structural dynamics [M]. New York, USA: McGraw-Hill Book Company, 1964: 315–327.