超高车辆与箱梁立交桥碰撞简化计算模型评估分析

郭玉旭; 席丰; 谭英华; 胡亚超; 刘锋

doi:10.11883/bzycj-2022-0029

超高车辆与箱梁立交桥碰撞简化计算模型评估分析

doi: 10.11883/bzycj-2022-0029

郭玉旭^{1, 2,},
席丰^{1, 2, ,},
谭英华^{1, 2},
胡亚超^{1, 3},
刘锋³

1.
山东建筑大学土木工程学院，山东济南 250101
2.
山东建筑大学建筑结构加固改造与地下空间工程教育部重点实验室，山东济南 250101
3.
山东科技大学土木工程与建筑学院，山东青岛 266590

基金项目: 国家自然科学基金（12172198，52078283）

详细信息

作者简介:
郭玉旭 (1997－　)，男，博士研究生，yxg1997@stu.cqu.edu.cn

通讯作者:
席　丰 (1963－　)，男，博士，教授，博士生导师，xifeng@sdjzu.edu.cn

中图分类号: O389; U447
计量
- 文章访问数: 833
- HTML全文浏览量: 310
- PDF下载量: 178
- 被引次数: 7
出版历程
- 收稿日期: 2022-01-19
- 修回日期: 2022-05-27
- 网络出版日期: 2022-06-01
- 刊出日期: 2023-03-05

Analysis on assessment of simplified compuational models for collision of over-height vehicles with box-girder flyovers

GUO Yuxu^{1, 2
,},
XI Feng^{1, 2
, ,},
TAN Yinghua^{1, 2},
HU Yachao^{1, 3},
LIU Feng³

1.
School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, Shandong, China
2.
Key Laboratory of Building Structural Retrofitting and Underground Space Engineering, Shandong Jianzhu University, Jinan 250101, Shandong, China
3.
College of Civil Engineering and Architecture, Shandong University of Science and Technology, Qingdao 266590, Shandong, China

摘要

摘要: 为了考察受超高车辆撞击装配式钢筋混凝土箱梁跨线桥的冲击动力和破坏行为，以一起近来发生的实际工程事故为案例进行精化有限元数值分析，并提出了双质量-并联弹簧（double mass-parallel spring, DM-PS）简化车辆模型，以有效地模拟超高车辆与桥梁的非对心碰撞行为。所建议DM-PS简化模型的有效性通过与两种广泛使用的车辆模型包括全尺（full scale, FS）模型和简单刚体（simple rigid, SR）模型的比较而得到充分地评估。计算结果表明：采用FS模型可得到与事故现场照片基本一致的跨线桥撞击区域破坏特征；SR模型高估结构的局部破坏，弱化结构的整体变形；DM-PS模型对于预测结构破坏具有较高的准确性。因此，所提出的DM-PS模型为超高车辆撞击桥梁结构防护设计提供了一个简单有效的分析手段。在此基础上，利用DM-PS模型进行了详细的结构行为参数分析，深入考察了车辆撞击速度、撞击质量、撞击位置以及结构形式等效应。所得到的结论为：相比撞击质量，结构的冲击动力行为对于撞击速度有更高的敏感性；跨中受撞和边跨受撞的变形和破坏模式有较大差异，边跨受撞对于单侧支座损伤更严重；箱梁内的箱板以及底板可以有效提高结构的抗冲击性能。
- 车辆撞击 /
- 钢筋混凝土结构 /
- 结构破坏 /
- 双质量-并联弹簧车辆模型
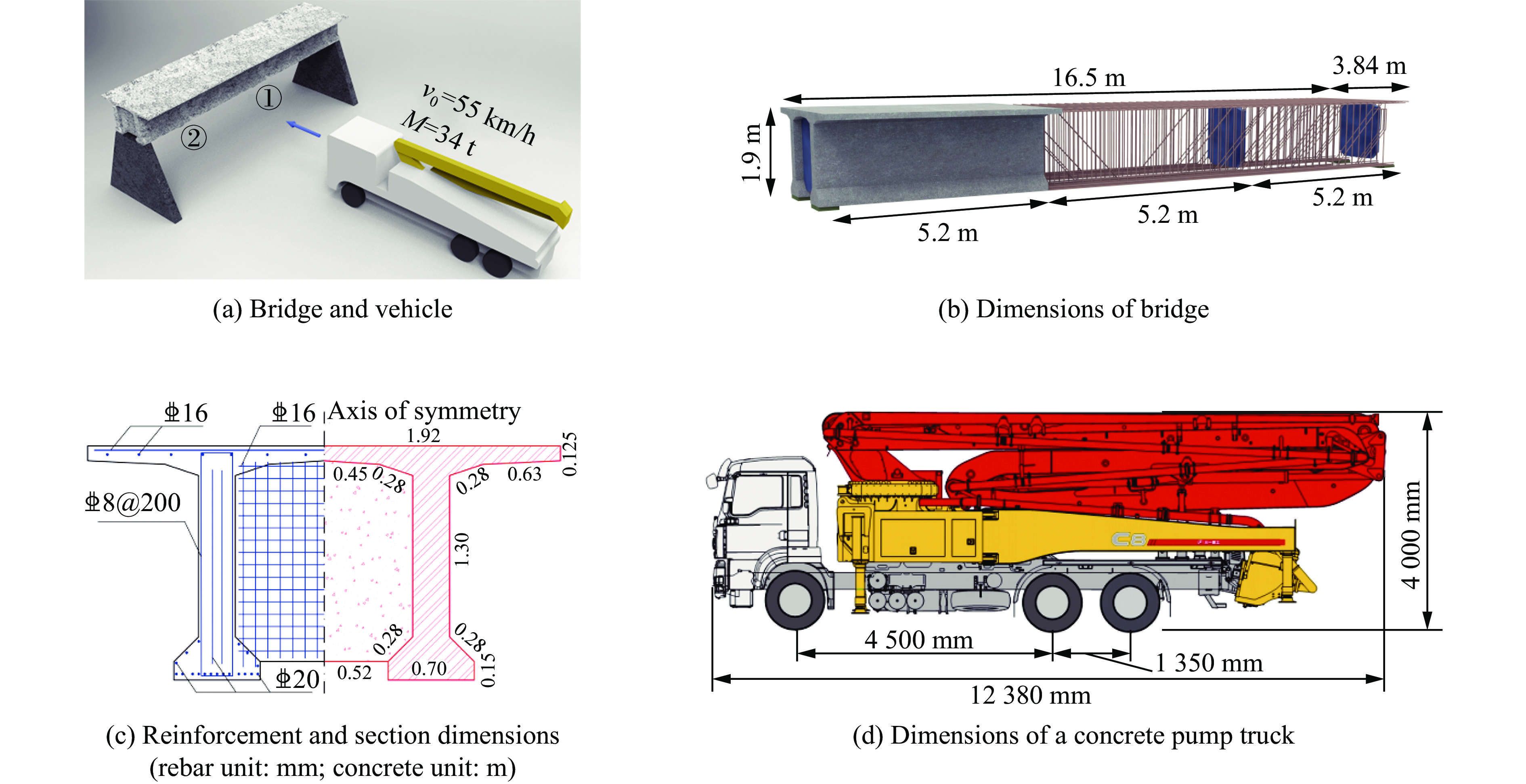
Abstract: To investigate the dynamical responses and failure behaviors of prefabricated reinforced-concrete (RC) box-girder flyovers caused by collision of over-height vehicles, a recent actual engineering accident is taken as an example to carry out refined numerical analysis by the finite element method, and a double mass-parallel spring (DM-PS) simplified vehicle model is proposed to effectively simulate the eccentric collision between the over-height vehicle and bridge superstructures. The effectiveness of the proposed DM-PS model is fully assessed through comparison with two widely-employed vehicle models, i.e., a full-scale (FS) model and a simple rigid (SR) model. The comparisons display that the failure characteristics of the collision area can be obtained by using the FS model, which is basically consistent with the photos of the accident scene; the SR model overestimates the local damage of the structure and underestimates the overall structural deformation; while the DM-PS model has high accuracy for predicting the structural failure. Therefore, the proposed DM-PS model can provide a simple and effective analysis tool for the protection design of bridge structures subjected to over-height vehicle collision. On this basis, a detailed parameter analysis of the structural behaviors is carried out by the DM-PS model, and the effects of vehicle collision velocity, mass, position, and structural form are investigated in depth. It is shown that the structural sensitivity of the impact dynamic behavior to the collision velocity of the vehicle is significantly greater than that of the collision mass of the vehicle; the deformation and failure modes of mid-span collision and side-span collision are quite different, and the damage of side-span collision to one side base is more serious; the box plate and reinforced plate in the box girder can effectively improve the structural impact resistance. Numerical results and conclusions can provide a reference for the crashworthiness design of bridges. The critical information of the finite element analysis process is presented in detail.
- vehicle collision /
- reinforced concrete structure /
- structural failure /
- double mass-parallel spring (DM-PS) model

HTML全文

图 1 车辆和箱桥结构

Figure 1. Vehicle and box-girder bridge structure

下载: 全尺寸图片幻灯片

图 2 桥梁有限元模型

Figure 2. A finite-element model of the bridge

下载: 全尺寸图片幻灯片

图 3 全尺寸车辆有限元模型

Figure 3. A full-scale (FS) vehicle finite-element (FE) model

下载: 全尺寸图片幻灯片

图 4 SR车辆模型

Figure 4. A simple-rigid (SR) vehicle model

下载: 全尺寸图片幻灯片

图 5 DM-PS车辆模型

Figure 5. DM-PS vehicle model

下载: 全尺寸图片幻灯片

图 6 混凝土单轴应力-应变曲线

Figure 6. Uniaxial stress-strain curves of concrete

下载: 全尺寸图片幻灯片

图 7 单元尺寸敏感性

Figure 7. Sensitivity to element size

下载: 全尺寸图片幻灯片

图 8 受撞击区域的破坏面对比

Figure 8. Failure comparison at collision area

下载: 全尺寸图片幻灯片

图 9 受撞击正面损伤云图

Figure 9. Damage contour of collision frontal

下载: 全尺寸图片幻灯片

图 10 桥面法向位移与切向位移

Figure 10. Normal and tangential displacement of the bridge deck

下载: 全尺寸图片幻灯片

图 11 不同瞬时箱梁结构损伤云图

Figure 11. Box girder damage contours at different instants

下载: 全尺寸图片幻灯片

图 12 SR模型计算结果

Figure 12. Simulation results by using the SR model

下载: 全尺寸图片幻灯片

图 13 DM-PS模型计算结果

Figure 13. Simulation results by using the DM-PS model

下载: 全尺寸图片幻灯片

图 14 能量分布对比

Figure 14. Comparison of energy distribution

下载: 全尺寸图片幻灯片

图 15 撞击力时程曲线对比

Figure 15. Comparison of collision force-time history curves

下载: 全尺寸图片幻灯片

图 16 具有加强底板的箱梁有限元模型

Figure 16. Box girder FE model with reinforced plate

下载: 全尺寸图片幻灯片

图 17 车辆质量和速度对破坏深度的影响

Figure 17. Effect of mass and velocity of vehicles on failure depth

下载: 全尺寸图片幻灯片

图 18 撞击力时程曲线

Figure 18. Collision force-time history curves

下载: 全尺寸图片幻灯片

图 19 桥体特征位移与支座损伤分析

Figure 19. Bridge characteristic displacement and base failure analysis

下载: 全尺寸图片幻灯片

图 20 受撞击正面SDEG云图

Figure 20. SDEG contours of collision frontal

下载: 全尺寸图片幻灯片

图 21 桥面损伤和结构破坏

Figure 21. Damage of the bridge deck and structural failure

下载: 全尺寸图片幻灯片

图 22 有无加强底板的结构破坏

Figure 22. Structural failure with or without reinforced plate

下载: 全尺寸图片幻灯片

图 23 桥面切向位移对比

Figure 23. Comparison of tangential displacement

下载: 全尺寸图片幻灯片

图 24 撞击后结构转角

Figure 24. Structural rotation angle after collision

下载: 全尺寸图片幻灯片

图 25 不同工况撞击后的结构转角

Figure 25. Structural rotation angles after collision under different working conditions

下载: 全尺寸图片幻灯片

图 26 不同工况下的混凝土破坏深度

Figure 26. Concrete failure depths after collision under different working conditions

下载: 全尺寸图片幻灯片

表 1 单元数目及类型

Table 1. Number and type of elements

项目单元数目尺寸/mm 单元类型

桥体 2 324 624 50 C3D8R
箱板 177 128 20 C3D8R
支座 3 368 20 C3D8R
钢筋 108 642 50 B31
地面 1 296 500 R3D4

下载: 导出CSV

表 2 模型工况

Table 2. Model working conditions

模型 M/t v_o/(m·s⁻¹) 箱梁类型-X 撞击位置-Y

M-v_o-XY 34/44/54 15/20/25 无底板/有底板跨中/边跨

下载: 导出CSV

参考文献(15)

[1]	HU Y C, TAN Y H, XI F. Failure assessment and virtual scenario reproduction of the progressive collapse of the FIU bridge [J]. Engineering Structures, 2021, 227: 111423. DOI: 10.1016/j.engstruct.2020.111423.
[2]	BUTH C E, BRACKIN M S, WILLIAMS W F, et al. Collision loads on bridge piers: phase 2. report of guidelines for designing bridge piers and abutments for vehicle collisions: 9-4973-2 [R]. Texas, USA: Texas Transportation Institute, 2011.
[3]	田力, 冯振宁. 超高车辆撞击预应力箱型梁桥上部结构的动态响应 [J]. 西南交通大学学报, 2016, 51(4): 632–638. DOI: 10.3969/j.issn.0258-2724.2016.04.005. TIAN L, FENG Z N. Dynamic response of superstructure of prestressed box-girder bridge to over-high truck impact [J]. Journal of Southwest Jiaotong University, 2016, 51(4): 632–638. DOI: 10.3969/j.issn.0258-2724.2016.04.005.
[4]	OZDAGLI A I, MOREU F, XU D, et al. Experimental analysis on effectiveness of crash beams for impact attenuation of overheight vehicle collisions on railroad bridges [J]. Journal of Bridge Engineering, 2020, 25(1): 04019133. DOI: 10.1061/(ASCE)BE.1943-5592.0001503.
[5]	XU L J, LU X Z, GUAN H, et al. Finite-element and simplified models for collision simulation between overheight trucks and bridge superstructures [J]. Journal of Bridge Engineering, 2013, 18(11): 1140–1151. DOI: 10.1061/(ASCE)BE.1943-5592.0000472.
[6]	AL-THAIRY H, WANG Y C. A simplified analytical method for predicting the critical velocity of vehicle impact on steel columns [J]. Journal of Constructional Steel Research, 2014, 92: 136–149. DOI: 10.1016/j.jcsr.2013.10.014.
[7]	陆新征, 卢啸, 张炎圣, 等. 超高车辆-桥梁上部结构撞击力的工程计算方法 [J]. 中国公路学报, 2011, 24(2): 49–55. DOI: 10.19721/j.cnki.1001-7372.2011.02.009. LU X Z, LU X, ZHANG Y S, et al. Engineering calculation method for collision force between over-height truck and bridge superstructure [J]. China Journal of Highway and Transport, 2011, 24(2): 49–55. DOI: 10.19721/j.cnki.1001-7372.2011.02.009.
[8]	HENG K, LI R W, LI Z R, et al. Dynamic responses of highway bridge subjected to heavy truck impact [J]. Engineering Structures, 2021, 232: 111828. DOI: 10.1016/j.engstruct.2020.111828.
[9]	陆新征, 何水涛, 黄圣楠. 超高车辆撞击桥梁上部结构研究: 破坏机理, 设计方法和防护对策 [M]. 北京: 中国建筑工业出版社, 2011: 54–55.
[10]	GORST N J S, WILLIAMSON S J, PALLETT P F, et al. Friction in temporary works: 071 [R]. Birmingham, UK: Health and Safety Executive, 2003.
[11]	LI X X. Parametric study on numerical simulation of missile punching test using concrete damaged plasticity (CDP) model [J]. International Journal of Impact Engineering, 2020, 144: 103652. DOI: 10.1016/j.ijimpeng.2020.103652.
[12]	ABAQUS Inc. ABAQUS analysis user’s manual [Z]. ABAQUS Inc., 2021.
[13]	张帝, 杨军, 曾丹, 等. 钢筋混凝土排架结构的抗爆破坏等级 [J]. 爆炸与冲击, 2020, 40(12): 121405. DOI: 10.11883/bzycj-2020-0012. ZHANG D, YANG J, ZENG D, et al. Damage grades of reinforced concrete bent structures against blast [J]. Explosion and Shock Waves, 2020, 40(12): 121405. DOI: 10.11883/bzycj-2020-0012.
[14]	LI X X L, WANG C, SATO J. Framework for dynamic analysis of radioactive material transport packages under accident drop conditions [J]. Nuclear Engineering and Design, 2020, 360: 110480. DOI: 10.1016/j.nucengdes.2019.110480.
[15]	庄茁, 张帆, 岑松, 等. ABAQUS非线性有限元分析与实例 [M]. 北京: 科学出版社, 2005: 110–115.

施引文献

期刊类型引用(3)

1.	陈甫君, 袁飞云, 于建华, 李小军, 岚涛, 郭达. 地震作用下不等高度桥墩多跨钢筋混凝土桥梁的碰撞效应与脆弱性. 科学技术与工程. 2025(17) 百度学术
2.	陈鹏程，尹小莉，王琳，路国运，焦晋峰. 连续两次侧向冲击下格构式钢构件的力学性能. 爆炸与冲击. 2025(04): 125-135 . 本站查看
3.	李全林. 城市人行天桥被撞击后的检测评估及分析. 工程建设与设计. 2024(24): 67-69 . 百度学术