Anti-penetration capability of pre-stressed confined concrete with truncated cone
-
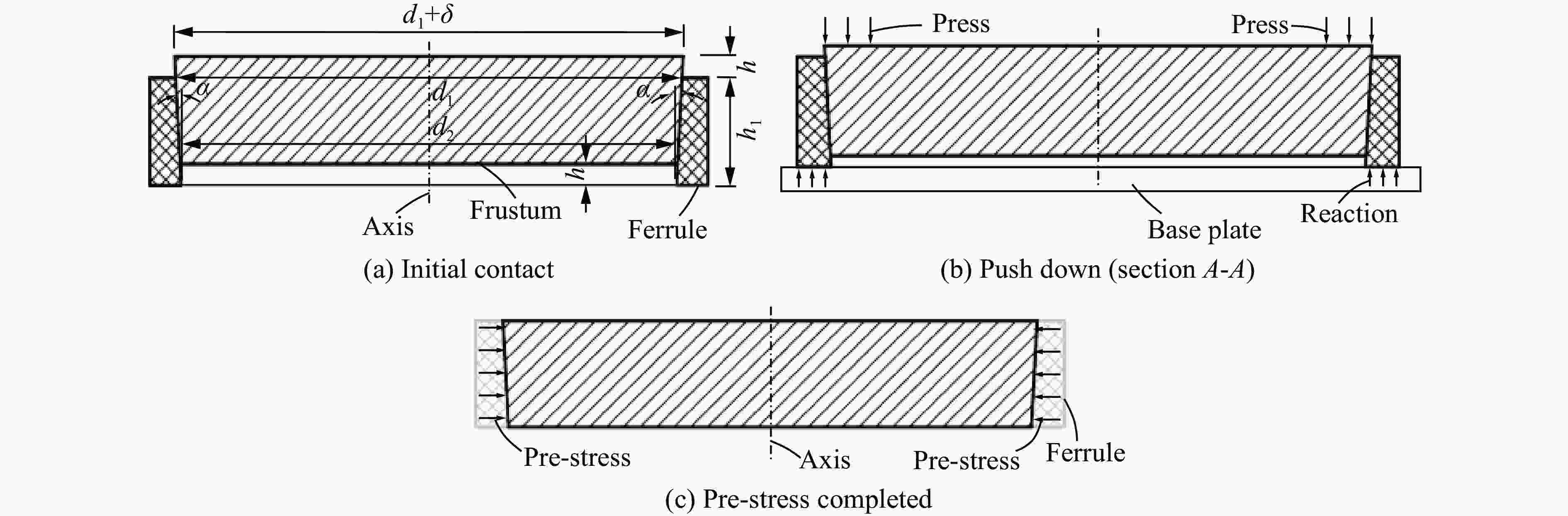
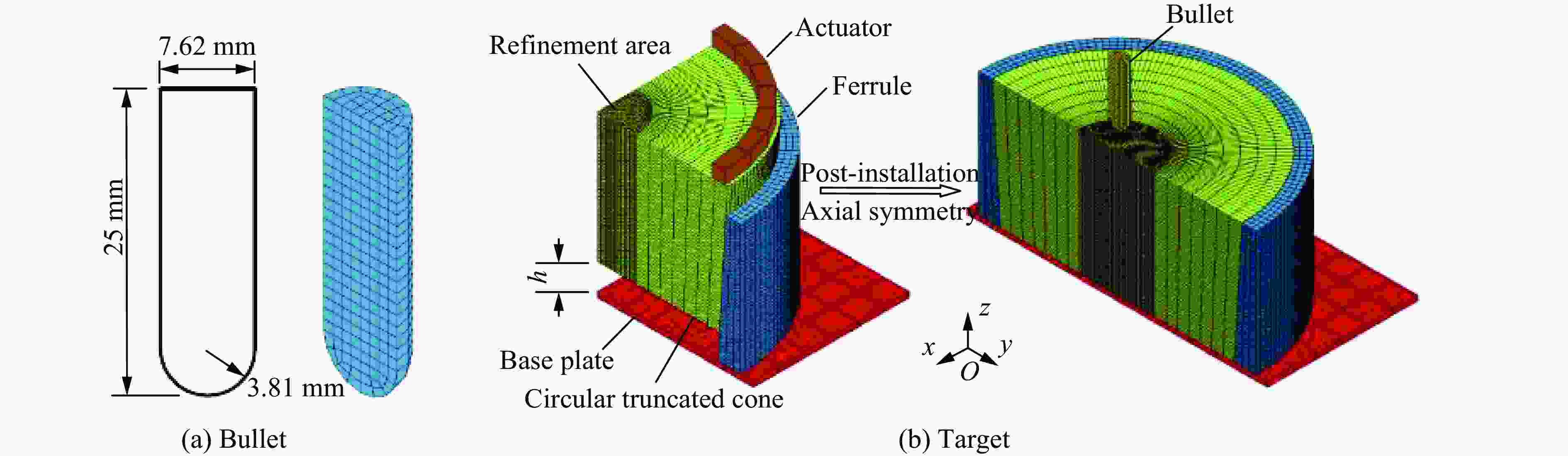
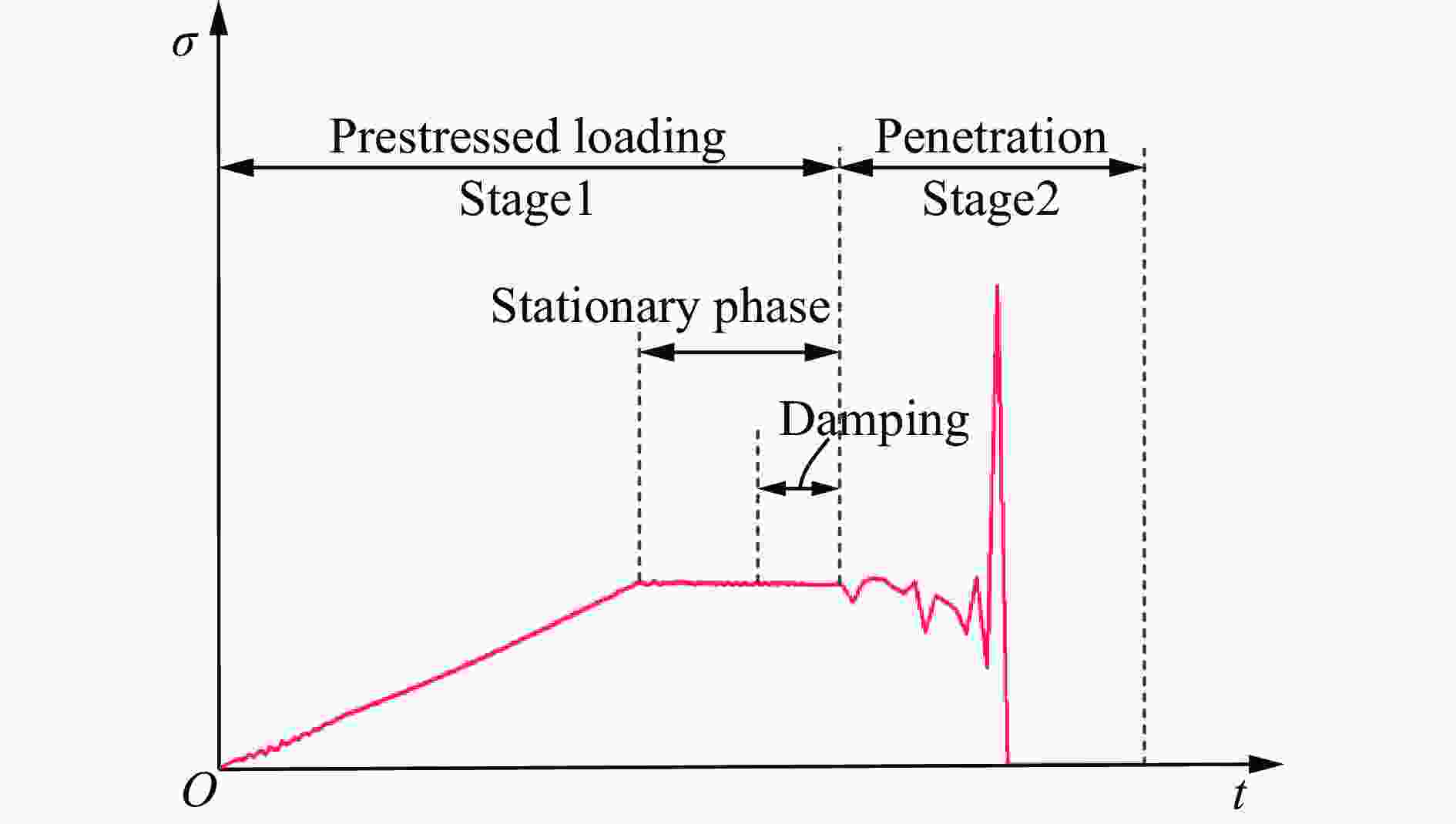
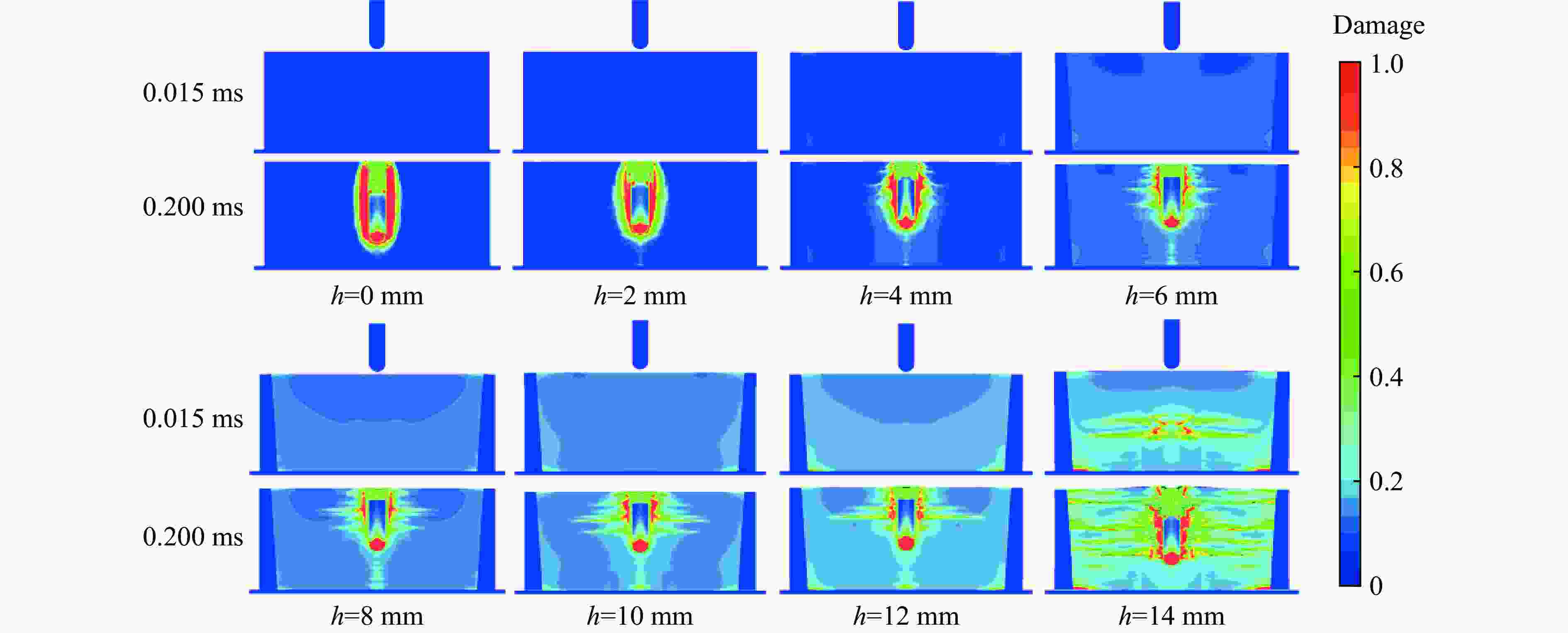
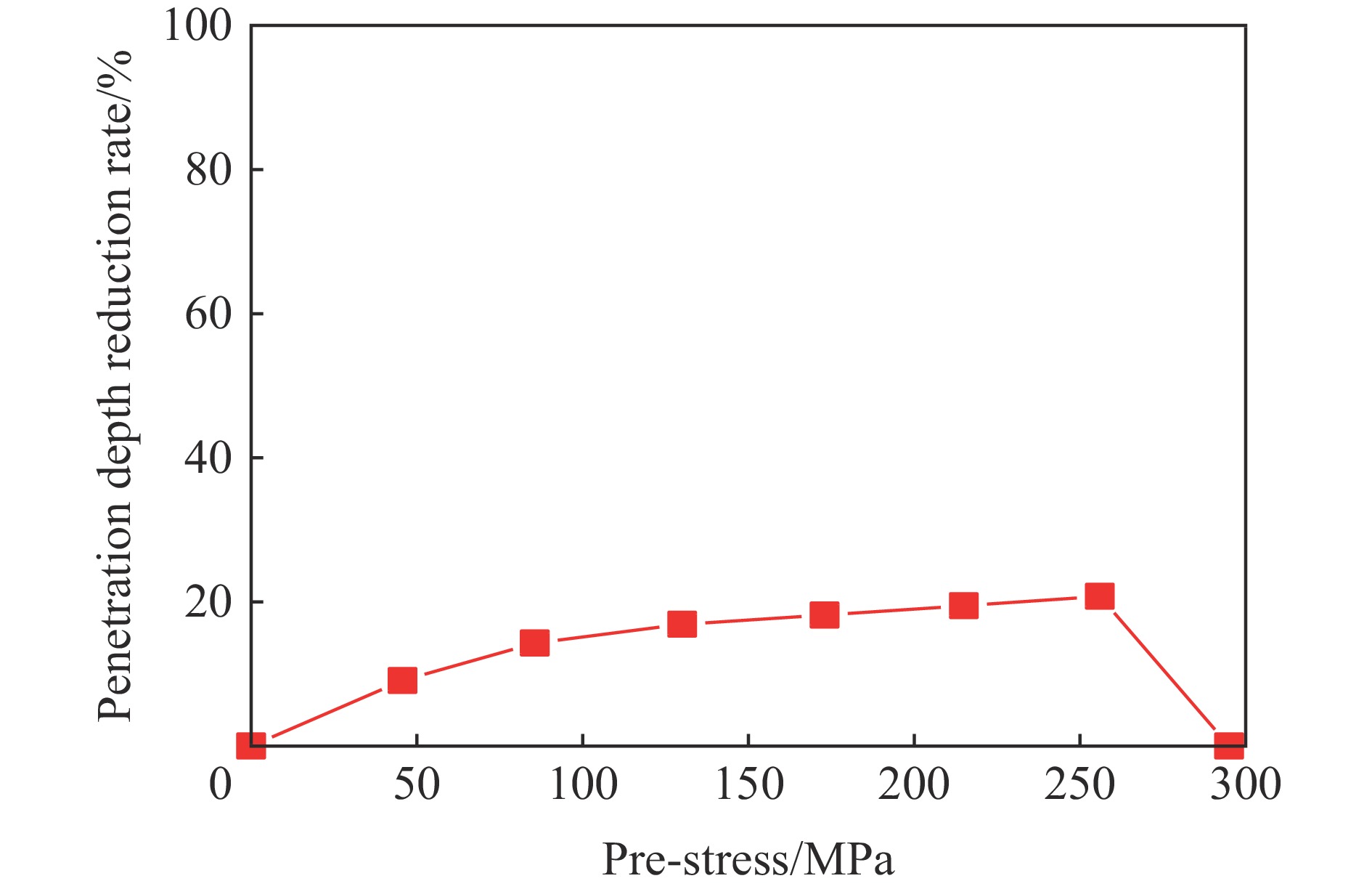
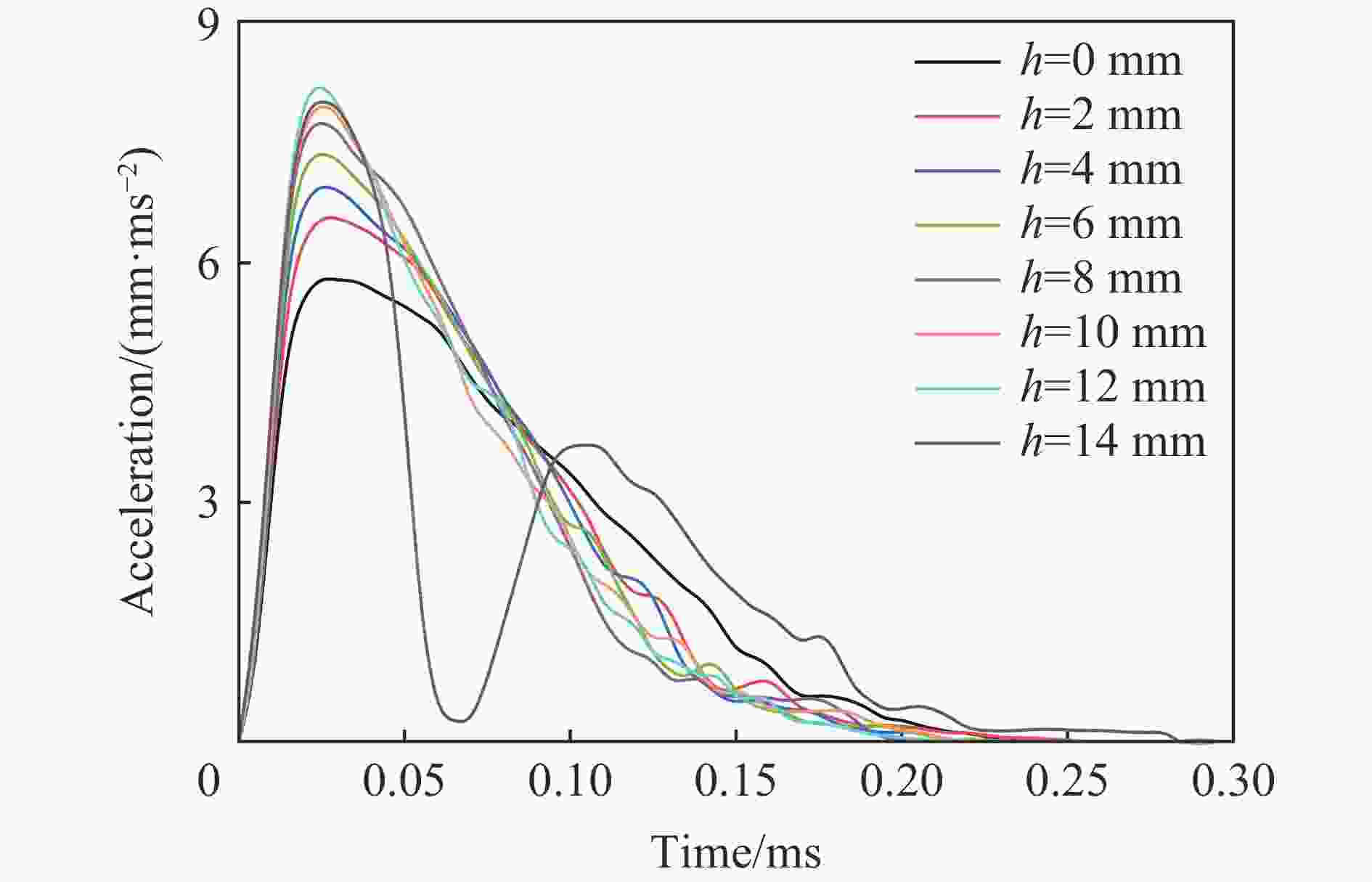
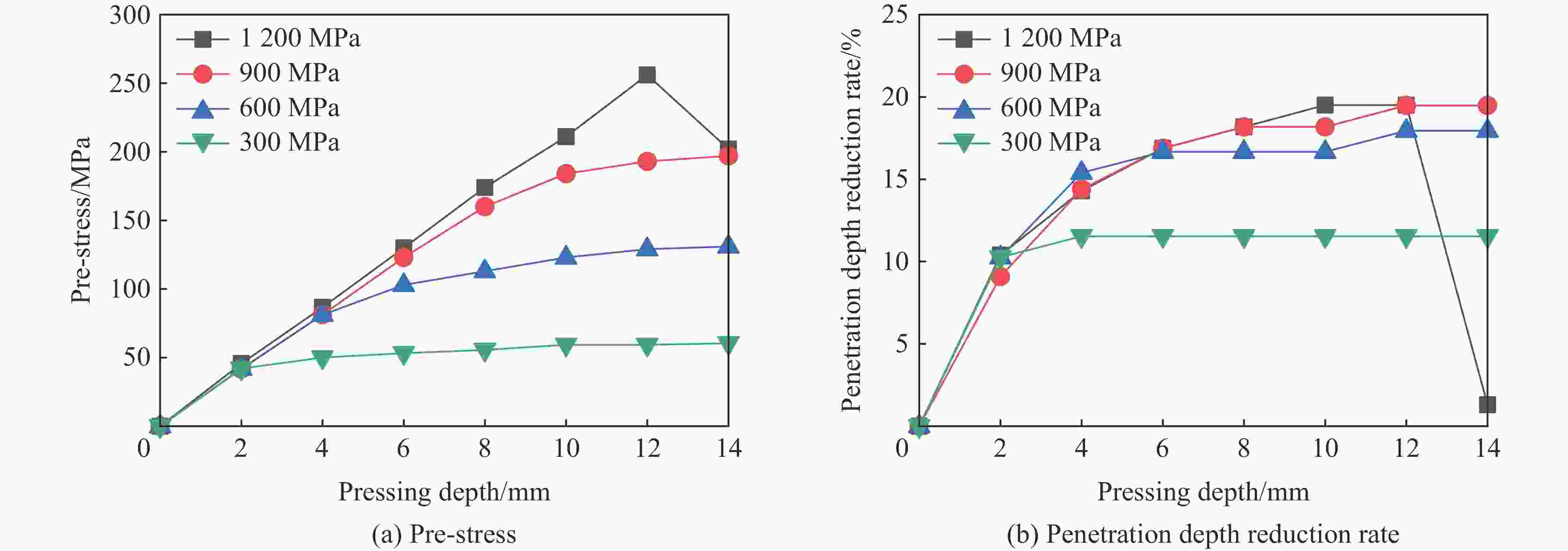
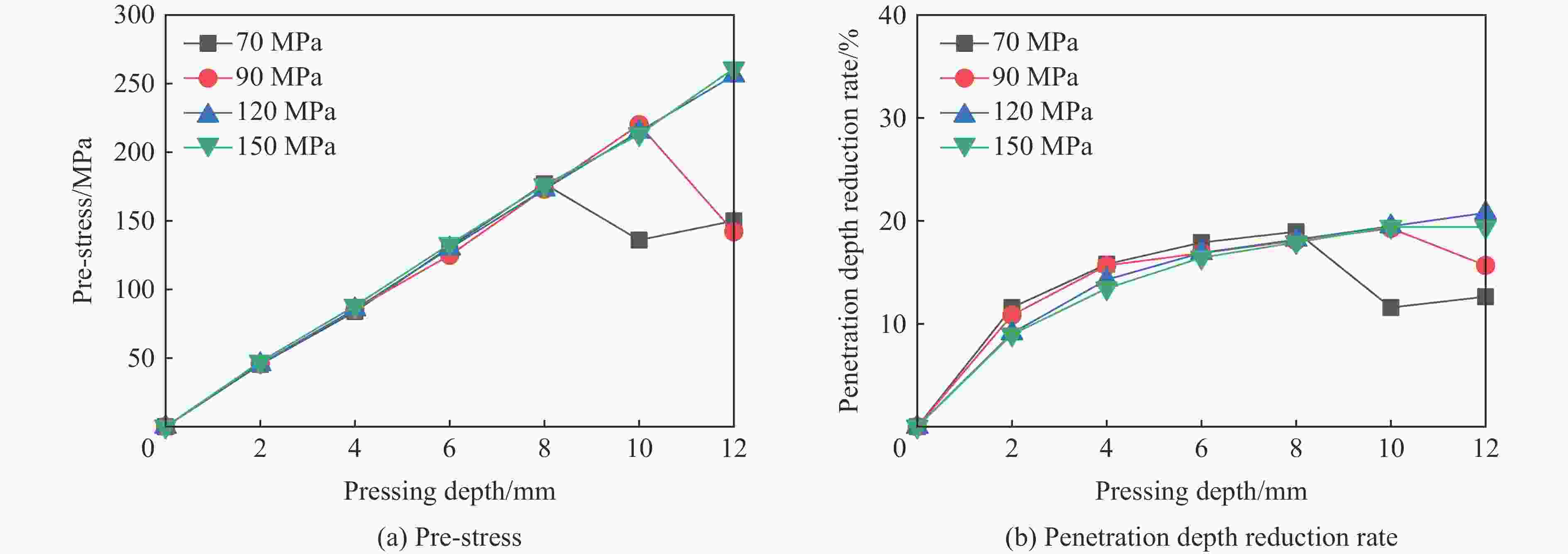
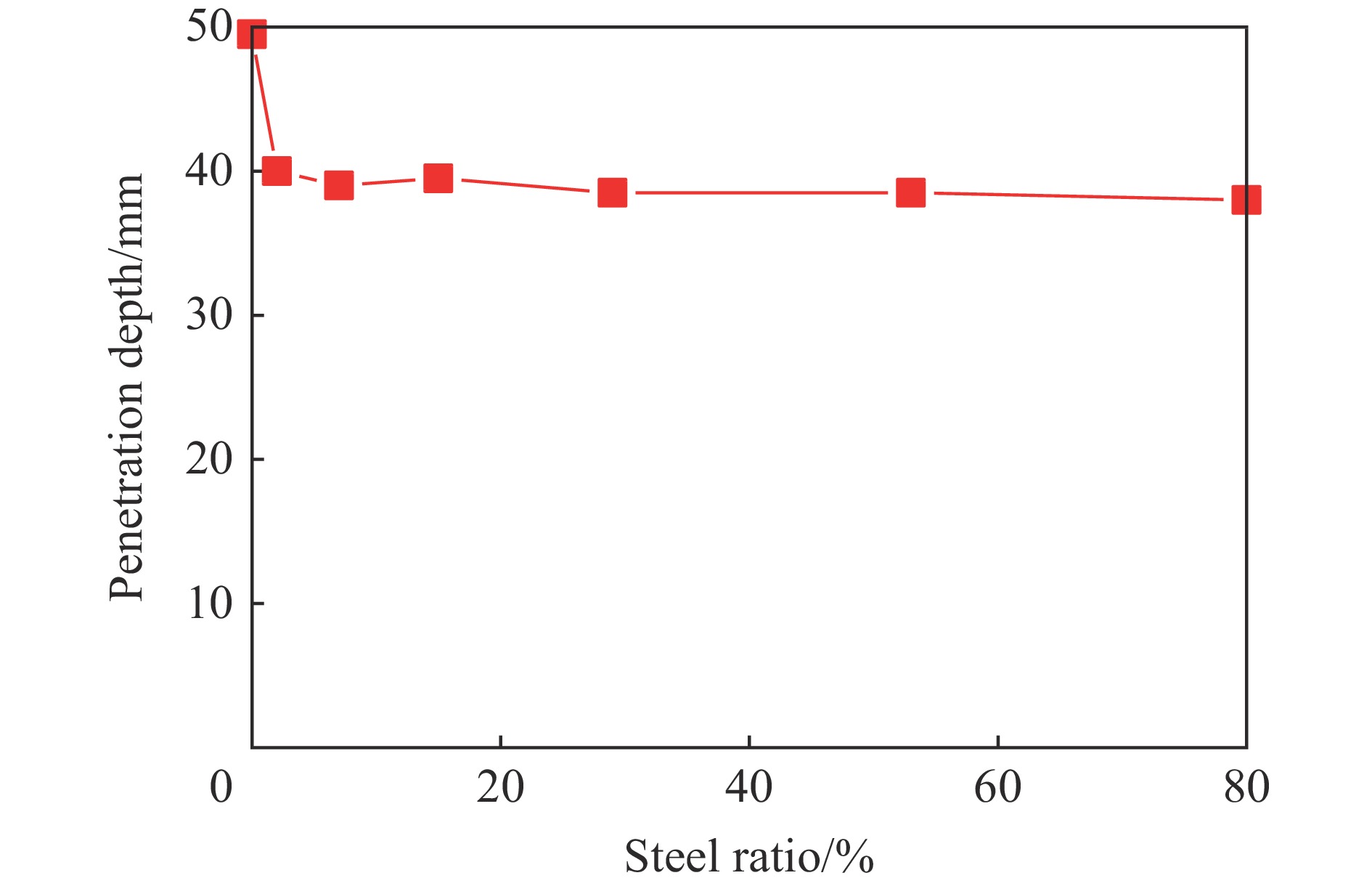
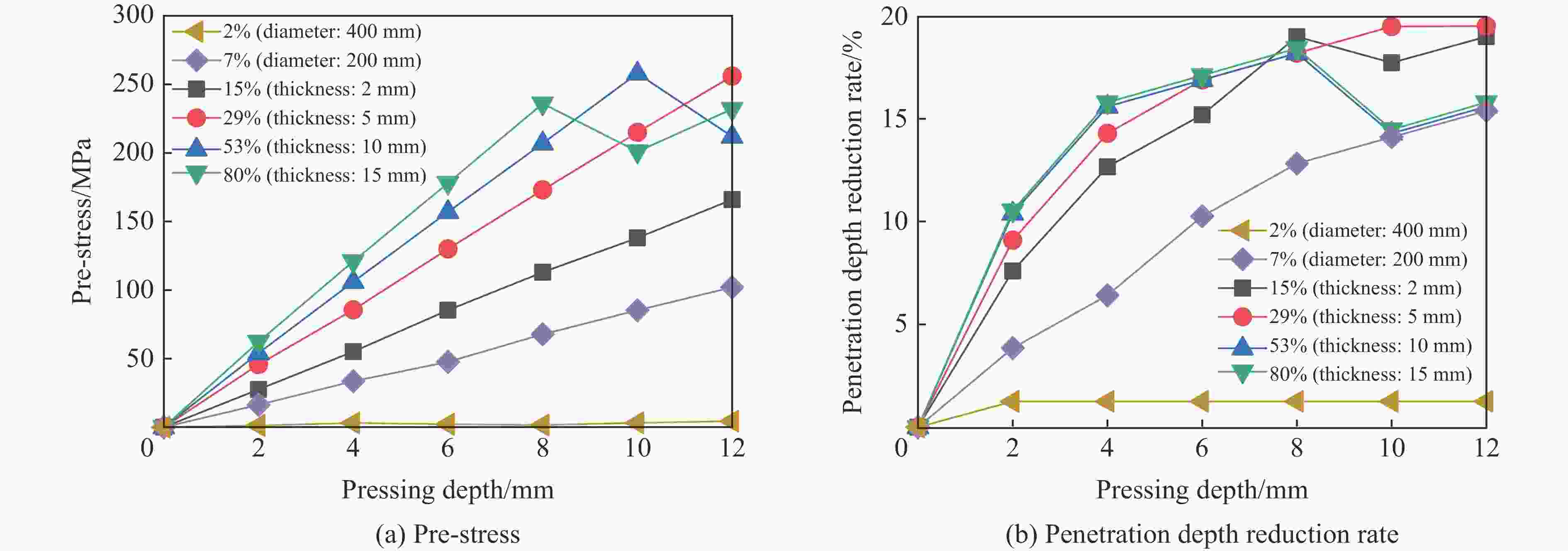
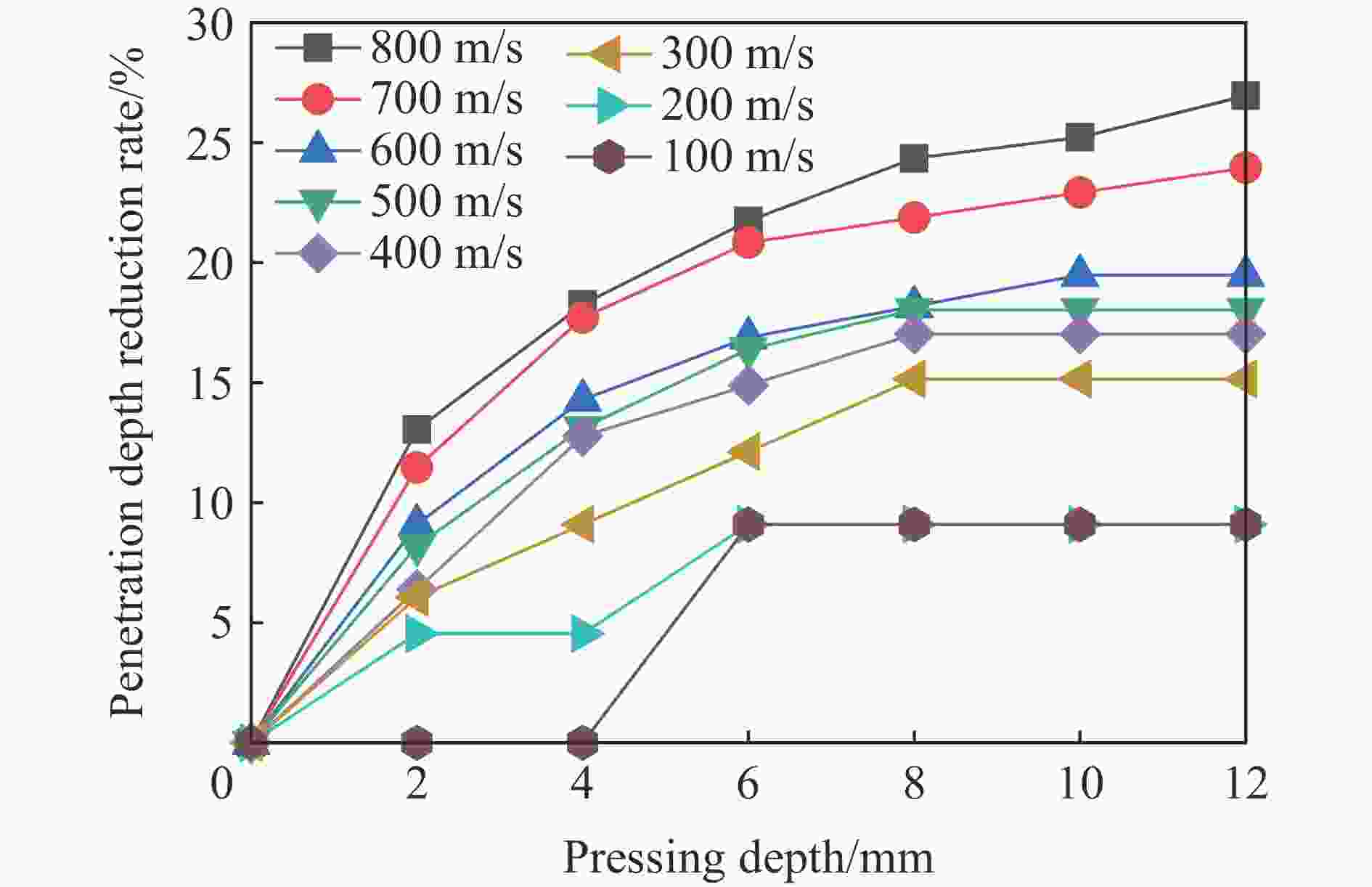
摘要: 在侧限约束条件下，混凝土材料的抗侵彻性能可得到较大提高，在此基础上施加预应力围压，其抗侵彻性能可进一步提高，但现有预应力方法对约束混凝土施加预应力较为困难。基于此，提出了一种相对简便的锥台嵌挤预应力约束方法，采用楔形块楔紧的原理，将锥面倾角为3°和直径微大于约束环的锥台形混凝土靶体挤入与之匹配的约束钢环内，通过锥面配合契紧的方式对混凝土靶体沿径向施加预应力，以锥台靶体的下压深度、盈差以及压入力的大小等指标控制预应力大小。采用LS-DYNA软件验证了该方法施加预应力的可行性，并通过重启动算法开展了预应力约束混凝土靶的抗侵彻性能研究。数值计算结果表明，靶体预应力随着其下压深度或盈差的增大近似线性增加，且混凝土靶体的抗侵彻性能随预应力增大而提高，但预应力过大时靶体内部发生损伤，导致其抗侵彻性能反而快速下降。对钢环强度、混凝土强度、含钢率和弹体速度等参数进行敏感性分析，结果表明，合理匹配钢环强度和混凝土强度，并选择合适的靶体含钢率，可有效提高靶体的预应力、抗侵彻性能以及钢材利用率；且弹体初速度越高，预应力对提高靶体抗侵彻性能的作用越明显。提出的锥台嵌挤预应力约束方法可为提高混凝土等脆性材料的抗侵彻性能提供一种新思路和方法。Abstract: The penetration resistance of concrete can be greatly improved by lateral confinement, and it would be continued to increase when pre-stress is further applied. However, the existing methods are difficult to realize the pre-stress on the confined concrete. In this paper, a relatively simple method for pre-stress confinement is proposed. Based on the principle of wedging the wedge-shaped block, a truncated cone-shaped concrete target with a cone inclination of 3° and a diameter slightly larger than the ferrule was squeezed into the matching steel ferrule, so the concrete target was pre-stressed along the radial direction by means of cone-shaped fitting and tightening, while the pre-stress was controlled by the indicators such as the pressing depth of the concrete target, the margin, and the pressing force. The feasibility of this method is then verified by simulation using LS-DYNA, and the penetration resistance of pre-stressed confined concrete is studied by the so-called restart algorithm. Numerical results demonstrate that the proposed method can provide enough radial pre-stress to the confined concrete target, and the pre-stress of the target increases approximately linearly with the increase of the pressing depth or the margin. Furthermore, within a certain range, the penetration resistance of the concrete target increases with the increase of pre-stress, while it decreases rapidly when the pre-stress is too high, which causes the damage of the concrete target. Parametric study on the parameters such as steel ferrule strength, concrete strength, steel ratio and projectile velocity, shows that reasonable matching of the steel ferrule strength with the concrete strength and selection of appropriate steel ratio of the target can effectively improve the pre-stress, penetration resistance of the target and the efficiency of steel; the higher the projectile velocity, the more obvious the effect of pre-stress on the improvement of the anti-penetration performance of the target. The proposed method for applying pre-stress provides a new approach to improve the anti-penetration capability of brittle materials such as concrete.
-
Key words:
- pre-stress /
- penetration /
- confinement /
- concrete /
- LS-DYNA
-
泡沫金属材料的率相关性能研究主要采用分离式霍普金森压杆(SHPB)动态压缩实验技术。由于泡沫铝复杂的微结构以及低阻抗、低波速、大变形等特点, 使其动态性能测试难度较大, 实验结果的离散性很大。同时, 由于泡沫铝材料制备方法多样, 泡沫铝的力学性能差异很大。迄今为止, 对泡沫铝应变率效应的研究尚没有得出一致的结论[1-2]。
V.S.Deshpande等[3]进行了0.001~5 000 s-1应变率范围内Alulight泡沫和Duocel泡沫的动、静态压缩实验, 得到闭孔泡沫铝和开孔泡沫铝均对应变率不敏感的结论。郭伟国等[4]对相对密度8.4%和4.5%的Duocel泡沫在0.001~500 s-1应变率下的形变和力学性能进行了系统的实验研究, 同样得出该材料对应变率不敏感的结论。K.A.Dannemann等[5]在Alporas泡沫和6101铝合金开孔泡沫(Duocel)的动、静态压缩实验中则发现, 400~2 500 s-1的应变率范围内闭孔泡沫铝具有明显的应变率效应, 开孔泡沫的应变率效应不明显。T.Mukai等[6-7]同样也得出了闭孔泡沫铝对应变率敏感的结论。程和法等[8-9]分别对相对密度0.363~0.419的开孔泡沫Al-Mg合金以及相对密度0.341~0.419的通孔泡沫铝, 在0.001~1 600 s-1和0.001~2 000 s-1应变率范围内的动、静态压缩力学性能进行了实验研究, 指出两种开孔泡沫材料均具有明显的应变率效应。田杰等[10]开展了4种不同基体材料泡沫铝的准静态和动态压缩实验, 得到的压缩应力应变曲线显示, 无论基体材料对应变率是否敏感性, 泡沫材料都表现出明显的应变率效应。张健等[11]对孔隙率60%~79%的闭孔泡沫铝在0.001~2 500 s-1应变率范围内的实验研究结果表明, 闭孔泡沫铝的应变率敏感性受孔隙率大小影响, 随着孔隙率的降低, 闭孔泡沫铝表现出明显的应变率效应, 高孔隙率闭孔泡沫铝对应变率基本不敏感。
尽管有很多泡沫铝对应变率敏感的结论, 但对于敏感性产生原因的解释不尽相同。K.A.Dannemann等[5]将其归结为泡孔内气体的黏性流动。胡时胜等[12]认为泡孔内气体的黏性流动引起的应力增加可忽略不计, 不可能是泡沫材料应变率敏感的根本原因, 敏感性主要是由泡孔结构的变形特性产生, 基体材料的应变率效应及泡孔的形状大小并不能对泡沫材料应变率的敏感性起主导作用。张健等[11]认为基体材料的应变率敏感性是泡沫材料应变率敏感性的决定性因素, 但影响程度受孔隙率大小影响, 随着孔隙率的增大敏感性降低; 微惯性、波效应和孔内气体压力对泡沫铝的平台应力不产生明显影响。
总体来说, 倾向于泡沫铝对应变率敏感的研究通常将敏感性产生原因归结为基体材料率相关性能、微结构惯性以及孔穴内部气体压力变化。而根据L.J.Gibson等[13]的研究结论, 可以认为, 孔穴气体压力变化对泡沫铝材料力学性能的影响很小, 不是引起泡沫铝材料应变率敏感的主要原因。此外, 尽管相对密度、应变率等参数不是泡沫铝材料是否存在应变率效应的决定因素, 但相对密度的变化可能会影响泡沫铝对应变率的敏感程度; 应变率(或加载速率)的变化可能会改变泡沫铝的变形机制, 进而影响泡沫铝材料应变率敏感性的产生原因。为此, 本文中, 研究基体材料率相关性能、微结构惯性对泡沫铝率相关性的影响, 分析相对密度与泡沫铝应变率敏感程度的关系, 以及应变率变化对泡沫铝动态压缩力学性能的影响。
1. 模型
1.1 三维随机球形泡孔模型
泡沫铝材料通常为无序开、闭孔混合结构。本文中采用Matlab和Abaqus软件生成了三维随机分布球形泡孔模型模拟泡沫铝材料的微细观结构, 模型几何边界呈周期性排列, 并采用代表性体积单元边长与泡孔孔径的比描述三维随机模型中泡孔的规模大小, 即:
δ=l/(2r) (1) 式中:δ为模型的泡孔规模大小, l为模型的边长, r为球形泡孔的半径。
图 1为泡孔规模δ=4, 孔隙率分别为65%、50%和35%的泡沫材料三维球形泡孔模型。模型采用四面体单元离散, 单元数量分别为218 032、306 139和377 064。
1.2 基体材料本构模型
采用Cowper-Symonds模型描述铝合金基体材料的应变率效应[11]:
σdy=σsy(1+(˙εC)1/P) (2) 式中:
为材料的动态屈服应力,
为材料的静态屈服应力,
为应变率, C、P为Cowper-Symonds应变率参数。
基体材料的弹塑性本构采用理想弹塑性模型。计算过程中, 应变率参数C和P分别为6 500 s-1和4, 杨氏模量为69 GPa, 泊松比为0.33, 静态屈服应力为250 MPa, 密度为2.7 g/mm3。另外, 当应变率参数C和P取值为零时, 表示基体材料率无关。
1.3 泡孔规模影响分析
泡孔模型在理论上应包含尽可能多的泡孔结构, 但过多的微结构将会导致计算量过大而使模型不具有实际应用价值, 需要综合考虑模型泡孔规模与得到可信结论之间的关系。为此, 分别构建了泡孔规模δ=2、δ=3和δ=4, 孔隙率范围35%~65%的一系列三维随机泡孔模型, 并采用Abaqus有限元软件分析了泡沫杨氏模量随相对密度的分布规律, 见图 2。
图 2 泡沫模型初始弹性模量随相对密度的分布Figure 2. Initial elastic modulus of foams versus foam relative densities可见, 泡孔规模δ=3时, 结果的离散性较小, 且模型没有明显尺度效应。所以采用泡孔规模δ=3的代表性体积单元模型用于后续分析。因此, 以下泡沫模型的动态力学性能模拟中, 采用的代表性体积单元模型尺寸为6 mm×6 mm×6 mm, 泡孔半径为1 mm。为便于施加压缩载荷, 在模型两端各添加一块刚性平板, 并对其中一块平板施加固支约束, 对另一块刚性平板施加恒定速率为v的位移载荷。刚性平板与泡孔模型接触, 泡孔模型自接触。泡沫材料的应变率可以表示为:
˙ε=vl (3) 式中:v为加载速率, l为代表性体积单元模型沿加载方向的尺寸。
以下计算采用Ansys/Ls-dyna有限元程序, 不考虑压缩过程中气体压力变化的影响。本文中应力、应变均指工程应力和工程应变。
2. 计算结果
2.1 应变率敏感因素
图 3为有限元计算的相对密度50%泡沫模型动态压缩应力应变曲线, 应变率为10~104 s-1。可见, 泡沫模型的压缩应力应变曲线显示出了典型的三阶段变形特征, 即线弹性段、塑性屈服平台段以及致密段; 且随着应变率的增加, 应力应变曲线的平台段逐渐抬高, 泡沫模型的屈服应力与应变率大小相关, 泡沫模型表现出明显的应变率敏感效应。
图 3 基体材料率相关泡沫模型动态压缩应力应变曲线Figure 3. Dynamic compressive stress-strain curves of foam models with rate-dependent cell material由此可以得到初步结论, 若基体材料对应变率敏感, 则泡沫铝材料也存在应变率敏感效应。至于泡沫铝应变率敏感效应是由基体材料的率相关性能引起的还是微结构惯性导致的, 还需要进一步分析。
当基体材料率无关时, 相对密度50%泡沫模型的动态压缩应力应变曲线见图 4。可见, 泡沫模型的压缩应力应变曲线同样表现出三阶段变形特征; 在中、低应变率(10~1 000 s-1)下, 随着应变率的增加, 应力应变曲线的平台段变化不大, 泡沫模型的压缩力学性能对应变率不敏感(见图 4(a)); 在高应变率(2 500~10 000 s-1)下, 随着应变率的增加, 应力应变曲线的平台段逐渐抬高, 泡沫模型表现出一定的应变率敏感特征(见图 4(b))。与图 3相比, 图 4(b)中平台应力随应变率的变化幅度小, 可见在高应变率下, 基体材料的率相关效应对泡沫模型的率相关性能仍具有重要影响。
图 4 基体材料率无关泡沫模型动态压缩应力应变曲线Figure 4. Dynamic compressive stress-strain curves of foam models with rate-independent cell material结合前面的分析可以得到以下结论:(1)在中、低应变率下, 泡沫铝应变率的敏感效应主要由基体材料的率相关性能引起, 微结构惯性的影响很小。(2)在高应变率下, 微结构惯性对泡沫铝应变率效应的影响逐渐增大, 此时泡沫铝率相关性能受基体材料的率相关性能和微结构惯性联合作用。
2.2 相对密度的影响
图 5为10~10 000 s-1应变率范围动态压缩载荷条件下, 泡沫铝流动应力随相对密度的分布。其中, 流动应力为各模型应力应变曲线上与0.2压缩应变所对应的平台段应力[9]。
图 5 动态压缩下泡沫铝流动应力与相对密度关系Figure 5. Flow stresses of aluminum foams versus foam relative densities under dynamic compressive loadingsL.J.Gibson等[13]给出了静态压缩条件下泡沫材料的塑性坍塌强度与相对密度关系式:
σplσys=aρn (4) 式中:σpl为泡沫材料的塑性坍塌强度, σys为基体材料的屈服强度, a和n为材料常数, ρ为泡沫相对密度。
采用上式对图 5中计算结果进行拟合, 可以得到不同应变率下a和n的结果, 见表 1, 拟合曲线见图 5。由表 1中的拟合计算结果发现:(1)随着应变率的提高, 比例系数a逐渐增大, 泡沫模型表现出应变率强化效应。(2)在中、低应变率下, 随着应变率的提高, 指数n保持不变, 表明相对密度变化对泡沫模型的应变率敏感程度基本没有影响。(3)在高应变率下, 随着应变率的提高, 指数n逐渐减小, 表明泡沫模型的应变率敏感程度与相对密度相关。
表 1 拟合结果Table 1. Fitting results of parameters˙ε/s-1 a n 10 0.698 1.72 100 0.784 1.72 1 000 0.942 1.72 2 500 1.03 1.68 5 000 1.13 1.66 10 000 1.27 1.64 2.3 应变率的影响
由式(4)可以得到应变率由
增加到
时, 泡沫铝材料塑性坍塌强度的相对变化量为:
αf=σpl(˙ε2)−σpl(˙ε1)σpl(˙ε1) (5) 当变化前后的应变率
和
位于中、低应变率范围内时, 注意到此时式(4)中系数n保持不变, 式(5)变为:
αf=a(˙ε2)−a(˙ε1)a(˙ε1) (6) 式中:
和
为应变率分别为
和
时, 对应的式(4)中比例系数a。
同样, 由式(4)可以得到应变率从
增加到
时, 泡沫铝基体材料屈服强度的相对变化量:
αs=σdy(˙ε2)−σdy(˙ε1)σdy(˙ε1)=(˙ε2)1/P−(˙ε1)1/PC1/P+(ˉε1)1/P (7) 基于上式计算可以得到, 当应变率从10 s-1增加到100和1 000s-1时, 泡沫铝基体材料屈服强度分别增加12.87%和35.74%。将表 1中的数值拟合结果代入式(6)则可以得到, 当应变率从10 s-1增加到100和1 000 s-1时, 泡沫铝材料塑性坍塌强度分别增加12.32%和34.96%。可见, 在中、低应变率下, 泡沫铝与基体材料对应变率的敏感程度接近, 此时, 基体材料的率相关性是泡沫铝应变率效应的主要影响因素。
分别基于式(5)和(7)可以得到, 应变率从2 500 s-1增加到5 000 s-1和10 000 s-1时, 相对密度分别为35%、50%和65%泡沫模型及其基体材料塑性坍塌强度的相对变化量, 见表 2。可见, 泡沫模型塑性坍塌强度的相对变化量比基体材料大; 随着相对密度升高, 泡沫模型塑性坍塌强度的相对变化量逐渐减小。(1)在高应变率下, 微结构惯性的影响逐渐增大, 使泡沫材料对应变率的敏感性进一步提高, 导致泡沫铝比铝合金材料具有更大的应变率敏感性。(2)在高应变率下, 随着相对密度的降低, 泡沫模型的应变率敏感程度提升。这表明相对密度较低泡沫铝的微结构惯性效应更加显著。
表 2 泡沫模型及其基体材料强度的变化Table 2. Variation of flow stress for foams and its cell material˙ε2/s-1 αf/% αs/% ρ=0.35 ρ=0.50 ρ=0.65 5 000 12.04 11.24 10.66 8.34 10 000 28.59 26.77 25.44 18.25 3. 结论
基于三维随机球形泡孔模型, 采用有限元方法, 对35%~65%相对密度范围内泡沫铝在10~10 000 s-1应变率下的动态压缩变形进行了数值模拟。计算结果表明:
(1) 在中、低应变率(10~1 000 s-1)下, 基体材料的率相关性是泡沫铝应变率效应的主要影响因素; 在高应变率(2 500~10 000 s-1)下, 泡沫铝应变率效应受基体材料率相关性能和微结构惯性共同作用。
(2) 在中、低应变率下, 泡孔结构的变形主要表现为准静态变形模式; 在高应变率下, 动态压缩变形机制逐渐起重要作用。
(3) 在中、低应变率下, 泡沫铝与基体材料对应变率的敏感程度接近; 在高应变率下, 泡沫铝比铝合金材料具有更大的应变率敏感性。
(4) 在高应变率下, 相对密度较低泡沫铝的微结构惯性效应更显著。
-
图 3 圆锥台靶体和约束环轴线的剖面尺寸
Figure 3. Axial section dimensions of circular target and ferrule
图 8 圆锥台靶体的von Mises应力云图
Figure 8. Von Mises stress nephogram of circular concrete target
图 10 混凝土靶内部的径向应力时程曲线
Figure 10. Time history curves of radial pre-stress of concrete target
图 11 靶体下压深度、盈差与预应力的关系
Figure 11. Relation between pressing depth, margin and pre-stress
图 12 钢环截面中心单元的应力和应变时程曲线
Figure 12. Time history curves of stress and strain in central elements of steel ferrule
图 14 预应力对侵彻深度下降率的影响
Figure 14. Effect of pre-stress on penetration depth reduction rate
图 16 钢环强度对预应力和侵彻深度下降率的影响
Figure 16. Effect of steel strength on pre-stress and penetration depth reduction rate
图 17 混凝土强度对预应力和侵彻深度下降率的影响
Figure 17. Effect of concrete strength on pre-stress and penetration depth reduction rate
图 18 无预应力靶含钢率对侵深的影响
Figure 18. Effect of steel ratio on penetration depth of non-prestressed target
图 19 含钢率对预应力和侵彻深度下降率的影响
Figure 19. Effect of steel ratio on pre-stress and penetration depth reduction rate
图 20 弹体初速度对预应力约束混凝土抗侵彻性能的影响
Figure 20. Effect of initial velocity of projectile on penetration depth reduction rate of pre-stressed concrete target
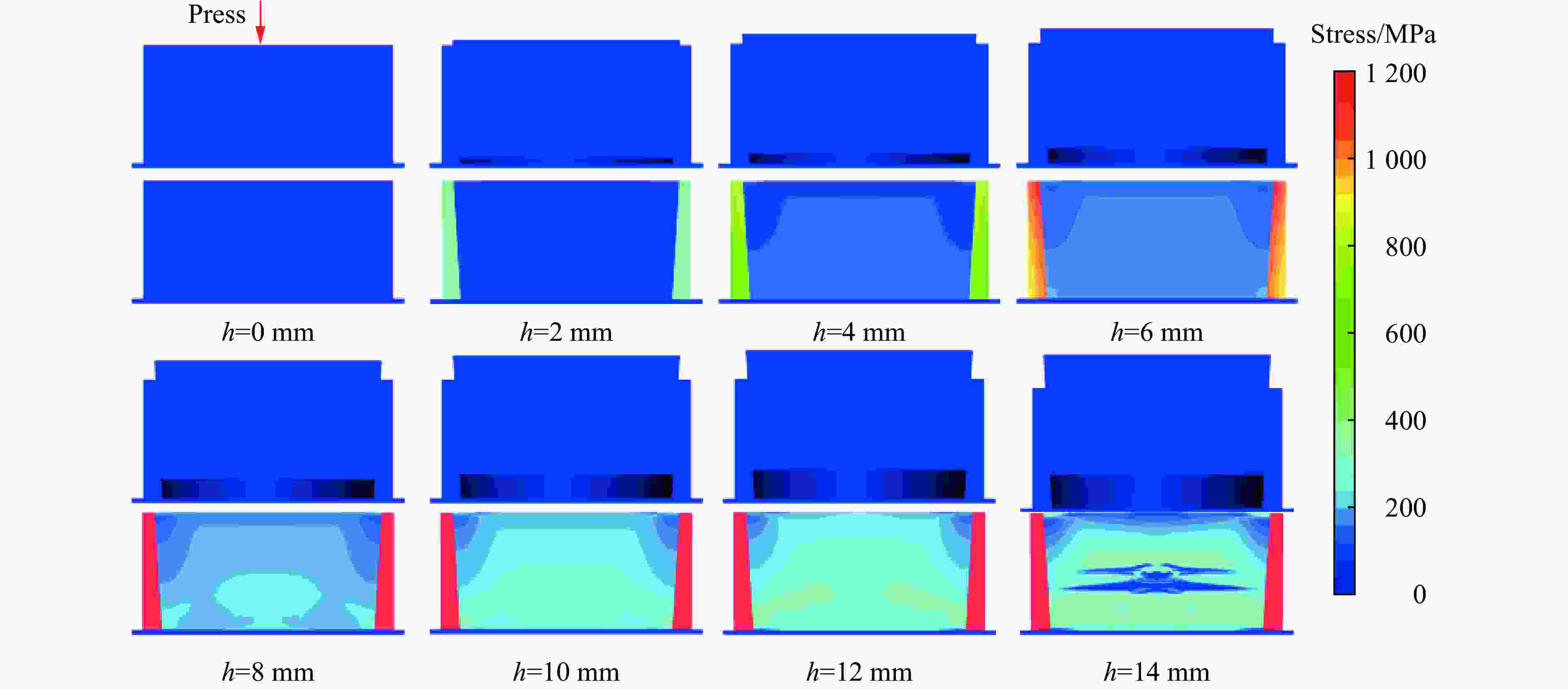
表 1 预应力工况设计
Table 1. Designed pre-stress conditions
工况 h/mm δ/mm 1 0 0 2 2 0.2 3 4 0.4 4 6 0.6 5 8 0.8 6 10 1.0 7 12 1.2 8 14 1.4 
下载: 导出CSV
-
[1] DANCYGIER A N, KATZ A, BENAMOU D, et al. Resistance of double-layer reinforced HPC barriers to projectile impact [J]. International Journal of Impact Engineering, 2014, 67: 39–51. DOI: 10.1016/j.ijimpeng.2014.01.001. [2] BRUHL J C, VARMA A H, JOHNSON W H. Design of composite SC walls to prevent perforation from missile impact [J]. International Journal of Impact Engineering, 2015, 75: 75–87. DOI: 10.1016/j.ijimpeng.2014.07.015. [3] WAN F, JIANG Z G, TAN Q H, et al. Response of steel-tube-confined concrete targets to projectile impact [J]. International Journal of Impact Engineering, 2016, 94: 50–59. DOI: 10.1016/j.ijimpeng.2016.03.012. [4] 甄明, 蒋志刚, 万帆, 等. 钢管约束混凝土抗侵彻性能试验 [J]. 国防科技大学学报, 2015, 37(3): 121–127. DOI: 10.11887/j.cn.201503020.ZHEN M, JIANG Z G, WAN F, et al. Steeltube confined concrete targets penetration experiments [J]. Journal of National University of Defense Technology, 2015, 37(3): 121–127. DOI: 10.11887/j.cn.201503020. [5] 万帆. 钢管约束混凝土抗侵彻性能与机理研究 [D]. 长沙: 国防科学技术大学, 2014.WAN F. Investigation on the anti-penetration properties and mechanism of steel-tube-confined concrete targets [D]. Changsha: National University of Defense Technology, 2014. [6] 石少卿, 尹平, 刘颖芳, 等. 玻璃纤维约束混凝土抗侵彻机理研究 [J]. 玻璃钢/复合材料, 2004(1): 6–7. DOI: 10.3969/j.issn.1003-0999(2004)01-006.SHI S Q, YIN P, LIU Y F, et al. Research on mechanism of anti-penetration of concrete confined with GFRP [J]. Fiber Reinforced Plastics Composites, 2004(1): 6–7. DOI: 10.3969/j.issn.1003-0999(2004)01-006. [7] 梁乔恒. UHMWPE纤维混凝土动态材料模型参数与抗多发打击研究 [D]. 长沙: 国防科学技术大学, 2016.LIANG Q H. Research on dynamic constitutive parameters and penetration properties resisted to multi-impact of UHMWPE fiber reinforced concrete [D]. Changsha: National University of Defense Technology, 2016. [8] 石少卿, 黄翔宇, 刘颖芳, 等. 多边形钢管混凝土短构件在防护工程中的应用 [J]. 混凝土, 2005(2): 95–98. DOI: 10.3969/j.issn.1002-3550.2005.02.027.SHI S Q, HUANG X Y, LIU Y F, et al. Application of polygonal short steel tube filled with concrete on the defense work [J]. Concrete, 2005(2): 95–98. DOI: 10.3969/j.issn.1002-3550.2005.02.027. [9] 王起帆, 石少卿, 王征, 等. 蜂窝遮弹层抗弹丸侵彻实验研究 [J]. 爆炸与冲击, 2016, 36(2): 253–258. DOI: 10.11883/1001-1455(2016)02-0253-06.WANG Q F, SHI S Q, WANG Z, et al. Experimental study on penetration-resistance characteristics of honeycomb shelter [J]. Explosion and Shock Waves, 2016, 36(2): 253–258. DOI: 10.11883/1001-1455(2016)02-0253-06. [10] 蒋志刚, 甄明, 刘飞, 等. 钢管约束混凝土抗侵彻机理的数值模拟 [J]. 振动与冲击, 2015, 34(11): 1–6. DOI: 10.13465/j.cnki.jvs.2015.11.001.JIANG Z G, ZHEN M, LIU F, et al. Simulation of anti-penetration mechanism of steel tube confined concrete [J]. Journal of Vibration and Shock, 2015, 34(11): 1–6. DOI: 10.13465/j.cnki.jvs.2015.11.001. [11] 徐松林, 单俊芳, 王鹏飞, 等. 三轴应力状态下混凝土的侵彻性能研究 [J]. 爆炸与冲击, 2019, 39(7): 071101. DOI: 10.11883/bzycj-2019-0034.XU S L, SHAN J F, WANG P F, et al. Penetration performance of concrete under triaxial stress [J]. Explosion and Shock Waves, 2019, 39(7): 071101. DOI: 10.11883/bzycj-2019-0034. [12] 陈丽娜, 单俊芳, 周李姜, 等. 应力状态对水泥砂浆侵彻性能的影响 [J]. 振动与冲击, 2020, 39(15): 32–40. DOI: 10.13465/j.cnki.jvs.2020.15.005.CHEN L N, SHAN J F, ZHOU L J, et al. Effects of stress state on penetration performance of cement mortar [J]. Journal of Vibration and Shock, 2020, 39(15): 32–40. DOI: 10.13465/j.cnki.jvs.2020.15.005. [13] 单俊芳. 三轴应力状态下混凝土动态力学性能及抗弹机理研究 [D]. 合肥: 中国科学技术大学, 2020.SHAN J F. Investigation on the dynamic mechanical properties and anti-bullet mechanism of concrete under triaxial static loading [D]. Hefei: University of Science and Technology of China, 2020. [14] SHERMAN D, BEN-SHUSHAN T. Quasi-Static impact damage in confined ceramic tiles [J]. International Journal of Impact Engineering, 1998, 21(4): 245–265. DOI: 10.1016/S0734-743X(97)00063-8. [15] ORPHAL D L, FRANZEN R R. Penetration of confined silicon carbide targets by tungsten long rods at impact velocities from 1.5 to 4.6 km/s [J]. International Journal of Impact Engineering, 1997, 19(1): 1–13. DOI: 10.1016/0734-743X(95)00064-H. [16] ORPHAL D L, FRANZEN R R, CHARTERS A C, et al. Penetration of confined boron carbide targets by tungsten long rods at impact velocities from 1.5 to 5.0 km/s [J]. International Journal of Impact Engineering, 1997, 19(1): 15–29. DOI: 10.1016/S0734-743X(96)00004-8. [17] ORPHAL D L, FRANZEN R R, PIEKUTOWSKI A J, et al. Penetration of confined aluminum nitride targets by tungsten long rods at 1.5−4.5 km/s [J]. International Journal of Impact Engineering, 1996, 18(4): 355–368. DOI: 10.1016/0734-743X(95)00045-C. [18] HU G L, RAMESH K T, CAO B Y, et al. The compressive failure of aluminum nitride considered as a model advanced ceramic [J]. Journal of the Mechanics and Physics of Solids, 2011, 59(5): 1076–1093. DOI: 10.1016/j.jmps.2011.02.003. [19] ZHANG R, HAN B, LI L, et al. Influence of prestress on ballistic performance of bi-layer ceramic composite armors: experiments and simulations [J]. Composite Structures, 2019, 227: 111258. DOI: 10.1016/j.compstruct.2019.111258. [20] HEARD H C, CLINE C F. Mechanical behaviour of polycrystalline BeO, Al2O3 and AlN at high pressure [J]. Journal of Materials Science, 1980, 15(8): 1889–1897. DOI: 10.1007/BF00550614. [21] 胡欣, 王富耻, 王扬卫, 等. 约束应力对AD95陶瓷动态硬度的影响 [J]. 稀有金属材料与工程, 2009, 38(S2): 1164–1166. DOI: 10.3321/j.issn:1002-185X.2009.z2.309.HU X, WANG F C, WANG Y W, et al. Effect of confined stress on dynamic hardness of ceramic AD95 [J]. Rare Metal Materials and Engineering, 2009, 38(S2): 1164–1166. DOI: 10.3321/j.issn:1002-185X.2009.z2.309. [22] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjective to large strain, high strain rates, and high pressure [C]//The 14th International Symposium on Ballistic. Quebec: American Defense Preparedness Association, 1993: 591–600. [23] KONG X Z, FANG Q, CHEN L, et al. A new material model for concrete subjected to intense dynamic loadings [J]. International Journal of Impact Engineering, 2018, 120: 60–78. DOI: 10.1016/j.ijimpeng.2018.05.006. [24] REN G M, WU H, FANG Q, et al. Parameters of Holmquist-Johnson-Cook model for high-strength concrete-like materials under projectile impact [J]. International Journal of Protective Structures, 2017, 8(3): 352–367. DOI: 10.1177/2041419617721552. [25] LSTC. LS-DYNA® keyword user’s manual, Version 971 [Z]. Livermore: Livermore Software Technology Corporation, 2007. [26] OTTOSEN N S, RISTINMAA M. The mechanics of constitutive modeling [M]. Amsterdam: Elsevier, 2005. [27] DENG Y H, TUAN C Y. Design of concrete-filled circular steel tubes under lateral impact [J]. ACI Structural Journal, 2013, 110(4): 691–702. [28] 李磊. 不同硬度30CrMnSiNi2A钢动态本构与损伤参数研究 [D]. 南京: 南京理工大学, 2017. [29] KONG X Z, FANG Q, ZHANG J H, et al. Numerical prediction of dynamic tensile failure in concrete by a corrected strain-rate dependent nonlocal material model [J]. International Journal of Impact Engineering, 2020, 137: 103445. DOI: 10.1016/j.ijimpeng.2019.103445. [30] KONG X Z, FANG Q, WU H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61–71. DOI: 10.1016/j.ijimpeng.2016.04.014. [31] 邓国强, 杨秀敏, 金乾坤. 侵彻爆炸效应数值计算新型岩石本构模型 [J]. 兵工学报, 2012, 33(S2): 375–380. [32] 邓国强, 杨秀敏. 超高速武器对地打击效应数值仿真 [J]. 科技导报, 2015, 33(16): 65–71. DOI: 10.3981/j.issn.1000-7857.2015.16.010.DENG G Q, YANG X M. Numerical simulation of damage effect of hyper velocity weapon on ground target [J]. Science & Technology Review, 2015, 33(16): 65–71. DOI: 10.3981/j.issn.1000-7857.2015.16.010. -
下载:
计量
- 文章访问数: 527
- HTML全文浏览量: 217
- PDF下载量: 68
- 被引次数: 0