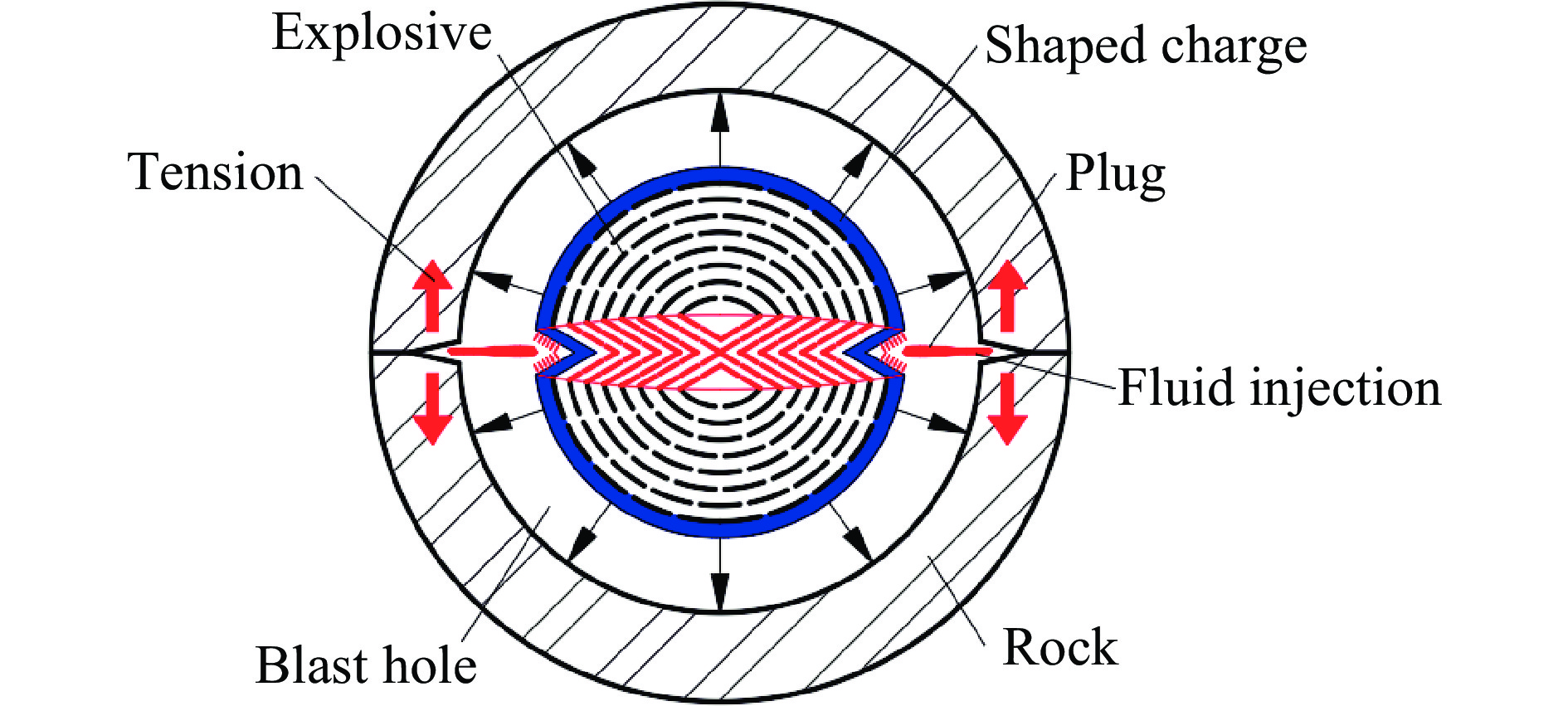
Optimum seam forming angle of bilinear shaped charge in engineering blasting
-
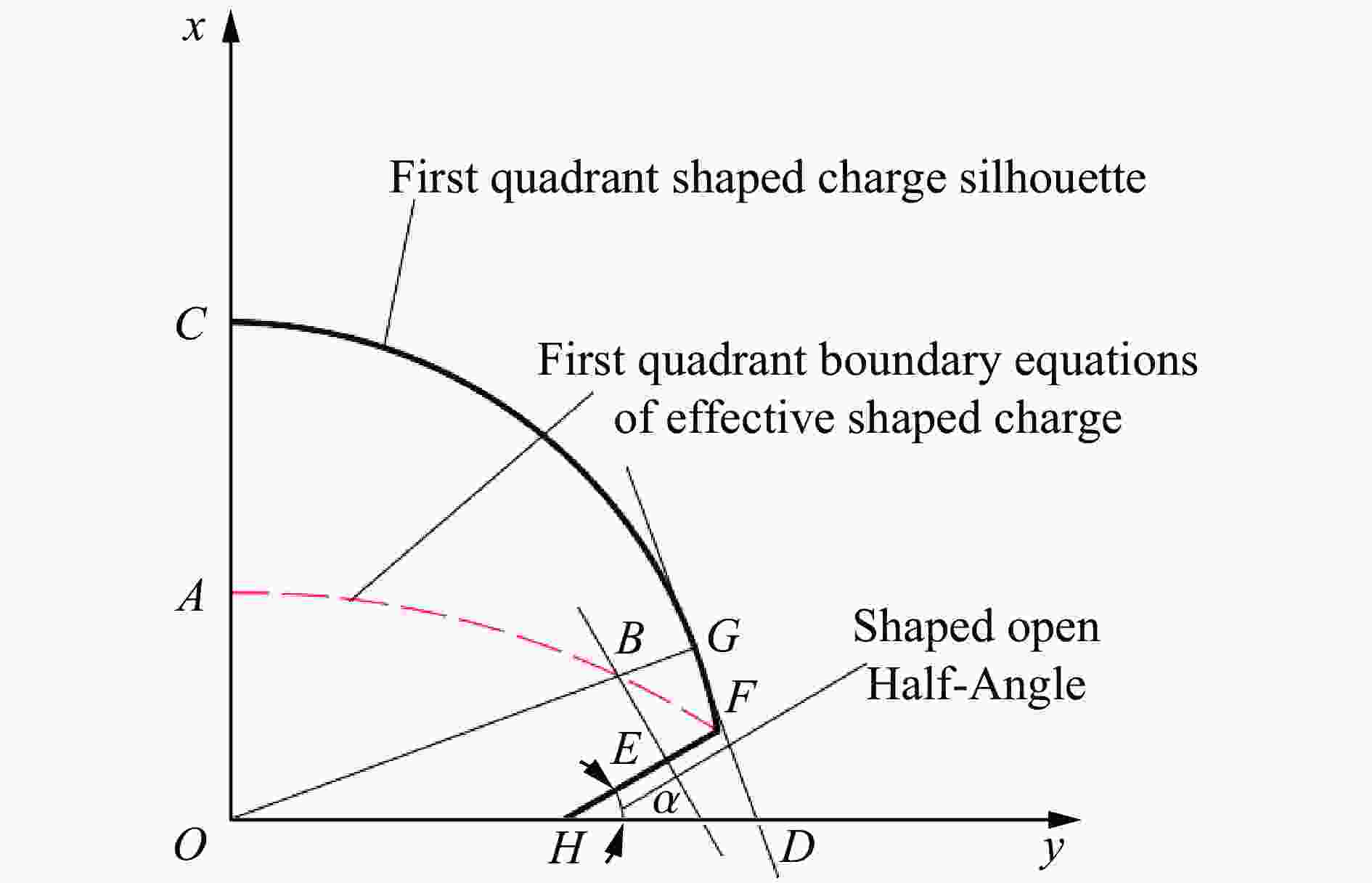
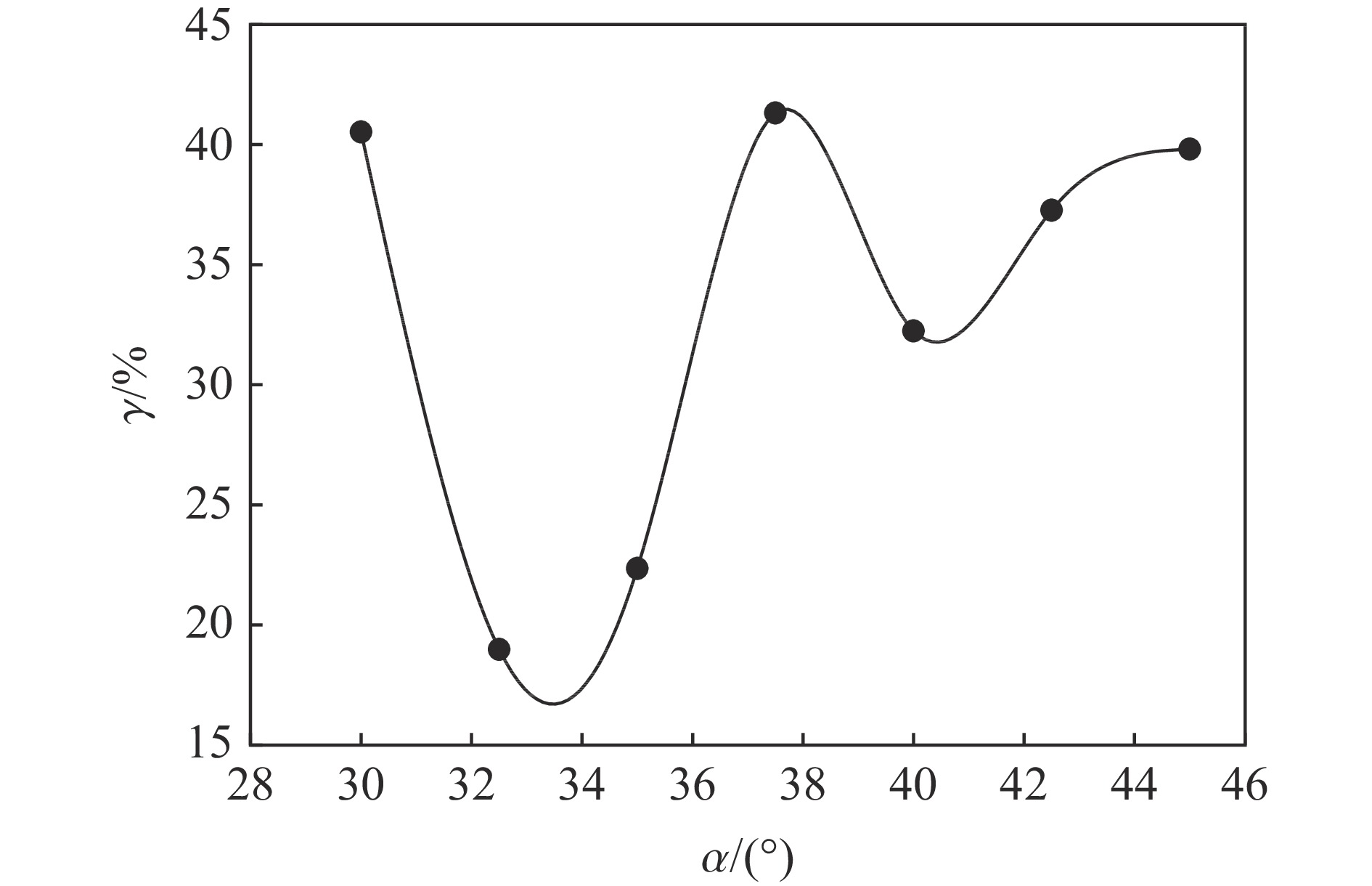
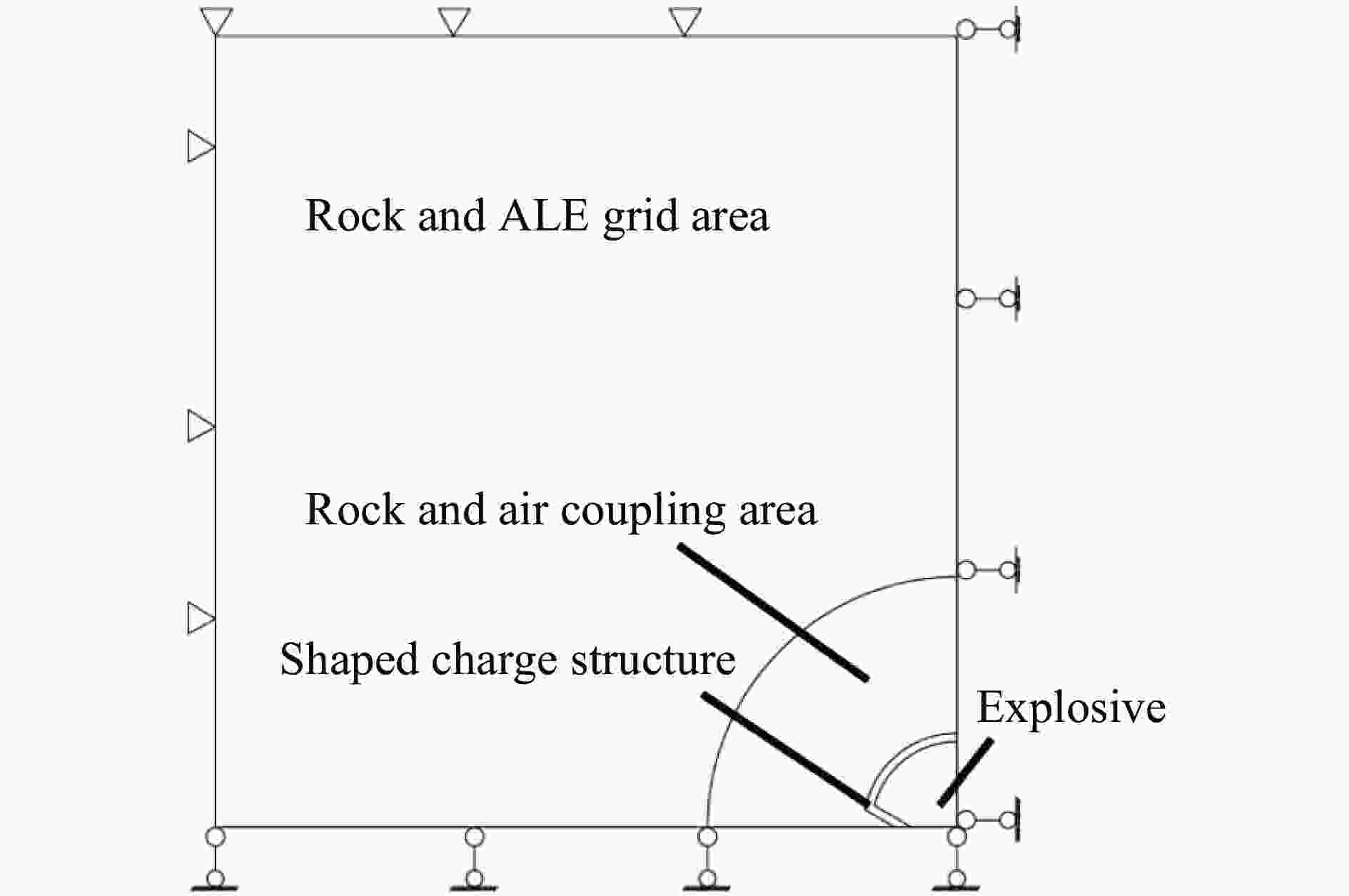
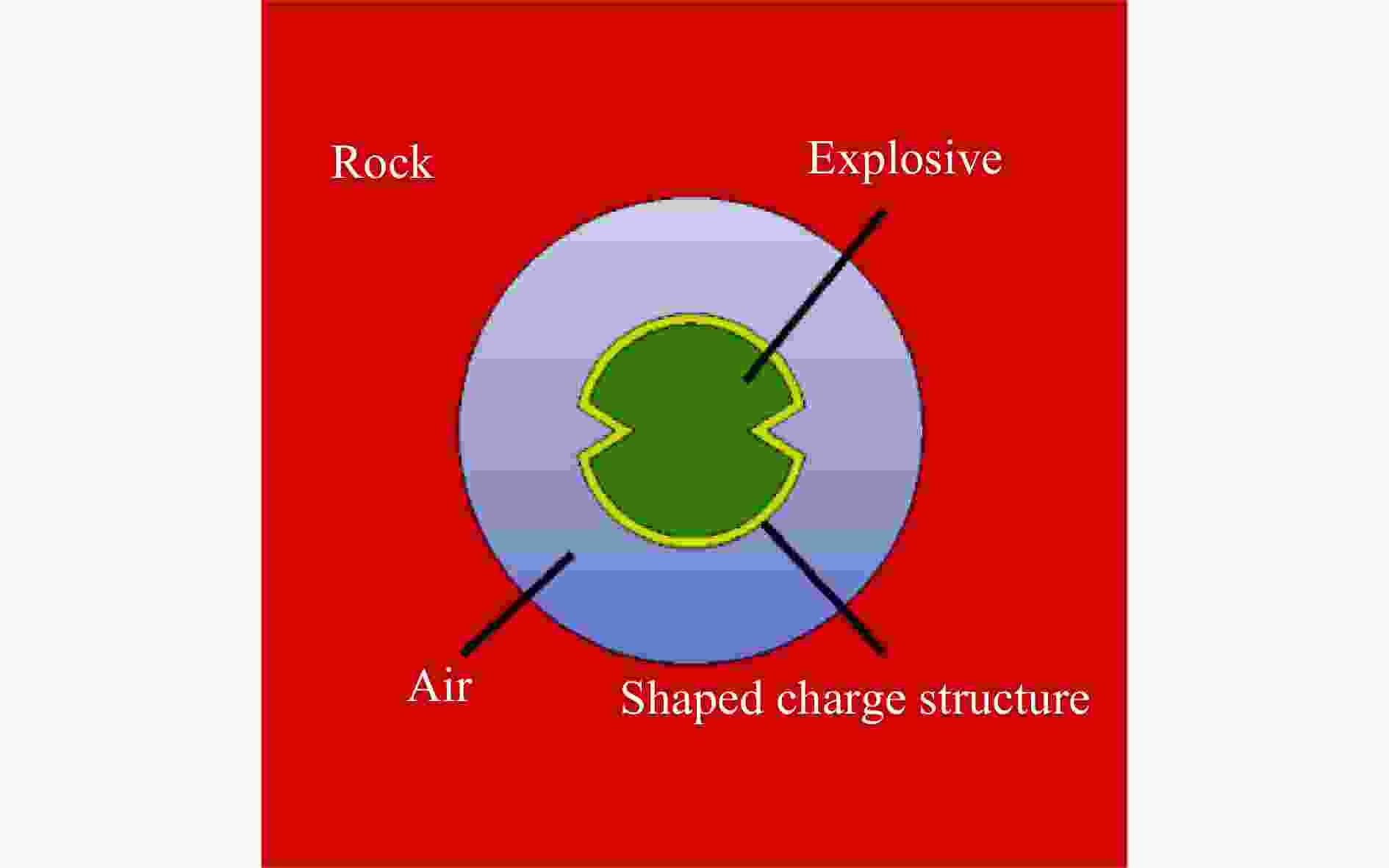
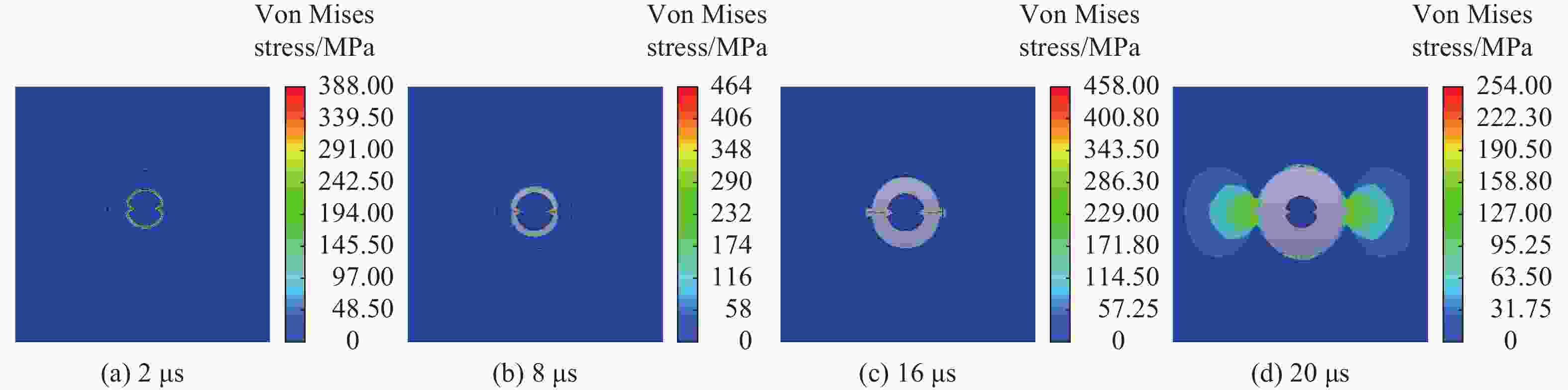
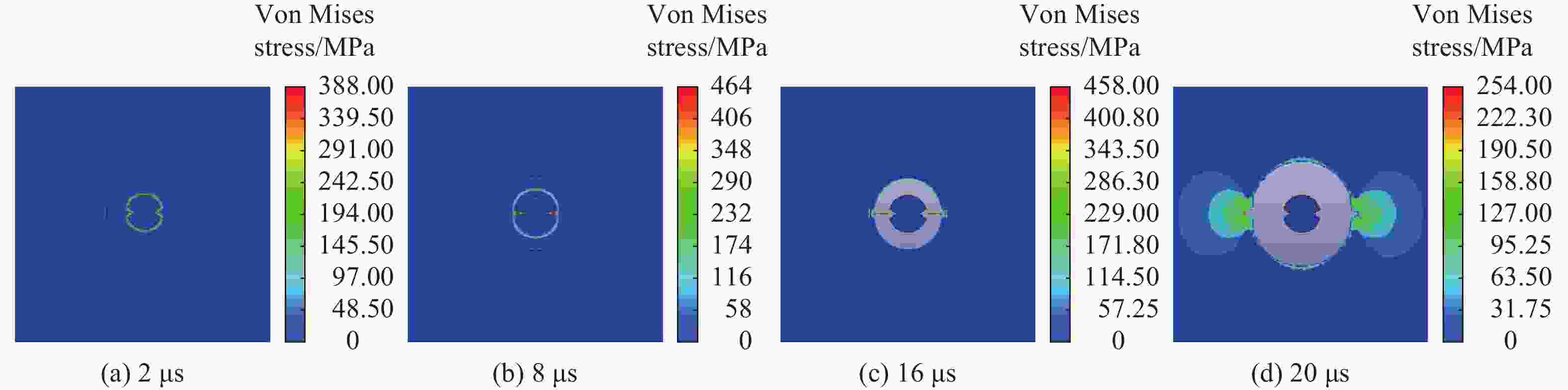
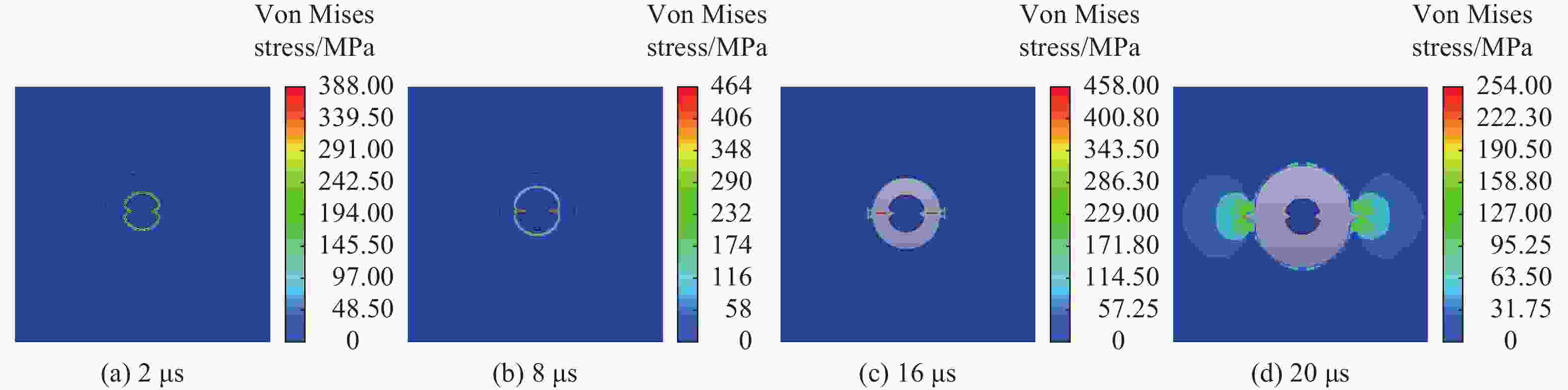
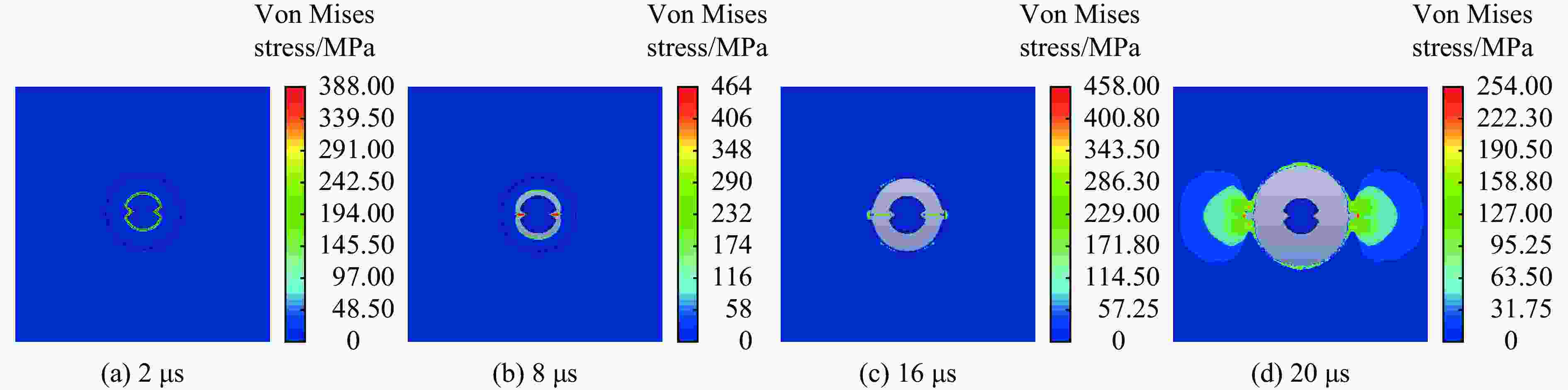
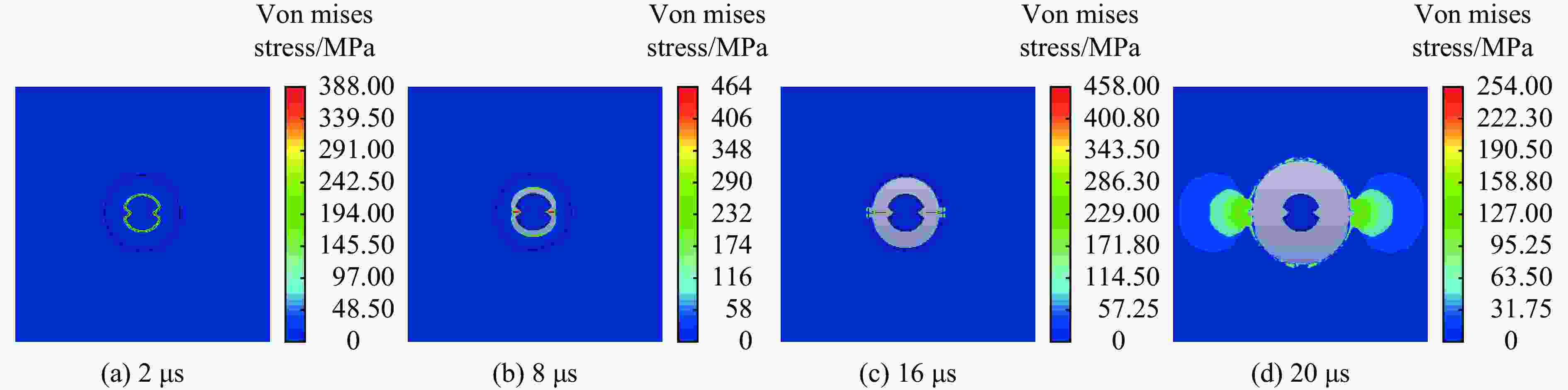
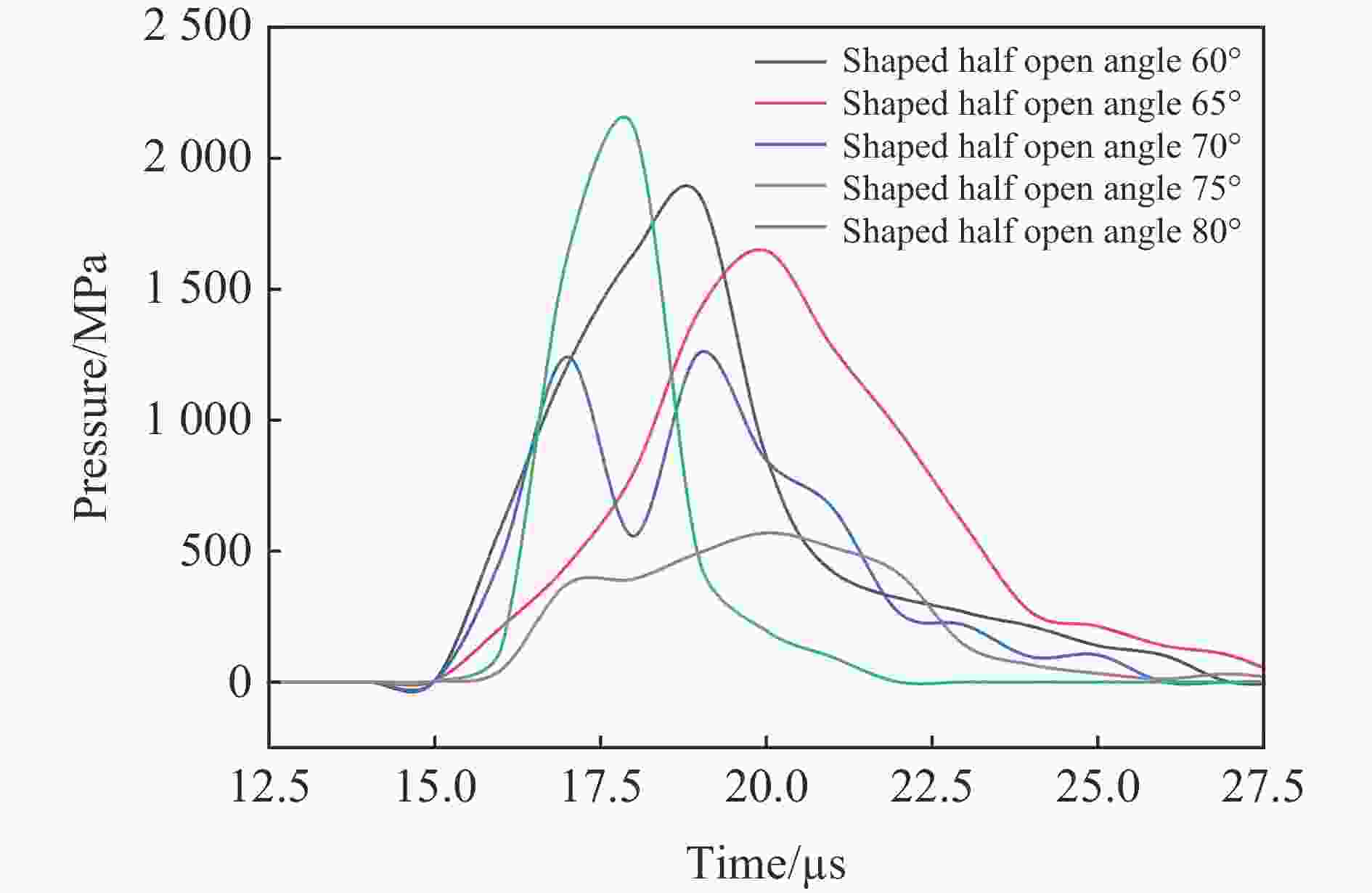
摘要: 为探究聚能张开角对双线型聚能药包结构炸药有效利用率和聚能效应的影响，通过瞬时爆轰假说理论对有效聚能炸药边界方程进行推导，分析不同聚能张开角聚能装药结构炸药的有效利用率；通过水泥砂浆物理模型试验，研究不同聚能张开角预裂孔成缝规律；采用LS-DYNA数值模拟软件，建立不同聚能张开角数值模型，揭示不同聚能张开角的双线型聚能结构药包射流的侵彻过程。研究结果表明聚能张开角为75°时，炸药产生聚能效应的有效利用率最大；聚能结构药包聚能槽张开角为75°时，预裂孔成缝效果明显优于聚能槽张开角为60°的聚能结构药包，沿聚能槽方向应力集中效应和侵彻深度最佳，炮孔壁上岩石单元最先达到应力峰值。针对聚能张开角为75°的双线型聚能结构药包开展了不同岩性预裂爆破现场试验，板岩和白云岩两种不同岩性，在孔距增大20%的条件下，双线型聚能预裂爆破效果优于常规预裂爆破。Abstract: To explore the influences of the opening angle of bilinear shaped charge on the effective utilization rate and energy gathering effect, the boundary equation of effective shaped charge was deduced through the theory of instantaneous detonation hypothesis. The effective utilization ratio of the shaped charge structure blasting with 60°, 65°, 70°, 75°, and 80° shaped charge angles was analyzed using the visual implicit functions of SymPy package based on Python language. Through the physical model tests of single-hole Plexiglas and double-hole cement mortar, the crack formation law of pre-cracked holes with different energy-gathering opening angles was studied. Using the LS-DYNA numerical simulation software, five numerical models with energy-gathered opening angles of 60°, 65°, 70°, 75°, and 80° were established to reveal the penetration process of the bilinear energy-gathered structure charge jet and the stress evolution law of the rock unit on the blast-hole wall with different energy-gathered opening angles. The research results show that the effective utilization ratio of the shaped explosives is the highest when the energy-gathered opening angle is 75°. The pre-split hole formation effect when the opening angle of the energy-concentrating groove of the shaped charge is 75° is better than that when the opening angle is 60°, and the stress concentration effect and penetration depth along the direction of the energy-concentrating groove are the best, and the rock unit on the blast-hole wall reaches the peak stress first. The pre-split blasting field tests of two lithologies of Slate and Dolomite were carried out for the double-line shaped energy-concentrated structure charge with the energy-gathering opening angle of 75°. In two different lithologies of Slate and Dolomite, under the condition that hole spacing was increased by 20%, the double-linear pre-split blasting effect of the shaped energy is better than that of the conventional pre-split blasting.
-
在不同厚度飞片相互撞击过程中，冲击波从材料自由表面反射，材料内部或近自由表面区域受到卸载稀疏波作用，如果延性金属材料内部的拉伸应力足够高，以孔洞形式的损伤将经历成核、增长和汇合演化过程，当微孔洞的数量和尺寸增长到一定阶段之后，它们的(强)相互作用就变得十分重要，这时，微孔洞之间的汇合以及细观尺度上的不稳定性将导致材料的最终破坏。实验结果分析表明：在强动态拉伸载荷作用下，孔洞汇合可能开始于孔洞成核后，并伴随损伤演化整个过程，此时，孔洞汇合对孔洞增长起到抑制作用[1]；孔洞增长不仅以孤立孔洞形式增长，而且可能主要以孔洞汇合形式增长[2]。因此，在连续损伤模型中耦合孔洞汇合的影响，有助于精细描述延性材料损伤演化过程、分析不同因素对损伤演化过程的影响[3-5]。
由于微孔洞之间强相互作用在理论分析方面遇到的困难，至今还没有一个较好的模型对孔洞汇合进行合理的描述[6]。一个合理的孔洞汇合模型不仅应给出开始汇合的准则，而且还应该对其间的应力松弛或材料软化予以适当的描述。当然要作以上分析是非常困难的，因而许多学者通过数值模拟两个孔洞之间的相互关系给出一些半经验性的孔洞汇合临界条件，即以孔洞之间的相互距离或临界损伤作为孔洞汇合的临界判据：T.Pardoen等[7]认为孔洞汇合的临界损伤依赖于微孔洞初始体积分数、加载应力三轴度及微孔洞形状；M.F.Horstemeyer等[8]采用微力学有限元计算方法研究准静态加载条件下两个孔洞之间的贯通行为，指出孔洞开始汇合的临界韧带距离依赖于边界条件和材料韧性，且约为2~8倍的孔洞直径；E.T.Seppala等[9]采用分子动力学方法对动态条件下铜材料中孔洞的增长和聚集行为进行了数值模拟，结果显示临界韧带距离约为0.5倍孔洞直径时，孔洞周围塑性区相遇，孔洞增长速度突然增加，从而导致孔洞汇合。此外，在理论分析方面，P.F.Thomson[10]简化了塑性极限载荷的滑移线场解, 提出了一种孔洞汇合的判断准则；D.L.Tonks等[11]进一步用高应变率下的随机滤渗理论解释了断裂点, 提出了一种通过孔洞聚集形成小尺度孔洞簇增长的模型；T.Pardoen等[12]讨论了基于微结构机理的孔洞汇合模型的进展，并指出因微孔洞汇合引起金属断裂过程最后阶段的模拟需要反映微结构演化重要信息的延性损伤模型。在过去的十多年里，孔洞汇合研究的重要进步是基于简单的孔隙度准则或临界应变准则发展为基于微观机理认识的进展。不过，目前的研究主要是分析相同大小孔洞间的汇合，还需要将其扩展到更一般的情况，即不同大小的孔洞之间的汇合问题；此外，对于孔洞汇合最初发生于相同的大孔洞之间、小孔洞之间亦或不同大小孔洞之间，目前还没有确切的说明。同时，现有的孔洞汇合模型严格来说是描述孔洞变形对损伤的影响，且一般采用指数函数来唯像描述孔洞汇合后损伤的快速增长[13]，而根据损伤度的定义，孔洞汇合时刻并没有引起损伤的改变，但实际却促进了损伤的快速发展，目前对于其物理机理至今仍处于探讨之中。
本文中基于两个不同大小孔洞之间的几何关联，给出孔洞汇合的临界判定方法，并基于能量守恒原理，揭示孔洞汇合后引起损伤增长的物理机理，同时，耦合孔洞汇合的影响，采用数值方法讨论孔洞汇合对延性金属层裂损伤演化特性的影响。
1. 孔洞汇合的判定方法
现阶段对于孔洞汇合机理的分析已经成为层裂损伤研究的主要关注点[14-16]，不过，现有的汇合判据还存在不足之处：距离判据没有考虑损伤的影响；损伤(或应力、应变)判据没有考虑孔洞大小的影响。此外，在强动态加载情况下，孔洞增长过程不易发生塑性局域化，孔洞几乎仍然保持球形形状，孔洞汇合时，损伤度较高，且孔洞之间产生相互接触，这可能是因为惯性对孔洞间的颈缩起了阻碍作用[14]，这种情况在一些层裂实验[17-18]以及裂纹扩展实验[19]中均可以观测到(见图 1)。因汇合前孔洞基本保持球形形状，且相邻孔洞间距较小，则因孔洞间基体材料颈缩引起孔洞变化对损伤的影响较小，因此相对于基于颈缩过程分析得到的孔洞汇合判据，采用孔洞间距离判据更加简单、适宜。
为此，我们考虑两个空心球壳之间的几何关联(见图 2)，并定义孔隙度：
α=b3/(b3−a3) 则孔洞间距离可以表示为：
d=[(αα−1)1/3−1](a1+a2) (1) 本文中仍将采用孔洞间的距离作为孔洞开始汇合的判据，并根据实验结果确定临界孔洞距离dcr(根据文献[2]的实验结果，本文中采用dcr=4min(a1, a2))，即当两个孔洞间的距离d≤dcr时，认为相应的两个孔洞之间发生汇合。与现有的距离计算方法不同，公式(1)不仅包含了孔洞大小，同时也包含了损伤度的影响。众所周知，在相同加载条件下小孔洞周边的应力集中更明显，同时，在大孔洞不变的情况下，小孔洞越小，其对应的损伤度越小，因此，孔洞汇合应该首先发生于最大孔洞与最小孔洞之间，这也从侧面说明了实验最后的观测结果以及相关的数值模拟结果中小孔洞很少的可能原因。
取a1=ka2、d=ma1=mka2，则公式(1)可以转化为损伤度D的表达式：
D=α−1α=[1+k1+(m+1)k]3 (2) 两个特例：
当m=k=1时，D=0.296，这与分析层裂问题时常采用的临界断裂损伤度相近；
当m=1时，有D=α−1α=limk→∞[1+k1+2k]3=0.125。
这与L.M.Brown等[20]和D.L.Tonks等[11]分析的孔洞汇合初始临界损伤度完全一致，换句话说，文献[11, 20]中所采用的孔洞汇合临界损伤度只是我们所讨论的特例，图 3显示了孔洞汇合损伤度与汇合孔洞相对大小比值之间的对应关系，同时，计算结果也显示了孔洞汇合损伤度的取值范围在0.296~0.125之间。
图 3 孔洞相对大小与孔洞汇合临界损伤度关系Figure 3. Critical damage for void coalescence vs. relative difference in size between two voids当k=10时，图 4显示了孔洞汇合损伤度与孔洞距离之间的对应关系。综合分析图 3~4和公式(2)可知，孔洞汇合是损伤、孔洞相对大小以及孔洞间距离综合影响的结果。对于材料性质、应力状态对孔洞汇合的影响：一方面，损伤与应力、应变耦合在一起[21]，损伤对孔洞汇合的影响也间接地反映了材料性质和应力状态对孔洞汇合的影响；另一方面，针对强加载情况，直至汇合前孔洞仍基本保持球形形状，因此，材料的性质和应力状态的影响主要反映在汇合前的孔洞增长过程。
图 4 孔洞间距离与孔洞汇合临界损伤度关系Figure 4. Critical damage for void coalescence vs. distance between two voids2. 孔洞汇合对损伤增长的影响
现有的孔洞汇合判据(模型)，包括距离判据或应力、应变判据(如Tonks模型和Thomason模型)，都是基于孔洞间材料颈缩过程得到的，描述的是汇合前孔洞的变化情况，而没有涉及孔洞汇合后对损伤的影响。对于在强动态拉伸载荷作用下，因汇合前孔洞基本保持球形形状，且孔洞间距很小，则孔洞间材料颈缩过程对损伤的影响减弱。目前已经有大量的文献研究孔洞间材料颈缩过程对损伤的影响，因此本文中忽略颈缩的影响，主要讨论孔洞汇合后对损伤度增长的影响。
孔洞汇合遵循能量守恒原则，即在孔洞汇合前后有：
Ei+Ek=ˉEi+ˉEk (3) 式中：Ei、Ek分别表示孔洞周围基体材料的内能和动能，Ei、Ek为孔洞汇合后对应的值。
对于内能的变化，在绝热条件下有：
˙e=−p∂v∂t (4) 式中：e、p、v分别表示单位体积的内能、压力和材料的相对比容。因基体材料不可压假设，并且假设孔洞汇合并没有改变材料内部的孔隙度，因此有：
∂v∂t=0 即孔洞汇合时内能守恒。
此外，针对单一的空心球壳，设r0为基体材料内部的Lagrange坐标，相应的r为Euler坐标，a0、α0为初始孔洞半径和初始孔隙度，则根据不可压缩假设有[21]：
r3=r30−a30α0−αα0−1 (5) ˙r=a303r2(α0−1)˙α (6) 则其动能可以表示为：
{E_{\rm{k}}} = \frac{1}{2}\int_a^b {4{\rm{ \mathsf{ π} }}\rho {r^2}{{\dot r}^2}{\rm{d}}r = \frac{{2{\rm{ \mathsf{ π} }}\rho }}{9}\frac{{a_0^6}}{{{{\left( {{\alpha _0} - 1} \right)}^2}}}\left[ {1 - {{\left( {\frac{{\alpha - 1}}{\alpha }} \right)}^{^{1/3}}}} \right]{{\dot \alpha }^2}\frac{1}{a}} (7) 损伤材料内部含有大量不同大小的孔洞，不妨将其等效为不同大小的空心球壳，且每一个空心球壳的内外径之比相同，即α和α0相同，这样不仅方便损伤的计算，而且可以间接地考虑孔洞之间的相互作用[22-23]。因孔洞汇合前后α、α0和基体材料的密度ρ不变，则根据动能守恒原则，由公式(7)有：
\dot {\bar \alpha} = \dot \alpha \sqrt {\frac{{\sum ({n_i}/{a_i})}}{{\sum ({N_j}/{R_j})}}} (8) 式中：{\dot \alpha }、ai以及ni为孔洞汇合前的孔隙度增长率、孔洞半径以及对应的孔洞数，{\dot {\bar \alpha} }、Rj以及Nj为孔洞汇合后的值。式(8)显示了因孔洞汇合引起的孔洞数减少、孔洞尺寸增加，从而造成孔隙度增长速度的提高，这也明确了因孔洞汇合引起损伤增长的物理机理。
3. 孔洞汇合影响的数值分析
对于延性金属层裂损伤的研究，我们已经建立了反映初始损伤及孔洞大小、惯性和材料弹塑性效应的层裂损伤物理统计描述方法[22]，同时，基于材料晶粒尺寸与潜在孔洞成核数之间的关系，构建了一个耦合晶粒尺寸影响的孔洞成核方程[24]。在前期工作的基础上，我们将孔洞汇合的影响引入到已有的层裂损伤模型中，即在计算损伤演化过程中，根据公式(1)，当孔洞间距离d≤dcr时，采用公式(8)调整孔隙度的增长率，同时结合相关文献对实验结果的分析[2]，探讨孔洞汇合对层裂损伤演化过程的影响。层裂实验靶材料分别选用30、60、100和200 μm等4种晶粒尺寸的高纯铜，靶厚均为4 mm；飞片材料为石英(Z-cut quartz)，厚度约2 mm，飞片速度约131 m/s。对4种靶材料的实验结果进行了数值模拟，同时，在30 μm晶粒尺寸高纯铜的计算模型中考虑了孔洞汇合的影响。计算中所采用的模型参数和材料参数均与我们前期的工作[22, 24]所采用的参数相同。
图 5显示了汇合对孔洞尺寸d增长的影响：因汇合以及汇合导致孔隙度增长率的提高，相对于没有考虑汇合的计算结果，孔洞尺寸迅速增长。图 6的计算结果显示：虽然孔洞汇合时损伤度没有增加，但因为汇合引起孔隙度增长率的提高，从而导致了损伤的快速增长。
图 7左图显示了晶粒尺寸、孔洞汇合对自由面速度vf的影响：随着材料平均晶粒尺寸的增加，自由面速度曲线的回跳点降低，即层裂强度增加，这与P.B.Trivedi等[25]对不同晶粒尺寸高纯铝层裂实验结果的分析在定性上一致；同时，对于平均晶粒尺寸为30 μm的材料，考虑孔洞汇合的影响，曲线回跳后的斜率显著增加，上升的幅度增高，图 7右图为对应的自由面速度曲线实验结果：平均晶粒尺寸dg=30、200 μm的损伤材料中存在大量的孔洞汇合现象，相对于没有发生孔洞汇合的自由面速度曲线(60、100 μm)，自由面速度曲线回跳后的斜率和上升的幅度增加[2]，关于孔洞汇合的计算结果和实验结果定性上符合也较好。
图 7 晶粒尺寸、孔洞汇合对自由面速度曲线的影响Figure 7. Influences of void coalescence and grain size on free surface velocities表 1列出了不同平均晶粒尺寸dg损伤材料内部层裂面处孔洞数N和平均孔洞直径dv的实验统计结果和数值计算结果(注：实验给出的是可观测到的孔洞数，而计算给出的是单位体积(cm3)内的孔洞数)。实验观测结果显示：随着晶粒尺寸的增加，损伤材料内部的孔洞数减少、平均孔洞尺寸增加。计算结果与实验定性符合。同时，对实验观测结果和计算结果的分析表明(30 μm样品)：孔洞汇合引起孔洞数减少、平均孔洞尺寸增加。
表 1 损伤材料内部孔洞数及孔洞大小的统计结果Table 1. Damage statisticsdg /μm N dv 实验 计算 实验 计算 30 236 11.460 38.1 12.17 0.044(考虑汇合) 37.12(考虑汇合) 60 363 3.236 22.7 22.36 100 267 1.421 33.0 34.51 200 111 0.566 55.1 42.60 图 8显示了选取不同孔洞汇合临界损伤度D对自由面速度曲线的影响：孔洞汇合发生越早，材料内部损伤发展越快，即自由面曲线回跳后曲线上升的斜率和幅度越大。
图 8 孔洞汇合临界损伤度对自由面速度曲线的影响Figure 8. Influences of critical damage for void coalescence on free surface velocities4. 结语
耦合孔洞汇合的影响是精细化描述延性金属材料层裂损伤演化过程的关键。针对强动态拉伸载荷作用下延性金属层裂损伤问题，尝试建立了一个反映材料损伤和材料内部孔洞之间几何信息的孔洞汇合判定方法，从而弥补了现有判据只考虑单一影响因素的不足。同时，基于孔洞汇合前后能量守恒原理，给出了孔洞汇合对损伤增长影响的关系式，明确了孔洞汇合引起损伤增长的物理机理。
将材料平均晶粒尺寸影响和孔洞汇合影响引入到层裂损伤模型中，结合相关文献的实验分析结果，数值计算分析结果显示：晶粒尺寸越小，损伤材料内部成核孔洞越多、平均孔洞尺寸越小，自由面速度回跳点增高(即层裂强度降低)、回跳后速度曲线上升的斜率降低；孔洞汇合引起回跳后速度曲线上升的斜率增加、损伤材料内部的孔洞数减少、平均孔洞尺寸增加。计算结果与实验结果定性上符合较好，从而在一定程度上推进了延性金属层裂损伤的微细观物理建模研究。
-
图 1 双线型聚能爆破能量示意图
Figure 1. Schematic diagram of the energy in bilinear shaped charge blasting
图 2 第一象限药柱炸药利用率函数模型
Figure 2. Functional model of explosive utilization ratio in the first quadrant
图 3 不同聚能张开半角有效聚能炸药边界方程
Figure 3. Boundary of effective shaped charge to the relative half opening angle
图 4 不同聚能张开半角炸药聚能效应有效利用率
Figure 4. Efficiency of shaped charge (γ) to the relative half opening angle (α)
图 14 张开角为60°的侵彻过程von Mises应力云图
Figure 14. Von Mises stress contour diagram of penetration process with an opening angle of 60°
图 15 张开角为65°的侵彻过程von Mises应力云图
Figure 15. Von Mises stress contour diagram of penetration process with an opening angle of 65°
图 16 张开角为70°的侵彻过程von Mises应力云图
Figure 16. Von Mises stress contour diagram of penetration process with an opening angle of 70°
图 17 张开角为75°的侵彻过程Mises应力云图
Figure 17. Von Mises stress contour diagram of penetration process with an opening angle of 75°
图 18 张开角为80°的侵彻过程von Mises应力云图
Figure 18. Von Mises stress contour diagram of penetration process with an opening angle of 80°
图 20 不同聚能张开角岩石单元H33925应力时程曲线
Figure 20. Stress-time history curves of rock element H33925 with different shaped opening angles
表 1 炸药性能参数
Table 1. Explosive performance parameters
炸药类型 爆速/（m·s−1） 密度/（g·cm−3） 爆热/（kJ·kg−1） 熔点/℃ 爆燃点/℃ 外观 黑索金 8750 1.89 6025 205 230 白色结晶粉末 
下载: 导出CSV
表 2 试验爆破参数
Table 2. Test parameters
组号 类型 药包直径/mm 装药量/g 炮孔深度/mm 炮孔直径/mm 备注 1 普通 6 0.6 80 8 无需定位 2 双线型聚能 6 0.6 80 8 需定位
下载: 导出CSV
表 3 水泥砂浆试件静态力学参数
Table 3. Static mechanical parameters of cement mortar
纵波波速/（m·s−1） 密度/（g·cm−3） 抗压强度/MPa 抗拉强度/MPa 泊松比 弹性模量/GPa 1 810 2.41 5.13 0.45 0.213 7.16
下载: 导出CSV
表 4 岩石材料参数
Table 4. Rock material parameters
参数符号 参数解释说明 取值 参数符号 参数解释说明 取值 {\rho }_{0} /（kg·m−3） 物质密度 2600 {p}_{\mathrm{crush}} 孔隙压实时压力 102 G/GPa 剪切模量 28.7 { {G}^{\mathrm{*} }_{\mathrm{c} } } 压缩屈服面参数 0.4 fc/MPa 单轴抗压强度 154 {{G}_{\mathrm{t}}}^{\mathrm{*}} 拉伸屈服面参数 0.7 N 孔隙度指数 0.697 {X}_{\mathrm{I}} 剪切模量缩减系数 0.5 {\beta }_{\mathrm{t}} 拉伸应变率指数 0.0115 {D}_{1} 初始损伤参数 0.04 {B}_{0} 状态方程参数 1.68 {D}_{2} 损伤参数 1 {B}_{1} 状态方程参数 1.68 {\beta }_{\mathrm{C}} 压缩应变率指数 0.0083 {\alpha }_{0} 初始孔隙度 1.0 {A}_{\mathrm{f}} 残余应力强度参数 1.62 T1 状态方程参数 30.64 {N}_{\mathrm{f}} 残余应力强度参数 0.6
下载: 导出CSV
表 5 炸药及其状态方程参数
Table 5. Explosive and its state equation parameters
密度/（kg·m−3） 爆速/（m·s−1） 压力/GPa JWL状态方程参数 {A}_{\mathrm{J}} /GPa {B}_{\mathrm{J}} /GPa R1 R2 \omega {E}_{\mathrm{J}} /GPa 1320 6690 16 586 21.6 5.81 1.77 0.282 7.38
下载: 导出CSV
表 6 聚能管材料参数
Table 6. Shaped tube material parameters
ρ/(g·cm−3) γ C1/(km·s−1) S1 E/(GPa) Y/MPa Hc/MPa n Tm/K 2.790 2.00 5.330 1.340 27.6 265 426 0.34 775 注：\rho 为红铜材料密度；\gamma 为Grüneisen系数；{C_1}为应变率硬化系数；E为弹性模量；{S_1}、Y、{H_{\text{c}}}为材料常数；n为应变硬化指数；{T_{\text{m}}}为常态下材料的熔化温度；
下载: 导出CSV
表 7 炸药性能参数
Table 7. Explosive performance parameters
炸药类型 爆速/(m·s−1) 密度/(g·cm−3) 猛度/mm 殉爆距离/cm 震源药柱 3500 1.6 18 6
下载: 导出CSV
表 8 预裂爆破参数(
H_1=12\;{\rm{m}} )Table 8. Pre-split blasting parameters (
H_1=12\;{\rm{m}} )类型 直径/mm 倾角/(°) 长度/m 间距/m 填塞长度/m 线装药密度/(kg·m−1) 类型 板岩碎裂岩 120 65 14 1 3 0.5 普通 板岩碎裂岩 120 65 14 1.2 3 0.5 双线型聚能 白云岩 120 65 14 1.2 3 0.8 普通 白云岩 120 65 14 1.44 3 0.8 双线型聚能
下载: 导出CSV
-
[1] 李胜林, 梁书锋, 李晨, 等. 露天矿山深孔台阶爆破技术的现状与发展趋势 [J]. 矿业科学学报, 2021, 6(5): 598–605. DOI: 10.19606/j.cnki.jmst.2021.05.009.LI S L, LIANG S F, LI C, et al. Current status and development trend of deep hole bench blasting technology in open-pit mines [J]. Journal of Mining Science and Technology, 2021, 6(5): 598–605. DOI: 10.19606/j.cnki.jmst.2021.05.009. [2] RUSTAN A. Linear shaped charges for contour blasting or stone cutting: full scale tests at Gårdlidenberget, Storsund [M]. Luleå Tekniska Universitet, 1983. [3] 罗勇, 沈兆武. 聚能药包在岩石定向断裂爆破中的应用研究 [J]. 爆炸与冲击, 2006, 26(3): 250–255. DOI: 10.11883/1001-1455(2006)03-0250-06.LUO Y, SHEN Z W. Application study on directional fracture controlled blasting with shaped charge in rock [J]. Explosion and Shock Waves, 2006, 26(3): 250–255. DOI: 10.11883/1001-1455(2006)03-0250-06. [4] 刘文革, 题正义, 黄文尧. 轴对称聚能药管及其聚能效应 [J]. 辽宁工程技术大学学报, 2006, 25(S2): 126–128.LIU W G, TI Z Y, HUANG W Y. New axisymmetric amplitude transformer of explosive and its mohaupt effect [J]. Journal of Liaoning Technical University, 2006, 25(S2): 126–128. [5] 杨仁树, 佟强, 杨国梁. 聚能管装药预裂爆破模拟试验研究 [J]. 中国矿业大学学报, 2010, 39(5): 631–635.YANG R S, TONG Q, YANG G L. Pre-splitting blasting with binding energy tube charges: simulations and experimental research [J]. Journal of China University of Mining & Technology, 2010, 39(5): 631–635. [6] 宋俊生, 王雁冰, 高祥涛, 等. 定向断裂控制爆破机理及应用 [J]. 矿业科学学报, 2016, 1(1): 16–28. DOI: 10.19606/j.cnki.jmst.2016.01.004.SONG J S, WANG Y B, GAO X T, et al. The mechanism of directional fracture controlled blasting and its application [J]. Journal of Mining Science and Technology, 2016, 1(1): 16–28. DOI: 10.19606/j.cnki.jmst.2016.01.004. [7] 梁洪达, 郭鹏飞, 孙鼎杰, 等. 不同聚能爆破模式应力波传播及裂纹扩展规律研究 [J]. 振动与冲击, 2020, 39(4): 157–164,184. DOI: 10.13465/j.cnki.jvs.2020.04.020.LIANG H D, GUO P F, SUN D J, et al. A study on crack propagation and stress wave propagation in different blasting modes of shaped energy blasting [J]. Journal of Vibration and Shock, 2020, 39(4): 157–164,184. DOI: 10.13465/j.cnki.jvs.2020.04.020. [8] 赵建平, 戴东波, 张振洋, 等. 线性聚能爆破时影响岩体损伤因素的灰色关联分析 [J]. 爆破, 2018, 35(4): 14–19. DOI: 10.3963/j.issn.1001-487X.2018.04.003.ZHAO J P, DAI D B, ZHANG Z Y, et al. Grey relational analysis of influencing factors of rock mass damage during linear shaped charge blasting [J]. Blasting, 2018, 35(4): 14–19. DOI: 10.3963/j.issn.1001-487X.2018.04.003. [9] 吴波, 韦汉, 徐世祥, 等. 基于SPH的椭圆双极线性聚能药包控制爆破数值模拟研究 [J]. 煤炭科学技术, 2022, 50(5): 135–142. DOI: 10.13199/j.cnki.cst.2019-1261.WU B, WEI H, XU S X, et al. Numerical analysis of controlled blasting of elliptic bipolar linear shaped charge based on SPH [J]. Coal science and Technology, 2022, 50(5): 135–142. DOI: 10.13199/j.cnki.cst.2019-1261. [10] 黄风雷, 张雷雷, 段卓平. 大锥角药型罩聚能装药侵彻混凝土实验研究 [J]. 爆炸与冲击, 2008, 28(1): 17–22. DOI: 10.11883/1001-1455(2008)01-0017-06.HUANG F L, ZHANG L L, DUAN Z P. Shaped charge with large cone angle for concrete target [J]. Explosion and Shock Waves, 2008, 28(1): 17–22. DOI: 10.11883/1001-1455(2008)01-0017-06. [11] 薛宪彬. 对称双线型聚能爆破技术数值模拟研究及应用 [J]. 工程爆破, 2017, 23(6): 26–29, 38. DOI: 10.3969/j.issn.1006-7051.2017.06.006.XUE X B. Numerical simulation analysis and application of symmetric bilinear shaped charge blasting technology [J]. Engineering Blasting, 2017, 23(6): 26–29, 38. DOI: 10.3969/j.issn.1006-7051.2017.06.006. [12] 秦健飞, 秦如霞, 李必红. 双聚能槽药柱的理论研究及其工程应用 [J]. 采矿技术, 2009, 9(5): 40–44. DOI: 10.13828/j.cnki.ckjs.2009.05.018. [13] 朱飞昊, 刘泽功, 高魁, 等. 构造带内巷道定向聚能爆破掘进围岩损伤特征试验研究 [J]. 岩石力学与工程学报, 2018, 37(9): 2037–2047. DOI: 10.13722/j.cnki.jrme.2018.0344.ZHU F H, LIU Z G, GAO K, et al. Experimental study on rock damage of roadway excavation by cumulative blasting in structural coal [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(9): 2037–2047. DOI: 10.13722/j.cnki.jrme.2018.0344. [14] 刘健, 刘泽功, 高魁, 等. 深孔定向聚能爆破增透机制模拟试验研究及现场应用 [J]. 岩石力学与工程学报, 2014, 33(12): 2490–2496. DOI: 10.13722/j.cnki.jrme.2014.12.014.LIU J, LIU Z G, GAO K, et al. Experimental study and application of directional focused energy blasting in deep boreholes [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2490–2496. DOI: 10.13722/j.cnki.jrme.2014.12.014. [15] 秦健飞. 双聚能预裂与光面爆破综合技术 [M]. 北京: 中国水利水电出版社, 2014: 45–70. [16] MEURER A, SMITH C P, PAPROCKI M, et al. SymPy: symbolic computing in python [J]. PeerJ Preprints, 2016, 6: e2083v1. DOI: 10.7287/PEERJ.PREPRINTS.2083V1. [17] 王汪洋. 隧道聚能水压控制爆破岩机理与参数优化研究 [D]. 南宁: 广西大学, 2019: 76–80.WANG W Y. Study on rock breaking mechanism and parameter optimization of cumulative hydraulic controlled blasting in tunnel [D]. Nanning: Guangxi University, 2019: 76–80. [18] MA G W, AN X M. Numerical simulation of blasting-induced rock fractures [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(6): 966–975. DOI: 10.1016/j.ijrmms.2007.12.002. [19] LIU K, LI Q Y, WU C Q, et al. A study of cut blasting for one-step raise excavation based on numerical simulation and field blast tests [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 109: 91–104. DOI: 10.1016/j.ijrmms.2018.06.019. [20] XIE L X, LU W B, ZHANG Q B, et al. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses [J]. Tunnelling and Underground Space Technology, 2017, 66: 19–33. DOI: 10.1016/j.tust.2017.03.009. 期刊类型引用(1)
1. 张凤国，刘军，何安民，赵福祺，王裴. 强冲击加载下延性金属卸载熔化损伤/破碎问题的物理建模及其应用. 物理学报. 2022(24): 284-292 . 
百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 714
- HTML全文浏览量: 191
- PDF下载量: 125
- 被引次数: 2