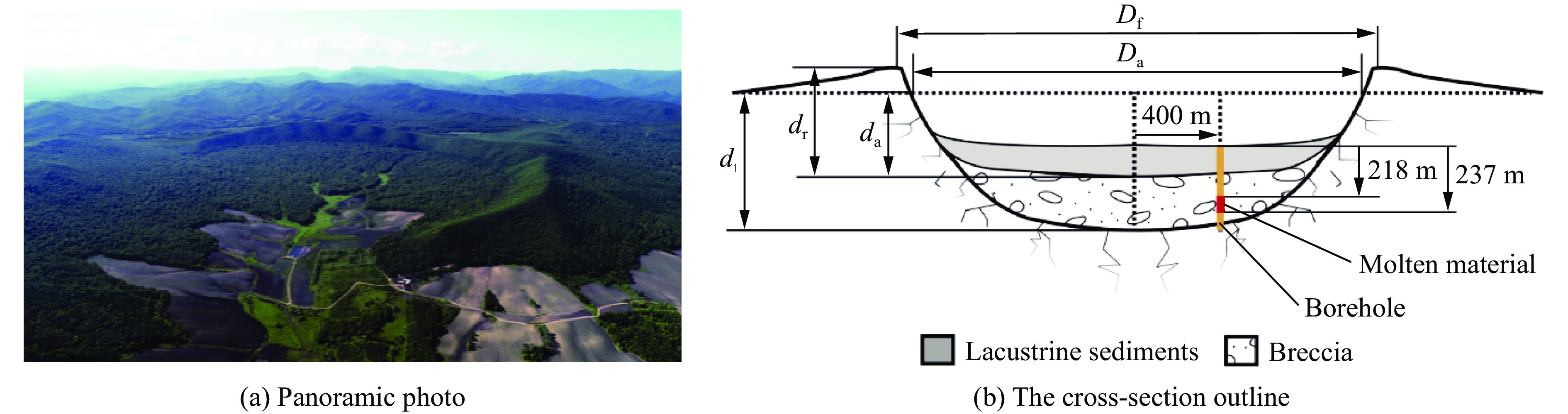
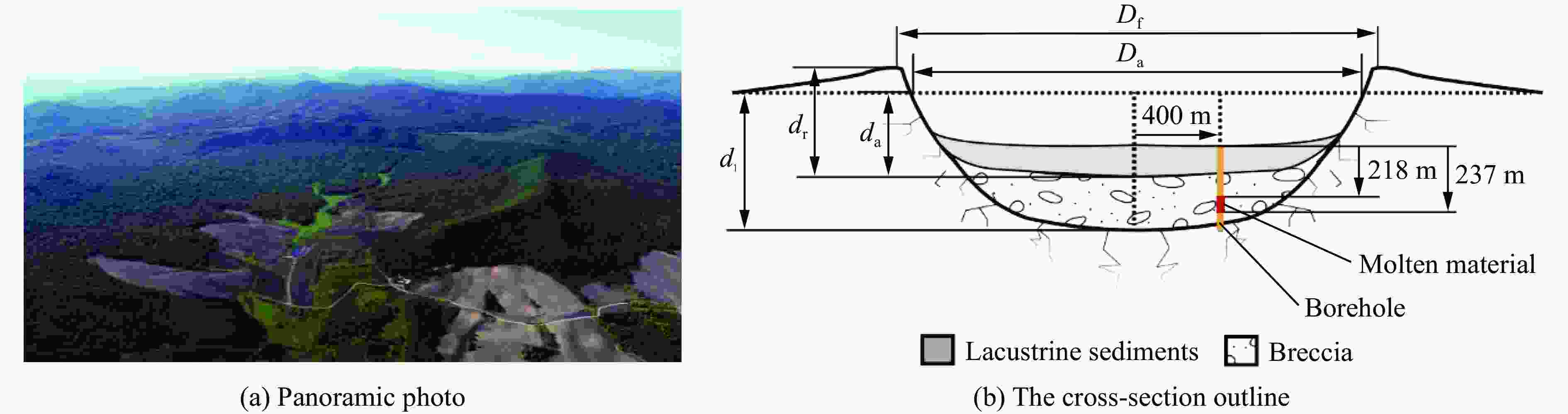
Numerical simulation of Yilan crater formation process
-
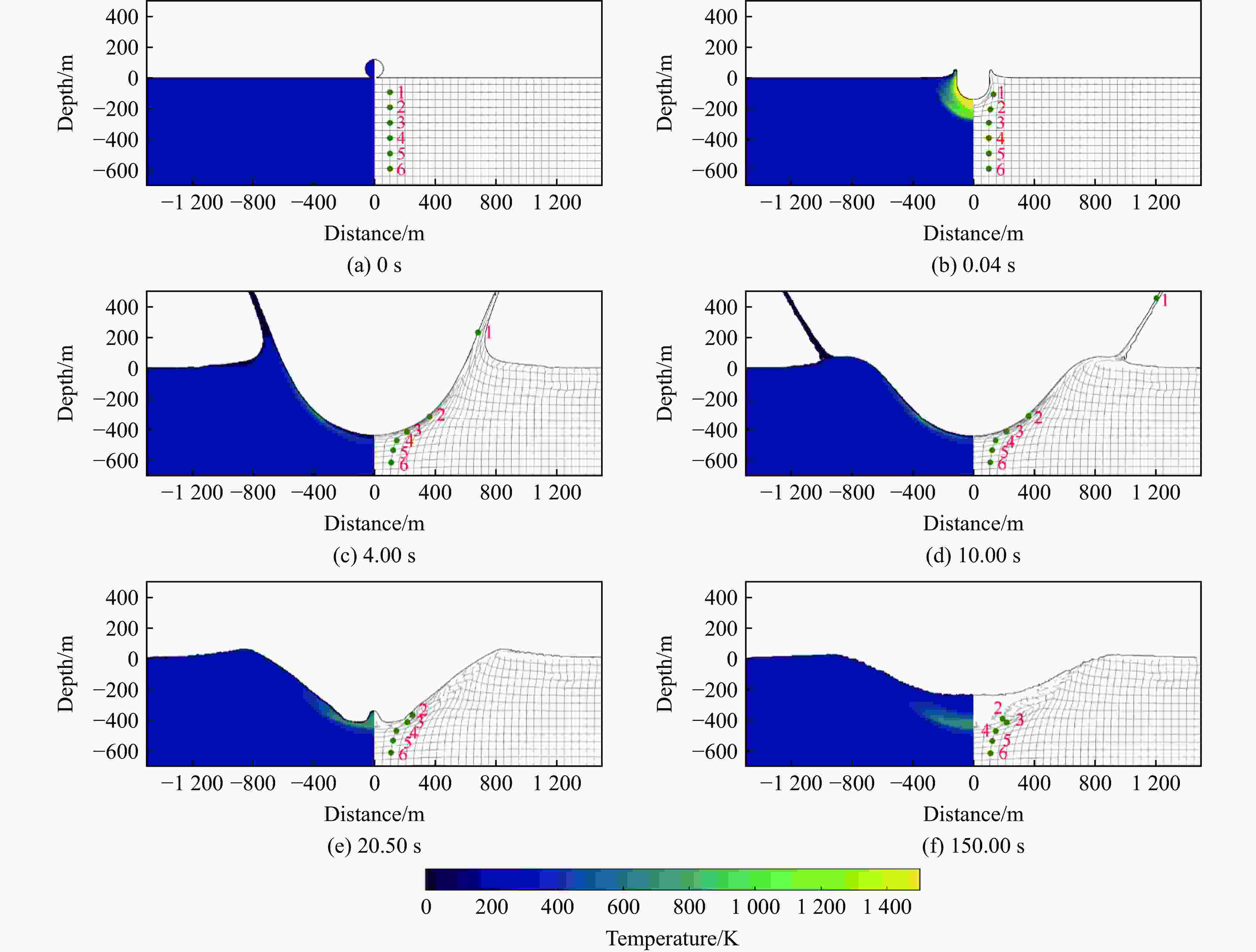
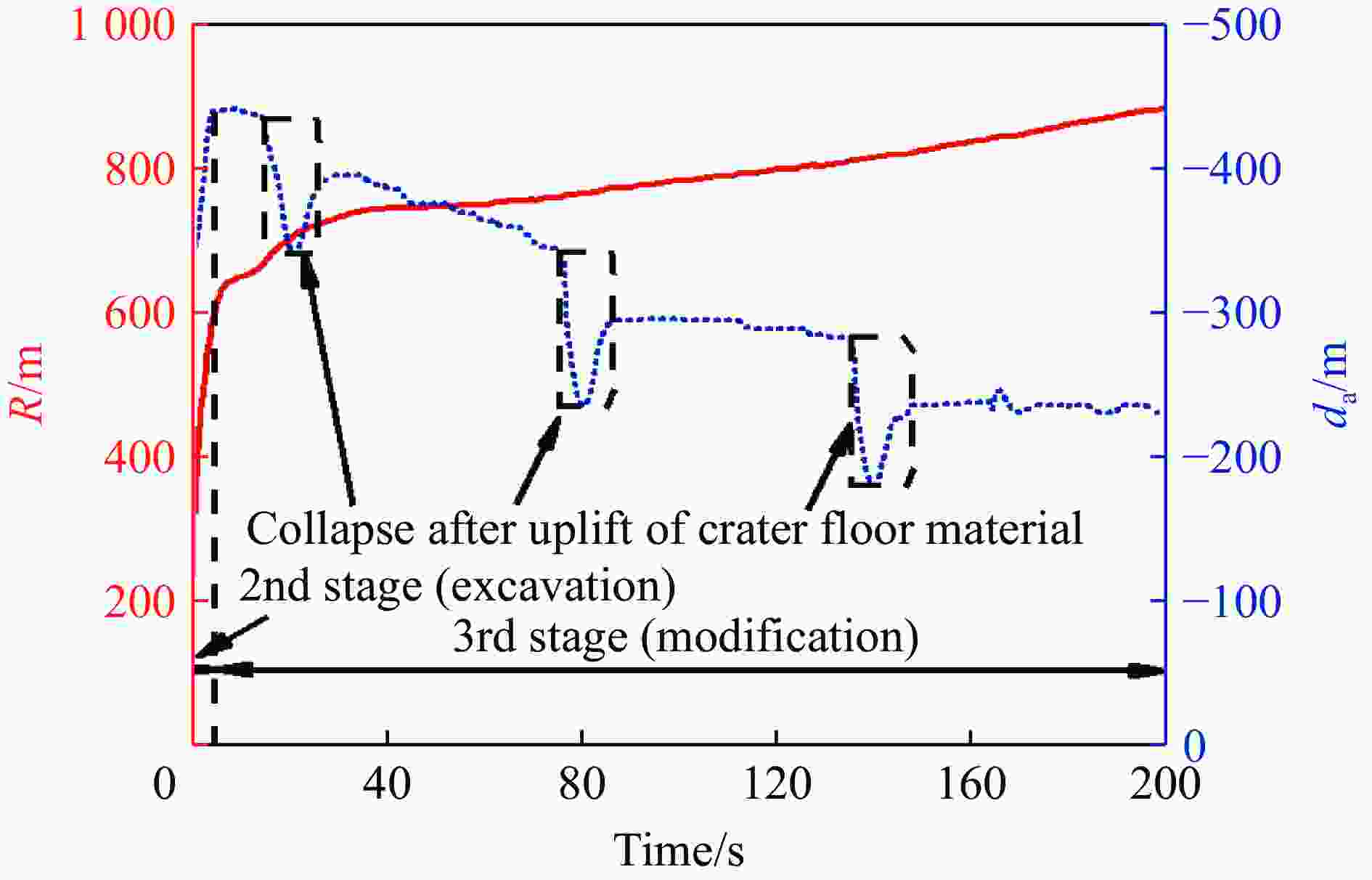
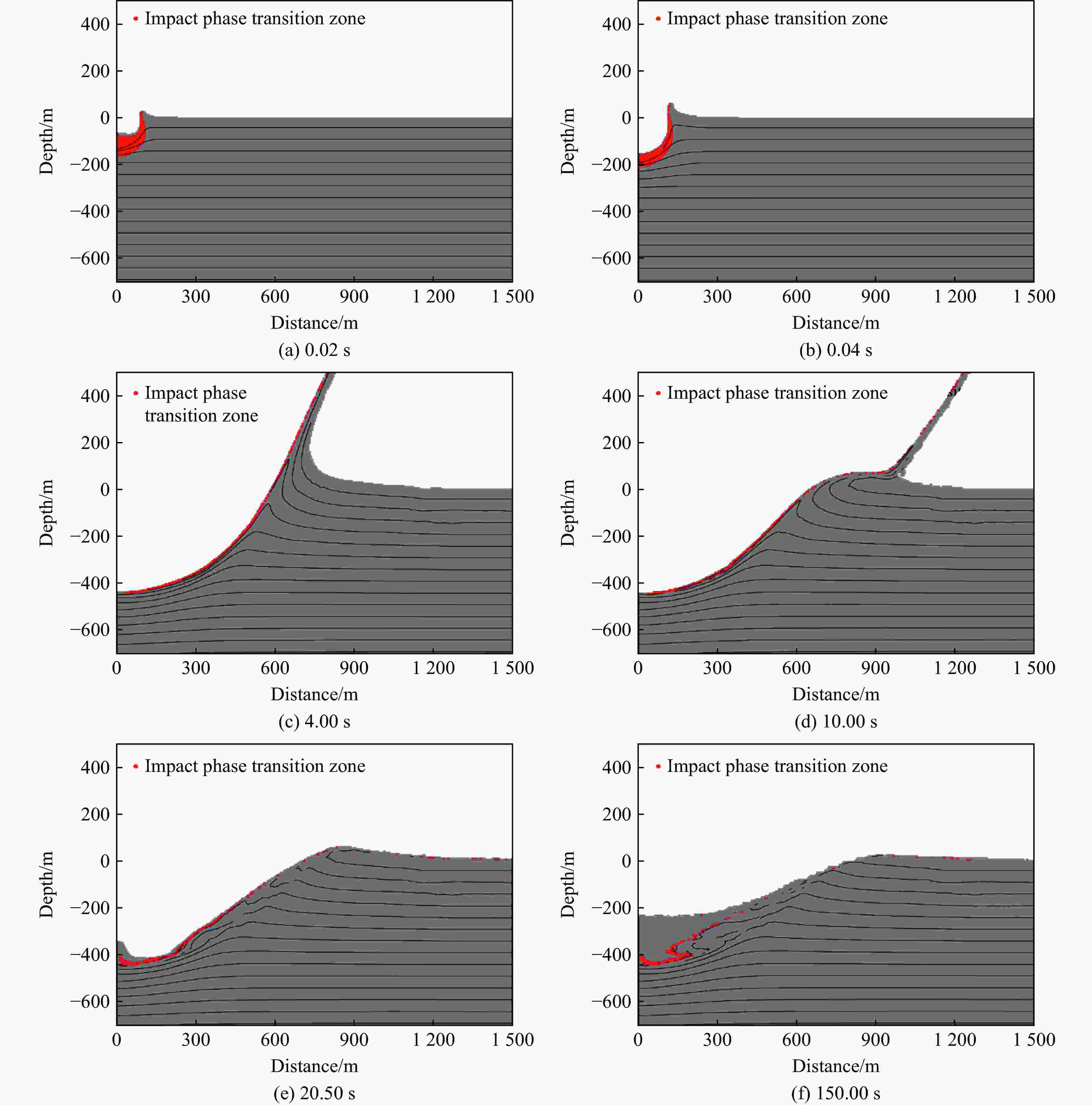
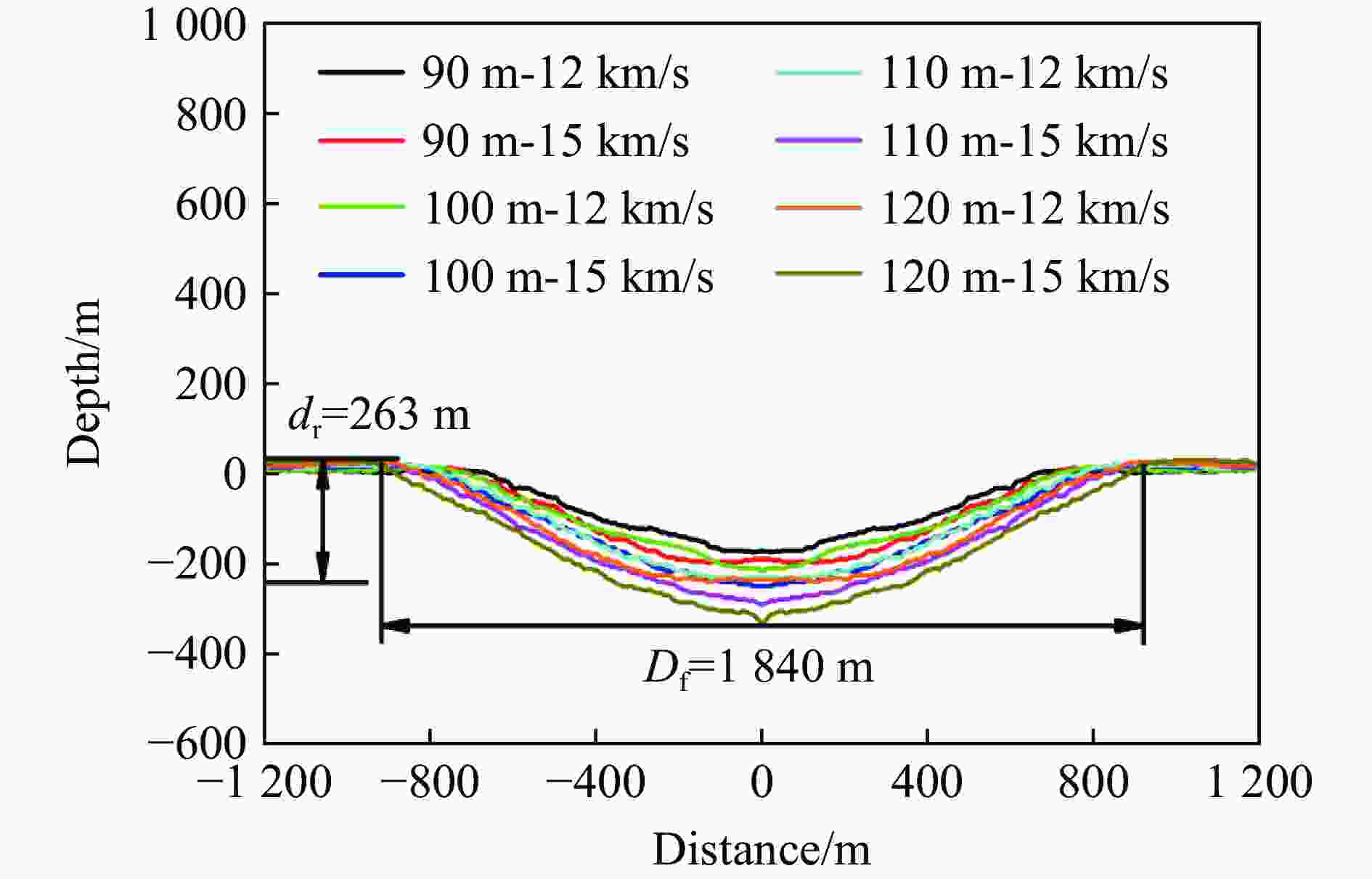
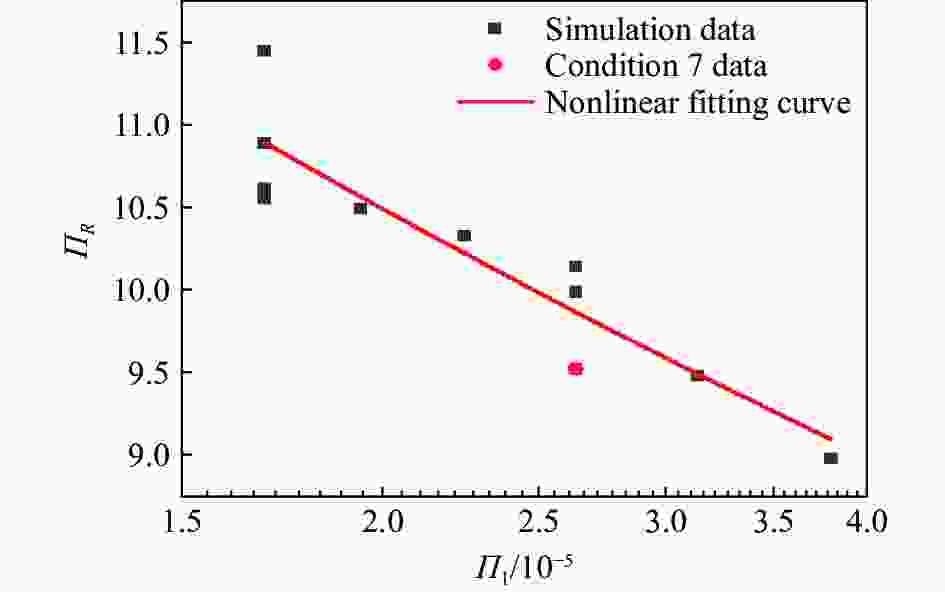
摘要: 基于iSALE-2D仿真代码对依兰陨石坑的形成过程进行了研究，采用欧拉算法开展数值模拟，探讨了依兰陨石坑的撞击条件，统计分析了成坑过程中熔化层的形成与分布规律，结合点源成坑相似律模型，拟合得到强度机制下的成坑半径关系式。研究结果表明一颗直径120 m、撞击速度12 km/s的花岗岩质小行星垂直撞击地表形成一个与依兰陨石坑形态相似的陨石坑，再现了成坑形成的3个阶段：接触与压缩阶段、开坑阶段、后期调整阶段。大部分熔体在坑底呈分层堆叠分布，少量熔体随抛射物沉积在靶体表面，呈离散状分布，完全熔化材料质量约为撞击体质量的24倍。直径120 m、撞击速度12 km/s工况模拟结果与拟合的成坑半径关系式结果相对误差10.3%。Abstract: The formation process of the Yilan crater was numerically studied based on the iSALE-2D simulation code. The Euler algorithm was used to carry out the numerical simulation, and eight groups of working conditions were simulated. According to the scaling law, it was determined that the projectile diameter range was 90 to 120 m, and the projectile velocity was 12 and 15 km/s. Simulation results under the corresponding working conditions within 150 s of impact were obtained, including the crater diameter, depth, and crater profile curve. The optimal impact conditions of the Yilan crater were studied, and the formation and distribution of the molten layer during the cratering process were statistically analyzed. Combined with the point source cratering similarity law model, the relationship of cratering radius under the strength mechanism was obtained by fitting. The research results show that, according to the comparison between the simulated data and actual exploration data, a granite asteroid with a diameter of 120 m and an impact velocity of 12 km/s vertically hits the surface, forming a crater with a shape similar to the Yilan crater. The crater has a final diameter of 1 840 m and a crater edge depth of 263 m, which is in good agreement with the exploration data of the Yilan crater. Three stages of crater formation were reproduced: contact and compression, excavation, and modification. The distribution of the impact melting layer of the target plate material during the crater formation under the simulated conditions were revealed. The material melted completely when the peak pressure exceeds 56 GPa during the impact process, and this process was completed within 20 ms. Most melts was distributed at the bottom of the crater in layers and stacks, and a small amount of melts was deposited discretely on the surface of the target plate. The mass of the completely melted material is about 24 times the projectile mass. The relative error between the simulation results and the fitted crater radius relational results under the conditions with 120 m diameter and 12 km/s impact velocity is 10.3%.
-
Key words:
- impact crater /
- iSALE-2D /
- hypervelocity impact /
- impact melting
-
图 3 重力初始化靶体岩石静压和靶体密度
Figure 3. Gravity-initialized lithostatic pressure and density of target
图 4 直径120 m、速度12 km/s的花岗岩质小行星撞击成坑3个阶段材料和温度分布
Figure 4. Material and temperature distributions in three stages of crater formation induced by the impact of a 120-m-diameter granitic asteroid with the velocity of 12 km/s
图 5 直径120 m、速度12 km/s的花岗岩质小行星撞击坑的半径和坑深随时间的演化
Figure 5. Time histories of the radius and depth of the crater induced by the impact of a 120-m-diameter granite asteroid with the velocity of 12 km/s
图 6 直径120 m、速度12 km/s的花岗岩质小行星撞击陨石坑形成过程花岗岩熔化层分布
Figure 6. Distribution of granite melt layers during the crater formation induced by the impact of a 120-m-diameter granite asteroid with the velocity of 12 km/s
图 7 无量纲化的花岗岩完全熔化质量与撞击体直径的关系
Figure 7. Dimensionless completely-melted granite mass varied with projectile diameter
图 8 不同模拟工况在计算结束时间150 s所对应的陨石坑剖面轮廓
Figure 8. The crater profiles corresponding to the different simulation conditions at the end time of 150 s
图 9 成坑半径拟合曲线与工况7数据的对比
Figure 9. Comparison of the crater radius fitting curve and the data of condition 7
表 1 模拟工况
Table 1. Simulation conditions
工况 dp /m u/(km∙s−1) t/s 1 90 12 150 2 90 15 150 3 100 12 150 4 100 15 150 5 110 12 150 6 110 15 150 7 120 12 150 8 120 15 150 
下载: 导出CSV
表 2 陨石坑熔化层分布
Table 2. Distribution of melted layers in craters
工况 dm /m mt /(1010 kg) 1 2.34 2 3.86 3 3.25 4 30～50 5.62 5 4.39 6 10～50 7.65 7 30～50 5.64 8 35～50 9.65
下载: 导出CSV
表 3 8组模拟工况在150 s坑形数据
Table 3. Crater shape data for eight simulation conditions at 150 s
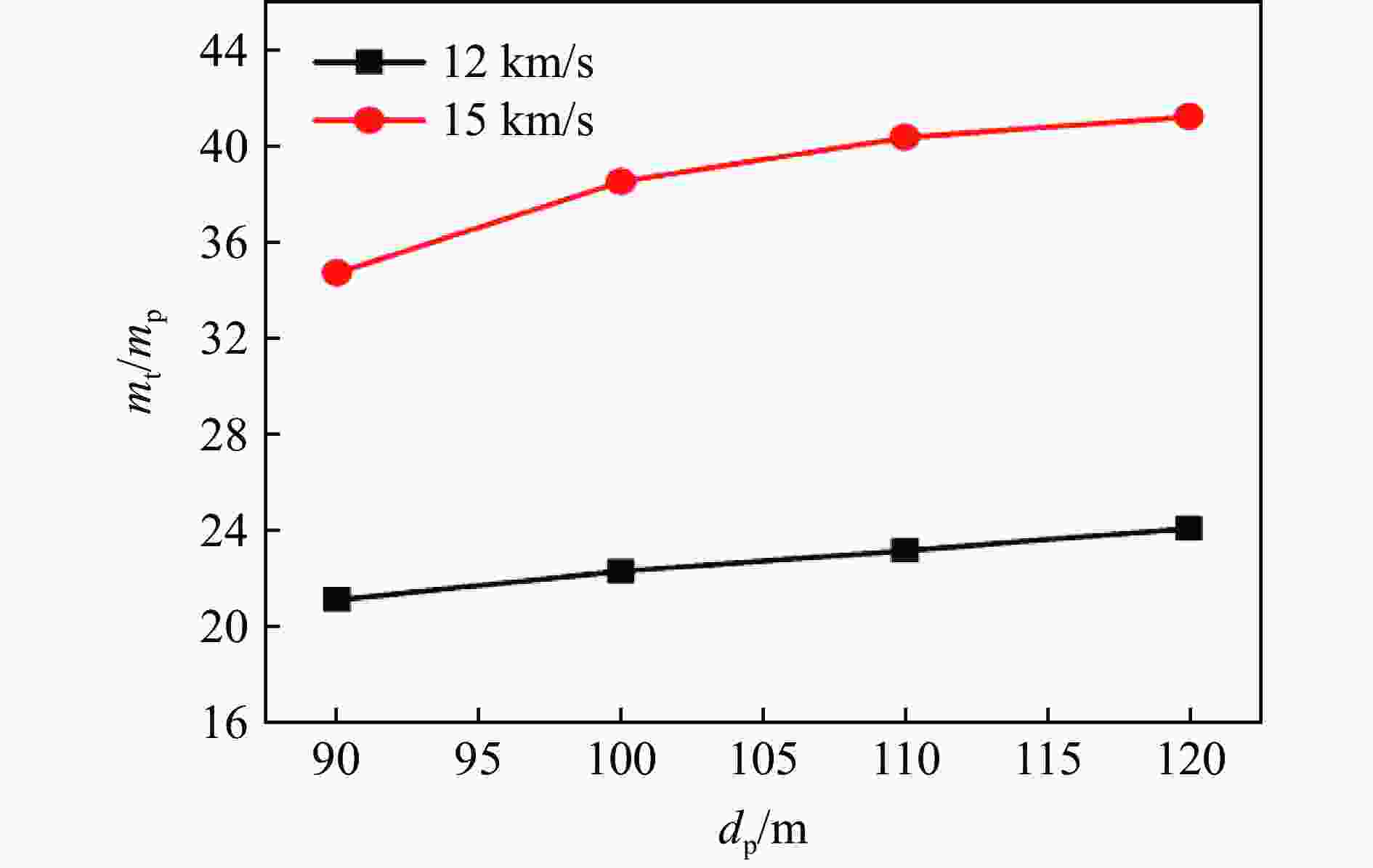
工况 dp/m u/(km∙s−1) Df/m dr/m dr/dp 1 90 12 1470 182 2.02 2 90 15 1660 208 2.31 3 100 12 1610 227 2.27 4 100 15 1710 269 2.69 5 110 12 1770 251 2.28 6 110 15 1930 317 2.88 7 120 12 1840 263 2.19 8 120 15 2040 359 2.99
下载: 导出CSV
-
[1] RUMPF C M, LEWIS H G, ATKINSON P M. Asteroid impact effects and their immediate hazards for human populations [J]. Geophysical Research Letters, 2017, 44(8): 3433–3440. DOI: 10.1002/2017GL073191. [2] 刘文近, 张庆明, 马晓荷, 等. 近地小天体对地撞击成坑模型研究进展 [J]. 爆炸与冲击, 2021, 41(12): 121404. DOI: 10.11883/bzycj-2021-0255.LIU W J, ZHANG Q M, MA X H, et al. A review of the models of near-Earth object impact cratering on Earth [J]. Explosion and Shock Waves, 2021, 41(12): 121404. DOI: 10.11883/bzycj-2021-0255. [3] SAITO T, KAIHO K, ABE A, et al. Numerical simulations of hypervelocity impact of asteroid/comet on the Earth [J]. International Journal of Impact Engineering, 2006, 33(1): 713–722. DOI: 10.1016/j.ijimpeng.2006.09.012. [4] IVANOV B. Cratering [J]. Planetary Science, 2020. DOI: 10.1093/acrefore/9780190647926.013.7. [5] IVANOV B A. Numerical modeling of the largest terrestrial meteorite craters [J]. Solar System Research, 2005, 39(5): 381–409. DOI: 10.1007/s11208-005-0051-0. [6] HALIM S H, BARRETT N, BOAZMAN S J, et al. Numerical modeling of the formation of Shackleton crater at the lunar south pole [J]. Icarus, 2021, 354: 113992. DOI: 10.1016/j.icarus.2020.113992. [7] YUE Z Y, DI K C. Hydrocode simulation of the impact melt layer distribution underneath Xiuyan Crater, China [J]. Journal of Earth Science, 2017, 28(1): 180–186. DOI: 10.1007/s12583-017-0741-9. [8] 陈鸣, 谢先德, 肖万生, 等. 依兰陨石坑: 我国东北部一个新发现的撞击构造 [J]. 科学通报, 2020, 65(10): 948–954. DOI: 10.1360/TB-2019-0704.CHEN M, XIE X D, XIAO W S, et al. Yilan crater, a newly identified impact structure in northeast China [J]. Chinese Science Bulletin, 2020, 65(10): 948–954. DOI: 10.1360/TB-2019-0704. [9] CHEN M, KOEBERL C, TAN D Y, et al. Yilan crater, China: Evidence for an origin by meteorite impact [J]. Meteoritics and Planetary Science, 2021, 56(7): 1274–1292. DOI: 10.1111/maps.13711. [10] AMSDEN A A, RUPPEL H M, HIRT C W. SALE: a simplified ALE computer program for fluid flow at all speeds [R]. Livermore, USA: Lawrence Livermore National Laboratory, 1980. DOI: 10.2172/5176006. [11] RADUCAN S D, DAVISON T M, COLLINS G S. Morphological diversity of impact craters on asteroid (16) psyche: insight from numerical models [J]. Journal of Geophysical Research: Planets, 2020, 125(9): e2020JE006466. DOI: 10.1029/2020JE006466. [12] ZHU M H, ARTEMIEVA N, MORBIDELLI A, et al. Reconstructing the late-accretion history of the Moon [J]. Nature, 2019, 571(7764): 226–229. DOI: 10.1038/s41586-019-1359-0. [13] DAVISON T M, COLLINS G S, ELBESHAUSEN D, et al. Numerical modeling of oblique hypervelocity impacts on strong ductile targets [J]. Meteoritics and Planetary Science, 2011, 46(10): 1510–1524. DOI: 10.1111/j.1945-5100.2011.01246.x. [14] COLLINS G S, MELOSH H J, MARCUS R A. Earth impact effects program: a web-based computer program for calculating the regional environmental consequences of a meteoroid impact on Earth [J]. Meteoritics & planetary science, 2005, 40(6): 817–840. DOI: 10.1111/j.1945-5100.2005.tb00157.x. [15] MELOSH H J. A hydrocode equation of state for SiO2 [J]. Meteoritics & planetary science, 2007, 42(12): 2079–2098. DOI: 10.1111/j.1945-5100.2007.tb01009.x. [16] PIERAZZO E, VICKERY A M, MELOSH H J. A reevaluation of impact melt production [J]. Icarus, 1997, 127(2): 408–423. DOI: 10.1006/icar.1997.5713. [17] COLLINS G S, MELOSH H J, IVANOV B A. Modeling damage and deformation in impact simulations [J]. Meteoritics and Planetary Science, 2004, 39(2): 217–231. DOI: 10.1111/j.1945-5100.2004.tb00337.x. [18] 李力. 火星壁垒撞击坑遥感探测及其形成机制的数值模拟研究 [D]. 北京: 中国科学院大学, 2016.LI L. Remote sensing observations and numerical simulation for the formation mechanism of Martian rampart craters [D]. Beijing, China: University of Chinese Academy of Sciences, 2016. [19] IVANOV B A, DENIEM D, NEUKUM G. Implementation of dynamic strength models into 2D hydrocodes: Applications for atmospheric breakup and impact cratering [J]. International Journal of Impact Engineering, 1997, 20(1): 411–430. DOI: 10.1016/S0734-743X(97)87511-2. [20] OHNAKA M. A shear failure strength law of rock in the brittle-plastic transition regime [J]. Geophysical Research Letters, 1995, 22(1): 25–28. DOI: 10.1029/94GL02791. [21] HOLSAPPLE K A, SCHMIDT R M. Point source solutions and coupling parameters in cratering mechanics [J]. Journal of Geophysical Research:Solid Earth, 1987, 92(B7): 6350–6376. DOI: 10.1029/JB092iB07p06350. [22] NAKAMURA A M, YAMANE F, OKAMOTO T, et al. Size dependence of the disruption threshold: laboratory examination of millimeter-centimeter porous targets [J]. Planetary and Space Science, 2015, 107: 45–52. DOI: 10.1016/j.pss.2014.07.011. [23] HOUSEN K R, HOLSAPPLE K A. Ejecta from impact craters [J]. Icarus, 2011, 211(1): 856–875. DOI: 10.1016/j.icarus.2010.09.017. -
计量
- 文章访问数: 568
- HTML全文浏览量: 142
- PDF下载量: 160
- 被引次数: 0