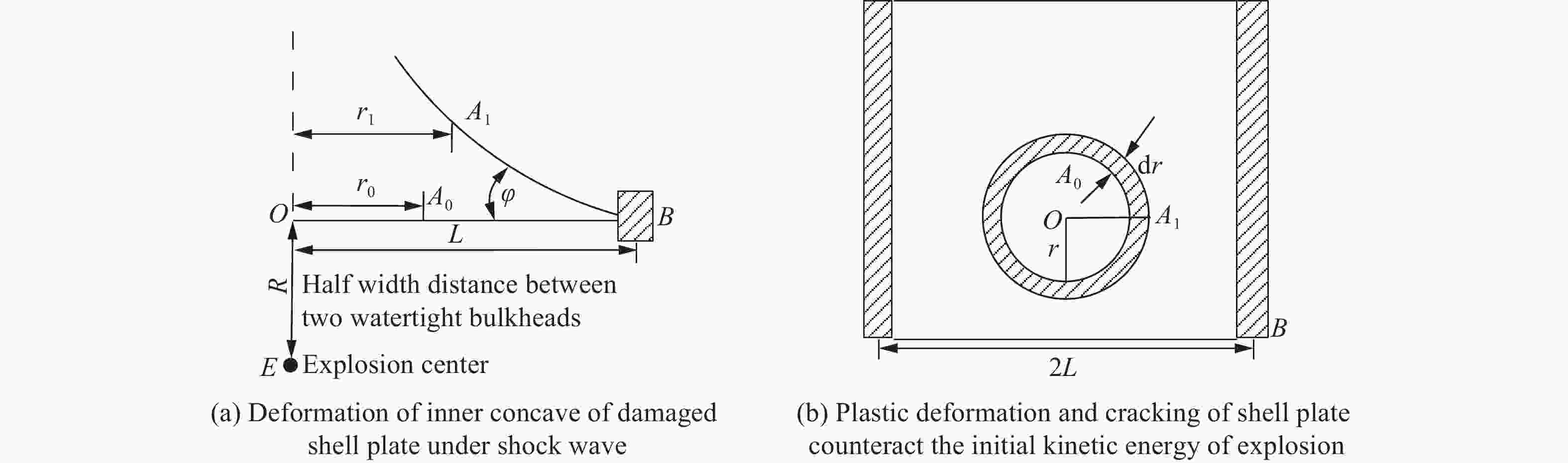
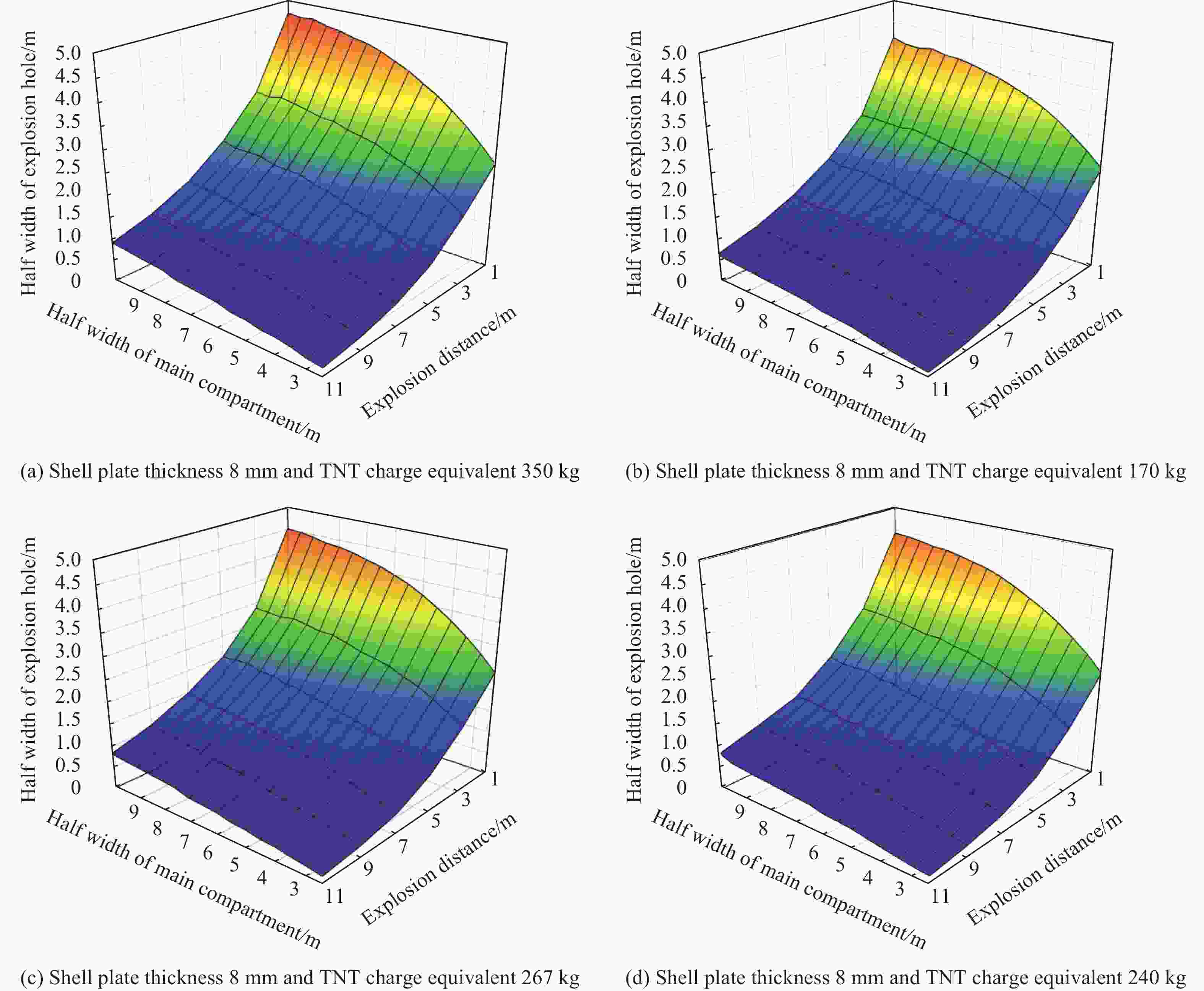
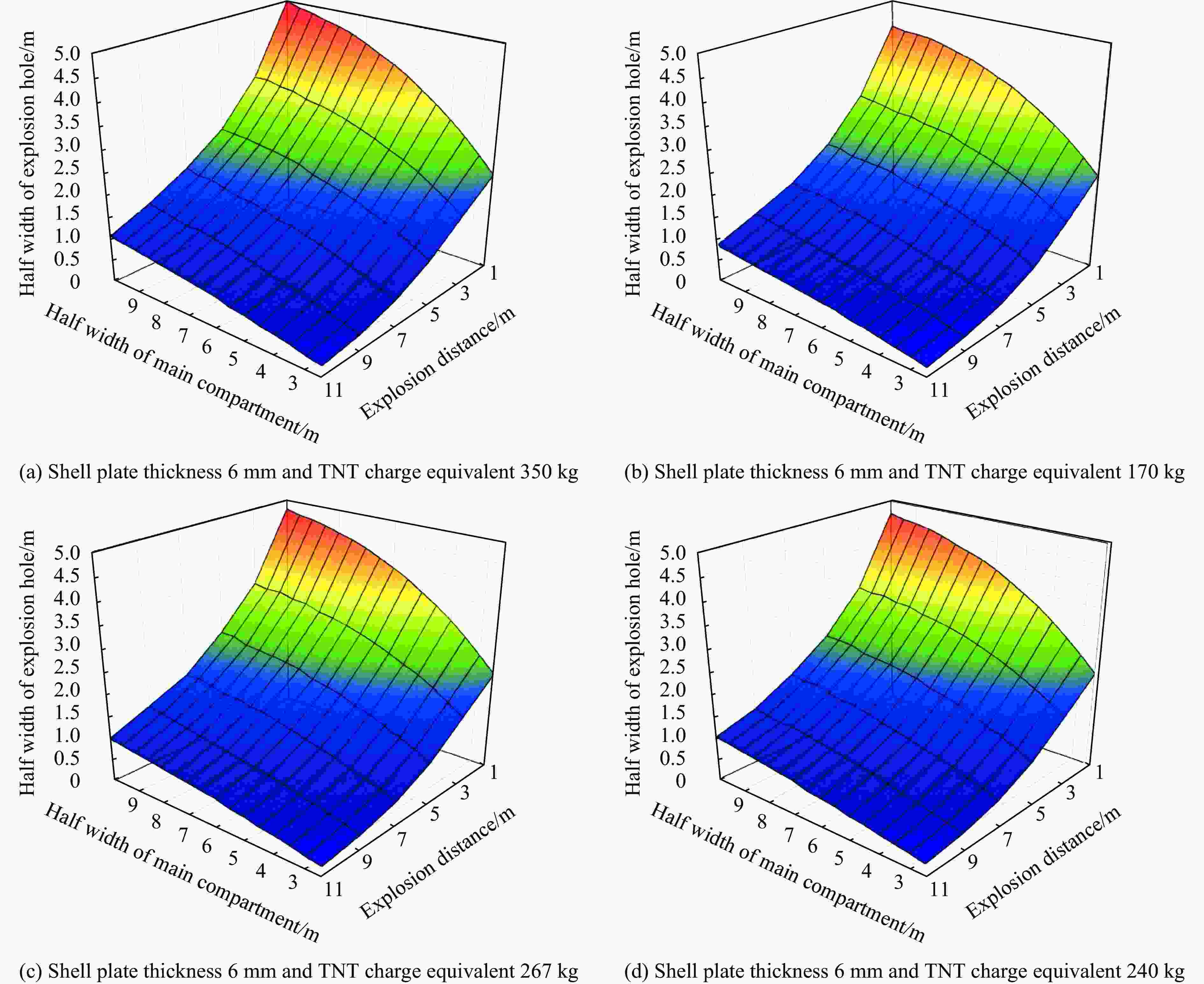
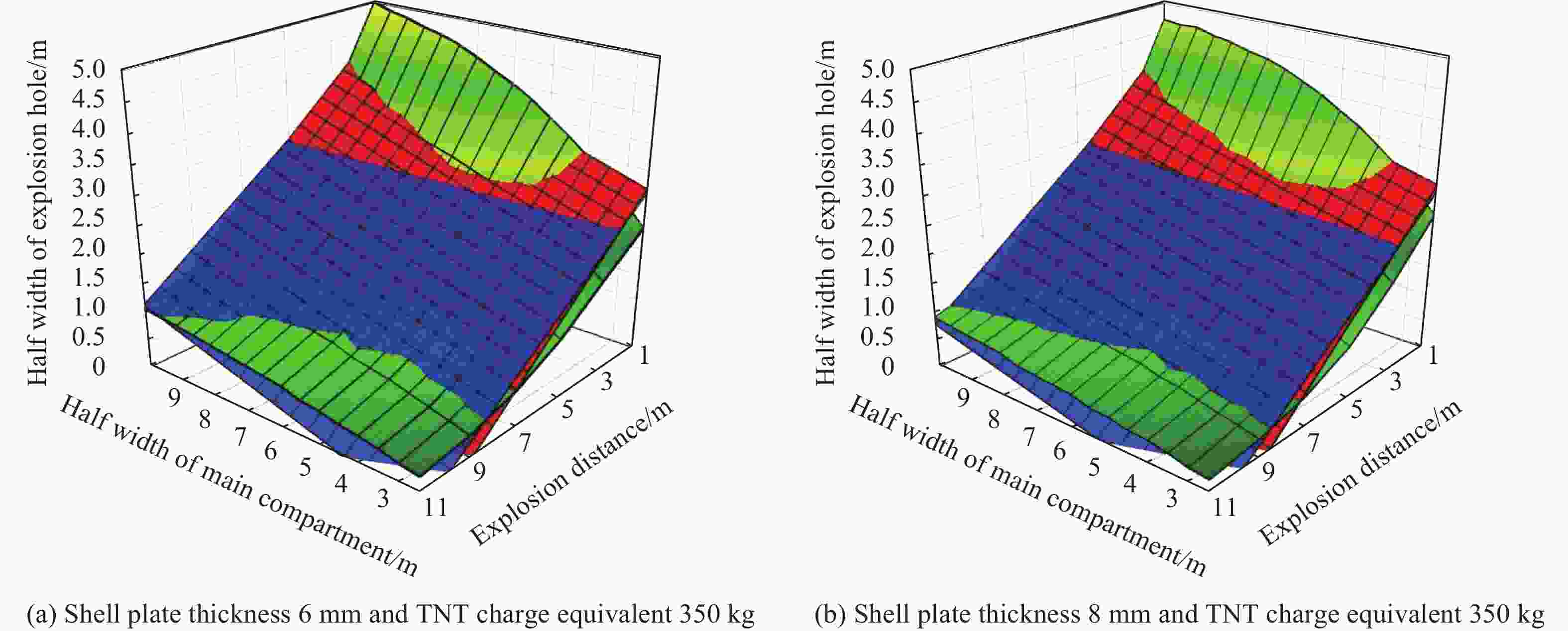
A two-step iterative method for damage calculation of a ship hullsubjected to underwater close-up non-contact explosion
-
摘要: 船体水下近距非接触爆炸产生的破口计算过程复杂，涉及船体板架、武器装药和爆距方位等诸多因素，工程实践中通常应用经验公式求解。基于舰船遭受定向型战斗部攻击、毁伤面近似垂直于毁伤轴和爆炸过程瞬时发生满足近似能量守恒基本条件，根据爆炸冲击波初始动能与爆炸作用区域结构塑性变形能等量传递的假设，给出了计算方法。考虑了附着加强筋的船体壳板等效厚度对抵御冲击波毁伤的影响，运用爆炸冲击波作用下船体壳板产生的极限应变超过板材动态极限应变导致壳板开裂这一基本原理，设计了两步迭代法计算流程，给出了简捷易用的迭代计算表格。针对4种典型装药当量冲击波作用下，5~20 m长度舱段，11 m以内爆炸距离，6 和8 mm这2种典型厚度船体壳板遭受爆炸冲击受损情况进行了768组数据计算。引入平面拟合方程，通过判断截平面相似度分析，给出了计算方法的适用性判据，探讨了计算参数的适用范围，以保证两步迭代法能够客观反映水下近距非接触爆炸的实际破坏效果。结合经验公式计算结果和破损舰船受损实测数据，对该方法进行了检验，实践表明：两步迭代法易于工程实践且具有较好的准确性。Abstract: The calculation of the break of ship hull caused by underwater close-range non-contact explosion is a complex process, involving many factors such as the hull frame, weapon charge, explosion distance and orientation, etc., so empirical formulas are usually used in engineering design. If the ship is attacked by a directional warhead, it is usually assumed that the damage surface is approximately perpendicular to the damage axis, and the explosion process instantaneously meets the basic condition on approximate energy conservation, then the calculation method is proposed according to the assumption that the initial kinetic energy of the explosion shock wave is equally transmitted to the plastic deformation energy of the structure in the explosion action area. Considering the effect of the equivalent thickness of the hull shell-plate attached with stiffeners on the resistance to shock wave damage, and using the fundamental principle that cracking of the shell plate will take place when the ultimate strain of the hull plate under the action of explosion shock wave exceeds the dynamic ultimate strain of the plate, the calculation flow of the two-step iterative method is designed, and a simple and easy-to-use iterative calculation table is given. 768 sets of data are calculated for the damage of hull shell-plates with the typical thicknesses of 6 mm and 8 mm under the action of four typical charge equivalent shock waves, with an explosion distance within 11 m, acting on a compartment with 5-20 m span. By introducing the plane fitting equation, the applicability criterion of the calculation method is given by judging the similarity analysis of the section plane, and the valid range of the calculation parameters is discussed to ensure that the two-step iteration method can objectively reflect the actual damage effect of the underwater short-range non-contact explosion. Combined with the calculation results of empirical formulas and the measured data of damaged ships, the method is verified. The practice shows that the two-step iterative method is easy for engineering practice and has good accuracy.
-
Key words:
- warship survivability /
- hull damage /
- underwater close-up explosion /
- breach calculation
-
图 1 炸点与船舶舱室之间的位置关系
Figure 1. Positional relationship between explosion point and ship cabin
图 2 水下近场非接触爆炸毁伤船体壳板基本原理
Figure 2. Basic principle of hull plate damaged by underwater near-field non-contact explosion
图 4 不同TNT装药当量对厚度8 mm船壳板产生的破坏作用计算结果
Figure 4. Calculation results of damage effect of different TNT charge equivalents on the 8-mm-thickness ship shell plate
图 5 不同TNT装药当量对厚度6 mm船壳板产生的破坏作用计算结果
Figure 5. Calculation results of damage effect of different TNT charge equivalents on 6-mm-thickness ship shell plate
图 6 TNT装药当量350 kg对不同厚度船板破坏作用计算结果平面型数据拟合方程
Figure 6. Calculation results of the destructive effect of TNT charge equivalent 350 kg on ship plates with different thicknesses
表 1 部分典型炸药的相似常数计算参数[10]
Table 1. Calculation parameters of similarity constants of some typical explosives[10]
炸药 kp kθ αp αθ TNT 52.5 0.094 1.13 −0.18 RS211鱼雷装药 59.6 0.101 1.17 −0.23 HLZY-1含铝炸药 49.0 0.132 1.11 −0.22 
下载: 导出CSV
表 2 水下爆炸船体破口计算表
Table 2. Calculation of hull break caused by underwater explosion
序号 项目 物理量 数值 说明 操作方法 1 装药量 W/kg 267 TNT当量 需要输入 2 爆炸产生的破口半径（半宽） R/m 2.71 计算结果，这个半宽数值对应中间完全撕裂破洞，实际破坏要比这个计算数值略小，这个结果越靠近炸点，与实际结果越接近。 输入半宽值试算，结果显示在C区域 3 炸药水中爆炸相似常数KE KE/（KPa∙m） 84.4 经验常数，根据实际查表由式（7）计算/采用TNT装药,代入公式时乘103 不输入 4 炸药水中爆炸相似常数αE αE 2.04 经验常数，根据实际查表由式（8）计算/采用TNT装药 不输入 5 两道水密隔墙之间的半宽距离 L/m 8.00 整个舱段长度为2L（m） 按水密段实际宽度一半输入 6 船壳板原始厚度 H/mm 8.000 直接输入不必转换成单位m 按实际输入 7 船壳板等效厚度（考虑加强筋） $ \bar{h} $/m 0.064 按实际板厚度8倍计算 不输入 8 爆距 R/m 3.00 炸点距离舷板垂直距离 按实际输入，接触爆炸可按0.01输入 9 爆炸区域冲击波初始动能 EK/（kg∙m2∙s−2） 3349689 A区域：炸药爆炸冲击波初始动能计算值 不输入，用与B区域结果比对 10 钢板强度 σ/MPa 235.00 直接输入不必转换成Pa，对于Q235钢板，此数值是235 MPa，船板一般取值235～440 MPa，代入公式时乘106 按实际输入 11 船壳板变形内凹陷试算角度 Φ/（°） 2.27 从0°～90°取数值试算 输入角度试算，结果显示在B区域 12 内凹陷角度转换弧度制 Φ/rad 0.04 此处是中间转换数值 不输入 13 爆破区计算作用动能 EA/（kg∙m2∙s−2） 3332283 B区域：爆炸冲击波做功近似转化为船壳板塑性变形能 不输入，用与A区域数值比对，直至EK=EA时止 14 动态极限应变 εm/% 0.2 钢板的极限应变是0.2% 不输入 15 计算极限应变 ε/% 0.2 C区域：此处计算得到临界极限应变 不输入 注：*以上计算方法适用于舱室跨度大于7 m，爆距小于9 m。
下载: 导出CSV
表 3 典型TNT装药当量爆炸破坏10 m跨度隔舱6 mm厚度舷板的计算结果
Table 3. Calculation results of equivalent explosion damage of typical TNT charge to 10 m span compartment and 6 mm thick sideboard
爆距/m 典型TNT当量条件下的破口半宽/m 350 kg 267 kg 240 kg 170 kg 9 0.92 0.87 0.81 0.76 11 0.66 0.61 0.56 0.51
下载: 导出CSV
表 4 典型TNT装药当量爆炸破坏10 m跨度隔舱8 mm厚度舷板的计算结果
Table 4. Calculation results of equivalent explosion damage of typical TNT charge to 10 m span compartment and 8 mm thick sideboard
爆距/m 典型TNT当量条件下的破口半宽/m 350 kg 267 kg 240 kg 170 kg 9 0.68 0.63 0.63 0.53 11 0.48 0.43 0.43 0.39
下载: 导出CSV
表 5 7 m以内跨度6 mm厚度舷板隔舱典型TNT装药当量爆距1 m破坏的计算结果
Table 5. Calculated damage results of typical TNT charge equivalent explosive distance of 1 m with span of 6 mm and the thickness of the bulkhead compartment within 7 m
隔舱跨度/m 典型TNT当量条件下的破口半宽/m 350 kg 267 kg 240 kg 170 kg 7 3.15 3.11 3.08 3.03 6 2.79 2.76 2.75 2.71 5 2.41 2.40 2.39 2.36
下载: 导出CSV
表 6 7 m以内跨度8 mm厚度舷板隔舱典型TNT装药当量爆距1 m破坏的计算结果
Table 6. Calculated damage results of typical TNT charge equivalent explosive distance of 1 m with span of 8 mm and the thickness of the bulkhead compartment within 7 m
隔舱跨度/m 典型TNT当量条件下的破口半宽/m 350 kg 267 kg 240 kg 170 kg 7 3.07 3.01 2.99 2.9 6 2.76 2.72 2.71 2.64 5 2.42 2.39 2.38 2.34
下载: 导出CSV
表 7 运用经验公式和两步迭代法的计算结果比较
Table 7. Comparison of calculation results between the empirical formula and the two-step iterative method
案例 运用吉田隆经验公式计算破坏半径 运用两步迭代法计算破坏半径 罗伯茨号 2.77 m 2.63 m 科尔号 3.29 m（装药181 kg）/4.07 m（装药317 kg） 5.07 m（装药181 kg）/5.67 m(装药317 kg)
下载: 导出CSV
-
[1] 吉田隆. 二次世界大战初期日本海军舰船在炸弹攻击下的损伤实例分析 [J]. 舰船科学, 1990(5): 70–81.YOSHIDA. Damage case analysis of Japanese navy ships subjected to bomb attack in the early of the second world war [J]. Ship Science, 1990(5): 70–81. [2] 朱锡, 白雪飞, 黄若波, 等. 船体板架在水下接触爆炸作用下的破口试验 [J]. 中国造船, 2003, 44(1): 46–51. DOI: 10.3969/j.issn.1000-4882.2003.01.007.ZHU X, BAI X F, HUANG R B, et al. Crevasse experiment research of plate membrance in vessels subjected to underwater contact explosion [J]. Shipbuilding of China, 2003, 44(1): 46–51. DOI: 10.3969/j.issn.1000-4882.2003.01.007. [3] 朱锡, 白雪飞, 张振华. 空中接触爆炸作用下船体板架塑性动力响应及破口研究 [J]. 中国造船, 2004, 45(2): 43–50. DOI: 10.3969/j.issn.1000-4882.2004.02.006.ZHU X, BAI X F, ZHANG Z H. Plastic dynamic response and crevasse research of ship panels subjected to air contact explosion [J]. Shipbuilding of China, 2004, 45(2): 43–50. DOI: 10.3969/j.issn.1000-4882.2004.02.006. [4] 牟金磊, 朱锡, 黄晓明, 等. 水下近场非接触爆炸作用下固支方板破口计算 [J]. 振动与冲击, 2011, 30(1): 37–39, 55. DOI: 10.3969/j.issn.1000-3835.2011.01.008.MU J L, ZHU X, HUANG X M, et al. Crevasse computation for a clamped square plate subjected to near-field noncontact underwater explosion [J]. Journal of Vibration and Shock, 2011, 30(1): 37–39, 55. DOI: 10.3969/j.issn.1000-3835.2011.01.008. [5] 陈海龙, 周姝, 孙丰等. 水下接触爆炸对舰船壳板的毁伤试验效果估算方法评估 [J]. 舰船科学技术, 2013, 35(10): 33–37. DOI: 10.3404/j.issn.1672-7649.2013.10.008.CHEN H L, ZHOU S, SUN F, et al. Estimation on estimation method of warship shell experimental damage subjected to underwater contact explosion [J]. Ship Science and Technology, 2013, 35(10): 33–37. DOI: 10.3404/j.issn.1672-7649.2013.10.008. [6] DIDOSZAK J M. Parametric studies of DDG-81 ship shock trail simulation[D]. California: Naval Postgraduate School Monterey, 2004: 140–161. [7] JULIE A K. Feasibility and design of blast mitigation systems for naval applications using water mist fire suppression systems [D]. Cambridge, MA: Massachusetts Institute of Technology. 2004: 9–11. [8] BOGDAN S. The effect of an underwater explosion on a ship [J]. Scientific Journal of Polish Naval Academy (PNA), 2015, 201(2): 57–73. DOI: 10.5604/0860889X.1172074. [9] 李志辉, 刘辉, 李其修,等. 水下非接触爆炸作用下舰船结构损伤评估 [J]. 舰船科学技术, 2012, 34(7): 40–44. DOI: 10.3404/j.issn.1672-7649.2012.07.008.LI Z H, LIU H, LI Q X, et al. Research on damage evaluation of ship structure in underwater non-contact explosion [J]. Ship Science and Technology, 2012, 34(7): 40–44. DOI: 10.3404/j.issn.1672-7649.2012.07.008. [10] 李金河, 赵继波, 谭多望,等. 炸药水中爆炸的冲击波性能 [J]. 爆炸与冲击, 2009, 29(2): 172–176.LI J H, ZHAO J B, TAN D W, et al. Underwater shock wave performances of explosives [J]. Explosion and Shock Waves, 2009, 29(2): 172–176. [11] 宫翔飞, 刘文韬, 张树道,等. 水下爆炸近场峰值压力的数值模拟 [J]. 爆炸与冲击, 2019, 39(4): 041409. DOI: 10.11883/bzycj-2017-0262.GONG X F, LIU W T, ZHANG S D, et al. Numerical simulation of peak pressure in near-field underwater explosion [J]. Explosion and Shock Waves, 2019, 39(4): 041409. DOI: 10.11883/bzycj-2017-0262. [12] HSU C Y, LIANG C C, TENG T L, et al. Numerical study of hovercraft main hull structural response subjected to shockwave from underwater explosion[C]// JAWAID M, AZAD A K, YOUSEFI M. International Conference on Advanced Material Science and Environmental Engineering (AMSEE 2016). Netherlands: Atlantis Press, 2016: 136–139. [13] GEBREHIWOT S Z, REMES H, KARTTUNEN A T. A Stress concentration factor for interacting surface notch and subsurface hole [J]. Rakenteiden Mekaniikka, 2018, 51(4): 20–37.DOI. DOI: 10.23998/rm.70292. [14] BRADLEY P. No higher honor: saving the USS samuel B: Roberts in the persian gulf[M]. Annapolis: Naval Institute Press, 2006: 16–27. -
计量
- 文章访问数: 464
- HTML全文浏览量: 94
- PDF下载量: 112
- 被引次数: 0