A study of dynamic constitutive model of frozen sandy soil considering confining pressure effect
-
摘要: 为描述主动围压作用下冻结砂土的动态力学特性,通过在朱-王-唐模型的非线性体上串联塑性体,建立了能够考虑围压效应的冻结砂土动态损伤本构模型;分析了损伤参数对应力-应变曲线特征、屈服点、峰值应力和峰值应变的影响规律,基于冻结砂土动力学试验数据确定了模型参数;通过将模型和试验数据进行对比,并对不同试验条件下模型的预测误差进行分析,验证了模型的适用性和准确性。结果表明,损伤参数对应力-应变曲线弹性阶段和屈服点无明显影响,而对塑性阶段和破坏阶段的影响较为显著,本构模型预测的应力-应变曲线与试验结果具有较好的一致性。模型能够预测围压引起冻结砂土塑性阶段占比大和屈服点明显的特征,且能够描述围压对冻结砂土动态强度的增强效应;不同负温和主动围压条件下,模型对峰值应力和屈服强度的预测效果优于峰值应变和屈服应变。
-
关键词:
- 冻结砂土 /
- 围压效应 /
- 分离式Hopkinson压杆 /
- 动态本构模型 /
- 屈服强度
Abstract: To describe the dynamic mechanical properties of frozen sandy soil under active confining pressure, a dynamic damage constitutive model, which could consider the effect of active confining pressure on the dynamic strength and deformation characteristics of frozen sandy soil, was established by connecting a plastic body to the nonlinear Zhu-Wang-Tang model. The effects of damage parameters on the characteristics of stress-strain curves, yield point, peak stress, and peak strain were analyzed. In addition, the model parameters were determined based on the dynamic test data of frozen sandy soil. The applicability and accuracy of the established model were verified by comparing the model with the test data and analyzing its prediction errors under different test conditions. The results show that the damage parameters have no significant effect on the elastic stage and yield point of the dynamic stress-strain curves. However, it significantly affects the plastic and failure stages. The stress-strain curves predicted by the established constitutive model are in good agreement with the test results. The model is appropriate in predicting the characteristics including large portion of the plastic stage and obvious yield point caused by active confining pressure. Moreover, the model can also describe the enhancement effect of confining pressure on the dynamic compressive strength of frozen sandy soil. The predictions of the model on the peak stress and yield stress are better than those on the peak strain and yield strain under different negative temperatures and active confining pressures. -
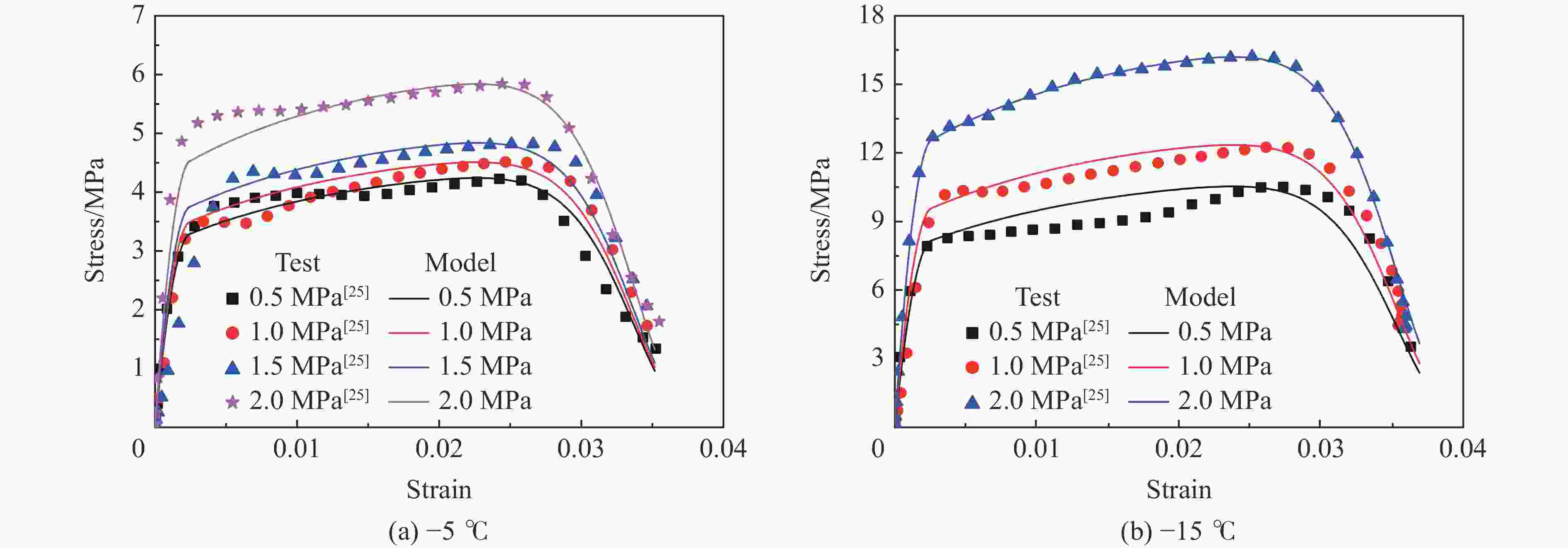
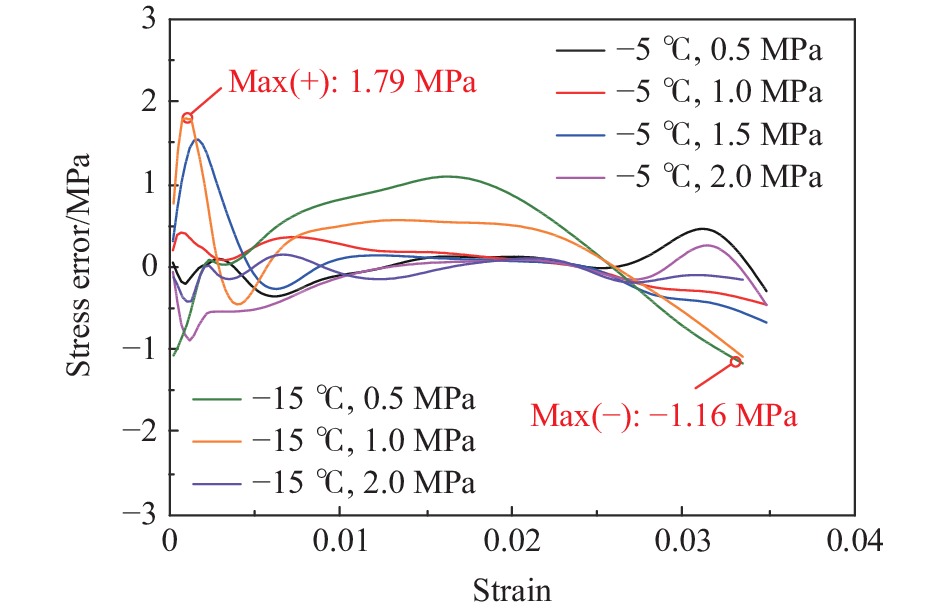
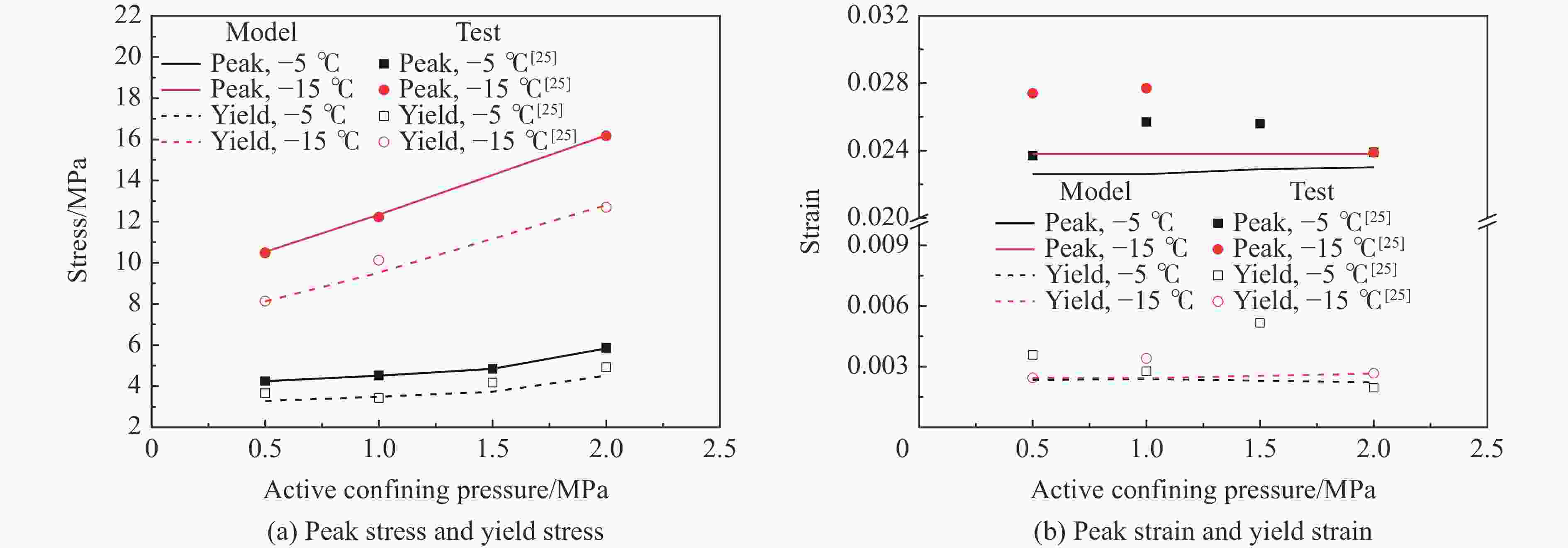
图 4 不同主动围压下本构模型曲线与试验结果的对比
Figure 4. Comparison of dynamic stress-strain curves by the modified constitutive model with the test results[25] under different active confining pressures
表 1 冻结砂土动态本构模型参数
Table 1. Dynamic constitutive model parameters of frozen sandy soil
温度/℃ 围压/MPa E0/MPa E1/MPa E2/MPa α/GPa β/GPa σs/MPa θ2/ms λ φ μ η −5 0.5 1920 45 130 −420 590 3.28 0.1 0.15 7.2 0.036 11.5 −5 1.0 1920 45 130 −420 590 3.49 0.1 0.15 7.2 0.036 11.5 −5 1.5 1920 45 130 −420 590 3.73 0.1 0.15 7.2 0.036 11.5 −5 2.0 1920 45 130 −420 590 4.51 0.1 0.15 7.2 0.036 11.5 −15 0.5 5030 60 210 −740 980 8.12 0.1 0.45 7.2 0.036 11.5 −15 1.0 5030 60 210 −740 980 9.52 0.1 0.45 7.2 0.036 11.5 −15 2.0 5030 60 210 −740 980 12.81 0.1 0.45 7.2 0.036 11.5 表 2 不同试验条件下冻结砂土的模型应力与试验应力的平均绝对误差、均方根误差和标准差
Table 2. Mean absolute errors, root mean square errors and standard deviations between the dynamical stresses of frozen sandy soil by the established model and the test ones under different test conditions
温度/℃ 围压/MPa 平均绝对误差/MPa 均方根误差/MPa 标准差/MPa −5 0.5 0.130 0.195 0.174 −5 1.0 0.177 0.279 0.240 −5 1.5 0.677 0.907 0.751 −5 2.0 0.315 0.493 0.356 −15 0.5 0.585 0.701 0.715 −15 1.0 0.615 1.034 0.794 −15 2.0 0.125 0.193 0.158 -
[1] 龙驭球, 崔京浩, 袁驷, 等. 力学筑梦中国 [J]. 工程力学, 2018, 35(1): 1–54. DOI: 10.6052/j.issn.1000-4750.2017.09.1000.LONG Y Q, CUI J H, YUAN S, et al. Build ‘Chinese dream’ with the assistance of mechanics [J]. Engineering Mechanics, 2018, 35(1): 1–54. DOI: 10.6052/j.issn.1000-4750.2017.09.1000. [2] 佘诗刚, 林鹏. 中国岩石工程若干进展与挑战 [J]. 岩石力学与工程学报, 2014, 33(3): 433–457. DOI: 10.13722/j.cnki.jrme.2014.03.001.SHE S G, LIN P. Some developments and challenging issues in rock engineering field in China [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(3): 433–457. DOI: 10.13722/j.cnki.jrme.2014.03.001. [3] 滕振超, 赵誉翔, 滕云超, 等. 冲击荷载作用下冻土区埋地管道动力响应试验研究 [J]. 地震工程与工程振动, 2021, 41(6): 168–176. DOI: 10.13197/j.eeev.2021.06.168.tengzc.016.TENG Z C, ZHAO Y X, TENG Y C, et al. Dynamic response test of buried pipeline in frozen soil area under impact load [J]. Earthquake Engineering and Engineering Dynamics, 2021, 41(6): 168–176. DOI: 10.13197/j.eeev.2021.06.168.tengzc.016. [4] 胡宏伟, 冯海云, 陈朗, 等. 非理想炸药在混凝土介质中的爆炸做功特性 [J]. 爆炸与冲击, 2018, 38(1): 197–203. DOI: 10.11883/bzycj-2016-0123.HU H W, FENG H Y, CHEN L, et al. Characteristic work capability of non-ideal explosives in concrete [J]. Explosion and Shock Waves, 2018, 38(1): 197–203. DOI: 10.11883/bzycj-2016-0123. [5] 王明洋, 岳松林, 李海波, 等. 超高速弹撞击岩石的地冲击效应等效计算 [J]. 岩石力学与工程学报, 2018, 37(12): 2655–2663. DOI: 10.13722/j.cnki.jrme.2018.0473.WANG M Y, YUE S L, LI H B, et al. An equivalent calculation method of ground shock effects of hypervelocity projectile striking on rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(12): 2655–2663. DOI: 10.13722/j.cnki.jrme.2018.0473. [6] 张爽, 武海军, 黄风雷. 刚性弹正侵彻钢筋混凝土靶阻力模型 [J]. 兵工学报, 2017, 38(11): 2081–2092. DOI: 10.3969/j.issn.1000-1093.2017.11.001.ZHANG S, WU H J, HUANG F L. Resistance model of rigid projectile penetrating into reinforced concrete target [J]. Acta Armamentarii, 2017, 38(11): 2081–2092. DOI: 10.3969/j.issn.1000-1093.2017.11.001. [7] 周晓松, 梅志远, 张焱冰. 复合材料夹层结构在舰艇碰撞防护中的研究进展 [J]. 爆炸与冲击, 2018, 38(3): 696–706. DOI: 10.11883/bzycj-2016-0303.ZHOU X S, MEI Z Y, ZHANG Y B. Research progress of composite sandwich structure in ship collision protection [J]. Explosion and Shock Waves, 2018, 38(3): 696–706. DOI: 10.11883/bzycj-2016-0303. [8] 谭仪忠, 刘元雪, 张裕, 等. 高寒高海拔多年冻土地区抗侵彻深度研究 [J]. 振动与冲击, 2015, 34(22): 9–12, 23. DOI: 10.13465/j.cnki.jvs.2015.22.002.TAN Y Z, LIU Y X, ZHANG Y, et al. Penetration depth of projectile body into high-cold and high-altitude permafrost area [J]. Journal of Vibration and Shock, 2015, 34(22): 9–12, 23. DOI: 10.13465/j.cnki.jvs.2015.22.002. [9] ZHU Z W, FU T T, ZHOU Z W, et al. Research on Ottosen constitutive model of frozen soil under impact load [J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 137: 104544. DOI: 10.1016/j.ijrmms.2020.104544. [10] ZHANG F L, ZHU Z W, MA W, et al. A unified viscoplastic model and strain rate-temperature equivalence of frozen soil under impact loading [J]. Journal of the Mechanics and Physics of Solids, 2021, 152: 104413. DOI: 10.1016/j.jmps.2021.104413. [11] 刘志强, 柳家凯, 王博, 等. 冻结黏土动态力学特性的SHPB试验研究 [J]. 岩土工程学报, 2014, 36(3): 409–416. DOI: 10.11779/CJGE201403002.LIU Z Q, LIU J K, WANG B, et al. Dynamic characteristics of frozen clay by using SHPB tests [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 409–416. DOI: 10.11779/CJGE201403002. [12] 胡时胜, 王礼立, 宋力, 等. Hopkinson压杆技术在中国的发展回顾 [J]. 爆炸与冲击, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17.HU S S, WANG L L, SONG L, et al. Review of the development of Hopkinson pressure bar technique in China [J]. Explosion and Shock Waves, 2014, 34(6): 641–657. DOI: 10.11883/1001-1455(2014)06-0641-17. [13] 罗飞, 张元泽, 朱占元, 等. 一种青藏高原冻结砂土蠕变本构模型 [J]. 哈尔滨工业大学学报, 2020, 52(2): 26–32. DOI: 10.11918/201810053.LUO F, ZHANG Y Z, ZHU Z Y, et al. Creep constitutive model for frozen sand of Qinghai-Tibet Plateau [J]. Journal of Harbin Institute of Technology, 2020, 52(2): 26–32. DOI: 10.11918/201810053. [14] 牛亚强, 赖远明, 王旭, 等. 基于Martin-Darvidenkov模型的冻结粉质黏土动力特性研究 [J]. 中国公路学报, 2019, 32(8): 58–65, 78. DOI: 10.19721/j.cnki.1001-7372.2019.08.005.NIU Y Q, LAI Y M, WANG X, et al. Dynamic characteristics of frozen silty clay based on Martin-Darvidenkov model [J]. China Journal of Highway and Transport, 2019, 32(8): 58–65, 78. DOI: 10.19721/j.cnki.1001-7372.2019.08.005. [15] ZHANG S J, DU H M, HARBOR J. The Effect of confining pressure and water content on compressive strength and deformation of ice-rich silty sand [J]. Permafrost and Periglacial Processes, 2017, 28(1): 298–305. DOI: 10.1002/ppp.1906. [16] 马芹永, 张经双, 陈文峰, 等. 人工冻土围压SHPB试验与冲击压缩特性分析 [J]. 岩土力学, 2014, 35(3): 637–640. DOI: 10.16285/j.rsm.2014.03.003.MA Q Y, ZHANG J S, CHEN W F, et al. Analysis of SHPB test and impact compression in confining pressure for artificial frozen soil [J]. Rock and Soil Mechanics, 2014, 35(3): 637–640. DOI: 10.16285/j.rsm.2014.03.003. [17] ZHANG H D, ZHU Z W, SONG S C, et al. Dynamic behavior of frozen soil under uniaxial strain and stress conditions [J]. Applied Mathematics and Mechanics, 2013, 34(2): 229–238. DOI: 10.1007/s10483-013-1665-x. [18] 马冬冬, 马芹永, 袁璞, 等. 主动围压状态人工冻结砂土SHPB试验与分析 [J]. 岩土力学, 2017, 38(10): 2957–2961, 2972. DOI: 10.16285/j.rsm.2017.10.024.MA D D, MA Q Y, YUAN P, et al. SHPB tests on artificial frozen sand and its analysis under active confining pressure [J]. Rock and Soil Mechanics, 2017, 38(10): 2957–2961, 2972. DOI: 10.16285/j.rsm.2017.10.024. [19] 马冬冬, 马芹永, 袁璞, 等. 冻结黏土单轴与主动围压状态SHPB试验对比分析 [J]. 振动与冲击, 2017, 36(19): 255–260. DOI: 10.13465/j.cnki.jvs.2017.19.039.MA D D, MA Q Y, YUAN P, et al. Comparison analysis and SHPB tests on artificial frozen clay in uniaxial load and confining pressure states [J]. Journal of Vibration and Shock, 2017, 36(19): 255–260. DOI: 10.13465/j.cnki.jvs.2017.19.039. [20] MA D D, MA Q Y, YUAN P. SHPB tests and dynamic constitutive model of artificial frozen sandy clay under confining pressure and temperature state [J]. Cold Regions Science and Technology, 2017, 136: 37–43. DOI: 10.1016/j.coldregions.2017.01.004. [21] 王礼立. 爆炸/冲击动力学学习研究中的若干疑惑 [J]. 爆炸与冲击, 2021, 41(1): 011401. DOI: 10.11883/bzycj-2020-0415.WANG L L. Some doubts in studying explosion/impact dynamics [J]. Explosion and Shock Waves, 2021, 41(1): 011401. DOI: 10.11883/bzycj-2020-0415. [22] ZHANG F L, ZHU Z W, FU T T, et al. Damage mechanism and dynamic constitutive model of frozen soil under uniaxial impact loading [J]. Mechanics of Materials, 2020, 140: 103217. DOI: 10.1016/j.mechmat.2019.103217. [23] 张龙辉, 张晓晴, 姚小虎, 等. 高应变率下航空透明聚氨酯的动态本构模型 [J]. 爆炸与冲击, 2015, 35(1): 51–56. DOI: 10.11883/1001-1455(2015)01-0051-06.ZHANG L H, ZHANG X Q, YAO X H, et al. Constitutive model of transparent aviation polyurethane at high strain rates [J]. Explosion and Shock Waves, 2015, 35(1): 51–56. DOI: 10.11883/1001-1455(2015)01-0051-06. [24] FU T T, ZHU Z W, ZHANG D, et al. Research on damage viscoelastic dynamic constitutive model of frozen soil [J]. Cold Regions Science and Technology, 2019, 160: 209–221. DOI: 10.1016/j.coldregions.2019.01.017. [25] 马冬冬. 动静组合加载下人工冻土动态力学特性及本构模型研究 [D]. 淮南, 安徽: 安徽理工大学, 2018.MA D D. Study on dynamic mechanical property and constitutive model of artificial frozen soil under coupled static and dynamic load [D]. Huainan, Anhui: Anhui University of Science and Technology, 2018. -






 下载:
下载: