Dynamic response and failure of sandwich beams with graded metal foam core under high-velocity impact
-
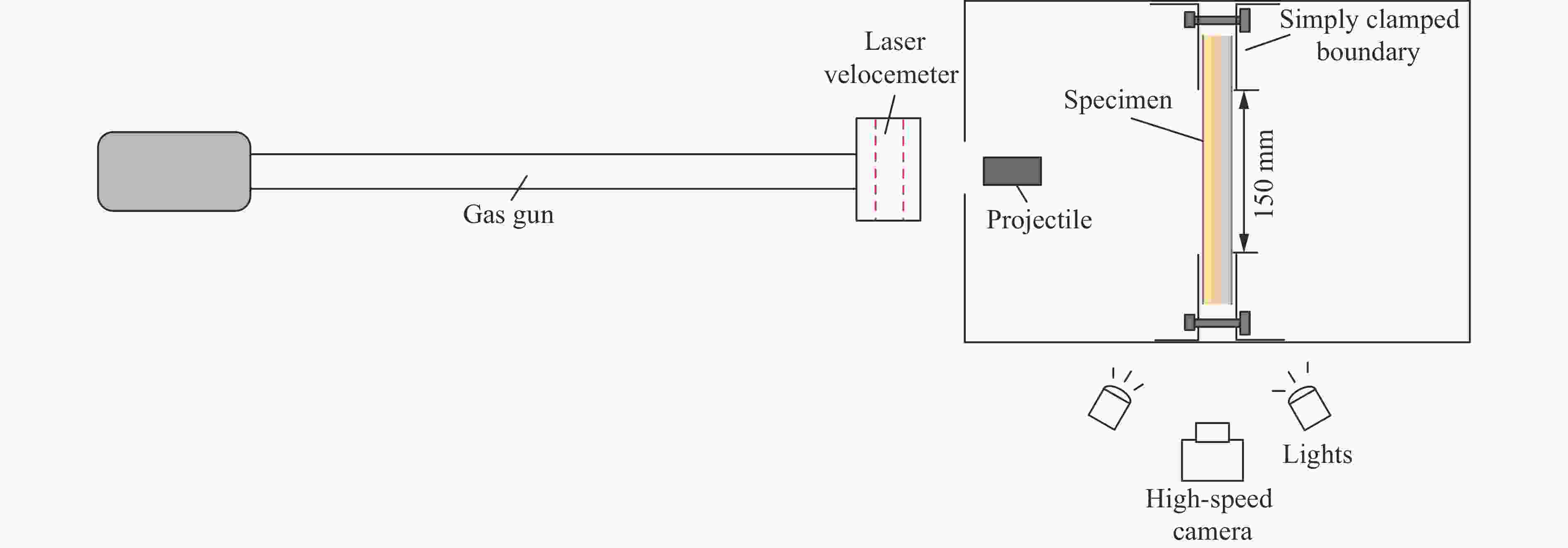
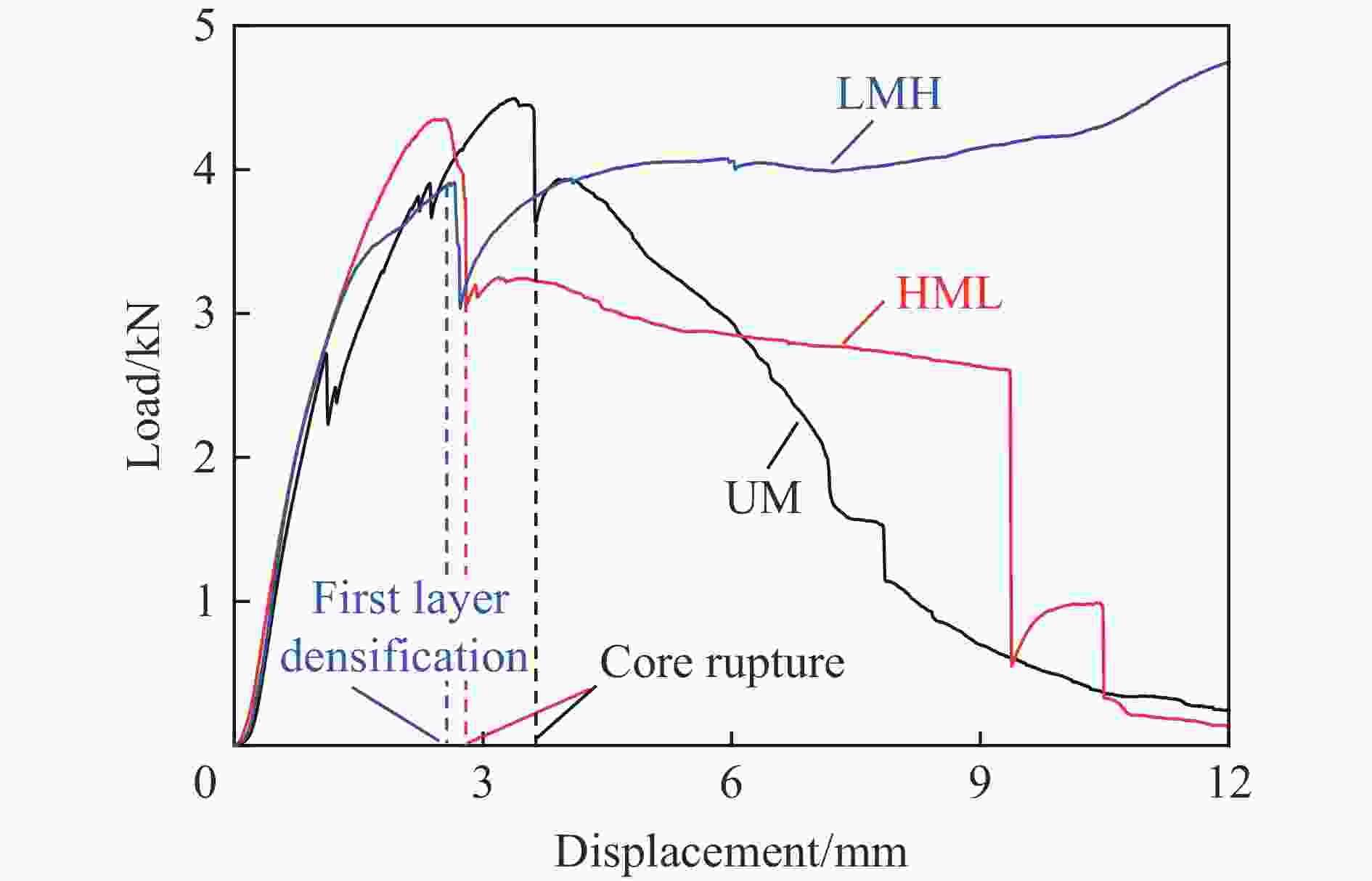
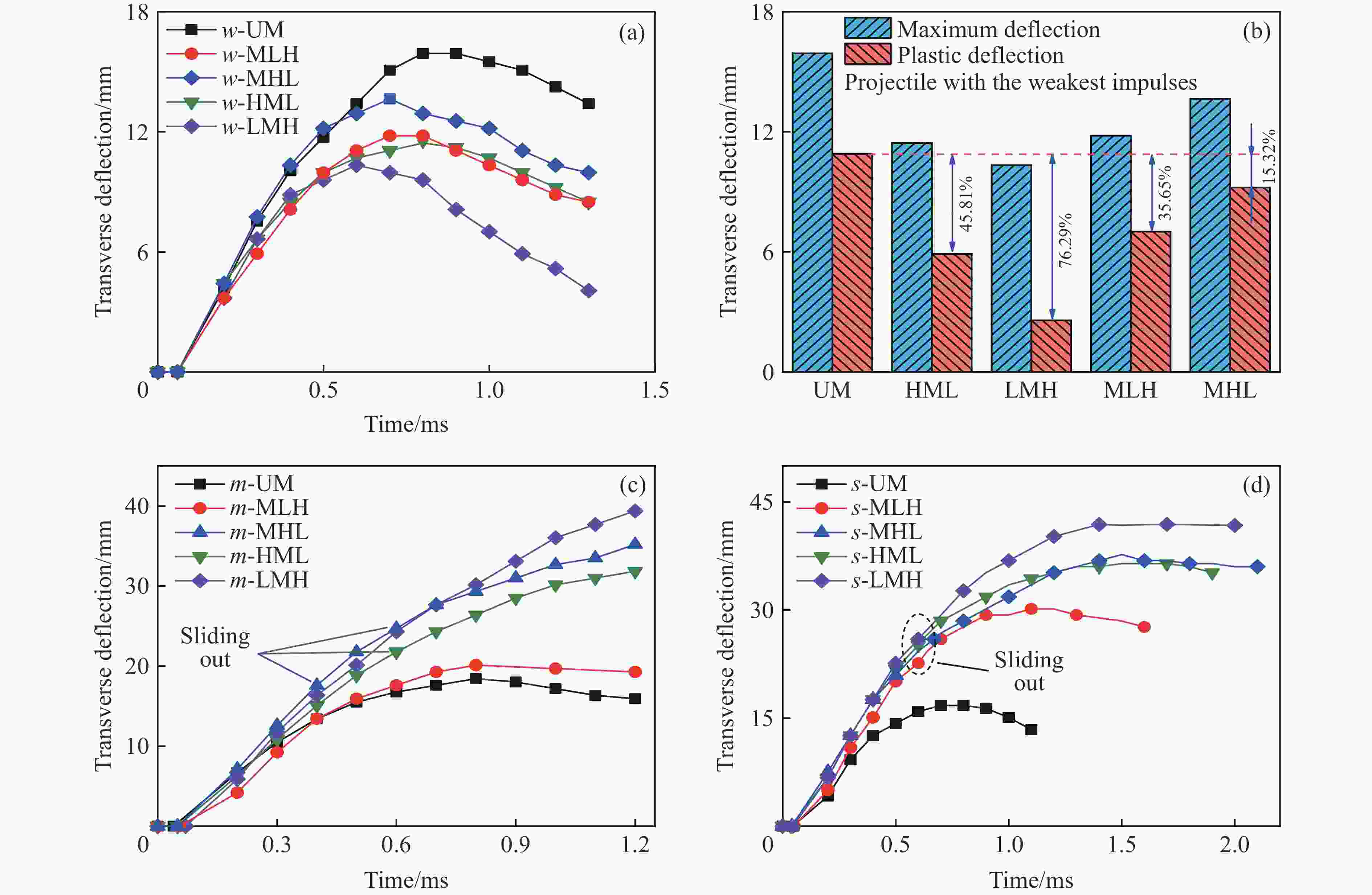
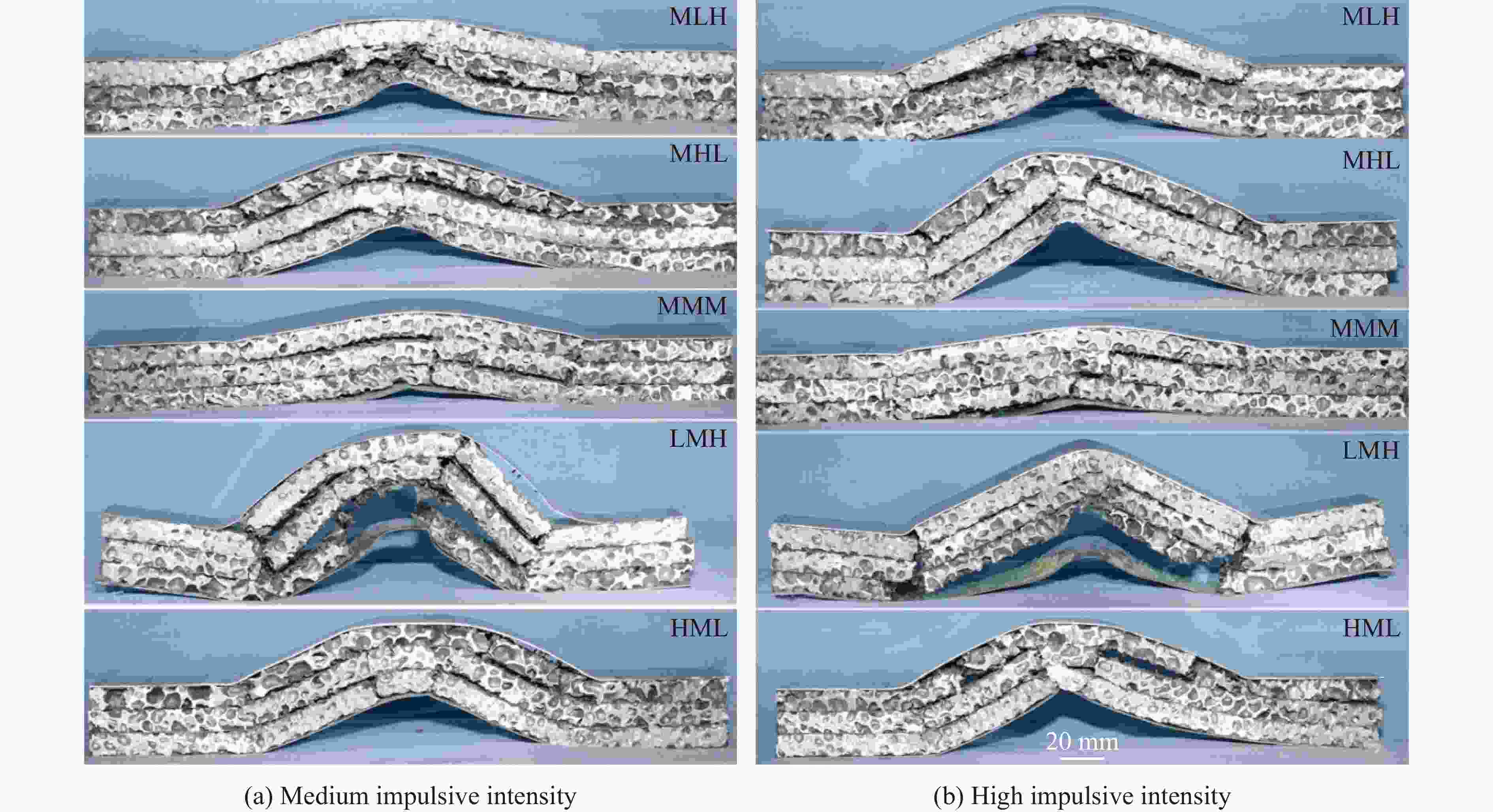
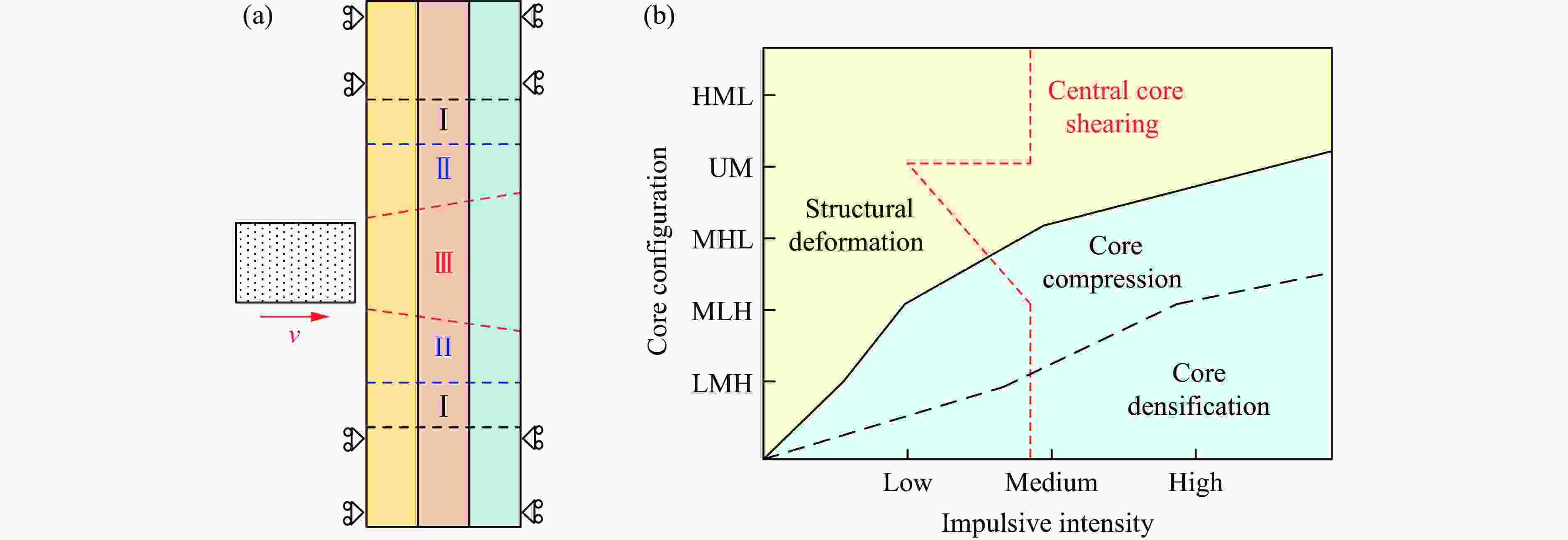
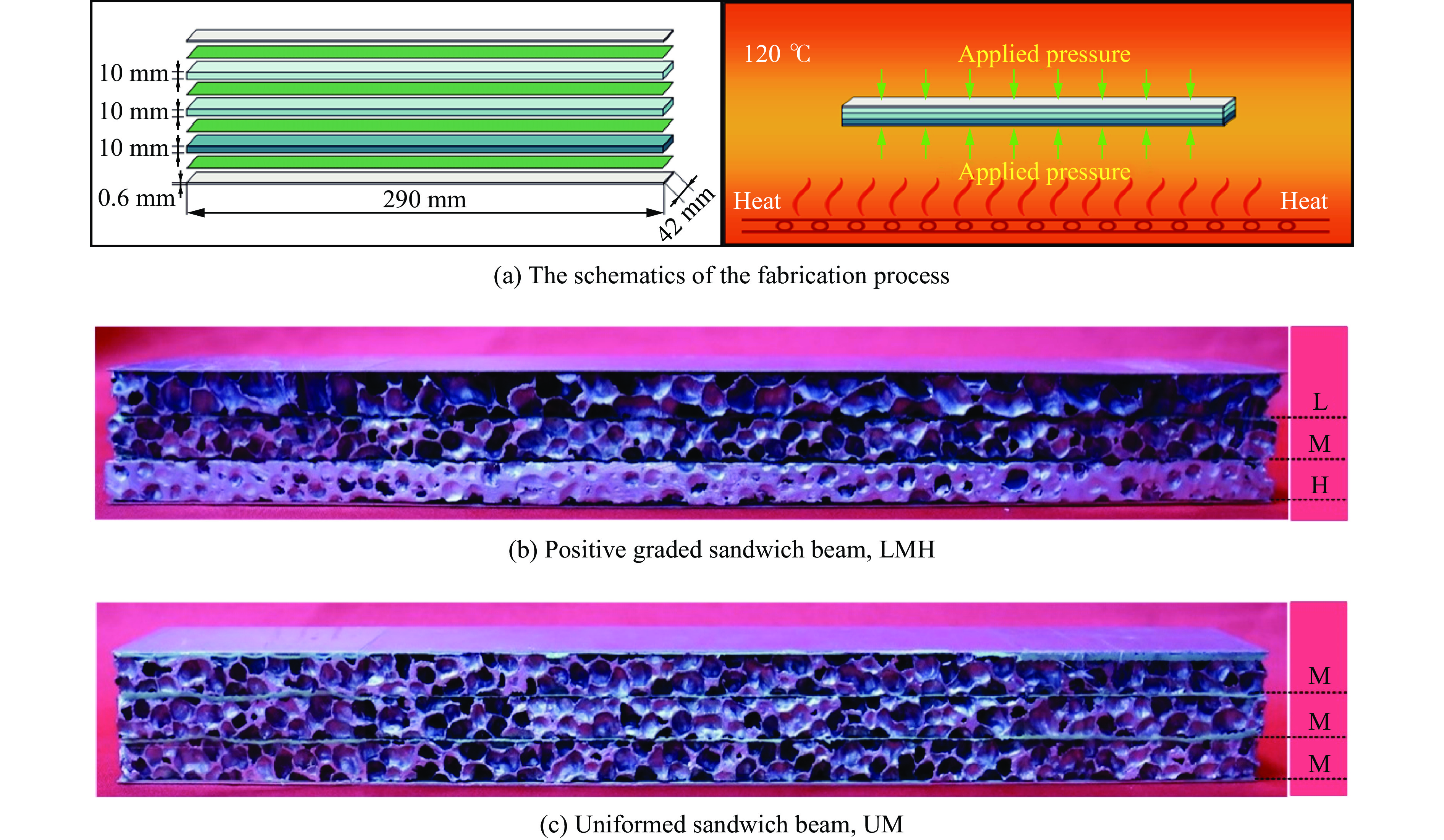
摘要: 采用泡沫弹冲击加载实验对梯度金属泡沫夹芯梁结构开展了不同冲击强度下的动态响应和失效研究，分析了由三种不同密度泡沫铝组成的等面密度的五种不同梯度的夹芯结构在夹支边界条件下的抗高速冲击性能，结合三点弯曲实验，研究梯度效应对夹芯结构抗冲击性能的影响。研究表明：密度梯度对结构的失效过程和失效模式有着明显的影响，且夹芯梁结构的初始失效模式对结构整体响应和主要的能量吸收机制起着主导作用；当冲击条件不足以使得均质芯材发生压缩时，均质及负梯度夹芯结构初始失效模式为整体弯曲变形，低强度芯层位于前两层的梯度结构随着冲击强度的变化出现不同程度的局部芯层压缩；当冲击强度较低时，梯度结构通过丰富的局部失效表现出明显优于均质结构的抗冲击变形能力；当冲击强度大于临界值时，均质结构具有更好的抗冲击变形能力。通过合理地设计密度梯度实现逐层压缩吸能，能够有效的提升防护结构的抗冲击性能。Abstract: The dynamic response and failure of sandwich beams with gradient metal foam core subjected to high-velocity impact are studied experimentally. The impact resistance of five sandwich beams with different density gradient arrangements but the same surface density composed of three aluminum foams with different densities is analyzed. All the sandwich beams are simply-clamped. Combined with the quasi-static three-point bending tests, the impact resistance of the gradient sandwich beams is evaluated in terms of dynamic deformation and failure modes by considering the effects of core density gradient and impulsive intensity. The results show that the density gradient effect significantly influences the dynamic response and failure mode. The initial failure mode plays an important role in the structural response and the predominant energy absorption mechanism. Since the impact condition can not produce the local compression of the medium-density core, the initial failure mode of the uniform and negative gradient sandwich structures is the overall bending deformation, while the local core compression is the initial failure mode of the other structures with weak cores located in the first two layers. When the impulsive intensity is low, the gradient sandwich beam has superior impact resistance to the uniform counterpart. With increasing intensity, once a critical intensity is exceeded, the gradient sandwich beam shows low bending resistance to the uniform counterpart. Therefore, the optimal design of the core density gradient can efficiently improve the impact resistance of the sandwich beams under the high-velocity impact, which is a valuable reference for engineering applications.
-
图 2 泡沫梯度夹芯梁结构高速冲击加载实验装置示意图
Figure 2. Experimental setup for the graded foam sandwich beams
图 3 典型泡沫铝梯度夹芯梁结构三点弯曲失效过程
Figure 3. Failure of typical gradient metal foam sandwich beams under the three-point bending
图 4 典型泡沫铝梯度夹芯梁结构三点弯曲载荷-位移关系
Figure 4. Load-displacement curve of the typical gradient metal foam sandwich beam under the three-point bending
图 5 低速冲击下金属梯度夹芯梁结构动态变形与失效
Figure 5. Dynamic deformation and failure modes of the gradient metal foam sandwich beams under the low impulsive intensity
图 6 中速和高速冲击下金属梯度夹芯梁结构动态变形与失效
Figure 6. Dynamic deformation and failure modes of the gradient metal foam sandwich beams under the medium and high impulsive intensities
图 7 不同冲击速度下梯度夹芯梁结构背板中点动态响应和变形
Figure 7. Central dynamic response and deformation of the gradient metal foam sandwich beams under the impulsive loads
图 8 均质泡沫铝夹芯梁结构低速冲击载荷作用下的失效模式
Figure 8. Failure modes of UM under the low impulsive intensity
图 9 梯度泡沫铝夹芯梁结构低速冲击载荷作用下的失效模式
Figure 9. Failure modes of the gradient metal foam sandwich beams under the low impulsive intensity
图 10 梯度泡沫铝夹芯梁结构冲击载荷作用下的失效模式
Figure 10. Failure modes of the gradient metal foam sandwich beams under the impulsive loads
图 11 梯度夹芯梁结构抗冲击失效模式
Figure 11. Failure modes of the gradient metal foam sandwich beams subjected to high-velocity impact
表 1 金属梯度夹芯结构高速冲击实验初始条件及结果
Table 1. Experimental conditions and results of the graded metal foam sandwich beams
编号 芯层 m0/g v0/
(m·s−1)I0 /
(N·s)wb/
mm编号 芯层 m0/g v0/
(m·s−1)I0 /
(N·s)wb/
mm编号 芯层 m0/g v0/
(m·s−1)I0 /
(N·s)wb/
mmw-UM MMM 21.00 157.0 3.30 10.89 m-UM MMM 21.54 226.4 4.88 12.57 s-UM MMM 19.00 266.3 5.06 9.21 w-HML HML 21.14 160.6 3.39 5.90 m-HML HML 19.14 234.4 4.49 25.97 s-HML HML 19.26 261.4 5.04 26.81 w-LMH LMH 21.83 175.9 3.84 2.58 m-LMH LMH 22.36 229.6 5.13 52.78 s-LMH LMH 21.47 260.8 5.60 23.46 w-MLH MLH 19.95 179.7 3.59 7.01 m-MLH MLH 20.44 240.0 4.91 15.50 s-MLH MLH 21.20 261.6 5.54 31.83 w-MHL MHL 21.29 176.4 3.76 9.22 m-MHL MHL 22.27 233.3 5.20 20.94 s-MHL MHL 22.69 263.5 5.98 38.53 注：(a) wb为塑性变形；(b) 本表中均质梯度（UM）、正梯度（LMH）和负梯度（HML）夹芯结构数据均来自于文献[19]。 
下载: 导出CSV
-
[1] SUN Y, LI Q M. Dynamic compressive behaviour of cellular materials: a review of phenomenon, mechanism and modelling [J]. International Journal of Impact Engineering, 2018, 112: 74–115. DOI: 10.1016/j.ijimpeng.2017.10.006. [2] LIU Z, MEYERS M A, ZHANG Z, et al. Functional gradients and heterogeneities in biological materials: design principles, functions, and bioinspired applications [J]. Progress in Materials Science, 2017, 88: 467–498. DOI: 10.1016/j.pmatsci.2017.04.013. [3] 王根伟, 刘冕, 宋辉, 等. 冲击载荷下径向密度排布对泡沫金属力学性能影响的研究 [J]. 爆炸与冲击, 2020, 40(7): 071401. DOI: 10.11883/bzycj-2019-0403.WANG G W, LIU M, SONG H, et al. Influence of radial density arrangement on mechanical properties of metal foam under impact loading [J]. Explosion and Shock Waves, 2020, 40(7): 071401. DOI: 10.11883/bzycj-2019-0403. [4] 叶楠, 张伟, 黄威, 等. PVC夹芯板在冲击载荷下的动态响应与失效模式 [J]. 爆炸与冲击, 2017, 37(1): 37–45. DOI: 10.11883/1001-1455(2017)01-0037-09.YE N, ZHANG W, HUANG W, et al. Dynamic response and failure mode of PVC sandwich plates subjected to impact loading [J]. Explosion and Shock Waves, 2017, 37(1): 37–45. DOI: 10.11883/1001-1455(2017)01-0037-09. [5] 敬霖, 王志华, 赵隆茂. 多孔金属及其夹芯结构力学性能的研究进展 [J]. 力学与实践, 2015, 37(1): 1–24. DOI: 10.6052/1000-0879-14-180.JING L, WANG Z H, ZHAO L M. Advances in studies of the mechanical performance of cellular metals and related sandwich structures [J]. Mechanics in Engineering, 2015, 37(1): 1–24. DOI: 10.6052/1000-0879-14-180. [6] WANG E, LI Q, SUN G. Computational analysis and optimization of sandwich panels with homogeneous and graded foam cores for blast resistance [J]. Thin-Walled Structures, 2020, 147: 106494. DOI: 10.1016/j.tws.2019.106494. [7] CUI L, KIERNAN S, GILCHRIST M D. Designing the energy absorption capacity of functionally graded foam materials [J]. Materials Science and Engineering A: Structural Materials: Properties, 2009, 507: 215–225. DOI: 10.1016/j.msea.2008.12.011. [8] HUANG W, XU H, FAN Z, et al. Compressive response of composite ceramic particle-reinforced polyurethane foam [J]. Polymer Testing, 2020, 87: 106514. DOI: 10.1016/j.polymertesting.2020.106514. [9] DESHPANDE V S, FLECK N A. Isotropic constitutive models for metallic foams [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(6/7): 1253–1283. DOI: 10.1016/S0022-5096(99)00082-4. [10] DANIEL I M, CHO J M, WERNER B T. Characterization and modeling of stain-rate-dependent behavior of polymeric foams [J]. Composites Part A: Applied Science and Manufacturing, 2013, 45: 70–78. DOI: 10.1016/j.compositesa.2012.10.003. [11] RADFORD D D, MCSHANE G J, DESHPANDE V S, et al. The response of clamped sandwich plates with metallic foam cores to simulated blast loading [J]. International Journal of Solids & Structures, 2006, 43: 2243–2259. [12] QIU X, DESHPANDE V S, FLECK N A. Impulsive loading of clamped monolithic and sandwich beams over a central patch [J]. Journal of the Mechanics and Physics of Solids, 2005, 53: 1015–1046. DOI: 10.1016/j.jmps.2004.12.004. [13] APETRE N A, SANKAR B V, AMBUR D R. Low-velocity impact response of sandwich beams with functionally graded core [J]. International Journal of Solids and Structures, 2006, 43(9): 2479–2496. DOI: 10.1016/j.ijsolstr.2005.06.003. [14] JING L, SU X, CHEN D, et al. Experimental and numerical study of sandwich beams with layered-gradient foam cores under low-velocity impact [J]. Thin-Walled Structures, 2019, 135: 227–244. DOI: 10.1016/j.tws.2018.11.011. [15] ZHANG W, QIN Q, LI K, et al. Effect of stepwise gradient on dynamic failure of composite sandwich beams with metal foam core subject to low-velocity impact [J]. International Journal of Solids and Structures, 2021, 228: 111125. DOI: 10.1016/j.ijsolstr.2021.111125. [16] 苏兴亚, 敬霖, 赵隆茂. 爆炸载荷下分层梯度泡沫铝夹芯板的失效模式与抗冲击性能 [J]. 爆炸与冲击, 2019, 39(6): 063103. DOI: 10.11883/bzycj-2018-0198.SU X Y, JING L, ZHAO L M. Failure modes and shock resistance of sandwich panels with layered-gradient aluminum foam cores under air-blast loading [J]. Explosion and Shock Waves, 2019, 39(6): 063103. DOI: 10.11883/bzycj-2018-0198. [17] ZHOU X F, JING L. Deflection analysis of clamped square sandwich panels with layered-gradient foam cores under blast loading [J]. Thin-Walled Structures, 2020, 157: 107141. DOI: 10.1016/j.tws.2020.107141. [18] RADFORD D D, DESHPANDE V S, FLECK N A. The use of metal foam projectiles to simulate shock loading on a structure [J]. International Journal of Impact Engineering, 2005, 31(9): 1152–1171. DOI: 10.1016/j.ijimpeng.2004.07.012. [19] FANG B P, HUANG W, XU H J, et al. High-velocity impact resistance of stepwise gradient sandwich beams with metal foam cores [J]. Thin-Walled Structures, 2022, 181: 110054. DOI: 10.1016/j.tws.2022.110054. -
计量
- 文章访问数: 695
- HTML全文浏览量: 162
- PDF下载量: 295
- 被引次数: 0