低温和低压环境下炸药爆炸冲击波的传播特性

李瑞; 李孝臣; 汪泉; 袁玉红; 洪晓文; 黄寅生

doi:10.11883/bzycj-2022-0188

低温和低压环境下炸药爆炸冲击波的传播特性

doi: 10.11883/bzycj-2022-0188

李瑞^{1, 2,},
李孝臣²,
汪泉^2, ,,
袁玉红³,
洪晓文⁴,
黄寅生³

1.
安徽理工大学煤炭安全精准开采国家地方联合工程研究中心，安徽淮南 232001
2.
安徽理工大学化学工程学院，安徽淮南 232001
3.
南京理工大学化学与化工学院，江苏南京 210094
4.
内蒙金属材料研究所，山东烟台 264003

基金项目: 国家自然科学基金（11872002）；安徽省自然科学基金（2208085QA26）；安徽理工大学煤炭安全精准开采国家地方联合工程研究中心开放基金（EC2021015）；安徽理工大学校级重点项目（xjzd2020-08）

详细信息

作者简介:
李　瑞（1987－　），男，博士，讲师，lirui_89@126.com

通讯作者:
汪　泉（1980－　），男，博士，教授，博士生导师，wqaust@163.com

中图分类号: O382.1; TJ55
计量
- 文章访问数: 1028
- HTML全文浏览量: 310
- PDF下载量: 220
- 被引次数: 4
出版历程
- 收稿日期: 2022-05-01
- 修回日期: 2022-06-30
- 网络出版日期: 2022-08-07
- 刊出日期: 2023-02-25

Propagation characteristics of blast wave in diminished ambient temperature and pressure environments

1.
Joint National-Local Engineering Research Centre for Safe and Precise Coal Mining, Anhui University of Science and Technology, Huainan 232001, Anhui, China
2.
School of Chemical Engineering, Anhui University of Science and Technology, Huainan 232001, Anhui, China
3.
School of Chemistry and Chemical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
4.
Inner Mongolia Metal Material Research Institute, Yantai 264003, Shandong, China

摘要

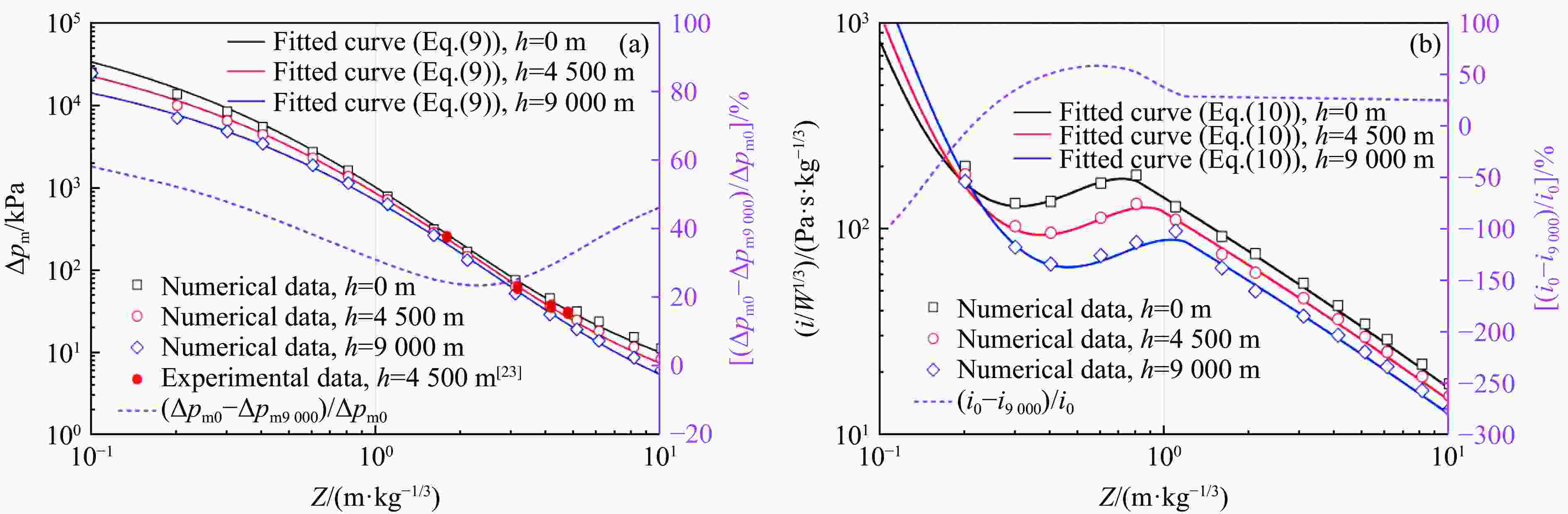
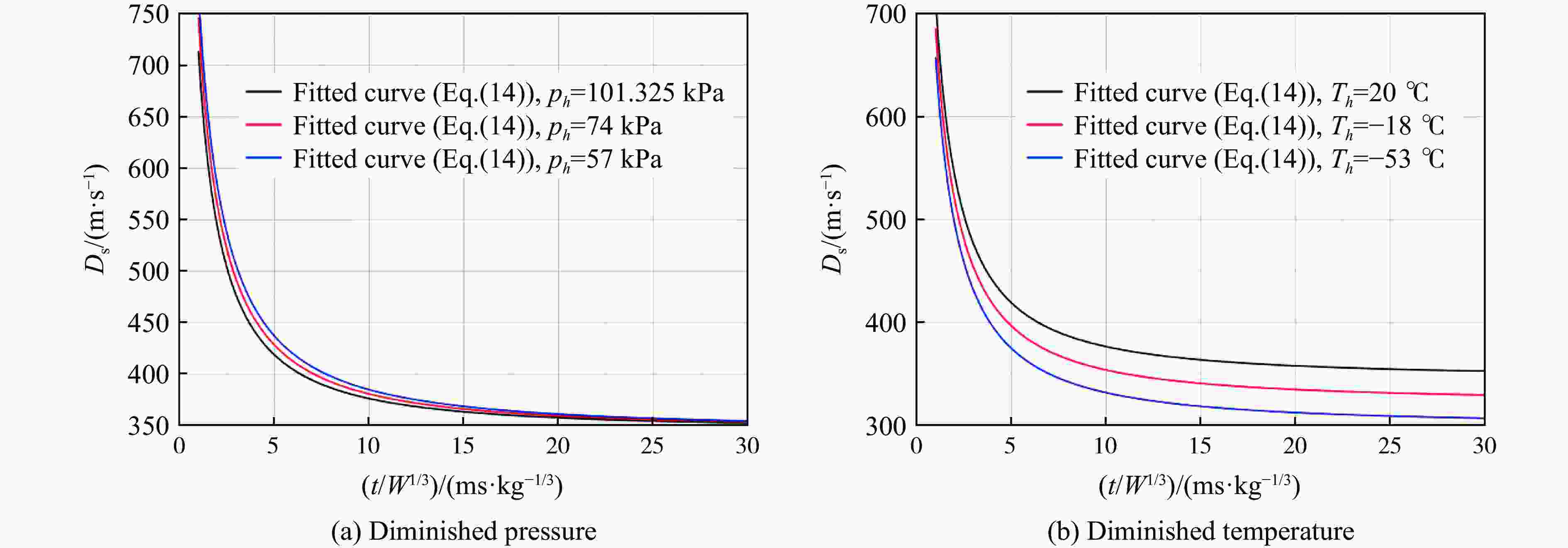
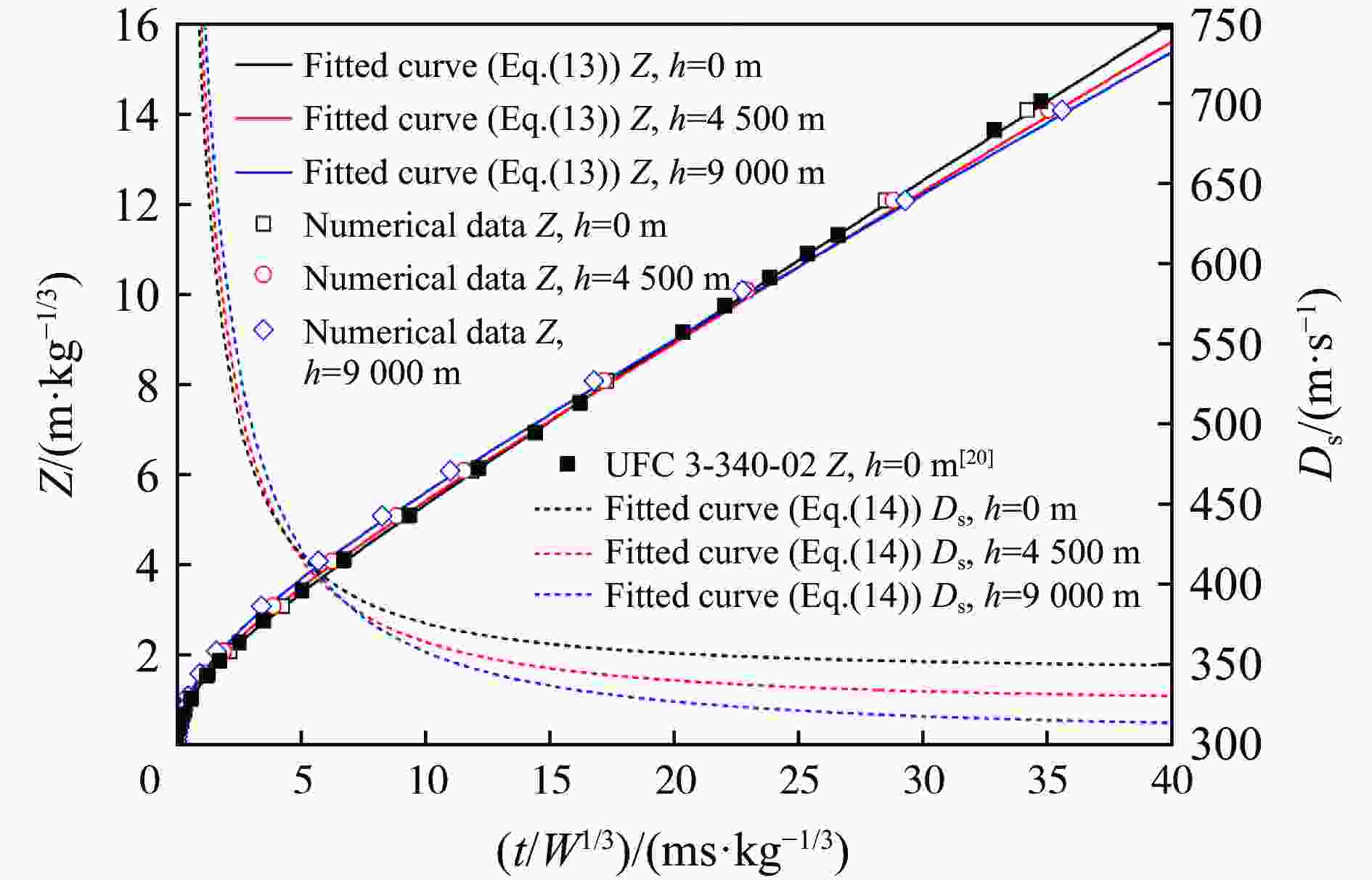
摘要: 针对高海拔或高空的低温、低压环境对炸药爆炸冲击波传播的影响，利用量纲分析理论和AUTODYN有限元软件，研究了低温、低压及海拔高度对炸药爆炸冲击波参量（峰值超压、比冲量和波阵面运动轨迹）的影响规律，建立了相应的计算公式，并通过数值模拟和实验数据进行了对比验证。结果表明，该计算公式可以有效预测低温和低压环境下炸药爆炸冲击波参量。环境压力降低，爆炸冲击波峰值超压和爆炸远场（比例距离Z>0.2 m/kg^1/3）比冲量减小，冲击波传播速度增大。环境温度降低，冲击波比冲量增大，传播速度降低，峰值超压影响不大。海拔高度在0~9 000 m范围内，每升高1000 m冲击波峰值超压和爆炸远场比冲量分别平均降低约3.9%和3.2%。海拔升高，爆炸近场冲击波传播速度升高，爆炸远场冲击波传播速度则降低。高海拔环境下低压对冲击波峰值超压和比冲量的影响大于低温，爆炸近场冲击波传播速度取决于低压的影响，爆炸远场冲击波传播速度取决于低温的影响。
- 爆炸冲击波 /
- 高海拔 /
- 低温环境 /
- 低压环境 /
- 传播特性
Abstract: The effects of different diminished ambient pressure, temperature and altitude from sea level on blast wave parameters (overpressure, impulse and wave front trajectory) were investigated by employing the dimensional analysis theory and the AUTODYN software. Meanwhile, the relationship equations between the blast wave parameters with the diminished pressure and temperature were established, which were verified by numerical simulations and experimental data. Results indicate that the equations can evaluate the blast wave parameters at diminished temperature and pressure effectively. It is noted that the blast wave overpressure and far-field (scaled distance Z>0.2 m/kg^1/3) impulse decrease, but the propagation velocity increases, as the ambient pressure decreases. The blast wave impulse increases, and the propagation velocity decreases, but has little effect on the overpressure, as the ambient temperature decreases. It is shown that when the altitude increases by 1000 m in the range from 0 to 9000 m above sea level, the overpressure and far-field impulse of the blast wave decrease in average by about 3.9% and 3.2%. In addition, the blast wave propagation velocity in the near field increases, but it in the farfield decreases with the altitude increase. The influences of the diminished pressure on the blast wave overpressure and impulse are greater than those of the diminished temperature at high altitudes. The blast wave propagation velocity depends on the diminished pressure in the near field, but on the diminished temperature in the far field.
- blast wave /
- high altitude /
- diminished temperature /
- diminished pressure /
- propagation characteristics

HTML全文

混凝土的耐久性直接关系到建筑结构的寿命及安全性和稳定性。在威胁混凝土结构耐久性的诸多因素中，盐腐蚀尤为突出。盐腐蚀多发生于滨海地区和盐渍土地区。地处滨海区域的建筑或直接建于海水中的混凝土结构，常年经受海水的浸泡和冲刷，遭受海水中Cl^-和SO₄^2-的侵蚀；在我国西部盐渍土区域，如新疆、甘肃、青海、宁夏等地，土壤中SO₄^2-的质量浓度最高可达4 200 mg/L，高出我国沿海海水中SO₄^2-约1倍，处于该地区的建筑，尤其是地下混凝土结构，受盐离子的侵蚀十分严重。Cl^-对混凝土保护层的腐蚀较为严重，可致其脱落，引起内部钢筋锈蚀；硫酸盐侵入混凝土内部引发石膏腐蚀和钙矾石腐蚀，导致混凝土内部结构发生膨胀破坏，明显弱化其各项静/动力学性能。虽然目前关于盐对混凝土的腐蚀研究较多，但是大多集中于静态力学性能^[1-5]、离子扩散^[6-8]及静态损伤模型^[9-11]等，对其在高应变率下的性能测试及动态本构模型仍需深入研究。

基于此，本文中利用∅100 mm分离式霍普金森压杆(split Hopkinson pressure bar，SHPB)实验装置，对受氯盐和硫酸盐腐蚀的混凝土进行动态力学性能研究，结合宏观唯象损伤统计理论和Weibull分布思想，建立混凝土受盐腐蚀后的动态统计损伤本构模型，并对模型进行验证。

1. 实验

1.1 材料和试件

制作混凝土试件所用的材料包括：42.5 R级普通硅酸盐水泥，由硅酸盐水泥熟料、质量分数为6%~20%的少量氧化物、适量磨细石膏等材料组成；石灰岩碎石，堆积密度为1.62 kg/L，粒径范围为5~20 mm；灞河中砂，堆积密度为1.5 kg/L，细度模数为2.8；自来水；F类(低钙)Ⅰ级粉煤灰。混凝土的设计强度为C30，试件尺寸为∅100 mm×50 mm，配合比如表 1所示。

表 1 混凝土配合比

Table 1. Mix proportions of concrete

kg/m³
水泥	水	灞河中砂	石灰岩碎石	粉煤灰
338	215	643	1 144	60

下载: 导出CSV

| 显示表格

试件浇筑完毕后在室内静置24 h后脱模，然后立即置于养护箱内，进行为期28 d的标准养护。

1.2 动态压缩实验

本实验设置两组腐蚀环境：氯盐和硫酸盐。将养护后的试件分别置于质量分数均为15%的NaCl和Na₂SO₄溶液中浸泡，腐蚀60 d后，利用∅100 mm的SHPB实验装置测试其在不同应变率下的动态力学性能。同时，设置一组空白对照组，该组试件不浸泡任何溶液，其余外部环境均相同。为便于分析，将浸泡于NaCl溶液和Na₂SO₄溶液中的试件分别标记为S1组、S2组，对照组标记为N组。

2. 实验结果

2.1 应力-应变曲线

在不同应变率下，各组试件的动态应力-应变(σ -ε)曲线如图 1所示。由图 1可知：随着应变率的升高，峰值应力逐渐增加，具有显著的应变率效应；同时应力-应变曲线的下降段总体上随着应变率的升高而逐渐向高应变方向移动，说明试件的变形程度不断增大。

图 1 3组混凝土试样的动态应力-应变曲线

Figure 1. Dynamic stress-strain curves of three groups of concrete specimens

下载: 全尺寸图片幻灯片

2.2 动态抗压强度

动态抗压强度(即峰值应力)为试件破坏时的应力，是衡量材料在动荷载作用下的强度规律的重要力学性能指标，直接反映材料的动力特性。为各组混凝土试件在不同冲击荷载作用下动态抗压强度f_{c, d}与平均应变率 ${\bar {\dot \varepsilon }}$ 的关系图。观察可知，f_{c, d}与 ${\bar {\dot \varepsilon }}$ 满足线性规律，对其进行线性拟合，可以得到如下关系式：

${\rm{N}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{c,d}}}} = 11.775\;6 + 0.584\;9\bar {\dot \varepsilon} ,\;\;\;{R^2} = 0.983\;2$

(1)

${\rm{S1}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{c}},{\rm{d}}}} = 11.3548 + 0.4577\bar {\dot \varepsilon} ,\quad {R^2} = 0.9066$

(2)

${\rm{S2}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{c}},{\rm{d}}}} = 26.1249 + 0.3173\bar {\dot \varepsilon} ,\quad {R^2} = 0.7692$

(3)

图 2 动态抗压强度-平均应变率曲线

Figure 2. Dynamic compressive strength vs. average strain rate

下载: 全尺寸图片幻灯片

由图 2以及式(1)~式(3)可知：随着应变率的升高，各组试件的f_{c, d}明显增大，且N组试件的f_{c, d}的增长率(拟合直线斜率)最大，即其应变率敏感性最强，S1组试件次之，S2组试件最小；相比于N组试件，S1组和S2组试件的f_{c, d}均有不同程度的下降，且S1组试件的降幅大于S2组。

测得N组、S1组和S2组混凝土试件的静态抗压强度(f_{c, s})分别为42.65、32.51和35.33 MPa。定义动态强度增长因子I：动态抗压强度f_{c, d}与静态抗压强度f_{c, s}的比值，即I=f_{c, d}/f_{c, s}。为I与应变率对数lg ${\bar {\dot \varepsilon }}$ 的关系图，对其进行线性拟合，得到：

${\rm{N}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;I = - 3.3168 + 2.4802\lg \bar {\dot \varepsilon} ,\quad {R^2} = 0.9562$

(4)

${\rm{S1}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;\;I = - 3.6205 + 2.6917\lg \bar {\dot \varepsilon} ,\quad {R^2} = 0.8615$

(5)

${\rm{S2}}\;组\;\;\;\;\;\;\;\;\;\;\;\;\;I = - 1.2031 + 1.4261\lg \bar {\dot \varepsilon} ,\quad {R^2} = 0.9424$

(6)

图 3 动态强度增长因子-平均应变率对数曲线

Figure 3. Dynamic increase factor vs. the logarithm of average strain rate

下载: 全尺寸图片幻灯片

观察图 3可知：对于3组试件，其动态强度增长因子I的线性相关性均较强；N组试件的I最小；S1组试件的I在较低的应变率下略低于S2组，而在较高的应变率下高于S2组。

试件被NaCl溶液腐蚀后，Cl^-与混凝土内部晶体或胶凝体发生一系列化学反应，破坏混凝土内部物质组成和结构，改变了原有水化产物的性质，导致水化硅酸钙胶凝体与水泥石的黏结性能下降，致使混凝土强度降低。Na₂SO₄溶液渗入混凝土内部后，同样产生结晶体，填充于混凝土内部孔隙，当结晶体累积到一定量后，对混凝土内部进行挤压，产生内应力；同时，当SO₄^2-进入混凝土内部后，与氢氧化钙和水化铝酸钙发生反应，生成钙矾石和石膏，反应后体积明显增大，亦产生内应力，严重时引发混凝土产生由内向外的裂缝，破坏骨料与水泥石的黏结，降低混凝土强度。图 4显示了通过扫描电镜(scanning electron microscope，SEM)观测的各组试件微观形貌。从图 4可以看出：N组试件因未受任何腐蚀，随着时间的增长，水化产物C─S─H凝胶逐渐增多，致密性较大，微观缺陷和损伤较小，强度持续增加；对于被盐腐蚀的试件(S1组和S2组)，其表面的絮状结晶体较多，且排列紧密，形成一层致密的晶体层，使裂缝内部产生一定挤压应力，致使试件的抗压强度较N组试件有所下降。

图 4 3组混凝土试样的扫描电镜图像

Figure 4. SEM images of three groups of concrete specimens

下载: 全尺寸图片幻灯片

3. 动态统计损伤本构模型

3.1 本构模型的构建

由于混凝土内部存在微裂纹、微孔洞等初始损伤，且裂纹密度和应变均服从Weibull分布，因此将混凝土视为连续介质，结合连续损伤力学，基于统计理论，建立统计损伤本构模型，即：

$\sigma=E \varepsilon(1-D)$

(7)

式中：E为混凝土无损状态下的弹性模量，D为损伤变量。

混凝土内部微裂纹密度和应变均服从Weibull分布，概率密度函数φ(ε)的表达式为^[12]：

$\varphi(\varepsilon)=\frac{m}{a}\left(\frac{\varepsilon}{a}\right)^{m-1} \exp \left[-\left(\frac{\varepsilon}{a}\right)^{m}\right]$

(8)

式中：a、m是与材料物理力学性质相关的系数。

3.2 模型参数的确定

根据连续损伤力学理论^[13]，可将混凝土视为多个“微元体”的组合，同时假定每个“微元体”所受的应力和损伤参量连续且均匀分布。设混凝土内部所有“微元体”的数量为N，受荷载作用后被破坏的“微元体”数为n，则统计损伤变量D定义为：

$D=n / N$

(9)

因此，在某一应变区间[ε，ε+dε]内，已破坏的“微元体”数为Nφ(ε)dε。当混凝土应变为ε时，已破坏的“微元体”数为^[14]：

$n(\varepsilon ) = \int_0^\varepsilon N \varphi (\varepsilon ){\rm{d}}\varepsilon = \int_0^\varepsilon N \frac{m}{a}{\left( {\frac{\varepsilon }{a}} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{\varepsilon }{a}} \right)}^m}} \right]{\rm{d}}\varepsilon = N\left\{ {1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{a}} \right)}^m}} \right]} \right\}$

(10)

将式(10)代入式(8)，可得混凝土的统计损伤演化方程：

$D = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{a}} \right)}^m}} \right]$

(11)

将式(11)代入式(7)，则本构模型变为：

$\sigma=E \varepsilon(1-D)=E \varepsilon \exp \left[-\left(\frac{\varepsilon}{a}\right)^{m}\right]$

(12)

在混凝土静态应力-应变曲线的上升段选取两点A、B，所对应的应力σ_A、σ_B分别为峰值强度的40%和60%，则此两点的斜率即为所需的弹性模量：

$E_{\mathrm{C}}=\frac{\sigma_{B}-\sigma_{A}}{\varepsilon_{B}-\varepsilon_{A}}$

(13)

式中：ε_A、ε_B分别表示A、B两点的应变。根据式(13)，可确定N组、S1组和S2组的弹性模量分别为43.52、35.79和36.62 GPa。

因此，只需再确定材料的物理力学性能参数a和m，即可完全确定该本构模型。由式(12)可得：

$\frac{\sigma}{E \varepsilon}=\exp \left[-\left(\frac{\varepsilon}{a}\right)^{m}\right]$

(14)

对式(14)等号两边取两次对数，得：

$\ln \left[-\ln \left(\frac{\sigma}{E \varepsilon}\right)\right]=m \ln \varepsilon-m \ln a$

(15)

令x=ln ε，y=ln[－ln(σ/Eε)]，则式(15)变为：

$y=m x-m \ln a$

(16)

基于各组混凝土试件的动态应力-应变曲线，可得本构模型参数a和m，见表 2。对a和m分别进行非线性拟合，得到其与平均应变率的关系：

${\rm{N}}\;组\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} a = - 230.9749 + 9.6460\bar {\dot \varepsilon} - 0.1308{{\bar {\dot \varepsilon} }^2} + 5.7874 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.9968\\ m = - 6.5354 + 0.2746\bar {\dot \varepsilon} - 0.0036{{\bar {\dot \varepsilon} }^2} + 0.1571 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.9708 \end{array} \right.$

(17)

${\rm{S1}}\;组\;\;\;\;\;\;\;\left\{ \begin{array}{l} a = - 367.7624 + 13.1099\bar {\dot \varepsilon} - 0.1503{{\bar {\dot \varepsilon} }^2} + 5.6978 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.8265\\ m = - 10.3671 + 0.3768\bar {\dot \varepsilon} - 0.0043{{\bar {\dot \varepsilon} }^2} + 0.1620 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.9958 \end{array} \right.$

(18)

${\rm{S2}}\;组\;\;\;\;\;\;\;\left\{ \begin{array}{l} a = 1.0190 - 0.0572\bar {\dot \varepsilon} + 0.0009{{\bar {\dot \varepsilon} }^2} - 0.0242 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.9945\\ m = 0.2623 - 0.0102\bar {\dot \varepsilon} + 0.0002{{\bar {\dot \varepsilon} }^2} - 0.0089 \times {10^{ - 4}}{{\bar {\dot \varepsilon} }^3},\quad {R^2} = 0.9824 \end{array} \right.$

(19)

表 2 不同应变率下模型参数

Table 2. Model parameters at different strain rates

样品组	${\bar {\dot \varepsilon }}$ /s^-1	a/10^-5	m	样品组	${\bar {\dot \varepsilon }}$ /s^-1	a/10^-5	m	样品组	${\bar {\dot \varepsilon }}$ /s^-1	a/10^-5	m
	55.07	3.68	0.162		62.73	13.01	0.190		29.45	0.04	0.102
	67.86	20.61	0.211		81.05	57.64	0.285		51.76	0.24	0.110
N	78.63	6.72	0.173	S1	92.98	11.05	0.171	S2	62.79	1.19	0.145
	91.41	0.10	0.094		102.95	2.17	0.096		73.37	4.52	0.169
	109.43	171.01	0.431		111.77	12.89	0.146		116.58	20.31	0.212

下载: 导出CSV

| 显示表格

将式(17)~式(19)分别代入式(12)，即可得到最终的动态统计损伤本构模型。

3.3 应变率效应修正

在2.2节中对试件的I与lg ${\bar {\dot \varepsilon }}$ 间的关系进行了线性拟合，拟合公式的形式为I=α+β lg ${\bar {\dot \varepsilon }}$ 。但是在实际工程应用中却习惯将其写成I=1+C lg ${\bar {\dot \varepsilon }}$ 的形式，其中C为应变率系数，因此需将此前的公式进行转换，如表 3所示。

表 3 动态强度增长因子与平均应变率对数的关系

Table 3. Relation of dynamic compressive strength increase factor with the logarithm of average strain rate

样品组	拟合公式	转换后的拟合公式	C
N	I=-3.316 8+2.480 2 lg ${\bar {\dot \varepsilon }}$	I=1-0.747 8 lg ${\bar {\dot \varepsilon }}$	-0.747 8
S1	I=-3.620 5+2.691 7 lg ${\bar {\dot \varepsilon }}$	I=1-0.743 5 lg ${\bar {\dot \varepsilon }}$	-0.743 5
S2	I=-1.203 1+1.426 1 lg ${\bar {\dot \varepsilon }}$	I=1-1.185 4 lg ${\bar {\dot \varepsilon }}$	-1.185 4

下载: 导出CSV

| 显示表格

综上所述，考虑应变率强化效应的动态统计损伤本构模型为：

$\sigma=E \varepsilon(1-D) K_{\varepsilon}$

(20)

式中：K_ε为应变率强化因子，K_ε=-C lg ${\bar {\dot \varepsilon }}$ 。最终的动态统计损伤本构模型的表达式为：

$\sigma = E\varepsilon \exp \left[ { - {{\left( {\frac{\varepsilon }{a}} \right)}^m}} \right]( - C\lg \bar {\dot \varepsilon} )$

(21)

3.4 模型验证

至此，动态统计损伤本构模型已构建完成，将实际的动态应力-应变曲线(部分)与计算曲线进行对比，如图 5所示。可以看出，各组试件的应力-应变实验曲线与相应的模型曲线吻合较好，虽然存在一定的偏差，但整体上能够较准确地描述各组混凝土试件在冲击荷载作用下的动态力学响应规律。

图 5 实验曲线与模型曲线的对比

Figure 5. Comparison of experimental and model curves

下载: 全尺寸图片幻灯片

模型中，将用于确定参数a、m及C值的动态应力-应变曲线记为基准曲线，因此图 5反映的是基准实验曲线与本构模型曲线的拟合程度。为进一步对模型进行验证，将模型曲线与各组非基准曲线作进一步的对比分析。分别取N组、S1组和S2组的非基准曲线，对应的应变率分别为95.79、67.15和82.64 s^-1，根据式(17)~式(19)计算得到a、m值，分别为：N组，a=1.207×10^-4，m=0.183；S1组，a=7.367×10^-4，m=0.360；S2组，a=0.774×10^-4，m=0.198。再由表 3及式(21)计算得到各应变率下的模型曲线，并与实际曲线进行对比，如图 6所示。由图 6可知，各组试样的应力-应变实验曲线与模型曲线同样具有较高的吻合度。由于该本构模型是基于统计理论、Weibull分布函数及部分假定构建而成，而试件的应力-应变行为受试件本身尺寸、内部结构及外界环境等影响，因此模型曲线与实验曲线之间的偏差在可接受范围之内。

图 6 模型验证

Figure 6. Model verification

下载: 全尺寸图片幻灯片

4. 结论

利用∅100 mm SHPB实验装置，对经质量分数均为15%的NaCl和Na₂SO₄溶液浸泡腐蚀的混凝土的动态力学性能进行了研究，建立并验证了混凝土腐蚀后的动态统计损伤本构模型，主要结论如下：

(1) 各组试件的动态抗压强度和动态强度增长因子均具有较强的应变率相关性，而受盐腐蚀后，各组试件的动态抗压强度均有不同程度的下降，且NaCl腐蚀试件的降幅大于Na₂SO₄腐蚀试件；

(2) 基于宏观唯象损伤统计理论和Weibull分布思想，将混凝土视为连续介质，以混凝土内部“微元体”定义损伤，构建动态统计损伤本构模型，各参数的物理意义明确，参数a和m精确控制着拟合曲线的形状、弯曲度和幅值等，同时计入应变率强化效应修正系数C；

(3) 动态统计损伤本构模型曲线与实验曲线的拟合度较高，能够较准确地描述各组混凝土试件在冲击荷载作用下的动态力学响应规律，模型曲线与实验曲线之间存在的偏差在可接受范围之内。

图 1 一维球对称楔形模型

Figure 1. A one-dimensional spherical symmetric wedge model

下载: 全尺寸图片幻灯片

图 2 不同网格尺寸的冲击波超压-时程曲线比较

Figure 2. Comparison of overpressure time history curves for different cell sizes

下载: 全尺寸图片幻灯片

图 3 标准大气环境下冲击波参量的理论、数值模拟与实验结果对比

Figure 3. Comparison among theoretical, numerical and experimental blast wave parameters in standard atmospheric environment

下载: 全尺寸图片幻灯片

图 4 低压环境下冲击波参量的理论、数值模拟与实验数据对比

Figure 4. Comparison among theoretical, numerical and experimental shock wave parameters in diminished pressure environments

下载: 全尺寸图片幻灯片

图 5 低温环境下冲击波参量的理论、数值模拟结果与实验结果的对比

Figure 5. Comparison among theoretical, numerical and experimental shock wave parameters in diminished temperature environments

下载: 全尺寸图片幻灯片

图 6 高海拔环境下冲击波参量的理论、数值模拟结果与实验结果的对比

Figure 6. Comparison among theoretical, numerical and experimental shock wave parameters in high-altitude environment

下载: 全尺寸图片幻灯片

图 7 不同低压和低温环境下爆炸冲击波波阵面的运动轨迹

Figure 7. Motion trajectories of blast wave in diminished pressure and temperature environments

下载: 全尺寸图片幻灯片

图 8 不同低压和低温环境下爆炸冲击波的传播速度

Figure 8. Propagation velocities of blast waves in diminished pressure and temperature environments

下载: 全尺寸图片幻灯片

图 9 不同海拔高度下爆炸冲击波波阵面运动轨迹及传播速度的理论、数值模拟结果与实验结果的对比

Figure 9. Theoretical, numerical and experimental comparison of shock wave parameters in different high-altitude environments

下载: 全尺寸图片幻灯片

表 1 爆炸冲击波传播问题中物理量的量纲幂次

Table 1. Dimensional power coefficients of physical quantities in the problem of blast wave propagation

基本量纲 E p ρ r Δp_m i t

M 1 1 1 0 1 1 0
L 2 −1 −3 1 −1 −1 0
T −2 −2 0 0 −2 −1 1

下载: 导出CSV

表 2 爆炸冲击波传播问题中物理量的量纲幂次（初等变换）

Table 2. Dimensional power coefficients of physical quantities in the problem of blast wave propagation (elementary transformation)

参考物理量 E p ρ r Δp_m i t

E 1 0 0 1/3 0 1/3 1/3
p 0 1 0 −1/3 1 1/6 −5/6
ρ 0 0 1 0 0 1/2 1/2

下载: 导出CSV

表 3 不同海拔高度下的大气参数

Table 3. Atmospheric parameters at different altitudes

h/m T_h/K p_h/kPa ρ_h/(kg∙m⁻³)

0 288.15 101.325 1.225
4 500 258.90 57.728 0.777
9 000 229.65 30.742 0.466

下载: 导出CSV

参考文献(24)

[1]	王兆祥, 常颖, 付昭旺, 等. 某型坦克炮常规弹药高原环境下打击效能试验 [J]. 火力与指挥控制, 2017, 42(5): 173–176. DOI: 10.3969/j.issn.1002-0640.2017.05.038. WANG Z X, CHANG Y, FU Z W, et al. Experimental study on operational effectiveness under plateau environment for certain type of tank cannon equipped with conventional ammunition [J]. Fire Control and Command Control, 2017, 42(5): 173–176. DOI: 10.3969/j.issn.1002-0640.2017.05.038.
[2]	李科斌, 李晓杰, 闫鸿浩, 等. 不同真空度下空中爆炸近场特性的数值模拟研究 [J]. 振动与冲击, 2018, 37(17): 270–276. DOI: 10.13465/j.cnki.jvs.2018.17.038. LI K B, LI X J, YAN H H, et al. Numerical simulation for near-field characteristics of air explosion under different degrees of vacuum [J]. Journal of Vibration and Shock, 2018, 37(17): 270–276. DOI: 10.13465/j.cnki.jvs.2018.17.038.
[3]	VELDMAN R L, NANSTEEL M W, CHEN C C T, et al. The effect of ambient pressure on blast reflected impulse and overpressure [J]. Experimental Techniques, 2017, 41(3): 227–236. DOI: 10.1007/s40799-017-0171-8.
[4]	汪泉, 陆军伟, 李志敏, 等. 负压条件下柱形爆炸罐内爆炸波传播规律 [J]. 兵工学报, 2021, 42(6): 1250–1256. DOI: 10.3969/j.issn.1000-1093.2021.06.015. WANG Q, LU J W, LI Z M, et al. Propagation law of explosion wave in columnar explosion tank under vacuum conditions [J]. Acta Armamentarii, 2021, 42(6): 1250–1256. DOI: 10.3969/j.issn.1000-1093.2021.06.015.
[5]	庞春桥, 陶钢, 周佩杰, 等. 高原环境下爆炸冲击波参数的有效预测方法 [J]. 振动与冲击, 2018, 37(14): 221–226. DOI: 10.13465/j.cnki.jvs.2018.14.031. PANG C Q, TAO G, ZHOU P J, et al. Effective method for predicting the parameters of shock waves in plateau environment [J]. Journal of Vibration and Shock, 2018, 37(14): 221–226. DOI: 10.13465/j.cnki.jvs.2018.14.031.
[6]	陈龙明, 李志斌, 陈荣, 等. 高原环境爆炸冲击波传播特性的实验研究 [J]. 爆炸与冲击, 2022, 42(5): 053206. DOI: 10.11883/bzycj-2021-0279. CHEN L M, LI Z B, CHEN R, et al. An experimental study on propagation characteristics of blast waves under plateau environment [J]. Explosion and Shock Waves, 2022, 42(5): 053206. DOI: 10.11883/bzycj-2021-0279.
[7]	IZADIFARD R A, FOROUTAN M. Blastwave parameters assessment at different altitude using numerical simulation [J]. Turkish Journal of Engineering and Enviromental Sciences, 2010, 34(1): 25–41. DOI: 10.3906/muh-0911-39.
[8]	BRIDGMAN P W. Dimensional analysis[M]. 2nd ed. New Haven, USA: Yale University Press, 1931: 40–46.
[9]	LEE E L, HORNIG, H C, KURY, J W. Adiabatic expansion of high explosive detonation products: TID 4500-UCRL 50422 [R]. Livermore, USA: Lawrence Livermore National Laboratory, 1968.
[10]	COWLER M S, VIRNBAUM N K. AUTODYN user Manual [M]. Oakland, USA: Century Dynamics Inc, 1989: 213–214.
[11]	BORGNAKKE C, SONNTAG R E. Fundamentals of thermodynamics [M]. 8th ed. Singapore: John Wiley & Sons, 2013: 110–120.
[12]	HENRYCH J. The dynamics of explosion and its use [M]. Amsterdam, the Netherlands: Elsevier, 1979: 124–132.
[13]	BRODE H L. Numerical solutions of spherical blast waves [J]. Journal of Applied Physics, 1955, 26(6): 766–775. DOI: 10.1063/1.1722085.
[14]	HELD M. Blast waves in free air [J]. Propellants, Explosives, Pyrotechnics, 1983, 8(1): 1–7. DOI: 10.1002/prep.19830080102.
[15]	SADOVSKIY M A. Mechanical action of air shock waves of explosion, based on experimental data [M]. Moscow, Russia: Nauka Press, 1952: 6–10.
[16]	BAJIĆ Z. Determination of TNT equivalent for various explosives [D]. Belgrade: University of Belgrade, 2007.
[17]	KINNEY G F, GRAHAM K J. Explosive shocks in air [M]. Berlin: Springer, 1985: 88–105.
[18]	MILLS C A. The design of concrete structures to resist explosions and weapon effects [C]//1st International Conference on Concrete for Hazard Protection. Edinburgh, UK, 1987: 61–73.
[19]	KINGERY C N, BULMASH G. Air-blast parameters from TNT spherical air burst and hemispherical surface burst: ARBRLTR-02555 [R]. Maryland, USA: US Army Ballistic Research Laboratory, 1984.
[20]	USA Department of Defense Explosives Safety Board. Structures to resist the effects of accidental explosions: UFC 3-340-02 [S]. Washington, USA: US Army Corps of Engineers, 2008.
[21]	DEWEY J M, SPERRAZZA J. The effect of atmospheric pressure and temperature on air shock: BRL report 721 [R]. Maryland, USA: Aberdeen Proving Ground, 1950.
[22]	钱翼稷. 空气动力学 [M]. 北京: 北京航空航天大学出版社, 2004: 17–21.
[23]	李志斌, 陈龙明, 陈荣, 等. 一种高原爆炸冲击波等效测试系统及测试方法: CN112378563A [P]. 2021-02-19. LI Z B, CHEN L M, CHEN R, et al. Plateau explosive shock wave equivalent test system and test method: CN112378563A [P]. 2021-02-19.
[24]	DEWEY J M. The properties of a blast wave obtained from an analysis of the particle trajectories [J]. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 1971, 324(1558): 275–299.

施引文献

期刊类型引用(1)
1. 赵继波, 孙承纬, 罗斌强, 蔡进涛, 王桂吉, 谭福利, 赵剑衡. 磁驱动等熵压缩实验构形的磁流体力学计算模拟. 力学学报. 2014(05): 685-693 . 百度学术
其他类型引用(3)

资源附件(0)

访问统计

图(9) / 表(3)

计量

文章访问数: 1028
HTML全文浏览量: 310
PDF下载量: 220
被引次数: 4

1. 实验
1.1 材料和试件
1.2 动态压缩实验
2. 实验结果
2.1 应力-应变曲线
2.2 动态抗压强度
3. 动态统计损伤本构模型
3.1 本构模型的构建
3.2 模型参数的确定
3.3 应变率效应修正
3.4 模型验证
4. 结论

基本量纲	E	p	ρ	r	Δp_m	i	t
M	1	1	1	0	1	1	0
L	2	−1	−3	1	−1	−1	0
T	−2	−2	0	0	−2	−1	1

参考物理量	E	p	ρ	r	Δp_m	i	t
E	1	0	0	1/3	0	1/3	1/3
p	0	1	0	−1/3	1	1/6	−5/6
ρ	0	0	1	0	0	1/2	1/2

h/m	T_h/K	p_h/kPa	ρ_h/(kg∙m⁻³)
0	288.15	101.325	1.225
4 500	258.90	57.728	0.777
9 000	229.65	30.742	0.466

低温和低压环境下炸药爆炸冲击波的传播特性

doi: 10.11883/bzycj-2022-0188

作者简介: 李 瑞（1987－ ），男，博士，讲师，lirui_89@126.com

通讯作者: 汪 泉（1980－ ），男，博士，教授，博士生导师，wqaust@163.com

计量

出版历程