实时高温作用下花岗岩冲击压缩力学特性研究

黄耀莹; 屈璐; 李宇白; 翟越; 谢怡帆

doi:10.11883/bzycj-2022-0196

实时高温作用下花岗岩冲击压缩力学特性研究

doi: 10.11883/bzycj-2022-0196

黄耀莹^1,,
屈璐^{1, 2, ,},
李宇白^{1, 2},
翟越^{1, 2},
谢怡帆¹

1.
长安大学地质工程与测绘学院，陕西西安 710064
2.
自然资源部矿山地质灾害成灾机理与防控重点实验室，陕西西安 710064

基金项目: 国家自然科学基金（41941019）；陕西省创新人才推进计划-科研创新团队（2021TD-55）；中央高校基本科研业务费专项（300102261101）

详细信息

作者简介:
黄耀莹（1999－　），女，硕士研究生，2021126140@chd.edu.cn

通讯作者:
屈　璐（1983－　），女，博士，讲师，qulu@chd.edu.cn

中图分类号: O383.2
计量
- 文章访问数: 571
- HTML全文浏览量: 167
- PDF下载量: 110
- 被引次数: 14
出版历程
- 收稿日期: 2022-05-09
- 修回日期: 2022-12-15
- 网络出版日期: 2023-01-05
- 刊出日期: 2023-02-25

Mechanical properties of granite under impact compression after real-time high temperature

HUANG Yaoying^1
,,
QU Lu^{1, 2
, ,},
LI Yubai^{1, 2},
ZHAI Yue^{1, 2},
XIE Yifan¹

1.
College of Geological Engineering and Geomatics, Chang’an University, Xi’an 710064, Shaanxi, China
2.
Key Laboratory of Mine Geological Disaster Mechanism and Prevention, Ministry of Natural Resources, Xi’an 710064, Shaanxi, China

摘要

摘要: 为研究实时高温作用对花岗岩冲击力学特性的影响，以川藏铁路色季拉山施工区域加里东期花岗岩为研究对象，利用分离式霍普金森杆（SHPB）及同步箱式电阻炉，对20～800 ℃实时高温下的花岗岩试件进行冲击压缩试验，分析高温作用及加载应变率对试件破碎特征、动态抗压强度及能量吸收情况的影响，基于粉晶X射线衍射分析矿物成分变化与花岗岩动力学强度的内在关联。研究表明：20～400 ℃高温试件以脆性劈裂破坏为主，碎片形态呈纺锤形，两端尖锐，而600 ℃高温试件以塑性破坏为主，形状趋于圆钝；试件峰值应力随温度升高具有先增大后减小的变化趋势，200 ℃时达到强度阈值，随后持续降低；单位体积岩石耗散能与加载应变率呈线性正相关关系，与温度呈二次函数关系，与峰值应力呈指数关系，拟合效果良好；石英、云母和长石三种主要矿物成分的含量波动、相态变化等因素共同导致花岗岩动力学强度在200 ℃后逐步劣化。
- 实时高温 /
- 花岗岩 /
- SHPB /
- 能量耗散 /
- XRD
Abstract: The study of thermal-mechanical coupling mechanism is of great significance to deep rock engineering such as rock tunnel fire, nuclear waste treatment and geothermal development. To investigate the effect of high temperature on the impact mechanical properties of granite, the real-time high temperature impact compression test was carried out on the granite specimen at 20～800 ℃. The Caledonian granite in the construction area of Sejila Mountain on Sichuan-Tibet Railway was taken as the research object, real-time high temperature impact compression tests were carried out on the specimens under five different temperatures ( 20, 200, 400, 600 and 800 ℃) with three average loading rates ( 72.8, 144.97 and 230.29 s⁻¹) by using the split Hopkinson pressure bar (SHPB) and synchronous box-type resistance furnace. The effects of high temperature and loading strain rate on the fracture characteristics, dynamic compressive strength and fractal dimension of the specimens were analyzed. The variation law of dissipated energy per unit volume was also studied and discussed. In addition, the intrinsic correlation between the change of mineral composition and the dynamic strength of granite was analyzed based on X-ray powder crystal diffraction. The results show that the brittle fracture of the specimens at 20 to 400 ℃ is dominant, and the fragments are spindle-shaped with sharp ends. The specimens at 600 ℃ are dominated by plastic failure, and their shapes tend to be round. The peak stress of specimens increases first and then decreases with the increase of temperature, reaches the strength threshold at 200 ℃, and then decreases continuously. The dissipated energy per unit volume of rock has a positive linear correlation with the loading strain rate and a quadratic function with the temperature, which shows a good fitting effect. The content fluctuation and phase change of the three main mineral components of quartz, mica and feldspar lead to the gradual deterioration of the dynamic strength of granite after 200 ℃.
- real-time high temperature /
- granite /
- SHPB /
- energy dissipation /
- XRD

HTML全文

随着高效毁伤技术的不断发展以及未来战争作战条件的多元化，武器弹药适应高海拔、高空，甚至太空等极端环境的需求日益突显^[1]。众所周知，高海拔或高空环境的一个重要特点就是环境温度显著低于平原地区，大气压力低于标准大气压，呈现低温和低压的环境状态。对于平原地区正常使用的常规武器弹药，在高海拔或高空等低温和低压环境使用时，炸药的爆炸能量释放受环境的影响如何，需要进行重新评估。

近年来，已有一些关于低压环境下炸药爆炸冲击波传播特性的相关研究报道。李科斌等^[2]利用AUTODYN有限元软件分析了不同真空度下爆炸近场冲击波参量的变化规律。Veldman等^[3]对不同初始环境压力下C-4炸药爆炸冲击波的传播规律进行了数值模拟和实验研究，发现环境压力对爆炸冲击波的正反射压力和比冲量影响显著。汪泉等^[4]通过抽真空爆炸系统对低压环境爆炸冲击波传播进行了实验研究，获得了不同低压条件对爆炸冲击波参量的影响规律。庞春桥等^[5]和陈龙明等^[6]以高海拔环境为研究背景，开展了低压条件下炸药爆炸冲击波传播的实验研究，给出了不同低压条件下炸药爆炸冲击波参量的预测公式。Izadifard等^[7]利用AUTODYN有限元软件对高海拔环境中的低压条件对炸药爆炸冲击波传播的影响进行了数值模拟研究，拟合得到了低压条件下爆炸冲击波参量的修正因子。目前，关于高海拔环境炸药爆炸冲击波传播规律的研究主要考虑了低压条件的影响，对于低温条件，特别是高海拔、高空等的低温和低压耦合环境对爆炸冲击波传播特性的影响缺乏系统研究。

本文中，拟通过量纲分析对低温和低压环境下炸药爆炸冲击波参量进行理论分析，利用AUTODYN有限元软件开展不同低温和低压环境下炸药爆炸冲击波传播的数值模拟，探讨低温、低压和海拔高度对爆炸冲击波参量的影响。

1. 爆炸冲击波参量的理论分析

1.1 爆炸冲击波参量的影响因素

炸药爆炸形成的冲击波对目标的破坏作用主要取决于冲击波正压区的特征参量，包括峰值超压Δp_m、比冲量i和冲击波到达时间t等。炸药在空气中爆炸时，影响爆炸冲击波参量的物理量有炸药爆炸释放的总能量E、空气环境压力p、空气密度ρ以及传播距离r。忽略空气介质的黏性和热传导，炸药爆炸冲击波参量可以表示为空气参数的函数形式：

$\left\{ \begin{gathered} \Delta {p_{\text{m}}} = {f_1}\left( {E,p,\rho ,r} \right) \\ i = {f_2}\left( {E,p,\rho ,r} \right) \\ t = {f_3}\left( {E,p,\rho ,r} \right) \\ \end{gathered} \right.$

(1)

1.2 爆炸冲击波参量的量纲分析

由Π定理^[8]可知，式(1)中7个物理量有3个基本量纲：M、L和T，对应3个独立的参考物理量，选择E、p和ρ作为参考物理量，各物理量的量纲幂次如表1所示。

表 1 爆炸冲击波传播问题中物理量的量纲幂次

Table 1. Dimensional power coefficients of physical quantities in the problem of blast wave propagation

基本量纲	E	p	ρ	r	Δp_m	i	t
M	1	1	1	0	1	1	0
L	2	−1	−3	1	−1	−1	0
T	−2	−2	0	0	−2	−1	1

下载: 导出CSV

| 显示表格

对表1进行类似矩阵初等变换，可以得到表2。

表 2 爆炸冲击波传播问题中物理量的量纲幂次（初等变换）

Table 2. Dimensional power coefficients of physical quantities in the problem of blast wave propagation (elementary transformation)

参考物理量	E	p	ρ	r	Δp_m	i	t
E	1	0	0	1/3	0	1/3	1/3
p	0	1	0	−1/3	1	1/6	−5/6
ρ	0	0	1	0	0	1/2	1/2

下载: 导出CSV

| 显示表格

根据Π定理^[8]，由表2可以得出爆炸冲击波参量峰值超压Δp_m、比冲量i以及冲击波到达时间t的无量纲表达式：

$\left\{ \begin{gathered} \frac{{\Delta {p_{\text{m}}}}}{p} = {f_1}\left( {\frac{r}{{{E^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \frac{i}{{{E^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}{p^{{1 \mathord{\left/ {\vphantom {1 6}} \right. } 6}}}{\rho ^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}} = {f_2}\left( {\frac{r}{{{E^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \frac{{t{p^{{5 \mathord{\left/ {\vphantom {5 6}} \right. } 6}}}}}{{{E^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}{\rho ^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}} = {f_3}\left( {\frac{r}{{{E^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}}{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \end{gathered} \right.$

(2)

对于空气，有状态方程pM_r=ρRT，式中R为理想气体常数，T为环境温度，M_r为空气相对分子质量；相同炸药爆炸释放的总能量E主要取决装药质量W。因此，式(2)可以转化为：

$\left\{ \begin{gathered} \frac{{\Delta {p_{\text{m}}}}}{p} = {f_1}\left( {Z{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \frac{{{T^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}i}}{{{W^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}{p^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}}} = {f_2}\left( {Z{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \frac{{{T^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}t}}{{{W^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}}} = {f_3}\left( {Z{p^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}} \right) \\ \end{gathered} \right.$

(3)

式中：Z为比例距离，Z=r/W^1/3。

从式(3)可以看出，炸药爆炸冲击波的比冲量i和冲击波到达时间t取决于环境温度T和环境压力p的影响，而爆炸冲击波峰值超压Δp_m则主要取决于环境压力p的影响。

2. 爆炸冲击波参量的数值模拟

2.1 计算模型

采用AUTODYN有限元软件对球形装药的自由场爆炸冲击波传播过程进行数值模拟研究。建立如图1所示的一维球对称楔形计算模型，模型由炸药和空气两部分组成，采用多物质Euler算法进行数值模拟。炸药为1 kg的TNT球形装药，起爆方式为装药中心点起爆，在空气域边界处设置非反射边界。空气域中设置一系列观测点（P₁～P₂₄）用于爆炸冲击波特征参量的结果输出。

图 1 一维球对称楔形模型

Figure 1. A one-dimensional spherical symmetric wedge model

下载: 全尺寸图片幻灯片

2.2 材料参数

炸药TNT采用JWL状态方程进行描述，具体表达式为^[9]：

$p = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){{\text{e}} ^{ - {R_1}V}}{\kern 1pt} {\kern 1pt} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){{\text{e}} ^{ - {R_2}V}} + \frac{{\omega E}}{V}$

(4)

式中：p为爆轰产物的压力，V为爆轰产物的相对比容，A、B、R₁、R₂、ω为常数，E为炸药体积内能。炸药TNT的JWL参数取自AUTODYN标准材料模型库^[10]。

对空气，采用理想气体状态方程描述，即：

$p = \left( {\gamma - 1} \right)\rho e$

(5)

式中：p为空气压力，γ为理想气体绝热指数，ρ为空气密度，e为空气的初始比内能。e取决于空气环境温度^[11]：

$e = {c_V}T$

(6)

式中：T为空气温度； ${c_V}$ 为空气的比定容热容，理想气体的比定容热容仅取决于温度^[11]。因此，以下数值模拟中，通过改变空气的初始密度和初始比内能，实现不同的低温和低压空气环境。

2.3 网格尺寸的收敛性分析

使用AUTODYN有限元软件对不同低温和低压环境下炸药爆炸冲击波的传播过程进行数值模拟，首先需要进行网格尺寸的收敛性分析，以确定数值模型合理的网格尺寸。为此，分别采用网格尺寸为0.5、1.0、2.0、3.0、5.0和10.0 mm进行爆炸冲击波传播的数值模拟研究。图2为Z=0.3, 2.0 m/kg^1/3 等2种比例距离下，不同网格尺寸数值模拟得到的爆炸冲击波超压-时程曲线。

图 2 不同网格尺寸的冲击波超压-时程曲线比较

Figure 2. Comparison of overpressure time history curves for different cell sizes

下载: 全尺寸图片幻灯片

从图2可以看出，随着网格尺寸的增大，冲击波波峰由陡峭变得平缓，波前压力由环境压力上升至峰值压力的斜率逐渐降低，冲击波压力波形逐渐失真。对比图2中2个比例距离下不同网格尺寸的冲击波超压-时程曲线，可以认为网格尺寸在0.5～2.0 mm尺寸范围内的数值模拟是收敛的。因此，为了保证数值模拟的收敛性，同时避免不必要的数值模拟计算时间，选择1.0 mm的网格尺寸进行后续冲击波传播过程的数值模拟研究。

3. 结果与分析

3.1 标准大气环境下爆炸冲击波参量

对于标准大气环境下炸药的爆炸冲击波参量已有大量的实验研究，并拟合得到了计算爆炸冲击波的峰值超压Δp_m和比冲量i的经验公式^{[7, 12-19]}。这些常用的计算爆炸冲击波参量的经验公式与数值模拟和UFC 3-340-02规范^[20]的对比结果如图3所示。从图3可以看出，这些经验公式的适用范围和计算结果互有差异，这是由于早期的测试条件落后，仪器精度不够等多种原因导致的。

图 3 标准大气环境下冲击波参量的理论、数值模拟与实验结果对比

Figure 3. Comparison among theoretical, numerical and experimental blast wave parameters in standard atmospheric environment

下载: 全尺寸图片幻灯片

从图3还可以看出，不同比例距离下炸药爆炸冲击波峰值超压Δp_m和比冲量i的数值模拟结果与UFC 3-340-02规范^[20]数据吻合较好，说明选择1.0 mm的网格尺寸进行数值模拟研究是合理的。分析图3可知，对于炸药爆炸冲击波的峰值超压Δp_m和比冲量i，Kinney-Grahm公式和Izadifard-Foroutan公式最接近UFC 3-340-02规范^[20]和数值模拟结果，相应的计算公式分别为^{[7, 17]}：

$\frac{{\Delta {p_{\text{m}}}}}{p} = \frac{{808\left[ {1 + {{\left( {{Z \mathord{\left/ {\vphantom {Z {4.5}}} \right. } {4.5}}} \right)}^2}} \right]}}{{\sqrt {1 + {{\left( {{Z / {0.048}}} \right)}^2}} \sqrt {1 + {{\left( {{Z / {0.32}}} \right)}^2}} \sqrt {1 + {{\left( {{Z / {1.35}}} \right)}^2}} }}\begin{array}{*{20}{c}} {{\text{ }}}&{0.053{\text{ }}{{\text{m}} / {{\text{k}}{{\text{g}}^{{\text{1}}/{\text{3}}}}}} {\text{≤}} Z {\text{≤}} 500} \end{array}{\text{ }}{{\text{m}} / {{\text{k}}{{\text{g}}^{{\text{1}}/{\text{3}}}}}}$

(7)

$\frac{i}{{{W^{{1/ 3}}}}} = \left\{ \begin{array}{ll} {10^{ - 3.423{{\left( {\lg Z} \right)}^4} - 10.143{{\left( {\lg Z} \right)}^3} - 7.558{{\left( {\lg Z} \right)}^2} - 1.614{\text{ }}\lg Z + 2.14}}& Z {\text{＜}} 0.8{\text{ }}{{\text{m}} / {{\text{k}}{{\text{g}}^{{\text{1}}/{\text{3}}}}}} \\ {10^{ - 0.07{{\left( {\lg Z} \right)}^2} - 0.853{\text{ }}\lg Z + 2.153}}& Z {\text{≥}} 0.8{\text{ }}{{\text{m}} / {{\text{k}}{{\text{g}}^{{\text{1}}/{\text{3}}}}}} \\ \end{array} \right.$

(8)

式中：Δp_m和p分别为爆炸冲击波峰值超压和环境压力，kPa；i为比冲量，Pa·s；W为装药量，kg。

3.2 低温和低压环境下的爆炸冲击波参量

经验公式(7)～(8)只能描述标准大气环境下炸药爆炸冲击波的峰值超压Δp_m和比冲量i，无法描述低温和低压环境下的炸药爆炸冲击波参量变化规律。为此，结合量纲分析推导的关系式(3)，根据相似准则对式(7)～(8)进行整理，可以得到描述低温和低压环境下炸药爆炸冲击波峰值超压Δp_m和比冲量i的计算公式分别为：

$\begin{split}&\dfrac{{\Delta {p_{\text{m}}}}}{{{p_h}}} = \dfrac{{808\left[ {1 + {{\left( {\dfrac{Z}{{4.5}}} \right)}^2}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{2}{3}}}} \right]}}{{\sqrt {1 + {{\left( {\dfrac{Z}{{0.048}}} \right)}^2}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{2}{3}}}} \sqrt {1 + {{\left( {\dfrac{Z}{{0.32}}} \right)}^2}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{2}{3}}}} \sqrt {1 + {{\left( {\dfrac{Z}{{1.35}}} \right)}^2}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{2}{3}}}} }}\\ &0.053{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{ - \frac{1}{3}}} {\text{≤}} Z {\text{≤}} 500{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{ - \frac{1}{3}}} \end{split}$

(9)

$\begin{split}&\dfrac{i}{{{W^{{1 / 3}}}}} =\\ &\left\{ \begin{array}{ll} {\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{\frac{2}{3}}} {\left( {\dfrac{{{T_0}}}{{{T_h}}}} \right)^{\frac{1}{2}}} {10^{ - 3.423{{\left\{ {\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right]} \right\}}^4} - 10.143{{\left\{ {\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right]} \right\}}^3} - 7.558{{\left\{ {\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right]} \right\}}^2} - 1.614\;\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right] + 2.14}}&Z {\text{＜}} 0.8{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{ - \frac{1}{3}}} \\ {\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{\frac{2}{3}}}{\left( {\dfrac{{{T_0}}}{{{T_h}}}} \right)^{\frac{1}{2}}}{10^{ - 0.07{{\left\{ {\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right]} \right\}}^2} - 0.853\;\lg \left[ {{\textit{Z}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}} \right] + 2.153}}&Z {\text{≥}} 0.8{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)^{ - \frac{1}{3}}} \end{array} \right. \end{split}$

(10)

式中： p_h和p₀分别为低压环境和标准大气环境下的环境压力，kPa；下标 h 为海拔高度，m；T_h和T₀分别为低压环境和标准大气环境下的环境温度，K；W为装药量，kg。

为了验证式(9)~(10)预测低压环境下炸药爆炸冲击波超压和比冲量的准确性，选择T_h=20 ℃，p_h= p₀, 2p₀/3, p₀/3进行理论计算和数值模拟研究，并与实验数据^[21]进行对比。相应的爆炸冲击波峰值超压Δp_m和比冲量i的理论计算、数值模拟与实验数据对比结果如图4所示。

图 4 低压环境下冲击波参量的理论、数值模拟与实验数据对比

Figure 4. Comparison among theoretical, numerical and experimental shock wave parameters in diminished pressure environments

下载: 全尺寸图片幻灯片

从图4可以看出，不同环境压力下冲击波参量的理论计算结果与数值模拟及实验结果吻合较好，说明式(9)～(10)和数值模拟能够较好地预测低压环境下炸药爆炸冲击波的峰值超压Δp_m和比冲量i。分析图4(a)可知，爆炸冲击波的峰值超压随着环境压力的降低而减小，爆炸近场的冲击波峰值超压下降幅度要大于爆炸远场。对于图4(b)，当Z<0.2 m/kg^1/3时，爆炸冲击波的比冲量随着环境压力的降低而略有增大；当Z>0.2 m/kg^1/3时，冲击波比冲量随着环境压力的降低而减小。

同样，为了验证式(9)~(10)预测低温环境下爆炸冲击波峰值超压和比冲量的准确性，选择环境压力p_h=101.325 kPa，环境温度T_h=20, −18, −53 ℃进行理论计算和数值模拟研究。相应的爆炸冲击波峰值超压Δp_m和比冲量i理论计算、数值模拟和实验数据的对比结果如图5所示。

图 5 低温环境下冲击波参量的理论、数值模拟结果与实验结果的对比

Figure 5. Comparison among theoretical, numerical and experimental shock wave parameters in diminished temperature environments

下载: 全尺寸图片幻灯片

从图5可以看出，不同环境温度下爆炸冲击波参量的理论计算、数值模拟与实验数据吻合较好，说明式(9)～(10)和数值模拟能够较好地预测低温环境下炸药爆炸冲击波的峰值超压Δp_m和比冲量i。分析图5可知，环境温度对爆炸冲击波的峰值超压Δp_m影响不大，但影响爆炸冲击波的比冲量i，冲击波比冲量i随环境温度降低而增大。

3.3 高海拔环境下的爆炸冲击波参量

高海拔环境是典型的低温和低压耦合大气环境，高海拔环境下环境温度和大气压力与海拔高度分别有如下关系^{[7, 22]}：

${T}_{h}=288.15-0.006\;5h\text{，}{p}_{h}=101.325{\left(1-\frac{h}{44\;330}\right)}^{5.255\;88}\;\;\;\;\;0{\text{≤}} h{\text{≤}} 11\;000\text{ m}$

(11)

根据关系式(11)和空气状态方程pM_r=ρRT，计算获得不同海拔高度h下的环境温度T_h、环境压力p_h和空气密度ρ_h，如表3所示。

表 3 不同海拔高度下的大气参数

Table 3. Atmospheric parameters at different altitudes

h/m	T_h/K	p_h/kPa	ρ_h/(kg∙m⁻³)
0	288.15	101.325	1.225
4 500	258.90	57.728	0.777
9 000	229.65	30.742	0.466

下载: 导出CSV

| 显示表格

将表3中不同海拔高度下的环境温度T_h和环境压力p_h代入式(5)～(6)，计算获得不同海拔高度下的空气状态参数，再利用AUTODYN有限元软件对不同海拔高度下炸药爆炸冲击波的传播过程进行数值模拟研究。同时，将表3中不同海拔高度下的大气参数代入式(9)～(10)，计算获得不同海拔高度下的爆炸冲击波峰值超压Δp_m和比冲量i。相应爆炸冲击波参量的理论计算、数值模拟与实验数据对比结果，以及冲击波超压Δp_m和比冲量i随海拔高度h增加的变化率如图6所示。

图 6 高海拔环境下冲击波参量的理论、数值模拟结果与实验结果的对比

Figure 6. Comparison among theoretical, numerical and experimental shock wave parameters in high-altitude environment

下载: 全尺寸图片幻灯片

从图6可以看出，不同海拔高度下爆炸冲击波参量的理论计算与数值模拟、实验结果吻合较好，表明式(9)～(10)能够较好地预测高海拔的低温和低压耦合大气环境下炸药爆炸冲击波的峰值超压Δp_m和比冲量i。分析图6(a)可知，爆炸冲击波的峰值超压Δp_m随海拔的升高而降低，海拔从0 m升至9 000 m时，冲击波峰值超压降低23.5%～58.2%，平均降低了35.3%。因此，海拔高度在0～9 000 m范围内，海拔每升高1 000 m，冲击波峰值超压平均降低约3.9%。对于图6(b)，Z<0.2m/kg^1/3时，爆炸冲击波的比冲量i随海拔的升高而增大，海拔从0 m升至9 000 m时，冲击波比冲量i增大0.8%～94.8%，平均增大了43.2%；当Z>0.2 m/kg^1/3时，爆炸冲击波的比冲量随海拔的升高而减小，海拔从0 m升至9 000 m时，冲击波比冲量i减小4.9%～58.8%，平均减小了28.4%。因此，海拔高度在0～9 000 m范围内，Z<0.2 m/kg^1/3时，海拔高度每升高1 000 m，比冲量i平均增大约4.8%；Z>0.2 m/kg^1/3时，海拔每升高1 000 m，比冲量i平均减小约3.2%。对比图4～6可知，炸药爆炸冲击波的峰值超压Δp_m随海拔的升高而减小，主要是由低压环境导致的，环境温度影响不大。Z<0.2 m/kg^1/3时，爆炸冲击波比冲量i随海拔的升高而增大，是由低压和低温条件共同促进作用导致的。Z>0.2 m/kg^1/3时，爆炸冲击波比冲量i随海拔的升高而减小，说明低压条件对冲击波比冲量的减弱作用大于低温条件的促进作用。综上分析，高海拔环境的低压和低温条件对爆炸冲击波参量有重要影响。相比于低温条件，高海拔环境下低压条件对爆炸冲击波参量的影响程度更高。

3.4 冲击波波阵面运动规律

Dewey^[24]通过实验数据拟合得到了标准大气环境下1 kg球形TNT装药的爆炸冲击波传播轨迹经验公式：

$r = A + B{a_0}t + C\ln (1 + {a_0}t) + D\sqrt {\ln (1 + {a_0}t)}$

(12)

式中：r为爆炸冲击波半径，m；A=0.055963，B=1.01751，C=−0.45403和D=2.05527为拟合系数；a₀=340.292 m/s为标准大气条件下的空气音速；t为爆炸冲击波的传播时间，s。

式(12)只能描述标准大气环境下1 kg TNT装药的爆炸冲击波传播轨迹，不能描述低温和低压环境下不同装药量的爆炸冲击波传播过程。为此，根据式(3)和相似准则，对式(12)进行整理，得到低温和低压环境下装药量为W的炸药爆炸冲击波传播轨迹计算公式：

$\begin{split}Z =& \left[ A + B{{\left( {\frac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\frac{{{a_0}t}}{{{W^{\frac{1}{3}}}}} + C\ln \left( {1 + {{\left( {\frac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\frac{{{a_0}t}}{{{W^{\frac{1}{3}}}}}} \right) +\right.\\ &\left.D\sqrt {\ln \left( {1 + {{\left( {\frac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\frac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\frac{{{a_0}t}}{{{W^{\frac{1}{3}}}}}} \right)} \right]{\left( {\frac{{{p_0}}}{{{p_h}}}} \right)^{\frac{1}{3}}}\end{split}$

(13)

式(13)两边对时间t求微分，可以得到冲击波的传播速度：

$\begin{split}{D_{\text{s}}} =& \left[ B + \dfrac{C}{{1 + {{\left( {\dfrac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\dfrac{{{a_0}t}}{{{W^{\frac{1}{3}}}}}}} +\right.\\ &\left.\dfrac{D}{{2\left( {1 + {{\left( {\dfrac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\dfrac{{{a_0}t}}{{{W^{\frac{1}{3}}}}}} \right)\sqrt {\ln \left( {1 + {{\left( {\dfrac{{{T_h}}}{{{T_0}}}} \right)}^{\frac{1}{2}}}{{\left( {\dfrac{{{p_h}}}{{{p_0}}}} \right)}^{\frac{1}{3}}}\dfrac{{{a_0}t}}{{{W^{\frac{1}{3}}}}}} \right)} }} \right]{\left( {\dfrac{{{T_h}}}{{{T_0}}}} \right)^{\frac{1}{2}}}{a_0} \end{split}$

(14)

式中：D_s为冲击波传播速度，m/s。

通过数值模拟过程中监测点位置及冲击波的超压-时程曲线，可以追踪得到爆炸冲击波波阵面的运动轨迹。不同低压和低温条件下炸药爆炸冲击波传播轨迹的理论计算、数值模拟与实验结果的比较如图7所示。从图7可以看出，不同低压和低温环境下炸药爆炸冲击波波阵面的运动轨迹理论计算结果与数值模拟、实验结果吻合较好，说明式(13)能够较好地预测低压和低温环境下炸药爆炸冲击波波阵面的运动轨迹。分析图7可知，对于相同的传播时间，爆炸冲击波的传播距离随环境压力的降低而增大，随环境温度的降低而减小。表明环境温度和环境压力对爆炸冲击波的传播速度都有重要影响。

图 7 不同低压和低温环境下爆炸冲击波波阵面的运动轨迹

Figure 7. Motion trajectories of blast wave in diminished pressure and temperature environments

下载: 全尺寸图片幻灯片

通过式(14)可以计算获得不同低温和低压条件下炸药爆炸冲击波的传播速度，如图8所示。从图8可以看出，大气环境压力降低，爆炸冲击波的传播速度升高，而大气环境温度降低，爆炸冲击波的传播速度降低。因此，图7中炸药爆炸冲击波的传播距离随环境压力的降低而增大，随环境温度的降低而减小。由图8可知，随着传播时间的延长，冲击波传播速度逐渐衰减，最终衰减为空气的音速。由于空气的音速主要取决于环境温度^[22]，进而图8中低压环境下爆炸冲击波的传播速度衰减趋于同一值（见图8(a)），低温环境下爆炸冲击波传播速度衰减趋于不同值（见图8(b)）。

图 8 不同低压和低温环境下爆炸冲击波的传播速度

Figure 8. Propagation velocities of blast waves in diminished pressure and temperature environments

下载: 全尺寸图片幻灯片

对于高海拔的典型低温和低压耦合环境，将表3中不同海拔高度下环境温度T_h和环境压力p_h代入式(5)～(6)，结合空气状态方程获得不同海拔高度下的空气状态参数，再利用AUTODYN有限元软件对不同海拔高度下爆炸冲击波传播过程进行数值模拟研究。同时，将表3中不同海拔高度下大气参数代入式(13)～(14)，计算获得不同海拔高度下爆炸冲击波运动轨迹和传播速度。不同海拔高度下爆炸冲击波波阵面运动轨迹和冲击波传播速度的理论计算、数值模拟与实验结果的对比如图9所示。

图 9 不同海拔高度下爆炸冲击波波阵面运动轨迹及传播速度的理论、数值模拟结果与实验结果的对比

Figure 9. Theoretical, numerical and experimental comparison of shock wave parameters in different high-altitude environments

下载: 全尺寸图片幻灯片

从图9可以看出，不同海拔高度下炸药爆炸冲击波波阵面运动轨迹的理论计算结果与数值模拟、实验结果吻合较好，表明式(13)可以较好地预测不同海拔高度下炸药爆炸冲击波波阵面的运动轨迹。分析图9可知，对于爆炸近场（Z＜8 m/kg^1/3），相同的传播时间内，炸药爆炸冲击波的传播距离随海拔的升高而增大，对于爆炸远场（Z＞10 m/kg^1/3），爆炸冲击波的传播距离随海拔的升高而减小。这是由于爆炸近场的冲击波传播速度随海拔的升高而升高，爆炸远场冲击波传播速度随海拔的升高而降低导致的（图9中不同海拔高度下的爆炸冲击波传播速度）。综合分析图7～9可知，高海拔环境下炸药爆炸冲击波的传播速度，对于爆炸近场主要取决于低压环境的影响，而对于爆炸远场主要取决于低温环境的影响。

4. 结　论

基于量纲分析理论和AUTODYN有限元软件，对不同低温、低压和高海拔条件下炸药爆炸冲击波的峰值超压、比冲量和波阵面运动轨迹等参量进行了理论分析和数值模拟，并与实验数据进行了对比验证，得到了不同低温和低压环境下炸药爆炸冲击波参量的变化规律，主要结论如下。

(1)通过量纲分析理论结合标准大气环境下冲击波参量经验公式，建立了预测低温和低压环境下炸药爆炸冲击波峰值超压、比冲量和波阵面运动轨迹的计算公式，并通过数值模拟和实验数据验证计算公式的预测准确性。

(2)大气环境参数影响着炸药爆炸冲击波参量，环境压力降低，爆炸冲击波的峰值超压和爆炸远场（Z>0.2 m/kg^1/3）比冲量减小，冲击波传播速度升高。环境温度降低，炸药爆炸冲击波的比冲量增大，传播速度降低，峰值超压影响不大。

(3)海拔高度在0～9 000 m范围内，每升高1 000 m冲击波峰值超压和爆炸远场比冲量分别平均降低约3.9%和3.2%。爆炸近场的冲击波传播速度随海拔的升高而升高，爆炸远场的冲击波传播速度随海拔的升高而降低。高海拔环境下低压条件对峰值超压和比冲量的影响程度高于低温条件，爆炸近场冲击波的传播速度主要取决于低压的影响，爆炸远场冲击波的传播速度则主要取决于低温的影响。

图 1 标准花岗岩试件

Figure 1. Standard granite specimens

下载: 全尺寸图片幻灯片

图 2 SHPB系统及同步智能箱式电阻炉

Figure 2. SHPB system and synchronous intelligent box-type resistance furnace

下载: 全尺寸图片幻灯片

图 3 同步高温炉测试系统结构示意

Figure 3. Sketch of synchronous high temperature furnace test system structure

下载: 全尺寸图片幻灯片

图 4 加载应变率曲线

Figure 4. Strain rate curves

下载: 全尺寸图片幻灯片

图 5 整形前后波形曲线

Figure 5. Waveforms without and with a pulse shaper

下载: 全尺寸图片幻灯片

图 6 800 ℃实时高温破碎试件

Figure 6. Broken specimen at 800 ℃ real-time high temperature

下载: 全尺寸图片幻灯片

图 7 74.8 s⁻¹应变率时，试件破碎形态

Figure 7. Fragmentation morphologies of the specimen at the strain rate of 74.8 s⁻¹

下载: 全尺寸图片幻灯片

图 8 144.97 s⁻¹应变率时，试件破碎形态

Figure 8. Fragmentation morphologies of the specimen at the strain rate of 144.97 s⁻¹

下载: 全尺寸图片幻灯片

图 9 230.29 s⁻¹应变率时，试件破碎形态

Figure 9. Fragmentation morphologies of the specimen at the strain rate of 230.29 s⁻¹

下载: 全尺寸图片幻灯片

图 10 破碎试件细节

Figure 10. Detail of the broken specimen

下载: 全尺寸图片幻灯片

图 11 应力-应变曲线

Figure 11. Stress-strain curves

下载: 全尺寸图片幻灯片

图 12 峰值应力与温度、冲击荷载关系

Figure 12. Relationship between peak stress and temperature and strain rate

下载: 全尺寸图片幻灯片

图 13 分形维数与温度、应变率关系

Figure 13. Relationship between fractal dimension and temperature and strain rate

下载: 全尺寸图片幻灯片

图 14 分形维数与峰值应力关系

Figure 14. Relationship between fractal dimension and peak stress

下载: 全尺寸图片幻灯片

图 15 能量时程曲线

Figure 15. Curve of energy

下载: 全尺寸图片幻灯片

图 16 体积能量与应变率关系

Figure 16. Relationship between volumic energy and strain rate

下载: 全尺寸图片幻灯片

图 17 体积能量与温度关系

Figure 17. Relationship between volumic energy and temperature

下载: 全尺寸图片幻灯片

图 18 动态抗压强度与体积能量关系

Figure 18. Relationship between fractal dimension and volumic energy of granite

下载: 全尺寸图片幻灯片

图 19 不同实时高温下花岗岩X衍射图谱

Figure 19. X-ray diffraction patterns of granite at different real-time high temperatures

下载: 全尺寸图片幻灯片

图 20 长石、云母相对含量之和与温度的关系

Figure 20. Relationship between the sum of feldspar and mica content and temperature

下载: 全尺寸图片幻灯片

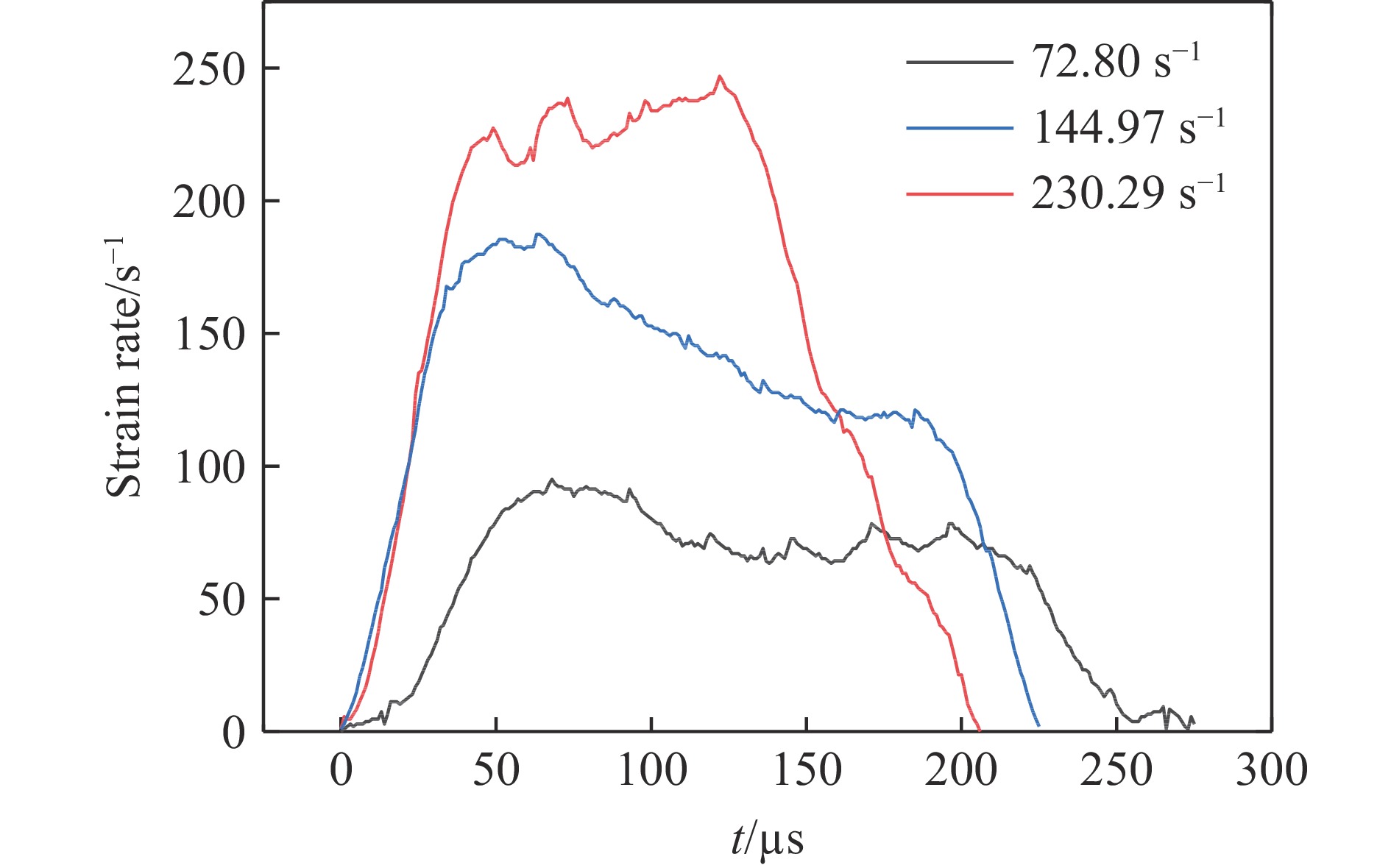
表 1 SHPB试验参数

Table 1. Parameters of the test

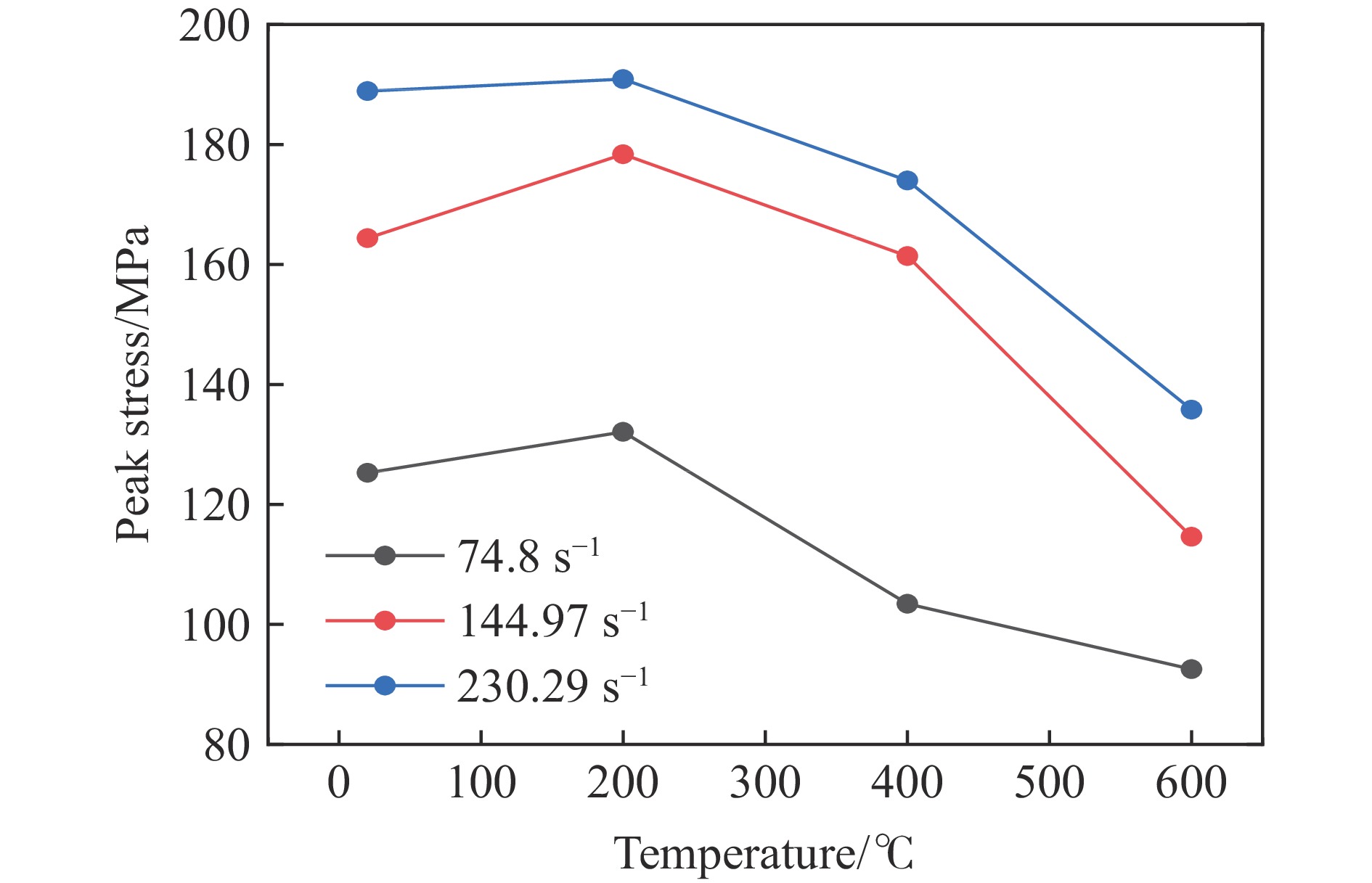
气压/MPa 冲击速率/（m∙s⁻¹）平均应变率/s⁻¹

0.2 5.4 74.80
0.4 8.8 144.97
0.6 11.3 230.29

下载: 导出CSV

表 2 峰值应力

Table 2. Peak stress

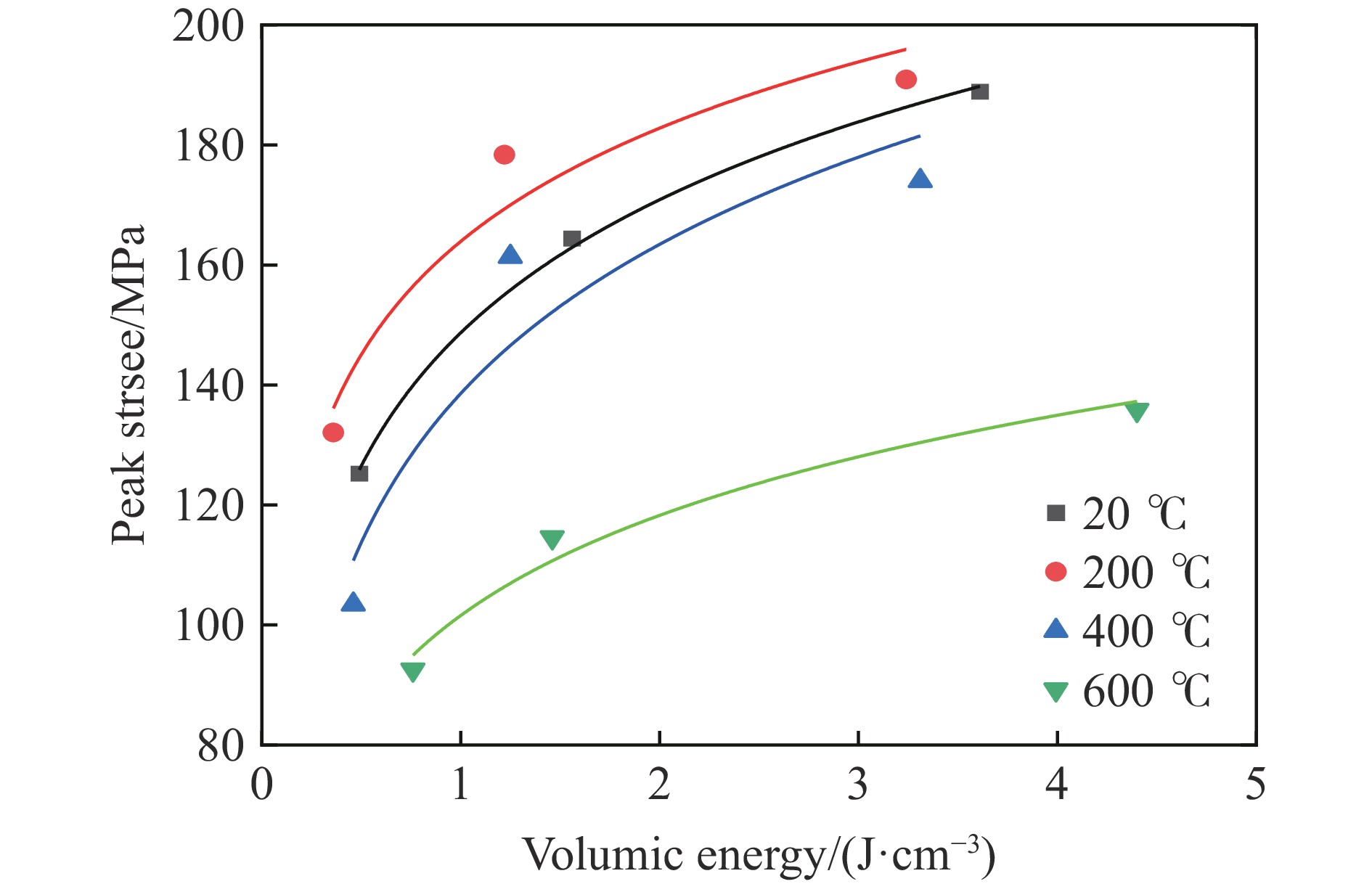
平均应变率/s⁻¹ 试件峰值应力/MPa
20 ℃ 200 ℃ 400 ℃ 600 ℃ 800 ℃

74.80 125.25 132.08 103.43 92.517 0
144.97 164.39 178.38 161.38 114.59 0
230.29 188.91 190.91 174.00 135.80 0

下载: 导出CSV

表 3 体积能量

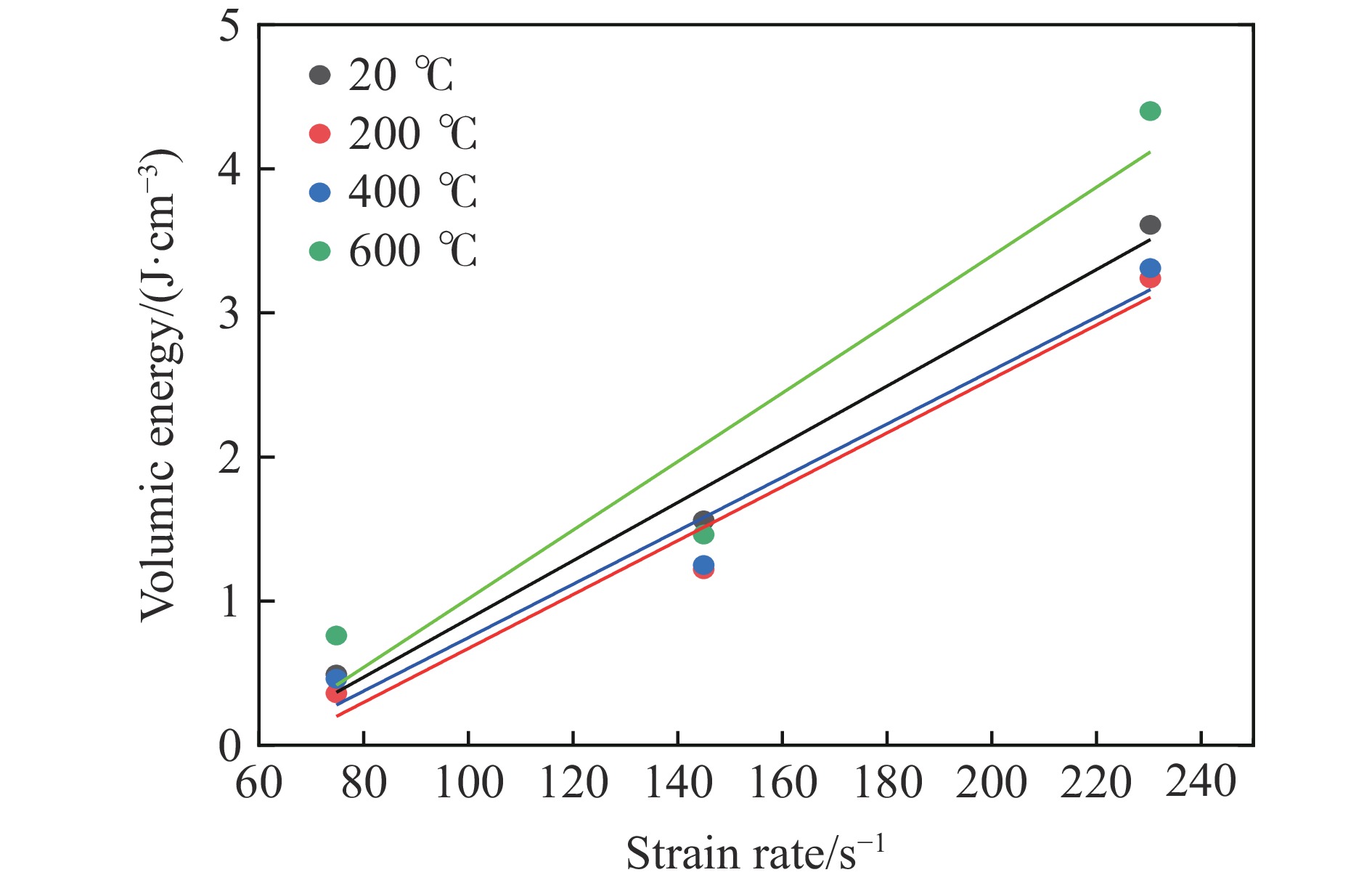
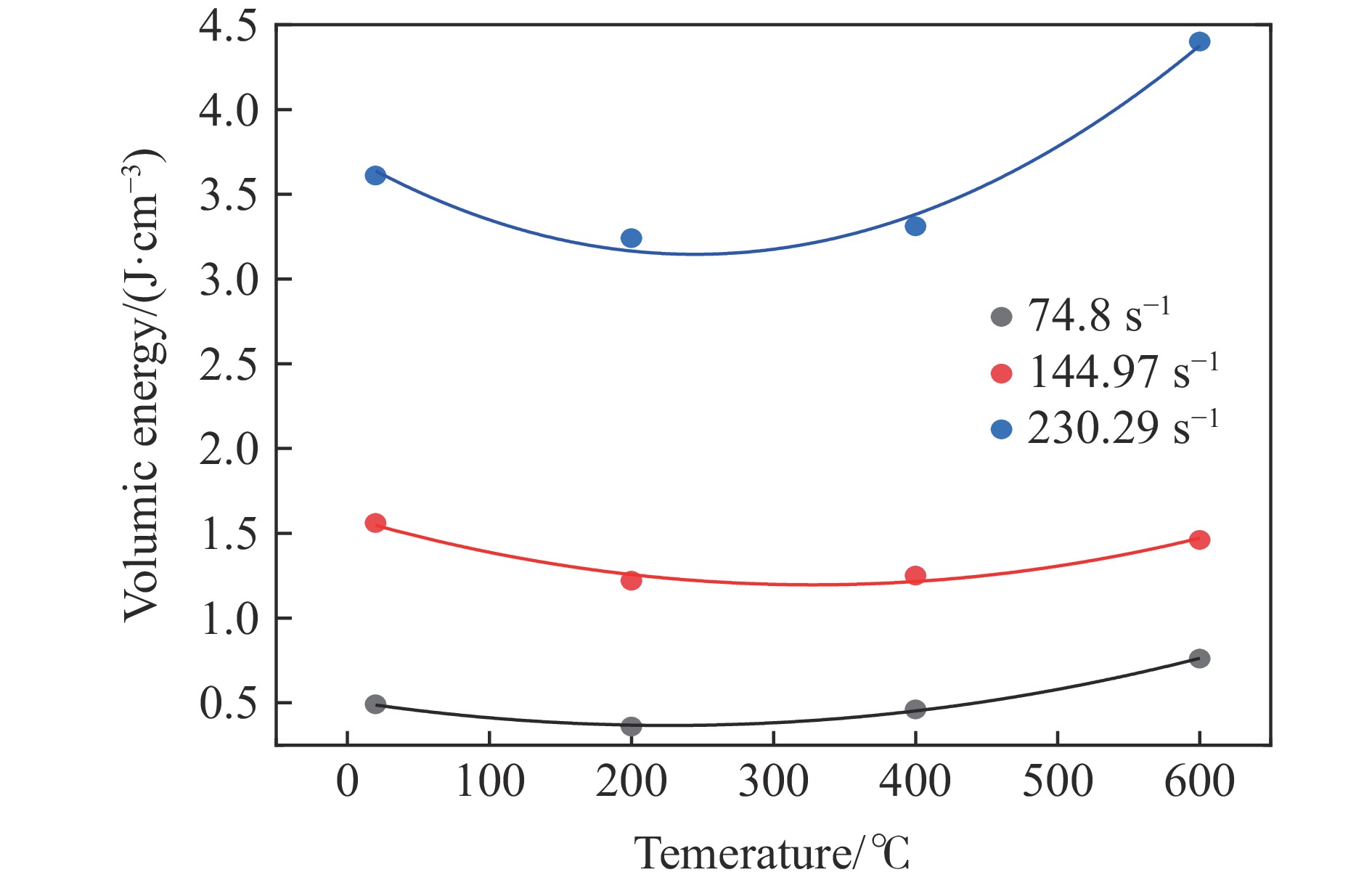
Table 3. Volumic energy

$\bar \varepsilon$ /s⁻¹ w/(J·cm⁻³)
20 ℃ 200 ℃ 400 ℃ 600 ℃ 800 ℃

74.80 0.49 0.36 0.46 0.76 0.49
144.97 1.56 1.22 1.25 1.46 1.56
230.29 3.61 3.24 3.31 4.40 3.61

下载: 导出CSV

表 4 矿物成分的质量分数（%）

Table 4. Mass fraction (%) of the components

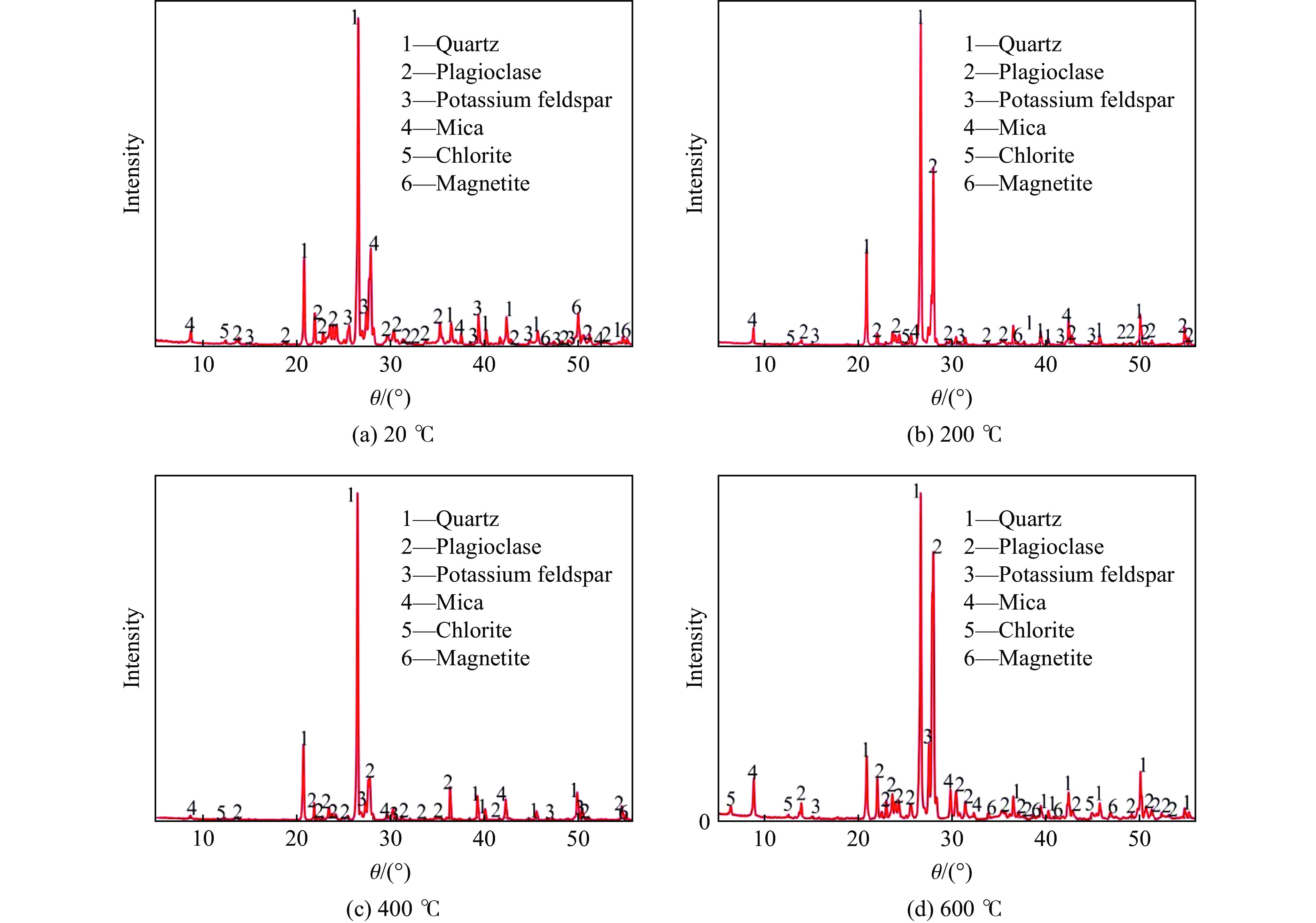
温度/℃ 石英长石云母绿泥石磁铁矿

20 53.4 32.2 7.2 2.2 5.0
200 52.5 35.6 8.4 1.7 0.5
400 77.4 17.1 3.4 1.4 0.7
600 33.3 50.0 13.2 1.5 0.6

下载: 导出CSV

参考文献(30)

[1]	闫治国, 朱合华, 梁利. 火灾高温下隧道衬砌管片力学性能试验 [J]. 同济大学学报(自然科学版), 2012, 40(6): 823–828. DOI: 10.3969/j.issn.0253-374x.2012.06.004. YAN Z G, ZHU H H, LIANG L. Experimental study on mechanical performance of lining segments in fire accidents [J]. Journal of Tongji University (Natural Science), 2012, 40(6): 823–828. DOI: 10.3969/j.issn.0253-374x.2012.06.004.
[2]	MARTÍN-GAMBOA M, IRIBARREN D, DUFOUR J. On the environmental suitability of high-and low-enthalpy geothermal systems [J]. Geothermics, 2015, 53: 27–37. DOI: 10.1016/j.geothermics.2014.03.012.
[3]	杨丹. 三次采油化学驱油技术现状与未来展望 [J]. 化学工程与装备, 2021(1): 216–217. DOI: 10.19566/j.cnki.cn35-1285/tq.2021.01.099.
[4]	唐红梅, 周云涛, 陈洪凯, 等. 地下工程爆破对危岩稳定性的影响 [J]. 爆炸与冲击, 2015, 35(2): 278–284. DOI: 10.11883/1001-1455(2015)02-0278-07. TANG H M, ZHOU Y T, CHEN H K, et al. Impact study on stability of unstable rock under underground construction blasting [J]. Explosion and Shock Waves, 2015, 35(2): 278–284. DOI: 10.11883/1001-1455(2015)02-0278-07.
[5]	罗生银, 窦斌, 田红, 等. 自然冷却后与实时高温下花岗岩物理力学性质对比试验研究 [J]. 地学前缘, 2020, 27(1): 178–184. DOI: 10.13745/j.esf.2020.1.19. LUO S Y, DOU B, TIAN H, et al. Comparative experimental study on physical and mechanical properties of granite after natural cooling and under real-time high temperature [J]. Earth Science Frontiers, 2020, 27(1): 178–184. DOI: 10.13745/j.esf.2020.1.19.
[6]	范飞林, 许金余. 大直径SHPB实验中的高温加载技术及其应用 [J]. 爆炸与冲击, 2013, 33(1): 54–60. DOI: 10.11883/1001-1455(2013)01-0054-07. FAN F L, XU J Y. High-temperature loading techniques in large-diameter SHPB experiment and its application [J]. Explosion and Shock Waves, 2013, 33(1): 54–60. DOI: 10.11883/1001-1455(2013)01-0054-07.
[7]	寇绍全, ALM O. 微裂隙和花岗岩的抗拉强度 [J]. 力学学报, 1987, 19(4): 366–373. DOI: 10.6052/0459-1879-1987-4-1987-045. KOU S Q, ALM O. Microcracks and the tensile strength of granite [J]. Acta Mechanica Sinica, 1987, 19(4): 366–373. DOI: 10.6052/0459-1879-1987-4-1987-045.
[8]	吴刚, 翟松韬, 王宇. 高温下花岗岩的细观结构与声发射特性研究 [J]. 岩土力学, 2015, 36(S1): 351–356. DOI: 10.16285/j.rsm.2015.S1.060. WU G, ZHAI S T, WANG Y. Research on characteristics of mesostructure and acoustic emission of granite under high temperature [J]. Rock and Soil Mechanics, 2015, 36(S1): 351–356. DOI: 10.16285/j.rsm.2015.S1.060.
[9]	赵阳升, 孟巧荣, 康天合, 等. 显微CT试验技术与花岗岩热破裂特征的细观研究 [J]. 岩石力学与工程学报, 2008, 27(1): 28–34. DOI: 10.3321/j.issn:1000-6915.2008.01.005. ZHAO Y S, MENG Q R, KANG T H, et al. Micro-CT experimental technology and meso-investigation on thermal fracturing characteristics of granite [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 28–34. DOI: 10.3321/j.issn:1000-6915.2008.01.005.
[10]	赵阳升, 万志军, 张渊, 等. 岩石热破裂与渗透性相关规律的试验研究 [J]. 岩石力学与工程学报, 2010, 29(10): 1970–1976. ZHAO Y S, WAN Z J, ZHANG Y, et al. Experimental study of related laws of rock thermal cracking and permeability [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1970–1976.
[11]	张静华, 王靖涛, 赵爱国. 高温下花岗岩断裂特性的研究 [J]. 岩土力学, 1987, 8(4): 11–16. DOI: 10.16285/j.rsm.1987.04.005. ZHANG J H, WANG J T, ZHAO A G. Fracture properies of granite at high temperature [J]. Rock and Soil Mechanics, 1987, 8(4): 11–16. DOI: 10.16285/j.rsm.1987.04.005.
[12]	王靖涛, 赵爱国, 黄明昌. 花岗岩断裂韧度的高温效应 [J]. 岩土工程学报, 1989, 11(6): 113–118. DOI: 10.3321/j.issn:1000-4548.1989.06.015. WANG J T, ZHAO A G, HUANG M C. Effect of high temperature on the fracture toughness of granite [J]. Chinese Journal of Geotechnical Engineering, 1989, 11(6): 113–118. DOI: 10.3321/j.issn:1000-4548.1989.06.015.
[13]	YIN T B, SHU R H, LI X B, et al. Comparison of mechanical properties in high temperature and thermal treatment granite [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1926–1937. DOI: 10.1016/S1003-6326(16)64311-X.
[14]	尹土兵, 李夕兵, 殷志强, 等. 高温后砂岩静、动态力学特性研究与比较 [J]. 岩石力学与工程学报, 2012, 31(2): 273–279. DOI: 10.3969/j.issn.1000-6915.2012.02.006. YIN T B, LI X B, YIN Z Q, et al. Study and comparison of mechanical properties of sandstone under static and dynamic loadings after high temperature [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 273–279. DOI: 10.3969/j.issn.1000-6915.2012.02.006.
[15]	王超, 尹土兵. 实时高温下与热处理后砂岩动态拉伸特性研究 [J]. 工程爆破, 2021, 27(6): 9–17,51. DOI: 10.19931/j.EB.20210022. WANG C, YIN T B. Study on dynamic tensile properties of sandstone at real-time high temperatures and after thermal treatment [J]. Engineering Blasting, 2021, 27(6): 9–17,51. DOI: 10.19931/j.EB.20210022.
[16]	许锡昌, 刘泉声. 高温下花岗岩基本力学性质初步研究 [J]. 岩土工程学报, 2000, 22(3): 332–335. DOI: 10.3321/j.issn:1000-4548.2000.03.014. XU X C, LIU Q S. A preliminary study on basic mechanical properties for granite at high temperature [J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 332–335. DOI: 10.3321/j.issn:1000-4548.2000.03.014.
[17]	王鹏, 许金余, 刘石, 等. 高温下砂岩动态力学特性研究 [J]. 兵工学报, 2013, 34(2): 203–208. DOI: 10.3969/j.issn.1000-1093.2013.02.012. WANG P, XU J Y, LIU S, et al. Research on dynamic mechanical properties of sandstone at high temperature [J]. Acta Armamentarii, 2013, 34(2): 203–208. DOI: 10.3969/j.issn.1000-1093.2013.02.012.
[18]	平琦, 吴波, 吴明静, 等. 高温状态下岩石SHPB实验方法探究 [J]. 中国多媒体与网络教学学报(上旬刊), 2021(2): 205–207.
[19]	刘石, 许金余. 高温作用对花岗岩动态压缩力学性能的影响研究 [J]. 振动与冲击, 2014, 33(4): 195–198. DOI: 10.3969/j.issn.1000-3835.2014.04.035. LIU S, XU J Y. Effect of high temperature on dynamic compressive mechanical properties of granite [J]. Journal of Vibration and Shock, 2014, 33(4): 195–198. DOI: 10.3969/j.issn.1000-3835.2014.04.035.
[20]	LI Y B, ZHAI Y, WANG C S, et al. Mechanical properties of Beishan granite under complex dynamic loads after thermal treatment [J]. Engineering Geology, 2020, 267: 105481. DOI: 10.1016/j.enggeo.2020.105481.
[21]	尹土兵. 考虑温度效应的岩石动力学行为研究 [D]. 长沙: 中南大学, 2012. YIN T B. Study on dynamic behavior of rocks considering thermai, effect [D]. Changsha: Central South University, 2012.
[22]	刘贵, 周永胜. 花岗岩剪切变形与矿物成分变化的高温高压实验 [J]. 地质通报, 2020, 39(11): 1840–1849. LIU G, ZHOU Y S. An experimental study of shear deformation and mineral composition changes of granite under the condition of high temperature and high pressure [J]. Geological Bulletin of China, 2020, 39(11): 1840–1849.
[23]	张森, 舒彪, 梁铭, 等. 不同冷却方式下高温花岗岩细观损伤量化和机理分析 [J]. 煤田地质与勘探, 2022, 50(2): 106–114. DOI: 10.3969/j.issn.1001-1986.2022.02.013. ZHANG S, SHU B, LIANG M, et al. Quantification and mechanism analysis of meso-damage of high-temperature granite under different cooling modes [J]. Coal Geology & Exploration, 2022, 50(2): 106–114. DOI: 10.3969/j.issn.1001-1986.2022.02.013.
[24]	王春, 熊宏威, 舒荣华, 等. 高温处理后含铜矽卡岩的动态力学特性及损伤破碎特征 [J]. 中国有色金属学报, 2022, 32(9): 2801–2818. WANG C, XIONG H W, SHU R H, et al. Dynamic mechanical characteristic and damage-fracture behavior of deep copper-bearing skarn after high temperature treatment [J]. The Chinese Journal of Nonferrous Metals, 2022, 32(9): 2801–2818.
[25]	徐小丽, 高峰, 张志镇, 等. 实时高温下加载速率对花岗岩力学特性影响的试验研究 [J]. 岩土力学, 2015, 36(8): 2184–2192. DOI: 10.16285/j.rsm.2015.08.008. XU X L, GAO F, ZHANG Z Z, et al. Experimental study of the effect of loading rates on mechanical properties of granite at real-time high temperature [J]. Rock and Soil Mechanics, 2015, 36(8): 2184–2192. DOI: 10.16285/j.rsm.2015.08.008.
[26]	张志镇, 高峰, 高亚楠, 等. 高温影响下花岗岩孔径分布的分形结构及模型 [J]. 岩石力学与工程学报, 2016, 35(12): 2426–2438. DOI: 10.13722/j.cnki.jrme.2016.0798. ZHANG Z Z, GAO F, GAO Y N, et al. Fractal structure and model of pore size distribution of granite under high temperatures [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2426–2438. DOI: 10.13722/j.cnki.jrme.2016.0798.
[27]	席道瑛. 花岗岩中矿物相变的物性特征 [J]. 矿物学报, 1994, 14(3): 223–227. DOI: 10.16461/j.cnki.1000-4734.1994.03.003. XI D Y. Physical characteristics of mineral phase transition in the granite [J]. Acta Mineralogica Sinica, 1994, 14(3): 223–227. DOI: 10.16461/j.cnki.1000-4734.1994.03.003.
[28]	许金余, 刘石. 大理岩冲击加载试验碎块的分形特征分析 [J]. 岩土力学, 2012, 33(11): 3225–3229. DOI: 10.16285/j.rsm.2012.11.005. XU J Y, LIU S. Research on fractal characteristics of marble fragments subjected to impact loading [J]. Rock and Soil Mechanics, 2012, 33(11): 3225–3229. DOI: 10.16285/j.rsm.2012.11.005.
[29]	ZHANG Z X, KOU S Q, JIANG L G, et al. Effects of loading rate on rock fracture: fracture characteristics and energy partitioning [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 745–762. DOI: 10.1016/S1365-1609(00)00008-3.
[30]	许金余, 吕晓聪, 张军, 等. 围压条件下岩石循环冲击损伤的能量特性研究 [J]. 岩石力学与工程学报, 2010, 29(S2): 4159–4165. XU J Y, LV X C, ZHANG J, et al. Research on energy properties of rock cyclical impact damage under confining pressure [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 4159–4165.

施引文献

期刊类型引用(12)

1.	赵伟成，翟红波，李尚青，毛伯永. 高原环境爆炸冲击波传播规律及计算模型研究. 火工品. 2025(01): 62-69 . 百度学术
2.	雒泓宇，胡宇鹏，冯晓伟，王峰军，李明海. 典型炸药对高海拔长直坑道内爆炸冲击波阵面温度传播特性的影响. 清华大学学报(自然科学版). 2025(04): 721-731 . 百度学术
3.	Rui Li，Minghang Hu，Rui Sun，Yajing Chen，Yan Li，Quan Wang，Xiaorong Cui. Triple point path prediction for height of burst explosion in high-altitude environment. Defence Technology. 2025(04): 109-119 . 必应学术
4.	汪泉，胡程，谢守冬，李孝臣，李志敏，涂唱畅，朱群龙，杨锐. 负压条件对T2/Q235爆炸焊接复合板界面的影响. 火炸药学报. 2024(01): 64-71 . 百度学术
5.	李勇，雒泓宇，冯晓伟，胡宇鹏，张军，李海涛. 海拔高度对长直坑道内爆炸冲击波传播的影响. 爆炸与冲击. 2024(03): 105-117 . 本站查看
6.	李瑞，杨耀勇，汪泉，徐小猛，洪晓文. 高海拔环境下运动装药的爆炸冲击波特性. 火炸药学报. 2024(02): 159-171 . 百度学术
7.	李超，何兆，马重夫，陈铭德. 凹陷地形对固体推进剂近地爆炸冲击波影响的数值分析. 工程爆破. 2024(02): 34-41 . 百度学术
8.	刘赛，韩体飞，王猛，陈凯强，刘广鹏，姜鑫，孙彦臣. 低温环境对乳化炸药爆炸性能的影响. 高压物理学报. 2024(04): 139-146 . 百度学术
9.	杨洋，杜红棉，郭晋杰，王孺豪. 基于深度学习的残缺冲击波信号构建方法. 中北大学学报(自然科学版). 2024(05): 687-694 . 百度学术
10.	刘泉，姚箭，宋先钊，蒋欣利，李斌，王永旭，张丹，解立峰，张国凯. 初始环境压力对RDX基温压炸药冲击波超压和温度的影响. 北京理工大学学报. 2024(09): 913-922 . 百度学术
11.	李子涵，程扬帆，王浩，朱守军，沈兆武. 负压环境对乳化炸药爆炸温度场和有害效应的影响. 爆炸与冲击. 2023(08): 30-42 . 本站查看
12.	杨锐，汪泉，谢守冬，李瑞，涂唱畅，徐小猛，李孝臣. 负压爆炸载荷作用下固支钢板变形研究. 高压物理学报. 2023(05): 82-90 . 百度学术

其他类型引用(2)

资源附件(0)

访问统计

图(20) / 表(4)

计量

文章访问数: 571
HTML全文浏览量: 167
PDF下载量: 110
被引次数: 14

1. 爆炸冲击波参量的理论分析
1.1 爆炸冲击波参量的影响因素
1.2 爆炸冲击波参量的量纲分析
2. 爆炸冲击波参量的数值模拟
2.1 计算模型
2.2 材料参数
2.3 网格尺寸的收敛性分析
3. 结果与分析
3.1 标准大气环境下爆炸冲击波参量
3.2 低温和低压环境下的爆炸冲击波参量
3.3 高海拔环境下的爆炸冲击波参量
3.4 冲击波波阵面运动规律
4. 结　论

1. 爆炸冲击波参量的理论分析
1.1 爆炸冲击波参量的影响因素
1.2 爆炸冲击波参量的量纲分析
2. 爆炸冲击波参量的数值模拟
2.1 计算模型
2.2 材料参数
2.3 网格尺寸的收敛性分析
3. 结果与分析
3.1 标准大气环境下爆炸冲击波参量
3.2 低温和低压环境下的爆炸冲击波参量
3.3 高海拔环境下的爆炸冲击波参量
3.4 冲击波波阵面运动规律
4. 结　论

参考文献(30)

施引文献

资源附件(0)

访问统计

气压/MPa	冲击速率/（m∙s⁻¹）	平均应变率/s⁻¹
0.2	5.4	74.80
0.4	8.8	144.97
0.6	11.3	230.29

平均应变率/s⁻¹	试件峰值应力/MPa
平均应变率/s⁻¹	20 ℃	200 ℃	400 ℃	600 ℃	800 ℃
74.80	125.25	132.08	103.43	92.517	0
144.97	164.39	178.38	161.38	114.59	0
230.29	188.91	190.91	174.00	135.80	0

$\bar \varepsilon$ /s⁻¹	w/(J·cm⁻³)
$\bar \varepsilon$ /s⁻¹	20 ℃	200 ℃	400 ℃	600 ℃	800 ℃
74.80	0.49	0.36	0.46	0.76	0.49
144.97	1.56	1.22	1.25	1.46	1.56
230.29	3.61	3.24	3.31	4.40	3.61

温度/℃	石英	长石	云母	绿泥石	磁铁矿
20	53.4	32.2	7.2	2.2	5.0
200	52.5	35.6	8.4	1.7	0.5
400	77.4	17.1	3.4	1.4	0.7
600	33.3	50.0	13.2	1.5	0.6

实时高温作用下花岗岩冲击压缩力学特性研究

doi: 10.11883/bzycj-2022-0196

作者简介: 黄耀莹（1999－ ），女，硕士研究生，2021126140@chd.edu.cn

通讯作者: 屈 璐（1983－ ），女，博士，讲师，qulu@chd.edu.cn

计量

出版历程

Mechanical properties of granite under impact compression after real-time high temperature

1. 爆炸冲击波参量的理论分析

1.1 爆炸冲击波参量的影响因素

1.2 爆炸冲击波参量的量纲分析

2. 爆炸冲击波参量的数值模拟

2.1 计算模型

2.2 材料参数

2.3 网格尺寸的收敛性分析

3. 结果与分析

3.1 标准大气环境下爆炸冲击波参量

3.2 低温和低压环境下的爆炸冲击波参量

3.3 高海拔环境下的爆炸冲击波参量

3.4 冲击波波阵面运动规律

4. 结 论

期刊类型引用(12)

其他类型引用(2)

计量

出版历程

目录

1. 爆炸冲击波参量的理论分析

1.1 爆炸冲击波参量的影响因素

1.2 爆炸冲击波参量的量纲分析

2. 爆炸冲击波参量的数值模拟

2.1 计算模型

2.2 材料参数

2.3 网格尺寸的收敛性分析

3. 结果与分析

3.1 标准大气环境下爆炸冲击波参量

3.2 低温和低压环境下的爆炸冲击波参量

3.3 高海拔环境下的爆炸冲击波参量

3.4 冲击波波阵面运动规律

4. 结 论

作者简介:
黄耀莹（1999－　），女，硕士研究生，2021126140@chd.edu.cn

通讯作者:
屈　璐（1983－　），女，博士，讲师，qulu@chd.edu.cn

4. 结　论

4. 结　论