舱内爆炸角隅汇聚反射冲击波超压特性研究

刘博文; 龙仁荣; 张庆明; 巨圆圆; 钟贤哲; 汪海洋; 刘文近

doi:10.11883/bzycj-2022-0232

舱内爆炸角隅汇聚反射冲击波超压特性研究

doi: 10.11883/bzycj-2022-0232

1.
北京理工大学爆炸科学与技术国家重点实验室，北京100081
2.
海军研究院，北京 100161

基金项目: 国家自然科学基金（11902356）

详细信息

作者简介:
刘博文（1996－　），男，硕士研究生，liubowen610@163.com

通讯作者:
龙仁荣（1982－　），男，博士，副教授，longrenrong@bit.edu.cn

中图分类号: O383; O344.7
计量
- 文章访问数: 649
- HTML全文浏览量: 165
- PDF下载量: 179
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-30
- 修回日期: 2022-08-17
- 网络出版日期: 2022-08-30
- 刊出日期: 2023-01-05

Study on the corner overpressure characteristics of concentrated reflected shock wave due to internal blast in cabin

1.
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
2.
Naval Research Institute, Beijing 100161, China

摘要

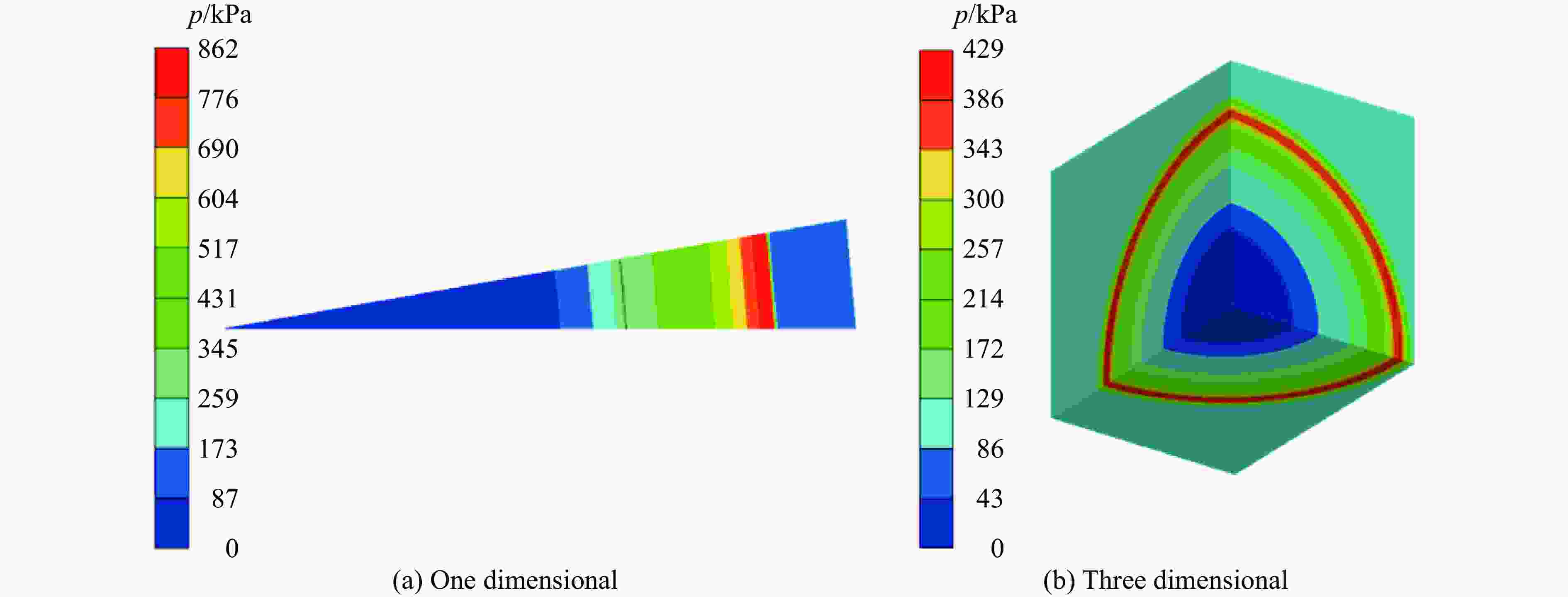
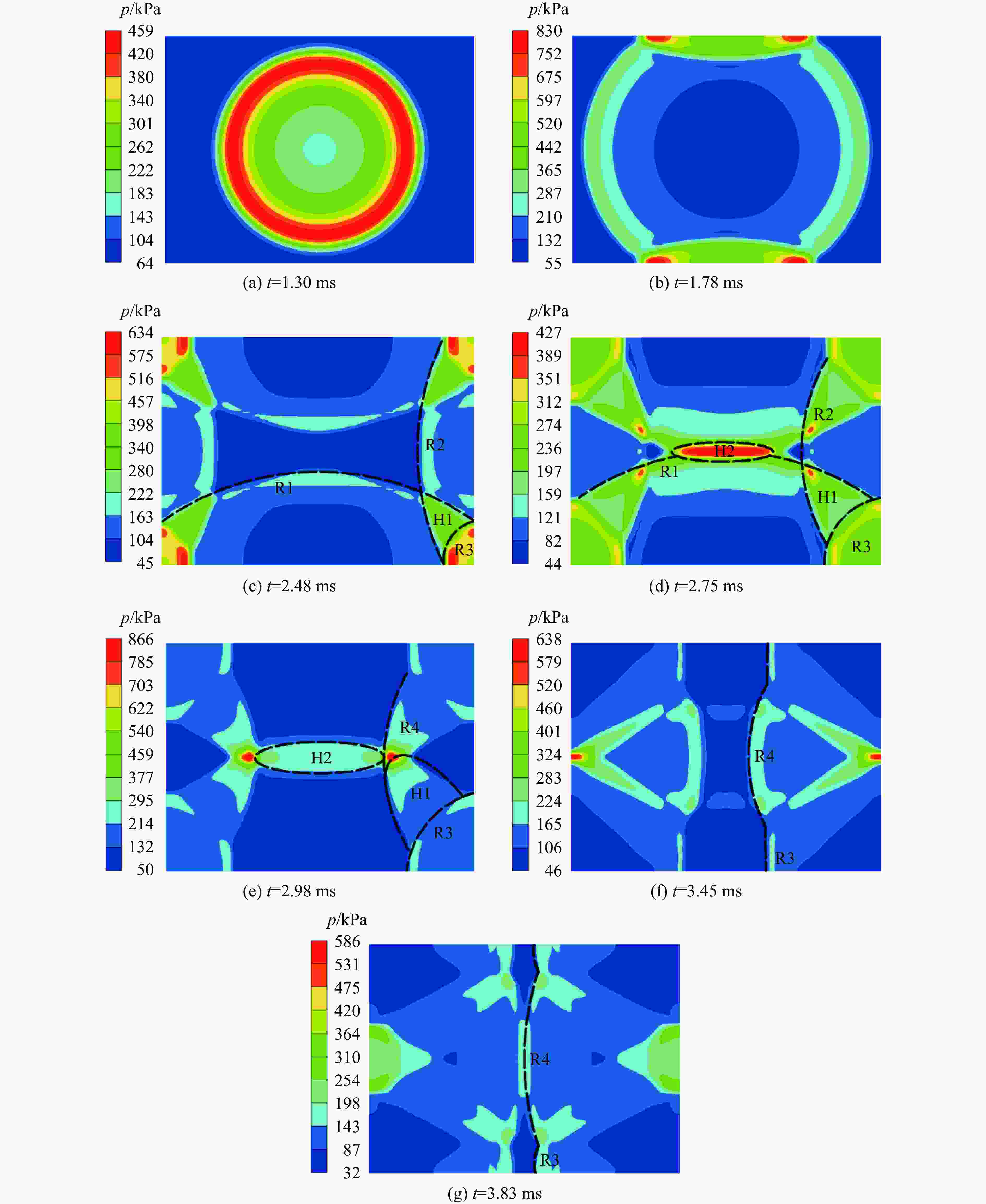
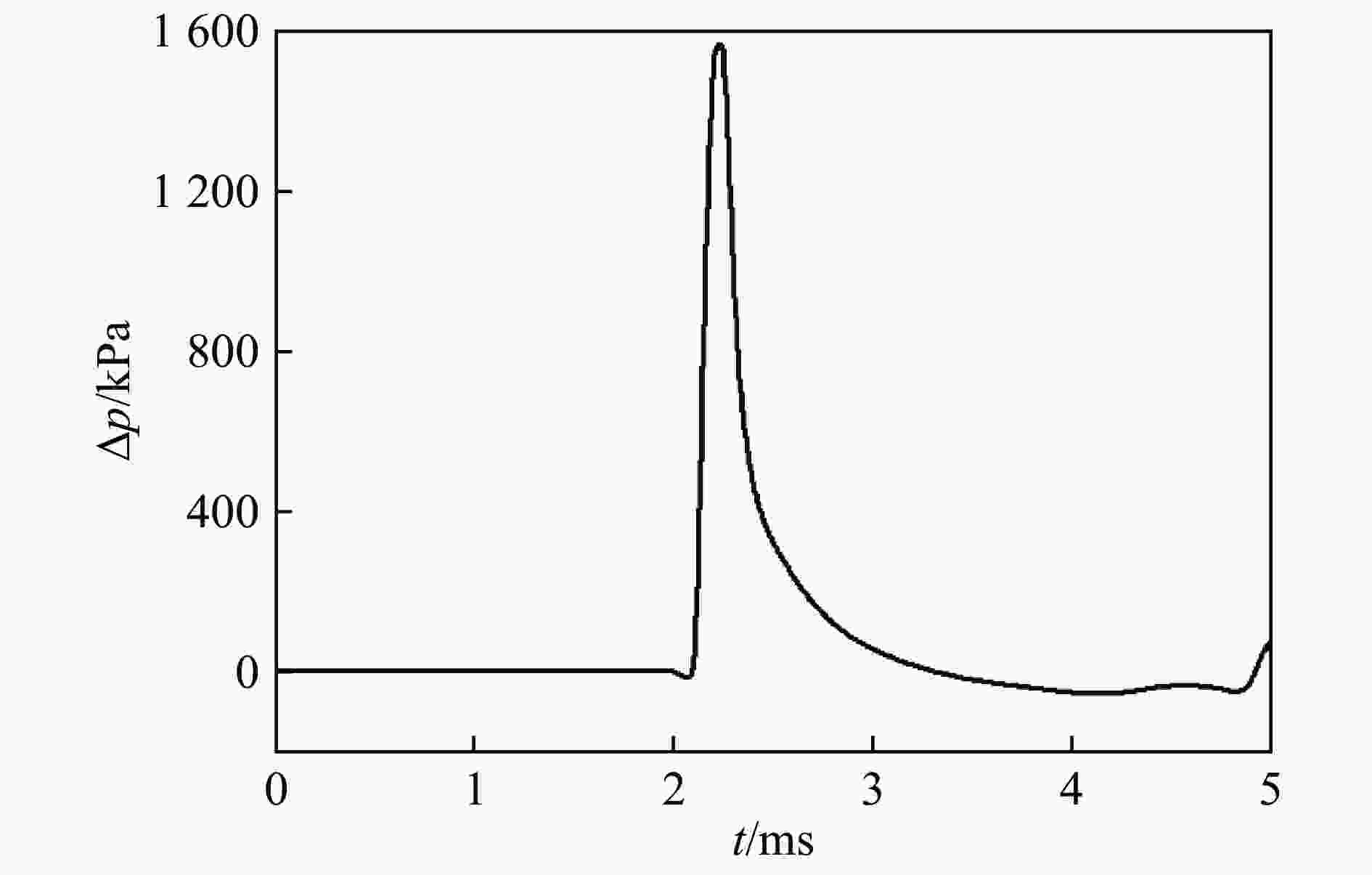
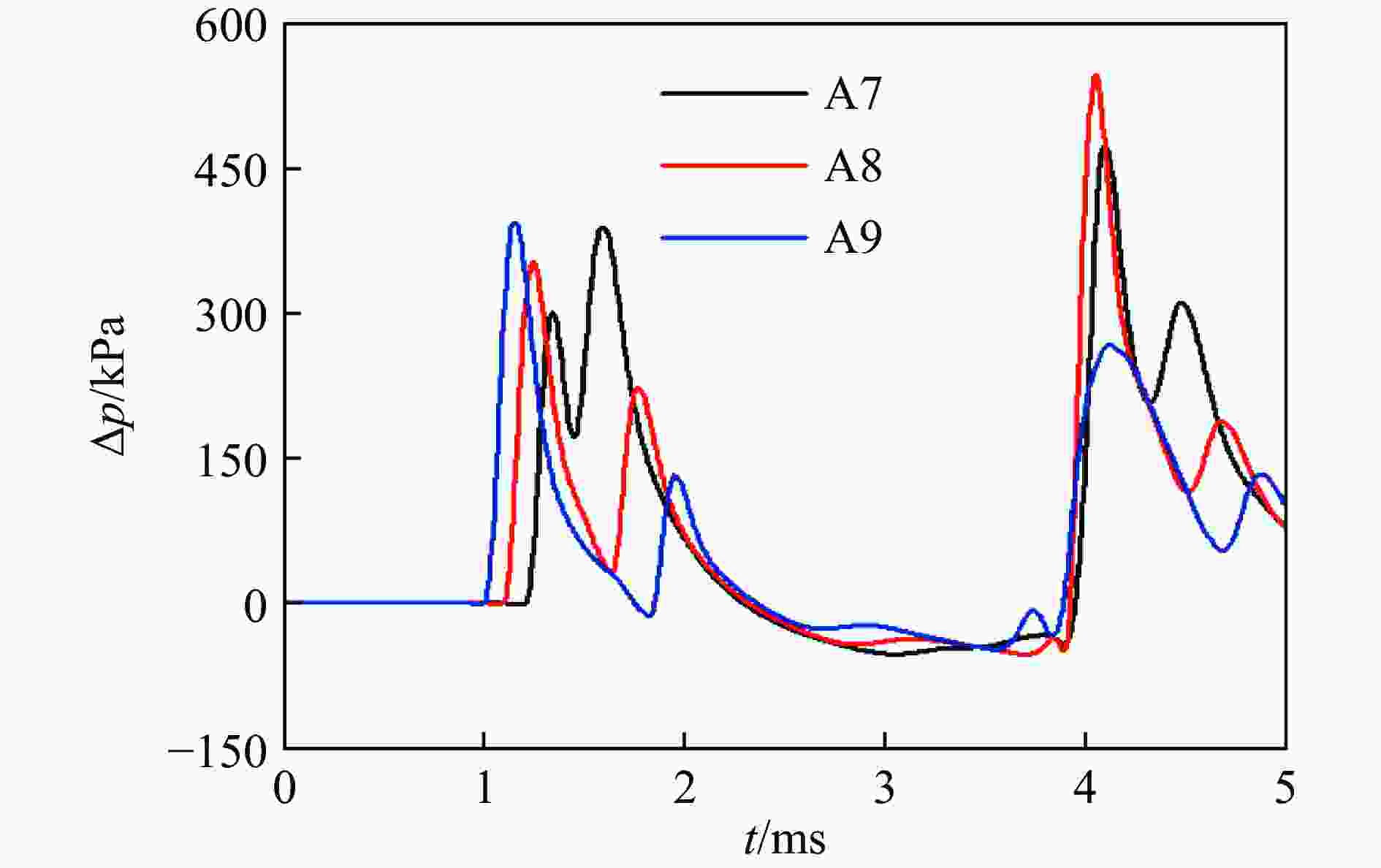
摘要: 为研究密闭舱室内爆角隅汇聚反射冲击波超压特性，利用缩比模型进行了某典型舱室内爆试验，得到远离角隅、两面角隅和三面角隅处的冲击波载荷，结合数值模拟研究了3种特征位置处冲击波传播规律及载荷特征。研究结果表明：远离角隅处壁面反射冲击波超压曲线呈现单峰结构，反射冲击波以球面波传播；距两面角隅一定范围内冲击波超压曲线呈现双峰结构，两面角隅冲击波超压曲线呈现单峰结构，角隅汇聚反射冲击波以椭球状传播；距三面角隅一定范围内冲击波超压曲线呈现多峰结构，三面角隅冲击波超压曲线呈现单峰结构，角隅汇聚反射冲击波以球面波传播；在合理假设条件下，根据量纲分析及数值模拟结果，得到首次冲击时角隅汇聚反射冲击波载荷经验计算公式。
- 舱内爆炸 /
- 角隅 /
- 冲击波 /
- 量纲分析
Abstract: In order to study the propagation law and load characteristics of shock wave at the corner due to the internal blast in a closed cabin, a typical cabin explosion test was carried out using a scaled model. Overpressure loads of shock wave in one-sided, two-sided and three-sided corners were obtained. The EULER-FCT algorithm in the AUTODYN software was used to simulate the explosion test in the cabin, and the shock wave propagation law and load characteristics at three characteristic positions were studied. The results show that the overpressure time history curve of the wall reflected shock wave far from the corner is a single-peak structure, and the reflected shock wave propagates in a spherical shape. Within a certain range from the two-sided corner, the shock wave overpressure curve is a double-peak structure. The shock wave overpressure time history curve at the edge of the two-sided corner is a single-peak structure. And the corner convergent shock wave propagates in an ellipsoid shape. The peak overpressure and specific impulse of the two-sided corner convergent shock wave are about 1.83 times and 3.77 times more than those of the wall reflected shock wave at the same position. Within a certain range from the three-sided corner, the shock wave overpressure curve is a multi-peak structure. The shock wave overpressure time history curve at the three-sided corner is a single-peak structure. And the corner convergent shock wave propagates in a spherical shape. The converging ability of the three-sided corner to the shock wave is stronger than that of the two-sided corner. The peak overpressure and specific impulse of the converging shock wave in the three-sided corner are about 7.6 times and 10.4 times those of the wall reflected shock wave at the same position. Under certain assumptions, according to dimensional analysis and numerical simulation of typical compartments under different TNT charge internal explosion conditions, an empirical calculation formula of corner convergent reflected shock wave load at the first impact was obtained.
- internal blast /
- corner /
- shock wave /
- dimensional analysis

HTML全文

图 1 试验舱室

Figure 1. Test cabin

下载: 全尺寸图片幻灯片

图 2 传感器位置示意图

Figure 2. Schematic of sensor positions

下载: 全尺寸图片幻灯片

图 3 舱内爆炸试验结果

Figure 3. Results of cabin explosion test

下载: 全尺寸图片幻灯片

图 4 数值模拟模型

Figure 4. Numerical simulation model

下载: 全尺寸图片幻灯片

图 5 冲击波压力云图

Figure 5. Shock wave pressure contours

下载: 全尺寸图片幻灯片

图 6 试验与数值模拟冲击波超压曲线对比

Figure 6. Comparison of shock wave overpressure curves between test and numerical simulation

下载: 全尺寸图片幻灯片

图 7 yOz平面不同时刻冲击波压力云图

Figure 7. Shock wave pressure contour at different times on the yOz plane

下载: 全尺寸图片幻灯片

图 8 三面角隅不同时刻冲击波压力云图

Figure 8. Shock wave pressure contours at different times at the three-sided corner

下载: 全尺寸图片幻灯片

图 9 舱室底面不同时刻冲击波压力云图

Figure 9. Shock wave pressure distribution at the bottom of the cabin at different times

下载: 全尺寸图片幻灯片

图 10 测点布置

Figure 10. Layout of measuring points layout

下载: 全尺寸图片幻灯片

图 11 两面角隅处测点冲击波超压曲线

Figure 11. Shock wave overpressure curve of the measuring points at the two-sided corner

下载: 全尺寸图片幻灯片

图 12 两面角隅冲击波与壁面反射冲击波峰值超压和比冲量的比值随装药量的变化

Figure 12. Ratio of peak overpressure and specific impulse of two-sided corner shock wave to wall-reflected shock wave as a function of charge

下载: 全尺寸图片幻灯片

图 13 三面角隅处测点6冲击波超压曲线

Figure 13. Shock wave overpressure curve of the measuring point 6 at the three-sided corner

下载: 全尺寸图片幻灯片

图 14 三面角隅冲击波与壁面反射冲击波峰值超压和比冲量的比值随装药量的变化

Figure 14. Ratio of the peak overpressure and the specific impulse of the three-sided corner shock wave to wall-reflected shock wave as a function of charge mass

下载: 全尺寸图片幻灯片

图 15 测点A7、A8和A9的冲击波超压曲线

Figure 15. Shock wave overpressure curves at measuring points A7, A8 and A9

下载: 全尺寸图片幻灯片

图 16 测点A12、A13和A14的冲击波超压曲线

Figure 16. Shock wave overpressure curves at measuring points A12, A13 and A14

下载: 全尺寸图片幻灯片

图 17 两面角隅和三面角隅汇聚反射冲击波作用范围

Figure 17. Range of converging reflected shock waves at the two-sided corner and the three-sided corner

下载: 全尺寸图片幻灯片

图 18 数值模拟布局

Figure 18. Numerical simulation layout

下载: 全尺寸图片幻灯片

图 19 两面角隅边线数值模拟结果与拟合公式对比

Figure 19. Comparison of two-sided corner simulation results and fitting formula

下载: 全尺寸图片幻灯片

图 20 三面角隅数值模拟结果与拟合公式对比图

Figure 20. Comparison of three-sided corner simulation results and fitting formula

下载: 全尺寸图片幻灯片

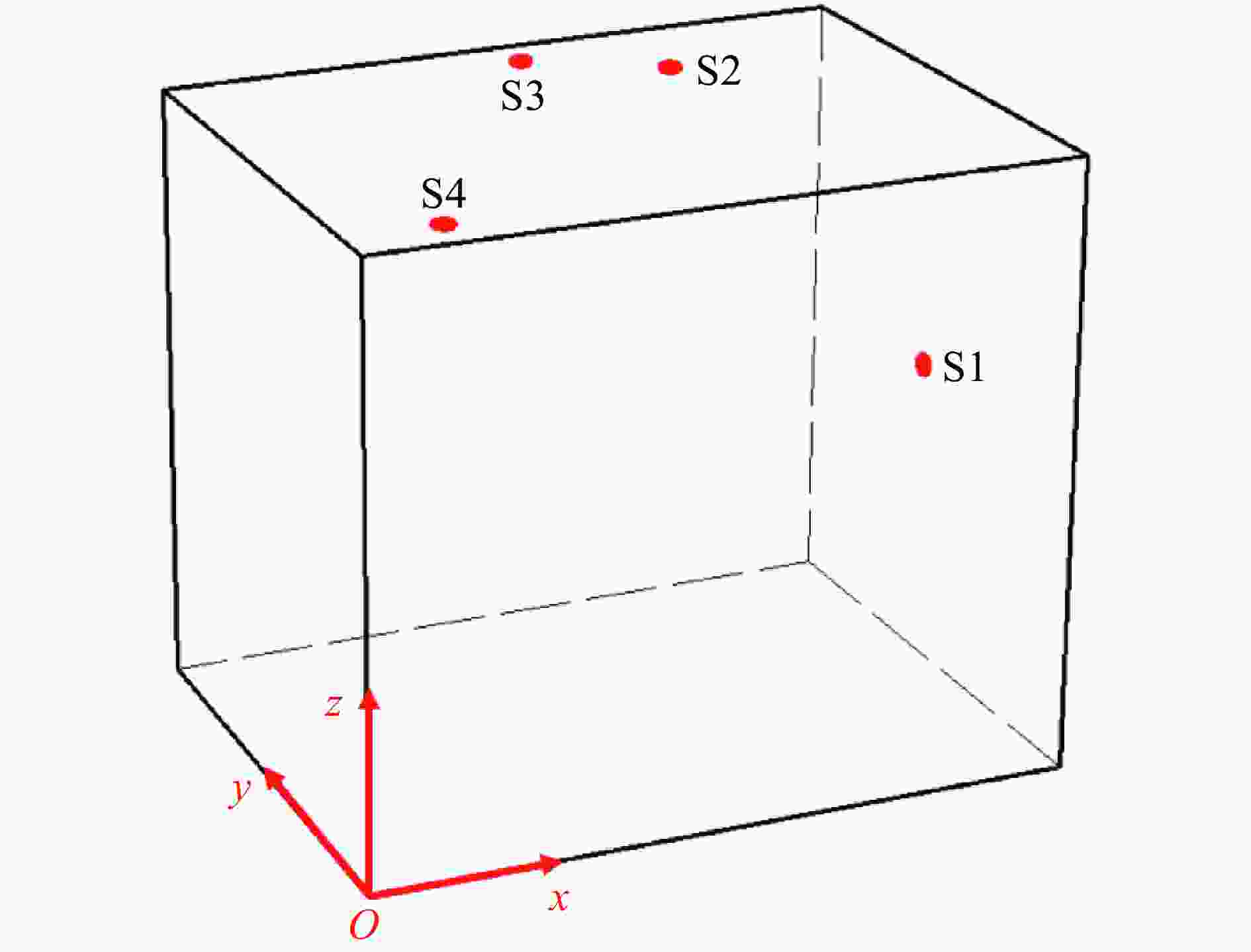
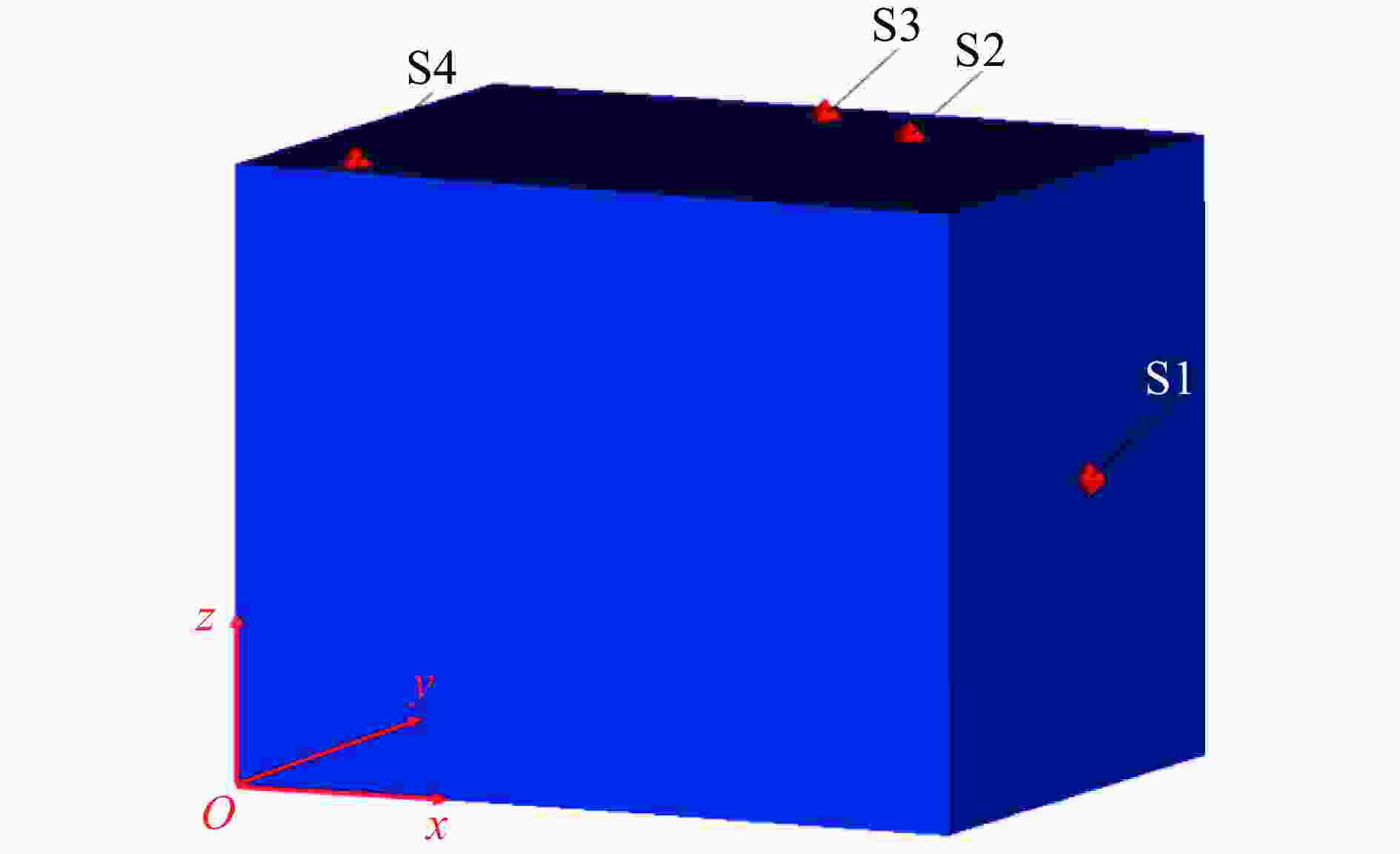
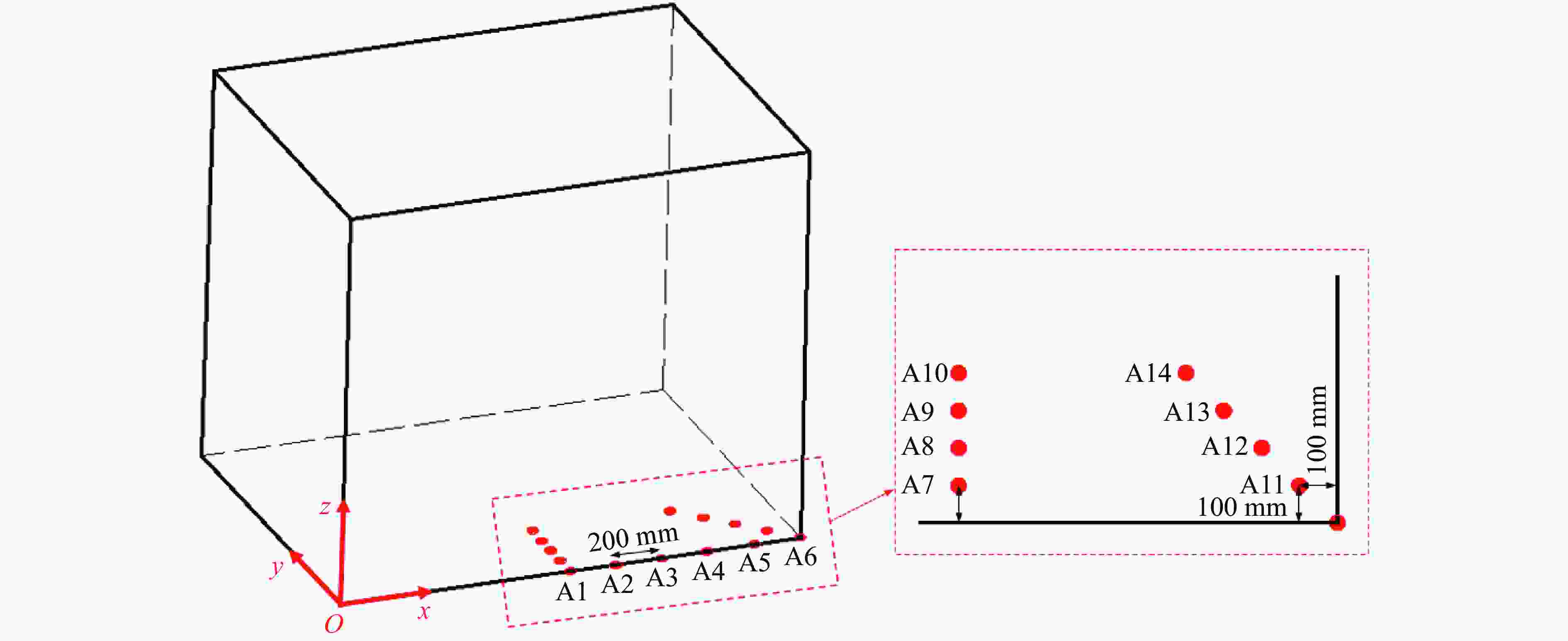
表 1 压力测点空间坐标

Table 1. Sensor coordinates

测点	x/m	y/m	z/m
S1	2.000	0.825	0.880
S2	1.349	1.130	1.750
S3	1.000	1.360	1.750
S4	0.270	0.140	1.750

下载: 导出CSV

表 2 各测点峰值超压和比冲量

Table 2. Overpressures and specific impulses at different measuring points

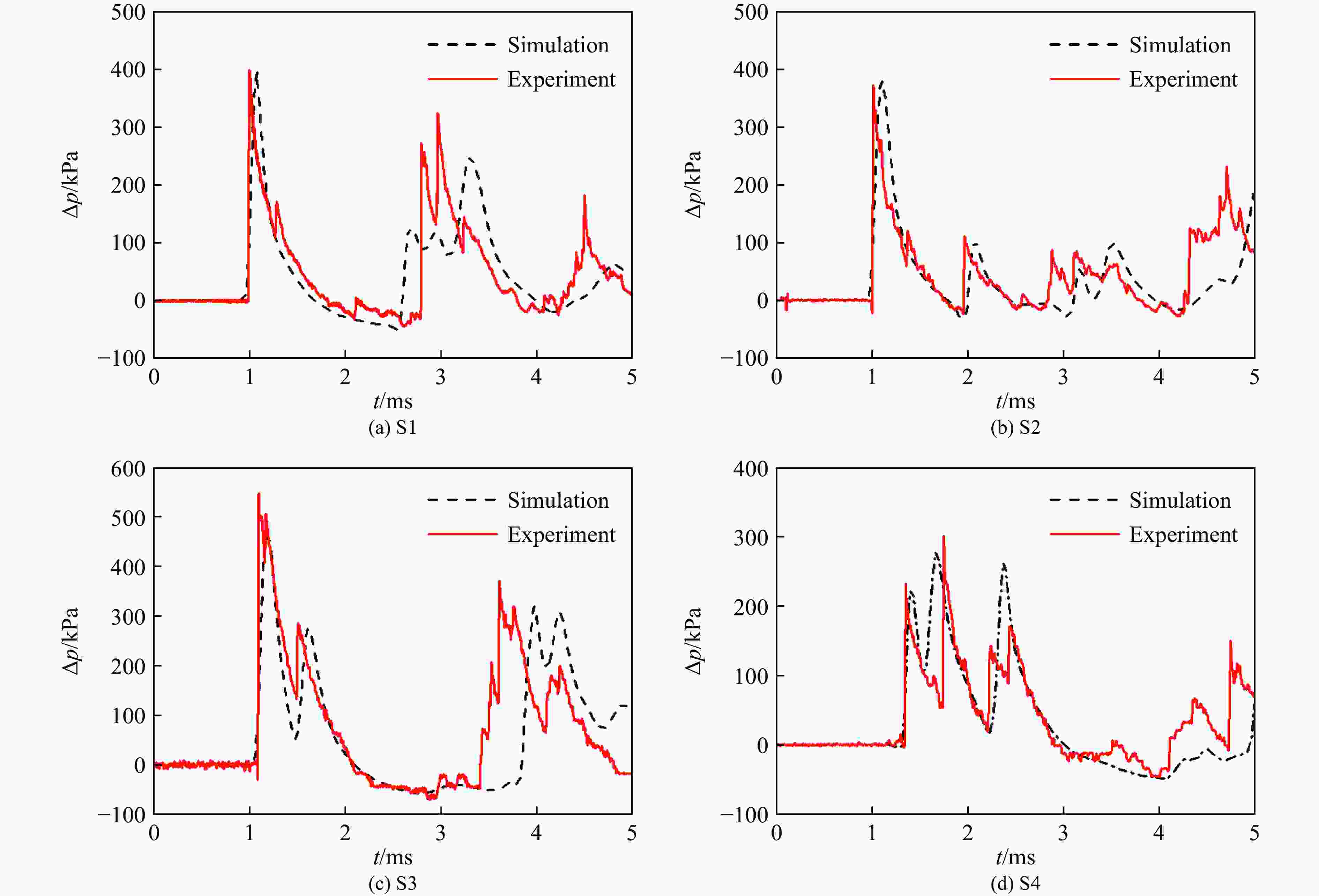
测点编号	距爆心距离/m	压力/kPa			比冲量/(Pa·s)
测点编号	距爆心距离/m	第1个峰值	第2个峰值	第3个峰值	比冲量/(Pa·s)
S1	1.00	401.22	*	*	93.48
S2	1.02	396.35	*	*	82.76
S3	1.07	528.87	326.64	*	154.24
S4	1.29	231.69	301.58	170.46	160.81
注：*表示该测点处没有后续压力峰值。

下载: 导出CSV

表 3 TNT炸药材料参数

Table 3. Material parameters of TNT

ρ_e/(kg·m⁻³)	D/(m·s⁻¹)	C₁/MPa	C₂/MPa	r₁	r₂	ω	v
1630	6930	3.74×10⁵	3.75×10³	4.15	0.9	0.35	1

下载: 导出CSV

表 4 试验与数值模拟结果对比

Table 4. Comparison of experimental and simulation results

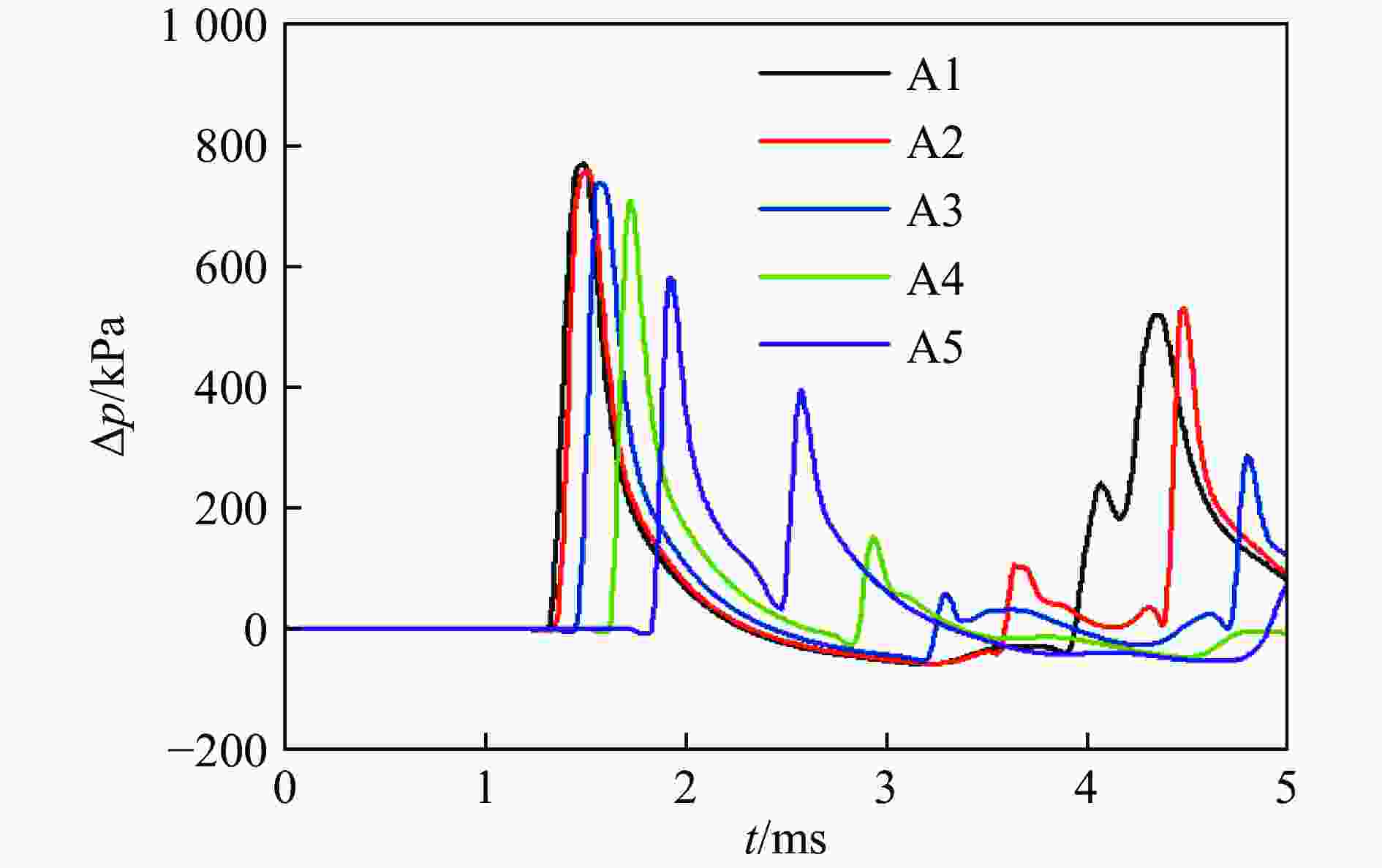
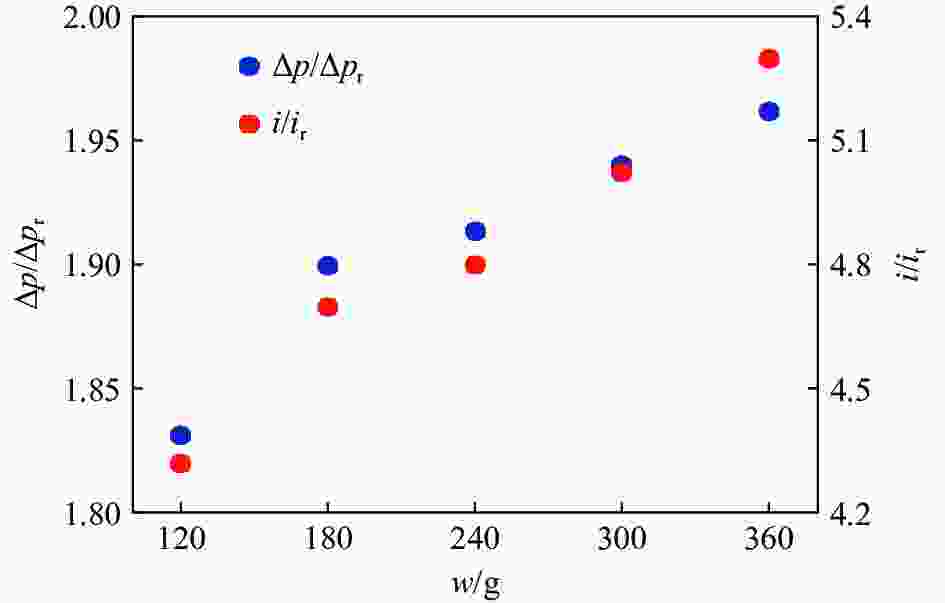
测点	超压/kPa		误差/%
测点	试验	数值模拟	误差/%
S1	401.22	396.99	−1.0
S2	396.35	378.64	−4.5
S3	528.87	461.56	−12.7
S4	231.69	224.49	−3.1

下载: 导出CSV

表 5 两面角隅汇聚反射冲击波与壁面反射冲击波对比

Table 5. Comparison of the two-sided corner convergent reflect shock waves and the wall reflected shock waves

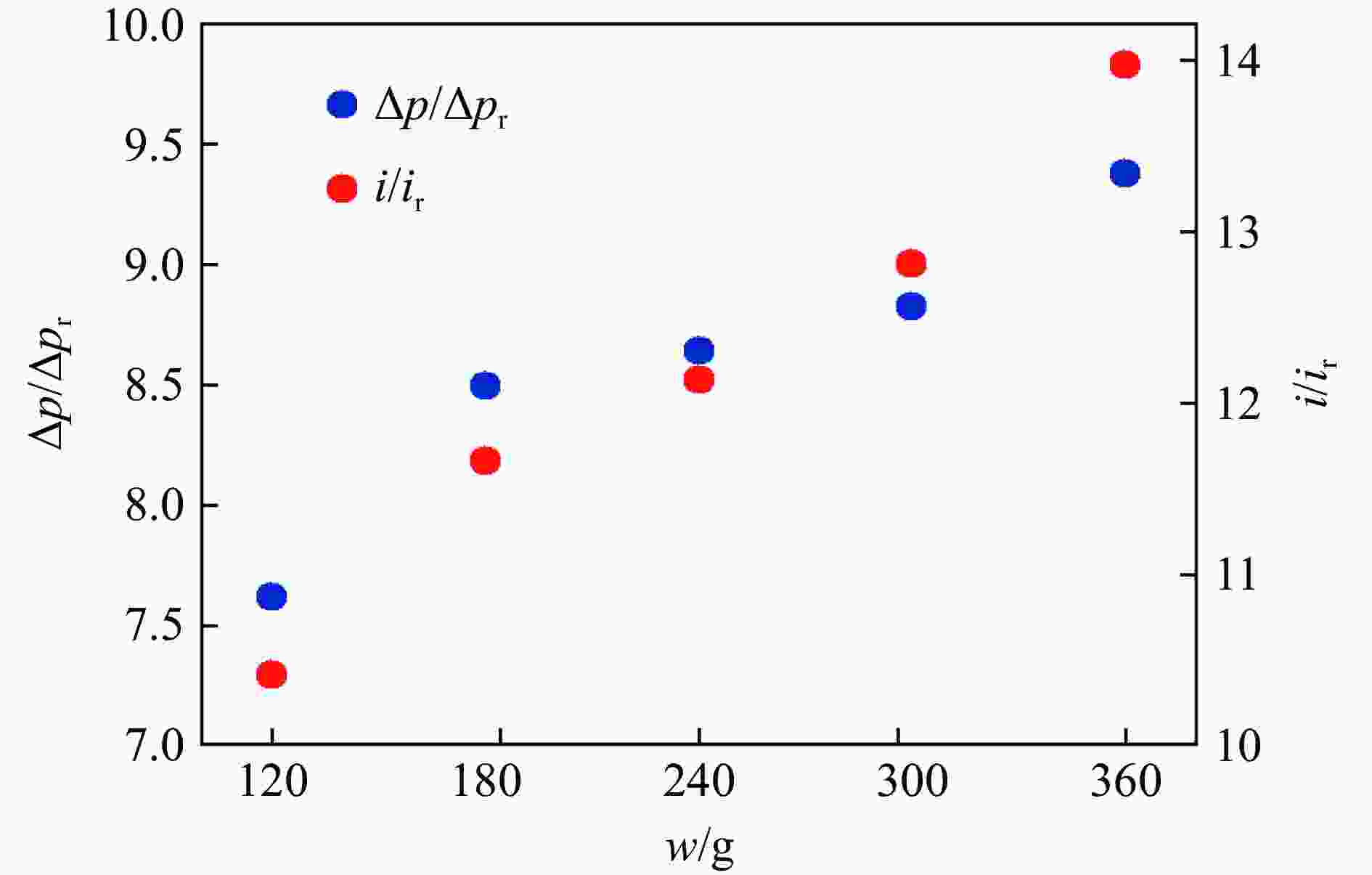
测点	Δp/kPa	i/(Pa·s)	Δp_r/kPa	i_r/(Pa·s)	Δp/Δp_r	i/i_r
A1	769.19	228.02	420.39	52.77	1.83	4.32
A2	756.34	222.03	403.43	51.99	1.87	4.27
A3	736.43	203.17	360.41	49.86	2.04	4.07
A4	707.06	176.29	305.71	46.81	2.31	3.77

下载: 导出CSV

表 6 测点空间坐标

Table 6. Measuring point coordinates

测点	L₁/m	L₂/m	L₃/m
1	1	1.5	1.75
2	1.125	1.5	1.75
3	1.25	1.5	1.75
4	1.375	1.5	1.75
5	1.5	1.5	1.75
6	2	1.5	0.875
7	2	1.5	1
8	2	1.5	1.125
9	2	1.5	1.25
10	2	1.5	1.375
11	2	0.75	1.75
12	2	0.875	1.75
13	2	1.0	1.75
14	2	1.125	1.75
15	2	1.25	1.75

下载: 导出CSV

表 7 两面角隅冲击波载荷数值模拟结果与拟合结果对比

Table 7. Comparison between simulation results and fitting results of shock wave load at the two-sided corner

w/kg	L₁/m	L₂/m	L₃/m	Δp/kPa		误差/%
w/kg	L₁/m	L₂/m	L₃/m	数值模拟	拟合	误差/%
0.16	1	1.5	1.75	1035.87	1099.89	6.2
0.22	1.125	1.5	1.75	1420.92	1447.98	1.9
0.28	1.25	1.5	1.75	1778.55	1768.30	−0.5
0.34	1.375	1.5	1.75	2094.97	2065.73	−1.4

下载: 导出CSV

表 8 三面角隅冲击波载荷数值模拟结果与拟合结果对比汇总表

Table 8. Comparison between simulation results and fitting results of shock wave load at the three-sided corner

w/kg	Δp/kPa		误差/%
w/kg	数值模拟	拟合	误差/%
0.16	2128.14	2105.47	−1.1
0.22	2957.61	2938.67	−0.6
0.28	3743.49	3782.76	1
0.34	4525.83	4635.46	2.4

下载: 导出CSV

表 9 不同尺寸下三面角隅处数值模拟结果与拟合结果对比

Table 9. Comparison of simulation results and fitting results at the three-sided corner under different sizes

H/m	w/kg	Δp/kPa		误差/%
H/m	w/kg	数值模拟	拟合	误差/%
1	0.6	75759.469	74112.974	−2.2
2	0.75	9961.668	10612.649	6.5
3	0.86	3508.824	3427.298	−2.3
4	0.95	1682.378	1539.208	−8.5
5	1.0	935.492	806.687	−13.7
6	1.1	666.898	502.730	−24.6

下载: 导出CSV

参考文献(18)

[1]	张同冰, 赵鹏铎, 李营. 基于AUTODYN的舱室内爆结构响应数值研究 [J]. 兵工学报, 2015, 36(S1): 103–107. ZHANG T B, ZHAO P D, LI Y. Numerical research on response of ship structure under internal explosion based on AUTODYN [J]. Acta Armamentarii, 2015, 36(S1): 103–107.
[2]	侯海量, 朱锡, 李伟, 等. 舱内爆炸冲击载荷特性实验研究 [J]. 船舶力学, 2010, 14(8): 901–907. DOI: 10.3969/j.issn.1007-7294.2010.08.011. HOU H L, ZHU X, LI W, et al. Experimental studies on characteristics of blast loading when exploded inside ship cabin [J]. Journal of Ship Mechanics, 2010, 14(8): 901–907. DOI: 10.3969/j.issn.1007-7294.2010.08.011.
[3]	侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析 [J]. 爆炸与冲击, 2007, 27(2): 151–158. DOI: 10.11883/1001-1455(2007)02-0151-08. HOU H L, ZHU X, MEI Z Y. Study on the blast load and failure mode of ship structure subject to internal explosion [J]. Explosion and Shock Waves, 2007, 27(2): 151–158. DOI: 10.11883/1001-1455(2007)02-0151-08.
[4]	李营, 张磊, 杜志鹏, 等. 舱室结构在战斗部舱内爆炸作用下毁伤特性的实验研究 [J]. 船舶力学, 2018, 22(8): 993–1000. DOI: 10.3969/j.issn.1007-7294.2018.08.009. LI Y, ZHANG L, DU Z P, et al. Experiment investigation on damage characteristic of cabins under warhead internal blast [J]. Journal of Ship Mechanics, 2018, 22(8): 993–1000. DOI: 10.3969/j.issn.1007-7294.2018.08.009.
[5]	姚熊亮, 屈子悦, 姜子飞, 等. 舰船舱内爆炸载荷特征与板架毁伤规律分析 [J]. 中国舰船研究, 2018, 13(3): 140–148. DOI: 10.19693/j.issn.1673-3185.01162. YAO X L, QU Z Y, JIANG Z F, et al. Analysis on characteristics of blast loading and stiffened plate damage due to internal blast in ship [J]. Chinese Journal of Ship Research, 2018, 13(3): 140–148. DOI: 10.19693/j.issn.1673-3185.01162.
[6]	BAKER W E, COX P A, WESTINE P S, et al. Explosion hazards and evaluation [M]. New York: Elsevier Scientific Publishing Company, 1983.
[7]	United Facility Creteria. Structures to resist the effects of accidental explosions, with Change 2: UFC 3-340-2 [S]. US Department of the Army, Navy and Air Force Technical Manual, 2008.
[8]	丁阳, 陈晔, 师燕超. 室内爆炸超压荷载简化模型 [J]. 工程力学, 2015, 32(3): 119–125,133. DOI: 10.6052/j.issn.1000-4750.2013.09.0874. DING Y, CHEN Y, SHI Y C. Simplified model of overpressure loading caused by internal blast [J]. Engineering Mechanics, 2015, 32(3): 119–125,133. DOI: 10.6052/j.issn.1000-4750.2013.09.0874.
[9]	陈鹏宇, 侯海量, 金键, 等. 舰船舱内爆炸载荷简化载荷计算模型 [J]. 舰船科学技术, 2020, 42(9): 22–29. DOI: 10.3404/j.issn.1672-7649.2020.09.005. CHEN P Y, HOU H L, JIN J, et al. Simplified calculation model for explosion loading in ship cabin [J]. Ship Science and Technology, 2020, 42(9): 22–29. DOI: 10.3404/j.issn.1672-7649.2020.09.005.
[10]	孔祥韶, 吴卫国, 李俊, 等. 角隅结构对舱内爆炸载荷影响的实验研究 [J]. 中国造船, 2012, 53(3): 40–50. DOI: 10.3969/j.issn.1000-4882.2012.03.007. KONG X S, WU W G, LI J, et al. Experimental research of influence of corner structure on blast loading under inner explosion [J]. Shipbuilding of China, 2012, 53(3): 40–50. DOI: 10.3969/j.issn.1000-4882.2012.03.007.
[11]	HU Y, WU C Q, LUKASZEWICZ M, et al. Characteristics of confined blast loading in unvented structures [J]. International Journal of Protective Structures, 2011, 2(1): 21–43. DOI: 10.1260/2041-4196.2.1.21.
[12]	姚迪, 罗刚, 谢伟, 等. 裸装药舱内爆炸压力载荷规律研究 [J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(1): 168–173. DOI: 10.3963/j.issn.2095-3844.2019.01.033. YAO D, LUO G, XIE W, et al. Study on the law of explosion pressure load in bare charge chamber [J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2019, 43(1): 168–173. DOI: 10.3963/j.issn.2095-3844.2019.01.033.
[13]	ZYSKOWSKI A, SOCHET I, MAVROT G, et al. Study of the explosion process in a small scale experiment-structural loading [J]. Journal of Loss Prevention in the Process Industries, 2004, 17(4): 291–299. DOI: 10.1016/j.jlp.2004.05.003.
[14]	FELDGUN V R, KARINSKI Y S, EDRI I, et al. On blast pressure analysis due to a partially confined explosion: Ⅱ. Numerical Studies [J]. International Journal of Protective Structures, 2012, 3(1): 61–79. DOI: 10.1260/2041-4196.3.1.61.
[15]	WU C Q, LUKASZEWICZ M, SCHEBELLA K, et al. Experimental and numerical investigation of confined explosion in a blast chamber [J]. Journal of Loss Prevention in the Process Industries, 2013, 2 6(4): 737-750. DOI: 10.1016/j.jlp.2013.02.001.
[16]	BENSELAMA A M, WILLIAM-LOUIS M J P, MONNOYER F. A 1D–3D mixed method for the numerical simulation of blast waves in confined geometries [J]. Journal of Computational Physics, 2009, 228(18): 6796–6810. DOI: 10.1016/j.jcp.2009.06.010.
[17]	北京工业学院八系《爆炸及其作用》编写组. 爆炸及其作用: 爆炸对目标的作用和穿甲作用 [M]. 北京: 国防工业出版社, 1979.
[18]	FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. Some characteristics of an interior explosion within a room without venting [J]. Structural Engineering and Mechanics, 2011, 38(5): 633–649. DOI: 10.12989/sem.2011.38.5.633.