在椭圆横截面弹体正侵彻下有限厚铝靶的破坏模式及响应特性

刘均伟; 张先锋; 赵瑶瑶; 魏海洋; 刘闯; 李鹏程

doi:10.11883/bzycj-2022-0249

在椭圆横截面弹体正侵彻下有限厚铝靶的破坏模式及响应特性

doi: 10.11883/bzycj-2022-0249

刘均伟^1,,
张先锋^1, ,,
赵瑶瑶²,
魏海洋^{1, 3},
刘闯¹,
李鹏程¹

1.
南京理工大学机械工程学院，江苏南京 210094
2.
江苏永丰机械有限责任公司，江苏淮安 211722
3.
北京航天长征飞行器研究所，北京 100074

基金项目: 国家自然科学基金（12141202，11790292）；中央高校基本科研业务费（30919011401）

详细信息

作者简介:
刘均伟（1996－　），男，博士研究生，liujunwei@njust.edu.cn

通讯作者:
张先锋（1978－　），男，博士，教授，lynx@njust.edu.cn

中图分类号: O385
计量
- 文章访问数: 367
- HTML全文浏览量: 134
- PDF下载量: 98
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-08
- 修回日期: 2022-08-25
- 网络出版日期: 2022-09-16
- 刊出日期: 2022-12-08

Failure modes and response characteristics of finite-thickness aluminum targets under normal penetration of elliptical cross-section projectiles

1.
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
2.
Jiangsu Yongfeng Machinery Co. Ltd., Huai’an 211722, Jiangsu, China
3.
Beijing Institute of Space Long March Vehicle, Beijing 100074, China

摘要

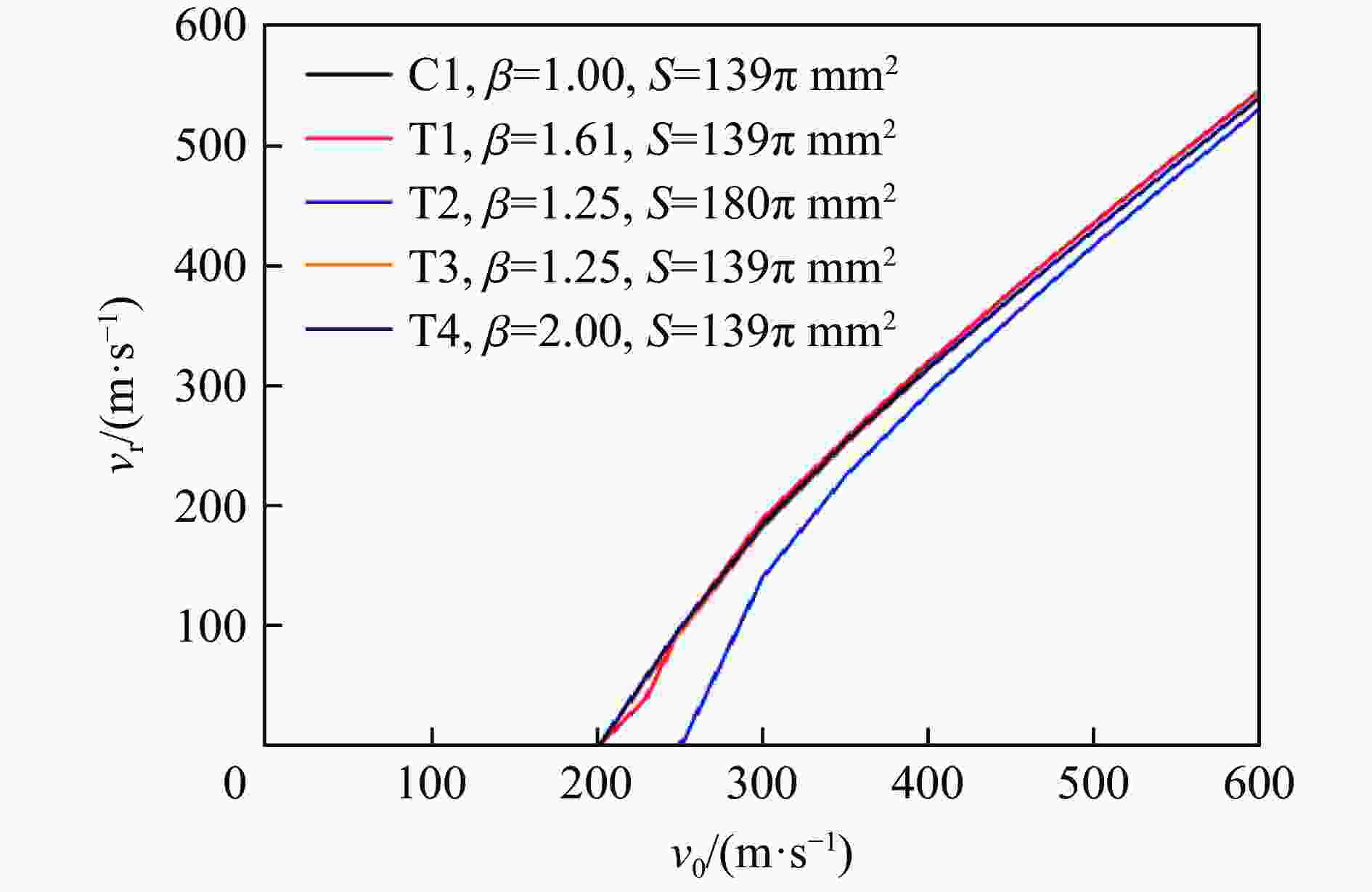
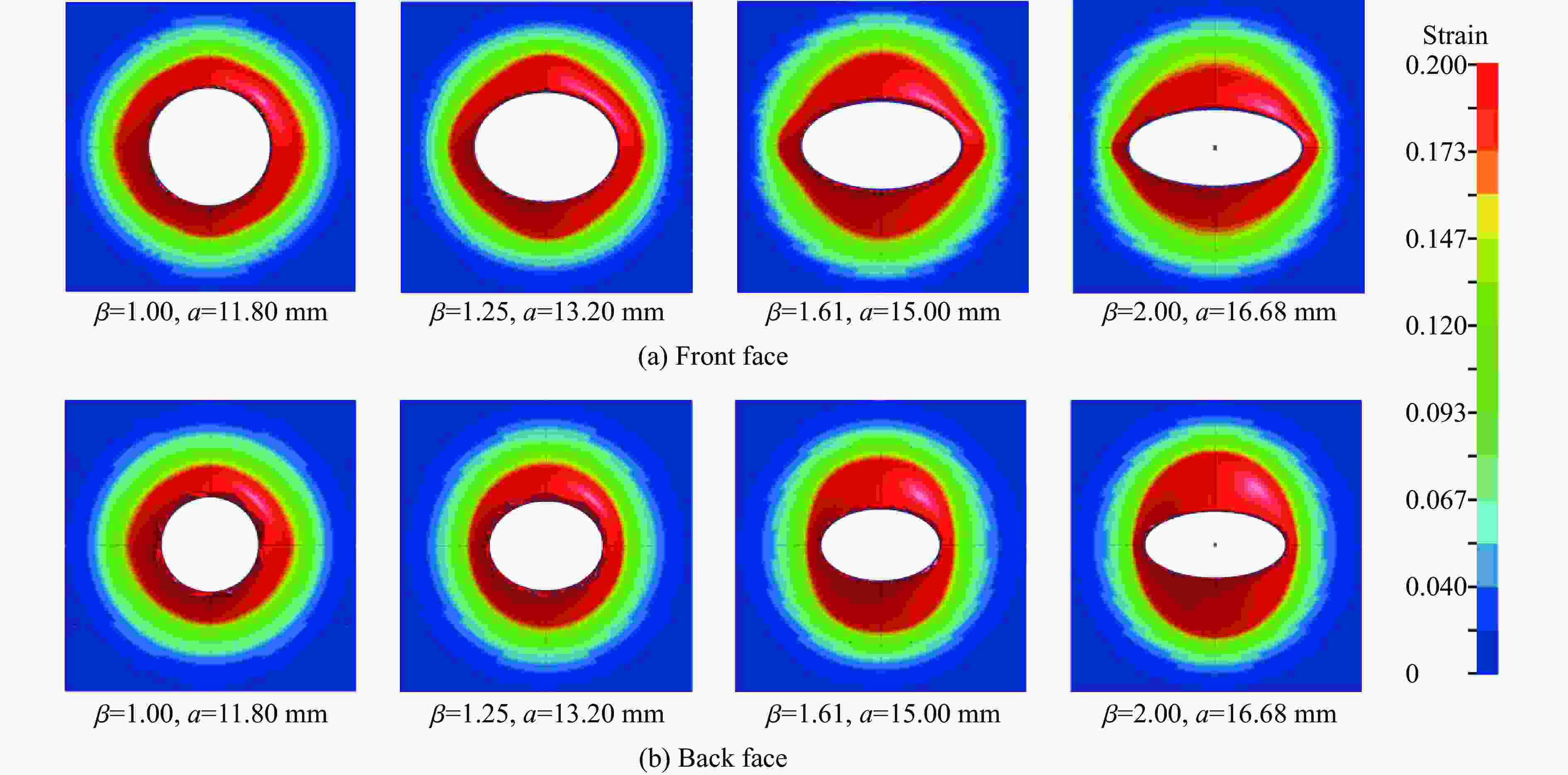
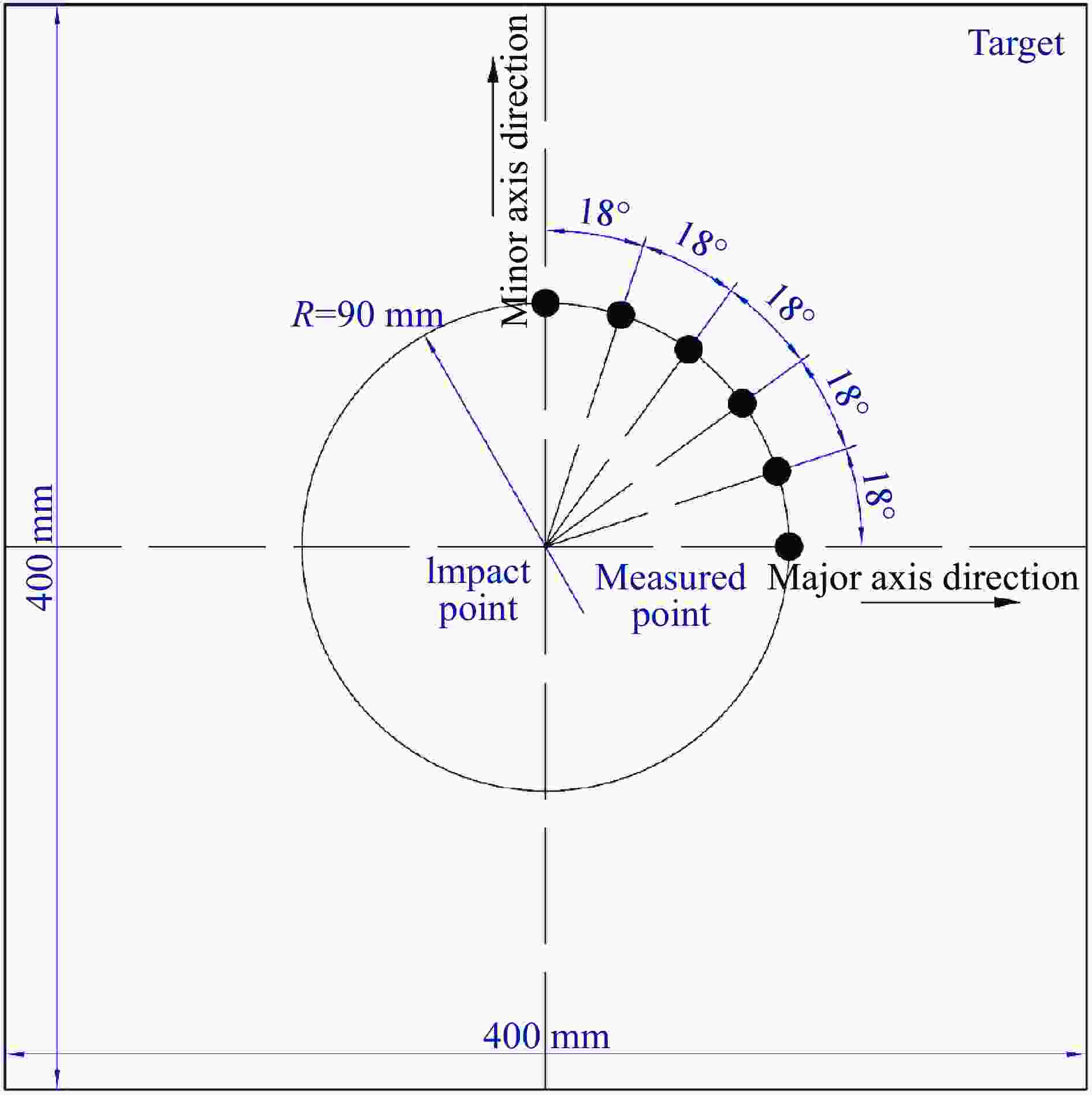
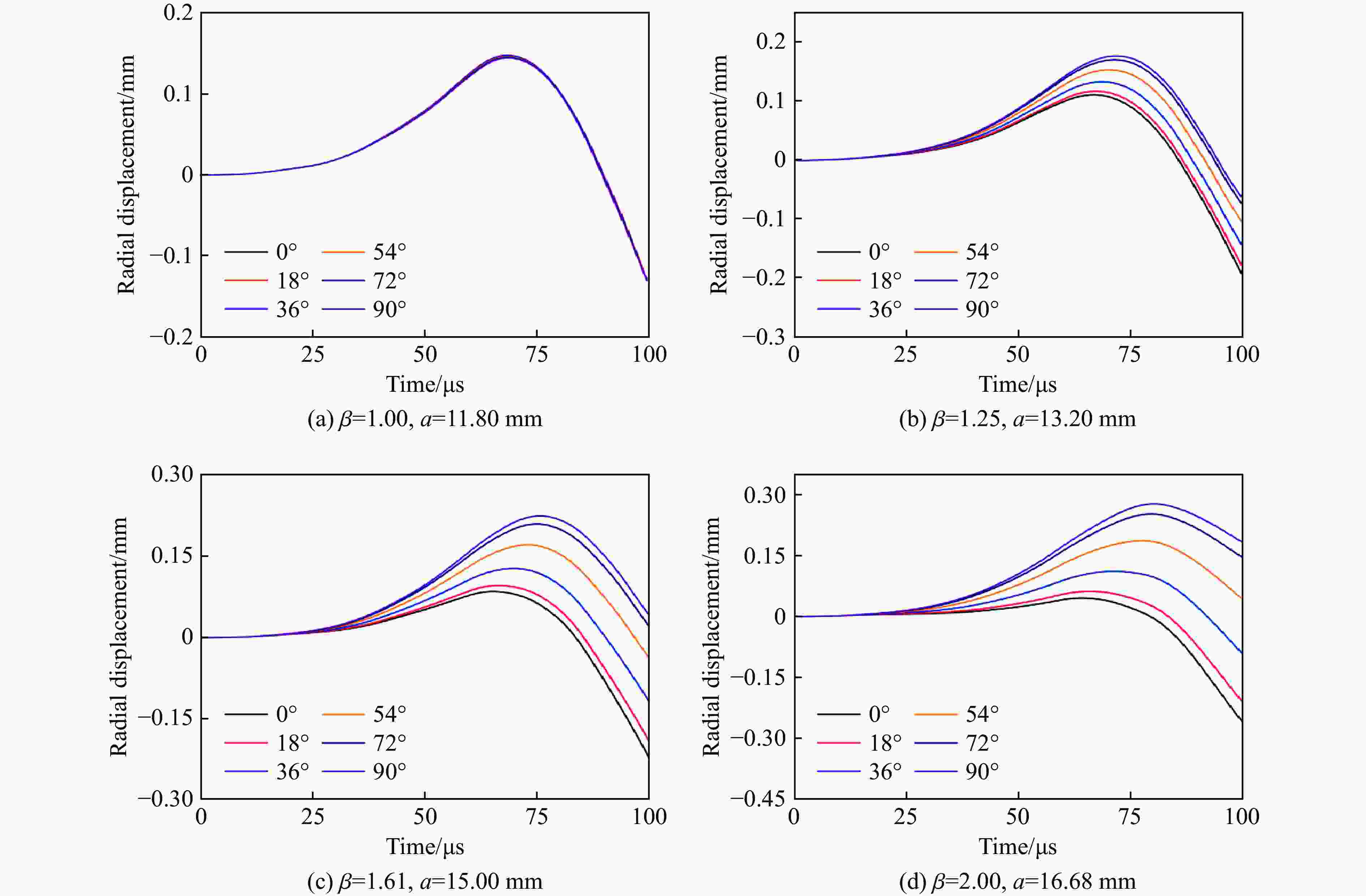
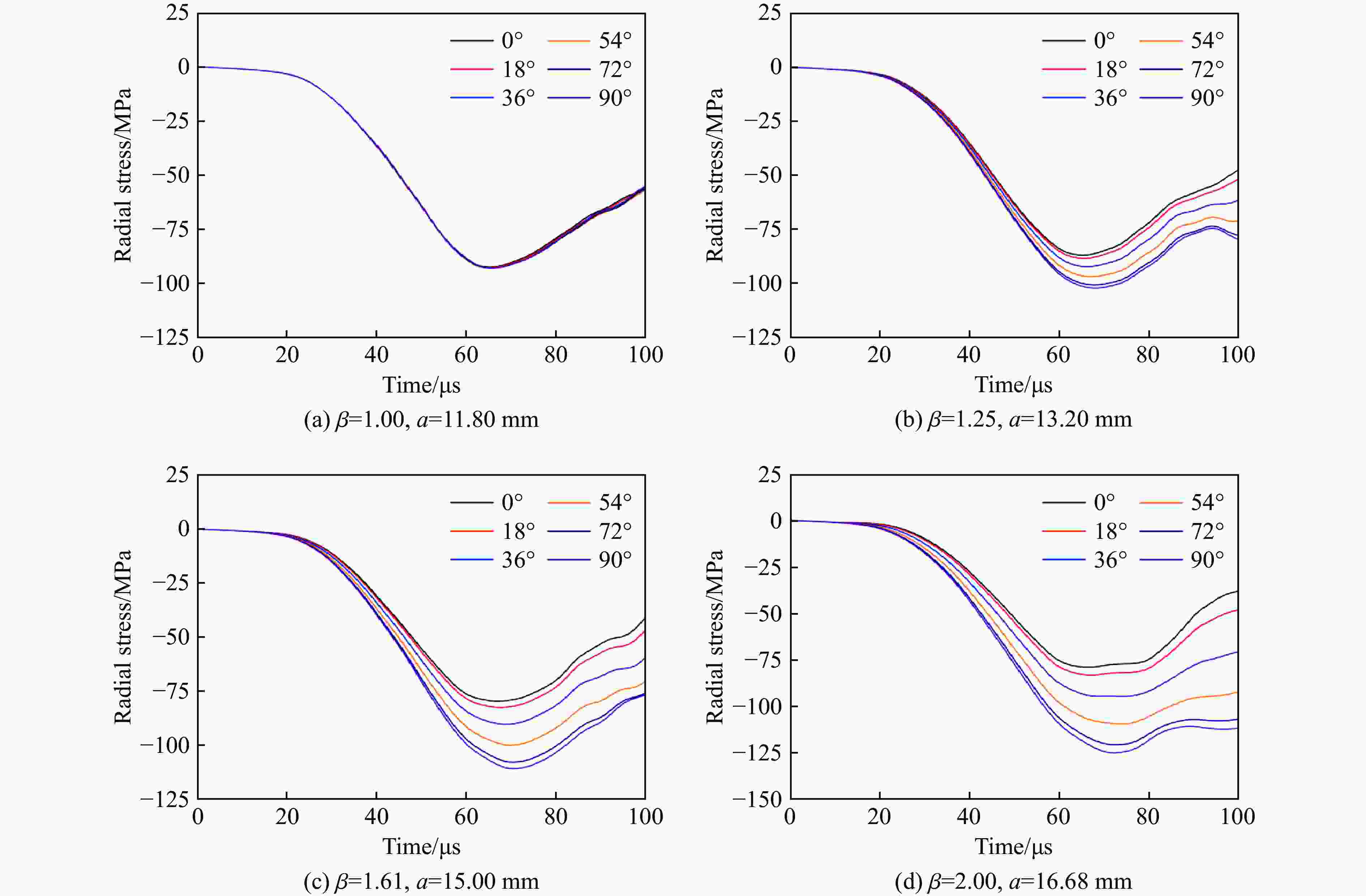
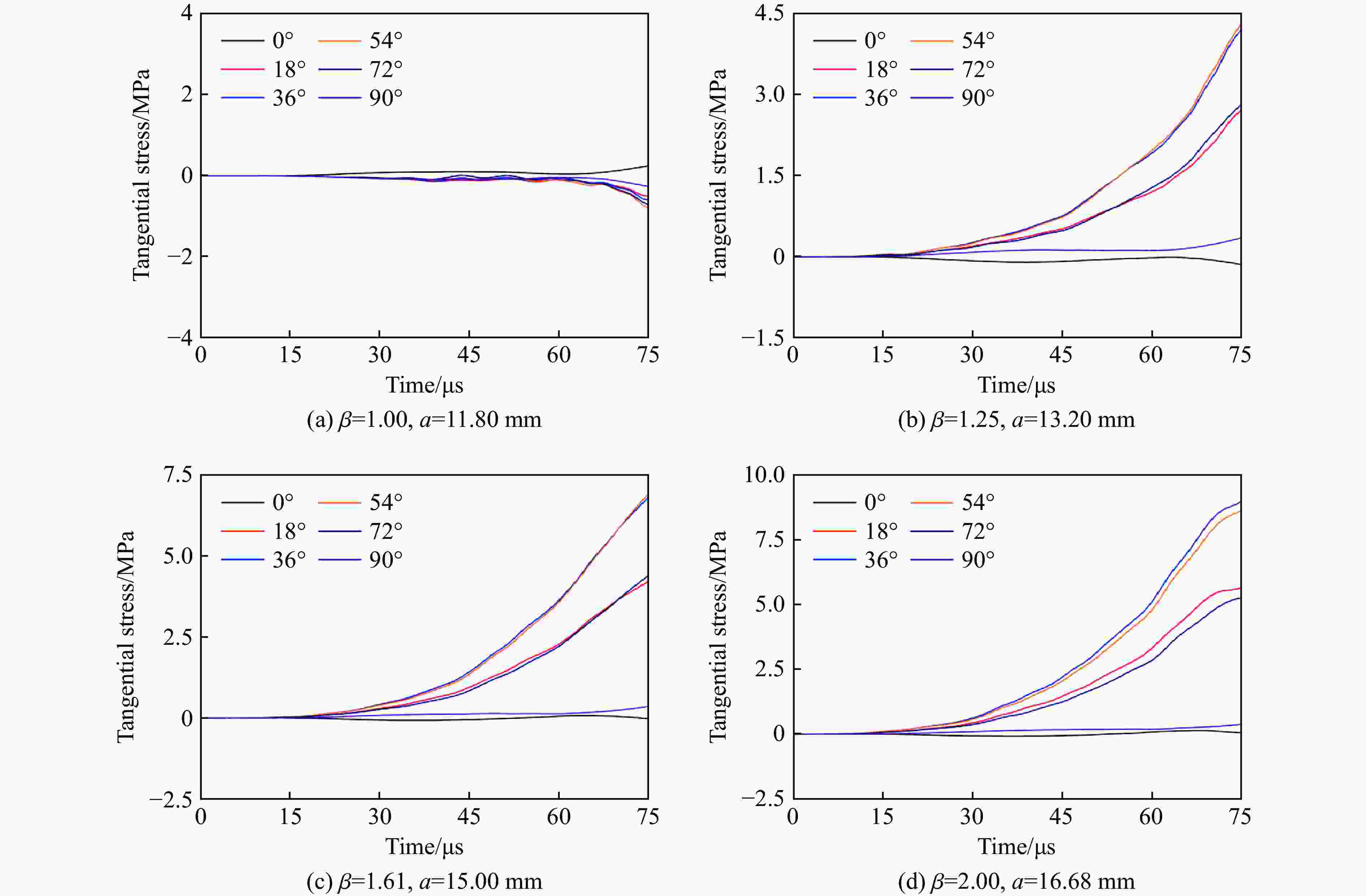
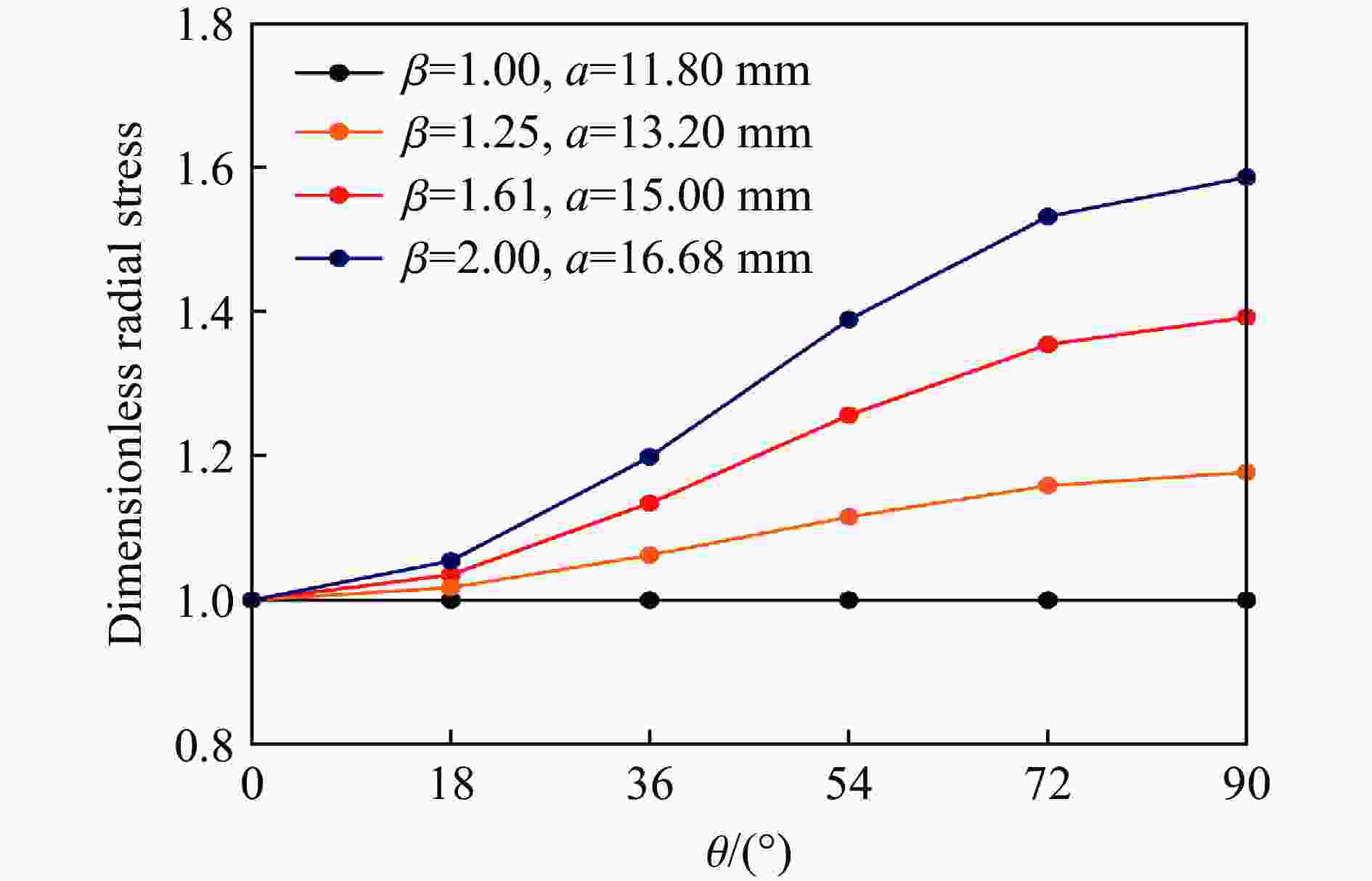
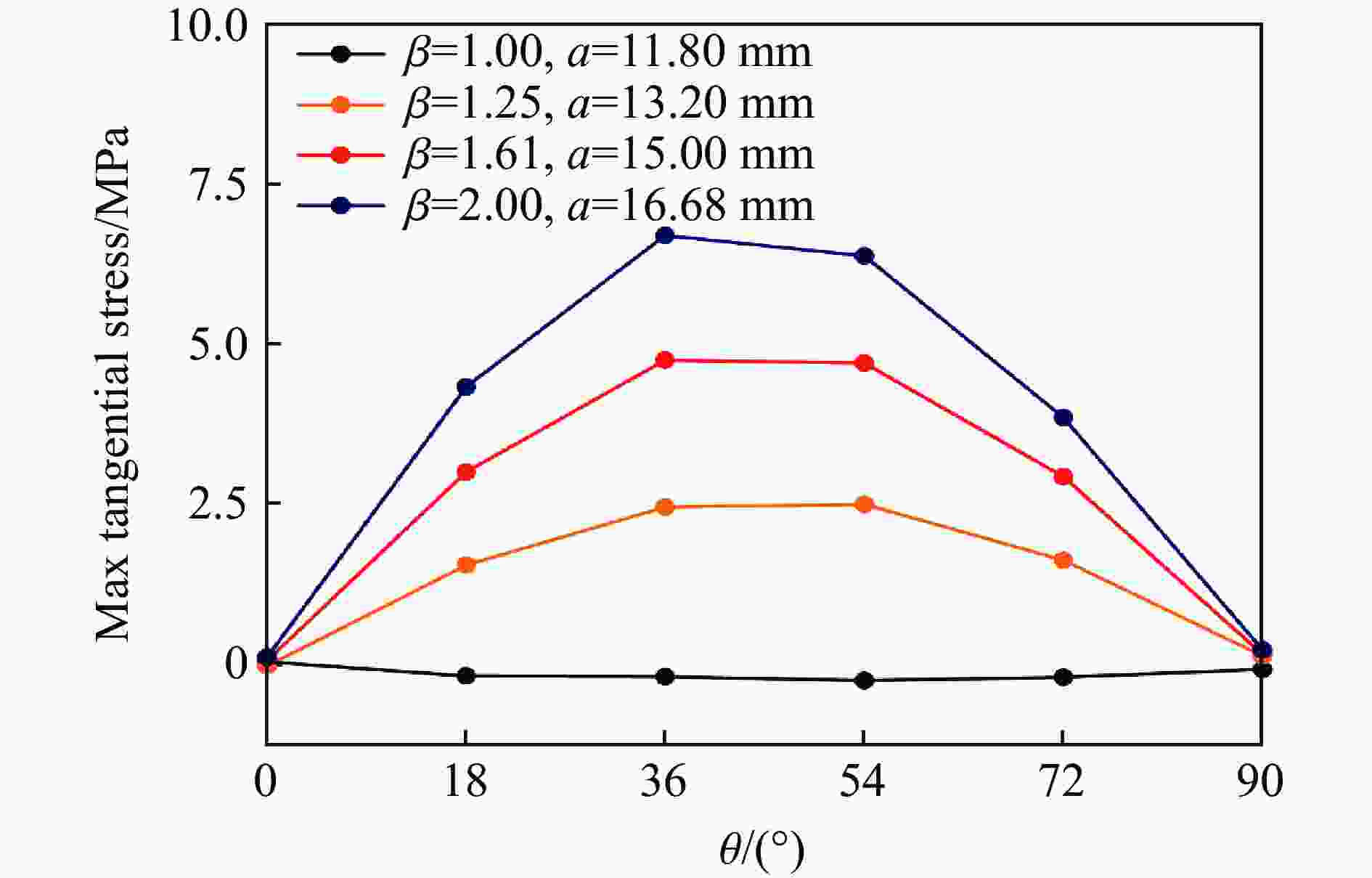
摘要: 基于30 mm口径弹道炮平台，开展了3种不同椭圆横截面弹体在200~600 m/s撞击速度范围内正侵彻2A12铝靶的实验，获得了2A12铝靶的破坏形貌及弹体的剩余速度。在此基础上，建立了相应的数值模型，结合实验结果验证了所建模型的有效性，并系统分析了弹体横截面长短轴长度比对靶体的破坏情况及响应特性的影响。研究结果表明：弹体最大横截面面积是影响弹体剩余速度的主要因素，而弹体横截面长短轴长度比对弹体剩余速度的影响较弱；在圆形横截面弹体侵彻下靶体背部形成的花瓣大小和形状一致，空间分布均匀，而在椭圆横截面弹体侵彻下，随着弹体横截面长短轴长度比的增大，靶体背部形成的花瓣数量增加、尺寸变小，且在短轴方向的花瓣数量和靶体表面隆起高度均大于长轴方向的；靶体在圆形横截面弹体侵彻下的径向位移、径向应力和切向应力与其在椭圆横截面弹体侵彻下的显著不同，前者沿周向方向各点的变化规律基本一致，靶体处于简单的压缩状态，切向应力为零，而后者各点的应力状态与弹体横截面长短轴长度比和周向角密切相关，靶体受到压缩和剪切应力的耦合作用。
- 铝靶 /
- 椭圆横截面弹体 /
- 长短轴长度比 /
- 剩余速度 /
- 正侵彻 /
- 径向位移 /
- 径向应力 /
- 切向应力
Abstract: By means of a 30-mm-caliber ballistic gun platform, a series of experiments were carried out on 2A12 aluminum targets subjected to normal penetration by three kinds of 30CrMnSi2A steel projectiles with different elliptical cross-section shapes in the striking velocity range from 200 m/s to 600 m/s. The residual velocities of the projectiles and the failure modes of the targets were experimentally obtained. Based on the experimental results, the corresponding numerical models were established and verified. And the influences of the major-to-minor axis length ratios of the projectile cross-sections on the failure modes and response characteristics of the targets were systematically analyzed. The results show as follows. The maximum cross-sectional areas of the projectiles are the main factor affecting the residual velocities of the projectiles, while the major-to-minor axis length ratios of the projectile cross-sections have little effect on the residual velocities. Therefore, in engineering applications, the engineering model for the circular cross-section projectile penetrating a target can be directly used to calculate the residual velocity of the elliptical cross-section projectile with the same maximum cross-sectional area. In addition, under normal penetration of the circular cross-section projectiles, the sizes, shapes and distribution of the petals induced at the back faces of the targets are uniform. However, under normal penetration of the elliptical cross-section projectiles, as the major-to-minor axis length ratios of the projectile cross-sections increase, the numbers of the petals induced at the back faces of the targets increase and the petal sizes decrease, and the petal numbers and the uplifted height in the minor axis direction are greater than those in the major axis direction. The radial displacement, radial stress and tangential stress of the targets under the normal penetration of the elliptical cross-section projectiles are obviously different from those of the targets under the normal penetration of the circular cross-section projectiles. Under normal penetrations of the circular cross-section projectiles, the above response characteristics of the targets change basically the same along the circumferential directions and the targets are under simple compression states with the tangential stress of zero. But, under normal penetrations of the elliptical cross-section projectiles, the stress states of different points of the targets are closely related to the major-to-minor axis length ratios and the circumferential angles of the projectiles, and the targets are subjected to the coupling effects of the compression and shear stresses.
- aluminum target /
- elliptical cross-section projectile /
- major-to-minor axis length ratio /
- residual velocity /
- normal penetration /
- radial displacement /
- radial stress /
- tangential stress

HTML全文

图 1 实验弹体

Figure 1. Projectiles used in the experiments

下载: 全尺寸图片幻灯片

图 2 实验靶体

Figure 2. Targets used in the experiments

下载: 全尺寸图片幻灯片

图 3 实验布局

Figure 3. Experimental layout

下载: 全尺寸图片幻灯片

图 4 C1-4弹体飞行姿态分析

Figure 4. Analysis of the flight attitude of the C1-4 projectile

下载: 全尺寸图片幻灯片

图 5 实验前后C1-4弹体对比

Figure 5. Comparison of the C1-4 projectile before and after the experiment

下载: 全尺寸图片幻灯片

图 6 不同横截面形状弹体侵彻下铝靶的破坏形貌

Figure 6. Damage of aluminum targets under normal penetration of the projectiles with different cross-section shapes

下载: 全尺寸图片幻灯片

图 7 有限元模型

Figure 7. Finite element models

下载: 全尺寸图片幻灯片

图 8 实验靶板破坏形态与数值模拟结果对比

Figure 8. Comparison of failure morphologies of targets between simulation and experiment

下载: 全尺寸图片幻灯片

图 9 不同横截面形状弹体剩余速度对比

Figure 9. Comparison of residual velocities of projectiles with different cross-section shapes

下载: 全尺寸图片幻灯片

图 10 弹体横截面长短轴长度比对靶体破坏形貌的影响

Figure 10. Influence of major-to-minor axis length ratios of the projectile cross-sections on damage morphologies of the targets

下载: 全尺寸图片幻灯片

图 11 靶体应变分布

Figure 11. Strain distribution of the targets

下载: 全尺寸图片幻灯片

图 12 数值模拟中靶体测点分布

Figure 12. Layout of measured points of targets in numerical simulation

下载: 全尺寸图片幻灯片

图 13 靶体沿周向方向的径向位移

Figure 13. Radial displacement of targets along circumferential direction

下载: 全尺寸图片幻灯片

图 14 靶体沿周向方向的径向应力

Figure 14. Radial stress of targets along circumferential direction

下载: 全尺寸图片幻灯片

图 15 靶体沿周向方向的切向应力

Figure 15. Tangential stress of targets along circumferential direction

下载: 全尺寸图片幻灯片

图 16 沿周向方向的无量纲径向位移

Figure 16. Dimensionless radial displacement of targets along circumferential direction

下载: 全尺寸图片幻灯片

图 17 沿周向方向的无量纲径向应力

Figure 17. Dimensionless radial stress of targets along circumferential direction

下载: 全尺寸图片幻灯片

图 18 沿周向方向的最大切向应力

Figure 18. The maximum tangential stress of targets along circumferential direction

下载: 全尺寸图片幻灯片

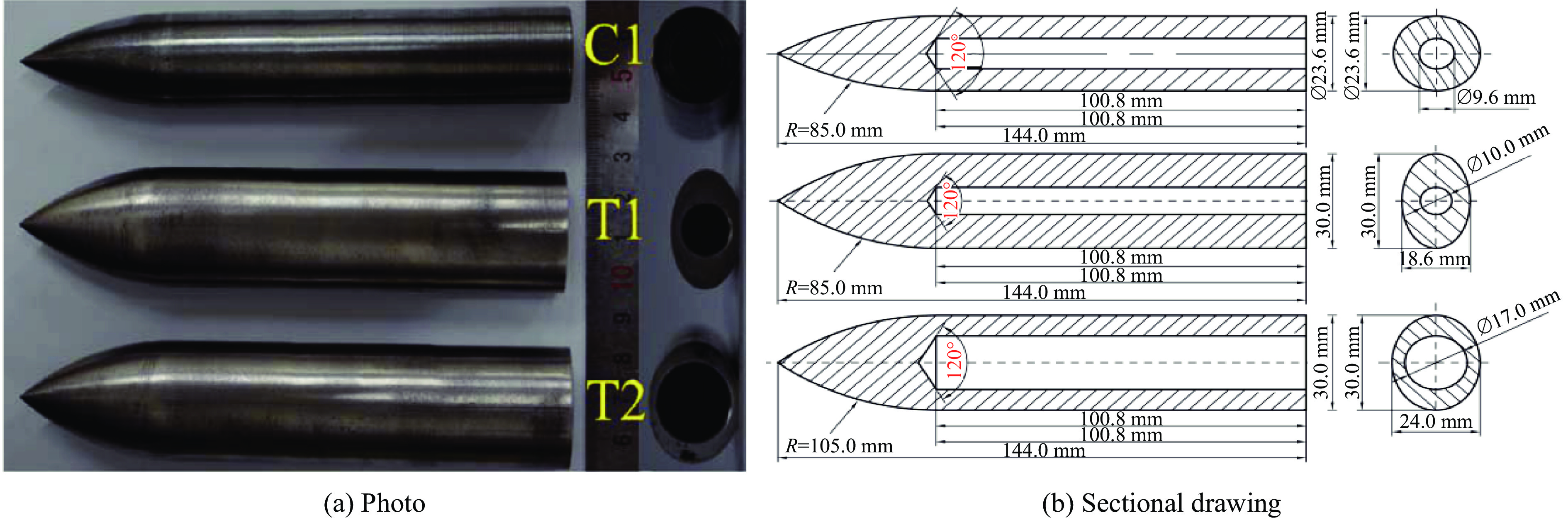
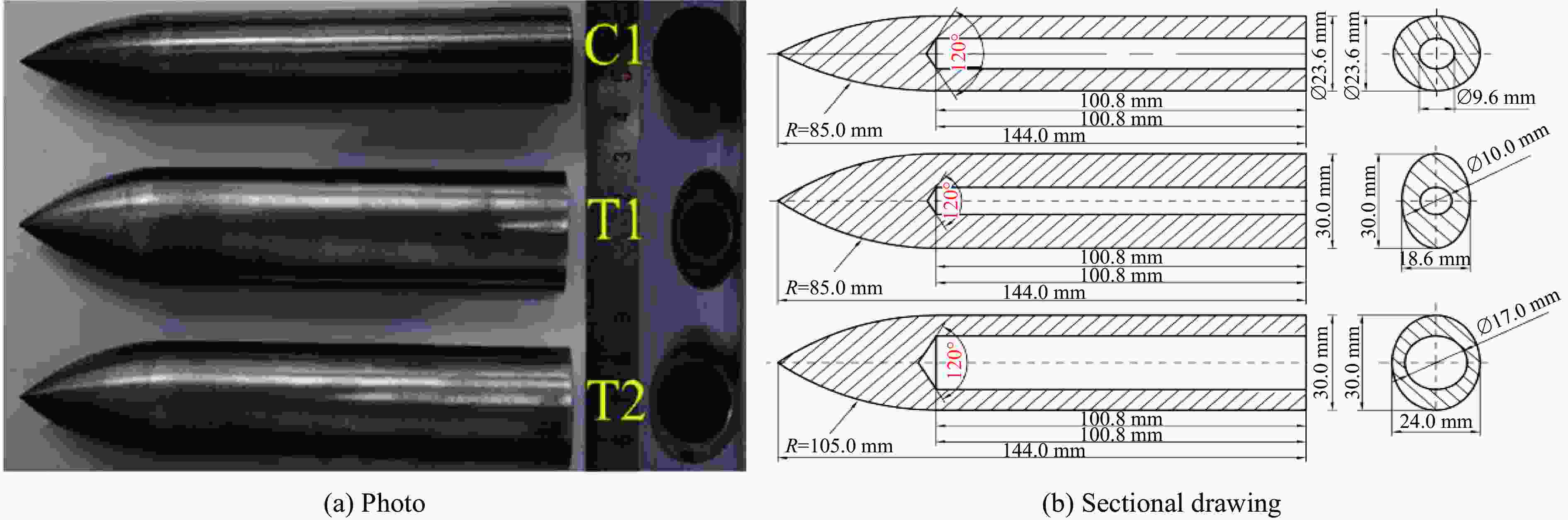
表 1 三种弹体主要参数

Table 1. Main parameters of three projectiles

弹体类型	弹体轮廓	2a/mm	2b/mm	β	L/mm	ψ	m/g
C1		23.6	23.6	1.00	43.2	3.6	360
T1		30.0	18.6	1.61	43.2	5.6	360
T2		30.0	24.0	1.25	43.2	3.5	360

下载: 导出CSV

表 2 弹体正侵彻铝靶的实验结果

Table 2. Experimental results for normal penetration of projectiles into aluminum targets

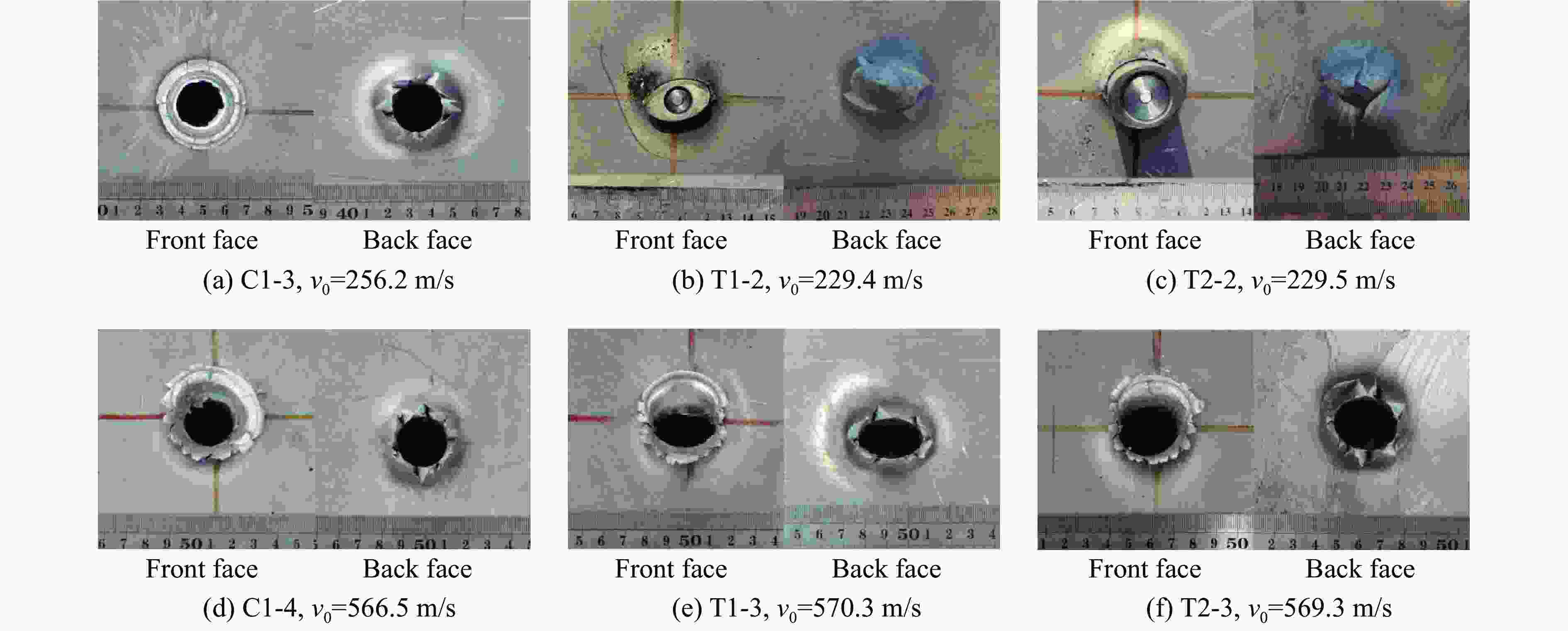
弹体	$ {v}_{0} $/(m·s⁻¹)	$ {v}_{\mathrm{r}} $/(m·s⁻¹)	$ \alpha $/(°)	$ \gamma $/(°)
C1-1	402.3	336.0	1.08	+0.63
C1-2	310.7	214.5	0.34	+0.19
C1-3	256.2	120.3	0.25	+0.17
C1-4	566.5	522.5	1.11	−0.68
T1-1	402.0	338.0	1.26	−0.62
T1-2	229.4	0	2.03	−1.51
T1-3	570.3	531.6	1.91	−1.49
T2-1	405.3	322.7	0.76	−0.30
T2-2	229.5	0	2.69	−2.39
T2-3	569.3	509.2	1.57	−1.13

下载: 导出CSV

表 3 材料参数

Table 3. Material parameters

材料	$\ \rho $/(g·cm⁻³)	G/GPa	μ	A/MPa	B/MPa	n	C	m	D₁
30CrMnSiNi2A^[25]	7.85	210	0.3
2A12铝^[26]	2.77	28	0.33	195	230	0.31	0.42	1	0.75

下载: 导出CSV

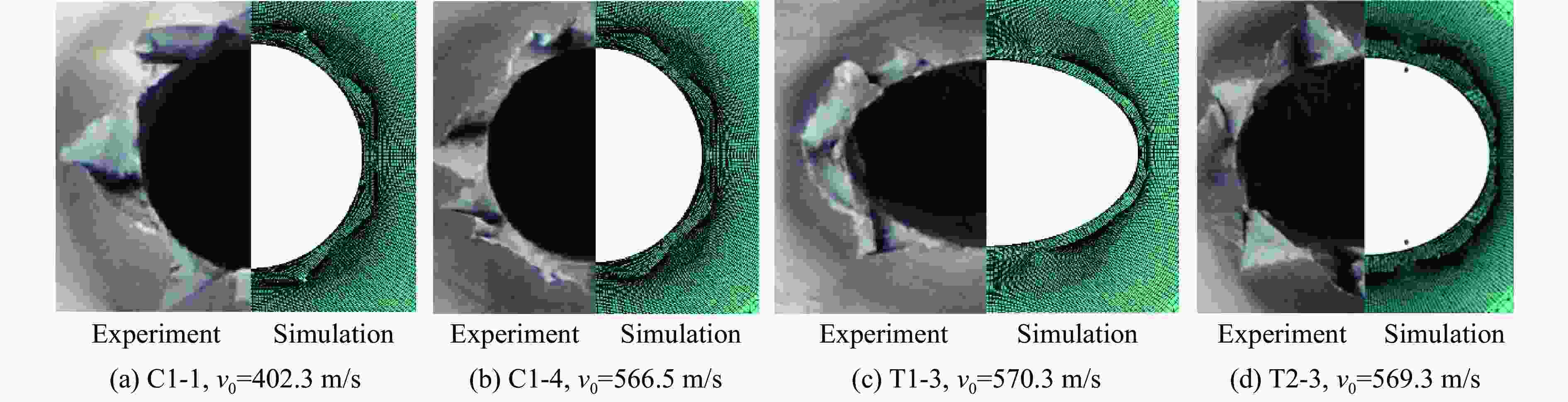
表 4 弹体剩余速度模拟结果与实验结果的对比

Table 4. Comparison of residual velocities of projectiles between simulation and experiment

弹体类型	v₀/(m·s⁻¹)	v_r/(m·s⁻¹)		ɛ_r/%
弹体类型	v₀/(m·s⁻¹)	实验	数值模拟	ɛ_r/%
C1	256.2	120.3	109.2	−9.2
	310.7	214.5	202.7	−5.5
	402.3	336.0	323.3	−3.8
	566.5	522.5	510.7	−2.3
T1	229.4	0	21.3
	402.0	338.0	323.5	−4.3
	570.3	531.6	514.5	−3.2
T2	229.5	0	0	0
	405.3	322.7	302.5	−6.3
	569.3	509.2	497.5	−2.3

下载: 导出CSV

表 5 靶体背部塑性应变区域范围对比

Table 5. Comparison of plastic strain ranges on the back of targets

弹体类型	2a/mm	2b/mm	长轴最大坐标/mm	短轴最大坐标/mm	长轴相对增量/%	短轴相对增量/%
C1	23.60	23.60	18.55	18.55	57.20	57.20
T3	26.40	21.10	17.30	18.08	31.06	71.37
T1	30.00	18.60	18.13	20.10	20.87	116.13
T4	33.36	16.68	19.13	22.30	14.69	167.39

下载: 导出CSV

参考文献(26)

[1]	VEDERNIKOV Y A, LEVIN V A, KHUDYAKOV Y S. Evolution and comparative analysis of group armor- and aeroballistics of ancient and modern ruled and poly-wedge arrows [J]. Bulletin of the Novosibirsk Computing Center. Series: Mathematical Modeling in Geophysics, 2005, 10: 93–116.
[2]	DAI X H, WANG K H, LI M R, et al. Rigid elliptical cross-section ogive-nose projectiles penetration into concrete targets [J]. Defence Technology, 2021, 17(3): 800–811. DOI: 10.1016/j.dt.2020.05.011.
[3]	MA X H, ZHANG Q M, ZHANG X W. A model for rigid asymmetric ellipsoidal projectiles penetrating into metal plates [J]. International Journal of Impact Engineering, 2022, 163: 104140. DOI: 10.1016/j.ijimpeng.2021.104140.
[4]	BEN-DOR G, DUBINSKY A, ELPERIN T. Optimal 3D impactors penetrating into layered targets [J]. Theoretical and Applied Fracture Mechanics, 1997, 27(3): 161–166. DOI: 10.1016/S0167-8442(97)00018-9.
[5]	BEN-DOR G, DUBINSKY A, ELPERIN T. A model for predicting penetration and perforation of FRP laminates by 3-D impactors [J]. Composite Structures, 2002, 56(3): 243–248. DOI: 10.1016/S0263-8223(02)00009-0.
[6]	YAKUNINA G Y. The construction of optimum three-dimensional shapes within the framework of a model of local interaction [J]. Journal of Applied Mathematics and Mechanics, 2000, 64(2): 289–298. DOI: 10.1016/S0021-8928(00)00051-4.
[7]	YAKUNINA G Y. The optimum non-conical and asymmetrical three-dimensional configurations [J]. Journal of Applied Mathematics and Mechanics, 2000, 64(4): 583–591. DOI: 10.1016/S0021-8928(00)00084-8.
[8]	WOO H J. Cavity expansion analysis of non-circular cross-sectional penetration problems [D]. Austin, Texas, USA: The University of Texas at Austin, 1997: 132–154.
[9]	BLESS S J. Penetration mechanics of non-circular rods [J]. AIP Conference Proceedings, 1996, 370(1): 1119–1122. DOI: 10.1063/1.50861.
[10]	杜忠华, 曾国强, 余春祥, 等. 异型侵彻体垂直侵彻半无限靶板试验研究 [J]. 弹道学报, 2008, 20(1): 19–21. DU Z H, ZENG G Q, YU C X, et al. Experimental research of novel penetrator vertically penetrating semi-infinite target [J]. Journal of Ballistics, 2008, 20(1): 19–21.
[11]	杜忠华, 朱建生, 王贤治, 等. 异型侵彻体垂直侵彻半无限靶板的分析模型 [J]. 兵工学报, 2009, 30(4): 403–407. DOI: 10.3321/j.issn:1000-1093.2009.04.005. DU Z H, ZHU J S, WANG X Z, et al. Analytical model on non-circular penetrator impacting semi-infinite target perpendicularly [J]. Acta Armamentarii, 2009, 30(4): 403–407. DOI: 10.3321/j.issn:1000-1093.2009.04.005.
[12]	高光发, 李永池, 刘卫国, 等. 长杆弹截面形状对垂直侵彻深度的影响 [J]. 兵器材料科学与工程, 2011, 34(3): 5–8. DOI: 10.3969/j.issn.1004-244X.2011.03.002. GAO G F, LI Y C, LIU W G, et al. Influence of the cross-section shapes of long rod projectile on the vertical penetration depth [J]. Ordnance Material Science and Engineering, 2011, 34(3): 5–8. DOI: 10.3969/j.issn.1004-244X.2011.03.002.
[13]	DONG H, LIU Z H, WU H J, et al. Study on penetration characteristics of high-speed elliptical cross-sectional projectiles into concrete [J]. International Journal of Impact Engineering, 2019, 132: 103311. DOI: 10.1016/j.ijimpeng.2019.05.025.
[14]	DONG H, WU H J, LIU Z H, et al. Penetration characteristics of pyramidal projectile into concrete target [J]. International Journal of Impact Engineering, 2020, 143: 103583. DOI: 10.1016/j.ijimpeng.2020.103583.
[15]	GAO X D, LI Q M. Trajectory instability and convergence of the curvilinear motion of a hard projectile in deep penetration [J]. International Journal of Mechanical Sciences, 2017, 121: 123–142. DOI: 10.1016/j.ijmecsci.2016.12.021.
[16]	高旭东, 李庆明. 带攻角斜侵彻混凝土的弹道偏转分析 [J]. 兵工学报, 2014, 35(Supp1 2): 33–39. GAO X D, LI Q M. Trajectory analysis of projectile obliquely penetrating into concrete target at attack angle [J]. Acta Armamentarii, 2014, 35(Supp1 2): 33–39.
[17]	王浩, 武海军, 闫雷, 等. 椭圆横截面弹体斜贯穿双层间隔薄钢板失效模式 [J]. 兵工学报, 2020, 41(Suppl 2): 1–11. DOI: 10.3969/j.issn.1000-1093.2020.S2.001. WANG H, WU H J, YAN L, et al. Failure mode of oblique perforation of truncated ogive-nosed projectiles with elliptic cross-section into double-layered thin steel plate with gap space [J]. Acta Armamentarii, 2020, 41(Suppl 2): 1–11. DOI: 10.3969/j.issn.1000-1093.2020.S2.001.
[18]	王浩, 潘鑫, 武海军, 等. 椭圆截面截卵形刚性弹体正贯穿加筋板能量耗散分析 [J]. 爆炸与冲击, 2019, 39(10): 103203. DOI: 10.11883/bzycj-2018-0350. WANG H, PAN X, WU H J, et al. Energy dissipation analysis of elliptical truncated oval rigid projectile penetrating stiffened plate [J]. Explosion and Shock Waves, 2019, 39(10): 103203. DOI: 10.11883/bzycj-2018-0350.
[19]	LANDKOF B, GOLDSMITH W. Petalling of thin, metallic plates during penetration by cylindro-conical projectiles [J]. International Journal of Solids and Structures, 1985, 21(3): 245–266. DOI: 10.1016/0020-7683(85)90021-6.
[20]	张中国, 黄风雷, 段卓平, 等. 弹体侵彻带加强筋结构靶的实验研究 [J]. 爆炸与冲击, 2004, 24(5): 431–436. DOI: 10.3321/j.issn:1001-1455.2004.05.009. ZHANG Z G, HUANG F L, DUAN Z P, et al. The experimental research for projectile penetrating the structural target with rebar [J]. Explosion and Shock Waves, 2004, 24(5): 431–436. DOI: 10.3321/j.issn:1001-1455.2004.05.009.
[21]	CHEN Y, WANG Y, TANG P, et al. Impact characteristics of stiffened plates penetrated by sub-ordnance velocity projectiles [J]. Journal of Constructional Steel Research, 2008, 64(6): 634–643. DOI: 10.1016/j.jcsr.2007.12.006.
[22]	SONG W D, NING J G, WANG J. Normal impact of truncated oval-nosed projectiles on stiffened plates [J]. International Journal of Impact Engineering, 2008, 35(9): 1022–1034. DOI: 10.1016/j.ijimpeng.2007.05.008.
[23]	徐双喜, 吴卫国, 李晓彬, 等. 截锥形弹穿甲单加筋板的破坏特性 [J]. 爆炸与冲击, 2011, 31(1): 62–68. DOI: 10.11883/1001-1455(2011)01-0062-07. XU S X, WU W G, LI X B, et al. Falure characteristics of a conical projectile penetrating single stiffened plate [J]. Explosion and Shock Waves, 2011, 31(1): 62–68. DOI: 10.11883/1001-1455(2011)01-0062-07.
[24]	LIU J W, ZHANG X F, WEI H Y, et al. Study on the penetration of elliptical cross-section projectiles into concrete targets: theory and experiment [J]. Latin American Journal of Solids and Structures, 2022, 19(3): 23. DOI: 10.1590/1679-78256939.
[25]	李磊, 张先锋, 吴雪, 等. 不同硬度30CrMnSiNi2A钢的动态本构与损伤参数 [J]. 高压物理学报, 2017, 31(3): 239–248. DOI: 10.11858/gywlxb.2017.03.005. LI L, ZHANG X F, WU X, et al. Dynamic constitutive and damage parameters of 30CrMnSiNi2A steel with different hardnesses [J]. Chinese Journal of High Pressure Physics, 2017, 31(3): 239–248. DOI: 10.11858/gywlxb.2017.03.005.
[26]	米双山, 张锡恩, 陶贵明. 钨球侵彻LY-12铝合金靶板的有限元分析 [J]. 爆炸与冲击, 2005, 25(5): 477–480. DOI: 10.11883/1001-1455(2005)05-0477-04. MI S S, ZHANG X E, TAO G M. Finite element analysis of spherical fragments penetrating LY-12 aluminum alloy target [J]. Explosion and Shock Waves, 2005, 25(5): 477–480. DOI: 10.11883/1001-1455(2005)05-0477-04.