Experimental and numerical simulation research on damage effect of jetting projectile charge (JPC) on reinforced concrete wall
-
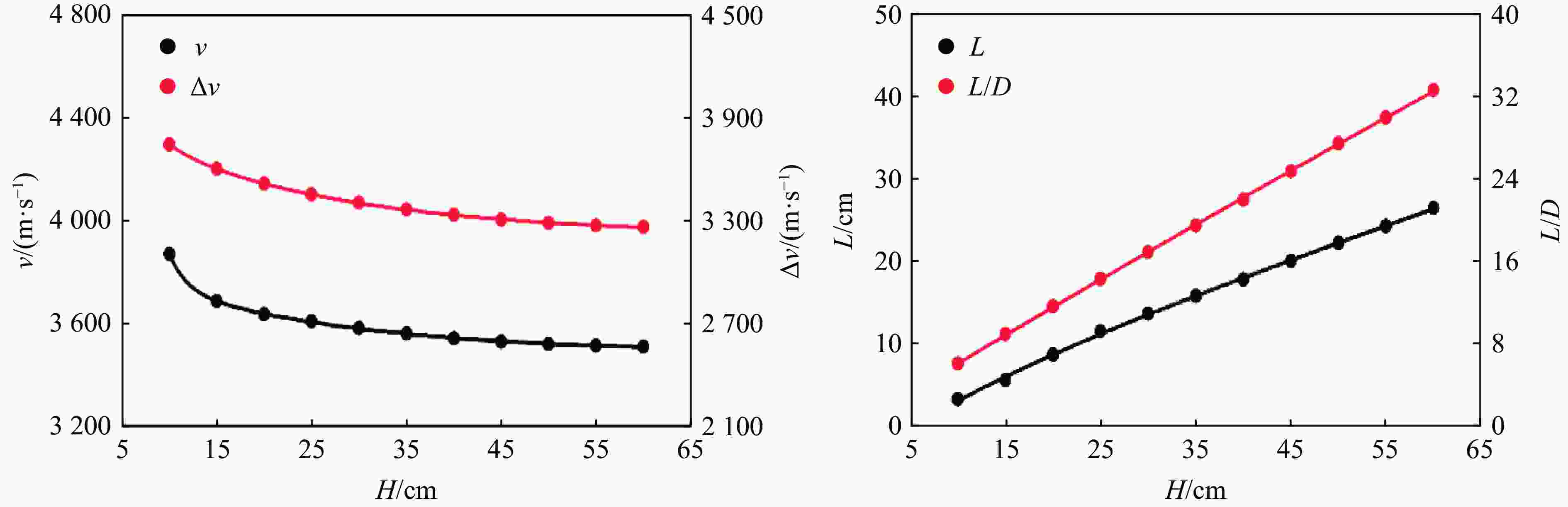
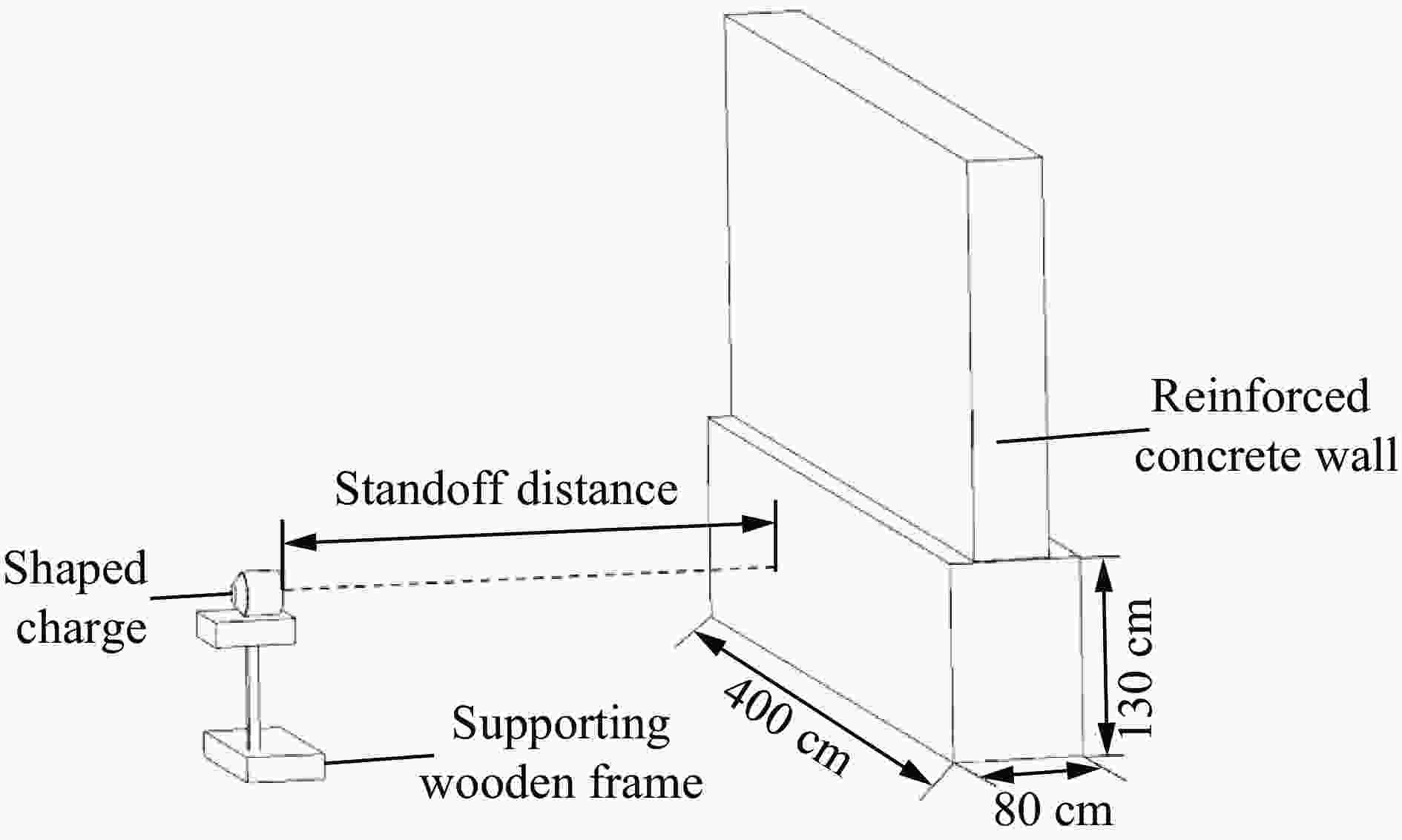
摘要: 为了满足高侵深和大穿孔的要求，设计一种聚能杆式弹丸（jetting projectile charge, JPC），开展大尺寸钢筋混凝土墙的毁伤效应试验。在此基础上，基于修正参数的K&C（Karagozian & Case）模型进行数值模拟，研究JPC高速侵彻和爆炸冲击波对钢筋混凝土墙的联合破坏作用，分析墙体厚度对破坏效果的影响规律。结果表明，在1.67倍和2.50倍装药直径的炸高条件下，JPC均能够有效贯穿80 cm（6.67倍装药直径）厚的钢筋混凝土墙，形成直径大于6 cm（0.50倍装药直径）的柱状孔洞；聚能装药的多载荷毁伤特性决定了钢筋混凝土墙的破坏结果，爆炸冲击波能够加剧墙体正面开坑和背面崩落的破坏范围；墙体厚度对于墙体正面漏斗坑的直径与深度及内部侵彻孔洞直径均无显著影响；随着墙体厚度增大，背面漏斗坑直径逐渐减小，深度却逐渐增大。
-
关键词:
- 聚能杆式弹丸(JPC) /
- 钢筋混凝土墙 /
- 侵彻 /
- 冲击波 /
- 联合破坏
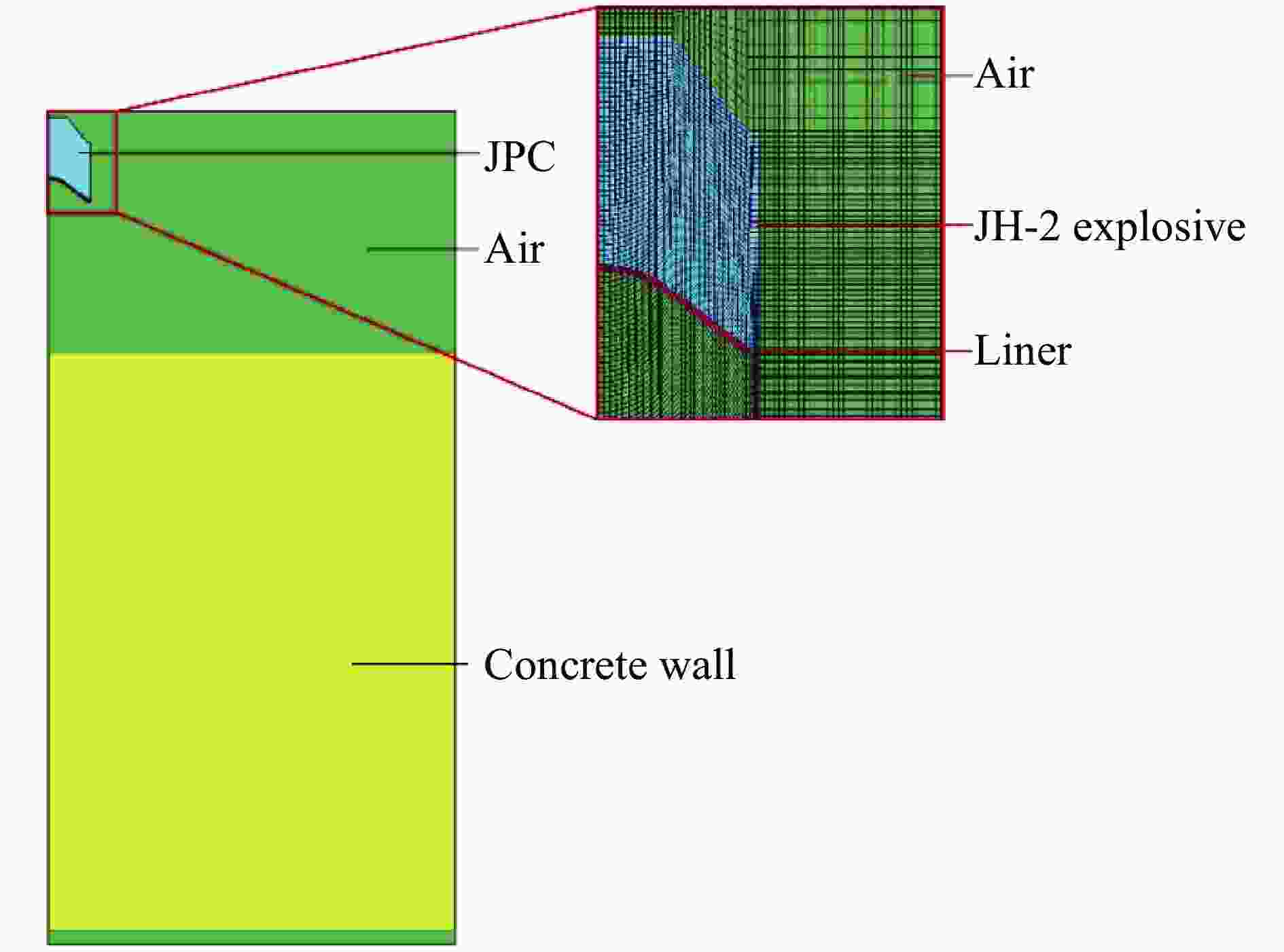
Abstract: To meet the requirements of a tandem penetrating warhead for high penetration depth and large perforation, a jetting projectile charge (JPC) was designed. The damage test of a large-scale reinforced concrete wall was carried out to analyze the impact of standoff distance on the damaging effect. By constructing a large air domain covering the whole reinforced concrete wall for the transmission of explosion shock wave and JPC, the coupling damage of JPC high-speed penetration and explosion shock wave to the reinforced concrete wall was considered. The damage evolution, strain rate and other parameters of the Karagozian & Case (K&C) model were modified, based on which a numerical model was established to simulate the whole process of the combined damage of JPC and explosion shock wave to the reinforced concrete wall. The reliability of the numerical model was fully verified by comparing the simulation and test results from the failure mode, crater depth and crater diameter of the reinforced concrete wall. On this basis, the combined damage effect of JPC and explosion shock wave on the reinforced concrete wall was further studied, and the influence of wall thickness on the damaging effect was analyzed. The results show that JPC can penetrate the reinforced concrete wall with a thickness of 80 cm (6.67 times of charge diameter) at the standoff distance of 1.67 times and 2.50 times of charge diameter, and form cylindrical holes with a diameter of more than 6 cm (0.50 times of charge diameter). The multi-load damage characteristic of shaped charge determines the damage result of the reinforced concrete wall, and the explosion shock wave can intensify the damage range of the front crater and back crater of the reinforced concrete wall. The wall thickness has no significant effect on the diameter and depth of the crater on the front of the wall and the diameter of the internal penetration hole. With the increase of the wall thickness, the crater diameter on the back gradually decreases and the crater depth on the back gradually increases.-
Key words:
- jetting projectile charge (JPC) /
- reinforced concrete wall /
- penetration /
- shock wave /
- combined damage
-
由于加载速率和惯性效应的影响，动态冲击作用下材料的断裂性能较静荷载作用下有明显的区别。尤其是含有内部缺陷(如裂缝、空洞等)的材料在冲击荷载作用下的断裂行为更加复杂。因此，研究缺陷对动态荷载下裂纹扩展的影响有着重要的意义。作为一种测定动态断裂参数常用的实验方法，三点弯曲实验得到了广泛使用[1]。姚学锋等[2]采用动态焦散线方法，对含偏置裂纹三点弯曲梁承受横向冲击的弯曲断裂行为进行了一系列动态断裂力学实验研究，给出了裂纹尖端应力场与梁中应力波传播的相互关系。J.F.Kalthoff等[3]首先将焦散线方法应用于动态断裂力学领域。姚学锋等[4]使用动焦散实验方法对三点弯曲梁冲击裂纹尖端初始曲线范围内的应力第二不变量分布进行研究，并分析了动荷载下裂纹起始扩展的条件及方向。杨仁树等[5]采用数字激光动态焦散线试验系统对含圆形孔与运动裂纹的相互作用机制进行了研究，分析了圆形孔对运动裂纹的断裂表面、裂纹扩展速度和应力强度因子的影响。黄明利等[6]利用岩石破裂过程分析程序，研究偏置裂纹位置的改变对三点弯曲梁的破坏模式的影响。A.S.Kobayashi等[7]得到了试件在动态剪切破坏过程中，裂纹尖端应力强度因子、动态能量释放率、裂纹扩展速度三者之间的关系。岳中文等[8]利用透射式焦散线实验系统，研究了三点弯曲梁预制裂纹与加载方向的夹角改变时，裂纹扩展速度及应力强度因子的变化规律。姚学锋等[9]采用动态焦散线实验研究了含预制裂纹三点弯曲梁扩展裂纹尖端动态能量释放率的分布规律。P.S.Theocaris等[10]利用动焦散方法研究了含预制裂纹的简支梁的断裂机制。杨仁树等[11]和岳中文等[12]研究了爆炸荷载作用下含缺陷介质的裂纹扩展规律。朱万成等[13]使用RFPA2D数值模拟方法模拟了偏三点弯曲岩石试样中的裂纹扩展路径。这些学者从不同角度对缺陷介质中裂纹扩展的规律进行了分析研究。然而，有关缺陷体与运动裂纹的相互作用关系以及缺陷体对运动裂纹传播方面的研究还存在一些不足。
本文中采用数字激光动态焦散线实验系统对不同倾角的预制裂纹缺陷与运动裂纹的相互作用机制进行研究，分析不同角度缺陷对运动裂纹扩展速度和尖端动态应力强度因子的影响。
1. 实验方法及计算原理
1.1 动态焦散线实验系统及操作方法
实验采用数字激光动态焦散线实验系统，如图 1所示。该系统包括高速数字照相机、激光光源、凸透镜、冲击加载装置及支架等设备。其中，采用高速数字照相机记录裂纹扩展过程中焦散斑图像的变化，其最高曝光速率可达106 s-1。激光光源为LWGL300-1500 mW型波长532 nm绿光激光光源。落锤质量为0.82 kg，下落高度为331 mm，击中试件时的速度为2.547 m/s。试件支架间距为190 mm。实验时，高速照相机曝光速率设定为1.5×105 s-1。
1.2 试件及其参数
实验试件材料为有机玻璃(PMMA)，PMMA材料的动态力学参数如下：纵波波速cp=2 320 m/s，横波波速cs=1 260 m/s，弹性模量Ed=6.1 GPa，泊松比ν=0.31，应力光学常量Ct=0.85×10-10 m2/N[14]。试件规格为220 mm×50 mm×5 mm。试件底边中部与试件中央位置分别预制1条裂纹，长度各为2 mm与5 mm，宽度均控制在0.3 mm以内。中央预制裂纹与水平方向夹角为α，且其中点在试件底边预制边裂纹正上方，并与试件中心重合。实验分为3组，第1组α=0°，第2组α=45°，第3组α=90°，为保证实验数据的准确性，每组实验重复5次。试件示意图如图 2所示。
1.3 实验计算原理
试件在裂纹开裂及扩展过程中，Ⅰ型裂纹占主导地位。裂纹尖端动态应力强度因子可以为[15]：
KI=2√2πF(v)3(3.17)5/2z0CtdeffD5/2 (1) 式中：D分别为沿裂纹方向的焦散斑最大直径，z0=900 mm为参考平面到物体平面的距离，Ct为试件材料的应力光学常数，v为裂纹扩展速度，deff为试件的有效厚度，F(v)为裂纹扩展时速度修正因子：
F(v)=4β1β2−(1+β22)2(1+β22)2(β21−β22) (2) 式中：β2i=1-(v/ci)2, i=1, 2;c1和c2分别为有机玻璃板中纵波速度和横波速度。当裂纹未起裂时，v=0, F(v)=1。当裂纹扩展时，F(v)恒小于1，在数据处理过程中F(v)常取为1[16]。
2. 实验结果及分析
2.1 裂纹扩展轨迹
图 3所示为冲击载荷下不同倾角预制缺陷试件的实验结果图。从图 3中可以看出，不同试件在冲击荷载作用下裂纹扩展轨迹的变化情况。将试件预制裂纹缺陷下方的扩展裂纹分别记为主裂纹A1、B1和C1，将预制裂纹缺陷上方的扩展裂纹记为次生裂纹。从实验结果看，预制裂纹缺陷可以抑制运动主裂纹的扩展并改变整个试件的裂纹扩展方向。倾角分别为0°、45°和90°预制裂纹缺陷试件的主裂纹A1、B1和C1扩展轨迹大致相同，其中主裂纹B1运动接近预制裂纹缺陷处略微向左倾斜，最终与预制裂纹缺陷垂直相交。可见预制裂纹缺陷倾角的改变对其主裂纹扩展轨迹影响较小。含0°倾角的预制裂纹缺陷试件主裂纹A1在与预制裂纹缺陷接触后，预制裂纹缺陷两端产生次生裂纹A2和A3，次生裂纹A2向上扩展轨迹向左略微倾斜，次生裂纹A3向上扩展轨迹向右略微倾斜。含45°倾角的预制裂纹缺陷试件主裂纹B1与预制裂纹缺陷接触后，预制裂纹缺陷上端产生次生裂纹B3，下端则产生向下扩展的次生裂纹B2，长度约为2 mm。含90°倾角的预制裂纹缺陷试件在预制裂纹上端产生次生裂纹C2。比较三者可以看出，含90°倾角的预制裂纹缺陷试件裂纹扩展轨迹较为平直。
2.2 动态焦散斑变化规律
图 4所示为不同倾角预制裂纹缺陷试件的裂纹尖端焦散斑系列图。
图 4 试件裂纹扩展的焦散斑图片Figure 4. Serial dynamic caustics patterns of crack propagation in specimens由图 4可知，主裂纹尖端和预制裂纹缺陷端部焦散斑大小均随时间变化而不断改变，反复多次。在t=1 053.33 μs时，主裂纹A1尖端焦散斑随裂尖开始移动；在t=886.67 μs时，主裂纹B1尖端焦散斑随裂尖开始移动；在t=1 093.33 μs时，主裂纹C1尖端焦散斑随裂尖开始移动。运动主裂纹A1、B1、C1尖端分别经过66.70、60.03和53.36 μs到达预制裂纹缺陷处。结果可知主裂纹C1所用时间最短。在t=1 093.33 μs时，0°倾角预制裂纹缺两端各形成1个焦散斑。在t=933.33 μs时，45°倾角预制裂纹缺端部形成2个焦散斑。在t=1 120.00 μs时，90°倾角预制裂纹缺端部形成2个焦散斑。运动主裂纹分别与0°和45°倾角预制裂纹相交时，主裂纹尖端的焦散斑迅速减小同时向预制裂纹缺陷两端移动，并与预制裂纹缺陷两端原有的焦散斑融合形成更大的焦散斑。随后预制裂纹缺陷端部起裂产生次生裂纹，次生裂纹向上扩展直至试件完全断裂。0°倾角预制裂纹缺陷端部2条次生裂纹在扩展过程初期，裂纹A2、A3尖端的焦散斑大小几乎相同。主裂纹C1与90°倾角预制裂纹缺陷相交时，主裂纹C1尖端的焦散斑与预制裂纹缺陷下端的焦散斑融合并迅速减小直到消失。同时，预制裂纹缺陷上端的焦散斑迅速增大，随后预制裂纹缺陷起裂。
2.3 裂纹扩展速度变化规律
为了计算结果合理，从每个实验的5组实验结果中取3组速度数据进行7次多项式拟合，进而得到裂纹扩展速度变化曲线，如图 5所示。从图 5中可以看出，主裂纹起裂后，积聚的能量得到释放，裂纹扩展速度迅速增加，并在最大值附近有轻微振荡，其中含倾角45°预制裂纹缺陷试件的振荡幅度最大，含倾角90°预制裂纹缺陷试件的振荡幅度最小。在t=1 113.34，953.34，1 140.00 μs时，运动主裂纹A1、B1和C1分别到达预制裂纹缺陷处。在主裂纹扩展过程中，含倾角0°预制裂纹缺陷试件的主裂纹A1最大扩展速度为466.67 m/s；含倾角45°预制裂纹缺陷试件的主裂纹B1最大扩展速度为469.02 m/s；含倾角90°预制裂纹缺陷试件的主裂纹C1最大扩展速度为491.57 m/s。主裂纹与预制裂纹缺陷接触时，次生裂纹不会立即起裂，这是因为预制裂纹缺陷端部是钝头，在此处起裂需要达到比运动裂纹尖端更高的应力强度因子。虽然扩展裂纹已经携带足够的能量，但仍需经过0~10 μs的时间积累更多能量，当应力集中超过材料断裂韧度时，次生裂纹才会起裂。次生裂纹起裂后，裂纹扩展速度迅速增至最大值，然后逐渐振荡下降至零。其中，含倾角0°预制裂纹缺陷试件次生裂纹最大扩展速度为275.31 m/s；含倾角45°预制裂纹缺陷试件次生裂纹最大扩展速度为336.86 m/s；含倾角90°预制裂纹缺陷试件的次生裂纹最大扩展速度为395.31 m/s。
2.4 动态应力强度因子变化规律
同样从每5组实验结果中取3组应力强度因子数据进行7次多项式拟合，进而可以得到裂纹扩展过程中裂尖动态应力强度因子随时间的变化曲线，如图 6所示。由图 6(a)可知，冲击荷载作用下含0°倾角的预制裂纹缺陷试件主裂纹尖端动态应力强度因子十分缓慢地振荡增大，说明能量正在逐渐积聚。在t=1 020 μs时，增加到起裂前的最大值1.80 MN/m3/2，之后动态应力强度因子迅速减小；在t=1 053.33 μs时，达到极小值1.23 MN/m3/2。随后再迅速增大，在t=1 086.67 μs时，达到峰值3.14 MN/m3/2，随后不断减小至零。在主裂纹A1扩展过程中，0°倾角预制裂纹缺陷两端的能量不断积累，预制裂纹缺陷尖端动态应力强度因子不断增大；t=1 120 μs时，分别达到峰值1.87和1.60 MN/m3/2，则次生裂纹A2、A3起裂，随后次生裂纹尖端动态应力强度因子振荡减小，最后降为零。由图 6(b)~(c)可以看出，含45°和90°倾角的预制裂纹缺陷试件主裂纹起裂前及扩展过程中，裂纹尖端动态应力强度因子的变化趋势与含0°倾角预制裂纹缺陷试件主裂纹相似。但是含45°和90°预制裂纹缺陷试件主裂纹起裂前，裂纹尖端动态应力强度因子的振荡幅度较小。在主裂纹扩展过程中，含0°预制裂纹缺陷试件主裂纹尖端动态应力强度因子的峰值为2.51 MN/m3/2，含45°预制裂纹缺陷试件主裂纹裂尖动态应力强度因子的峰值为2.75 MN/m3/2，含90°预制裂纹缺陷试件主裂纹裂尖动态应力强度因子的峰值为3.27 MN/m3/2。可见，主裂纹扩展过程中，随着预制裂纹缺陷倾斜角度的增大，裂尖动态应力强度因子的峰值增大。0°预制裂纹缺陷端部次生裂纹A2、A3起裂时的裂尖动态应力强度因子分别为1.78和1.60 MN/m3/2，45°预制裂纹缺陷端部次生裂纹B3起裂时的裂尖动态应力强度因子为2.29 MN/m3/2，90°预制裂纹缺陷端部次生裂纹C2起裂时的裂尖动态应力强度因子为3.10 MN/m3/2。随着预制裂纹缺陷倾角的增大，预制裂纹缺陷端部次生裂纹起裂时的裂尖动态应力强度因子也增大。
图 6 动态应力强度因子与时间关系Figure 6. Relationship between dynamic stress intensity factor and time3. 结论
(1) 冲击载荷下，运动主裂纹与预制裂纹贯通时，次生裂纹没有立即起裂，因为预制裂纹缺陷端部是钝头，在此处起裂需要达到比运动裂纹尖端更大的应力强度因子，因此需要经过0~10 μs的时间积累更高的能量，次生裂纹才会起裂。
(2) 当预制裂纹缺陷倾斜角度增大时，运动主裂纹尖端动态应力强度因子的峰值则会增大，同时，次生裂纹起裂时的动态应力强度因子也会增大。
(3) 运动主裂纹扩展速度先迅速增大，然后基本保持匀速扩展；次生裂纹扩展速度先迅速增大，然后不断震荡并逐渐下降，直到试件完全断裂。
-
图 2 JPC成型过程(t=0, 15, 18, 24, 31, 62, 131 μs)
Figure 2. Forming process of the JPC (t=0, 15, 18, 24, 31, 62, 131 μs)
图 4 JPC成型参数随炸高变化
Figure 4. Forming parameters of the JPC varing with standoff distance
图 7 钢筋混凝土墙的破坏结果（炸高20 cm）
Figure 7. Failure of the reinforced concrete wall (standoff distance is 20 cm)
图 8 钢筋混凝土墙的破坏结果（炸高30 cm）
Figure 8. Failure of the reinforced concrete wall (standoff distance is 30 cm)
图 10 JPC聚能装药破坏钢筋混凝土墙的数值模型
Figure 10. Numerical model of reinforced concrete wall damaged by the JPC
图 11 钢筋混凝土墙破坏的数值模拟结果
Figure 11. Numerical simulation results of reinforced concrete wall failure
图 12 JPC聚能装药破坏钢筋混凝土墙的应力云图
Figure 12. Stress cloud diagram of reinforced concrete wall damaged by the JPC
图 13 钢筋混凝土墙背面破坏过程
Figure 13. Failure process of the back of the reinforced concrete wall
图 14 钢筋混凝土墙破坏的应力云图
Figure 14. Stress cloud diagram of failure of reinforced concrete wall
图 15 减小空气域后JPC聚能装药破坏钢筋混凝土墙的数值模型
Figure 15. Numerical model of reinforced concrete wall damaged by the JPC after reducing air domain
图 16 不同尺寸空气域的数值模拟结果对比（炸高20 cm）
Figure 16. Comparison of numerical simulation results of different air domains (standoff distance is 20 cm)
图 17 不同尺寸空气域的数值模拟结果对比（炸高30 cm）
Figure 17. Comparison of numerical simulation results of different air domains (standoff distance is 30 cm)
图 18 不同厚度钢筋混凝土墙的损伤分布
Figure 18. Damage distribution of the reinforced concrete wall with different thicknesses
图 19 不同厚度钢筋混凝土墙的破坏变化
Figure 19. Damage of reinforced concrete wall with different thicknesses
ρ/（g·cm−3） C4 C5 E0/MPa V 1.225×10−3 0.4 0.4 0.25 1 
下载: 导出CSV
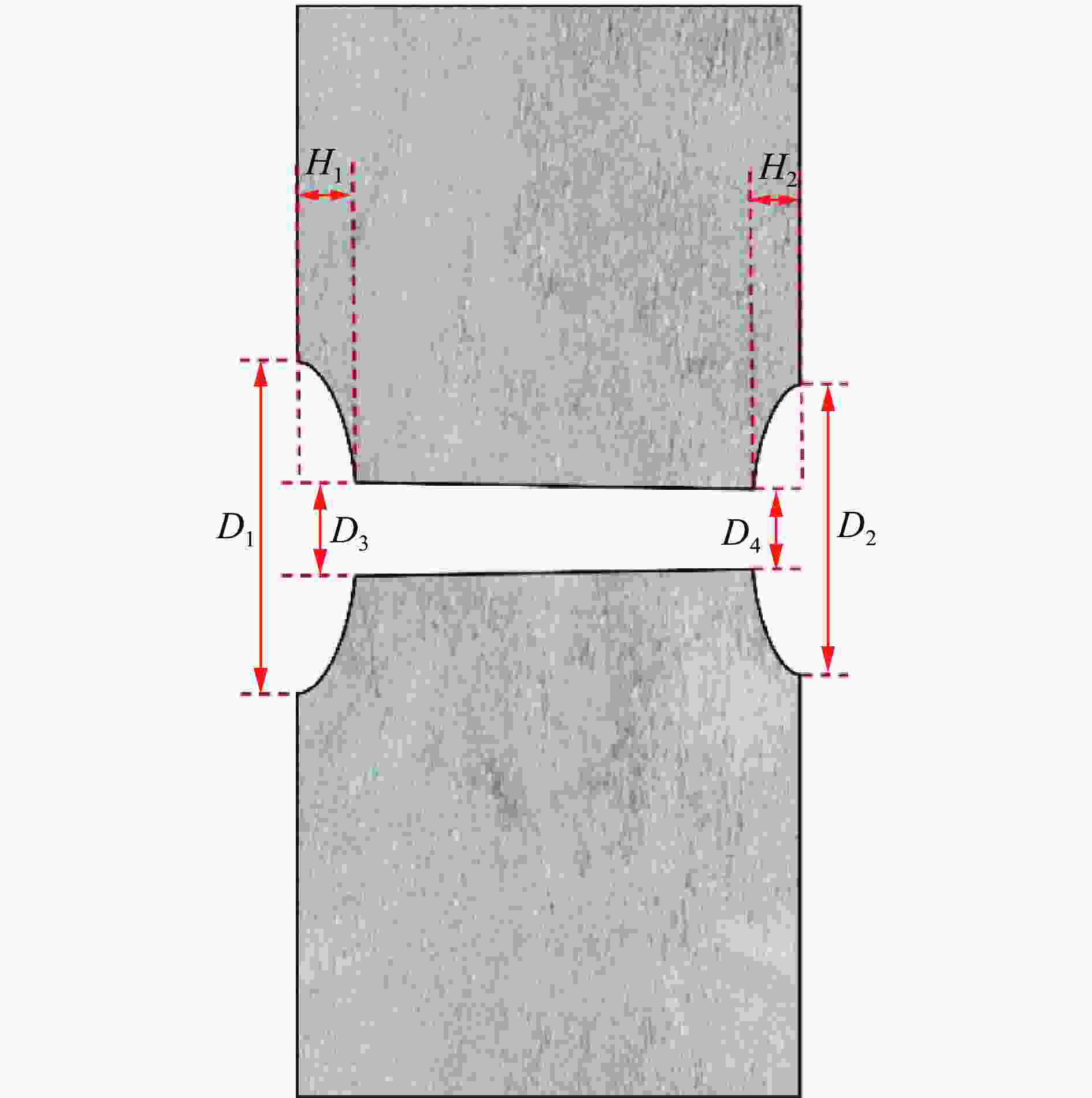
ρ/（g·cm−3） A/GPa B/GPa R1 R2 ω E0/GPa 1.7 630 6.801 4.1 1.3 0.36 10
下载: 导出CSV
ρ/（g·cm−3） A/GPa B/GPa n c m Tm/K Tr/K 8.96 0.09 0.292 0.31 0.025 1.09 1356 293
下载: 导出CSV
表 4 钢筋混凝土墙毁伤试验结果
Table 4. Test results of the reinforced concrete wall
炸高/cm D1/cm D2/cm D3/cm D4/cm H1/cm H2/cm 20 57.5 40.5 6.5 6.2 9.8 10.4 30 39.3 54.8 6.3 6.5 8.8 12.6
下载: 导出CSV
表 5 混凝土材料参数
Table 5. Material parameters of concrete
ρ/（g·cm−3） A0/MPa 泊松比 b1 b2 长度单位换算系数 压力单位换算系数 2.3 28 0.2 0.82 1.03 0.3937 1.45×107
下载: 导出CSV
表 6 钢筋混凝土墙破坏的数值模拟与试验结果对比（炸高20 cm）
Table 6. Comparison between numerical simulation results and test results (standoff distance is 20 cm)
方法 D1/cm D2/cm D3/cm D4/cm H1/cm H2/cm 试验结果 57.5 40.5 6.5 6.2 9.8 10.4 数值模拟 62.4 44.4 5.9 5.6 9.4 11.5 相对误差/% 8.5 9.6 9.2 9.7 4.1 10.6
下载: 导出CSV
表 7 钢筋混凝土墙破坏的数值模拟与试验结果对比（炸高30 cm）
Table 7. Comparison between numerical simulation results and test results (standoff distance is 30 cm)
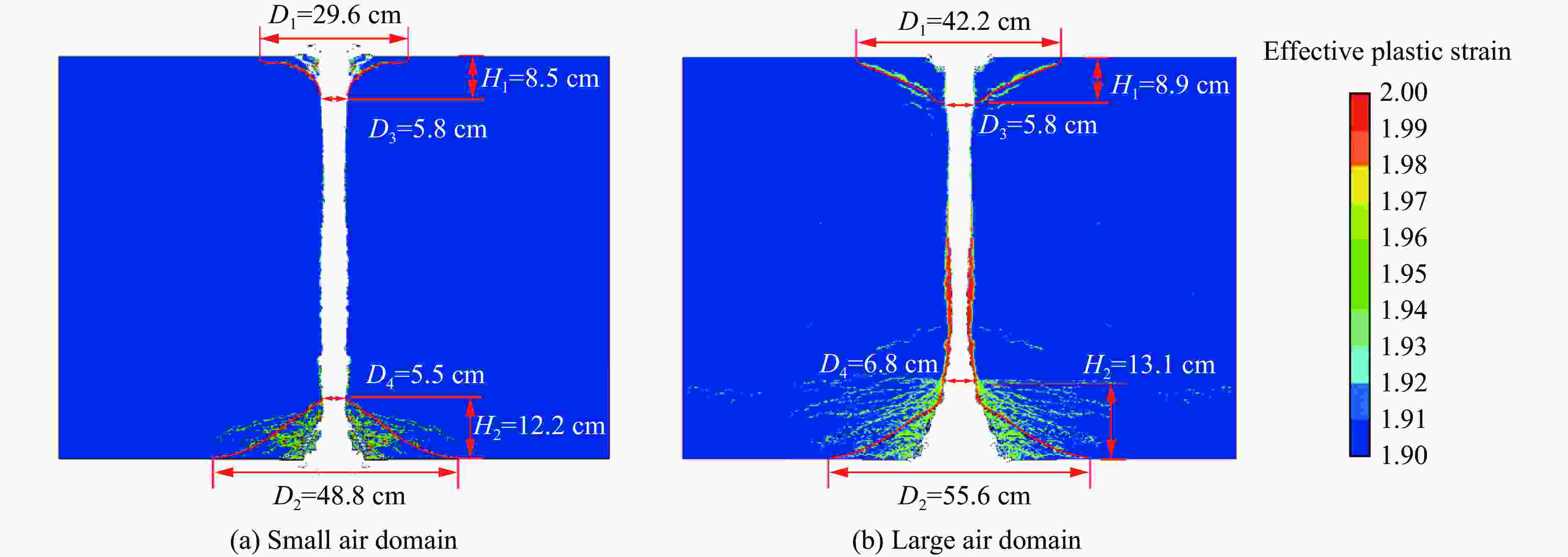
方法 D1/cm D2/cm D3/cm D4/cm H1/cm H2/cm 试验结果 39.3 54.8 6.3 6.5 8.8 12.6 数值模拟 42.2 55.6 5.8 6.8 8.9 13.1 相对误差/% 7.4 1.5 7.9 4.6 1.1 4.0
下载: 导出CSV
表 8 不同厚度钢筋混凝土墙破坏的数值模拟结果
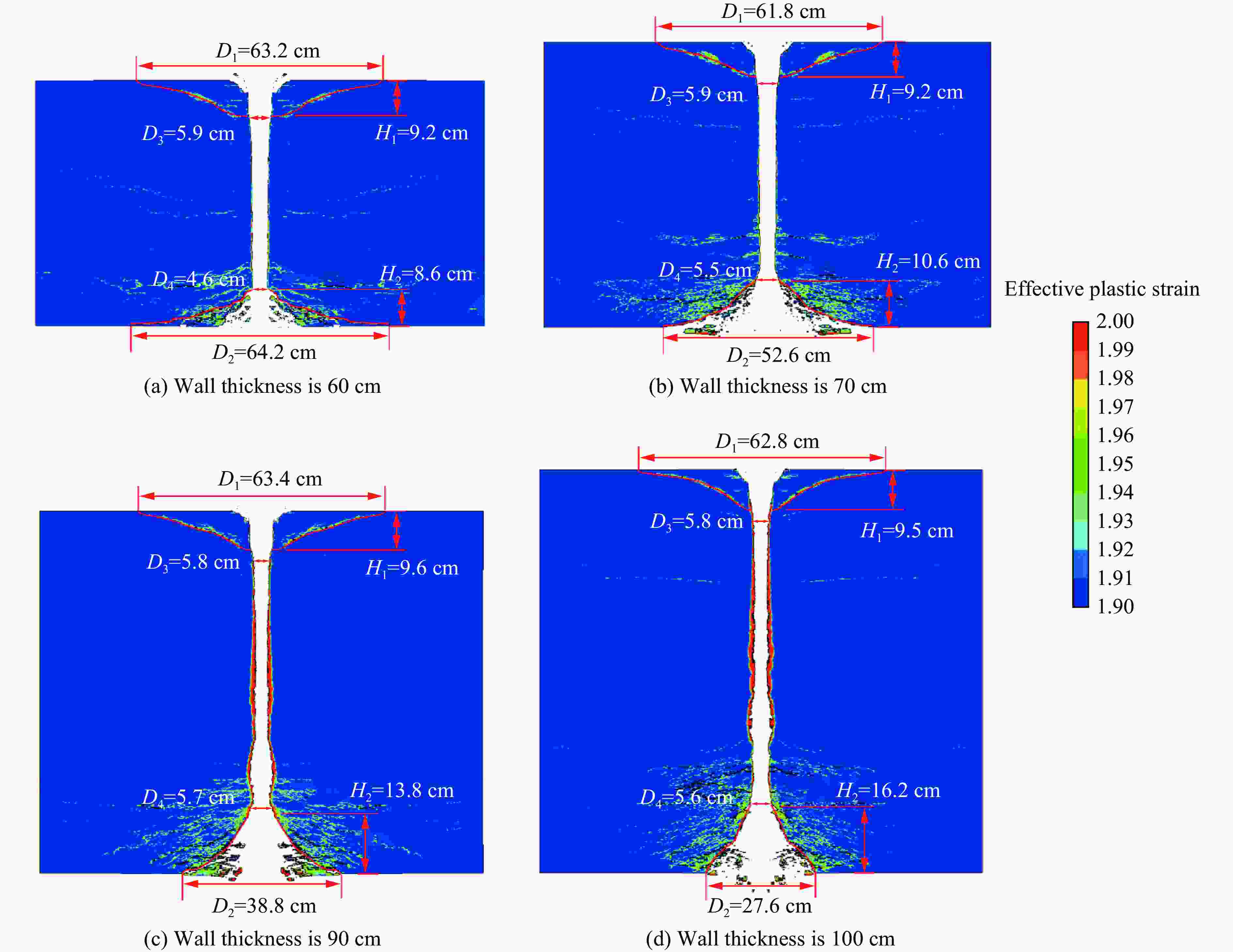
Table 8. Simulation results of reinforced concrete wall with different thickness
δ/cm D1/cm D2/cm D3/cm D4/cm H1/cm H2/cm H3/cm H3/δ 60 63.2 64.2 5.9 4.6 9.2 8.6 42.2 0.703 70 61.8 52.6 5.9 5.5 9.2 10.6 50.2 0.717 80 62.4 44.4 5.9 5.6 9.4 11.5 59.1 0.738 90 63.4 38.8 5.8 5.7 9.6 13.8 66.6 0.740 100 62.8 27.6 5.8 5.6 9.5 16.2 74.3 0.743
下载: 导出CSV
-
[1] 张雷雷, 黄风雷, 段卓平. 爆炸成型杆式侵彻体对混凝土靶侵彻研究 [J]. 弹箭与制导学报, 2006(SA): 1140–1142. DOI: 10.3969/j.issn.1673-9728.2006.02.361.ZHANG L L, HUANG F L, DUAN Z P. Studies about jetting projectiles charge’s penetration to concrete target [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006(SA): 1140–1142. DOI: 10.3969/j.issn.1673-9728.2006.02.361. [2] 李成兵, 沈兆武, 裴明敬. 聚能杆式弹丸侵彻混凝土实验研究 [J]. 振动与冲击, 2007(7): 85–88,183. DOI: 10.3969/j.issn.1000-3835.2007.07.020.LI C B, SHEN Z W, PEI M J. Experimental investigation of rod-shaped projectile penetrating concrete [J]. Journal of Vibration and Shock, 2007(7): 85–88,183. DOI: 10.3969/j.issn.1000-3835.2007.07.020. [3] 顾文彬, 胡亚峰, 刘建青, 等. 基于等质量变壁厚球缺罩聚能杆式射流成型特性研究 [J]. 爆破器材, 2013, 42(4): 14–19. DOI: 10.3969/j.issn.1001-8352.2013.04.004.GU W B, HU Y F, LIU J Q, et al. Characteristic study on jetting projectile charge formation of variable thickness sphere liner based on equi-mass [J]. Explosive Materials, 2013, 42(4): 14–19. DOI: 10.3969/j.issn.1001-8352.2013.04.004. [4] 付恒, 陈智刚. 等壁厚球缺形装药结构优化设计 [J]. 爆破器材, 2016, 45(5): 17–22. DOI: 10.3969/j.issn.1001-8352.2016.05.004.FU H, CHEN Z G. Optimization design of hemispherical charge structure with equal thickness [J]. Explosive Materials, 2016, 45(5): 17–22. DOI: 10.3969/j.issn.1001-8352.2016.05.004. [5] 张钧, 陈智刚, 李小军, 等. 变壁厚球缺罩杆式射流的形成与侵彻性能研究 [J]. 爆破器材, 2016, 45(1): 39–42. DOI: 10.3969/j.issn.1001-8352.2016.01.009.ZHANG J, CHEN Z G, LI X J, et al. Formation and penetration performances of jetting penetrator charge of hemispherical liners with variable thickness [J]. Explosive Materials, 2016, 45(1): 39–42. DOI: 10.3969/j.issn.1001-8352.2016.01.009. [6] 王维占, 冯顺山, 李小军, 等. 局部变壁厚球缺型药型罩侵彻威力性能的数值模拟及试验验证 [J]. 火炸药学报, 2018, 41(4): 420–424. DOI: 10.14077/j.issn.1007-7812.2018.04.018.WANG W Z, FENG S S, LI X J, et al. Numerical simulation and experimental verification of the penetrating power performance of hemispherical liner with locally variable-walled thickness [J]. Chinese Journal of Explosives & Propellants, 2018, 41(4): 420–424. DOI: 10.14077/j.issn.1007-7812.2018.04.018. [7] 张毅, 王志军, 崔斌, 等. 不同结构钛合金罩战斗部侵彻混凝土数值模拟 [J]. 兵器材料科学与工程, 2015, 38(2): 95–98. DOI: 10.14024/j.cnki.1004-244x.2015.02.008.ZHANG Y, WANG Z J, CUI B, et al. Numerical simulation on concrete target penetrated by warhead of different titanium alloy shaped charge [J]. Ordnance Material Science and Engineering, 2015, 38(2): 95–98. DOI: 10.14024/j.cnki.1004-244x.2015.02.008. [8] LI J, HAO H. Numerical study of concrete spall damage to blast loads [J]. International Journal of Impact Engineering, 2014, 68: 41–55. DOI: 10.1016/j.ijimpeng.2014.02.001. [9] WU J, ZHOU Y M, ZHANG R, et al. Numerical simulation of reinforced concrete slab subjected to blast loading and the structural damage assessment [J]. Engineering Failure Analysis, 2020, 118: 104926. DOI: 10.1016/j.engfailanal.2020.104926. [10] HU F, WU H, FANG Q, et al. Numerical simulations of shaped charge jet penetration into concrete-like targets [J]. International Journal of Protective Structures, 2017, 8(2): 237–259. DOI: 10.1177/2041419617706863. [11] LI W B, WANG X M, LI W B. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator [J]. International Journal of Impact Engineering, 2010, 37(4): 414–424. DOI: 10.1016/j.ijimpeng.2009.08.008. [12] GERAMI N D, LIAGHAT G H, MOGHADAS G H R S, et al. Analysis of liner effect on shaped charge penetration into thick concrete targets [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2017, 39(8): 3189–3201. DOI: 10.1007/s40430-017-0797-6. [13] WANG C, MA T B, NING J G. Experimental investigation of penetration performance of shaped charge into concrete targets [J]. Acta Mechanica Sinica, 2008, 24(3): 345. DOI: 10.1007/s10409-008-0160-3. [14] WU Y C, CRAWFORD J E. Numerical modeling of concrete using a partially associative plasticity model [J]. Journal of Engineering Mechanics, 2015, 141(12): 04015051. DOI: 10.1061/(ASCE)EM.1943-7889.0000952. [15] HONG J, FANG Q, CHEN L, et al. Numerical predictions of concrete slabs under contact explosion by modified K&C material model [J]. Construction and Building Materials, 2017, 155(11): 1013–1024. DOI: 10.1016/j.conbuildmat.2017.08.060. [16] MAO L, BARNETT S, BEGG D, et al. Numerical simulation of ultra high performance fibre reinforced concrete panel subjected to blast loading [J]. International Journal of Impact Engineering, 2014, 64: 91–100. DOI: 10.1016/j.ijimpeng.2013.10.003. [17] KONG X Z, FANG Q, LI Q M, et al. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact [J]. International Journal of Impact Engineering, 2017, 108: 217–228. DOI: 10.1016/j.ijimpeng.2017.02.016. [18] LIN X S, GRAVINA R J. An effective numerical model for reinforced concrete beams strengthened with high performance fibre reinforced cementitious composites [J]. Materials and Structures, 2017, 50(5): 212. DOI: 10.1617/s11527-017-1085-8. [19] LEE M J, PARK G K, KIM S W, et al. Damage characteristics of high-performance fiber-reinforced cement composites panels subjected to projectile impact [J]. International Journal of Mechanical Sciences, 2022, 214: 106919. DOI: 10.1016/j.ijmecsci.2021.106919. [20] CRAWFORD J E, WU Y C, MAGALLANES J M, et al. The importance of shear-dilatancy behaviors in RC columns [J]. International Journal of Protective Structures, 2013, 4(3): 341–377. DOI: 10.1260/2041-4196.4.3.341. [21] LI J, ZHANG Y X. Evaluation of constitutive models of hybrid-fibre engineered cementitious composites under dynamic loadings [J]. Construction and Building Materials, 2012, 30: 149–160. DOI: 10.1016/j.conbuildmat.2011.11.031. [22] 许香照, 马天宝, 郝莉. 大口径聚能装药侵彻厚混凝土靶板的数值模拟及实验研究 [J]. 中国科学:技术科学, 2016, 46(4): 339–348. DOI: 10.1360/N092016-00004.XU X Z, MA T B, HAO L. Experimental and numerical investigation on heavy-caliber shaped-charge penetration in thick concrete target [J]. Scientia Sinica: Technologica, 2016, 46(4): 339–348. DOI: 10.1360/N092016-00004. [23] ABDEL-KADER M. Numerical predictions of the behaviour of plain concrete targets subjected to impact [J]. International Journal of Protective Structures, 2018, 9(3): 313–346. DOI: 10.1177/2041419618759109. [24] XU H, WEN H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials [J]. International Journal of Impact Engineering, 2013, 60: 76–81. DOI: 10.1016/j.ijimpeng.2013.04.005. [25] MALVAR L J, ROSS C. A review of strain rate effects for concrete in tension [J]. ACI Materials Journal, 1998, 95: 735–739. [26] KONG X Z, FANG Q, ZHANG J H, et al. Numerical prediction of dynamic tensile failure in concrete by a corrected strain-rate dependent nonlocal material model [J]. International Journal of Impact Engineering, 2020, 137: 103445. DOI: 10.1016/j.ijimpeng.2019.103445. [27] Comite Euro-International Du Beton. CEB-FIP model code 1990: design code[M]. London:Thomas Telford Publishing, 1993. [28] YANKELEVSKY D, FELDGUN V. The embedment of a high velocity rigid ogive nose projectile into a concrete target [J]. International Journal of Impact Engineering, 2020, 144: 103631. DOI: 10.1016/j.ijimpeng.2020.103631. [29] LI Q M, TONG D J. Perforation thickness and ballistic limit of concrete target subjected to rigid projectile impact [J]. Journal of Engineering Mechanics, 2003, 129(9): 1083–1091. DOI: 10.1061/(ASCE)0733-9399(2003)129:9(1083. [30] LI P P, BROUWERS H J H, YU Q L. Influence of key design parameters of ultra-high performance fibre reinforced concrete on in-service bullet resistance [J]. International Journal of Impact Engineering, 2020, 136: 103434. DOI: 10.1016/j.ijimpeng.2019.103434. [31] MENG C M, TAN Q H, JIANG Z G, et al. Approximate solutions of finite dynamic spherical cavity-expansion models for penetration into elastically confined concrete targets [J]. International Journal of Impact Engineering, 2018, 114: 182–193. DOI: 10.1016/j.ijimpeng.2018.01.001. [32] CAO Y Y, YU Q L, TANG W H, et al. Numerical investigation on ballistic performance of coarse-aggregated layered UHPFRC [J]. Construction and Building Materials, 2020, 250: 118867. DOI: 10.1016/j.conbuildmat.2020.118867. 期刊类型引用(0)
其他类型引用(3)
-
下载:
计量
- 文章访问数: 565
- HTML全文浏览量: 235
- PDF下载量: 109
- 被引次数: 3