基于分数阶模型的牡蛎壳动力学特性研究

袁良柱; 陆建华; 苗春贺; 王鹏飞; 徐松林

doi:10.11883/bzycj-2022-0318

基于分数阶模型的牡蛎壳动力学特性研究

doi: 10.11883/bzycj-2022-0318

袁良柱^1,,
陆建华¹,
苗春贺¹,
王鹏飞¹,
徐松林^{1, 2, ,}

1.
中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽合肥 230027
2.
中国地震局地震预测研究所高压物理与地震科技联合实验室，北京 100036

基金项目: 国家自然科学基金（11672286, 11872361）；中央高校基本科研业务费专项资金（WK2480000008）；中石油与中科院重大战略合作项目（2015A-4812）；高压物理与地震科技联合实验室室开放基金（2019HPPES01）

详细信息

作者简介:
袁良柱（1998－　），男，博士研究生，ylzustcedu@mail.ustc.edu.cn

通讯作者:
徐松林（1971－　），男，博士，研究员，博士生导师，slxu99@ustc.edu.cn

中图分类号: O347
计量
- 文章访问数: 634
- HTML全文浏览量: 215
- PDF下载量: 112
- 被引次数: 0
出版历程
- 收稿日期: 2022-07-21
- 修回日期: 2022-10-11
- 网络出版日期: 2022-11-21
- 刊出日期: 2023-01-05

Dynamic properties of oyster shells based on a fractional-order model

1.
CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, Anhui, China
2.
United Laboratory of High-Pressure Physics and Earthquake Science, Institute of Earthquake Forecasting, China Earthquake Administration, Beijing 100036, China

摘要

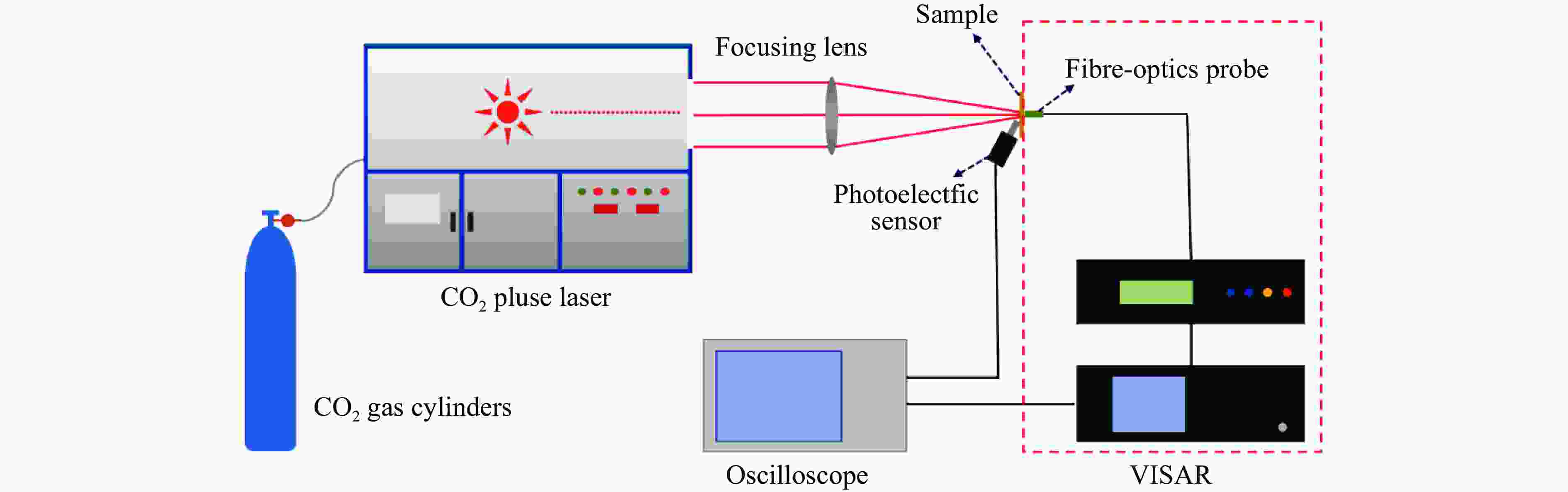
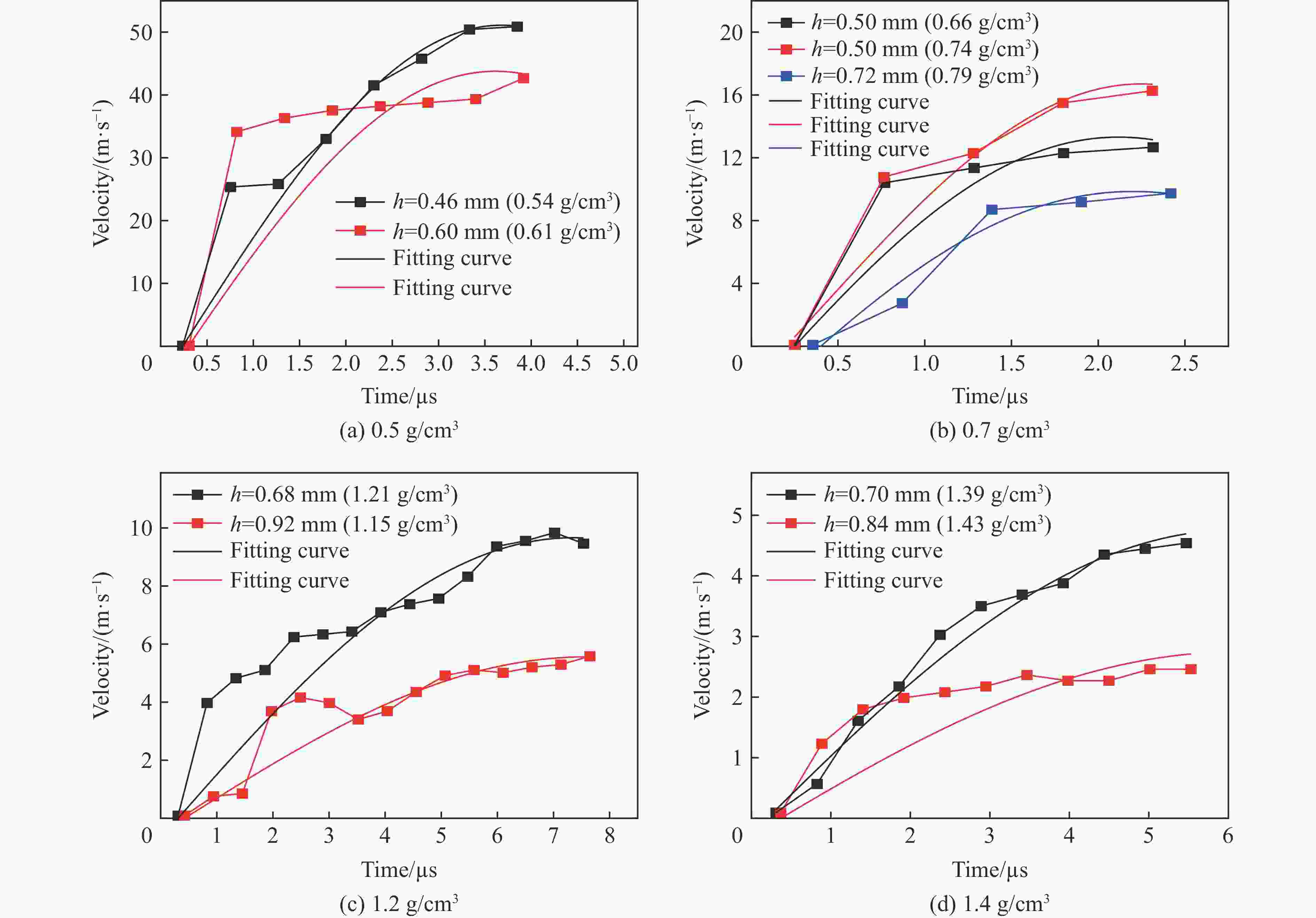
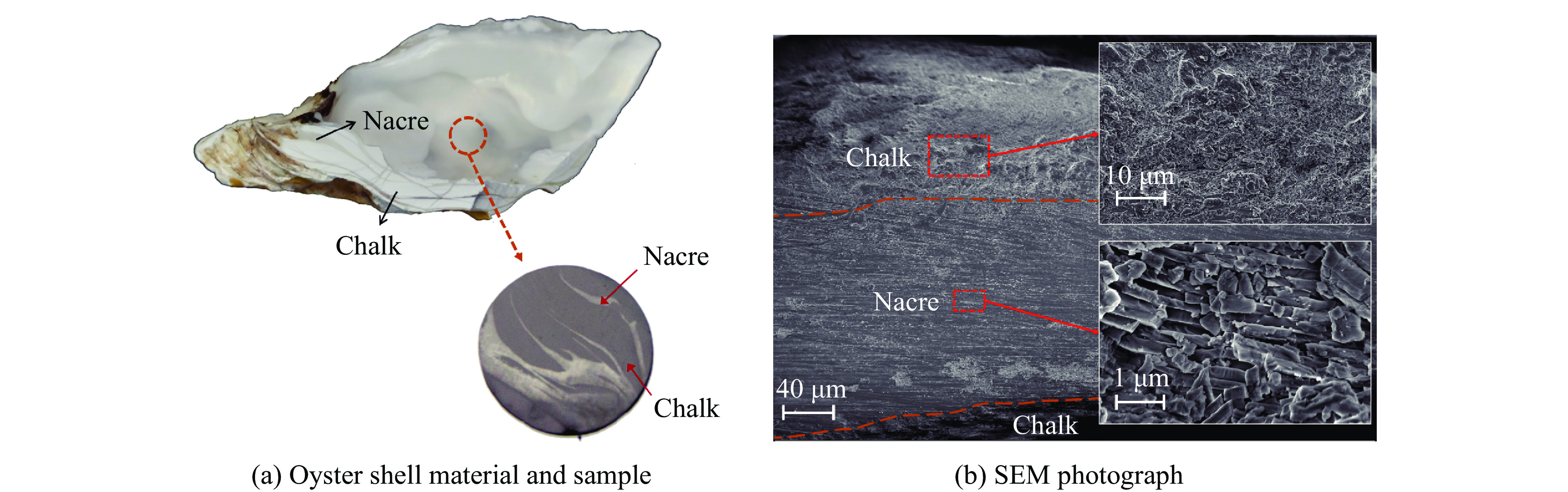
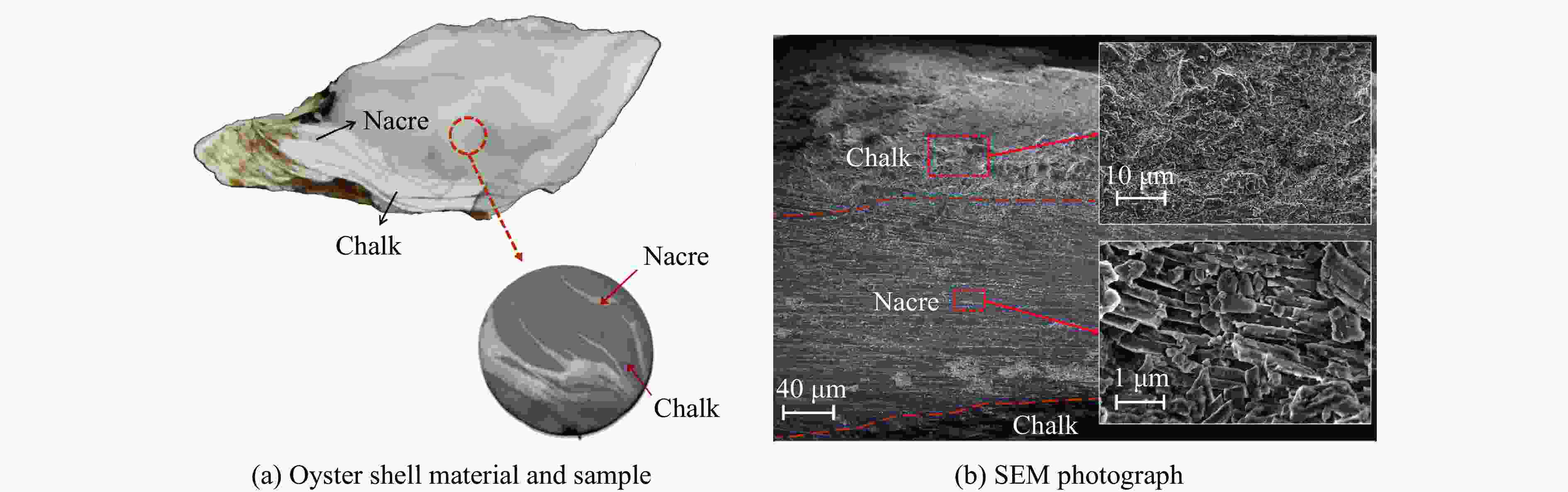
摘要: 贝壳、牡蛎等天然材料因其轻质高强的力学特性在材料设计等领域受到了广泛的关注，但由于材料本身结构的复杂性，对其力学行为的研究十分困难。近年来，分数阶模型在研究材料的力学特性上取得了成功，相比传统模型，分数阶模型可以更好地表征复杂介质的应力或应变与时间的关系。因此，本文从波传播理论出发，以分数阶模型作为材料本构，得到了复杂介质的波传播控制方程。通过Laplace变换得到了控制方程的解析解，并通过Laplace数值逆变换分析了波的衰减对分数阶模型中参量的敏感性，讨论了不同于材料弹性、黏性的材料“惯性”特性。接着，基于解析解和多种实验测试信号，给出了得到分数阶模型参数的拟合式子。以牡蛎材料作为研究对象，利用CO₂脉冲激光器进行小试样的冲击加载、应用两点激光干涉测速系统（laser interferometer velocimetry system, VISAR）对表面粒子的速度进行测量，得到了4种密度下不同厚度的牡蛎壳试样的粒子速度时程曲线，再结合上述理论方法分析得到了牡蛎壳试样的Abel模型和分数阶Maxwell模型的参数，模型参数反映了牡蛎壳试样的细微观结构特征。结果发现：牡蛎壳试样的密度越大，即在细微观上具有砖泥结构的珍珠层的占比越高，速度衰减越大，试样的黏性越大；这是由于CO₂激光脉冲器发射的激光波长与牡蛎壳试样珍珠层的砖泥结构间的缝隙尺寸相近，使得激光在冲击牡蛎壳试样中的珍珠层时发生较大的散射。
- 分数阶导数 /
- 本构模型 /
- 牡蛎壳 /
- 脉冲激光 /
- 动力学特性
Abstract: Natural materials such as shells and oysters have attracted extensive attention in the field of material design due to their lightweight and high-strength mechanical properties. However, due to the complex structure of shells, it is very difficult to study their mechanical behavior. In recent years, fractional-order models have been successful in studying the mechanical properties of materials. Compared with the traditional constitutive model, the fractional model can better characterize the relationship between the complex media’s stress or strain and time. Therefore, based on wave propagation theory and by using the time-dependent fractional-order model as the material constitutive model, the complex medium is simplified to the uniform medium, and its governing equation is obtained by then. The analytic solution of the governing equation which is a function of space coordinate x and Laplace variable s is obtained by the Laplace transform. It is hard to obtain the analytical solution of space coordinate x and time t directly through the inverse Laplace transform, so the numerical inverse Laplace transform is used to obtain the numerical solution of the governing equation in the time domain. The sensitivity of wave attenuation to parameters in the fractional model is analyzed. The inertial properties, which are different from the elastic and viscous properties of materials, are also discussed by analyzing the attenuation characteristics of stress waves when the order α is 0, 1.0, and 2.0 respectively. Then, based on the analytical solution of the governing equation and a variety of experimental test signals, a fitting formula is given to obtain the parameters of the fractional model. Oyster material with layered structure is taken as the research object. To obtain the local dynamic mechanical properties of oyster samples, the CO₂ pulse laser was used to carry out the impact loading of the small sample due to the high variability of the density distribution of oyster samples, and the two-point laser interferometer velocimetry system (VISAR) was used to measure the surface particle velocity. The particle velocity time history curve of the oyster sample with different densities and thicknesses was obtained. Combined with the above fitting formula, the parameters of the Abel model and Maxwell fractional differential model of oyster samples were obtained by fixing and unfixing the values of fractional order α, and the model parameters reflected the fine microstructure characteristics of oyster samples. The results show that the higher the density of the oyster sample is, the higher the proportion of nacre with brick and mortar structure in fine and micro, the greater the velocity attenuation, and the greater the viscosity of the oyster sample. The laser wavelength emitted by the CO₂ laser pulse is similar to the size of the gap between brick and mortar structures in the nacre of the oyster sample, so the laser has a large scattering when it impacts the nacre of the oyster sample, which causes the velocity attenuation. This study has a good reference significance for the study of the dynamic properties of meso-isomeric and macro-continuous complex media.
- fractional derivative /
- constitutive model /
- oyster shell /
- pulse laser /
- dynamic properties

HTML全文

图 1 牡蛎壳材料、圆形实验试样、试样纵剖面电镜照片与局部放大

Figure 1. Oyster shell material, circular sample, longitudinal section electron microscopy (SEM) and local magnification

下载: 全尺寸图片幻灯片

图 2 CO₂脉冲加载与激光干涉测速系统(VISAR)

Figure 2. CO₂ pulse loading and laser interferometer velocimetry system (VISAR)

下载: 全尺寸图片幻灯片

图 3 几种分数阶本构模型

Figure 3. Several fractional differential constitutive models

下载: 全尺寸图片幻灯片

图 4 单个半脉宽正弦函数

Figure 4. Single half pulse width sine function

下载: 全尺寸图片幻灯片

图 5 正弦波在Abel黏壶模型介质的衰减

Figure 5. Attenuation of a single half pulse width sine wave in Abel model media

下载: 全尺寸图片幻灯片

图 6 当α分别为1.0和2.0时的波传播特性

Figure 6. The property of wave propagation when the order α is 1.0 and 2.0 , respectively

下载: 全尺寸图片幻灯片

图 7 参数α、η和E对幅值衰减的影响

Figure 7. Influence of parameters α, η and E on amplitude attenuation

下载: 全尺寸图片幻灯片

图 8 各个密度下不同厚度牡蛎试样的速度信号及拟合曲线

Figure 8. Velocity signals and fitting curves of oyster samples with different thicknesses and densities

下载: 全尺寸图片幻灯片

图 9 牡蛎试样分数阶模型的拟合曲线及参数与牡蛎试样密度的关系

Figure 9. The fitting curve of the fractional model of the oyster sample and relationship between parameters and oyster sample density

下载: 全尺寸图片幻灯片

表 1 牡蛎壳试样分数阶模型的拟合参数

Table 1. Fitting parameters of the fractional model of the oyster sample

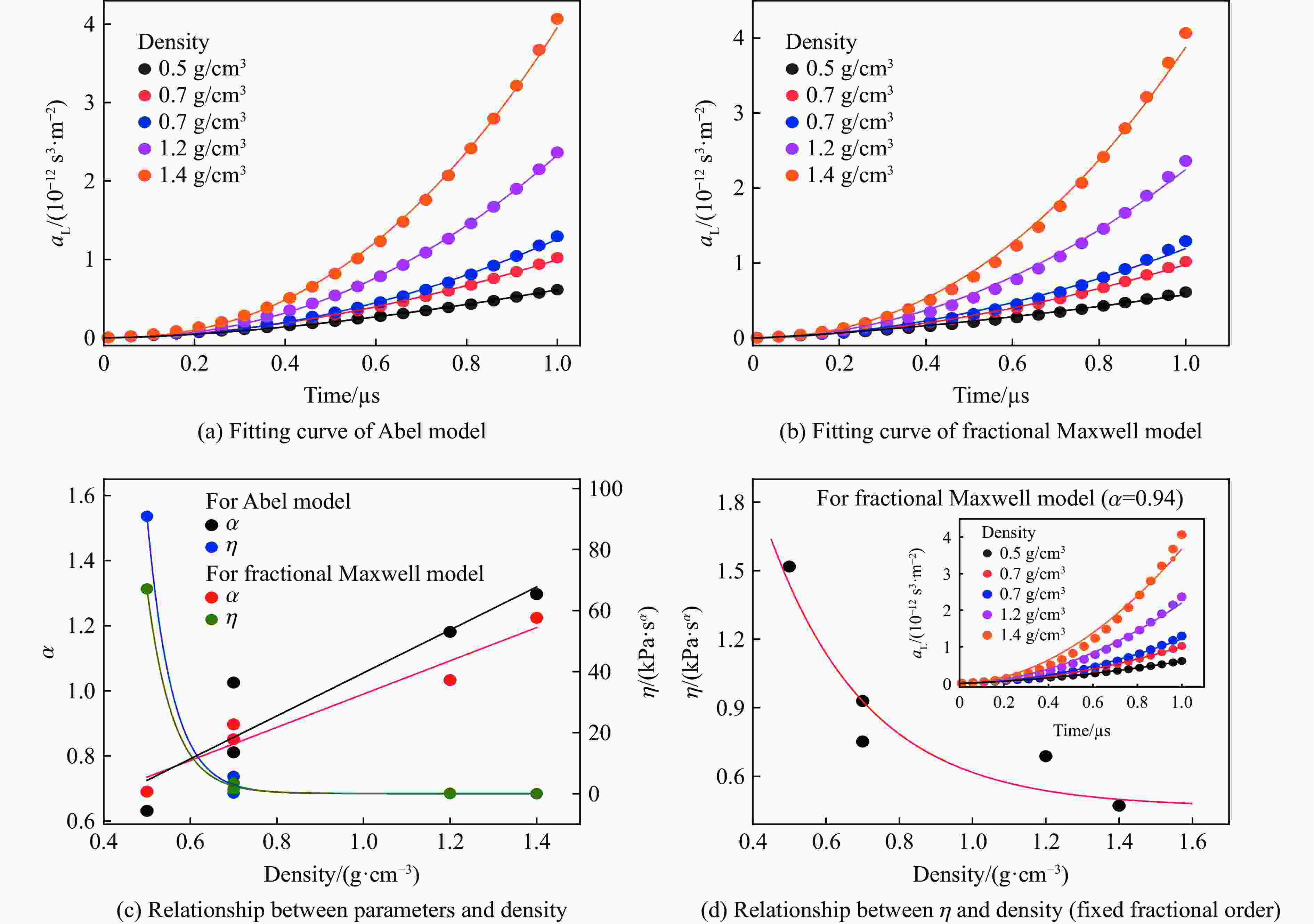
材料本构	密度/(g·cm⁻³)	α	E/GPa	η/(Pa·s^α)
Abel模型	0.5	0.631	-	9.09×10⁴
	0.7	0.811	-	5.65×10³
	0.7	1.025	-	192.12
	1.2	1.181	-	17.84
	1.4	1.297	-	2.19
分数阶Maxwell模型	0.5	0.690	2.21	6.71×10⁴
	0.7	0.851	7.34	3.55×10³
	0.7	0.897	7.67	1.45×10³
	1.2	1.033	12.88	170.01
	1.4	1.224	15.40	6.76

下载: 导出CSV

表 2 固定分数阶阶数情况下，牡蛎壳试样分数阶Maxwell模型的拟合参数

Table 2. Fitting parameters of fractional Maxwell model for oyster shell samples in the case of fixed fractional order

材料本构	密度/(g·cm⁻³)	α	E/GPa	η/(Pa·s^α)
分数阶Maxwell模型	0.5	0.94	2.44	1518.00
	0.7		7.67	929.35
	0.7		7.82	751.88
	1.2		13.15	687.85
	1.4		16.46	471.30

下载: 导出CSV

参考文献(33)

[1]	杨挺青. 黏弹性力学 [M]. 武汉: 华中理工大学出版社, 1992: 1–28.
[2]	JI B H, GAO H J. Mechanical properties of nanostructure of biological materials [J]. Journal of the Mechanics and Physics of Solids, 2004, 52: 1963–1990. DOI: 10.1016/j.jmps.2004.03.006.
[3]	MAO L B, GAO H L, YAO H B, et al. Synthetic nacre by predesigned matrix-directed mineralization [J]. Science, 2016, 354: 107–110. DOI: 10.1126/science.aaf8991.
[4]	GAO H L, CHEN S M, MAO L B, et al. Mass production of bulk artificial nacre with excellent mechanical properties [J]. Nature Communications, 2017(8): 287. DOI: 10.1038/s41467-017-00392-z.
[5]	WU K J, SONG Z Q, ZHANG S S, et al. Discontinuous fibrous Bouligand architecture enabling formidable fracture resistance with crack orientation insensitivity [J]. Proceedings of the National Academy of Sciences, 2020, 117(27): 15465–15472. DOI: 10.1073/pnas.2000639117.
[6]	HUANG Z W, LI H Z, PAN Z L, et al. Uncovering high-strain rate protection mechanism in nacre [J]. Scientific Reports, 2011(1): 148. DOI: 10.1038/srep00148.
[7]	徐松林, 刘永贵, 席道瑛等. 弹性波在含双裂纹岩体中的传播分析 [J]. 地球物理学报, 2012, 55(3): 944–952. DOI: 10.6038/j.issn.0001-5733.2012.03.024. XU S L, LIU Y G, XI D Y, et al. Analysis of propagation of elastic wave in rocks with double-crack model [J]. Chinese Journal of Geophysics, 2012, 55(3): 944–952. DOI: 10.6038/j.issn.0001-5733.2012.03.024.
[8]	谭子翰, 徐松林, 刘永贵, 等. 含多种尺寸缺陷岩体中的弹性波散射 [J]. 应用数学和力学, 2013, 34(1): 38–48. DOI: 10.3879/j.issn.1000-0887.2013.01.005. TAN Z H, XU S L, LIU Y G, et al. Scattering of elastic waves by multi-size defects in rock mass [J]. Applied Mathematics and Mechanics, 2013, 34(1): 38–48. DOI: 10.3879/j.issn.1000-0887.2013.01.005.
[9]	WANG P F, XU S L, LI Z B, et al. Experimental investigation on the strain-rate effect and inertia effect of closed-cell aluminum foam subjected to dynamic loading [J]. Materials Science and Engineering A, 2014, 620: 253–261. DOI: 10.1016/j.msea.2014.10.026.
[10]	MIAO C H, XU S L, SONG Y P, et al. Influence of stress state on dynamic breakage of quartz glass spheres subjected to lower velocity impacting [J]. Powder Technology, 2022, 397: 117081. DOI: 10.1016/j.powtec.2021.117081.
[11]	HUANG J Y, HU S S, XU S L, et al. Fractal crushing of granular materials under confined compression at different strain rates [J]. International Journal of Impact Engineering, 2017, 106: 259–265. DOI: 10.1016/j.ijimpeng.2017.04.021.
[12]	TING T C T, MUKUNOKI I. A theory of viscoelastic analogy for wave propagation normal to the layering of a layered medium [J]. Journal of Applied Mechanics, 1979, 46(2): 329–336. DOI: 10.1115/1.3424550.
[13]	张鸣, 王道荣, 单俊芳, 等. 石英纤维布叠层材料冲击性能研究 [J]. 实验力学, 2018, 33(2): 183–193. DOI: 10.7520/1001-4888-17-201. ZHANG M, WANG D R, SHAN J F, et al. Investigation on impact properties of quartz fiber cloth laminated material [J]. Journal of Experimental Mechanics, 2018, 33(2): 183–193. DOI: 10.7520/1001-4888-17-201.
[14]	李毅, 苗春贺, 徐松林, 等. 梯度密度黏弹性材料的波传播研究 [J]. 爆炸与冲击, 2021, 41(1): 013202. DOI: 10.11883/bzycj-2020-0313. LI Y, MIAO C H, XU S L, et al. Wave propagation in density-graded viscoelastic material [J]. Explosion and Shock Waves, 2021, 41(1): 013202. DOI: 10.11883/bzycj-2020-0313.
[15]	李毅. 梯度密度黏弹性材料的冲击响应研究 [D]. 合肥: 中国科学技术大学, 2020: 17–74. DOI: 10.27517/d.cnki.gzkju.2021.001407. LI Y. Investigation of dynamic response in density-graded viscoelastic material [D]. Hefei, Anhui, China: University of Science and Technology of China, 2021: 17–74. DOI: 10.27517/d.cnki.gzkju.2021.001407.
[16]	陈文, 孙洪广, 李西成, 等. 力学与工程问题的分数阶导数建模 [M]. 北京: 科学出版社, 2010: 12–56.
[17]	BAGLEY R L. Power law and fractional calculus model of viscoelasticity [J]. AIAA Journal, 1989, 27(10): 1412–1417. DOI: 10.2514/3.10279.
[18]	雷经发, 许孟, 刘涛, 等. 聚氯乙烯弹性体静动态力学性能及本构模型 [J]. 爆炸与冲击, 2020, 40(10): 103103. DOI: 10.11883/bzycj-2019-0249. LEI J F, XU M, LIU T, et al. Static/dynamic mechanical properties and a constitutive model of a polyvinyl chloride elastomer [J]. Explosion and Shock Waves, 2020, 40(10): 103103. DOI: 10.11883/bzycj-2019-0249.
[19]	段宇星, 杨强, 赵苗苗, 等. 弹性体材料应变率相关力学行为模型 [J]. 橡胶工业, 2020, 67(12): 899–903. DOI: 10.12136/j.issn.1000-890X.2020.12.0899. DUAN Y X, YANG Q, ZHAO M M, et al. Strain rate-related mechanical behavior model of elastomer material [J]. China Rubber Industry, 2020, 67(12): 899–903. DOI: 10.12136/j.issn.1000-890X.2020.12.0899.
[20]	WANG P F, YANG J L, SUN G Z, et al. Twist induced plasticity and failure mechanism of helical carbon nanotube fibers under different strain rates [J]. International Journal of Plasticity, 2018, 110: 74–94. DOI: 10.1016/j.ijplas.2018.06.007.
[21]	WANG P F, YANG J L, ZHANG X, et al. Dynamic behavior of carbon nanofiber-modified epoxy with the effect of polydopamine-coated interface [J]. Mechanics of Advanced Materials and Structures, 2018: 1827–1839. DOI: 10.1080/15376494.2018.1529843.
[22]	薛晓. 碳纳米管纤维的动静态力学性能研究 [D]. 合肥: 中国科学技术大学, 2020: 53–61. DOI: 10.27517/d.cnki.gzkju.2020.000565. XUE X. Investigation of dynamic and quasi-static mechanical properties of carbon nanotube fibers [D]. Hefei, Anhui, China: University of Science and Technology of China, 2020: 53–61. 10.27517/d.cnki.gzkju.2020.000565.
[23]	XUE X, WANG P F, GONG M, et al. Time-dependent microstructural evolution mechanisms of twisted carbon nanotube fibers under tension and relaxation [J]. International Journal of Plasticity, 2021, 136: 102866. DOI: 10.1016/j.ijplas.2020.102866.
[24]	赵永玲, 侯之超. 基于分数导数的橡胶材料两种粘弹性本构模型 [J]. 清华大学学报(自然科学版), 2013, 53(3): 378–383. DOI: 10.16511/j.cnki.qhdxxb.2013.03.004. ZHAO Y L, HOU Z C. Two viscoelastic constitutive models of rubber materials using fractional derivations [J]. Journal of Tsinghua University (Science and Technology), 2013, 53(3): 378–383. DOI: 10.16511/j.cnki.qhdxxb.2013.03.004.
[25]	BAGLEY R L, TORRVIK P J. A theoretical basis for the application of fractional calculus to viscoelasticity [J]. Journal of Rheology, 1983, 27(3): 201–210. DOI: 10.1122/1.549724CODEN:JORHD2.
[26]	寇磊. 分数阶微分型双参数黏弹性地基矩形板受荷响应 [J]. 力学季刊, 2013, 34(1): 154–160. DOI: 10.3969/j.issn.0254-0053.2013.01.020. KOU L. Response of rectangular plate on fractional derivative two-parameter viscoelastic foundation [J]. Chinese Quarterly of Mechanics, 2013, 34(1): 154–160. DOI: 10.3969/j.issn.0254-0053.2013.01.020.
[27]	尹耀得, 赵德敏, 刘建林, 等. 丙烯酸弹性体的率相关分数阶黏弹性模型研究 [J]. 力学学报, 2022, 54(1): 154–162. DOI: 10.6052/0459-1879-21-445. YIN Y D, ZHAO D M, LIU J L, et al. Study on the rate dependency of acrylic elastomer-based fractional viscoelastic model [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(1): 154–162. DOI: 10.6052/0459-1879-21-445.
[28]	ZHAO D M, YIN Y D, LIU J L. A fractional finite strain viscoelastic model of dielectric elastomer [J]. Applied Mathematical Modelling, 2021, 100: 564–579. DOI: 10.1016/j.apm.2021.08.023.
[29]	ROSSIKHIN Y A, SHITIKOVA M V. Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results [J]. Applied Mechanics Reviews, 2009, 63: 010801. DOI: 10.1115/1.4000563.
[30]	冯卓意, 陈雪梅. 贝壳资源的深加工利用 [J]. 材料科学与工程学报, 2022, 40(1): 123–128. DOI: 10.14136/j.cnki.issn1673-2812.2022.01.020. FENG Z Y, CHEN X M. Research on the processing technology of seashell resource [J]. Journal of Materials Sciense and Engineering, 2022, 40(1): 123–128. DOI: 10.14136/j.cnki.issn1673-2812.2022.01.020.
[31]	孙晋美, 郭万林. 贝壳珍珠母多级结构的化学-力学稳定性 [J]. 中国科学:物理学力学天文学, 2009, 39(11): 1654–1663. SUN J M, GUO W L. Chemical-mechanical stability of the hierarchical structure of shell nacre [J]. Scientia Sinica: Physica, Mechanica and Astronomica, 2009, 39(11): 1654–1663.
[32]	CONNOLLY J A. The numerical solution of fractional and distributed order differential equations [D]. Liverpool, UK: University of Liverpool, 2004: 13–48.
[33]	张元林. 工程数学(积分变换) [M]. 4版. 北京: 高等教育出版社, 2010: 85–88.