超高性能混凝土HJC本构模型参数确定及应用

宋帅; 杜闯; 李艳艳

doi:10.11883/bzycj-2022-0343

超高性能混凝土HJC本构模型参数确定及应用

doi: 10.11883/bzycj-2022-0343

宋帅^1,,
杜闯^{1, 2, ,},
李艳艳¹

1.
河北工业大学土木与交通学院，天津 300401
2.
河南省特种防护材料重点实验室，河南洛阳 471023

基金项目: 河北省高等学校科学研究项目（ZD2022140）；河南省特种防护材料重点实验室基金（SZKFJJ202005）

详细信息

作者简介:
宋　帅（1994－　），硕士研究生，s3401920284@163.com

通讯作者:
杜　闯（1976－　），博士，讲师，duch_1@sina.com

中图分类号: O382
计量
- 文章访问数: 1239
- HTML全文浏览量: 334
- PDF下载量: 472
- 被引次数: 23
出版历程
- 收稿日期: 2022-08-08
- 修回日期: 2022-11-10
- 网络出版日期: 2022-11-18
- 刊出日期: 2023-05-05

Determination and application of the HJC constitutive model parameters for ultra-high performance concrete

SONG Shuai^1
,,
DU Chuang^{1, 2
, ,},
LI Yanyan¹

1.
School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China
2.
Henan Key Laboratory of Special Protective Materials, Luoyang 471023, Henan, China

摘要

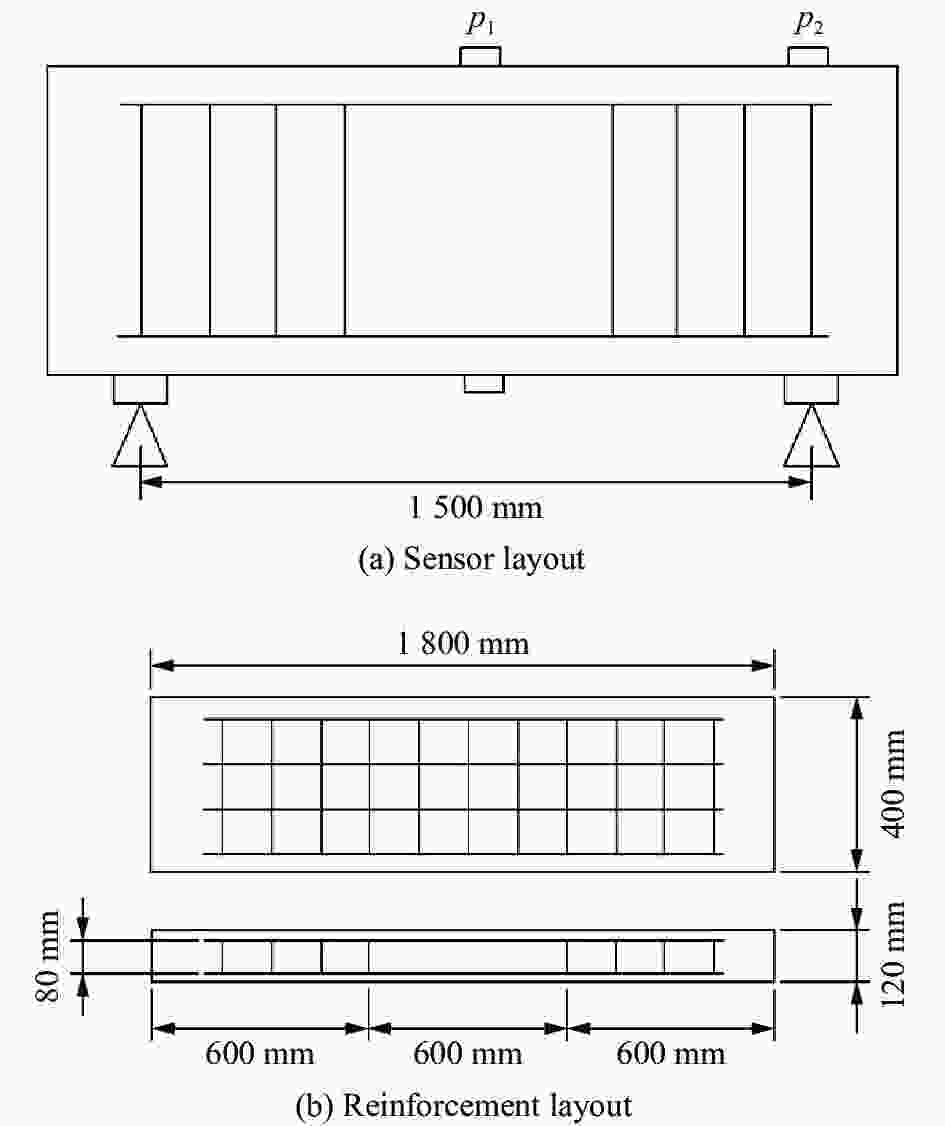
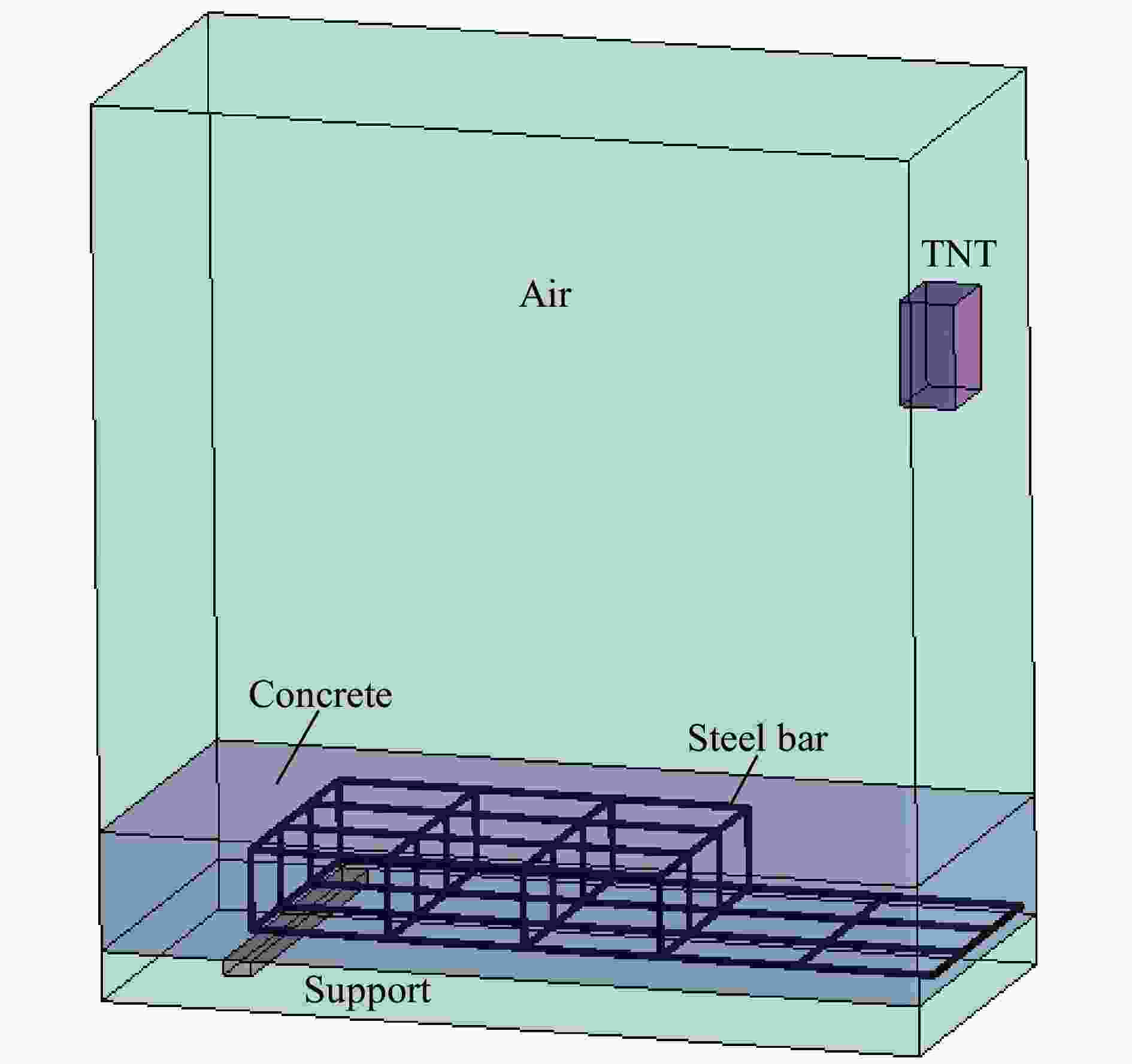
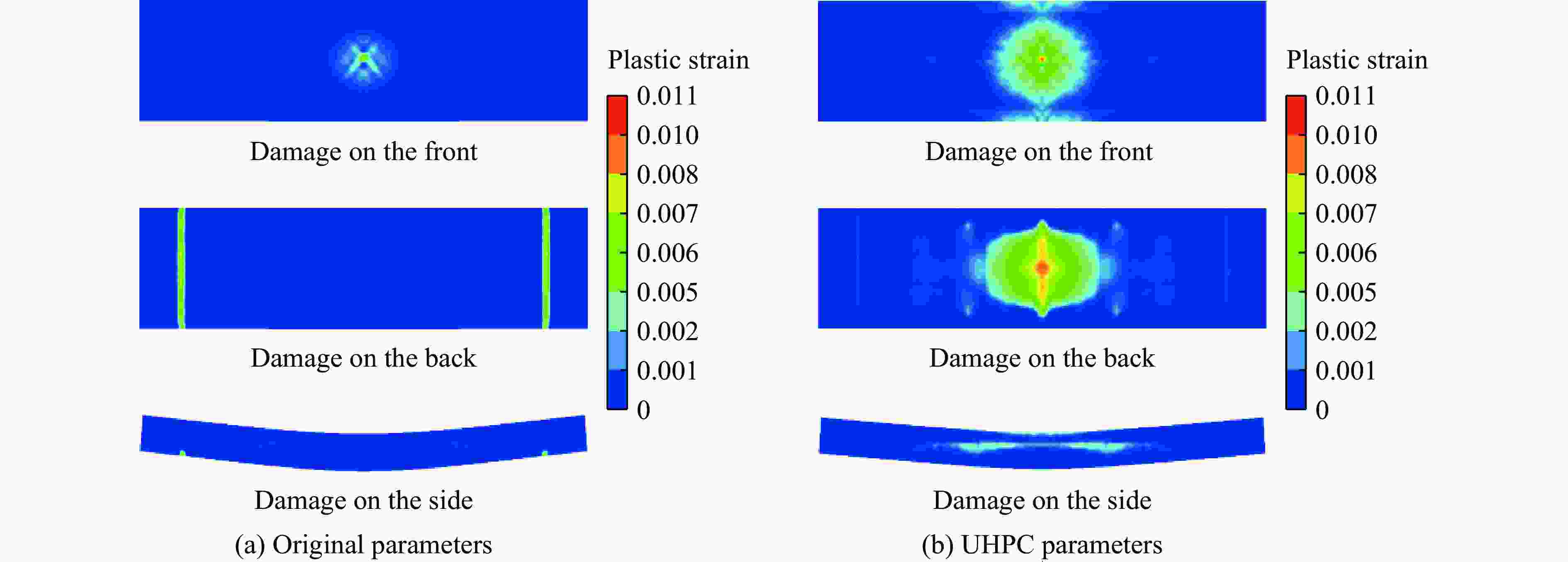
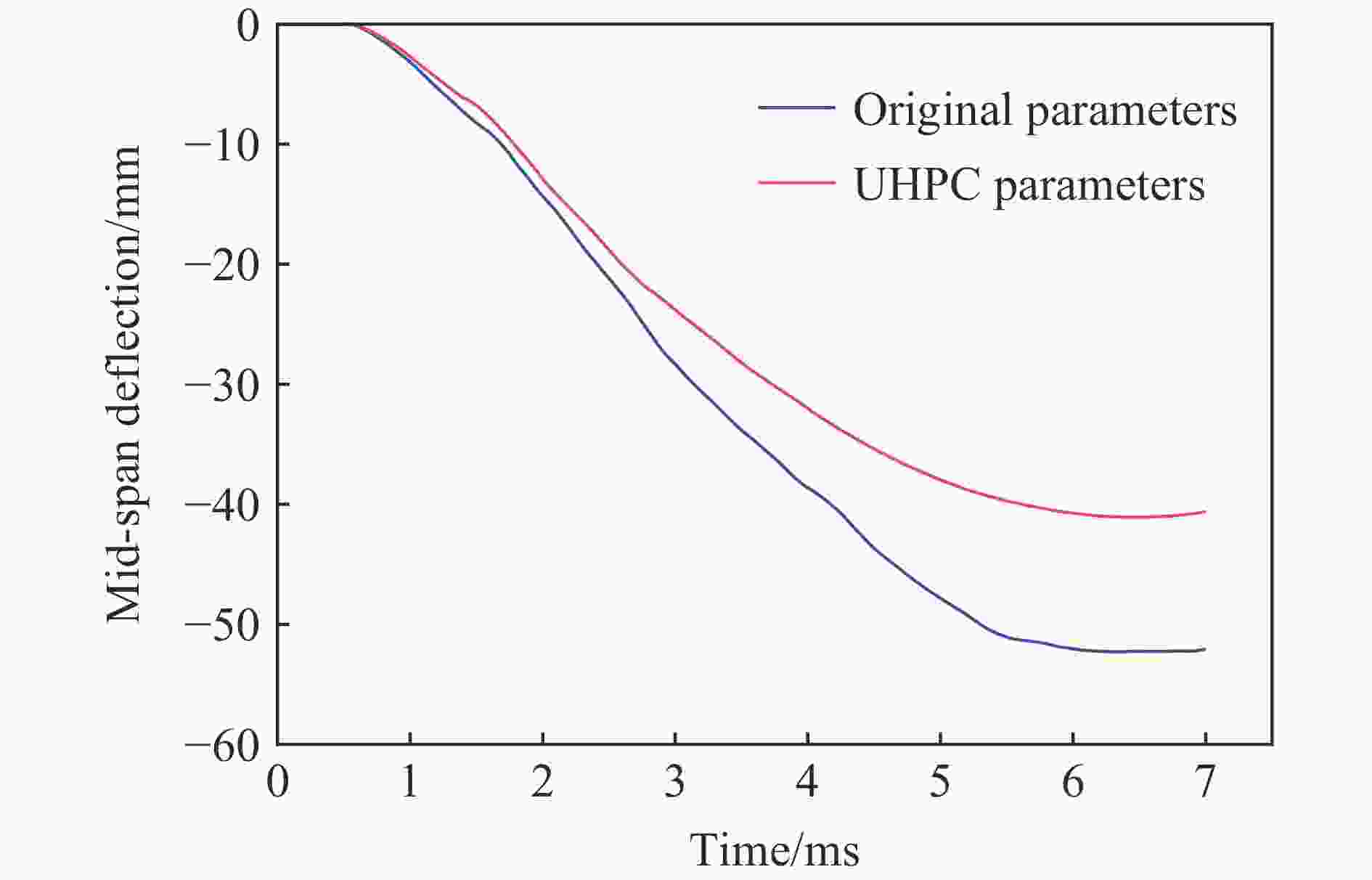
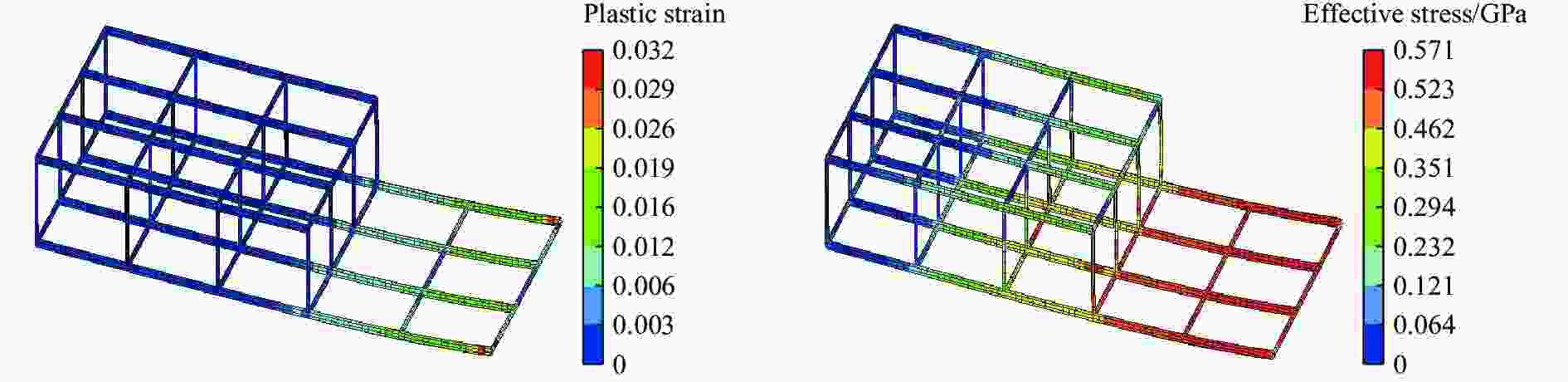
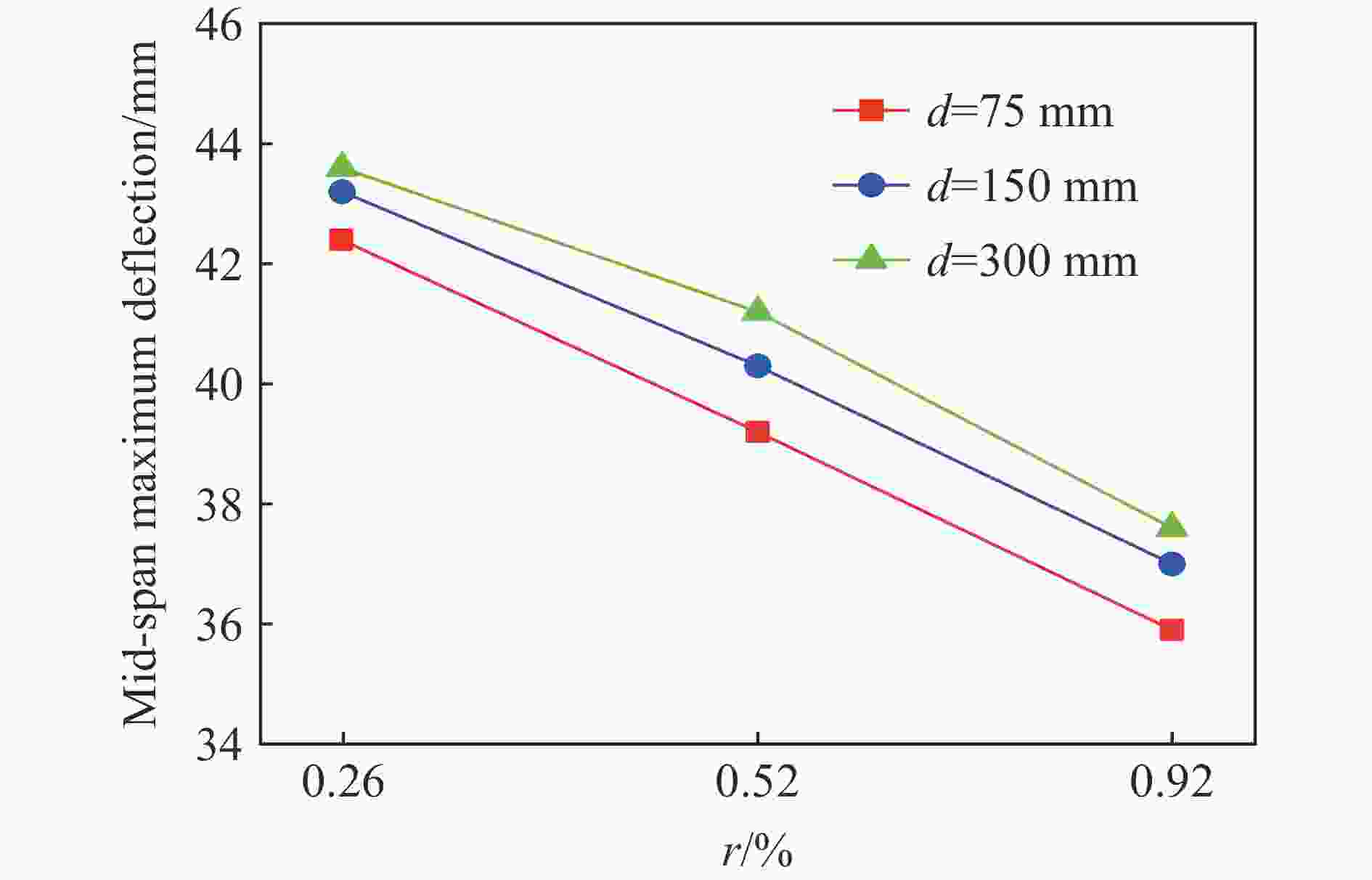
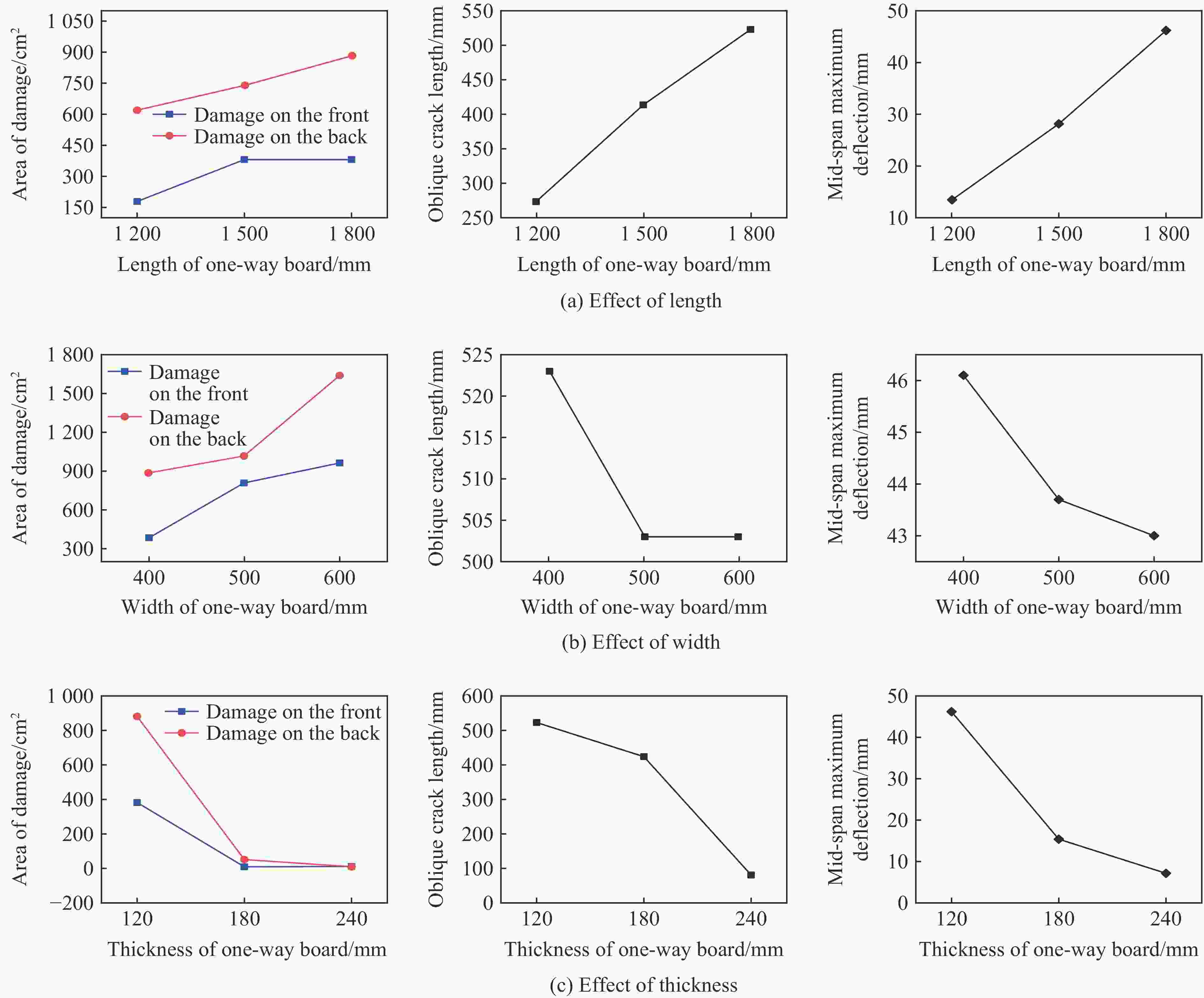
摘要: 在超高性能混凝土的数值模拟中，合理地确定其本构模型参数是提高计算精度和设计可靠度的基础。基于超高性能混凝土单轴压缩试验、霍普金森压杆试验和已有的三轴围压试验等，确定了超高性能混凝土的Holmquist-Johnson-Cook (HJC)本构模型参数。利用LS_DYNA软件模拟单向板爆炸试验，通过与试验中单向板的损伤程度和最大挠度进行对比，验证了已确定参数的有效性。为了进一步了解超高性能混凝土构件的抗爆机理，采用已确定的参数对单向板爆炸工况进行数值模拟，分析配筋和尺寸变化对爆炸结果的影响。结果表明，在爆炸过程中，提高纵筋配筋率可以减小单向板的跨中最大挠度，适当加密箍筋可以减小单向板侧面的斜裂缝长度。超高性能混凝土单向板具有明显的尺寸效应，其中厚度和长度变化对爆炸结果的影响最突出。
- 超高性能混凝土 /
- HJC本构模型 /
- 参数确定 /
- 单向板 /
- 最大挠度 /
- 配筋率
Abstract: The parameters of the Holmquist-Johnson-Cook (HJC) constitutive model for ultra-high performance concrete (UHPC) were determined based on uniaxial compression test, split Hopkinson pressure bar (SHPB) test and existing tri-axial compression test and so on, in order to improve the calculation accuracy and design reliability. In the determination process of parameters, the parameters of the HJC constitutive model were divided into five categories. The yield-surface parameters were determined by the static failure surface equation, the parameters of state equation were determined by the p-μ relation, the damage parameters were determined according to relevant literature, the basic physical parameters were determined according to the test, and so on. LS_DYNA was used to simulate the explosion test of the one-way slab. Firstly, the finite element model of the one-way slab was established. The HJC constitutive model was used for the UHPC, and the linear reinforcement model was used for the reinforcement material. The reinforcement and UHPC were connected by common joints. The air and explosive models were established, and the fluid-solid coupling method was used for calculation. The effectiveness of the determined parameters was verified by comparing the simulation results with the damage degree and the maximum deflection of the one-way slab in the test. In order to further understand the anti-blast mechanism of the UHPC members, the determined parameters were used to conduct numerical simulation on the one-way slab explosion condition, and the influences of reinforcement and size effect on the explosion result were analyzed. Results show that during the explosion process, the maximum mid-span deflection of the one-way slab can be reduced by increasing the longitudinal reinforcement ratio, and the length of oblique cracks on the side of the one-way slab can be reduced by properly encrypted stirrups. The UHPC one-way slab has an obvious size effect, and the variation of its thickness and length has the greatest influence on the explosion result.
- ultra-high performance concrete /
- HJC constitutive model /
- parameter determination /
- one-way slab /
- maximum deflection /
- reinforcement ratio

HTML全文

图 1 静态失效强度与静水压力之间的关系

Figure 1. Relationship between static failure strength and hydrostatic pressure

下载: 全尺寸图片幻灯片

图 2 不同应变率下的等效应力与静水压力之间的关系

Figure 2. Relationship between the effective-stress and hydrostatic pressure under different strain rates

下载: 全尺寸图片幻灯片

图 3 UHPC单轴抗压强度与应变率之间的关系

Figure 3. Relationship between uniaxial compressive strength and strain rate of UHPC

下载: 全尺寸图片幻灯片

图 4 HJC本构模型状态方程

Figure 4. HJC constitutive model equation of states

下载: 全尺寸图片幻灯片

图 5 试验工况

Figure 5. Test layout

下载: 全尺寸图片幻灯片

图 6 有限元模型

Figure 6. Finite element model

下载: 全尺寸图片幻灯片

图 7 不同材料参数下的塑性损伤模拟效果对比

Figure 7. Comparison of simulation effects of plastic damage under different material parameters

下载: 全尺寸图片幻灯片

图 8 不同材料参数下跨中挠度的时程曲线

Figure 8. Time history curves of mid-span deflection under different material parameters

下载: 全尺寸图片幻灯片

图 9 1/2模型的钢筋塑性应变和等效应力分布

Figure 9. Distributions of plastic strain and equivalent stress of reinforcement in the 1/2 model

下载: 全尺寸图片幻灯片

图 10 不同箍筋间距下跨中最大挠度与配筋率的关系

Figure 10. Relationship between mid-span maximum deflection and reinforcement ratio under different stirrup spacings

下载: 全尺寸图片幻灯片

图 11 不同配筋率下斜裂缝长度与箍筋间距的关系

Figure 11. Relationship between oblique crack length and stirrup spacing under different reinforcement ratios

下载: 全尺寸图片幻灯片

图 12 单向板的尺寸效应

Figure 12. Dimension effects of the one-way slab

下载: 全尺寸图片幻灯片

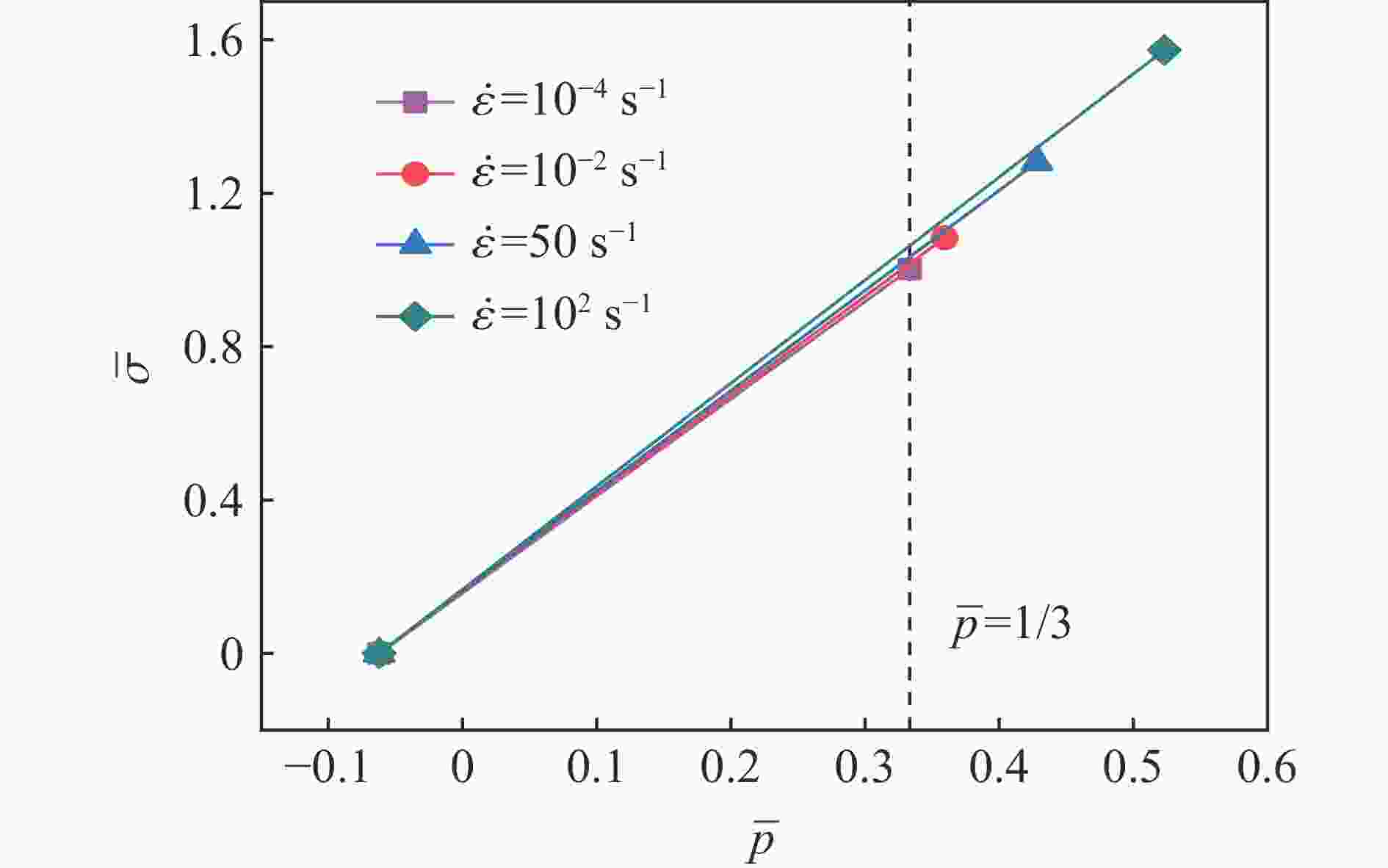
表 1 不同应变率下的UHPC力学参数

Table 1. UHPC mechanical parameters under different strain rates

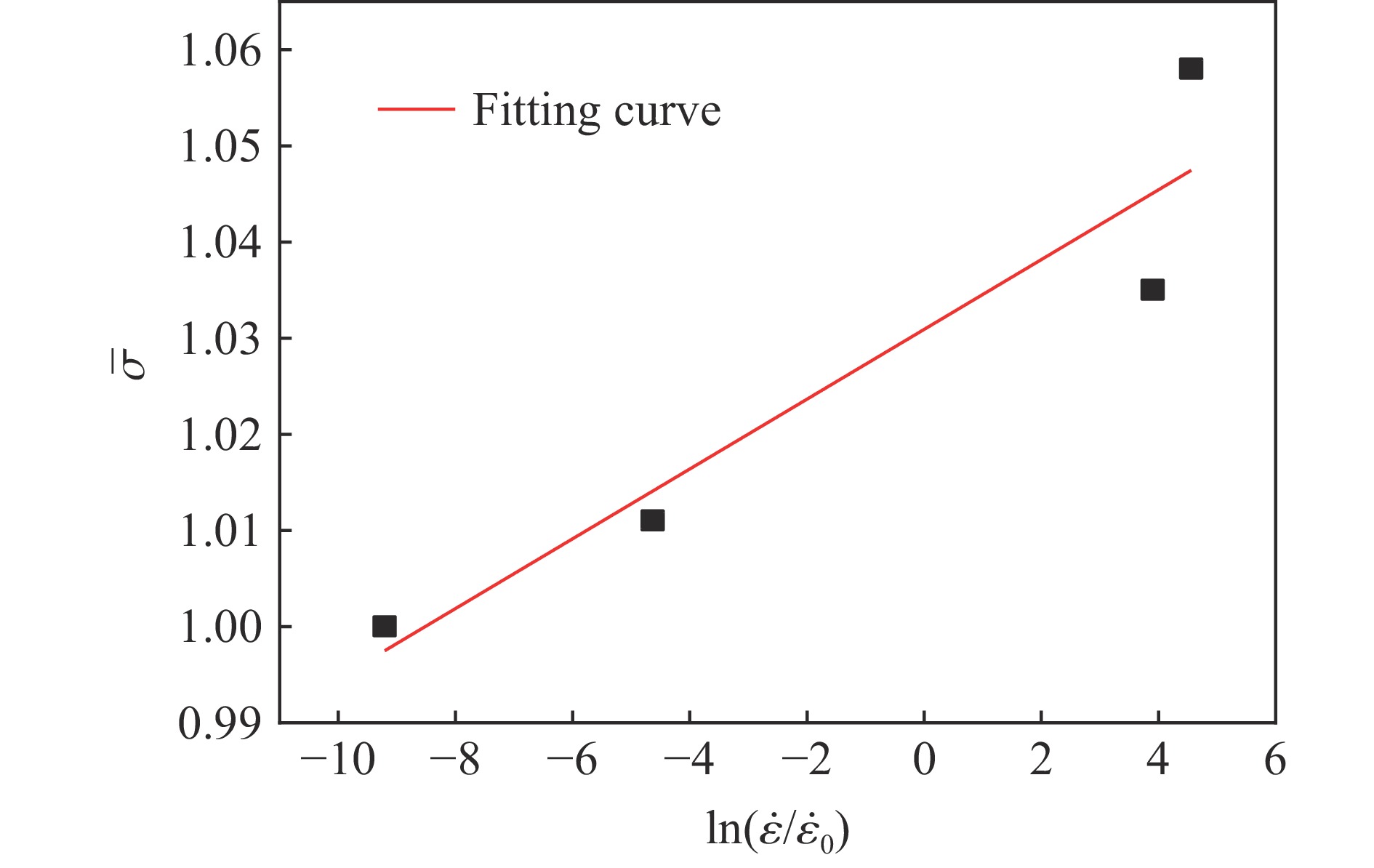
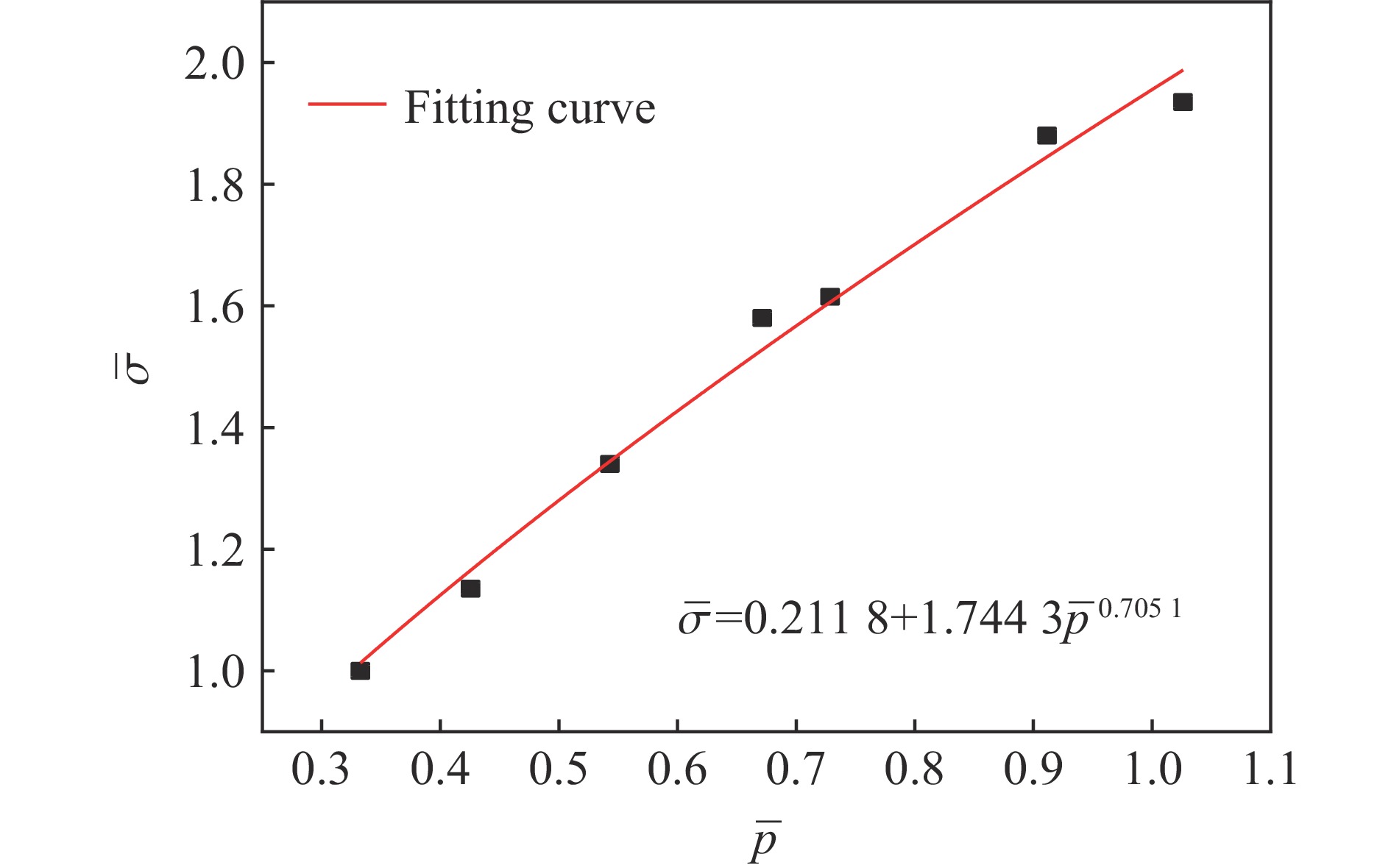
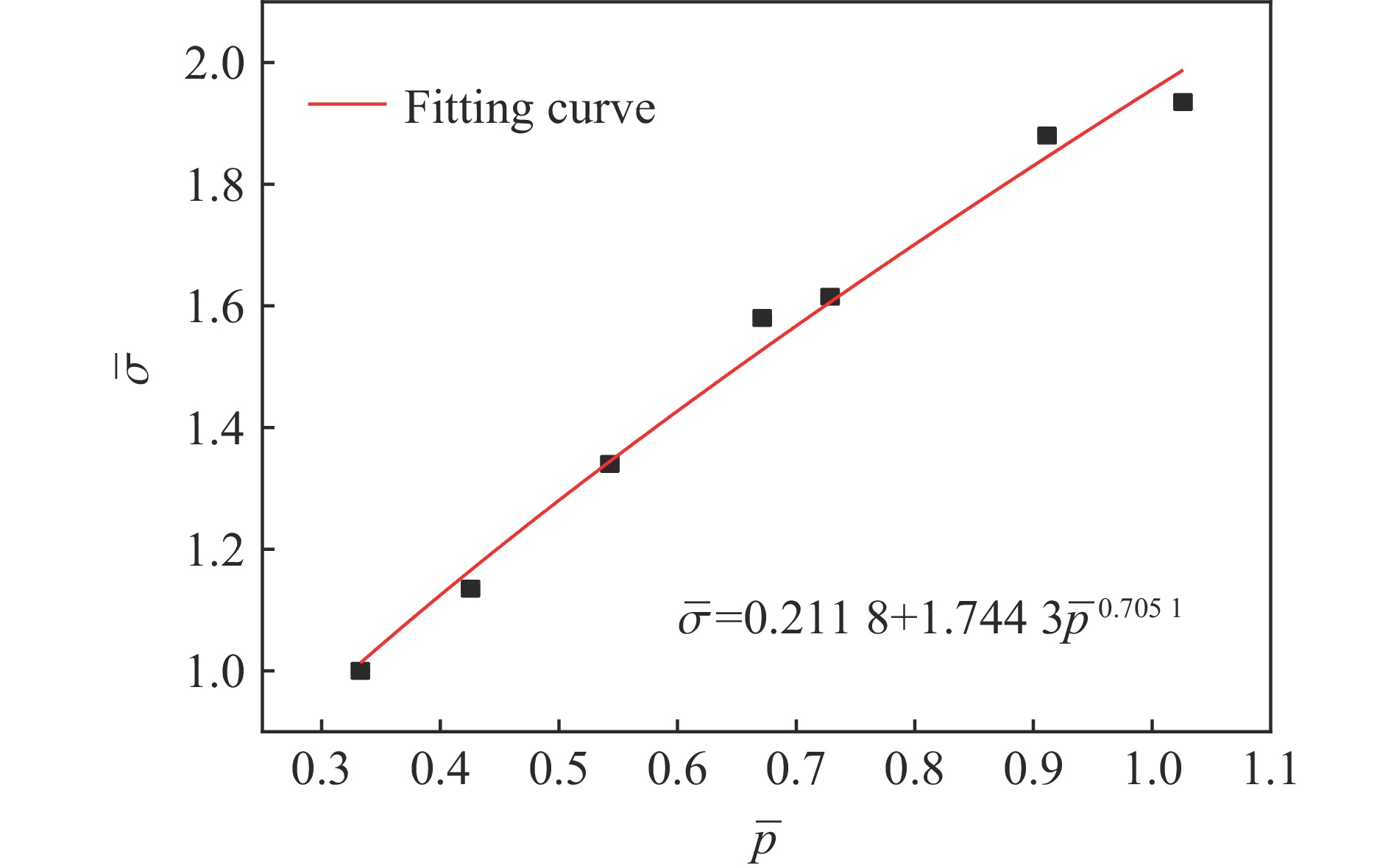
应变率/s⁻¹	抗压强度/MPa	$\overline \sigma$	$\overline p$
10⁻⁴	105.0	1.000 0	0.333 3
10⁻²	113.3	1.079 0	0.359 7
50	134.6	1.281 9	0.427 3
10²	164.7	1.568 6	0.522 9

下载: 导出CSV

表 2 超高性能混凝土HJC模型参数

Table 2. HJC model parametrs of UHPC

A	B	N	C	T/MPa	S_fmax	ε_efmin	D₁	D₂	f_s	${\dot \varepsilon _0}$ /s⁻¹
0.232 8	1.744 3	0.705 1	0.003 6	7.12	7.0	0.018 1	0.04	1.0	0.1725	1

p_c/MPa	p_l/MPa	μ_c	μ_l	K₁/GPa	K₂/GPa	K₃/GPa	σ_c/MPa	G/GPa	ρ/(g·cm⁻³)
35.0	235.0	0.0011	0.0383	46.4	−195.0	416.6	105.0	20.37	2.67

下载: 导出CSV

表 3 钢筋本构模型参数

Table 3. Parameters of reinforcement constitutive models

材料	密度/(g·cm⁻³)	弹性模量/GPa	泊松比	屈服应力/MPa	切线模量/GPa	失效应变
受拉钢筋	7.85	200	0.25	524	1.61	0.10
箍筋	7.85	200	0.25	423	1.91	0.08

下载: 导出CSV

表 4 修正前的原始参数

Table 4. Original parameters before correction

A	B	N	C	T/MPa	S_fmax	ε_efmin	D₁	D₂	f_s	${\dot \varepsilon _0}$ /s⁻¹
0.76	1.6	0.61	0.007	7.12	7.0	0.01	0.04	1.0	−	1

p_c/MPa	p_l/MPa	μ_c	μ_l	K₁/GPa	K₂/GPa	K₃/GPa	σ_c/MPa	G/GPa	ρ/(g·cm⁻³)
16.0	800.0	0.001	0.1	85.0	−171.0	208.0	105.0	20.37	2.67

下载: 导出CSV

表 5 单向板各方向尺寸变化

Table 5. Dimension change of one-way plate in each direction

长度/mm	宽度/mm	厚度/mm
1 200	400	120
1 500	500	180
1 800	600	240

下载: 导出CSV

参考文献(40)

[1]	LI J, WU C Q, HAO H. An experimental and numerical study of reinforced ultra-high performance concrete slabs under blast loads [J]. Materials and Design, 2015, 82: 64–76. DOI: 10.1016/j.matdes.2015.05.045.
[2]	WANG Y Z, WANG Y B, ZHAO Y Z, et al. Experimental study on ultra-high performance concrete under triaxial compression [J]. Construction and Building Materials, 2020, 263: 120225. DOI: 10.1016/j.conbuildmat.2020.120225.
[3]	LI J, WU C Q, HAO H, et al. Experimental investigation of ultra-high performance concrete slabs under contact explosions [J]. International Journal of Impact Engineering, 2016, 93: 62–75. DOI: 10.1016/j.ijimpeng.2016.02.007.
[4]	杜忠, 胡福. 高延性混凝土(HDC)在抗爆间室中的防护效果评估 [J]. 工程建设与设计, 2019(22): 9–10. DOI: 10.13616/j.cnki.gcjsysj.2019.11.204. DU Z, HU F. Evaluation of the protective effect of high-ductility concrete (HDC) in anti-explosion chamber [J]. Construction and Design for Engineering, 2019(22): 9–10. DOI: 10.13616/j.cnki.gcjsysj.2019.11.204.
[5]	辛健. 爆炸作用下RHT模型参数敏感性分析 [J]. 舰船电子工程, 2019, 39(4): 111–113, 122. DOI: 10.3969/j.issn.1672-9730.2019.04.024. XIN J. Sensitivity analysis of RHT model parameters under explosive attack [J]. Ship Electronic Engineering, 2019, 39(4): 111–113, 122. DOI: 10.3969/j.issn.1672-9730.2019.04.024.
[6]	RIEDEL W, THOMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes [C] // Proceeding of the 9th International Symposium, Interaction of the Effects of Munitions with Structures. Berlin: ISIEMS, 1999: 315–322.
[7]	MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D [J]. International Journal of Impact Engineering, 1997, 19(9/10): 847–873. DOI: 10.1016/S0734-743X(97)00023-7.
[8]	HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates and high pressures [C] // 14th International Symposium on Ballistics. Quebec: American Defense Preparedness Association, 1993: 591–600.
[9]	杜闯, 宋帅, 张江鹏. 爆炸冲击作用下三种混凝土本构模型对比研究 [J]. 兵器装备工程学报, 2022, 43(11): 49–56. DOI: 10.11809/bqzbgcxb2022.11.007. DU C, SONG S, ZHANG J P. Comparative study on three concrete constitutive models under blast loading [J]. Journal of Ordnance Equipment Engineering, 2022, 43(11): 49–56. DOI: 10.11809/bqzbgcxb2022.11.007.
[10]	张凤国, 李恩征. 混凝土撞击损伤模型参数的确定方法 [J]. 弹道学报, 2001, 13(4): 12–16, 23. DOI: 10.3969/j.issn.1004-499X.2001.04.003. ZHANG F G, LI E Z. A method to determine the parameters of the model for concrete impact and damage [J]. Journal of Ballistics, 2001, 13(4): 12–16, 23. DOI: 10.3969/j.issn.1004-499X.2001.04.003.
[11]	韩莉, 吴萍. 动荷载作用下混凝土HJC本构模型 [J]. 绿色环保建材, 2018(11): 3–4. DOI: 10.16767/j.cnki.10-1213/tu.2018.11.002.
[12]	LIU Y, HUANG F L, MA A E. Numerical simulations of oblique penetration into reinforced concrete targets [J]. Computers and Mathematics with Applications, 2011, 61(8): 2168–2171. DOI: 10.1016/j.camwa.2010.09.006.
[13]	张志刚, 李姝雅, 瘳红建. 爆炸荷载下碳纤维布加固混凝土板的抗弯性能研究 [J]. 应用力学学报, 2008, 25(1): 150–153. ZHANG Z G, LI S Y, LIAO H J. Flexural resistance of concrete plate strengthened with CFRP under explosive loading [J]. Chinese Journal of Applied Mechanics, 2008, 25(1): 150–153.
[14]	张志华, 刘磊, 王亚, 等. 混凝土爆破试验及数值模拟 [J]. 矿冶, 2018, 27(6): 34–37. DOI: 10.3969/j.issn.1005-7854.2018.06.008. ZHANG Z H, LIU L, WANG Y, et al. Blasting experiment and numerical simulation of concrete [J]. Mining and Metallurgy, 2018, 27(6): 34–37. DOI: 10.3969/j.issn.1005-7854.2018.06.008.
[15]	任根茂, 吴昊, 方秦, 等. 普通混凝土HJC本构模型参数确定 [J]. 振动与冲击, 2016, 35(18): 9–16. DOI: 10.13465/j.cnki.jvs.2016.18.002. REN G M, WU H, FANG Q, et al. Determinations of HJC constitutive model parameters for normal strength concrete [J]. Journal of Vibration and Shock, 2016, 35(18): 9–16. DOI: 10.13465/j.cnki.jvs.2016.18.002.
[16]	陈睿, 刘杰, 韩旭, 等. 混凝土材料动态本构参数的分阶段计算反求技术 [J]. 爆炸与冲击, 2014, 34(3): 315–321. DOI: 10.11883/1001-1455(2014)03-0315-07. CHEN R, LIU J, HAN X, et al. A multi-stage computational inverse technique for identification of the dynamic constitutive parameters of concrete [J]. Explosion and Shock Waves, 2014, 34(3): 315–321. DOI: 10.11883/1001-1455(2014)03-0315-07.
[17]	张社荣, 宋冉, 王超, 等. 碾压混凝土HJC动态本构模型修正及数值验证 [J]. 振动与冲击, 2019, 38(12): 25–31. DOI: 10.13465/j.cnki.jvs.2019.12.004. ZHANG S R, SONG R, WANG C, et al. Modification of a dynamic constitutive model—HJC model for roller-compacted concrete and numerical verification [J]. Journal of Vibration and Shock, 2019, 38(12): 25–31. DOI: 10.13465/j.cnki.jvs.2019.12.004.
[18]	熊益波, 陈剑杰, 胡永乐, 等. 混凝土Johnson-Holmquist本构模型关键参数研究 [J]. 工程力学, 2012, 29(1): 121–127. XIONG Y B, CHEN J J, HU Y L, et al. Study on the key parameters of the Johnson-Holmquist constitutive model for concrete [J]. Engineering Mechanics, 2012, 29(1): 121–127.
[19]	李鹏. 钢管混凝土柱爆炸作用下试验及动态本构模型研究 [D]. 广州: 广州大学, 2016: 64–71. LI P. Test and dynamic constitutive model study of CFST column under blast load [D]. Guangzhou, Guangdong, China: Guangzhou University, 2016: 64–71.
[20]	张若棋, 丁育青, 汤文辉, 等. 混凝土HJC、RHT本构模型的失效强度参数 [J]. 高压物理学报, 2011, 25(1): 15–22. DOI: 10.11858/gywlxb.2011.01.003. ZHANG R Q, DING Y Q, TANG W H, et al. The failure strength parameters of HJC and RHT concrete constitutive models [J]. Chinese Journal of High Pressure Physics, 2011, 25(1): 15–22. DOI: 10.11858/gywlxb.2011.01.003.
[21]	DU Y X, WEI J, LIU K, et al. Research on dynamic constitutive model of ultra-high performance fiber-reinforced concrete [J]. Construction and Building Materials, 2020, 234: 117386. DOI: 10.1016/j.conbuildmat.2019.117386.
[22]	过镇海, 王传志. 多轴应力下混凝土的强度和破坏准则研究 [J]. 土木工程学报, 1991, 24(3): 1–14. DOI: 10.15951/j.tmgcxb.1991.03.001. GUO Z H, WANG C Z. Investigation of strength and failure criterion of concrete under multi-axial stresses [J]. China Civil Engineering Journal, 1991, 24(3): 1–14. DOI: 10.15951/j.tmgcxb.1991.03.001.
[23]	仵鹏涛. 三向应力状态下超高性能混凝土材料静态力学性能研究 [D]. 天津: 天津大学, 2019: 40–44. DOI: 10.27356/d.cnki.gtjdu.2019.004796. WU P T. Study of static mechanical properties of ultra-high performance concrete under triaxial stress states [D]. Tianjin, China: Tianjin University, 2019: 40–44. DOI: 10.27356/d.cnki.gtjdu.2019.004796.
[24]	薛文. 落锤冲击作用下RC梁的动力响应研究 [D]. 武汉: 华中科技大学, 2016: 42–54. XUE W. Study on dynamic response of RC beams under drop hammer impact [D]. Wuhan, Hubei, China: Huazhong University of Science and Technology, 2016: 42–54.
[25]	王志亮, 毕程程, 李鸿儒. 混凝土爆破损伤的SPH-FEM耦合法数值模拟 [J]. 爆炸与冲击, 2018, 38(6): 1419–1428. DOI: 10.11883/bzycj-2017-0209. WANG Z L, BI C C, LI H R. Numerical simulation of blasting damage in concrete using a coupled SPH-FEM algorithm [J]. Explosion and Shock Waves, 2018, 38(6): 1419–1428. DOI: 10.11883/bzycj-2017-0209.
[26]	陈星明, 刘彤, 肖正学. 混凝土HJC模型抗侵彻参数敏感性数值模拟研究 [J]. 高压物理学报, 2012, 26(3): 313–318. DOI: 10.11858/gywlxb.2012.03.011. CHEN X M, LIU T, XIAO Z X. Numerical simulation study of parameter sensitivity analysis on concrete HJC model [J]. Chinese Journal of High Pressure Physics, 2012, 26(3): 313–318. DOI: 10.11858/gywlxb.2012.03.011.
[27]	汪衡, 董静, 顾振中, 等. HJC模型参数对侵彻效应影响度的数值研究 [J]. 兵器装备工程学报, 2020, 41(3): 200–204. DOI: 10.11809/bqzbgcxb2020.03.040. WANG H, DONG J, GU Z Z, et al. Numerical study on the effect of HJC model parameters on penetration [J]. Journal of Ordnance Equipment Engineering, 2020, 41(3): 200–204. DOI: 10.11809/bqzbgcxb2020.03.040.
[28]	胡志豪. 超高性能混凝土的气体渗透性能研究 [D]. 长沙: 湖南大学, 2021: 49–51. DOI: 10.27135/d.cnki.ghudu.2021.001461. HU Z H. Experimental study on gas permeability of ultra-high performance concrete [D]. Changsha, Hunan, China: Hunan University, 2021: 49–51. DOI: 10.27135/d.cnki.ghudu.2021.001461.
[29]	王政. 弹靶侵彻动态响应的理论与数值分析 [D]. 上海: 复旦大学, 2005: 39–40.
[30]	BEISSEL S R, JOHNSON G R. An abrasion algorithm for projectile mass loss during penetration [J]. International Journal of Impact Engineering, 2000, 24(2): 103–116. DOI: 10.1016/S0734-743X(99)00146-3.
[31]	严少华, 钱七虎, 周早生, 等. 高强混凝土及钢纤维高强混凝土高压状态方程的实验研究 [J]. 解放军理工大学学报, 2000, 1(6): 49–53. DOI: 10.7666/j.issn.1009-3443.20000610. YAN S H, QIAN Q H, ZHOU Z S, et al. Experimental study of equation of state for high-strength concrete and high-strength fiber concrete [J]. Journal of PLA University of Science and Technology, 2000, 1(6): 49–53. DOI: 10.7666/j.issn.1009-3443.20000610.
[32]	孙玉祥, 王杰, 武海军, 等. 混凝土高压状态方程实验与数值模拟研究 [J]. 爆炸与冲击, 2020, 40(12): 121401. DOI: 10.11883/bzycj-2020-0002. SUN Y X, WANG J, WU H J, et al. Experiment and simulation on high-pressure equation of state for concrete [J]. Explosion and Shock Waves, 2020, 40(12): 121401. DOI: 10.11883/bzycj-2020-0002.
[33]	高乐. 活性粉末混凝土高压状态方程研究 [D]. 广州: 广州大学, 2011: 51–53. GAO L. Research on high pressure equation of RPC [D]. Guangzhou, Guangdong, China: Guangzhou University, 2011: 51–53.
[34]	唐鸽, 江少恩, 巫顺超, 等. 用Hugoniot数据计算高压状态方程 [J]. 强激光与粒子束, 2009, 21(11): 1737–1740. TANG G, JIANG S E, WU S C, et al. Deducing equation of state under high pressure from Hugoniot data [J]. High Power Laser and Particle Beams, 2009, 21(11): 1737–1740.
[35]	蒋国平, 焦楚杰, 肖波齐. 高强混凝土气体炮试验与高压状态方程研究 [J]. 物理学报, 2012, 61(2): 026701. DOI: 10.7498/aps.61.026701. JIANG G P, JIAO C J, XIAO B Q. High-pressure state equation of high strength concrete investigated with the gas gun experiment [J]. Acta Physica Sinica, 2012, 61(2): 026701. DOI: 10.7498/aps.61.026701.
[36]	孙其然, 李芮宇, 赵亚运, 等. HJC模型模拟钢筋混凝土侵彻实验的参数研究 [J]. 工程力学, 2016, 33(8): 248–256. DOI: 10.6052/j.issn.1000-4750.2014.12.1094. SUN Q R, LI R Y, ZHAO Y Y, et al. Investigation on parameters of HJC model applied to simulate perforation experiments of reinforced concrete [J]. Engineering Mechanics, 2016, 33(8): 248–256. DOI: 10.6052/j.issn.1000-4750.2014.12.1094.
[37]	林琛, 徐建军, 杨晋伟, 等. 基于HJC模型的钢筋混凝土侵彻仿真失效准则与参数 [J]. 探测与控制学报, 2017, 39(2): 100–105. LIN C, XU J J, YANG J W, et al. The failure criterions and parameters of HJC model based perforation simulation [J]. Journal of Detection and Control, 2017, 39(2): 100–105.
[38]	石少卿, 康建功, 汪敏, 等. ANSYS/LS-DYNA在爆炸与冲击领域内的工程应用 [M]. 北京: 中国建筑工业出版社, 2011.
[39]	汪维, 张舵, 卢芳云, 等. 方形钢筋混凝土板的近场抗爆性能 [J]. 爆炸与冲击, 2012, 32(3): 251–258. DOI: 10.11883/1001-1455(2012)03-0251-08. WANG W, ZHANG D, LU F Y, et al. Anti-explosion performances of square reinforced concrete slabs under close-in explosions [J]. Explosion and Shock Waves, 2012, 32(3): 251–258. DOI: 10.11883/1001-1455(2012)03-0251-08.
[40]	LIN X S. Numerical simulation of blast responses of ultra-high performance fibre reinforced concrete panels with strain-rate effect [J]. Construction and Building Materials, 2018, 176: 371–382. DOI: 10.1016/j.conbuildmat.2018.05.066.

施引文献

期刊类型引用(11)

1.	鄢庆祺, 阮舒敏, 徐天赐, 刘卫星, 王志璇, 赵坪锐. 列车荷载作用下无砟轨道层间非吻合接触损伤机理. 铁道标准设计. 2025(07) 百度学术
2.	张鑫，刘泽功，常帅，陈响升，薛勇林，朱家亮，宋鑫. 爆破荷载作用下煤岩本构模型参数特性研究. 振动与冲击. 2025(05): 263-277 . 百度学术
3.	楼晓明，林杰，王新龙，刘怀宇，王广. 球面爆轰波下不同孔径耦合装药孔壁压力沿炮孔轴向分布特征. 哈尔滨工业大学学报. 2025(03): 148-159 . 百度学术
4.	张旭，刘晓辉，刘楚佳，罗盈. 高温大理岩的动态能量耗散机理及破坏特征. 爆炸与冲击. 2025(06): 68-80 . 本站查看
5.	王子琛. 白云石大理岩HJC本构参数确定及应用. 科技创新与应用. 2024(11): 72-75+80 . 百度学术
6.	谢全敏，刘文文，晏理想. 某大型深埋罐室围岩和混凝土试验及本构模型研究. 武汉理工大学学报. 2024(03): 48-55 . 百度学术
7.	骆柯，牛雷雷，朱万成，王聪，赵蔚. 不同冻结状态下含单裂隙岩石动态抗拉特性研究. 有色金属(矿山部分). 2024(04): 124-132+141 . 百度学术
8.	宁鹏博，刘军，赵硕，李瑶. 钢纤维增强混凝土动态力学性能及HJC本构模型参数标定. 中国建材科技. 2024(03): 20-25 . 百度学术
9.	漆涛，陶铁军，田兴朝，谢财进，万安桐，张厚英. 大断面隧道“楔形掏槽+高能孔”布设方法研究. 爆破. 2024(03): 95-103+120 . 百度学术
10.	李干，李杰，宋春明，李孝臣，王明洋. 花岗岩的动态力学性能、本构模型与状态方程研究. 力学与实践. 2023(05): 952-959 . 百度学术
11.	朱明，宫能平，穆朝民，蔡天宇，章雨. 高温后钢纤维自密实混凝土动、静态力学性能研究. 硅酸盐通报. 2023(11): 3895-3905 . 百度学术