Design of concrete shield against the combination of penetration and explosion of warheads
-
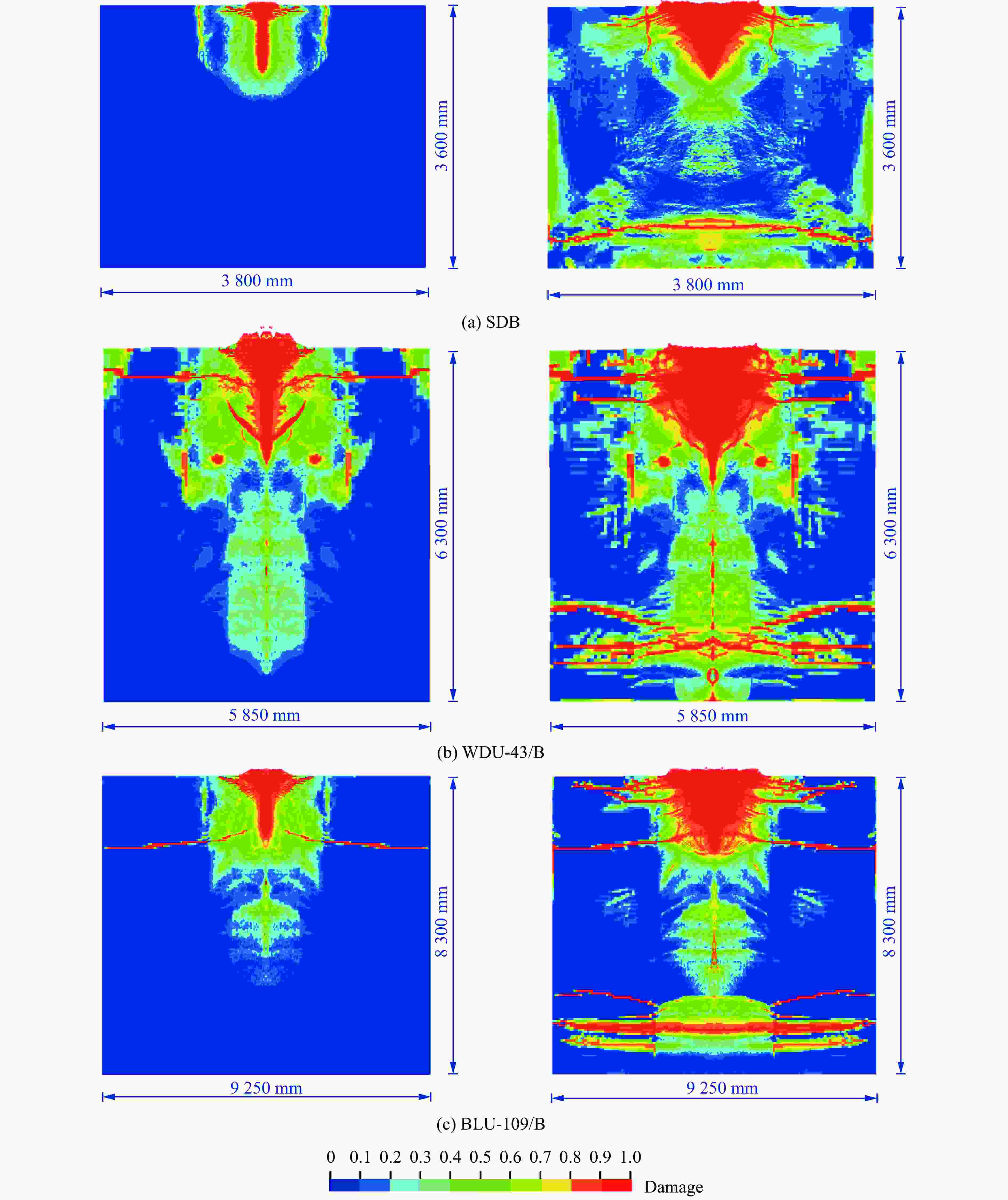
摘要: 准确评估战斗部侵彻爆炸作用下混凝土遮弹层的损伤破坏可为防护工程设计提供重要参考。首先基于Karagozian & Case（K&C）模型框架建立了新型混凝土动态损伤本构模型，其中强度面综合考虑了静水压力、Lode角、应变率和损伤；独立描述了拉伸和压缩损伤，并考虑了拉压之间的连续过渡以及剪切变形和体积压缩对损伤的贡献。随后，开展了半无限厚混凝土靶体的105 mm口径弹体侵彻爆炸联合作用试验。进一步通过对上述试验和已有有限厚混凝土靶板的预制孔埋置装药爆炸试验进行数值仿真分析，验证了所建立的本构模型、参数取值和有限元分析方法在描述混凝土动态阻力、损伤演化和开裂行为方面的准确性。最后，确定了SDB、WDB-43/B和BLU-109/B三种典型战斗部以声速侵彻爆炸普通混凝土的临界贯穿和临界震塌厚度。结果表明：SDB、WDB-43/B和BLU-109/B战斗部侵彻爆炸作用下混凝土的临界贯穿厚度分别为1.4、3.4和3.8 m，临界震塌厚度分别为3.6、6.3和8.3 m；由于携带炸药量的差异，不同战斗部侵彻爆炸下的临界贯穿和临界震塌厚度与侵彻深度的比值非定值，相应的比值范围分别为1.49~2.13和2.90~4.66。Abstract: Accurately evaluating the damage and failure of concrete shield subjected to combination of penetration and explosion of warheads can provide an important reference for the design of protective structures. Firstly, based on the frame of Karagozian & Case (K&C) model, a newly dynamic-damage constitutive model was established. The hydrostatic pressure, Lode angle, strain rate, and damage were all considered in strength surface. The tension and compression damages were described separately with a continued transition. Besides, the contribution of shear deformation and hydrostatic compression were also considered. Then, the combined penetration and explosion test of 105-mm-caliber projectile on the semi-infinite concrete target was conducted. The corresponding numerical simulation was conducted to verify the accuracy of the constitutive model, the parameters, and the finite element analysis approach in describing the dynamic resistance of concrete. Furthermore, by conducting the numerical simulations of the existing prefabricated hole charge explosion test on the finite concrete plane, the accuracy of the established constitutive model, parameters, and finite element analysis approach in describing the damage evolution and cracking behavior of concrete was validated. Finally, the perforation limit and scabbing limit of normal strength concrete subjected to the combination of penetration and explosion of three typical warheads at sound velocity were determined. The results show that, the perforation limits of the SDB, WDU-43/B, and BLU-109/B warheads are 1.4, 3.4 and 3.8 m, respectively. The scabbing limit are 3.6, 6.3 and 8.3 m, respectively. Due to the differences of the explosive mass in warheads, the ratios of perforation limit and scabbing limit under combined penetration and explosion to the depth of penetration are not constant. The corresponding ratio ranges are 1.49−2.13 and 2.90−4.66, respectively.
-
含铝炸药有较高的爆热和较强的作功能力，成为含能材料领域的研究热点。含铝炸药能量释放特性与理想炸药较大的不同主要在于，铝粉通常在CJ面后与气相产物发生二次反应，且随着铝粉含量的增加，含铝炸药的爆速降低[1-3]。铝粉的表面被一层氧化铝薄膜所覆盖，厚度通常为3～5 nm[4]，铝粉反应通常发生在氧化铝膜破裂后。含铝炸药中铝粉的反应延滞时间为爆轰波到达后铝粉氧化膜发生破裂且与气相产物发生反应所需要的时间，而铝粉氧化膜的破裂与多种因素有关（如铝核升温、熔化导致的热应力，氧化铝膜晶变、熔化，冲击波的作用导致的颗粒变形等）。研究含铝炸药中铝粉的反应起始时间，可以加深认识含铝炸药中铝粉的反应过程，为含铝炸药配方设计及应用提供参考。
低压下的铝粉燃烧实验表明，铝粉的燃烧时间与铝粉粒度之间满足dn关系[5]。由于含铝炸药爆轰时的高温、高压，很难直接测量产物中铝粉的反应情况，通常通过宏观爆轰性能测试，反推炸药中的铝粉反应情况。含铝炸药中铝粉的反应速率的实验研究主要有光谱法[6-8]、圆筒实验法[9-10]、飞片撞击法[11-12]、水下爆炸法等[13-14]，由以上方法已得到一些定性认识（如铝粉的反应与约束条件，炸药组分，铝颗粒的尺寸、形状等相关），而对于炸药中铝粉反应的时间尺度，目前尚未形成较统一的认识。对铝粉二次反应起始时间已进行了一定的研究。曾亮等[15]利用电导率方法，对TNT/Al炸药中铝粉的反应起始时间进行了测量，结果表明粒径2、10 μm铝粉的反应起始时间分别为0.4、1.5 μs。Tao[16]利用激光速度干涉仪，分别测量了PETN和TNT含铝炸药与窗口的界面粒子速度，并依此标定了炸药的点火增长模型参数，进而计算了炸药的反应速率，并通过计算结果推断，粒径5 或18 μm铝粉会在1.5 μs内与PETN炸药的爆轰产物完全反应。Manner等[17]对HMX/Al（粒径3.2 μm）和HMX/LiF炸药进行了圆筒实验，结果表明2 μs内铝粉发生了显著的反应。Chan[18]对含铝炸药中铝粉的反应起始时间进行理论分析，认为当铝颗粒表面温度超过高压下铝的熔点时铝粉开始反应，则10 μm铝粉的反应起始时间为0.1 μs。以上大部分研究表明，微米级铝粉的反应起始时间在2 μs以内，但不同研究者给出的铝粉反应的具体起始时间差异较大，还有待进一步研究。
利用激光干涉法测量炸药与窗口的界面速度，可以获得炸药的爆轰波结构，进而可以分析反应区附近铝粉的反应情况，相比飞片法、圆筒实验法等，界面粒子速度法的结构响应更快（纳秒级）。本文中，将测量两种RDX/Al炸药和一种RDX/LiF炸药的爆轰波结构，分析爆轰产物中铝粉的反应延滞时间及反应区附近铝粉的反应情况，拟为爆轰产物环境下铝粉的反应动力学建模提供参考。
1. 实 验
测试系统主要由火炮、蓝宝石飞片、待测炸药、LiF光学窗口、光纤测速探头和光子多普勒测速仪（photon Doppler velocimetry, PDV）等组成，如图1所示。利用口径57 mm的火炮发射蓝宝石飞片撞击炸药产生一维平面波。在炸药背面安装
∅ 20 mm×11 mm的LiF窗口，LiF窗口与炸药接触面有厚约0.7 μm的铝镀膜。如图2所示，在背部靶架上安装3个光纤探头P1、P2和P3（在图1中仅示意P1），其中P1探头焦点正对炸药中心，P2和P3对称分布在P1两侧，与中心距离均为3.8 mm。在实验记录的时间内，被测区域不受侧向稀疏波的影响，始终为一维平面爆轰波。实验前，将炸药安装在爆炸罐中的炮管正前方，通过爆炸罐上的光纤法兰连接测试用探头与罐外仪器，最后对爆炸罐抽真空。光子多普勒测速仪为中国工程物理研究院流体物理研究研制，测速范围上限可达9 km/s。采用窗口傅里叶变换方法处理数据，速度时间分辨率为3 ns。不确定度主要由PDV测试的不确定度、窗口和探头安装导致的不确定度、炸药不均匀导致的不确定度3方面决定 ，速度的相对合成标准不确定度为2%。
由于炸药与LiF的阻抗有差别，实验测得的界面粒子速度并非炸药稳定爆轰时的波后粒子速度。因此，可利用冲击阻抗匹配公式计算炸药反应区内的压力[19]：
pCJ=12uCJ(ρ0(c0+λuCJ)+ρDCJ) (1) 式中：pCJ为待测炸药的爆压，uCJ为CJ点对应的界面粒子速度，ρ0为窗体材料初始密度，c0为窗体材料初始声速，λ为窗体材料冲击绝热线常数，ρ为待测炸药初始密度，DCJ为待测炸药CJ爆速。
采用压装工艺，制备了3种RDX基炸药，配方见表1。药柱的尺寸为
∅ 40 mm×30 mm。其中，铝粉为球形，粒径分别为2和10 μm，纯度大于99.8%；氟化锂粉末平均粒径为2.5 μm，纯度大于99%。氟化锂的密度、冲击阻抗、分子量与铝比较接近，且其化学性质较稳定，不会与炸药气相产物发生反应，在炸药产物中主要以惰性物质形式存在。通过含氟化锂炸药与含铝炸药的对比，可以评估铝粉的反应情况。铝和氟化锂的主要物理参数见表2，表中Tm、Tb、cV和K分别为熔点、沸点、比定容热容和导热系数。表 1 三种RDX基炸药的配方和参数Table 1. Components and characteristics of three kinds of explosives炸药 w/% 粒径/μm 密度/(g·cm−3) D/(m·s−1) RDX Al LiF 黏合剂 RF15 80 0 15 5 2.5 1.809 8141±40 RA15(2 μm) 80 15 0 5 2.0 1.803 8072±40 RA15(10 μm) 80 15 0 5 10.0 1.795 8070±40 表 2 铝和氟化锂的物理参数对比Table 2. Comparison of the main characteristics of Al and LiF材料 ρ0/(g·cm−3) Tm/K Tb/K cV/(J·g−1·K−1) K/(W·m−1·K−1) c0/(km·s−1) λ 铝 2.700 933 2 740 1.176 210 5.325 1.338 氟化锂 2.638 1 143 1.513 11.3 5.176 1.359 2. 结果与分析
2.1 界面粒子速度
对3种炸药均做了1发实验。实验中，测量了蓝宝石飞片速度，结果为(1 256±30) m/s；根据蓝宝石和待测炸药冲击绝热线，计算可得炸药中的输入压力约为8 GPa；该压力下炸药的到爆轰距离约为3 mm，可得到炸药稳定爆轰的传播距离约为27 mm。图3为实验测得的炸药爆轰波界面速度，每发实验均获得了3个数据。同一炸药不同探头之间的速度曲线差异较小，表明测试精度较高。
2.2 铝粉反应起始时间
每发实验3个位置的界面粒子平均值如图4所示。单个探头速度的相对不确定度为2%，多个探头速度平均值的相对不确定度约为1%。由图4可见，在CJ点前的反应区内，3种炸药的界面粒子变化趋势较一致，为了更清晰地呈现这个变化趋势，对CJ点附近的曲线进行了放大，如图5所示。由图5可见，von Neumann峰处3种炸药的界面粒子速度为1.8～1.9 km/s，在随后的15 ns内速度迅速下降到约1.6 km/s，该过程对应着RDX的分解反应。Pei等[20]对RDX基PBX炸药的爆轰反应区进行了测量（见图6），得到稳态爆轰条件下RDX基PBX炸药的爆轰反应时间为(14±3) ns，与本文含铝炸药的测试结果基本一致。由于铝粉与气相爆轰产物间的反应属于分子间的反应，在如此短的时间内，铝粉难以发生反应，可以认为RDX完全分解的点即为CJ点；考虑测试误差，可以认为3种炸药CJ点的速度均为(1 640±20) m/s，可计算3种炸药的爆压为27.6 GPa，对应CJ点等熵绝热指数为3.26。CJ点后到0.5 μs，含LiF炸药的界面粒子速度始终高于含铝炸药的，这是因LiF粉末与铝粉间的热力学性质差异导致。
图 4 三种炸药的平均界面粒子速度曲线Figure 4. Average interface particle velocity curves of three explosives
图 5 CJ点附近三种炸药的平均界面粒子速度曲线Figure 5. Average of interface particle velocitiy curves of three explosives near the CJ point在CJ点附近，气相爆轰产物与固体添加物之间会发生动量和热量的交换[21]。动量的交换主要与固相产物的冲击阻抗相关，因此，铝粉和LiF粉末之间的差异较小。而热量的交换主要与添加物的导热系数及颗粒粒径相关，铝的导热系数为210 W/(m·K)，远大于LiF的导热系数11.3 W/(m·K)，因此，在反应区附近，LiF粉末吸收的热量更少，对应的产物动能更大，相应的产物界面粒子速度也更高。含铝炸药和含LiF炸药界面粒子速度差最大出现在170 ns，此时，含LiF炸药的界面粒子速度为1 544 m/s，比含铝炸药的界面粒子速度1 455 m/s高7%。
随后，含铝炸药与含LiF炸药的界面粒子速度差越来越小，在0.6 μs时含2 μm铝炸药的界面粒子速度开始超过含LiF炸药的，在0.8 μs时含10 μm铝炸药的界面粒子速度开始超过含LiF炸药的。这表明，该时间段内，铝粉已经发生了反应。在0.4 μs时含2 μm铝炸药的界面粒子速度开始超过含10 μm铝炸药的，两者速度差最大出现在0.72 μs时，此时含2 μm铝炸药的界面粒子速度为1 308 m/s，比含10 μm铝炸药的界面粒子速度（1 257 m/s）高4%。这表明，铝粉粒径越小，炸药反应延滞时间越短。综合以上，两种粒度含铝炸药反应延滞时间为0.4～0.8 μs。在1.3 μs时含2和10 μm铝炸药的界面粒子速度分别为1 110和1 082 m/s，比含LiF炸药的界面粒子速度1 004 m/s分别提高了11%和8%，这时反应已经比较显著。
2.3 铝粉反应度
在铝粉反应的初始阶段，含铝炸药与含LiF炸药的主要成分相似，因此以含LiF炸药的等熵形式状态方程作为参考线，构建含铝炸药的状态方程[22]：
p(e,v)=pS,RF15(v)+Γ(v)v(e−eS,RF15(v))=pS,RF15(v)+Γ(v)vQλ (2) 式中：Q为铝粉与气相爆轰产物反应释放的总能量，
λ 为铝粉的反应度，Γ(v) 为爆轰产物Grüneisen系数，v为爆轰产物相对比容。为了分析铝粉的反应情况，需要联系界面粒子速度与炸药的状态方程。在反应区，铝粉反应产生的压力变化为弱扰动波，该条件下，以含LiF炸药为参考，铝粉反应产生的压力变化与界面粒子速度有关系：
Δp=p(e,v)−pS,RF15(v)=ρcΔu (3) 式中：ρ为炸药产物的密度，c为产物的声速，
Δu 为因铝粉反应导致的界面粒子速度变化。联立式(2)～(3)，可得：
λ=cΔuΓ(v)Q (4) 产物的压力同时受比容（决定冷压）和内能（决定热压）的影响，为便于分析内能对产物压力的影响，并分析铝粉的反应放能情况，本文中选择比容相同的时刻，以排除产物比容对产物压力的影响。为此，对炸药的界面粒子速度进行积分，如图7所示。选取界面粒子速度位移相同的时刻（比容相同）：炸药RA15 (10 μm)与RF15比容相同的时刻为1.1 μs，对应的界面粒子速度差为81 m/s；炸药RA15 (2 μm)与RF15比容相同的时刻为1.3 μs，对应的界面粒子速度差为74 m/s。为了获得上述时刻产物的密度、比容，针对本文的实验模型进行了数值模拟，其中炸药RF15的状态方程数据通过圆筒实验[9]拟合获得，数值模拟的炸药界面粒子速度如图8所示。初期，数值模拟的界面粒子速度与实验结果有一定差异，这是因数值模型中没有考虑炸药的反应过程而仅采用了产物的状态方程；在150 ns后，数值模拟结果与实验结果一致性较好。通过数值模拟，获得在1.1和1.3 μs时产物的相对比容v分别为0.86和0.89。
图 8 实验和模拟的炸药RF15界面粒子速度曲线Figure 8. Experimental and simulated interface particle velocity curves of explosive RF15爆轰产物的声速为：
c=√∂p∂ρ=(ρ0ρ2(AR1exp(−R1V)+AR2exp(−R2V)+C(1+ω)V−(2+ω)))1/2 (5) 在1.1和1.3 μs时，c分别为5 444和5 277 m/s，Q为1.8 ～3.0 MJ/kg，则炸药RA15 (2 μm)在1.1 μs时的反应度为18.4%～30.6%，炸药RA15 (10 μm)在1.3 μs时的反应度为16.3%～27.1%，两者的差距较小。由低压下铝粉燃烧实验，铝粉的燃烧时间t与铝粉的初始粒度d之间满足t=dn关系，n通常为1～2。取n为1，由该公式，2和10 μm铝粉炸药的反应度应有显著差异。而本文的结果与之不同，这说明爆轰产物环境下铝粉的反应机制与低压下铝粉的燃烧过程有较大差异。Li等[23]利用圆筒实验研究了铝粉粒度对铝粉反应速率的影响，结果表明，因爆轰产物中铝颗粒的破碎，铝粉颗粒大小对反应速率影响较小。本文的结果与圆筒实验结果[23]基本一致。
3. 结 论
(1)含铝炸药爆轰波结构与理想炸药有较大差异，其界面粒子速度曲线没有明显的拐点，反应初期因气相产物与添加物之间温度、速度的非平衡性，RDX/Al炸药的界面粒子速度低于RDX/LiF炸药的，随后因铝粉反应放能，使RDX/Al炸药的界面粒子速度高于RDX/LiF炸药的。
(2)微米铝粉在CJ面前不发生反应，2、10 μm铝粉RDX/Al炸药的爆轰波结构没有明显差异， 二者的反应延滞时间小于0.8 μs。
(3)爆轰产物环境下铝粉的反应机制与低压下有较大差异，反应速率受铝粉粒度的影响不明显，在本文中，两种粒度铝粉炸药的反应度为16%～31%。结果可提升对含铝炸药中铝粉反应过程的认识，为爆轰产物环境下铝粉的反应动力学建模提供参考。
-
图 5 普通混凝土单轴压缩应力-应变曲线
Figure 5. Compressive stress-strain relation of normal strength concrete
图 16 三种战斗部打击下混凝土靶体的损伤云图
Figure 16. Damage contours of concrete targets subjected to three warheads
图 18 三种战斗部打击下混凝土靶体的损伤云图
Figure 18. Damage contours of concrete targets subjected to three warheads
表 1 动态损伤本构模型中的强度面和损伤参数
Table 1. Parameters of the strength surface and the damage for the dynamic-damage constitutive model
Smax p0 dh1 ds1 d2 εfrac A m 13fc −0.16fc 0.000 35 0.000 84 1 0.007 1.03 0 
下载: 导出CSV
表 2 动态损伤本构模型的状态方程参数
Table 2. Parameters of the equation of state for the dynamic-damage constitutive model
μ1 μ2 μ3 μ4 μ5 μ6 μ7 μ8 μ9 μ10 0 0.0015 0.0043 0.0101 0.0305 0.0513 0.0726 0.0943 0.1740 0.2080 p1/μ2 p2/μ2 p3/μ2 p4/μ2 p5/μ2 p6/μ2 p7/μ2 p8/μ2 p9/μ2 p10/μ2 0 1 2.18 3.50 6.65 10.03 14.23 21.77 127.10 194.40 Ku,1 Ku,2 Ku,3 Ku,4 Ku,5 Ku,6 Ku,7 Ku,8 Ku,9 Ku,10 1 1 1.014 1.065 1.267 1.470 1.672 1.825 4.107 5.000
下载: 导出CSV
表 3 试验与数值模拟结果对比
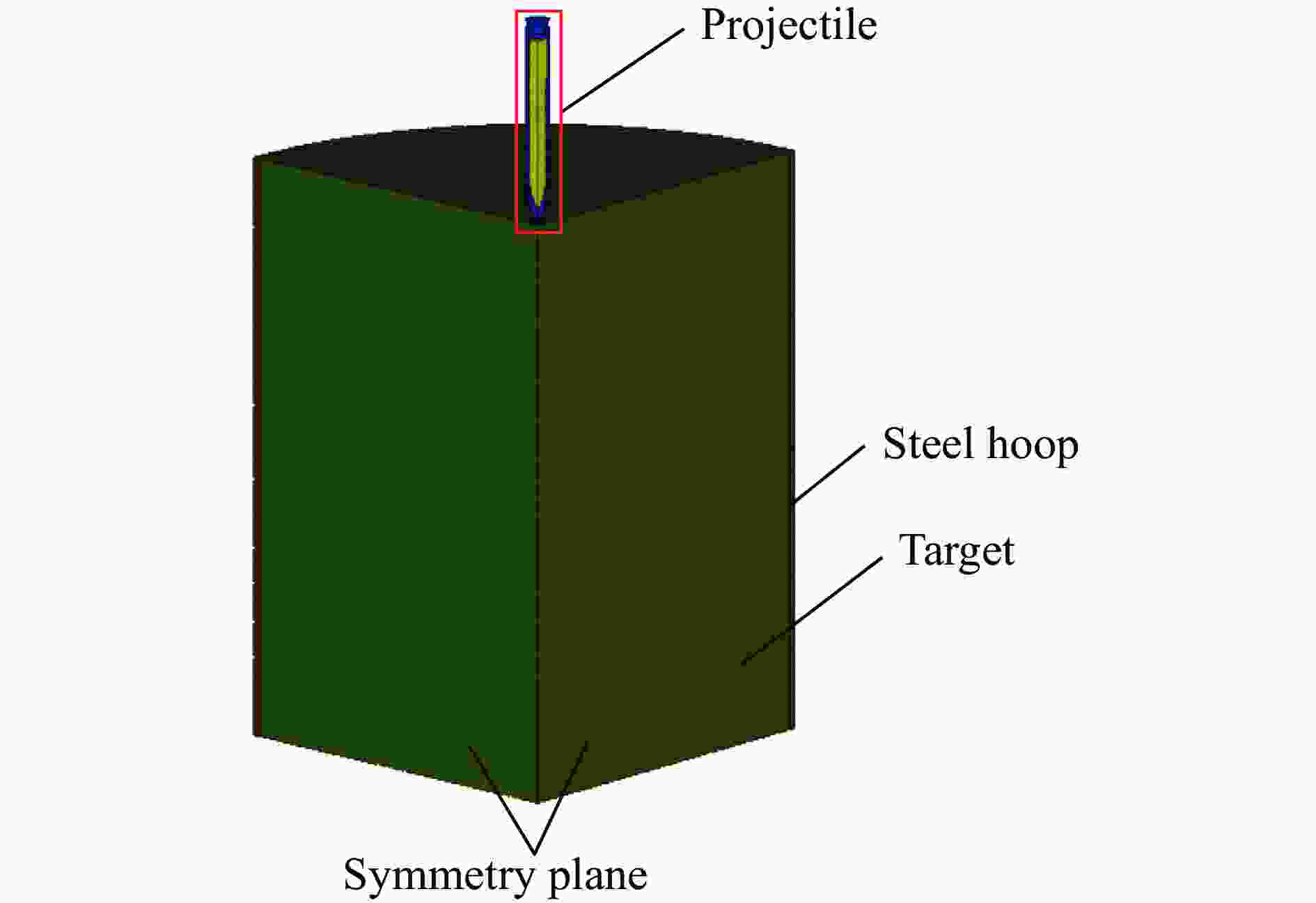
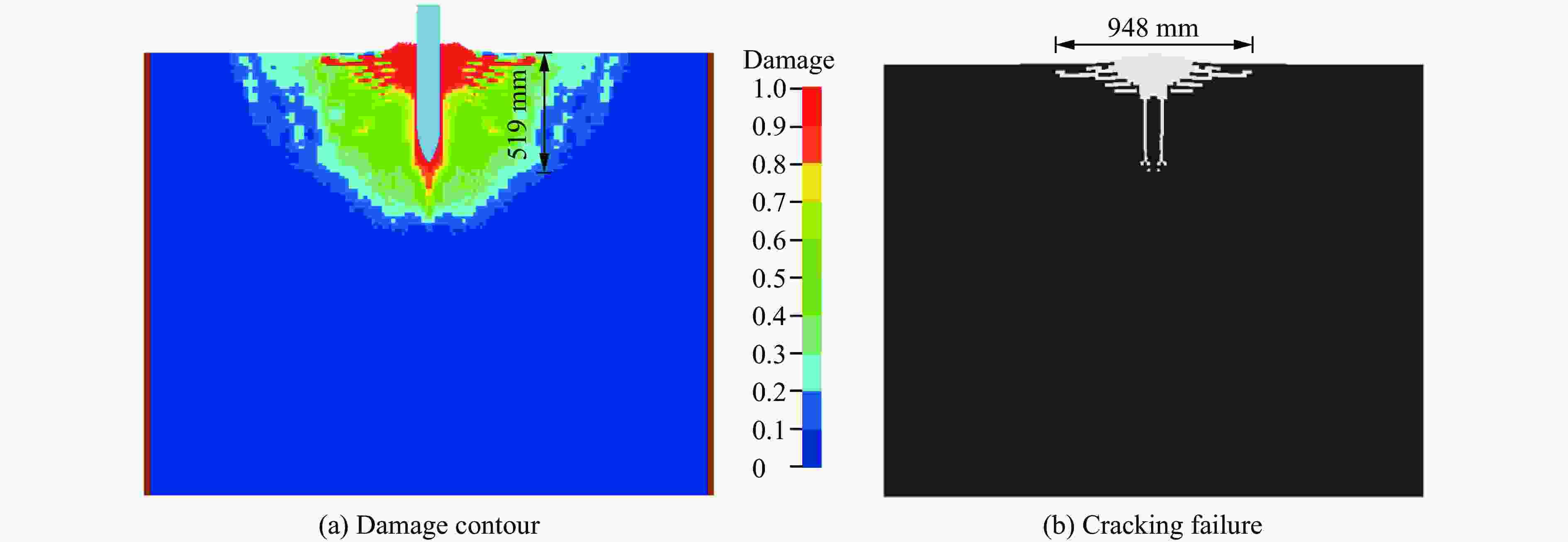
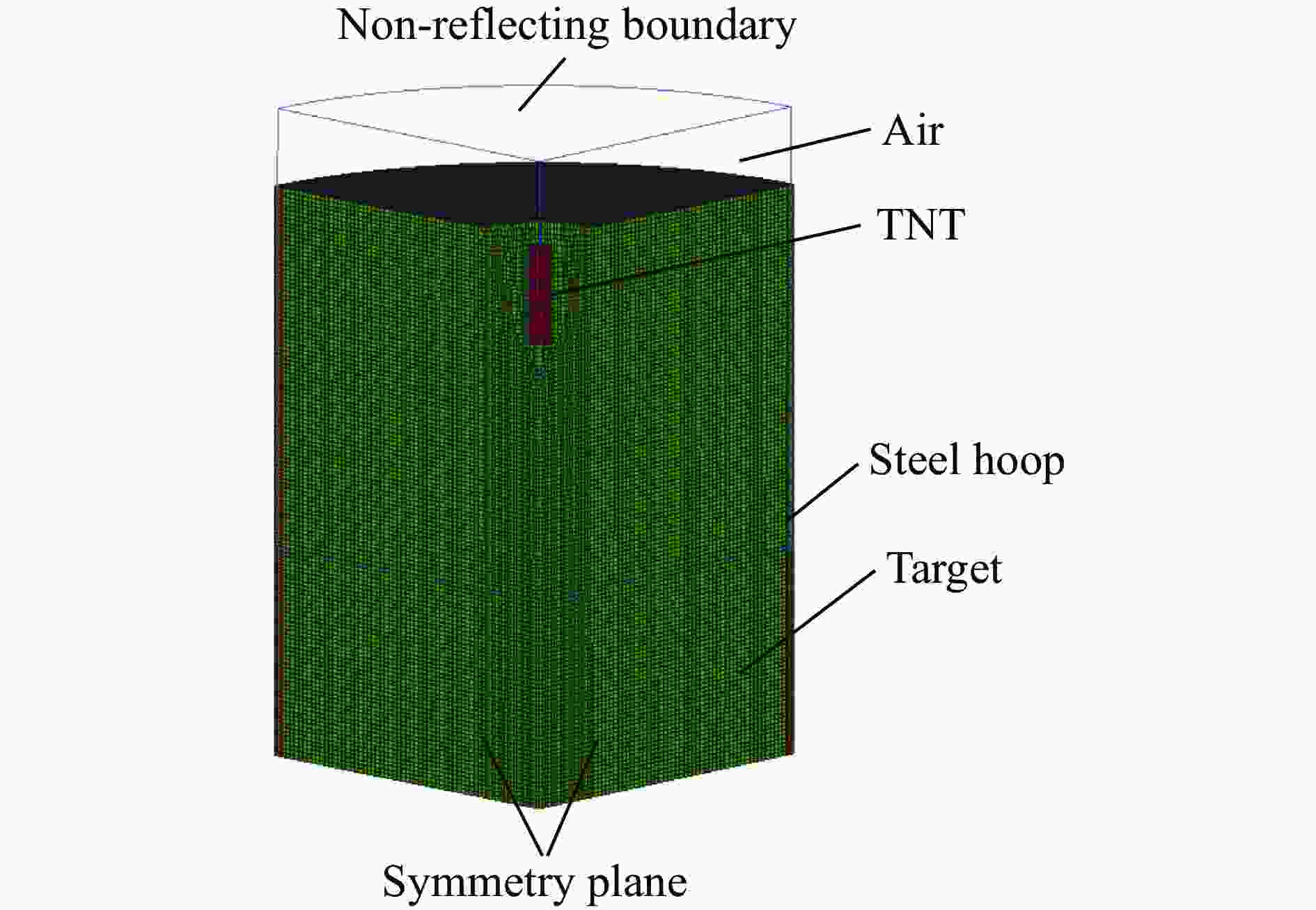
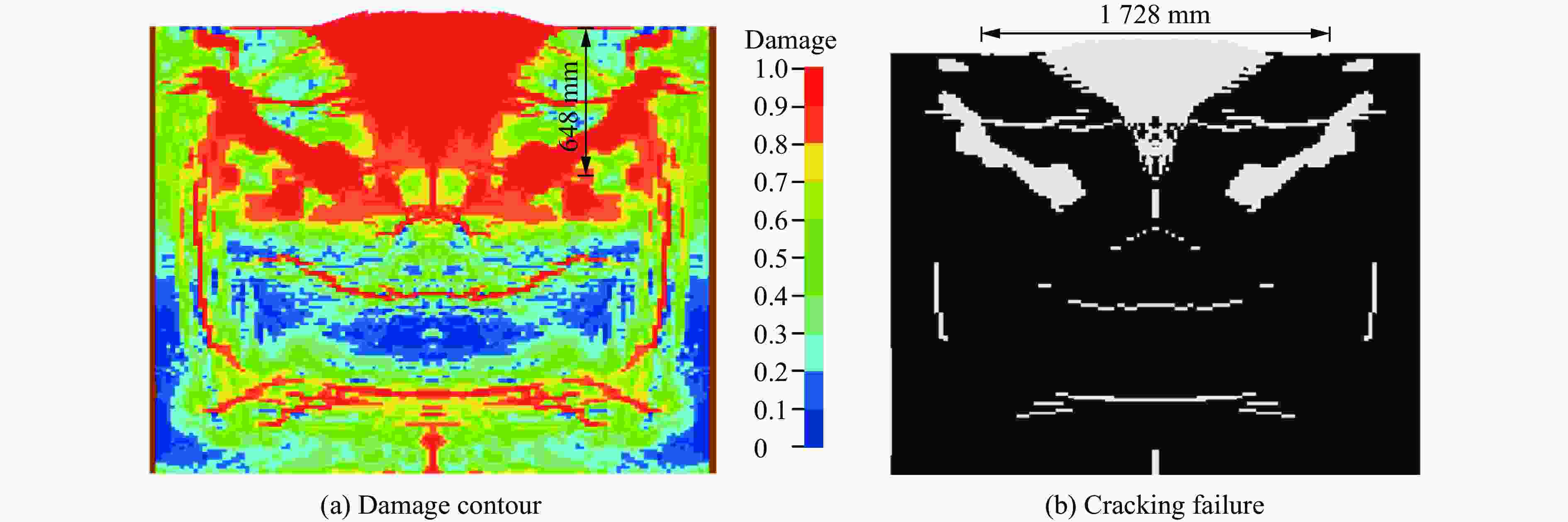
Table 3. Comparisons of test data and simulation results
试验 深度 开坑直径 试验/mm 模拟/mm 相对误差/% 试验/mm 模拟/mm 相对误差/% 侵彻 515 519 0.8 1 176 948 −19.4 爆炸 680 648 −4.7 1 671 1 728 3.4
下载: 导出CSV
表 4 TNT炸药的模型和状态方程参数
Table 4. Parameters for material model and the equation of state of the explosive TNT
密度/(kg·m−3) 爆速/(m·s−1) CJ爆压/GPa AJWL/GPa BJWL/GPa R1 R2 ω 1630 6930 21 374 375 4.15 1.0 0.35
下载: 导出CSV
表 5 空气的模型和状态方程参数
Table 5. Parameters for material model and the equation of state of the air
ρ/(kg·m−3) C4 C5 E0/Pa 1.29 0.4 0.4 2.5×105
下载: 导出CSV
表 6 三种战斗部参数
Table 6. Parameters of three warheads
战斗部 直径/
mm总质量/
kg长度/
mm壁厚/
mm头部曲
径比等效TNT
质量/kgSDB 152 113 1800 10.8 3 23 WDU-43/B 234 454 2400 41.5 9 100 BLU-109/B 368 874 2510 25.4 3 324
下载: 导出CSV
表 7 三种战斗部打击下的模拟结果
Table 7. Simulation results of three warheads
战斗部 侵彻作用 侵彻爆炸联合作用 临界贯穿厚度/m D1 D2 临界震塌厚度/m D3 D4 深度/m 开坑直径/mm 深度/m 开坑直径/mm SDB 0.94 1066 1.03 1656 1.4 1.49 1.36 3.6 3.83 3.50 WDU-43/B 2.17 1806 2.45 2180 3.4 1.57 1.39 6.3 2.90 2.57 BLU-109/B 1.78 2554 2.18 3556 3.8 2.13 1.74 8.3 4.66 3.81
下载: 导出CSV
-
[1] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates and high pressures [C]// Proceedings of the 14th International Symposium on Ballistics, 1993. [2] RIEDEL W, THOMA K, HIERMAIER S, et al. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes [C]// Proceedings of the 9th International Symposium on Interaction of the Effect of Munitions with Structures. Berlin-Strausberg, 1999. [3] MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D [J]. International Journal of Impact Engineering, 1997, 19(9/10): 847–873. DOI: 10.1016/S0734-743X(97)00023-7. [4] KONG X Z, FANG Q, WU H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61–71. DOI: 10.1016/j.ijimpeng.2016.04.014. [5] TU Z G, LU Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations [J]. International Journal of Impact Engineering, 2009, 36(1): 132–146. DOI: 10.1016/j.ijimpeng.2007.12.010. [6] KONG X Z, FANG Q, LI Q M, et al. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact [J]. International Journal of Impact Engineering, 2017, 108: 217–228. DOI: 10.1016/j.ijimpeng.2017.02.016. [7] WEERHEIJM J, VAN DOORMAAL J C A M. Tensile failure of concrete at high loading rates: new test data on strength and fracture energy from instrumented spalling tests [J]. International Journal of Impact Engineering, 2007, 34(3): 609–626. DOI: 10.1016/j.ijimpeng.2006.01.005. [8] FORRESTAL M J, FREW D J, HANCHAK S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles [J]. International Journal of Impact Engineering, 1996, 18(5): 465–476. DOI: 10.1016/0734-743X(95)00048-F. [9] 陈小伟, 张方举, 杨世全, 等. 动能深侵彻弹的力学设计(Ⅲ): 缩比实验分析 [J]. 爆炸与冲击, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-10.CHEN X W, ZHANG F J, YANG S Q, et al. Mechanics of structural design of EPW (Ⅲ): Investigations on the reduced-scale tests [J]. Explosion and Shock Waves, 2006, 26(2): 105–114. DOI: 10.11883/1001-1455(2006)02-0105-10. [10] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743x(94)80024-4. [11] FREW D J, HANCHAK S J, GREEN M L, et al. Penetration of concrete targets with ogive-nose steel rods [J]. International Journal of Impact Engineering, 1998, 21(6): 489–497. DOI: 10.1016/S0734-743X(98)00008-6. [12] 孙传杰, 卢永刚, 张方举, 等. 新型头形弹体对混凝土的侵彻 [J]. 爆炸与冲击, 2010, 30(3): 269–275. DOI: 10.11883/1001-1455(2010)03-0269-07.SUN C J, LU Y G, ZHANG F J, et al. Penetration of cylindrical-nose-tip projectiles into concrete targets [J]. Explosion and Shock Waves, 2010, 30(3): 269–275. DOI: 10.11883/1001-1455(2010)03-0269-07. [13] 黄蒙, 欧卓成, 段卓平, 等. 刚性弹体侵彻混凝土的相似性研究 [J]. 兵工学报, 2016, 37(S2): 176–180.HUANG M, OU Z C, DUAN Z P, et al. A study of similarity Analysis of hard projectile penetrating into concrete [J]. Acta Armamentarii, 2016, 37(S2): 176–180. [14] 邓勇军, 陈小伟, 钟卫洲, 等. 弹体正侵彻钢筋混凝土靶的试验及数值模拟研究 [J]. 爆炸与冲击, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001.DENG Y J, CHEN X W, ZHONG W Z, et al. Experimental and numerical study on normal penetration of a projectile into a reinforced concrete target [J]. Explosion and Shock Waves, 2020, 40(2): 023101. DOI: 10.11883/bzycj-2019-0001. [15] 马天宝, 武珺, 宁建国. 弹体高速侵彻钢筋混凝土的实验与数值模拟研究 [J]. 爆炸与冲击, 2019, 39(10): 103301. DOI: 10.11883/bzycj-2018-0275.MA T B, WU J, NING J G. Experimental and numerical study on projectiles’ high-velocity penetration into reinforced concrete [J]. Explosion and Shock Waves, 2019, 39(10): 103301. DOI: 10.11883/bzycj-2018-0275. [16] 左魁, 张继春, 曾宪明, 等. BLU-109B模型弹在岩石介质中成坑效应试验研究 [J]. 岩石力学与工程学报, 2007, 26(S1): 2767–2671. DOI: 10.3321/j.issn:1000-6915.2007.z1.027.ZUO K, ZHANG J C, ZENG X M, et al. Experimental study on formation of craters in rock with BLU-109B earth penetrating model projectiles [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 2767–2671. DOI: 10.3321/j.issn:1000-6915.2007.z1.027. [17] GENG H, LU H, SUN S Z, et al. Experimental study and damage effect analysis of concrete structures under the combined loadings of penetration and explosion [J]. Shock and Vibration, 2020, 2020: 2137945. DOI: 10.1155/2020/2137945. [18] SUN S Z, LU H, YUE S L, et al. The composite damage effects of explosion after penetration in plain concrete targets [J]. International Journal of Impact Engineering, 2021, 153: 103862. DOI: 10.1016/j.ijimpeng.2021.103862. [19] WU H, LI Y C, FANG Q, et al. Scaling effect of rigid projectile penetration into concrete target: 3D mesoscopic analyses [J]. Construction and Building Materials, 2019, 208: 506–524. DOI: 10.1016/j.conbuildmat.2019.03.040. [20] 彭永, 卢芳云, 方秦, 等. 弹体侵彻混凝土靶体的尺寸效应分析 [J]. 爆炸与冲击, 2019, 39(11): 113301. DOI: 10.11883/bzycj-2018-0402.PENG Y, LU F Y, FANG Q, et al. Analyses of the size effect for projectile penetrations into concrete targets [J]. Explosion and Shock Waves, 2019, 39(11): 113301. DOI: 10.11883/bzycj-2018-0402. [21] 程月华, 姜鹏飞, 吴昊, 等. 考虑尺寸效应的典型钻地弹侵彻混凝土深度分析 [J]. 爆炸与冲击, 2022, 42(6): 063302. DOI: 10.11883/bzycj-2021-0373.CHENG Y H, JIANG P F, WU H, et al. On penetration depth of typical earth-penetrating projectiles into concrete targets considering the scaling effect [J]. Explosion and Shock Waves, 2022, 42(6): 063302. DOI: 10.11883/bzycj-2021-0373. [22] LAI J Z, GUO X J, ZHU Y Y. Repeated penetration and different depth explosion of ultra-high performance concrete [J]. International Journal of Impact Engineering, 2015, 84: 1–12. DOI: 10.1016/j.ijimpeng.2015.05.006. [23] FAN Y, CHEN L, YU R Q, et al. Experimental study of damage to ultra-high performance concrete slabs subjected to partially embedded cylindrical explosive charges [J]. International Journal of Impact Engineering, 2022, 168: 104298. DOI: 10.1016/j.ijimpeng.2022.104298. [24] GERSTLE K B, ZIMMERMAN R M, WINKLER H, et al. Behavior of concrete under multiaxial stress states [J]. Journal of the Engineering Mechanics Division, 1980, 106(6): 1383–1403. DOI: 10.1061/JMCEA3.0002671. [25] KUPFER H B, GERSTLE K H. Behavior of concrete under biaxial stresses [J]. Journal of the Engineering Mechanics Division, 1969, 99(4): 853–866. DOI: 10.1061/JMCEA3.0001789. [26] WILLIAMS E M, AKERS S A, REED P A. Laboratory characterization of fine aggregate cementitious material: ERDC/GSL TR-05-16 [R]. Vicksburg, MS: Geotechnical and Structures Laboratory, US Army Engineer Research and Development Center, 2005. [27] RANKINE W J M. Manual of applied mechanics [M]. London: Griffin, 1876. [28] XU H, WEN H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials [J]. International Journal of Impact Engineering, 2013, 60: 76–81. DOI: 10.1016/j.ijimpeng.2013.04.005. [29] LS-DYNA. Keywords user’s manual. version 971 [M]. Livermore: Livermore Software Technology Corporation, 2012. [30] LIM J C, OZBAKKALOGLU T. Stress-strain model for normal- and light-weight concretes under uniaxial and triaxial compression [J]. Construction and Building Materials, 2014, 71: 492–509. DOI: 10.1016/j.conbuildmat.2014.08.050. [31] MURRAY Y D. User manual for LS-DYNA concrete material model 159 [M]. Washington DC: US Department of Transportation, 2007. FHWA-HRT-05-062. [32] SARGIN M. Stress-strain relationships for concrete and the analysis of structural concrete sections [M]. Waterloo: Solid Mechanics Division, University of Waterloo, 1971. [33] HORDIJK D A. Local approach to fatigue of concrete [D]. Delft: Delft University of Technology, 1991. [34] CUI J, HAO H, SHI Y C, et al. Experimental study of concrete damage under high hydrostatic pressure [J]. Cement and Concrete Research, 2017, 100: 140–152. DOI: 10.1016/j.cemconres.2017.06.005. [35] SIMO J C, HUGHES T J R. Computational inelasticity [M]. New York: Springer, 1998. DOI: 10.1007/b98904. [36] XU H, WEN H M. A computational constitutive model for concrete subjected to dynamic loadings [J]. International Journal of Impact Engineering, 2016, 91: 116–125. DOI: 10.1016/j.ijimpeng.2016.01.003. [37] WANG Y, KONG X Z, FANG Q, et al. Modelling damage mechanisms of concrete under high confinement pressure [J]. International Journal of Impact Engineering, 2021, 150: 103815. DOI: 10.1016/j.ijimpeng.2021.103815. [38] ATTARD M M, SETUNGE S. Stress-strain relationship of confined and unconfined concrete [J]. Material Journal, 1996, 93(5): 432–442. DOI: 10.14359/9847. [39] 王银, 孔祥振, 方秦, 等. 弹体对混凝土材料先侵彻后爆炸损伤破坏效应的数值模拟研究 [J]. 爆炸与冲击, 2022, 42(1): 013301. DOI: 10.11883/bzycj-2021-0132.WANG Y, KONG X, FANG Q, et al. Numerical investigation on damage and failure of concrete targets subjected to projectile penetration followed by explosion [J]. Explosion and Shock Waves, 2022, 42(1): 013301. DOI: 10.11883/bzycj-2021-0132. 期刊类型引用(6)
1. 程月华，吴昊，岑国华，张瑜. 侵彻爆炸联合作用下超高性能混凝土遮弹层设计. 爆炸与冲击. 2025(01): 90-103 . 
本站查看2. 杨石刚，徐国琳，杨亚，罗泽. 战斗部对钢纤维混凝土结构的侵爆复合破坏效应. 兵器装备工程学报. 2025(02): 1-10 . 
百度学术3. 吴昊，张瑜，程月华，岑国华. 典型战斗部侵彻爆炸下块石混凝土的遮弹层设计. 爆炸与冲击. 2025(04): 111-124 . 本站查看4. 吴昊，岑国华，程月华，张瑜. 基于战斗部侵彻动爆一体化效应的遮弹层设计. 爆炸与冲击. 2025(05): 90-105 . 本站查看5. 刘蒙莎，高戈，蒋迪. 预应力钢筋混凝土结构抗侵彻性能试验及数值模拟研究. 原子能科学技术. 2024(S1): 75-86 . 百度学术6. 张嘉庆，商飞. 连续打击下钢筋混凝土靶标应变响应研究. 国外电子测量技术. 2024(12): 109-114 . 百度学术其他类型引用(2)
-
下载:
百度学术
计量
- 文章访问数: 829
- HTML全文浏览量: 238
- PDF下载量: 191
- 被引次数: 8