Uncertainty quantification of magnetically driven quasi-isentropic compression experiments based on the Monte Carlo method
-
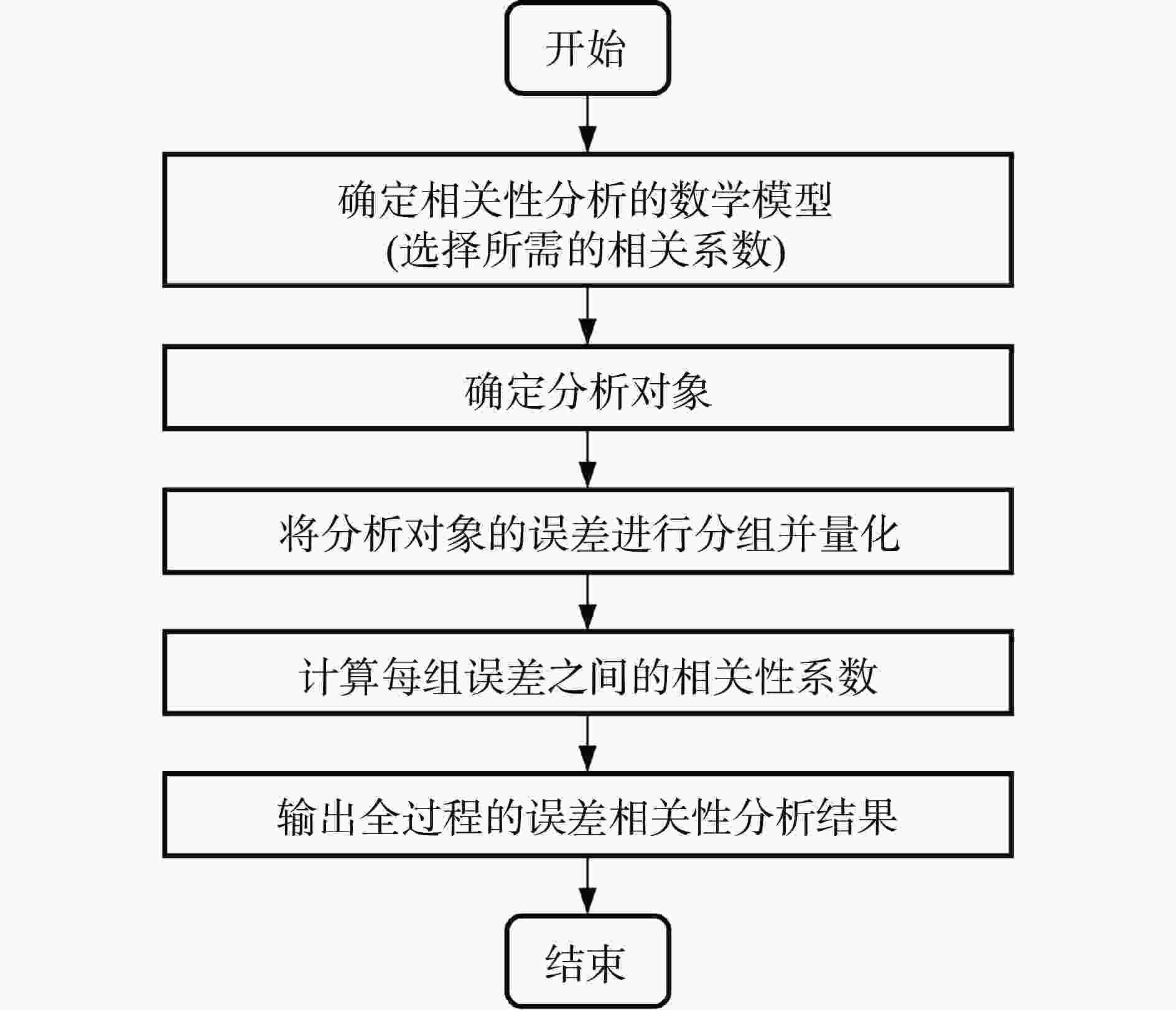
摘要: 磁驱动准等熵压缩实验是研究材料偏离Hugoniot状态高压物性和动力学行为的重要实验技术之一，开展不确定量化评估具有重要意义和价值。基于Monte Carlo原理，结合磁驱动准等熵压缩实验过程分析、Lagrange分析和特征线正向数据处理方法建立了适用于此类实验的Monte Carlo不确定度量化评估方法，实现利用磁驱动准等熵压缩实验获取材料声速、应力、应变等物理量以及状态方程和本构关系等物理模型的不确定度量化评估。利用建立的不确定度评估方法，对文献中已开展的钽、铜和NiTi合金的磁驱动准等熵压缩实验结果进行不确定度量化评估与分析。结果表明，基于本文中方法的评估结果与国外文献以相同原理得到的评估结果一致。对基于CQ-4装置开展的NiTi合金磁驱动准等熵压缩实验的评估结果表明，设计的磁驱动准等熵压缩实验是一种可靠的精密物理实验。在此基础上，深入讨论了磁驱动准等熵压缩实验的误差相关性和敏感性。结果表明：台阶样品厚度和粒子速度的测量是影响实验精度的主要因素。
-
关键词:
- 磁驱动准等熵压缩 /
- 不确定度 /
- Monte Carlo方法 /
- 量化评估
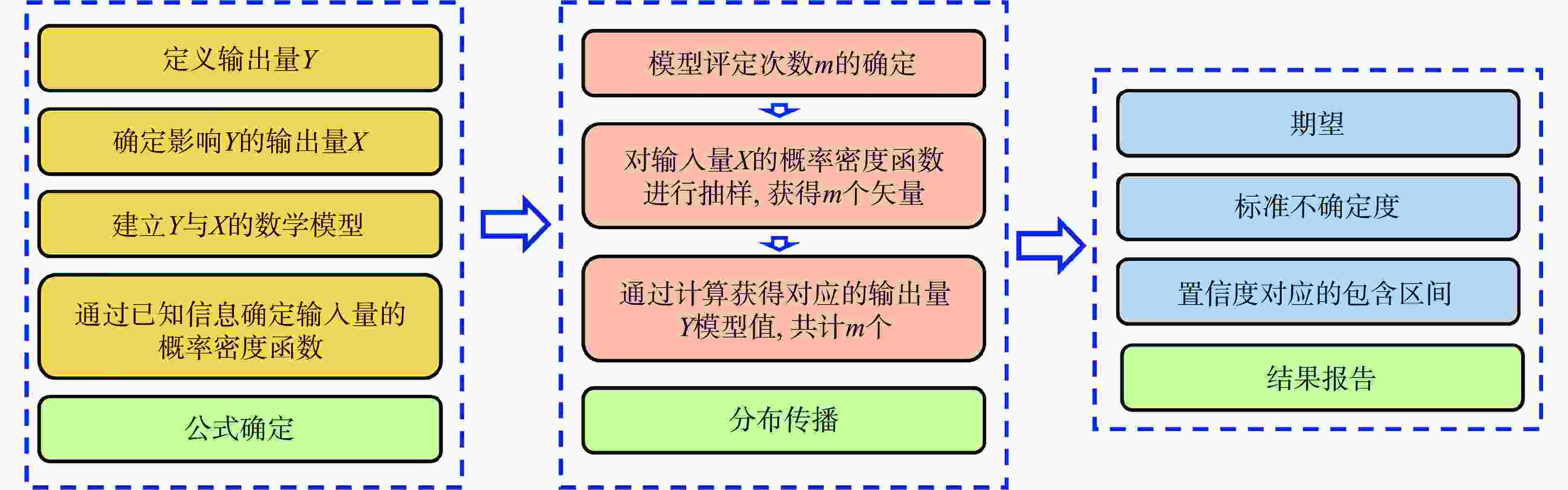
Abstract: Magnetically driven quasi-isentropic compression is one of the important experimental techniques to study high-pressure physics and dynamic behaviors of materials under off Hugoniot states. It is of great significance to carry out quantitative evaluation of experimental uncertainty. By combining with the process analysis of magnetically driven quasi-isentropic compression experiments and two forward data processing methods, an uncertainty quantitative evaluation method was established for such experiments based on the Monte Carlo method (MCM). The uncertainty quantification evaluations of physical quantities such as sound speed, stress, strain, and the parameters of equations of state and constitutive models were realized. Compared with the conventional method such as guide to the expression of uncertainty in measurement (GUM), the MCM uncertainty evaluation is more applicable to the cases in which the probability distribution of the input quantities is non-symmetric and the measurement model is non-linear. In fact, the uncertainty evaluation results obtained by the MCM is reasonable and not the ones under the maximum estimation condition. Employing the law of large numbers, nested cycle setting of the probability density functions (PDF) and nested loop construction of virtual samples makes the uncertainty evaluation results more accurate. By using the established MCM uncertainty evaluation method, the uncertainty evaluations of the experimental results of tantalum and copper samples under magnetically-driven quasi-isentropic compression were quantitatively analyzed firstly. The results are consistent with the data proposed in the literatures, which proves the correctness and reliability of our method. And then, the quantitative evaluation was conducted on magnetically-driven quasi-isentropic compression experiments of NiTi alloy carried out on a CQ-4 device. The results show that the experiments on the CQ-4 device are reliable and precise for high-pressure physics and material dynamics studies. Finally, the error correlation and sensitivity of magnetically-driven quasi-isentropic compression experiments were discussed in depth, and the results show that the measurements of step sample thickness and particle velocity are the main factors affecting the experimental accuracy but have different influence weights. This work has important guiding significance for studying high-pressure physics and dynamic behaviors of materials by using magnetically-driven quasi-isentropic compression experimental technology. -
图 1 磁驱动准等熵压缩实验原理图
Figure 1. A principle of magnetically-driven quasi-isentropic compression experiment
图 2 基于Monte Carlo原理评价不确定度的主要阶段
Figure 2. The main stages of evaluation uncertainty based on the Monte Carlo method
图 3 磁驱动准等熵压缩实验的Monte Carlo不确定度评价流程
Figure 3. Monte Carlo uncertainty evaluation process for magnetically-driven quasi-isentropic compression experiments
图 9 自由面速度历史曲线的虚拟样本构造结果
Figure 9. Band construction results of virtual samples for free surface velocity profiles
图 12 应力应变的不确定度评价结果及其极大估计
Figure 12. Uncertainty evaluations and their great estimates of stress and strain
图 14 两种数据处理方法的不确定度评价结果比较
Figure 14. Comparison of uncertainty evaluation results by two kinds of data processing methods
图 16 自由面速度历史曲线基于时序误差和速度误差的模拟带
Figure 16. Simulation bands of free surface velocity histories based on time deviation and velocity deviation
图 17 插值前后变量的映射关系
Figure 17. Mapping relationships of variables before and after interpolation
图 20 输出量误差与输入量误差的敏感系数
Figure 20. Sensitivity coefficients of the output deviation and input deviation
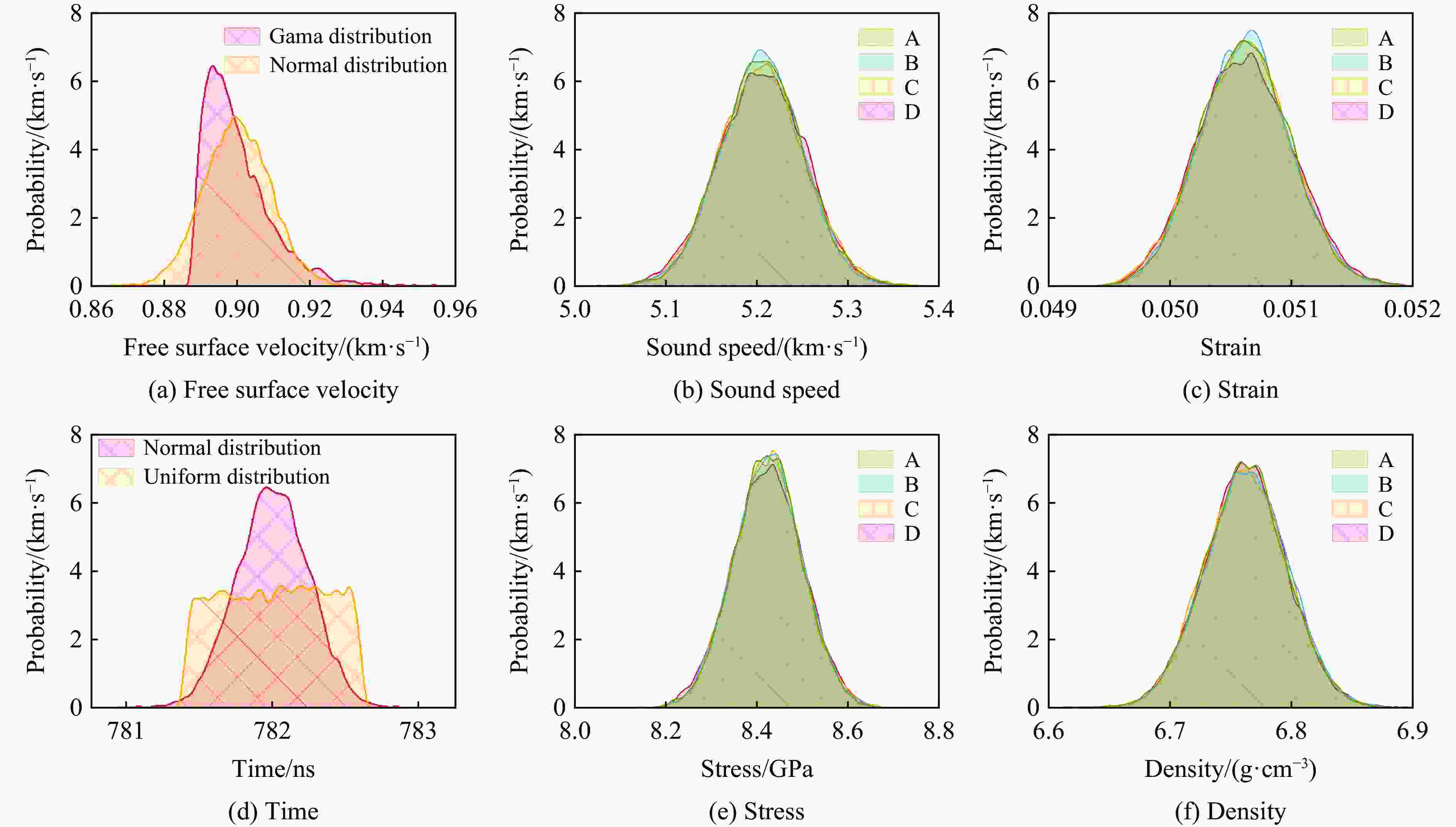
表 1 分布形式设置
Table 1. Settings of distribution form
设定形式名称 时间分布形式 自由面速度分布形式 A 正态分布 正态分布 B 正态分布 伽马分布 C 均匀分布 正态分布 D 均匀分布 伽马分布 
下载: 导出CSV
-
[1] SINARS D B, SWEENEY M A, ALEXANDER C S, et al. Review of pulsed power-driven high energy density physics research on Z at Sandia [J]. Physics of Plasmas, 27(7):, 2020, 27(7): 070501. DOI: 10.1063/5.0007476. [2] 王桂吉, 罗斌强, 陈学秒, 等. 磁驱动平面准等熵加载装置, 实验技术及应用研究新进展 [J]. 爆炸与冲击, 2021, 41(12): 62–83. DOI: 10.11883/bzycj-2021-0119.WANG G J, LUO B Q, CHEN X M, et al. Recent progress on the experimental facilities, techniques and applications of magnetically driven quasi-isentropic compression [J]. Explosion and Shock Waves, 2021, 41(12): 62–83. DOI: 10.11883/bzycj-2021-0119. [3] 孙承纬, 赵剑衡, 王桂吉, 等. 磁驱动准等熵平面压缩和超高速飞片发射实验技术原理、装置及应用 [J]. 力学进展, 2012, 42(2): 206–219. DOI: 10.6052/1000-0992-2012-2-20120208.SUN C W, ZHAO J H, WANG G J, et al. Progress in magnetic loading techniques for isentropic compression experiments and ultra-high velocity flyer launching [J]. Advances in Mechanics, 2012, 42(2): 206–219. DOI: 10.6052/1000-0992-2012-2-20120208. [4] DAVIS J P, KNUDSON M D , SHULENBURGER L, et al. Mechanical and optical response of [100] lithium fluoride to multi-megabar dynamic pressures [J]. Journal of Applied Physics, 2016, 120(16): 165901. DOI: 10.1063/1.4965869. [5] DAVIS J P, BROWN J L, KNUDSON M D, et al. Analysis of shockless dynamic compression data on solids to multi-megabar pressures: application to tantalum [J]. Journal of Applied Physics, 2014, 116(20): 2734–2224. DOI: 10.1063/1.4902863. [6] DAVIS J P. Experimental measurement of the principal isentrope for aluminum 6061-T6 to 240 GPa [J]. Journal of Applied Physics, 2006, 99(10): 782. DOI: 10.1063/1.2196110. [7] HALL C A, ASAY J R, KNUDSON M D, et al. Experimental configuration for isentropic compression of solids using pulsed magnetic loading [J]. Review of Scientific Instruments, 2001, 72(9): 3587–3595. DOI: 10.1063/1.1394178. [8] SEAGLE C T, DAVIS J P, MD KNUDSON. Mechanical response of lithium fluoride under off-principal dynamic shock-ramp loading [J]. Journal of Applied Physics, 2016, 120(16): 033515–984. DOI: 10.1063/1.4965990. [9] 罗斌强, 张红平, 种涛, 等. 磁驱动斜波压缩实验结果的不确定度分析 [J]. 高压物理学报, 2017, 31(3): 295–300. DOI: 10.11858/gywlxb.2017.03.011.LUO B Q, ZHANG H P, CHONG T, et al. Experimental uncertainty analysis of magnetically driven ramp wave compression [J]. Chinese Journal of High Pressure Physics, 2017, 31(3): 295–300. DOI: 10.11858/gywlxb.2017.03.011. [10] 张红平, 罗斌强, 王桂吉, 等. 基于特征线反演的斜波加载实验数据处理与分析 [J]. 高压物理学报, 2016, 30(2): 7. DOI: 10.11858/gywlxb.2016.02.006.ZHANG H P, LUO B Q, WANG G J, et al. Inverse characteristic analysis of ramp loading experiments [J]. Chinese Journal of High Pressure Physics, 2016, 30(2): 7. DOI: 10.11858/gywlxb.2016.02.006. [11] BROWN J L, ALEXANDER C S, ASAY J R, et al. Extracting strength from high pressure ramp-release experiments [J]. Journal of Applied Physics, 2013, 114(22): 223518–223516. DOI: 10.1063/1.4847535. [12] WANG G J, LUO B Q, ZHANG X P, et al. A 4 MA, 500 ns pulsed power generator CQ-4 for characterization of material behaviors under ramp wave loading [J]. The Review of Scientific Instruments, 2013, 84(1): 015117. DOI: 10.1063/1.4788935. [13] 经福谦. 动高压原理与技术 [M]. 2版. 北京: 科学出版社, 1999: 222–223. [14] SONG H, WU X, HUANG C, et al. Measurement of fast-changing low velocities by photonic Doppler velocimetry [J]. The Review of Scientific Instruments, 2012, 83(7): 073301. DOI: 10.1063/1.4731014. [15] 马云, 胡绍楼, 汪小松, 等. 样品-窗口界面运动速度的VISAR测试技术 [J]. 高压物理学报, 2003, 17(4): 290–294. DOI: 10.3969/j.issn.1000-5773.2003.04.008.MA Y, HU S L, WANG X S, et al. VISAR measurement on interface velocity between shocked specimen and window [J]. Chinese Journal of High Pressure Physics, 2003, 17(4): 290–294. DOI: 10.3969/j.issn.1000-5773.2003.04.008. [16] 罗斌强, 张红平, 赵剑衡, 等. 斜波压缩实验数据的正向Lagrange处理方法研究 [J]. 爆炸与冲击, 2017, 37(2): 243–248. DOI: 10.11883/1001-1455(2017)02-0243-06.LUO B Q, ZHANG H P, ZHAO J H, et al. Lagrangian forward analysis in data processing of ramp wave compression experiments [J]. Explosion And Shock Waves, 2017, 37(2): 243–248. DOI: 10.11883/1001-1455(2017)02-0243-06. [17] LUO B Q, JIN Y S, LI M, et al. Direct calculation of sound speed of materials under ramp wave compression [J]. AIP Advances, 2018, 8(11). DOI: 10.1063/1.5047479. [18] 张红平, 孙承纬, 李牧, 等. 准等熵实验数据处理的反积分方法研究 [J]. 力学学报, 2011, 43(1): 105–111. DOI: 10.6052/0459-1879-2011-1-lxxb2010-053.ZHANG H P, SUN C W, LI M, et al. Backward integration method in data processing of quasi-isentropic compression experiment [J]. Chinese Journal of Theoretical Applied Mechanics, 2011, 43(1): 105–111. DOI: 10.6052/0459-1879-2011-1-lxxb2010-053. [19] HAYES D B. Backward integration of the equations of motion to correct for free surface perturbations: AC04-94AL85000 [R]. Office of Scientific & Technical Information Technical Reports, 2001. DOI: 10.2172/783087. [20] 许淑艳. 蒙特卡罗方法在实验核物理中的应用 [M]. 2版. 北京: 原子能出版社, 2006: 3. [21] 国家质量监督检验检疫总局. 用蒙特卡洛法评定测量不确定度: JJF 1059.2—2012 [S]. 北京: 中国质检出版社, 2013. [22] 国家市场监督管理总局, 中国国家标准化管理委员会. 测量不确定度评定和表示补充文件1: 基于蒙特卡洛方法的分布传播: GB/T 27419—2018 [S]. 北京: 中国标准出版社, 2018. [23] DENG J X, DENG Y, CHEONG K H. Combining conflicting evidence based on Pearson correlation coefficient and weighted graph [J]. International Journal of Intelligent Systems, 2021, 36(12): 7443–7460. DOI: 10.1002/int.22593. [24] BROWN J L, ALEXANDER C S, ASAY J R, et al. Flow strength of tantalum under ramp compression to 250GPa [J]. Journal of Applied Physics, 2014, 115(4): 10340–1177. DOI: 10.1063/1.4863463. [25] VALE C D, MAURELLI V A. Simulating multivariate nonnormal distributions [J]. Psychometrika, 1983, 48(3): 465–471. DOI: 10.1007/BF02293687. [26] KRAUS R G, DAVIS J P, SEAGLE C T, et al. Dynamic compression of copper to over 450 GPa: a high-pressure standard [J]. Physical Review B, 2016, 93(13): 134105. DOI: 10.1103/physrevb.93.134105. [27] ZHANG X P, WANG G J, LUO B Q, et al. Mechanical response of near-equiatomic NiTi alloy at dynamic high pressure and strain rate [J]. Journal of Alloys, 2017, 731: 569–576. DOI: 10.1016/j.jallcom.2017.10.080. -
点击查看大图
计量
- 文章访问数: 427
- HTML全文浏览量: 115
- PDF下载量: 87
- 被引次数: 0