弹体侵彻超高性能混凝土反弹效应理论初探

朱擎; 李述涛; 陈叶青; 马上

doi:10.11883/bzycj-2022-0513

弹体侵彻超高性能混凝土反弹效应理论初探

doi: 10.11883/bzycj-2022-0513

军事科学院国防工程研究院，北京 100036

详细信息

作者简介:
朱　擎（1997－　），男，博士研究生，zq953783236@163.com

通讯作者:
李述涛（1984－　），男，博士，高级工程师，list16@tsinghua.org.cn

中图分类号: O385
计量
- 文章访问数: 340
- HTML全文浏览量: 84
- PDF下载量: 115
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-14
- 修回日期: 2023-03-01
- 网络出版日期: 2023-03-24
- 刊出日期: 2023-09-11

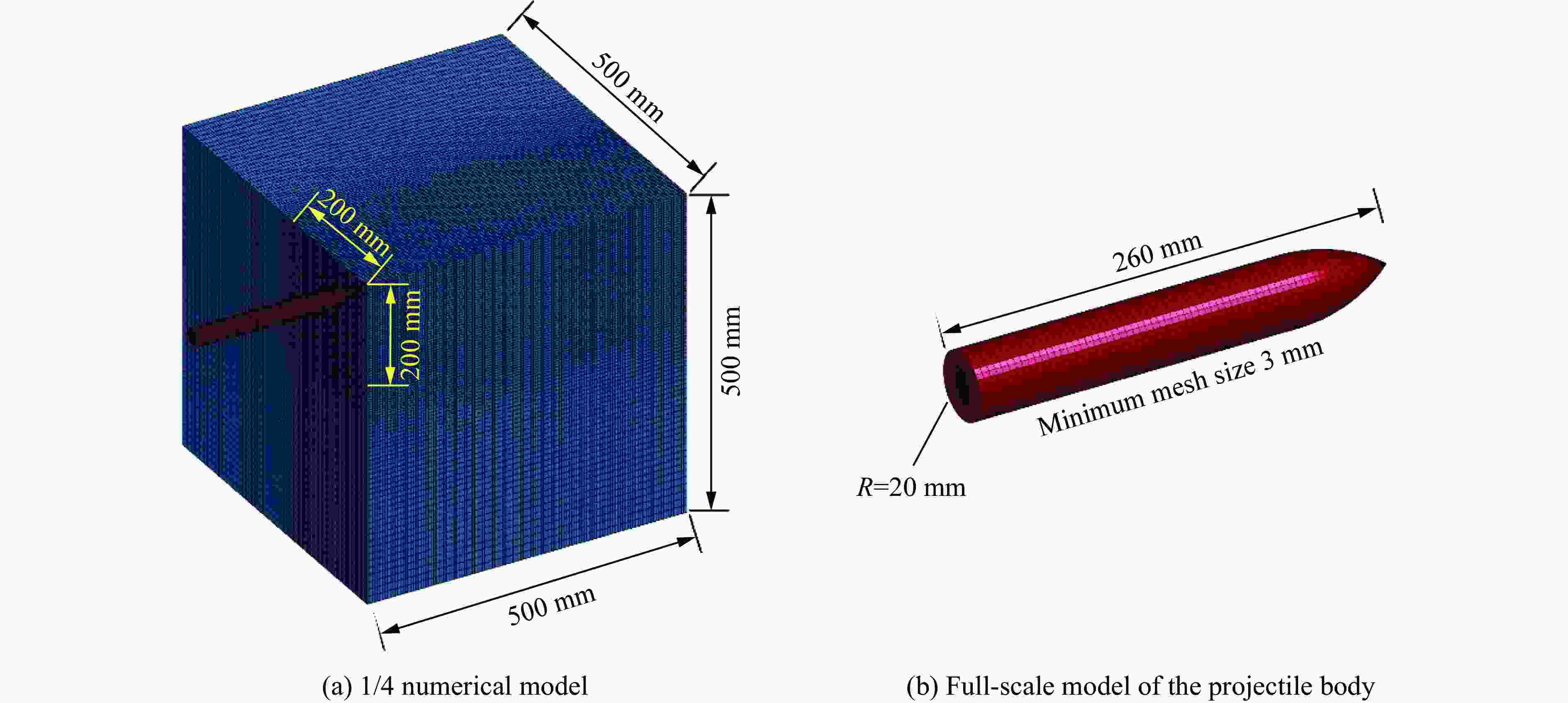
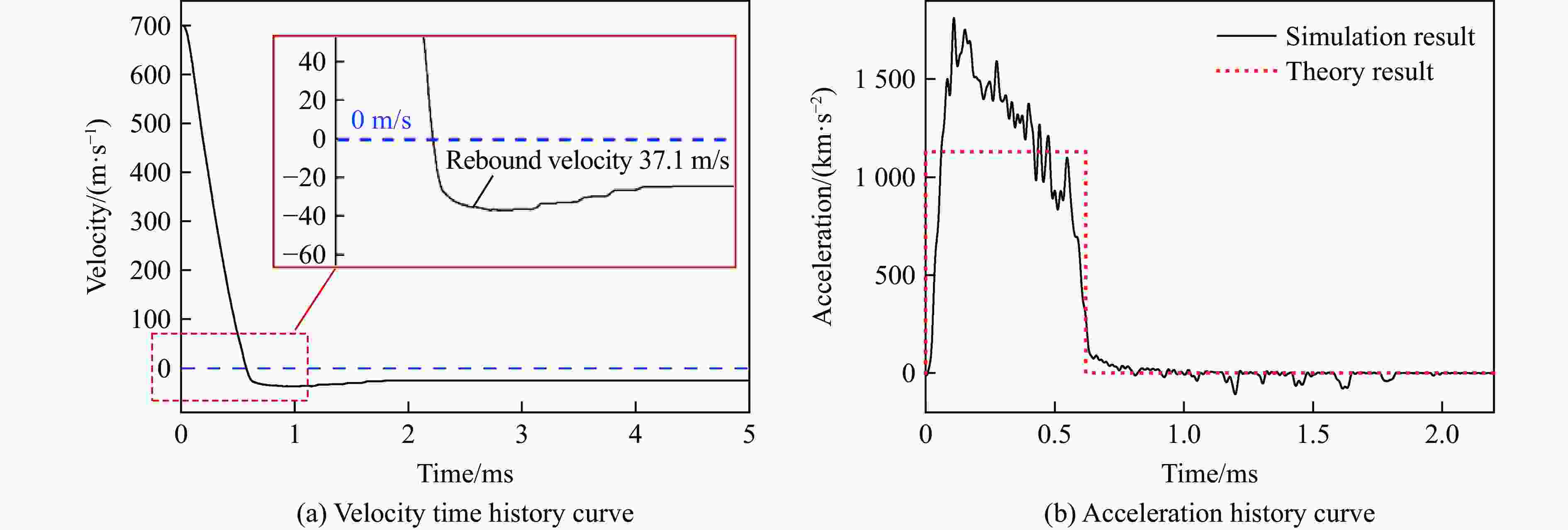
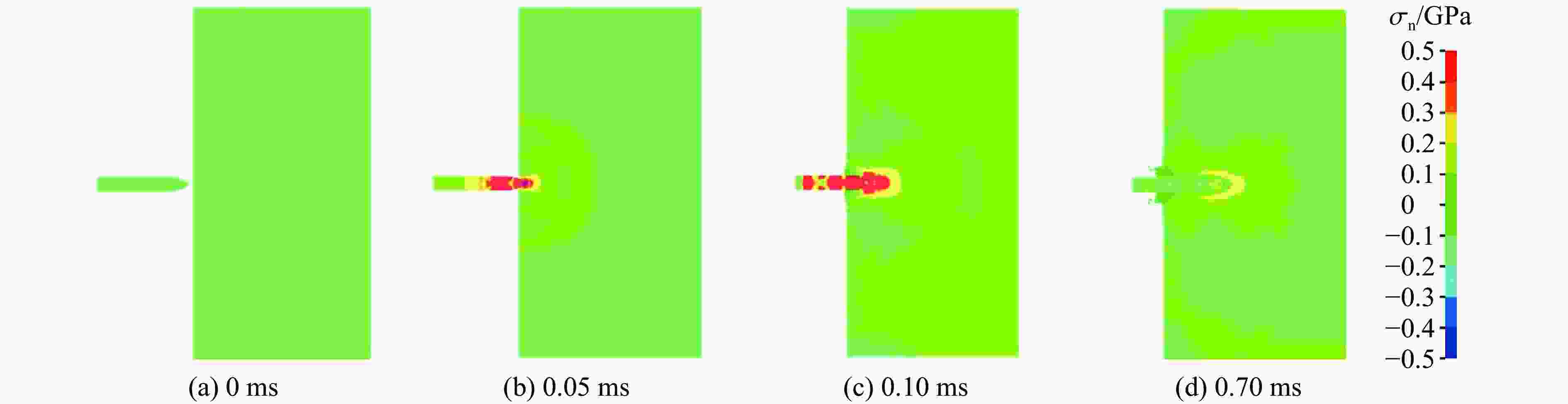
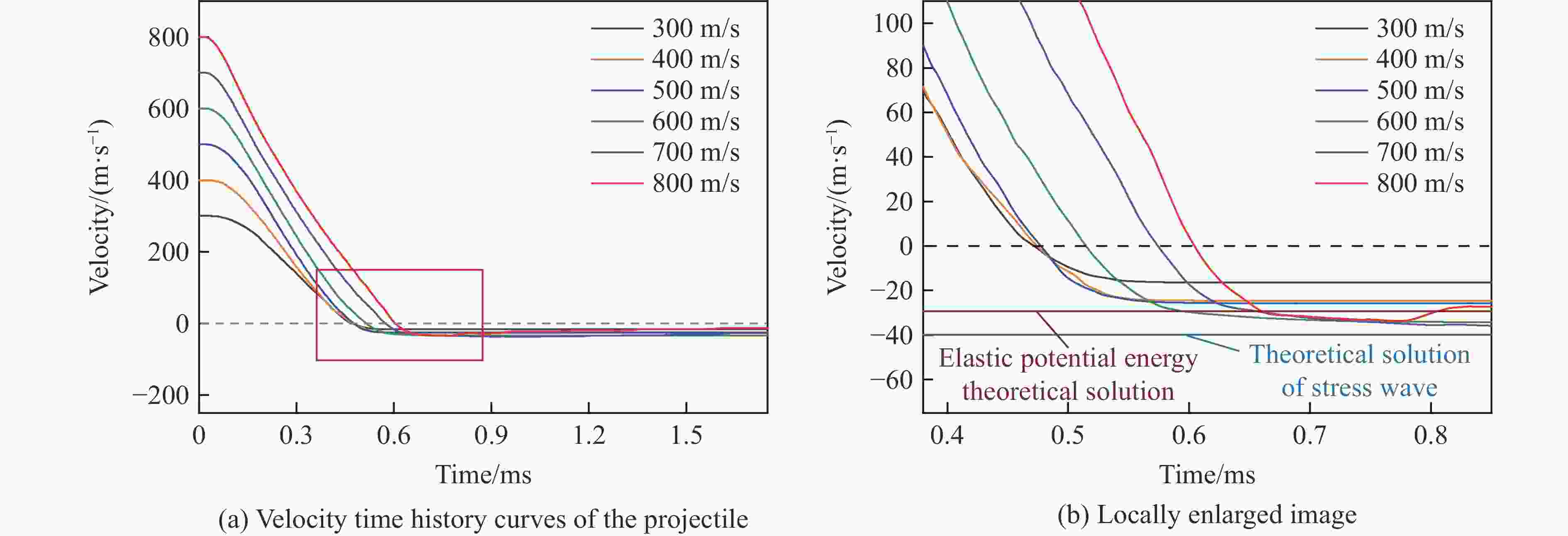
Preliminary theoretical study on the rebound effect of projectiles penetrating ultra-high performance concrete targets

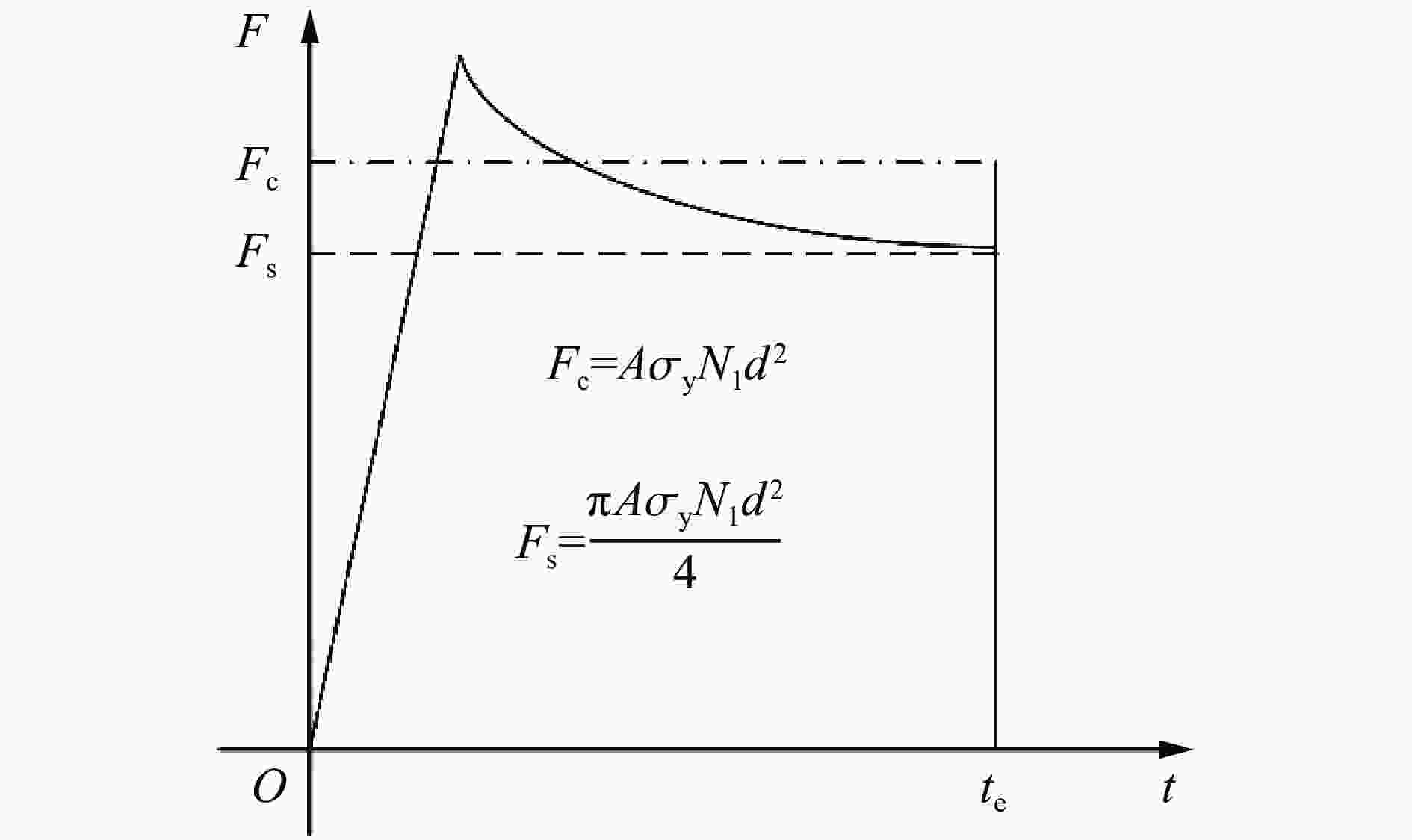
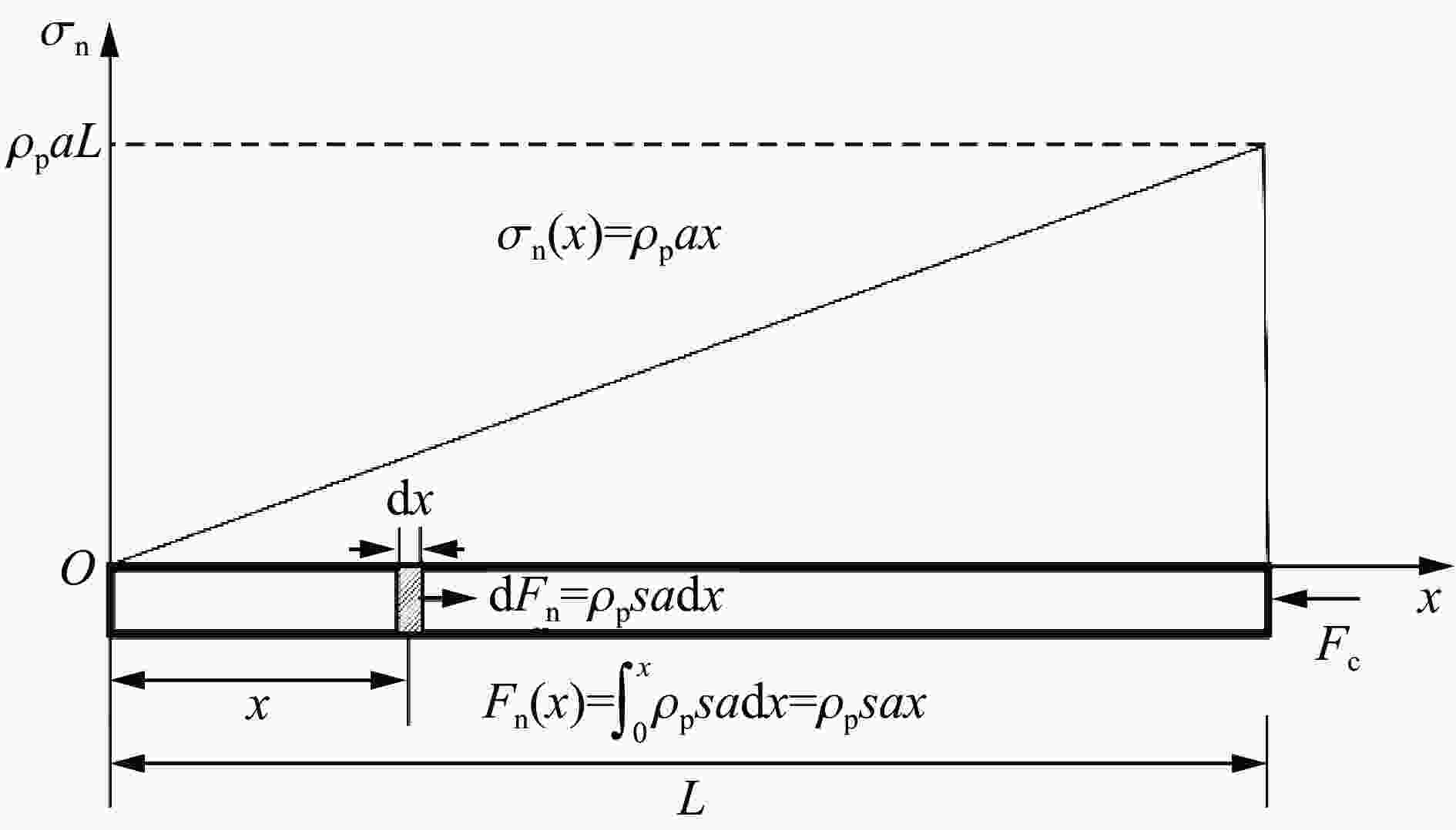
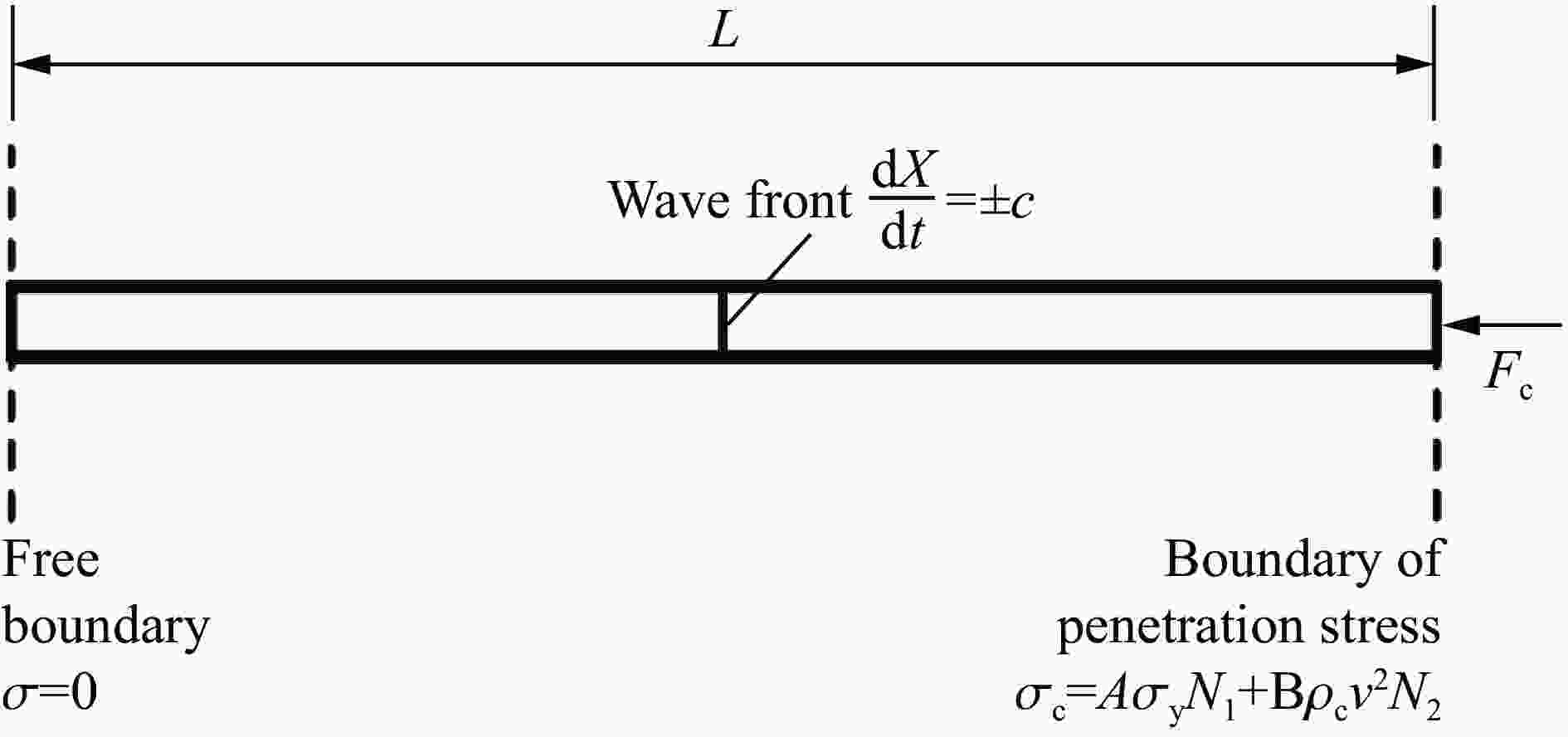
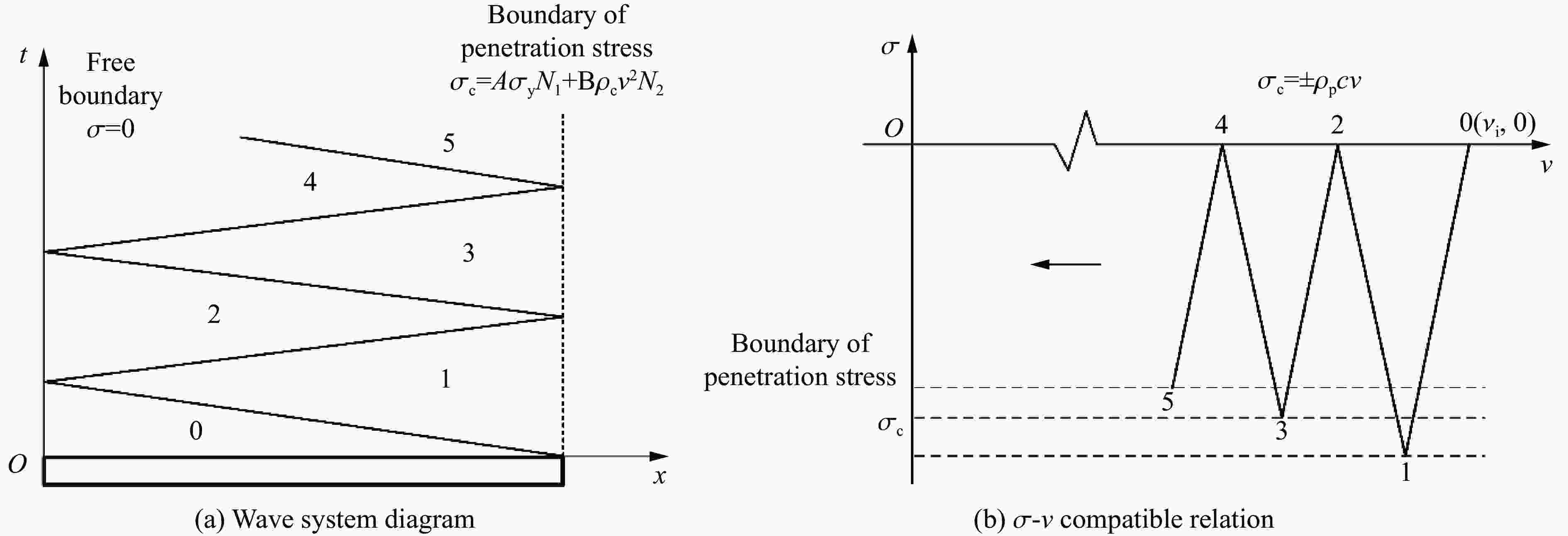
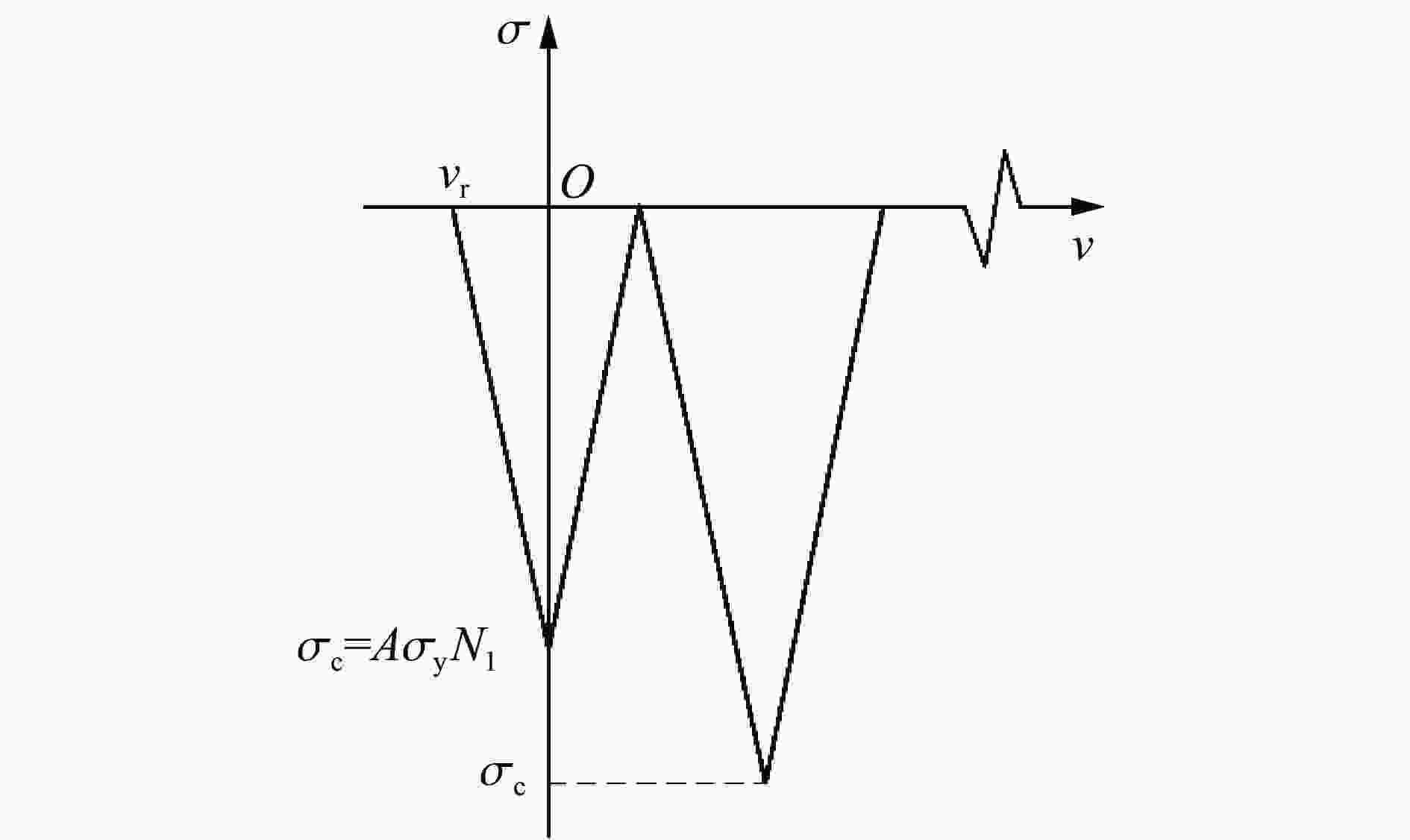
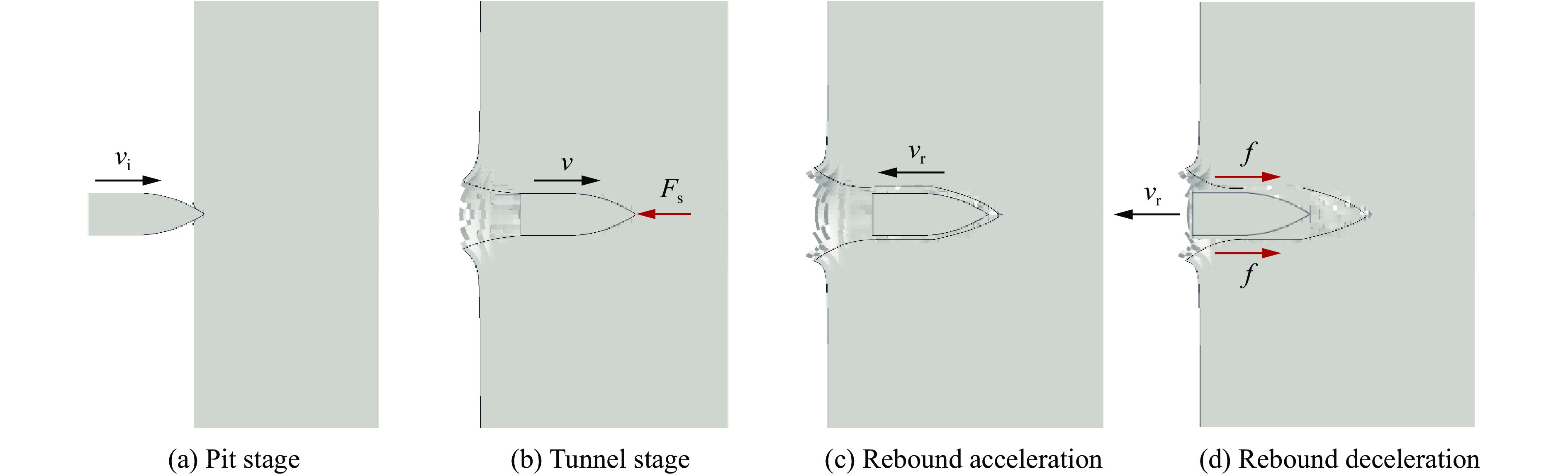
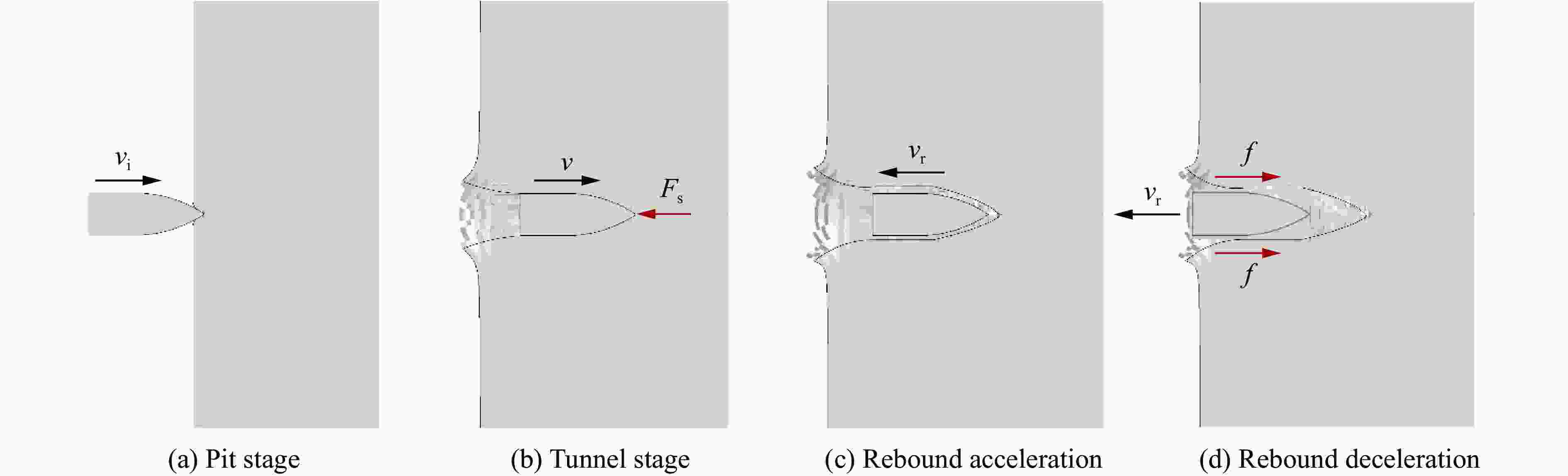
Institute of Defense Engineering, Academy of Military Sciences, Beijing 100036, China

摘要

摘要: 为了探究弹体在侵彻超高性能混凝土过程中弹体出现的反弹现象，基于空腔膨胀理论，分析了弹体从侵彻到反弹全过程的受力情况；分别以一维弹性杆弹性势能模型和一维应力波模型为理论基础，推导得到两种反弹速度的解析解，分析了影响反弹速度的物理量；通过数值模拟复现了弹体反弹现象，验证了理论模型的合理性，数值计算结果和两种解析解吻合良好。研究表明：侵彻阻力使弹体积累变形势能，侵彻结束后变形势能释放造成弹体反弹；反弹初速与着靶速度无关，与靶体材料的屈服强度和弹头形状系数等成正比，与弹体弹性模量和密度成反比。
- 弹体侵彻 /
- 超高性能混凝土 /
- 反弹效应 /
- 理论模型
Abstract: It is a developing trend of protection engineering to use high resistance materials such as ultra-high performance concrete to construct bullet-shielding structures. The phenomenon of projectile body rebound was found in the tests of projectile body penetrating ultra-high performance concrete. The projectile rebound effect is very important in the study of engineering protection, weapon damage and warhead design. In order to study the rebound velocity of projectile body after penetration and its influencing factors, the stress of projectile body from penetration to rebound was analyzed. Based on the expression of penetration resistance given by the cavity expansion theory, a one-dimensional elastic bar potential energy model was established from the perspective of the accumulation of deformation energy by penetration resistance, and a one-dimensional stress wave model was established from the perspective of stress wave generated by penetration resistance. The analytical solutions of the rebound velocity were derived from the two models respectively, and the physical quantities affecting the rebound velocity were analyzed. Through numerical simulation, the rebound phenomenon of the projectile body after penetrating the ultra-high performance concrete is reproduced, and the numerical results of the rebound velocity agree well with the two analytical solutions. Through numerical calculation of the same penetration model with different material parameters, the relationship between the rebound velocity and the material parameters in the analytical solution is verified, and the reliability of the theoretical model is proved. The results show that the projectile body accumulates deformation potential energy due to penetration resistance, and the projectile body bounces back due to the release of deformation potential energy after penetration. The initial rebound velocity is independent of the target velocity, proportional to the target material, yield strength and warhead shape coefficient, and inversely proportional to the elastic modulus and density of the projectile body. The results can preliminarily predict the rebound velocity and provide a reference for the design of ultra-high performance concrete protective structure and warhead.
- penetration of projectile /
- ultra-high performance concrete /
- rebound effect /
- theoretical model

HTML全文

图 1 弹体侵彻阶段受力状态

Figure 1. Force state of projectile body in each stage of penetration

下载: 全尺寸图片幻灯片

图 2 侵彻过程中弹体侵彻阻力时程曲线

Figure 2. Time history curve of projectile penetration resistance during penetration

下载: 全尺寸图片幻灯片

图 3 一维杆弹性势能模型

Figure 3. One-dimensional rod elastic potential energy model

下载: 全尺寸图片幻灯片

图 4 一维弹性波模型

Figure 4. One-dimensional elastic wave model

下载: 全尺寸图片幻灯片

图 5 弹性杆中弹性波波系图及其相容关系

Figure 5. The pattern of elastic wave system in elastic rod and its compatibility relation

下载: 全尺寸图片幻灯片

图 6 弹体左端面最后一次反射的相容关系示意图

Figure 6. Schematic diagram of the compatibility relation of the last reflection of the left face of the projectile body

下载: 全尺寸图片幻灯片

图 7 文献[24]中侵彻试验的数值计算模型

Figure 7. Numerical calculation model of penetration test in reference [24]

下载: 全尺寸图片幻灯片

图 8 文献[24]中网格尺寸收敛性分析

Figure 8. Analysis of unit size convergence in reference [24]

下载: 全尺寸图片幻灯片

图 9 侵彻坑直径D的试验结果与数值计算结果对比

Figure 9. Comparison of test results and numerical results of penetration pit diameter D

下载: 全尺寸图片幻灯片

图 10 弹体速度时程曲线和反弹速度理论解

Figure 10. Time history curves of projectile velocity and theoretical solutions to rebound velocity

下载: 全尺寸图片幻灯片

图 11 弹体侵彻超高性能混凝土有限元模型

Figure 11. Numerical model of projectile penetration into ultra high performance concrete

下载: 全尺寸图片幻灯片

图 12 3925-105-700的速度与加速度时程曲线

Figure 12. 3925-105-700 velocity and acceleration time history curve

下载: 全尺寸图片幻灯片

图 13 弹体侵彻方向的应力云图

Figure 13. Stress cloud diagram of projectile in penetration direction

下载: 全尺寸图片幻灯片

图 14 弹体7850-210速度时程曲线数值解和理论解的对比

Figure 14. Comparison of velocity time history curves of numerical and theoretical solutions of missile 7850-210

下载: 全尺寸图片幻灯片

图 15 弹体3925-105速度时程曲线数值解和理论解的对比

Figure 15. Comparison of velocity time history curves of numerical and theoretical solutions of missile 3925-105

下载: 全尺寸图片幻灯片

图 16 反弹速度数值解和理论解与侵彻初速之间的关系

Figure 16. The relationship between numerical and theoretical solutions of rebound velocity and initial penetration velocity

下载: 全尺寸图片幻灯片

图 17 两类弹体侵彻速度与反弹速度的对比

Figure 17. Comparison of penetration velocity and rebound velocity of two types of projectile bodies

下载: 全尺寸图片幻灯片

表 1 超高性能混凝土K&C模型参数^[24]

Table 1. K&C model parameters fot the ultra-high performance concrete^[24]

a₀/MPa	a₁	a₂/MPa⁻¹	a_1f	a_2f/MPa⁻¹	a_0y/MPa	a_1y	a_2y/MPa⁻¹
60.48	0.446 3	0.001 052	0.4417	0.000 989	38.32	0.625	0.003 090

ρ_c/(kg·m⁻³)	ν	f_t/MPa	b₁	b₂	b₃	Ω	W/mm
2 567	0.2	12	0.15	−4.39	1.15	0.75	2
注：a₀、a₁、a₂、a_1f、a_2f、a_0y、a_1y为失效面参数，ν为泊松比，f_t为抗拉强度，b₁、b₂、b₃为损伤参数，Ω为剪胀参数，W为试件宽度。

下载: 导出CSV

表 2 侵彻深度的试验与数值计算结果

Table 2. Experimental and numerical results of penetration depth

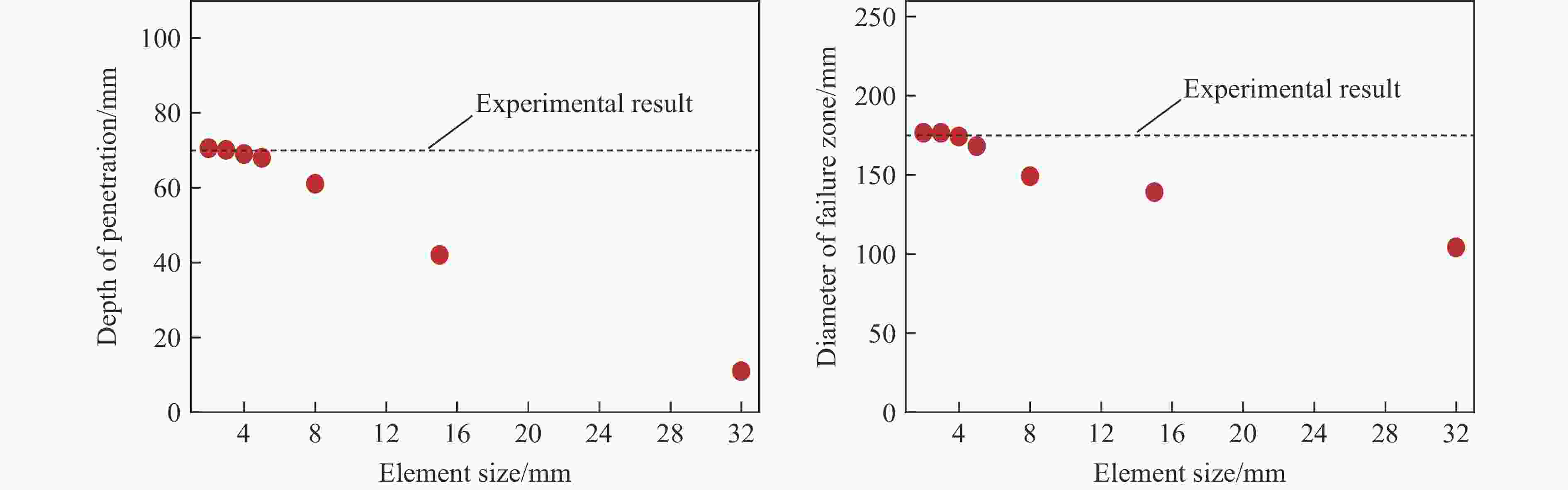
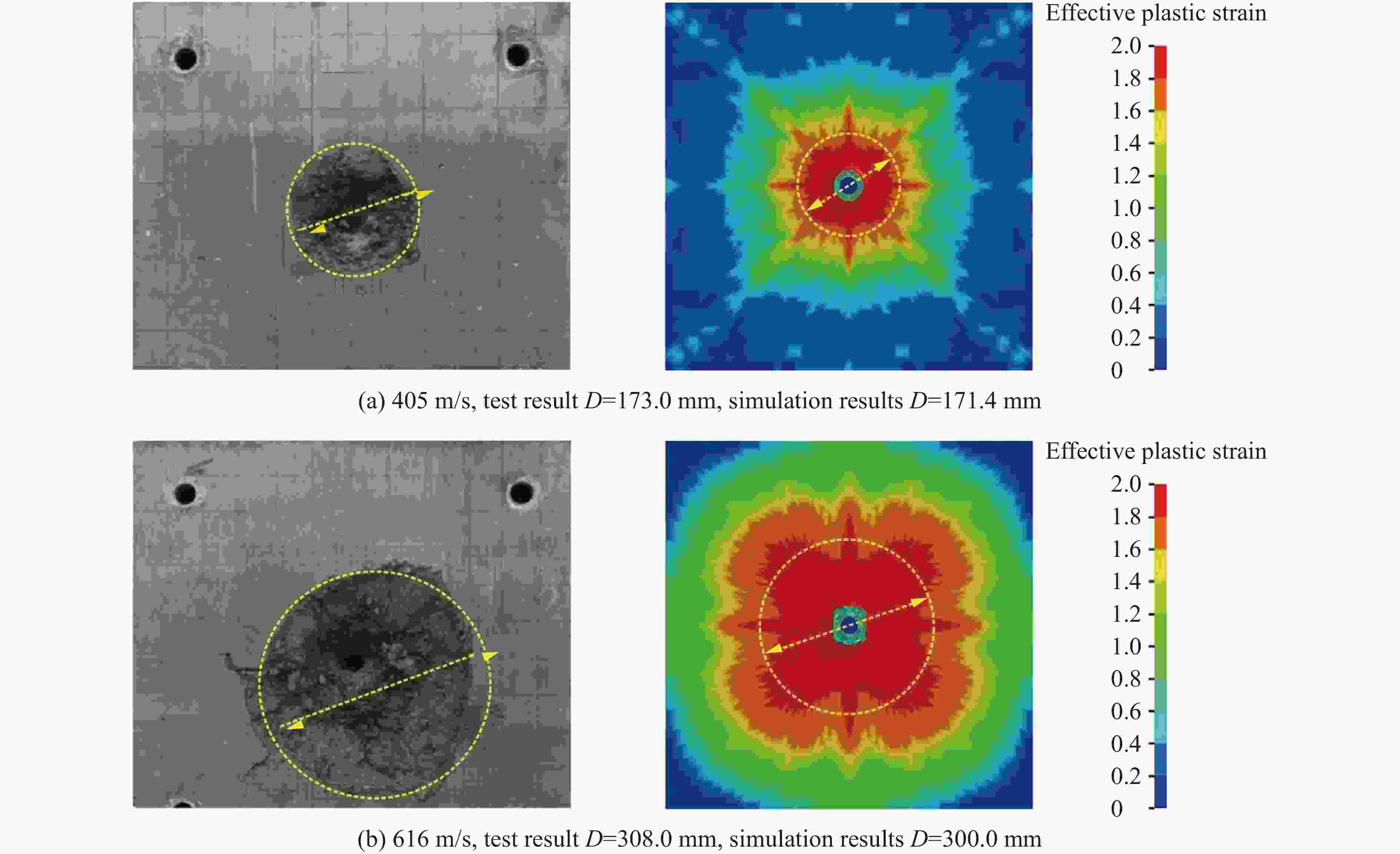
侵彻初速/(m·s⁻¹)	试验侵彻深度/mm	数值模拟侵彻深度/mm	误差/%
405	70	69	1.43
616	120	109	9.17

下载: 导出CSV

表 3 反弹速度的数值计算结果和理论预测值

Table 3. The results of numerical calculation and theoretical prediction of the rebound velocity

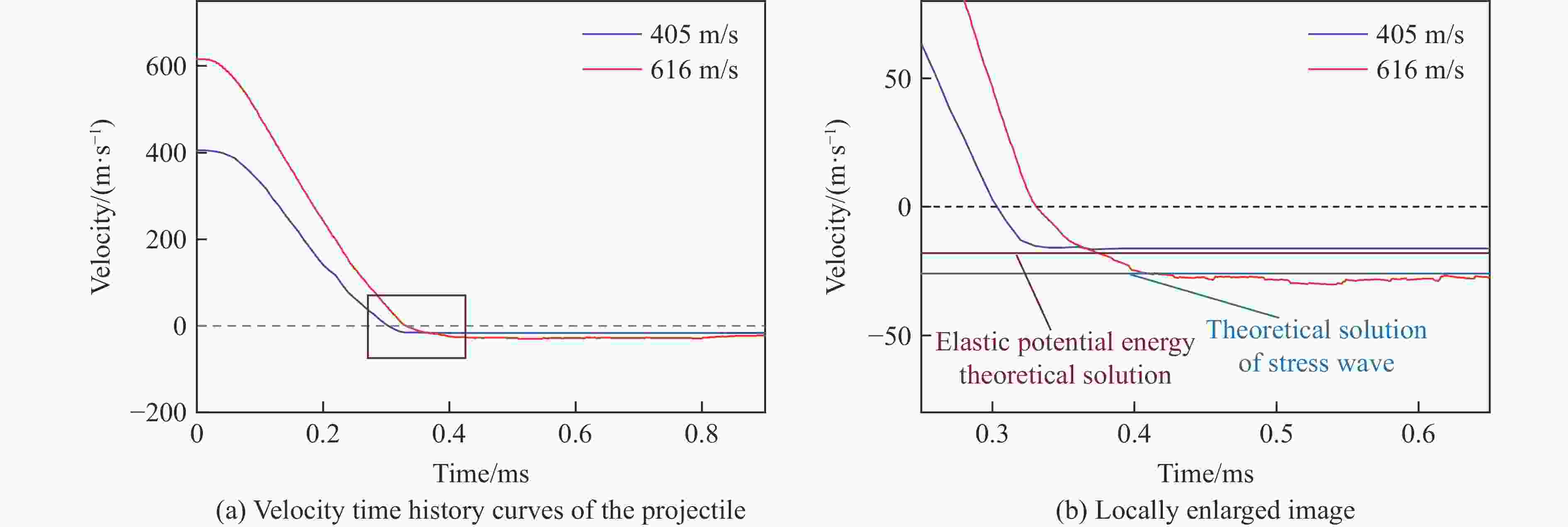
弹体	v_i/(m·s⁻¹)	v_r/(m·s⁻¹)			与数值模拟的误差/%
弹体	v_i/(m·s⁻¹)	数值模拟	弹性势能模型	一维弹性波模型	弹性势能模型	一维弹性波模型
7850-210	300	8.2	14.12	19.2	44.0	57.3
	400	10.6	14.12	19.2	24.4	44.8
	500	17.0	14.12	19.2	−20.0	11.5
	600	13.3	14.12	19.2	5.7	30.7
	700	16.7	14.12	19.2	−17.9	13.0
	800	15.9	14.12	19.2	−12.4	17.2
3925-105	300	16.3	28.25	38.4	42.8	57.5
	400	24.5	28.25	38.4	14.0	36.2
	500	25.8	28.25	38.4	9.4	32.8
	600	34.2	28.25	38.4	−20.0	10.9
	700	37.1	28.25	38.4	−30.2	3.40
	800	33.7	28.25	38.4	−18.3	12.2

下载: 导出CSV

参考文献(24)

[1]	YU R, SPIESZ P, BROUWERS H J H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) [J]. Cement and Concrete Research, 2014, 56: 29–39. DOI: 10.1016/j.cemconres.2013.11.002.
[2]	戎志丹, 孙伟. 粗集料对超高性能水泥基材料动态力学性能的影响 [J]. 爆炸与冲击, 2009, 29(4): 361–366. DOI: 10.11883/1001-1455(2009)04-0361-06. RONG Z D, SUN W. Influences of coarse aggregate on dynamic mechanical behaviors of ultrahigh-performance cementitious composites [J]. Explosion and Shock Waves, 2009, 29(4): 361–366. DOI: 10.11883/1001-1455(2009)04-0361-06.
[3]	张文华, 张云升, 陈振宇. 超高性能混凝土抗缩比钻地弹侵彻试验及数值仿真 [J]. 工程力学, 2018, 35(7): 167–175, 186. DOI: 10.6052/j.issn.1000-4750.2017.03.0237. ZHANG W H, ZHANG Y S, CHEN Z Y. Penetration test and numerical simulation of ultral-high performance concrete with a scaled earth penetrator [J]. Engineering Mechanics, 2018, 35(7): 167–175, 186. DOI: 10.6052/j.issn.1000-4750.2017.03.0237.
[4]	ZHANG W H, ZHANG Y S, ZHANG G R. Static, dynamic mechanical properties and microstructure characteristics of ultra-high performance cementitious composites [J]. Science and Engineering of Composite Materials, 2012, 19(3): 237–245. DOI: 10.1515/secm-2011-0136.
[5]	任辉启, 穆朝民, 刘瑞朝, 等. 精确制导武器侵彻效应与工程防护 [M]. 北京: 科学出版社, 2016.
[6]	程月华, 吴昊, 谭可可, 等. 装甲钢/UHPC复合靶体抗侵彻性能试验与数值模拟研究 [J]. 爆炸与冲击, 2022, 42(5): 053302. DOI: 10.11883/bzycj-2021-0278. CHENG Y H, WU H, TAN K K, et al. Experimental and numerical studies on penetration resistance of armor steel/UHPC composite target [J]. Explosion and Shock Waves, 2022, 42(5): 053302. DOI: 10.11883/bzycj-2021-0278.
[7]	隋树元, 王树山. 终点效应学 [M]. 北京: 国防工业出版社, 2000: 7.
[8]	FORRESTAL M J, LUK V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid [J]. Journal of Applied Mechanics, 1988, 55(2): 275–279. DOI: 10.1115/1.3173672.
[9]	FORRESTAL M J, LUK V K, BRAR N S. Perforation of aluminum armor plates with conical-nose projectiles [J]. Mechanics of Materials, 1990, 10(1/2): 97–105. DOI: 10.1016/0167-6636(90)90020-G.
[10]	FORRESTAL M J, BRAR N S, LUK V K. Penetration of strain-hardening targets with rigid spherical-nose rods [J]. Journal of Applied Mechanics, 1991, 58(1): 7–10. DOI: 10.1115/1.2897183.
[11]	陈小伟. 穿甲/侵彻力学的理论建模与分析 [M]. 北京: 科学出版社, 2019: 9.
[12]	CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2.
[13]	BATRA R C, WRIGHT T W. Steady state penetration of rigid perfectly plastic targets [J]. International Journal of Engineering Science, 1986, 24(1): 41–54. DOI: 10.1016/0020-7225(86)90147-3.
[14]	FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements [J]. International Journal of Impact Engineering, 2003, 28(5): 479–497. DOI: 10.1016/S0734-743X(02)00108-2.
[15]	FORRESTAL M J, WARREN T L. Penetration equations for ogive-nose rods into aluminum targets [J]. International Journal of Impact Engineering, 2008, 35(8): 727–730. DOI: 10.1016/j.ijimpeng.2007.11.002.
[16]	FREW D J, FORRESTAL M J, CARGILE J D. The effect of concrete target diameter on projectile deceleration and penetration depth [J]. International Journal of Impact Engineering, 2006, 32(10): 1584–1594. DOI: 10.1016/j.ijimpeng.2005.01.012.
[17]	ROSENBERG Z, DEKEL E. The penetration of rigid long rods-revisited [J]. International Journal of Impact Engineering, 2009, 36(4): 551–564. DOI: 10.1016/j.ijimpeng.2008.06.001.
[18]	陈小伟, 李继承. 刚性弹侵彻深度和阻力的比较分析 [J]. 爆炸与冲击, 2009, 29(6): 584–589. DOI: 10.11883/1001-1455(2009)06-0584-06. CHEN X W, LI J C. Analysis of penetration depth and resistive force in the deep penetration of a rigid projectile [J]. Explosion and Shock Waves, 2009, 29(6): 584–589. DOI: 10.11883/1001-1455(2009)06-0584-06.
[19]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets [J]. International Journal of Impact Engineering, 1994, 15(4): 395–405. DOI: 10.1016/0734-743X(94)80024-4.
[20]	CHEN X W. Dynamics of metallic and reinforced concrete targets subjected to projectile impact [D]. Singapore: Nanyang Technological University, 2003.
[21]	ROSENBERG Z, VAYIG Y, MALKA-MARKOVITZ A. The scaling issue in the penetration of concrete targets by rigid projectiles: revisited [J]. International Journal of Impact Engineering, 2020, 140: 103561. DOI: 10.1016/j.ijimpeng.2020.103561.
[22]	ROSENBERG Z, VAYIG Y, MALKA-MARKOVITZ A, et al. More on the perforation of concrete slabs by rigid projectiles [J]. International Journal of Impact Engineering, 2022, 162: 104138. DOI: 10.1016/j.ijimpeng.2021.104138.
[23]	余同希, 邱信明. 冲击动力学 [M]. 北京: 清华大学出版社, 2011.
[24]	ZHANG F L, SHEDBALE A S, ZHONG R, et al. Ultra-high performance concrete subjected to high-velocity projectile impact: implementation of K&C model with consideration of failure surfaces and dynamic increase factors [J]. International Journal of Impact Engineering, 2021, 155: 103907. DOI: 10.1016/j.ijimpeng.2021.103907.