基于3D细观模型的混凝土动态压缩行为分析

张湘茹; 程月华; 吴昊

doi:10.11883/bzycj-2022-0541

基于3D细观模型的混凝土动态压缩行为分析

doi: 10.11883/bzycj-2022-0541

同济大学土木工程学院，上海 200092

基金项目: 国家自然科学基金（52078379）

详细信息

作者简介:
张湘茹（1999－　），女，硕士研究生，2032542@tongji.edu.cn

通讯作者:
程月华（1994－　），女，博士，yhcheng@tongji.edu.cn

中图分类号: O347.3
计量
- 文章访问数: 547
- HTML全文浏览量: 121
- PDF下载量: 265
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-01
- 修回日期: 2023-04-17
- 网络出版日期: 2023-04-26
- 刊出日期: 2024-02-06

Analysis on dynamic compressive behavior of concrete based on a 3D mesoscale model

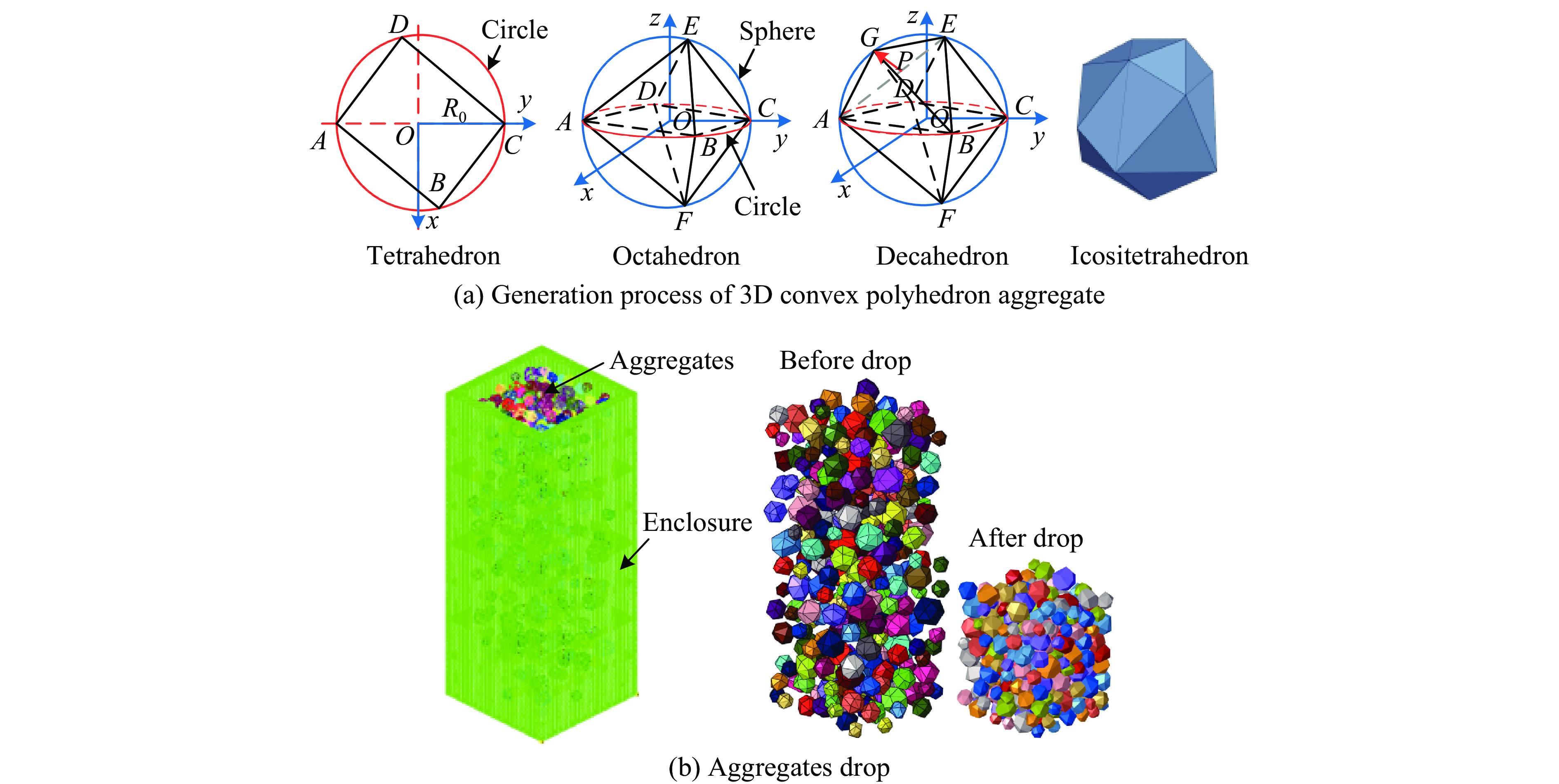
College of Civil Engineering, Tongji University, Shanghai 200092, China

摘要

摘要: 通过建立混凝土的3D细观模型，在细观尺度上分析动态压缩荷载作用下混凝土材料内部裂缝的产生和发展、损伤演化和动态强度及其影响因素。首先，基于传统的“生成-投放”法生成粒径、形状和空间分布均随机的凸多面体粗骨料模型，并通过骨料沉降和粒径缩放实现粗骨料的大体积率（达50%）和可调控；使用四面体网格划分骨料和砂浆表征其真实物理形状；使用界面粘结接触表征界面过渡区（ITZ）提升计算效率。进一步通过对比不同粗骨料粒径混凝土的分离式霍普金森压杆（SHPB）试验数据与模拟结果，如杆上应变时程、试件动态应力-应变曲线和试件损伤破坏模式，验证了建立的混凝土3D细观有限元模型、参数确定方法和数值仿真方法的准确性。最后，分析了30~100 s⁻¹应变率范围内骨料粒径（4~8、10~14和22~26 mm）、体积率（20%、30%和40%）和类型（石灰岩、花岗岩和玄武岩）对混凝土动态压缩强度的影响。结果表明：粗骨料粒径增大，混凝土动态压缩强度先增大后减小；粗骨料体积率越高，混凝土动态压缩强度越大；混凝土动态压缩强度随粗骨料强度的增加而提高。
- 混凝土 /
- 3D细观模型 /
- 动态力学行为 /
- 粘结接触 /
- 应变率效应
Abstract: As the most widely used construction material, concrete is common in military protection and civil transportation infrastructures. During its services life, concrete may bear dynamic loads such as high-speed penetration, blast and impact of vehicle, ship, rockfall and so on. On the mesoscale, concrete is three-phase material composed of mortar, coarse aggregates and interface transition zone (ITZ). The concrete 3D mesoscale model was established to analyze the crack generation and development, damage evolution, dynamic strength and its influencing factors of concrete. Firstly, randomly distributed convex polyhedron aggregates of random shapes and sizes were modeled based on the conventional “take-and-place” method and Monte Carlo algorithm, and drop of aggregates under gravity were simulated in finite element software LS-DYNA to make aggregates more dense, improving aggregate volume fraction to 50%. After that, aggregate size was reduced by a trial value to control aggregate volume fraction conveniently. Then, aggregates and mortar were meshed with tetrahedral elements to display their actual physical shapes. Besides, ITZ was represented by interface cohesive contact which equals zero-thickness bonding elements to improve computational efficiency. Furthermore, SHPB simulations of different coarse aggregates sizes concrete were conducted and the accuracy of finite element model, parameter determination method and numerical simulation methods were proved by comparing test and simulated bar strain-time history, dynamic stress-strain curves and failure patterns of specimens. Finally, influences of the aggregate size (4−8, 10−14 and 22−26 mm), volume fraction (20%, 30% and 40%) and type (limestone, granite and basalt) on concrete dynamic compressive strength under the strain rate within 30−100 s⁻¹ were analyzed. It shows that the dynamic compressive strength of concrete increases first and then decreases with the increase of aggregate size; the dynamic compressive strength of concrete increases with the increase of volume fraction; the dynamic compressive strength of concrete increases with the increase of aggregate strength.
- concrete /
- 3D mesoscale model /
- dynamic mechanical behavior /
- cohesive contact /
- strain rate effect

HTML全文

图 1 随机多面体粗骨料生成与沉降

Figure 1. Generation and drop of random polyhedral aggregates

下载: 全尺寸图片幻灯片

图 2 骨料缩放示意图及不同骨料体积率混凝土剖面

Figure 2. Schematic diagram of aggregates reductions and cross sections of concrete with different aggregate volume fractions

下载: 全尺寸图片幻灯片

图 3 布尔运算与网格划分

Figure 3. Boolean operation and mesh generation

下载: 全尺寸图片幻灯片

图 4 准静态单轴压缩与SHPB试验有限元模型

Figure 4. Finite element models of quasi-static uniaxial compression and SHPB tests

下载: 全尺寸图片幻灯片

图 5 杆上反射和透射波的网格敏感性

Figure 5. Convergence of mesh sizes on incident and transmitted stress waves

下载: 全尺寸图片幻灯片

图 6 RHT模型^[21]

Figure 6. RHT model^[21]

下载: 全尺寸图片幻灯片

图 7 砂浆的RHT压缩应变率效应参数修正

Figure 7. Modification of RHT compressive strain rate parameters for mortar

下载: 全尺寸图片幻灯片

图 8 牵引-分离关系曲线

Figure 8. Traction-separation law

下载: 全尺寸图片幻灯片

图 9 试验与模拟得到样品M的准静态应力-应变曲线对比

Figure 9. Comparison of quasi-static stress-strain curve between test and simulation of sample M

下载: 全尺寸图片幻灯片

图 10 试验与模拟得到样品G6的准静态应力-应变曲线对比

Figure 10. Comparison of quasi-static stress-strain curve between test and simulation of sample G6

下载: 全尺寸图片幻灯片

图 11 试验与模拟得到样品G12的准静态应力-应变曲线对比

Figure 11. Comparisons of quasi-static stress-strain curve between test and simulation of sample G12

下载: 全尺寸图片幻灯片

图 12 试验与模拟得到样品G24的准静态应力-应变曲线对比

Figure 12. Comparisons of quasi-static stress-strain curve between test and simulation of sample G24

下载: 全尺寸图片幻灯片

图 13 SHPB有限元模型应力平衡校核

Figure 13. Stress equilibrium check of SHPB finite element model

下载: 全尺寸图片幻灯片

图 14 平均应变率计算方法

Figure 14. Calculation method of average strain rate

下载: 全尺寸图片幻灯片

图 15 试验与模拟波形曲线对比（工况M-65 s⁻¹）

Figure 15. Comparison of test and simulated waveforms of case M-65 s⁻¹

下载: 全尺寸图片幻灯片

图 16 试验与模拟波形曲线对比（工况G6-85 s⁻¹）

Figure 16. Comparison of test and simulated waveforms of case G6-85 s⁻¹

下载: 全尺寸图片幻灯片

图 17 试验与模拟波形曲线对比（工况G12-60 s⁻¹）

Figure 17. Comparison of test and simulated waveforms of case G12-60 s⁻¹

下载: 全尺寸图片幻灯片

图 18 试验与模拟波形曲线对比（工况G24-80 s⁻¹）

Figure 18. Comparison of test and simulated waveforms of case G24-80 s⁻¹

下载: 全尺寸图片幻灯片

图 19 试验与模拟得到样品M的动态应力-应变曲线对比

Figure 19. Comparison of test and simulated dynamic stress-strain curves of sample M

下载: 全尺寸图片幻灯片

图 20 试验与模拟得到样品G6的动态应力-应变曲线对比

Figure 20. Comparison of test and simulated dynamic stress-strain curves of sample G6

下载: 全尺寸图片幻灯片

图 21 试验与模拟得到样品G12的动态应力-应变曲线对比

Figure 21. Comparison of test and simulated dynamic stress-strain curves of sample G12

下载: 全尺寸图片幻灯片

图 22 试验与模拟得到样品G24的动态应力-应变曲线对比

Figure 22. Comparison of test and simulated dynamic stress-strain curves of sample G24

下载: 全尺寸图片幻灯片

图 23 砂浆试件破坏模式

Figure 23. Failure patterns of mortar specimens

下载: 全尺寸图片幻灯片

图 24 不同骨料粒径混凝土试件破坏模式

Figure 24. Failure patterns for concrete specimens of different coarse aggregate sizes

下载: 全尺寸图片幻灯片

图 25 试件G24-50 s⁻¹破坏过程

Figure 25. Damage process of specimen G24-50 s⁻¹

下载: 全尺寸图片幻灯片

图 26 不同粒径骨料混凝土试件动态应力-应变曲线

Figure 26. Dynamic stress-strain curves for concrete specimens with different aggregate sizes

下载: 全尺寸图片幻灯片

图 27 不同骨料体积率混凝土试件动态应力-应变曲线

Figure 27. Dynamic stress-strain curves for concrete specimens of different aggregate volume fractions

下载: 全尺寸图片幻灯片

图 28 不同类型骨料混凝土试件动态应力-应变曲线

Figure 28. Dynamic stress-strain curves for concrete specimens of different aggregate types

下载: 全尺寸图片幻灯片

表 1 砂浆的RHT模型参数

Table 1. RHT model parameters of mortar

参数类型	参数	符号	取值	参数类型	参数	符号	取值
基本强度参数	拉压强度比	$ f_{{\mathrm{t}}} ^{\text{*}} $	0.18	失效面参数	失效面参数	A_f	1.6
基本强度参数	剪压强度比	$ f_{\mathrm{s}}^* $	0.1		失效面指数	N	0.61
弹性屈服面参数	压缩屈服面参数	$ g_{\mathrm{c}}^* $	0.53		拉压子午比	Q₀	0.6805
弹性屈服面参数	拉伸屈服面参数	$ g_{\mathrm{t}}^* $	0.7		罗德角相关系数	B_L	0.0105
残余强度面参数	残余强度参数	A_r	1.4		压缩应变率指数	$ {\beta _{\mathrm{c}}} $	5.64×10⁻³
残余强度面参数	残余强度指数	n_r	0.61		拉伸应变率指数	$ {\beta _{{\mathrm{t}}} } $	0.02
硬化段参数	剪切模量缩减系数	$ \xi $	0.9		参考压缩应变率	$ \dot \varepsilon _0^{\mathrm{c}} $	3×10⁻⁵ s⁻¹
软化段参数	损伤参数	D₁	0.02		参考拉伸应变率	$ \dot \varepsilon _0^{\mathrm{t}} $	3×10⁻⁶ s⁻¹
	损伤指数	D₂	1		过渡压缩应变率	$ \dot \varepsilon _{\mathrm{p}}^{\mathrm{c}} $	30 s⁻¹
	最小失效应变	$ \varepsilon _{\text{p}}^{\text{m}} $	0.01		过渡拉伸应变率	$ \dot \varepsilon _{\mathrm{p}}^{\mathrm{t}} $	30 s⁻¹

下载: 导出CSV

表 2 不同类型骨料HJC材料参数^[31-32]

Table 2. HJC model parameters of different aggregate types^[31-32]

岩石	ρ₀/(kg·m⁻³)	f_c/MPa	G/GPa	T/MPa	A₀	B₀
石灰石^[31]	2300	60	10.1	4	0.55	1.23
花岗岩^[31]	2660	154	28.7	12.2	0.3	2.5
玄武岩^[32]	2800	200	25.2	14.65	0.79	2.5

N	$ \sigma _{\max }^ * $	C₀	$ {\dot \varepsilon _0} $	D₁	D₂	e_f,min
0.89	20	0.0097	1×10⁻⁶	0.04	1	0.01
0.79	15	0.0097	1×10⁻⁶	0.04	1	0.01
0.7	15	0.007	1×10⁻⁶	0.04	1	0.01

P_c/MPa	P_l/GPa	K₁/GPa	K₂/GPa	K_3/GPa	μ_c	μ_l
20	2	39	−223	550	0.00125	0.174
51	1.2	12	25	42	0.00162	0.012
67.7	1.2	12	25	42	0.0012	0.012
注：ρ₀为密度，f_c为压缩强度，G为剪切模量，T为最大拉伸静水压力，A₀、B₀、N、$ \sigma _{\max }^ * $、C₀为强度面参数，$ {\dot \varepsilon _0} $为应变率效应参数，D₁、D₂、e_f,min为损伤参数，P_c、P_l、K₁、K₂、K₃、μ_c、μ_l为状态方程参数。

下载: 导出CSV

参考文献(33)

[1]	GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869–886. DOI: 10.1016/S0734-743X(01)00020-3.
[2]	KLEPACZKO J R, BRARA A. An experimental method for dynamic tensile testing of concrete by spalling [J]. International Journal of Impact Engineering, 2001, 25(4): 387–409. DOI: 10.1016/S0734-743X(00)00050-6.
[3]	BRARA A, CAMBORDE F, KLEPACZKO J R, et al. Experimental and numerical study of concrete at high strain rates in tension [J]. Mechanics of Materials, 2001, 33(1): 33–45. DOI: 10.1016/S0167-6636(00)00035-1.
[4]	DIAMARUYA M, KOBAYASHI H, NONAKA T. Impact tensile strength and fracture of concrete [J]. Journal de Physique Archives IV, 1997, 7(C3): 253–258. DOI: 10.1051/jp4:1997345.
[5]	REINHARDT H W, ROSSI P, VAN MIER J G M. Joint investigation of concrete at high rates of loading [J]. Materials and Structures, 1990, 23(3): 213–216. DOI: 10.1007/bf02473020.
[6]	TEDESCO J W, ROSS C A, MCGILL P B, et al. Numerical analysis of high strain rate concrete direct tension tests [J]. Computers & Structures, 1991, 40(2): 313–327. DOI: 10.1016/0045-7949(91)90357-R.
[7]	WEERHEIJM J, VAN DOORMAAL J C A M. Tensile failure of concrete at high loading rates: new test data on strength and fracture energy from instrumented spalling tests [J]. International Journal of Impact Engineering, 2007, 34(3): 609–626. DOI: 10.1016/j.ijimpeng.2006.01.005.
[8]	KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [J]. Proceedings of the Physical Society, Section B, 1949, 62(11): 676–700. DOI: 10.1088/0370-1301/62/11/302.
[9]	HAO Y, HAO H, JIANG G P, et al. Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests [J]. Cement and Concrete Research, 2013, 52: 63–70. DOI: 10.1016/j.cemconres.2013.05.008.
[10]	王江波, 丁俊升, 王晓东, 等. 粗骨料粒径对混凝土动态压缩行为的影响研究 [J]. 爆炸与冲击, 2022, 42(2): 023101. DOI: 10.11883/bzycj-2021-0147. WANG J B, DING J S, WANG X D, et al. Effect of coarse aggregate size on the dynamic compression behavior of concrete [J]. Explosion and Shock Waves, 2022, 42(2): 023101. DOI: 10.11883/bzycj-2021-0147.
[11]	郭瑞奇, 任辉启, 张磊, 等. 基于混凝土细观骨料模型的SHPB仿真模拟研究 [J]. 振动与冲击, 2019, 38(22): 107–116. DOI: 10.13465/j.cnki.jvs.2019.22.015. GUO R Q, REN H Q, ZHANG L, et al. Simulation for SHPB tests based on a mesoscopic concrete aggregate model [J]. Journal of Vibration and Shock, 2019, 38(22): 107–116. DOI: 10.13465/j.cnki.jvs.2019.22.015.
[12]	ZHOU X Q, HAO H. Modelling of compressive behaviour of concrete-like materials at high strain rate [J]. International Journal of Solids and Structures, 2008, 45(17): 4648–4661. DOI: 10.1016/j.ijsolstr.2008.04.002.
[13]	PAJĄK M, BARANOWSKI P, JANISZEWSKI J, et al. Experimental testing and 3D meso-scale numerical simulations of SCC subjected to high compression strain rates [J]. Construction and Building Materials, 2021, 302: 124379. DOI: 10.1016/j.conbuildmat.2021.124379.
[14]	LV T H, CHEN X W, DENG Y J, et al. Further numerical investigation on concrete dynamic behaviors with considering stress non-equilibrium in SHPB test based on the waveform features [J]. Acta Mechanica Sinica, 2020, 36(4): 873–886. DOI: 10.1007/s10409-020-00974-z.
[15]	WU Z Y, ZHANG J H, YU H F, et al. Experimental and mesoscopic investigation on the dynamic properties of coral aggregate concrete in compression [J]. Science China Technological Sciences, 2021, 64(6): 1153–1166. DOI: 10.1007/s11431-020-1739-y.
[16]	ZHOU R X, SONG Z H, LU Y. 3D mesoscale finite element modelling of concrete [J]. Computers & Structures, 2017, 192: 96–113. DOI: 10.1016/j.compstruc.2017.07.009.
[17]	WANG X F, ZHANG M Z, IVKOV A P. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete [J]. International Journal of Solids and Structures, 2016, 80: 310–333. DOI: 10.1016/j.ijsolstr.2015.11.018.
[18]	SHENG P Y, ZHANG J Z, JI Z. An advanced 3D modeling method for concrete-like particle-reinforced composites with high volume fraction of randomly distributed particles [J]. Composites Science and Technology, 2016, 134: 26–35. DOI: 10.1016/j.compscitech.2016.08.009.
[19]	GRUNWALD C, SCHAUFELBERGER B, STOLZ A, et al. A general concrete model in hydrocodes: verification and validation of the Riedel-Hiermaier-Thoma model in LS-DYNA [J]. International Journal of Protective Structures, 2017, 8(1): 58–85. DOI: 10.1177/2041419617695977.
[20]	LSTC. LS-DYNA keyword user's manual volume I-II, version R11 [R]. CA, USA: Livermore Software Technology Corporation, 2018.
[21]	CHEN D, WU H, FANG Q. Simplified micro-model for brick masonry walls under out-of-plane quasi-static and blast loadings [J]. International Journal of Impact Engineering, 2023, 174: 104529. DOI: 10.1016/j.ijimpeng.2023.104529.
[22]	Federation Internationale du Beton. FIB model code for concrete structures [S]. Switzerland: Comite Euro-International du Beton, 2010. DOI: 10.1002/9783433604090.
[23]	JIN L, YU W X, DU X L, et al. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates [J]. International Journal of Impact Engineering, 2019, 125: 1–12. DOI: 10.1016/j.ijimpeng.2018.10.011.
[24]	MALEKI M, RASOOLAN I, KHAJEHDEZFULY A, et al. On the effect of ITZ thickness in meso-scale models of concrete [J]. Construction and Building Materials, 2020, 258: 119639. DOI: 10.1016/j.conbuildmat.2020.119639.
[25]	WANG J M, LI X, JIVKOV A P, et al. Interfacial transition zones in concrete meso-scale models: balancing physical realism and computational efficiency [J]. Construction and Building Materials, 2021, 293: 123332. DOI: 10.1016/j.conbuildmat.2021.123332.
[26]	CHEN W N, SONG B. Split Hopkinson (Kolsky) bar: design, testing and applications [M]. Beijing: National Defense Industry, 2011.
[27]	LV T H, CHEN X W, CHEN G. Analysis on the waveform features of the split Hopkinson pressure bar tests of plain concrete specimen [J]. International Journal of Impact Engineering, 2017, 103: 107–123. DOI: 10.1016/j.ijimpeng.2017.01.004.
[28]	AL-SALLOUM Y, ALMUSALLAM T, IBRAHIM S M, et al. Rate dependent behavior and modeling of concrete based on SHPB experiments [J]. Cement and Concrete Composites, 2015, 55: 34–44. DOI: 10.1016/j.cemconcomp.2014.07.011.
[29]	苏新春, 蒋国平. 混凝土材料骨料效应SHPB实验研究 [J]. 四川建材, 2017, 43(10): 22–23. DOI: 10.3969/j.issn.1672-4011.2017.10.011. SU X C, JIANG G P. SHPB experimental study on aggregate effect of concrete materials [J]. Sichuan Building Materials, 2017, 43(10): 22–23. DOI: 10.3969/j.issn.1672-4011.2017.10.011.
[30]	HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures [C]// Proceedings of the 14th International Symposium on Ballistics. Quebec, Canada: IBC, 1993: 591–600.
[31]	WANG X H, ZHANG S R, DAI J G, et al. Evaluation of base damage and stability of concrete gravity dam subjected to underwater explosion [J]. Structures, 2022, 38: 1502–1514. DOI: 10.1016/j.istruc.2022.03.012.
[32]	宫俊, 吴昊, 方秦, 等. 刚玉骨料超高性能水泥基材料抗侵彻试验和细观数值模拟 [J]. 振动与冲击, 2017, 36(1): 55–63. DOI: 10.13465/j.cnki.jvs.2017.01.008. GONG J, WU H, FANG Q, et al. Test and mesoscale numerical simulation for corundum-aggregate ultra-high performance cementitious composites against projectile penetration [J]. Journal of Vibration and Shock, 2017, 36(1): 55–63. DOI: 10.13465/j.cnki.jvs.2017.01.008.
[33]	ZHANG W H, ZHANG Y S. Research on the static and dynamic compressive properties of high performance cementitious composite (HPCC) containing coarse aggregate [J]. Archives of Civil and Mechanical Engineering, 2015, 15(3): 711–720. DOI: 10.1016/j.acme.2014.12.006.