Y型通风采煤工作面瓦斯爆炸传播规律模拟研究

刘佳佳; 张扬; 张翔; 聂子硕

doi:10.11883/bzycj-2023-0018

Y型通风采煤工作面瓦斯爆炸传播规律模拟研究

doi: 10.11883/bzycj-2023-0018

刘佳佳^{1, 2, 3, 4,},
张扬¹,
张翔¹,
聂子硕¹

1.
河南理工大学安全科学与工程学院，河南焦作 454003
2.
安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽淮南 232001
3.
河南理工大学煤炭安全生产与清洁高效利用省部共建协同创新中心，河南焦作 454003
4.
河南理工大学瓦斯地质与瓦斯治理国家重点实验室培育基地，河南焦作 454003

基金项目: 国家自然科学基金（52074106）；河南省优秀青年科学基金（232300421061）；河南理工大学创新型科研团队项目（T2023-3）；深部煤矿采动响应与灾害防控国家重点实验室开放基金（SKLMRDPC22KF11）

详细信息

作者简介:
刘佳佳（1985－　），男，博士，副教授，博士生导师，liujiajia@hpu.edu.cn

中图分类号: O382
计量
- 文章访问数: 320
- HTML全文浏览量: 66
- PDF下载量: 54
- 被引次数: 0
出版历程
- 收稿日期: 2023-01-16
- 修回日期: 2023-04-06
- 网络出版日期: 2023-04-25
- 刊出日期: 2023-08-31

Simulation study on propagation characteristics of gas explosion in Y-shaped ventilated coal face

LIU Jiajia^{1, 2, 3, 4
,},
ZHANG Yang¹,
ZHANG Xiang¹,
NIE Zishuo¹

1.
College of Safety Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, Henan, China
2.
State Key Laboratory of Mining Response and Disaster Prevention and Control in Deep Coal Mines, Anhui University of Science and Technology, Huainan 232001, Anhui, China
3.
State Collaborative Innovation Center of Coal Work Safety and Clean-Efficiency Utilization, Henan Polytechnic University, Jiaozuo 454003, Henan, China
4.
State Key Laboratory Cultivation Base for Gas Geology and Gas Control, Henan Polytechnic University, Jiaozuo 454003, Henan, China

摘要

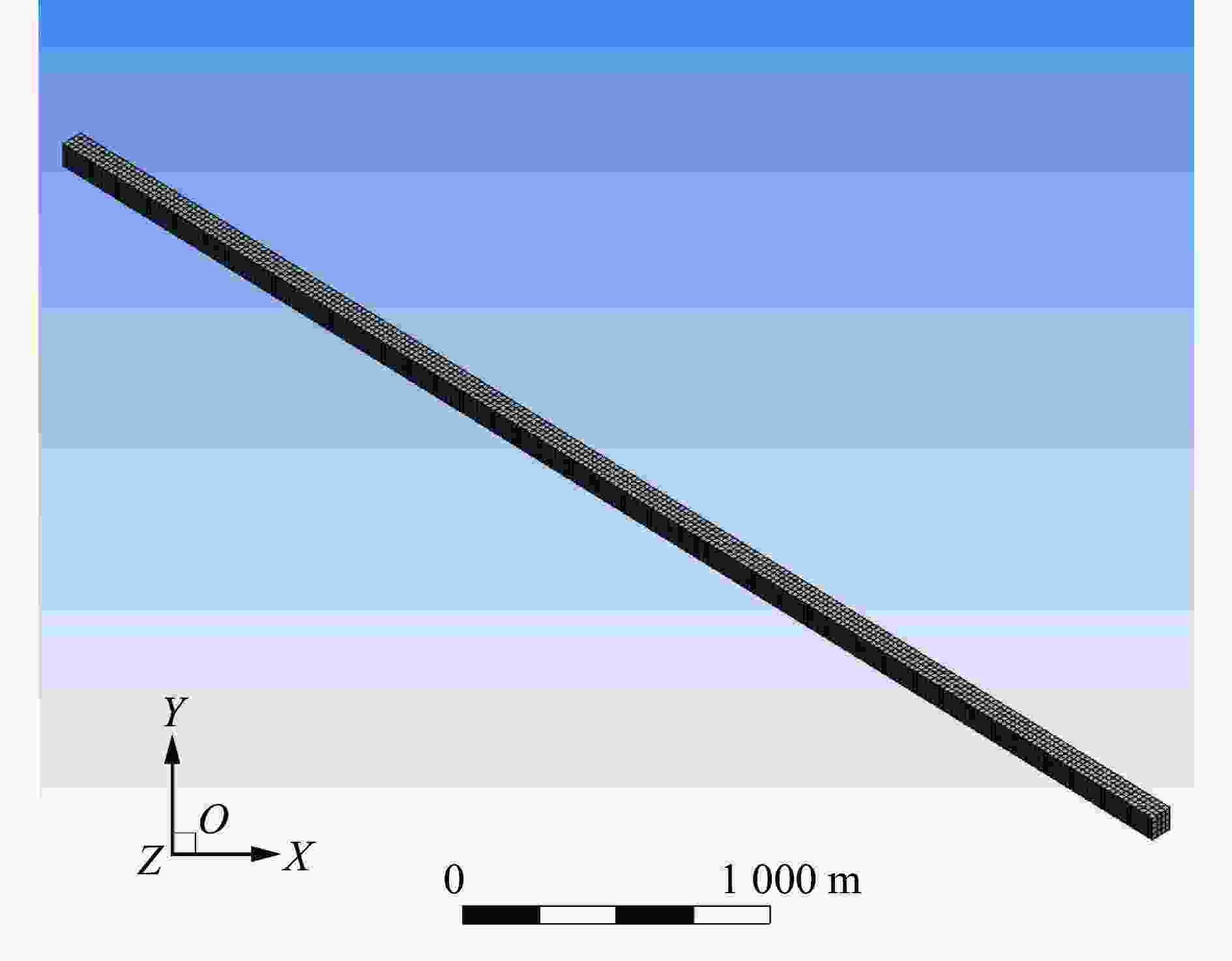
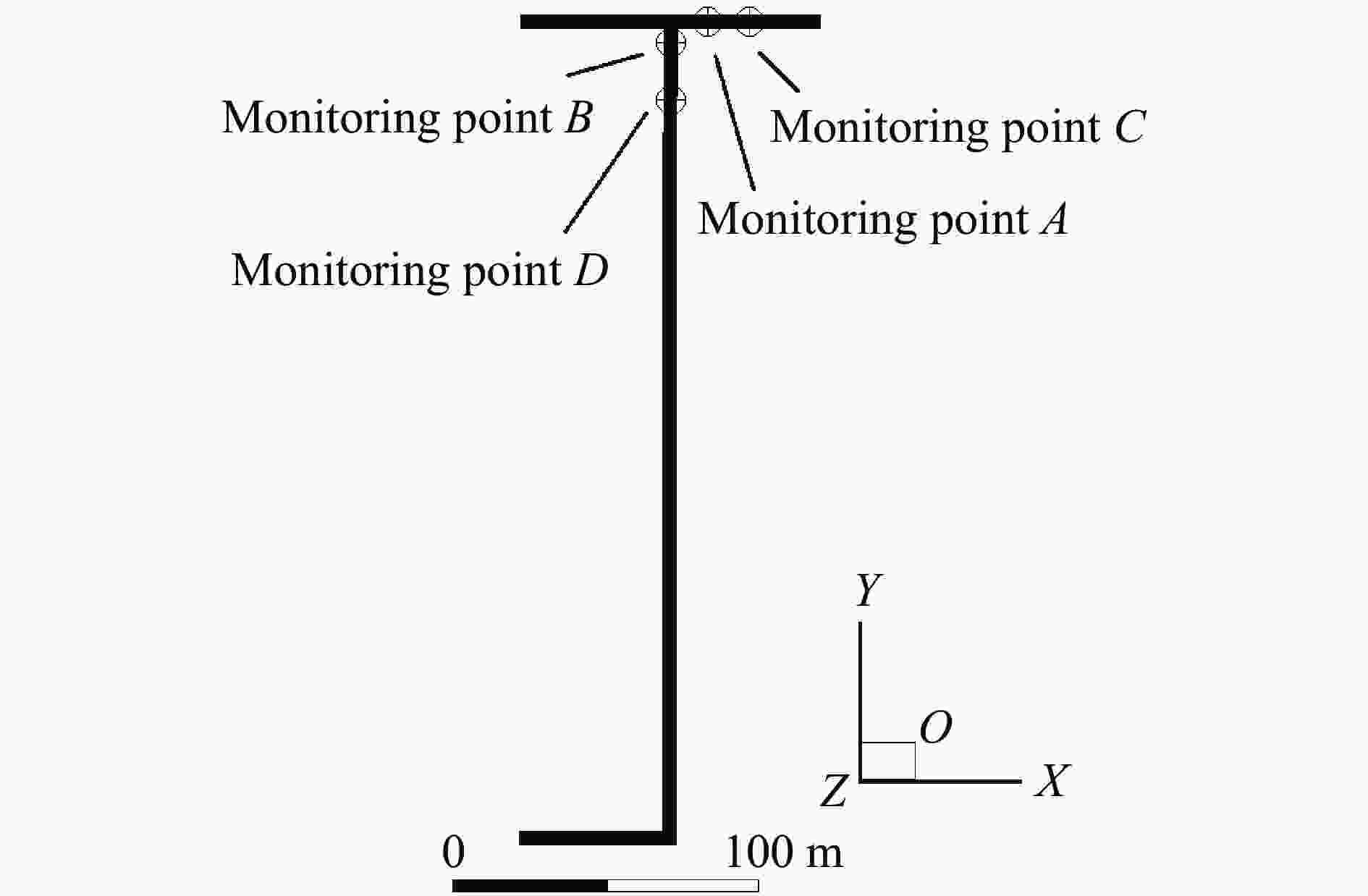
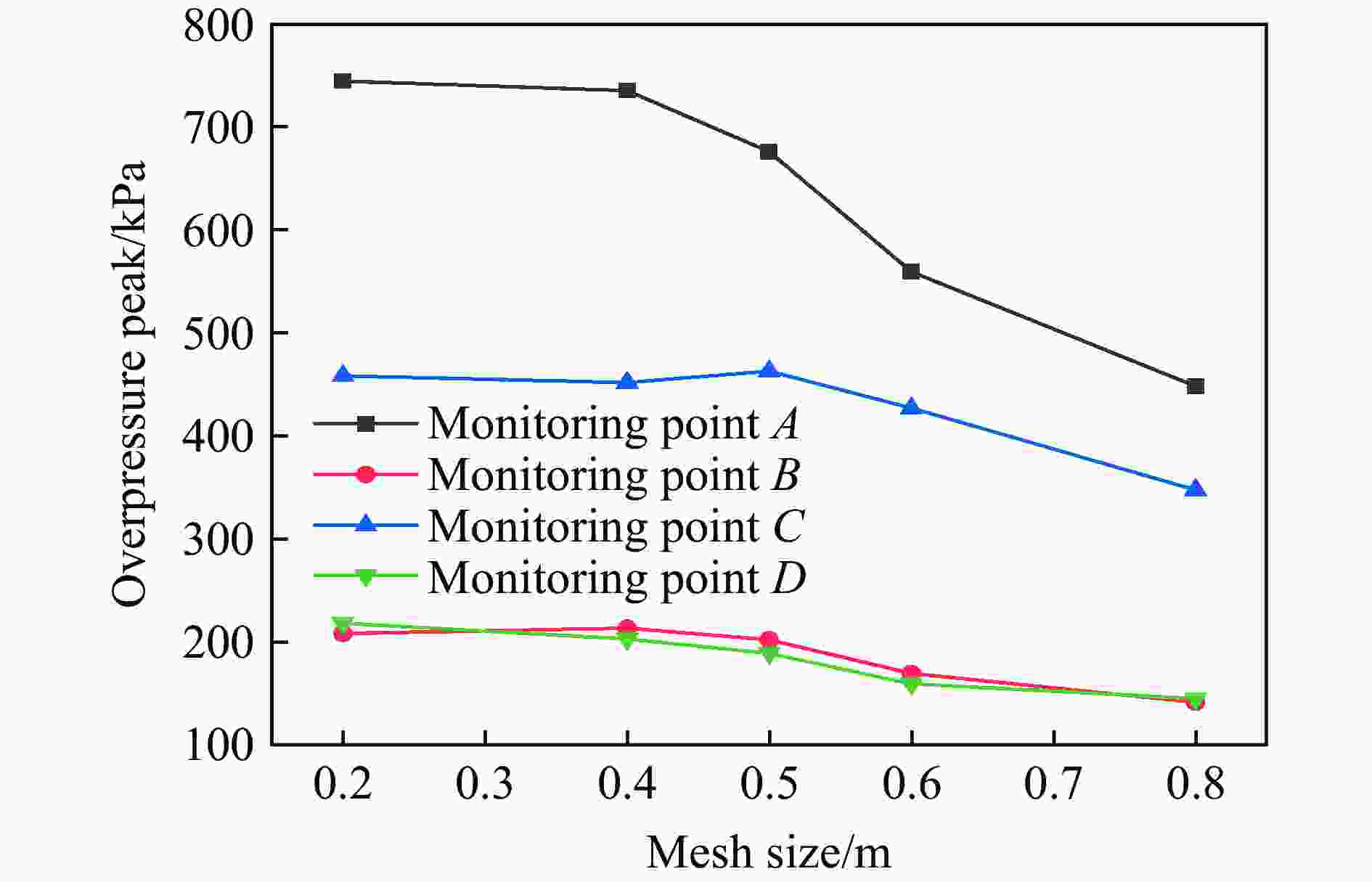
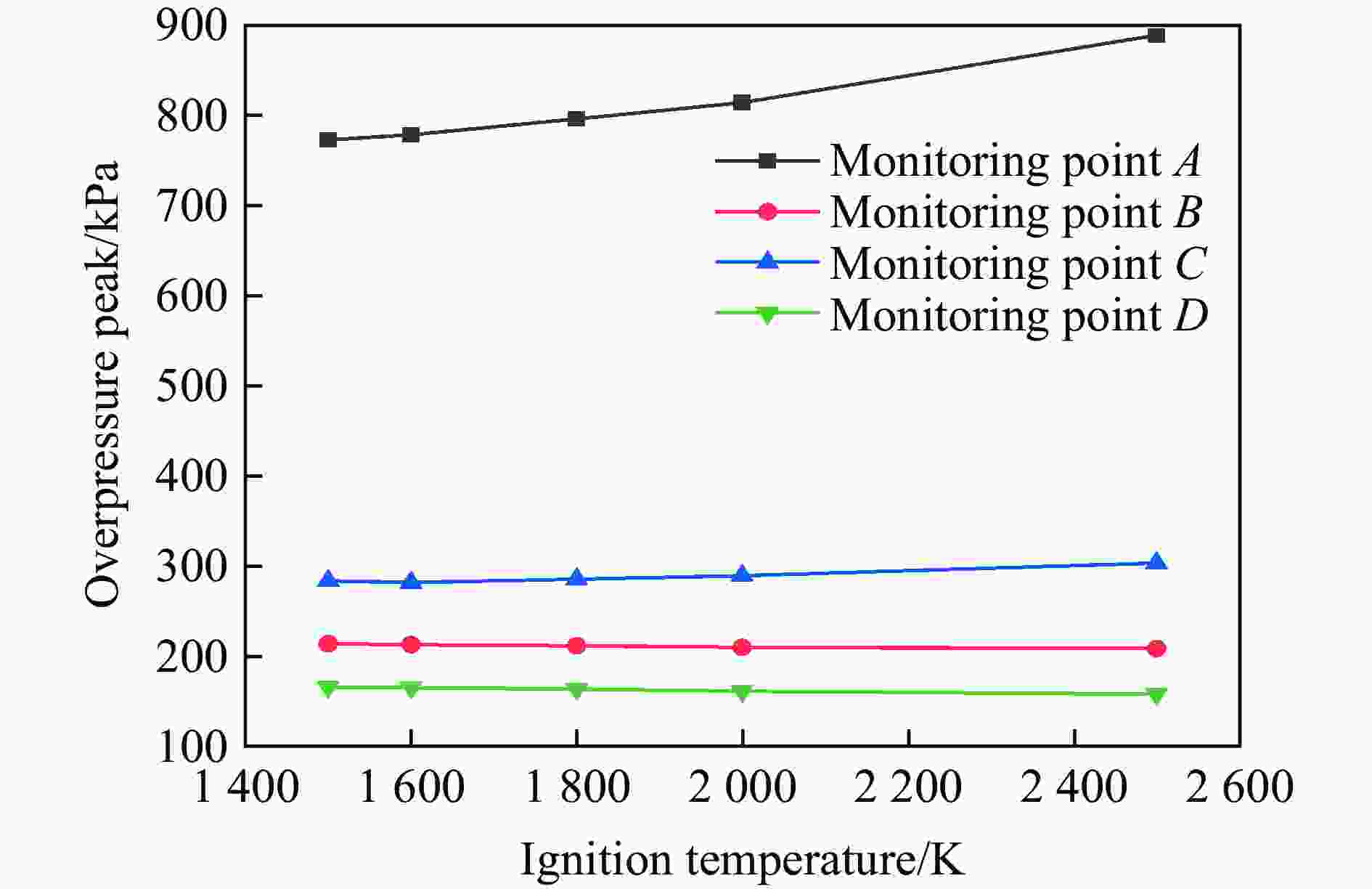
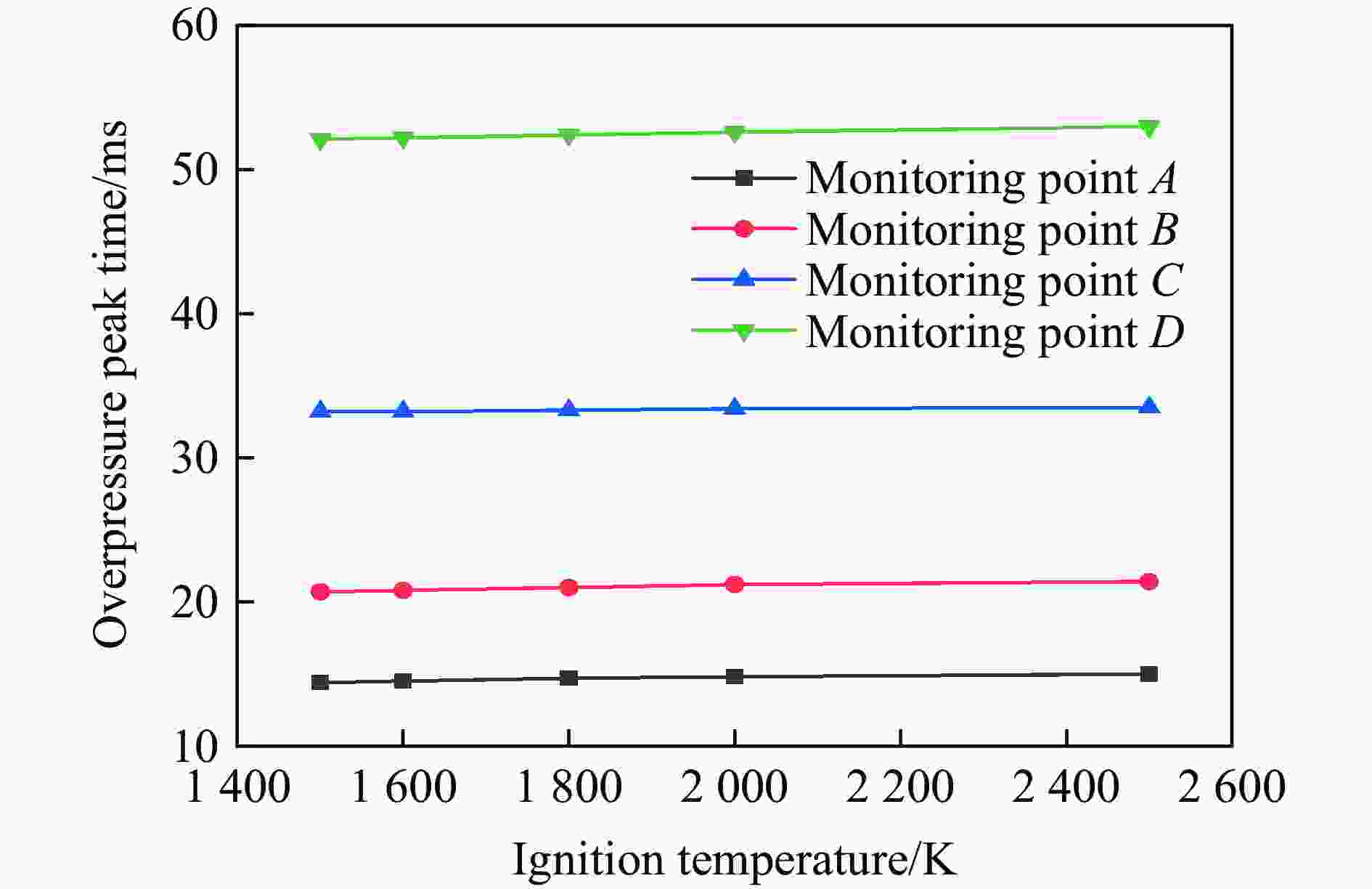
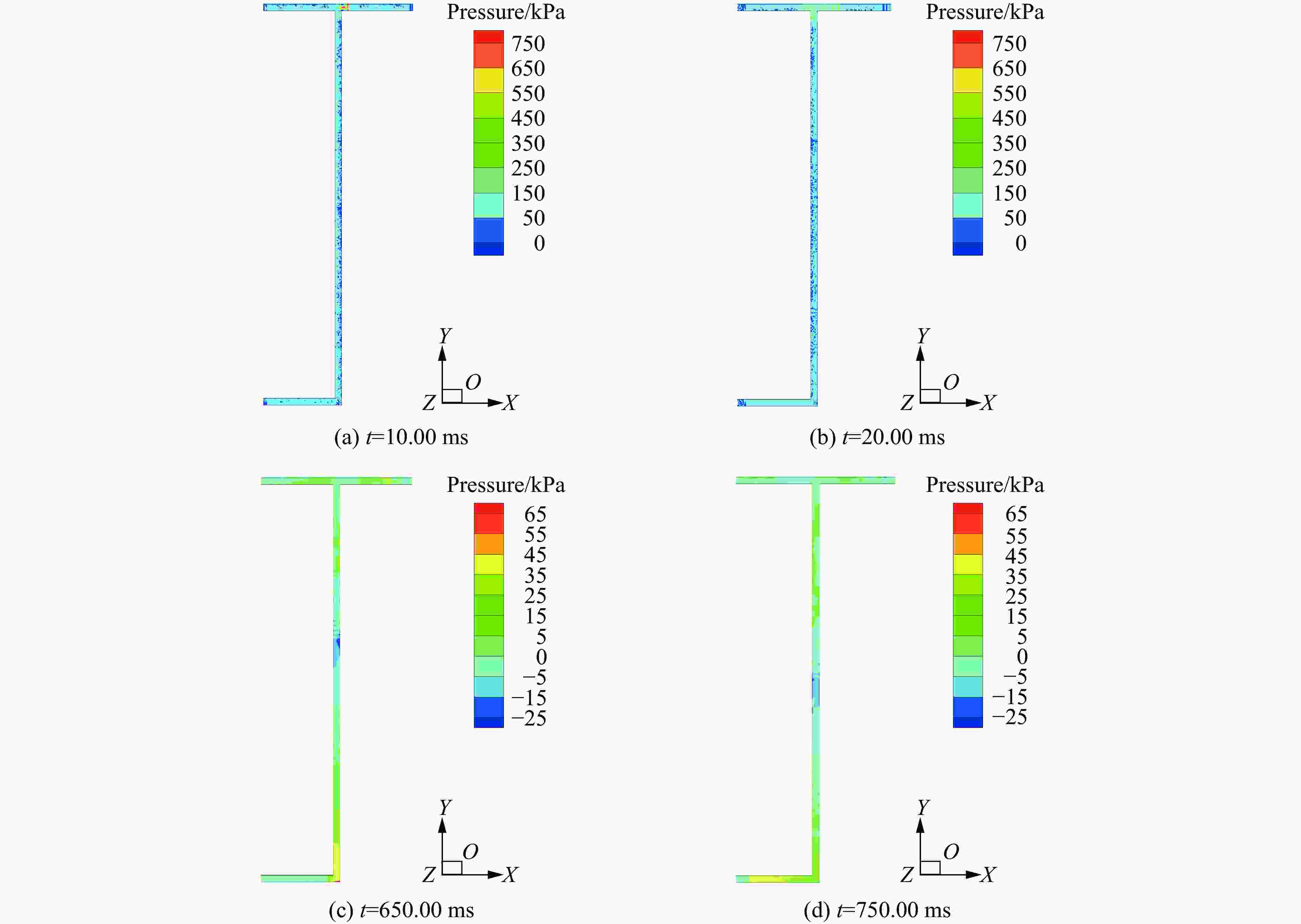
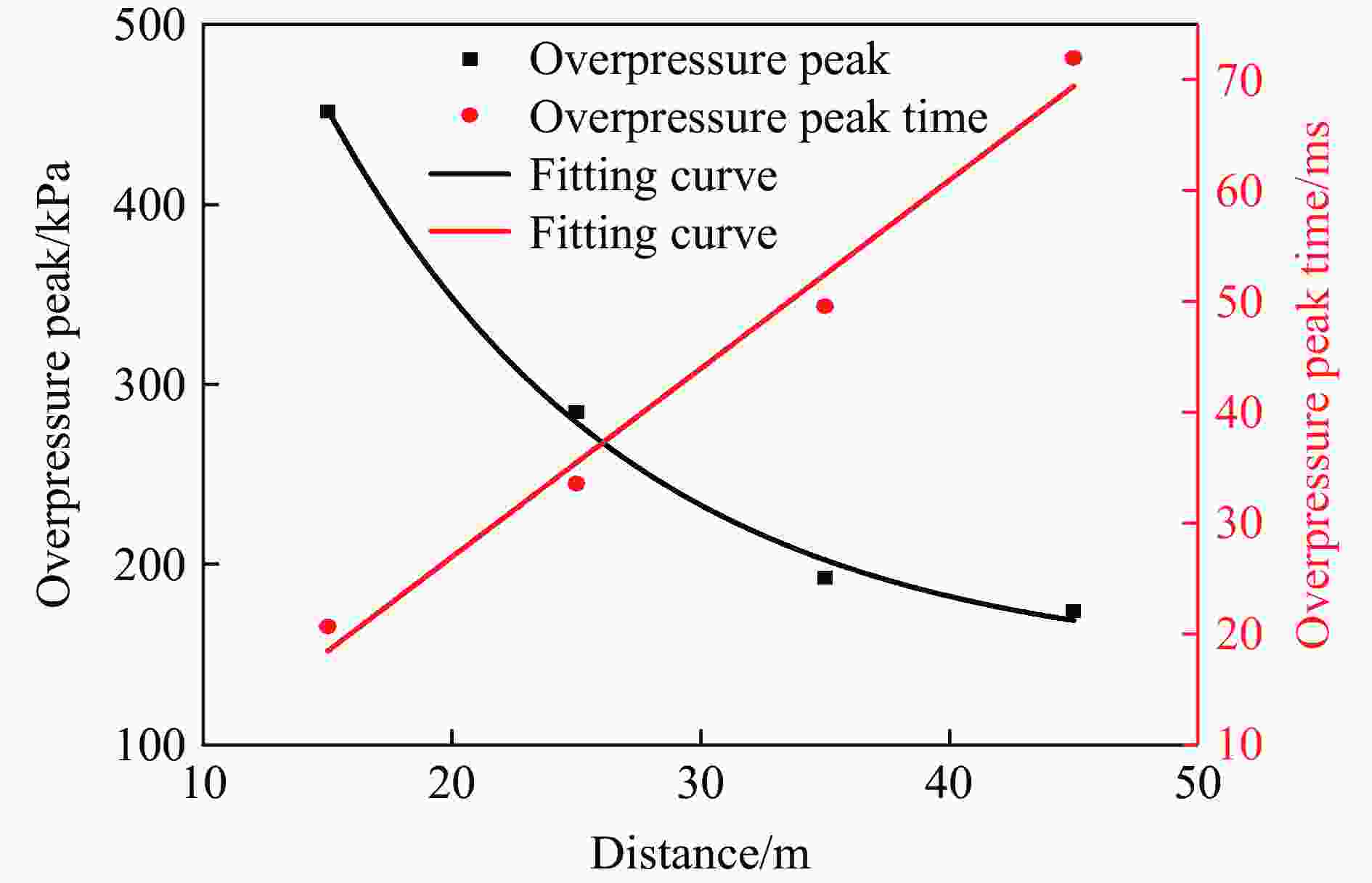
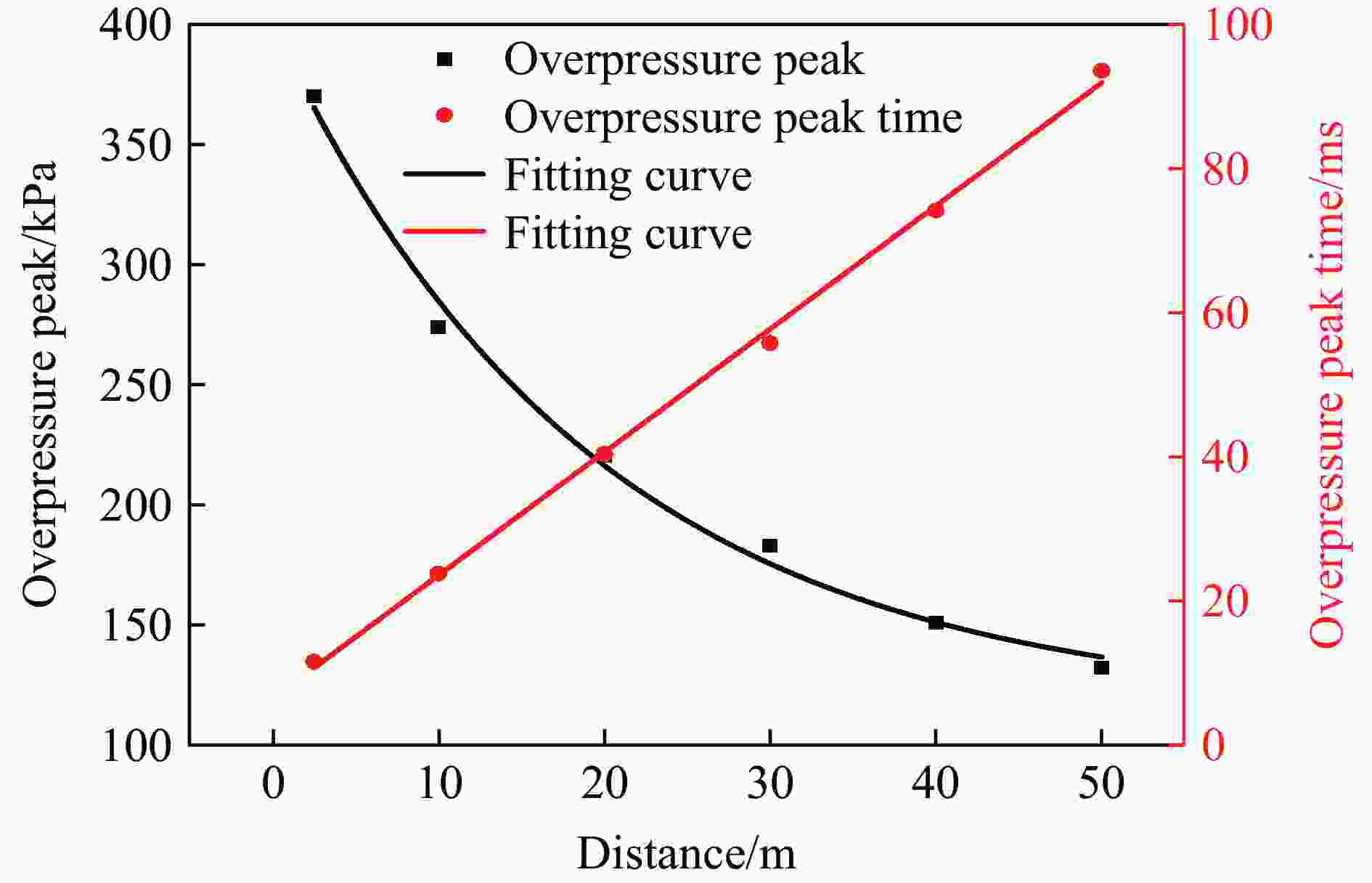
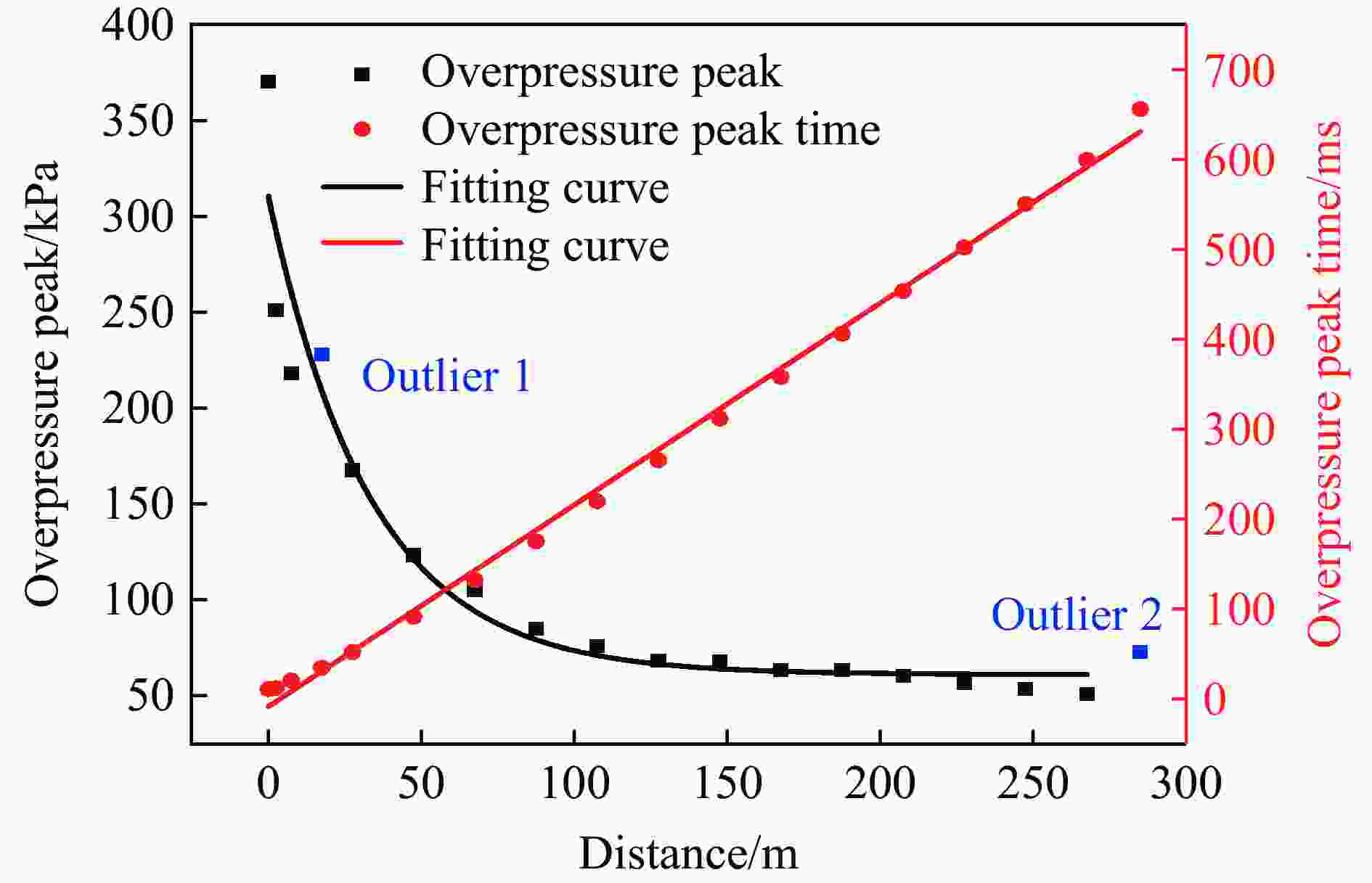
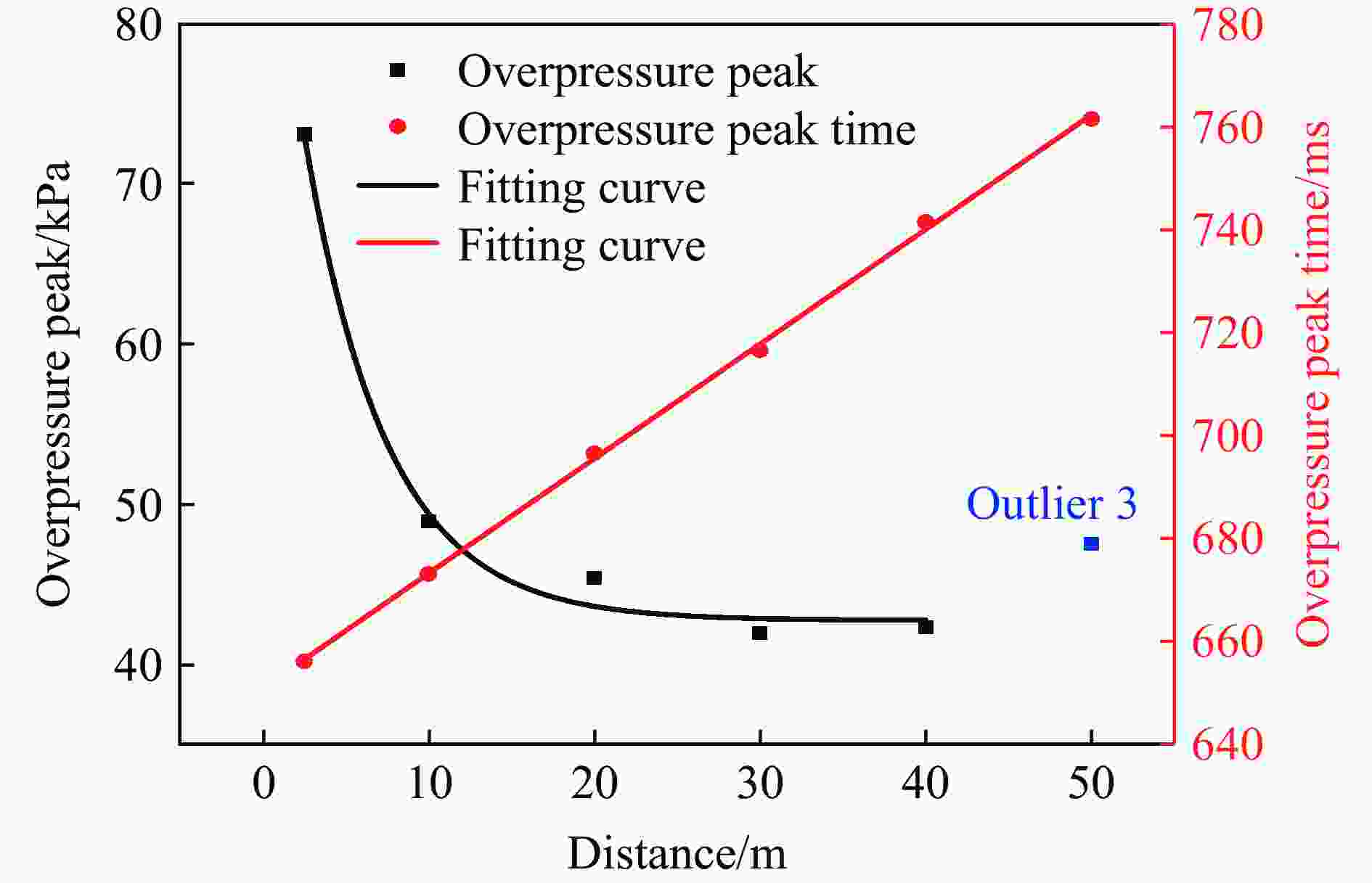
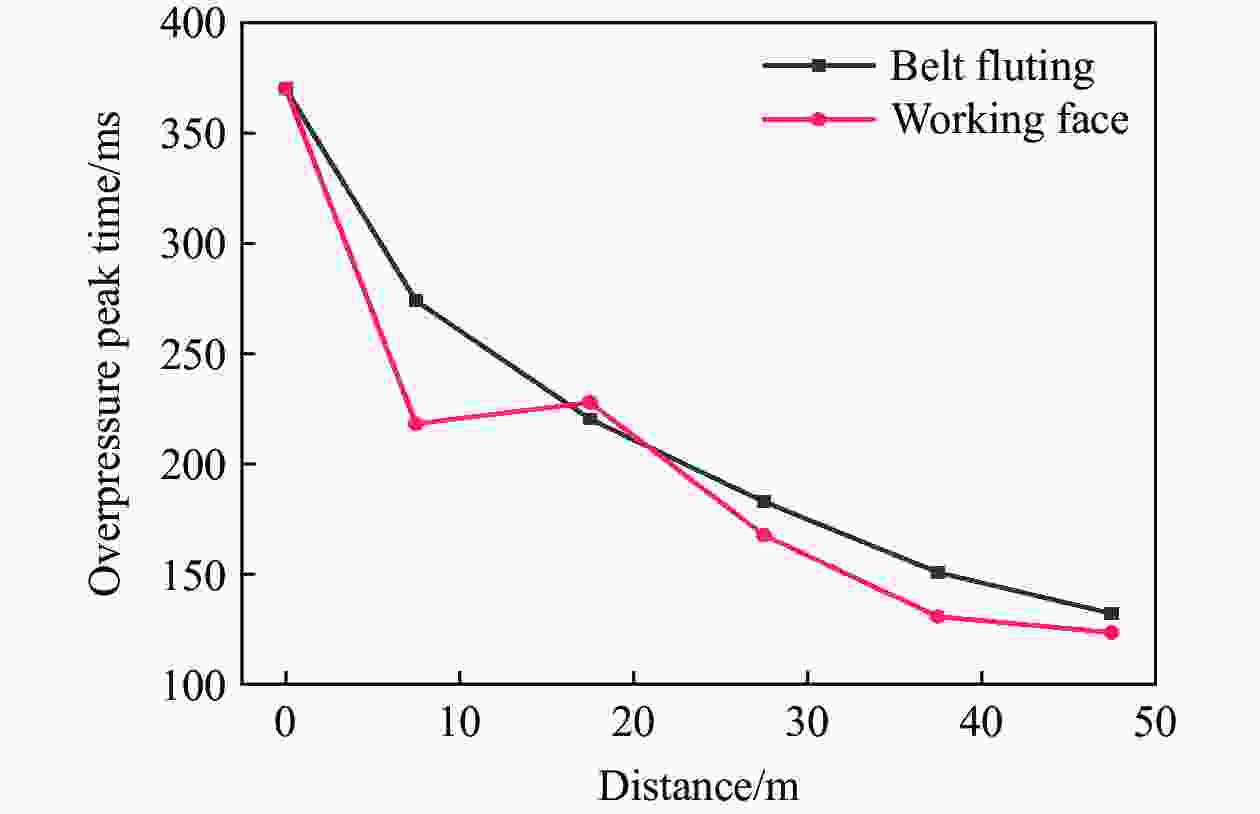
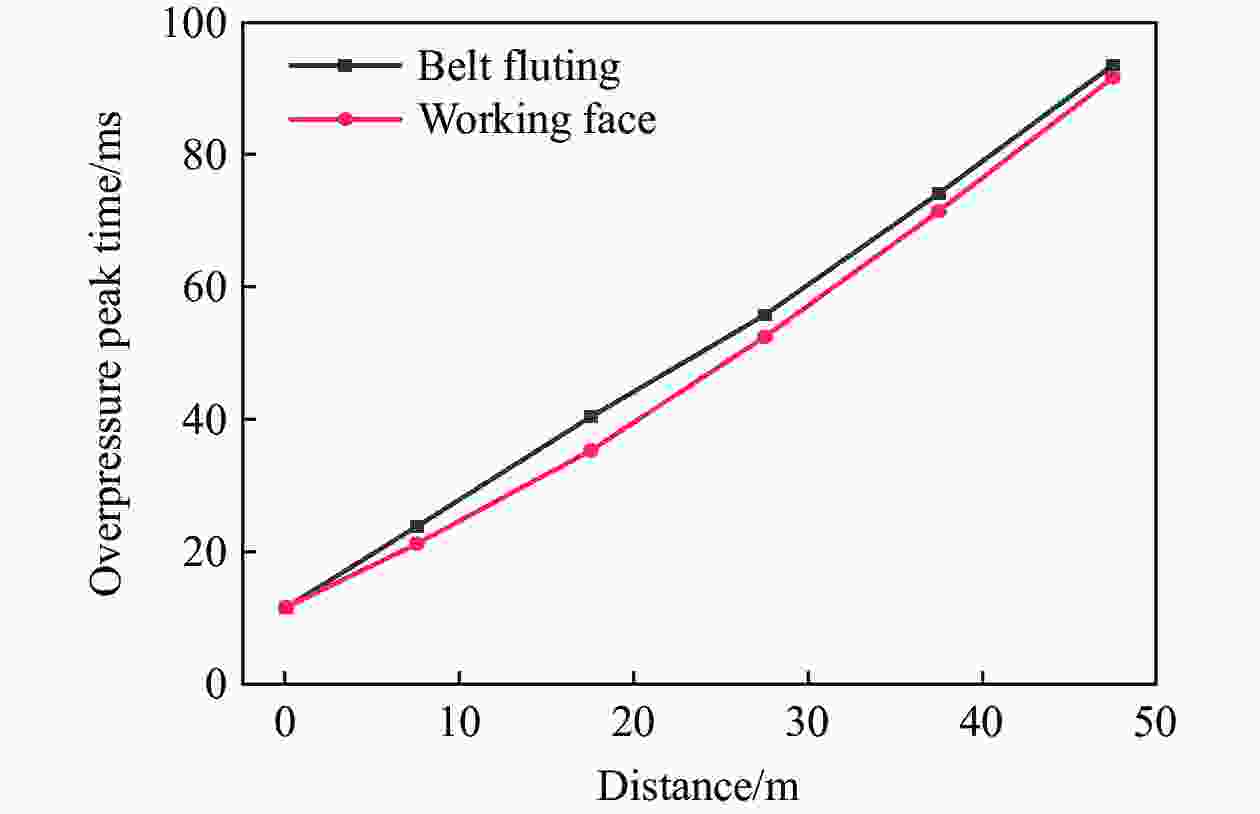
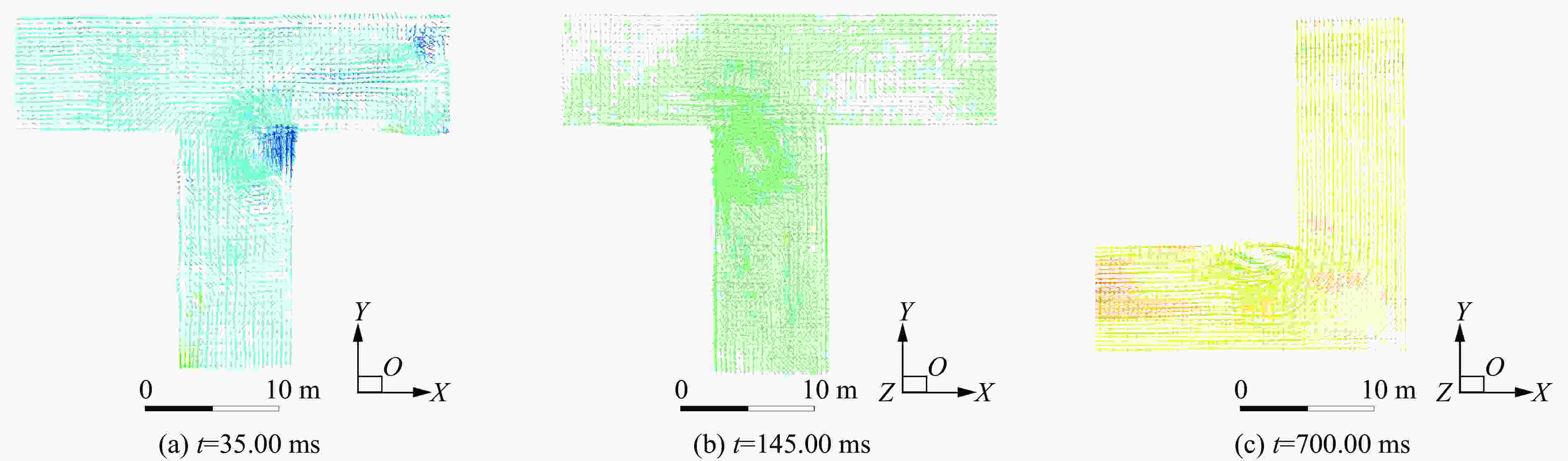
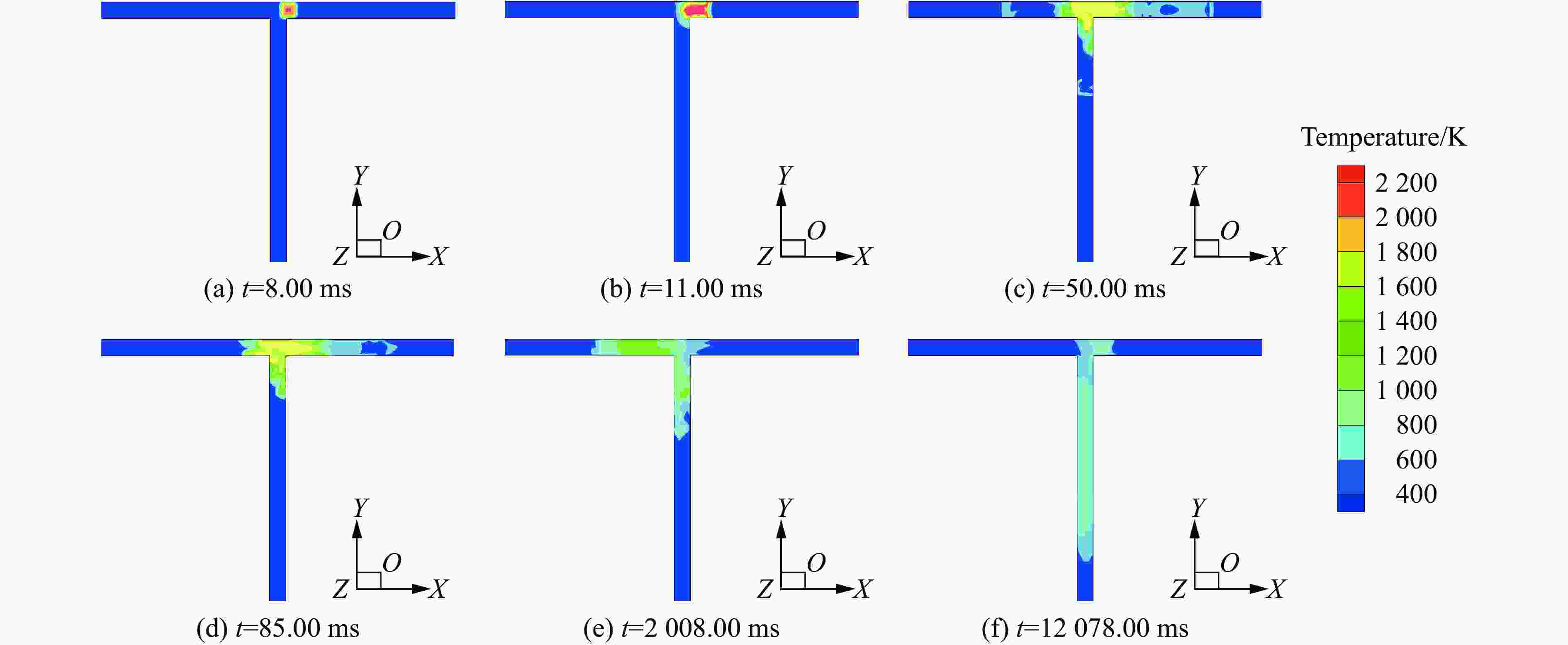
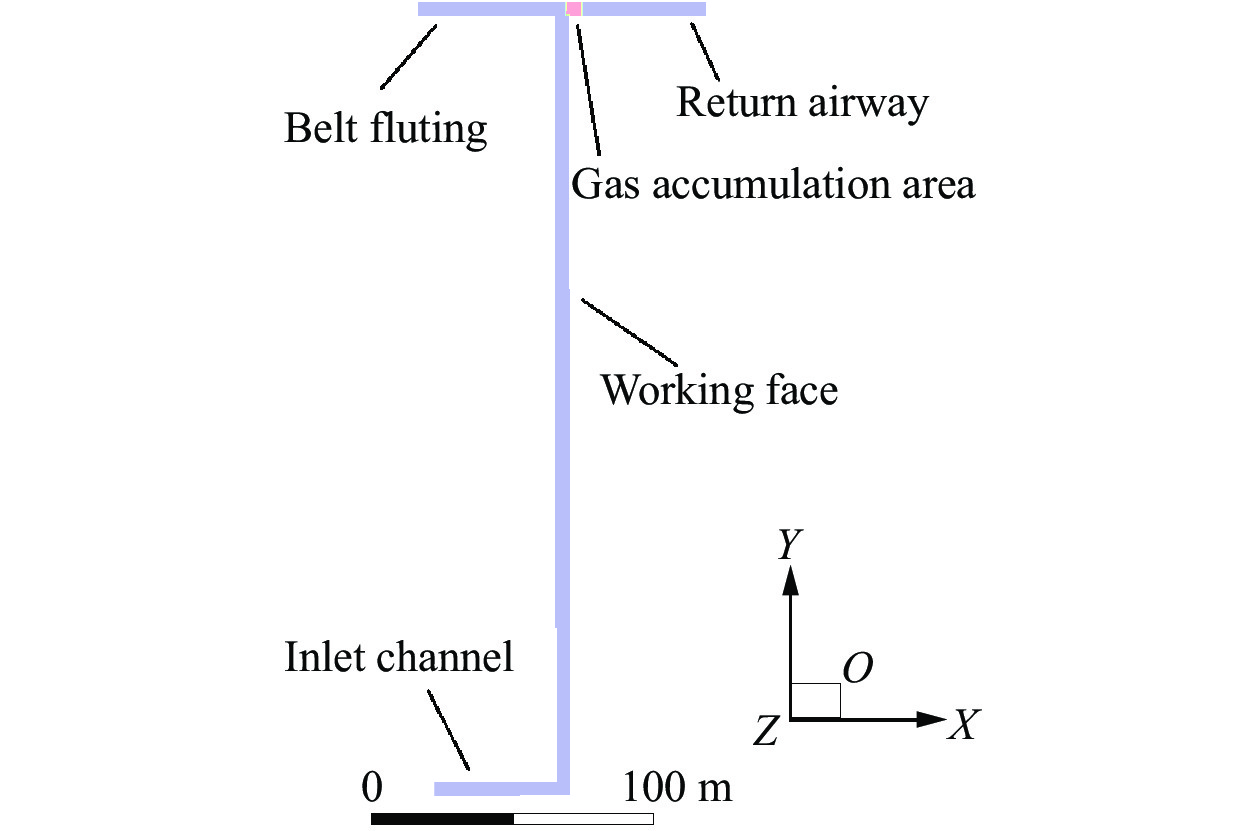
摘要: 针对Y型通风采煤工作面的瓦斯爆炸传播规律，利用Fluent模拟软件，结合余吾煤矿N2105工作面实际情况开展了数值模拟研究。结果表明：模拟结果与前人的实验结果之间的最大相对误差为11.3%，最小相对误差仅为1.7%，验证了数学模型的可靠性；确定了瓦斯爆炸数值模拟最合理的关键参数网格尺寸、迭代步长和点火温度分别为0.4 m、0.10 ms和1 800 K；进风顺槽、胶带顺槽、回风巷道和工作面的瓦斯爆炸超压峰值与爆源之间的距离符合指数函数关系，到达超压峰值所需时间与爆源之间的距离符合线性函数关系；距巷道分叉口7.5 m处，工作面超压衰减率为41.03%，胶带顺槽超压衰减率为25.99%，发生爆炸时胶带顺槽内更危险；工作面分叉处湍流区由右侧逐渐向左侧移动，且巷道分叉处超压峰值会增大；回风巷道火焰消散时间最短，胶带顺槽火焰消散时间次之，工作面火焰消散时间最长；胶带顺槽和回风巷道火焰消散方向与瓦斯爆炸初期火焰传播方向相反，工作面火焰消散方向与瓦斯爆炸初期火焰传播方向一致。
- Y型通风 /
- 采煤工作面 /
- 瓦斯爆炸 /
- 超压峰值 /
- 火焰传播
Abstract: To study the propagation law of gas explosion in a Y-shaped ventilated coal face, the simulation software of Fluent was used to carry out numerical simulation research combined with the actual situation of the N2105 working face in the Yuwu Coal Mine. Firstly, the reliability of the mathematical model in this paper was demonstrated. In addition, the simulation parameters were optimized to make the results fit the actual situation. Finally, a numerical simulation was carried out. The results show that the maximum error between the simulation results and the previous experimental results is 11.3%, and the minimum error is only 1.7%, which verifies the reliability of the mathematical model in this paper. The most reasonable key parameters for the numerical simulation of gas explosion were determined including mesh size, iteration step size and ignition temperature, which are 0.4 m, 0.10 ms and 1 800 K, respectively. The overpressure peak of the gas explosion in the air inlet channel, belt fluting, return airway, and working face and its distance from the explosion source accords with an exponential function, and the relationship between the time required to reach the overpressure peak and the distance from the explosion source is linear. The overpressure attenuation ratio of the working face is 41.03% at 7.5 m away from the tunnel bifurcation, and the overpressure attenuation ratio of the belt fluting is 25.99%. Belt fluting is more dangerous in the event of a gas explosion. In the bifurcation of the working face, the turbulent flow zone gradually moves from the right side to the left side, and the overpressure peak at the bifurcation of the roadway increases. The flame dissipation of the return airway is the fastest, followed by the flame dissipation of the belt fluting, and the flame dissipation of the working face is the slowest. The direction of the flame dissipation in the belt fluting and return airway is opposite to the direction of the flame propagation in the early stage of the gas explosion, while the direction of the flame dissipation in the working face is consistent with the direction of the flame propagation in the early stage of the gas explosion.
- Y-shaped ventilation /
- coal face /
- gas explosion /
- overpressure peak /
- flame propagation

HTML全文

图 1 余吾煤矿N2105工作面的三维物理模型

Figure 1. A 3D physical model of N2105 working face in Yuwu Coal Mine

下载: 全尺寸图片幻灯片

图 2 模拟管道示意图

Figure 2. Schematic diagram of simulated pipeline

下载: 全尺寸图片幻灯片

图 3 参数优化监测点示意图

Figure 3. Parameter optimization monitoring points

下载: 全尺寸图片幻灯片

图 4 超压峰值随网格尺寸的变化

Figure 4. Variations of overpressure peak with mesh size

下载: 全尺寸图片幻灯片

图 5 超压峰值到达时间随网格尺寸的变化

Figure 5. Variations of overpressure peak arrival time with mesh size

下载: 全尺寸图片幻灯片

图 6 超压峰值随迭代步长的变化

Figure 6. Variation of overpressure peak with time step

下载: 全尺寸图片幻灯片

图 7 超压峰值到达时间随迭代步长的变化

Figure 7. Variation of overpressure peak arrival time with time step

下载: 全尺寸图片幻灯片

图 8 超压峰值随点火温度的变化

Figure 8. Variation of overpressure peak with ignition temperature

下载: 全尺寸图片幻灯片

图 9 超压峰值到达时间随点火温度的变化

Figure 9. Variation of overpressure peak arrival time with ignition temperature

下载: 全尺寸图片幻灯片

图 10 瓦斯爆炸超压传播云图

Figure 10. Contours of gas explosion overpressure propagation

下载: 全尺寸图片幻灯片

图 11 回风巷道瓦斯爆炸传播规律

Figure 11. Gas explosion propagation law in return airway

下载: 全尺寸图片幻灯片

图 12 胶带顺槽瓦斯爆炸传播规律

Figure 12. Gas explosion propagation law along belt fluting

下载: 全尺寸图片幻灯片

图 13 工作面瓦斯爆炸传播规律

Figure 13. Gas explosion propagation law of working face

下载: 全尺寸图片幻灯片

图 14 进风顺槽瓦斯爆炸传播规律

Figure 14. Gas explosion propagation law in the inlet channel

下载: 全尺寸图片幻灯片

图 15 爆炸超压峰值对比

Figure 15. Comparison of gas explosion overpressure peaks

下载: 全尺寸图片幻灯片

图 16 爆炸超压峰值到达时间对比

Figure 16. Comparison of overpressure peak arrival time of gas explosion

下载: 全尺寸图片幻灯片

图 17 瓦斯爆炸超压矢量图

Figure 17. Vector diagrams of gas explosion overpressure

下载: 全尺寸图片幻灯片

图 18 火焰的温度云图

Figure 18. Contours of flame temperature variation

下载: 全尺寸图片幻灯片

表 1 爆炸超压模拟结果与实验结果的对比

Table 1. Comparison between simulation and experimental results of explosion overpressure

爆心距/m	爆炸超压/kPa		相对误差/%
爆心距/m	实验	模拟	相对误差/%
2.0	181.850	193.915	6.6
2.5	178.860	175.819	–1.7
3.0	167.663	156.085	–6.9
3.5	159.170	141.142	–11.3
4.0	139.672	129.495	–7.3
4.5	120.682	117.704	–2.4

下载: 导出CSV

表 2 网格分布

Table 2. Grid distribution

网格尺寸/m	网格节点数	网格数	平均网格质量
0.8	24 402	17 535	0.985
0.6	48 188	36 834	0.996
0.5	77 528	61 600	1.000
0.4	154 280	128 817	0.999
0.2	1 087 294	990 000	0.999

下载: 导出CSV

参考文献(29)

[1]	中国能源中长期发展战略研究项目组. 中国能源中长期2030—2050发展战略研究 [M]. 北京: 科学出版社, 2011.
[2]	EMAMI S D, RAJABI M, HASSAN C R C, et al. Experimental study on premixed hydrogen/air and hydrogen-methane/air mixtures explosion in 90 degree bend pipeline [J]. International Journal of Hydrogen Energy, 2013, 38(32): 14115–14120. DOI: 10.1016/j.ijhydene.2013.08.056.
[3]	BLANCHARD R, ARNDT D, GRATZ R, et al. Explosions in closed pipes containing baffles and 90 degree bends [J]. Journal of Loss Prevention in the Process Industries, 2010, 23(2): 253–259. DOI: 10.1016/j.jlp.2009.09.004.
[4]	孟显华, 谢岩森. 甲烷体积分数及巷道结构对甲烷爆炸特性影响研究 [J]. 中国安全科学学报, 2021, 31(S1): 136–142. DOI: 10.16265/j.cnki.issn1003-3033.2021.S1.024. MENG X H, XIE Y S. Study on influence of methane’s volume fraction and roadway structure on methane explosion characteristics [J]. China Safety Science Journal, 2021, 31(S1): 136–142. DOI: 10.16265/j.cnki.issn1003-3033.2021.S1.024.
[5]	YUAN X Q, ZHOU J, LIN Z Y, et al. Numerical study of detonation diffraction through 90-degree curved channels to expansion area [J]. International Journal of Hydrogen Energy, 2017, 42(10): 7045–7059. DOI: 10.1016/j.ijhydene.2017.01.206.
[6]	CAO X Y, FAN L T, CUI Y Y, et al. Effect of connected vessels structure on methane explosion characteristics [J]. Journal of Loss Prevention in the Process Industries, 2022, 77: 104789. DOI: 10.1016/j.jlp.2022.104789.
[7]	ZHANG L L, YANG Q Y, SHI B M, et al. Influences of a pipeline’s bending angle on the propagation law of coal dust explosion induced by gas explosion [J]. Combustion Science and Technology, 2021, 193(5): 798–811. DOI: 10.1080/00102202.2019.1673381.
[8]	QIU J W, JIANG B Y, TANG M Y, et al. Effect of different bend pipes on the propagation characteristics of premixed methane-air explosion in confined spaces [J]. Geofluids, 2021, 2021: 6635156. DOI: 10.1155/2021/6635156.
[9]	LIU J J, ZHANG Y, CHEN S Q, et al. Simulation study of gas explosion propagation law in coal mining face with different ventilation modes [J]. Frontiers in Energy Research, 2022, 10: 846500. DOI: 10.3389/fenrg.2022.846500.
[10]	马恒, 陈晓军, 荆德吉. H型通风巷道瓦斯爆炸及泄爆过程模拟研究 [J]. 中国安全科学学报, 2021, 31(1): 45–51. DOI: 10.16265/j.cnki.issn1003-3033.2021.01.007. MA H, CHEN X J, JING D J. Simulation study on gas explosion and discharge process in H-type ventilation roadway [J]. China Safety Science Journal, 2021, 31(1): 45–51. DOI: 10.16265/j.cnki.issn1003-3033.2021.01.007.
[11]	高建良, 吴泽琳, 王文祺, 等. 瓦斯爆炸冲击波在角、并联巷道内传播规律对比研究 [J]. 安全与环境学报, 2021, 21(6): 2494–2499. DOI: 10.13637/j.issn.1009-6094.2020.1012. GAO J L, WU Z L, WANG W Q, et al. Comparative study on the propagation law of gas explosion shock wave in the diagonal and parallel roadway [J]. Journal of Safety and Environment, 2021, 21(6): 2494–2499. DOI: 10.13637/j.issn.1009-6094.2020.1012.
[12]	高智慧, 李雨成, 张欢, 等. 瓦斯爆炸在角联通风管网中的传播特性研究 [J]. 中国安全生产科学技术, 2022, 18(8): 72–78. DOI: 10.11731/j.issn.1673-173x.2022.07.001. GAO Z H, LI Y C, ZHANG H, et al. Study on propagation characteristics of gas explosion in diagonal ventilation pipe network [J]. Journal of Safety Science and Technology, 2022, 18(8): 72–78. DOI: 10.11731/j.issn.1673-173x.2022.07.001.
[13]	景国勋, 朱斯佳, 贺祥. 不同封闭情况下T型中瓦斯爆炸传播规律实验研究 [J]. 中国安全生产科学技术, 2021, 17(7): 84–90. DOI: 10.11731/j.issn.1673-193x.2021.07.014. JING G X, ZHU S J, HE X. Experimental study on propagation laws of gas explosion in T-shaped pipe under different enclosed conditions [J]. Journal of Safety Science and Technology, 2021, 17(7): 84–90. DOI: 10.11731/j.issn.1673-193x.2021.07.014.
[14]	丁浩, 杜玉晶, 解北京. 负压腔体抑制T型瓦斯爆炸数值模拟 [J]. 煤矿安全, 2021, 52(7): 1–8. DOI: 10.13347/j.cnki.mkaq.2021.07.001. DING H, DU Y J, XIE B J. Numerical simulation of negative pressure cavity suppression of T-pipe gas explosion [J]. Safety in Coal Mines, 2021, 52(7): 1–8. DOI: 10.13347/j.cnki.mkaq.2021.07.001.
[15]	YAN Z, YUAN S, LI Z, et al. Study on inhibitory effect of cavity on gas explosion propagation [J]. Geofluids, 2021, 2021: 6674425. DOI: 10.1155/2021/6674425.
[16]	周辉, 穆朝民, 刘伟, 等. 空腔体长度对抑制瓦斯爆炸性能的影响研究 [J]. 中国安全科学学报, 2019, 29(9): 107–112. DOI: 10.16265/j.cnki.issn1003-3033.2019.09.017. ZHOU H, MU C M, LIU W, et al. Influence of cavity length on gas explosion suppression [J]. China Safety Science Journal, 2019, 29(9): 107–112. DOI: 10.16265/j.cnki.issn1003-3033.2019.09.017.
[17]	时本军, 穆朝民, 马海峰, 等. 腔体影响全巷道甲烷爆炸冲击波传播的特性 [J]. 煤炭学报, 2020, 45(S2): 841–849. DOI: 10.13225/j.cnki.jccs.2020.0791. SHI B J, MU C M, MA H F, et al. Cavity effect on the characteristics of methane blast wave propagation in the whole roadway [J]. Journal of China Coal Society, 2020, 45(S2): 841–849. DOI: 10.13225/j.cnki.jccs.2020.0791.
[18]	WANG J, WU Y, ZHENG L G, et al, Study on the propagation characteristics of hydrogen/methane/air premixed flames in variable cross-section ducts [J]. Process Safety and Environmental Protection, 2020, 135: 135–143. DOI: 10.1016/j.psep.2019.12.029.
[19]	LI Z, CHEN L, YAN H C, et al. Gas explosions of methane-air mixtures in a large-scale tube [J]. Fuel, 2021, 285: 119239. DOI: 10.1016/j.fuel.2020.119239.
[20]	GAO K, LIU Z Y, WU C Q, et al. Effect of low gas concentration in underground return tunnels on characteristics of gas explosions [J]. Process Safety and Environmental Protection, 2021, 152: 679–691. DOI: 10.1016/j.psep.2021.06.045.
[21]	罗振敏, 刘利涛, 王涛, 等. C₂H₆、C₂H₄、CO与H₂对甲烷爆炸压力及动力学特性影响 [J]. 工程科学学报, 2022, 44(3): 339–347. DOI: 10.13374/j.issn2095-9389.2020.10.22.002. LUO Z M, LIU L T, WANG T, et al. Effect of C₂H₆, C₂H₄, CO and H₂ on the explosion pressure and kinetic characteristics of methane [J]. Chinese Journal of Engineering, 2022, 44(3): 339–347. DOI: 10.13374/j.issn2095-9389.2020.10.22.002.
[22]	梁国栋. 2种气体状态下瓦斯爆炸极限范围的研究 [J]. 现代矿业, 2019, 35(9): 211–213. DOI: 10.3969/j.issn1674-6082.2019.09.064. LIANG G D. Study on the limit range of gas explosion in two kinds of gas conditions [J]. Modern Mining, 2019, 35(9): 211–213. DOI: 10.3969/j.issn1674-6082.2019.09.064.
[23]	贾泉升, 司荣军, 李润之, 等. 定容条件下瓦斯爆炸超压及爆后气体成分试验研究 [J]. 煤矿安全, 2019, 50(12): 1–5. DOI: 10.13347/j.cnki.mkaq.2019.12.001. JIA Q S, SI R J, LI R Z, et al. Experimental study on overpressure and gas composition after gases explosion under constant volume condition [J]. Safety in Coal Mines, 2019, 50(12): 1–5. DOI: 10.13347/j.cnki.mkaq.2019.12.001.
[24]	任搴华, 赵耀江, 周家川. Y型通风系统采空区漏风规律相似模拟实验研究 [J]. 中国煤炭, 2012, 38(3): 98–101. DOI: 10.19880/j.cnki.ccm.2012.03.026. REN Q H, ZHAO Y J, ZHOU J C. Similar simulation of air leakage law in goaf with Y-shape ventilation system [J]. China Coal, 2012, 38(3): 98–101. DOI: 10.19880/j.cnki.ccm.2012.03.026.
[25]	徐景德. 矿井瓦斯爆炸冲击波传播规律及影响因素的研究 [D]. 北京: 中国矿业大学, 2003: 31–33. XU J D. The study on gas explosion wave propagation law and affected factors in mine [D]. Beijing, China: China University of Mining and Technology, 2013: 31–33.
[26]	陈鹏, 李艳超, 黄福军, 等. 方孔障碍物对瓦斯火焰传播影响的实验与大涡模拟 [J]. 爆炸与冲击, 2017, 37(1): 21–26. DOI: 10.11883/1001-1455(2017)01-0021-06. CHEN P, LI Y C, HUANG F J, et al. LES approach to premixed methane/air flame propagating in the closed duct with a square-hole obstacle [J]. Explosion and Shock Waves, 2017, 37(1): 21–26. DOI: 10.11883/1001-1455(2017)01-0021-06.
[27]	李蒙, 杜扬, 李国庆, 等. 含90°直角弯管结构受限空间油气泄压爆炸实验与大涡模拟研究 [J]. 化工学报, 2018, 69(12): 5370–5378. DOI: 10.11949/j.issn.0438-1157.20180519. LI M, DU Y, LI G Q, et al. Experimental and large eddy simulation study on gasoline-air mixture explosions in semi-confined pipe with 90º right-angle bend [J]. CIESC Journal, 2018, 69(12): 5370–5378. DOI: 10.11949/j.issn.0438-1157.20180519.
[28]	温小萍, 余明高, 邓浩鑫, 等. 小尺度受限空间内瓦斯湍流爆燃大涡模拟 [J]. 化工学报, 2016, 67(5): 1837–1843. DOI: 10.11949/j.issn.0438-1157.20151219. WEN X P, YU M G, DENG H X, et al. Large eddy simulation of gas turbulent deflagration in small-scale confined space [J]. CIESC Journal, 2016, 67(5): 1837–1843. DOI: 10.11949/j.issn.0438-1157.20151219.
[29]	洪溢都, 林柏泉, 朱传杰. 开口型内瓦斯爆炸冲击波动压的数值模拟 [J]. 爆炸与冲击, 2016, 36(2): 198–209. DOI: 10.11883/1001-1455(2016)02-0198-12. HONG Y D, LIN B Q, ZHU C J. Simulation on dynamic pressure of premixed methane/air explosion in open-end pipes [J]. Explosion and Shock Waves, 2016, 36(2): 198–209. DOI: 10.11883/1001-1455(2016)02-0198-12.