Theoretical study on the dynamic response of rectangular liquid storage structure under explosion-induced ground shock
-
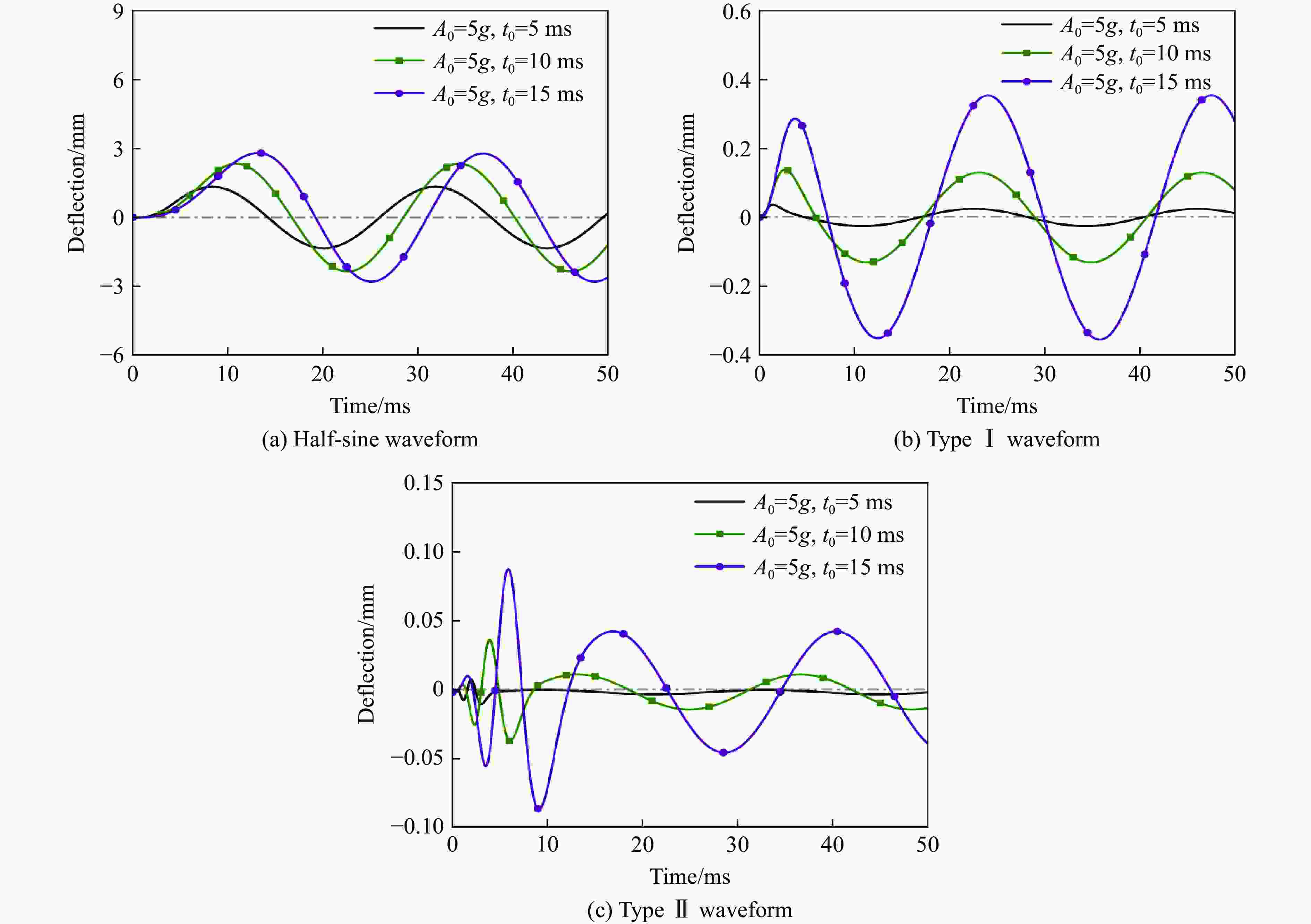
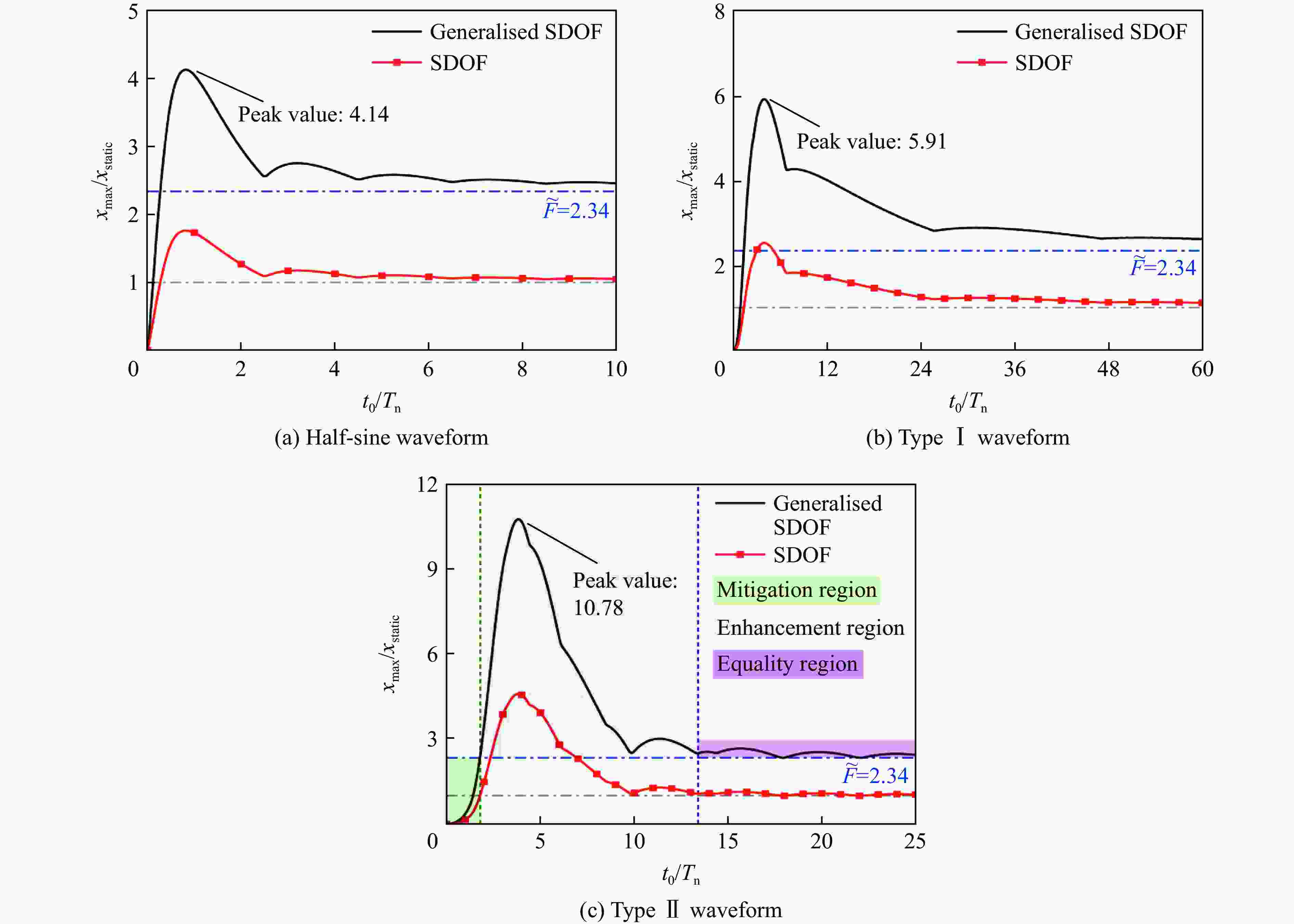
摘要: 为完善防护工程储液结构设计与评估体系，开展了爆炸冲击地震动作用下储液结构动力响应理论研究。将矩形储液结构简化为具有分布弹性的广义单自由度体系，采用虚功原理建立水平地震动下结构运动方程，通过双向梁函数组合法、Rayleigh法和Duhamel积分法分别得到储液结构壁板振型、振动频率和动力响应，进而构建地震响应谱。利用爆炸冲击震动模拟平台开展模型试验，结构测点应变、动水压力计算值与试验数据基本一致，验证了理论方法。通过算例分析储液率、地震动要素对模型结构动力响应的影响，构建爆炸地震动下储液结构挠度响应谱，结果表明：随储液率增加，结构基频降低，地震动激励特征因子先提高后降低，后者反映流固耦合对地震作用的强化效应先增强后减弱；弹性范围内，随地震动加速度峰值提高，结构挠度响应线性提高；地震动加速度持时和波形改变影响频谱特性，使挠度响应发生非线性变化；典型波形爆炸地震动的作用效果均可划分为相对于等效静力作用的缓和区、增强区和等效区；以响应谱峰值作为最不利响应进行防护设计偏于保守，考虑场地爆炸参数范围进行计算可提高工程设计的经济性。Abstract: To improve the design and evaluation system of liquid storage structure (LSS) in protection engineering, theoretical research on the dynamic response of LSS subjected to explosion-induced ground shock has been carried out. The rectangular LSS was simplified into a generalised single-degree-of-freedom system with distributed elasticity. The motion equation under horizontal ground shock was established based on the virtual work principle. The vibration mode function, vibration frequency, and dynamic response of the rectangular plate were obtained using the two-way beam function combination, the Rayleigh method, and the Duhamel’s integration method, respectively. The influences of liquid filling ratio, and ground-shock essentials (i.e. the peak, duration, waveform of ground acceleration) on the dynamic response of the model LSS were analysed by calculation examples. The maximum deflection was used as an index to build the dynamic response spectrum of the LSS subjected to explosion-induced ground shocks. The results showed that, with the increase of liquid filling ratio, the fundamental frequency of the structure decreases, and the characteristic factor of ground motion excitation first increase and then decrease. The latter reflects that the strengthening effect of fluid-structure interaction on seismic action is first enhanced and then weakened. Within the elastic range, as the peak value of ground acceleration increases, the deflection response of the LSS increases linearly. The varations in the duration and waveform of ground acceleration affect the spectrum characteristics, causing the nonlinear changes of deflection response. The effects of explosion-induced ground shocks featured by various typical waveforms can be divided into the mitigation, enhancement, and equality regions relative to the equivalent static action. It is conservative to take the peak of response spectrum as the most adverse response for protection design, whereas the calculation considering the range of site explosion parameters would improve the economy of engineering design. The proposed simplified theoretical method meets the requirement of preliminary rapid calculation and provides a reference for the protection design of LSS.
-
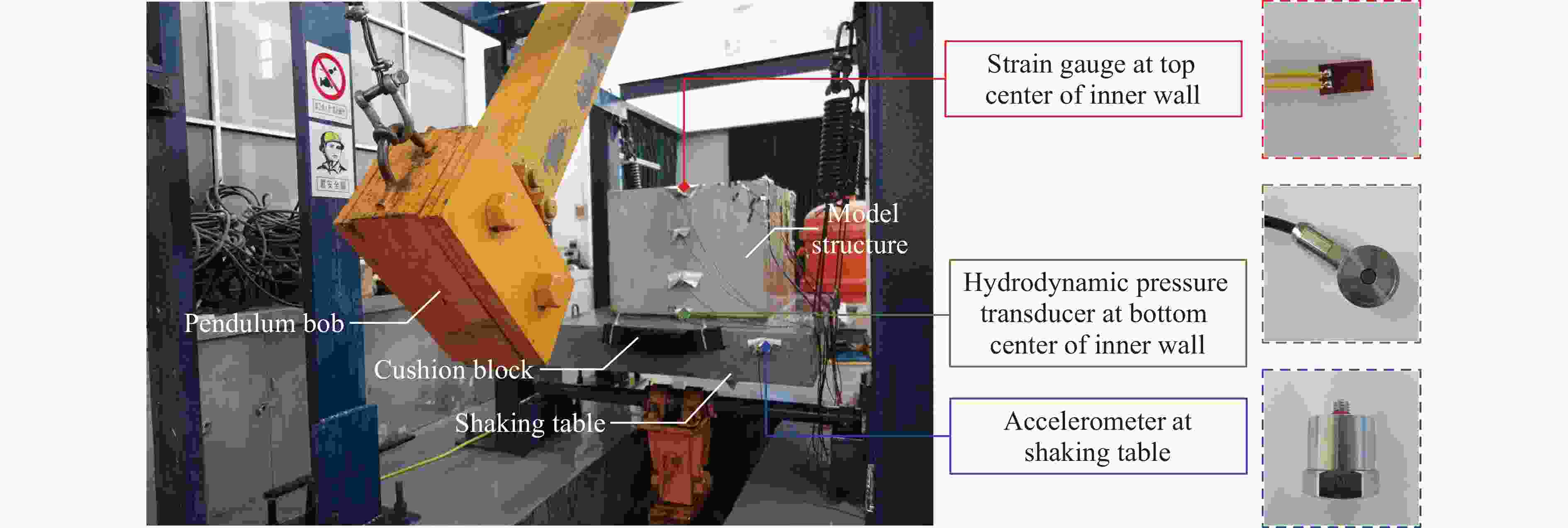
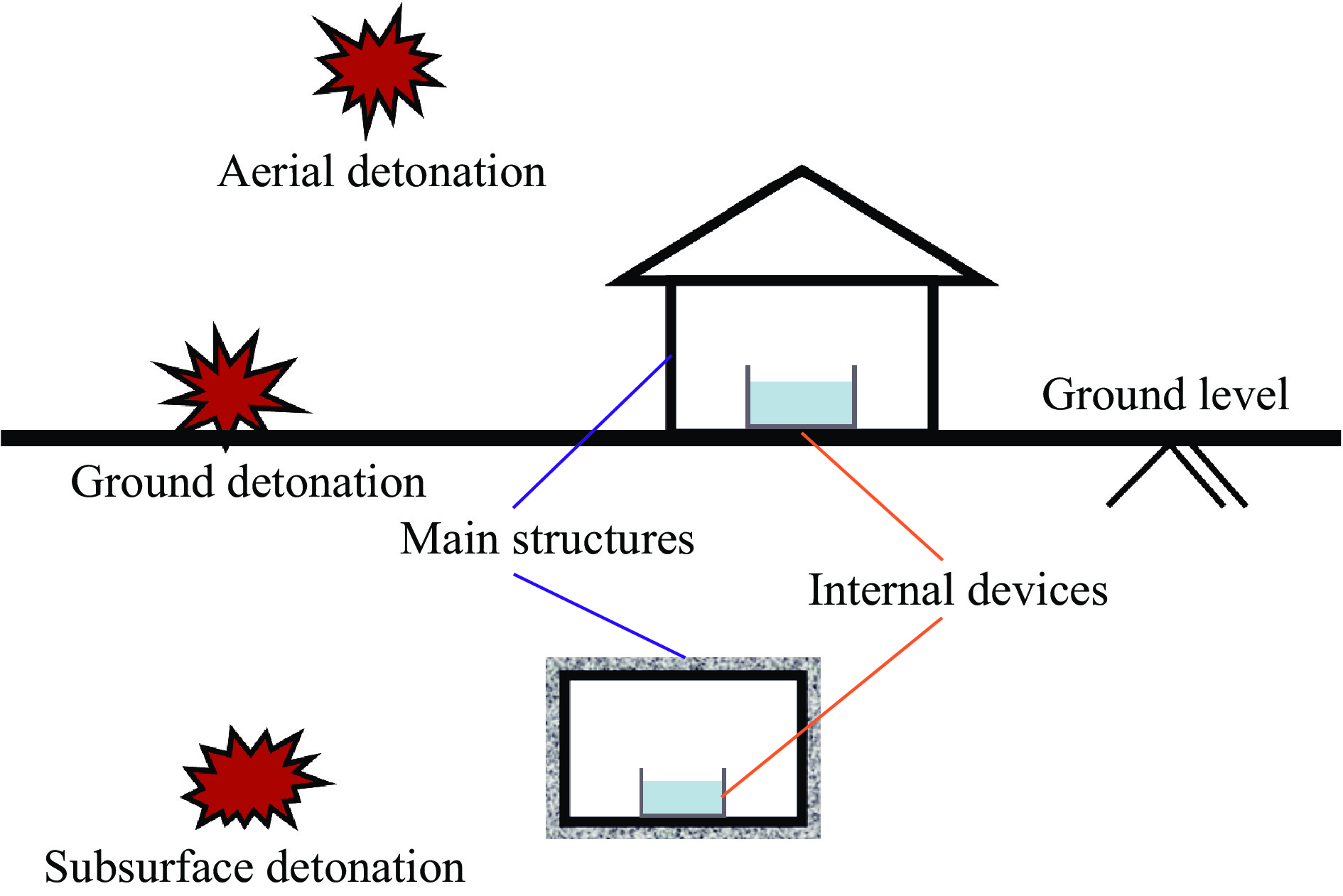
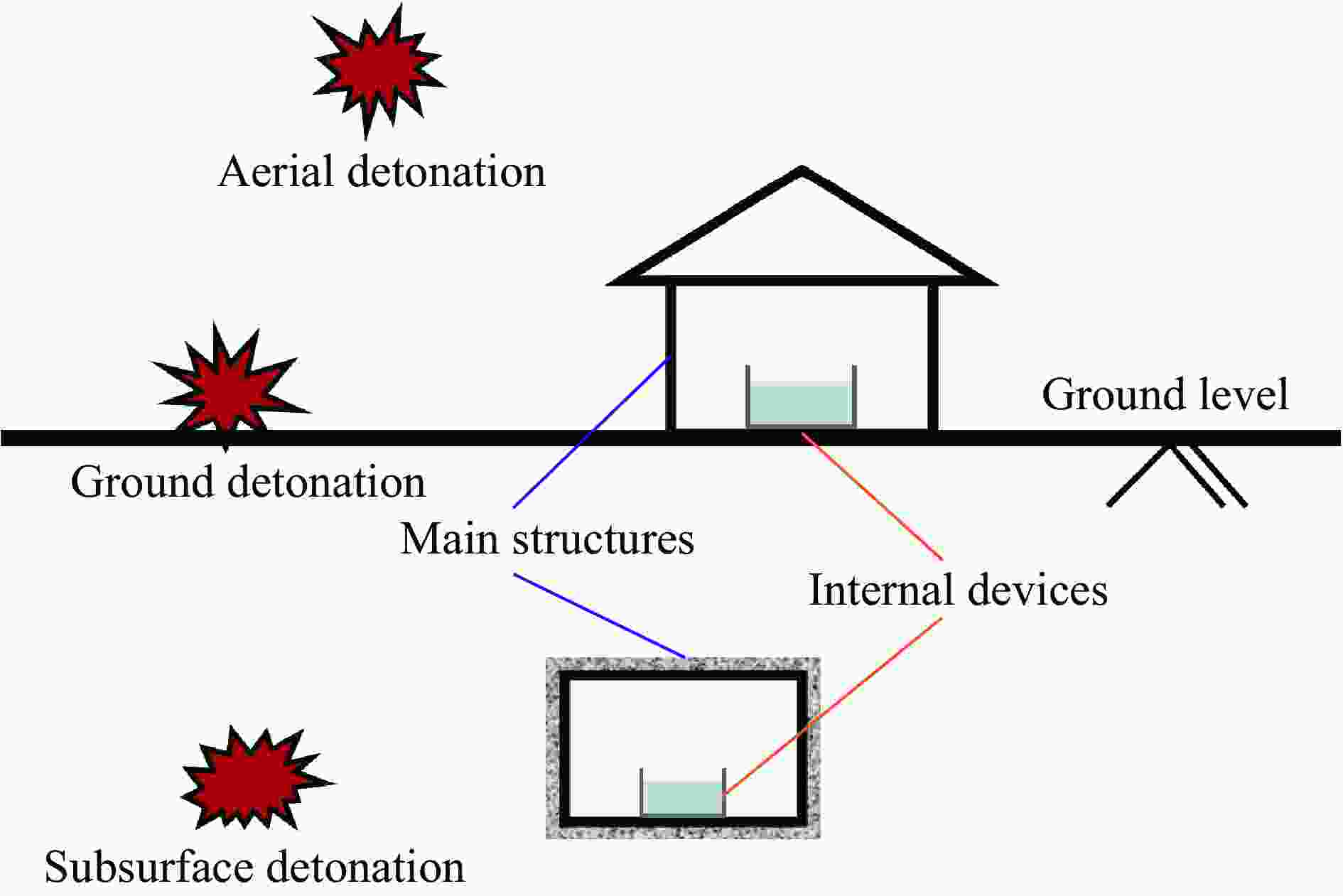
图 1 作为主体结构内部设备的储液结构[8]
Figure 1. Liquid storage structure (LSS) as an internal device in the main structure
图 4 不同摆锤高度下振动台输入加速度时程曲线
Figure 4. Time-history curves of input acceleration of shaking table at different pendulum heights
图 5 结构应变理论计算结果与试验数据对比
Figure 5. Comparison between the calculation results and test data for structural strain
图 6 动水压力理论计算结果与试验数据对比
Figure 6. Comparison between the calculation results and test data for hydrodynamic pressure
图 7 典型爆炸地震动波形的归一化加速度时程曲线
Figure 7. Normalised acceleration time-history curves of typical explosion-induced ground shock waveforms
图 10 广义刚度、基频、特征因子随储液率的变化
Figure 10. Variation in generalised stiffness, fundamental frequency, and characteristic factors with liquid filling ratio
图 11 不同储液率下储液结构挠度时程曲线
Figure 11. Deflection time-history curves of the LSS with different liquid filling ratios
图 12 不同地震动加速度峰值下储液结构挠度时程曲线
Figure 12. Deflection time-history curves of the LSS under ground shocks with different peak accelerations
图 13 不同地震动加速度持时下储液结构挠度时程曲线
Figure 13. Deflection time-history curves of the LSS under ground shocks with different acceleration durations
图 14 典型爆炸地震动下储液结构标准化挠度响应谱
Figure 14. Standardised deflection response spectra of the LSS under typical explosion-induced ground shock
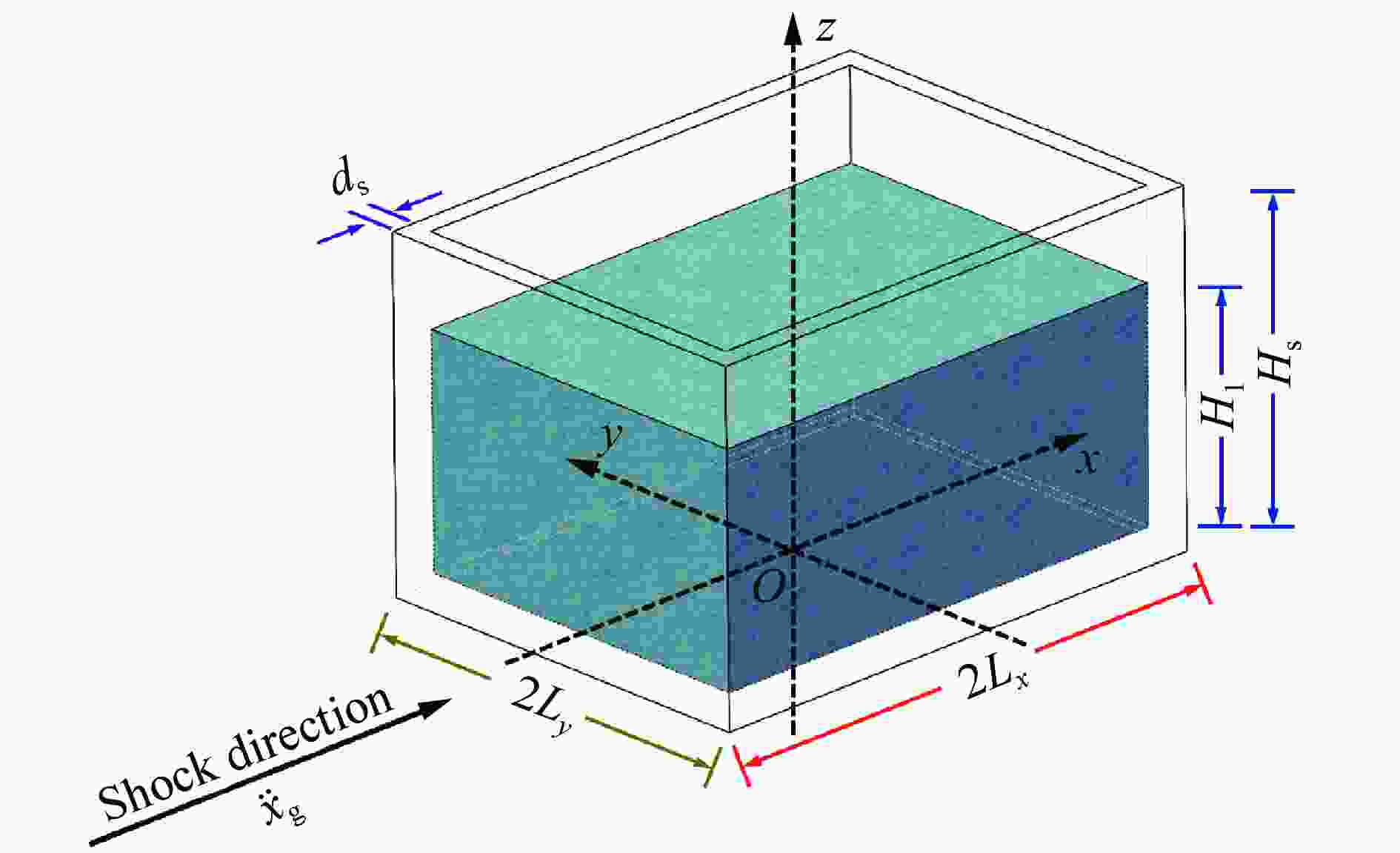
表 1 储液结构模型计算参数
Table 1. Calculation parameters of LSS model
2Lx/m 2Ly/m Hs/m ds/m ρs/(kg·m−3) E/GPa ν Hl/m ρl/(kg·m−3) 1.18 0.88 0.74 0.01 7930 203 0.3 0.30 1000 注：储液结构长、宽、高计算参数由外壁尺寸减去结构厚度，取内壁尺寸。 
下载: 导出CSV
表 2 弹性嵌固梁一阶频率系数
Table 2. First order frequency coefficient value of elastic embedded beam
K 0 0.5 1 3 5 7 10 20 30 100 ∞ β1 3.142 3.284 3.399 3.710 3.897 4.025 4.156 4.374 4.471 4.641 4.730
下载: 导出CSV
表 3 储液结构动力特性参数
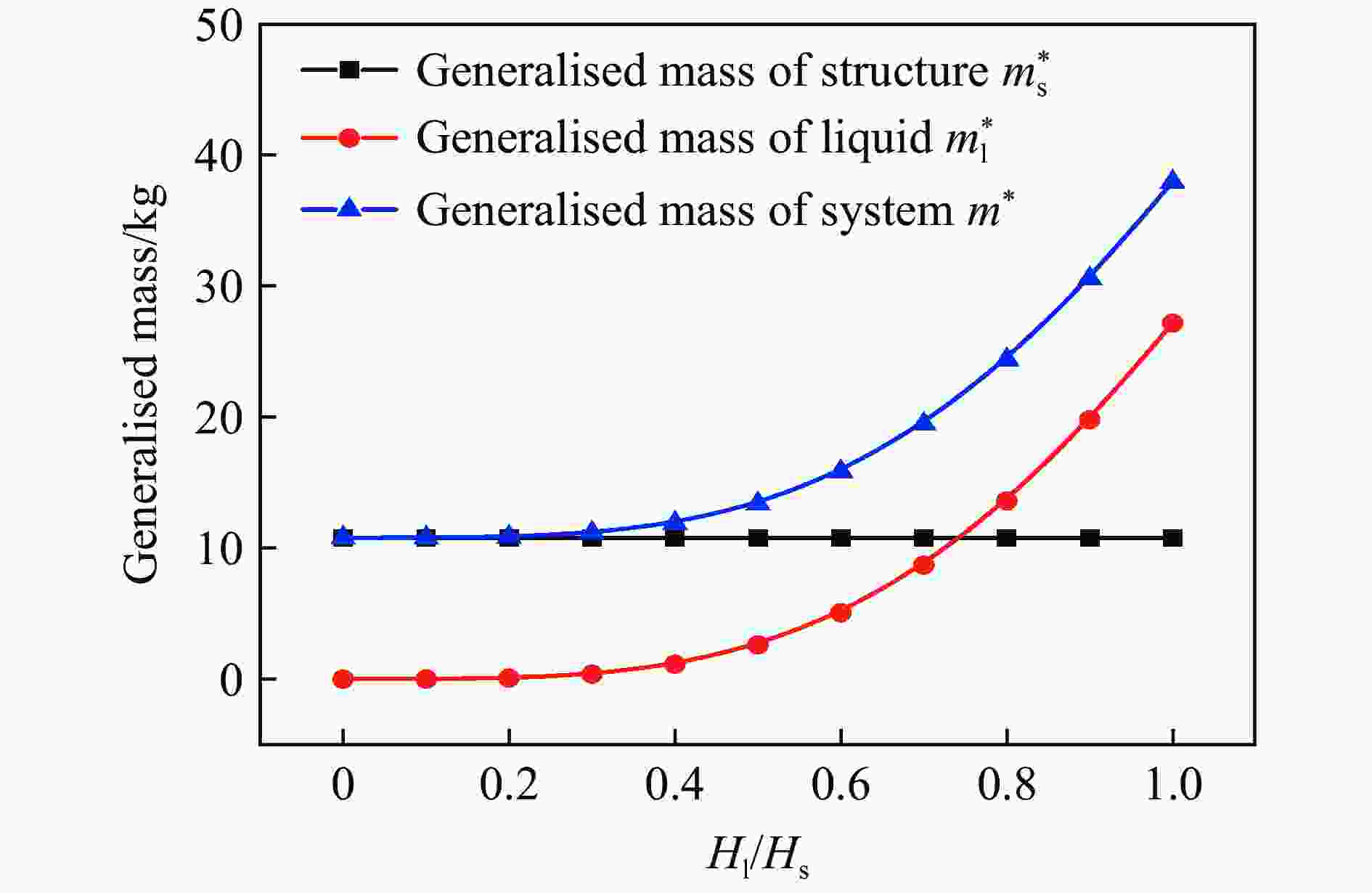
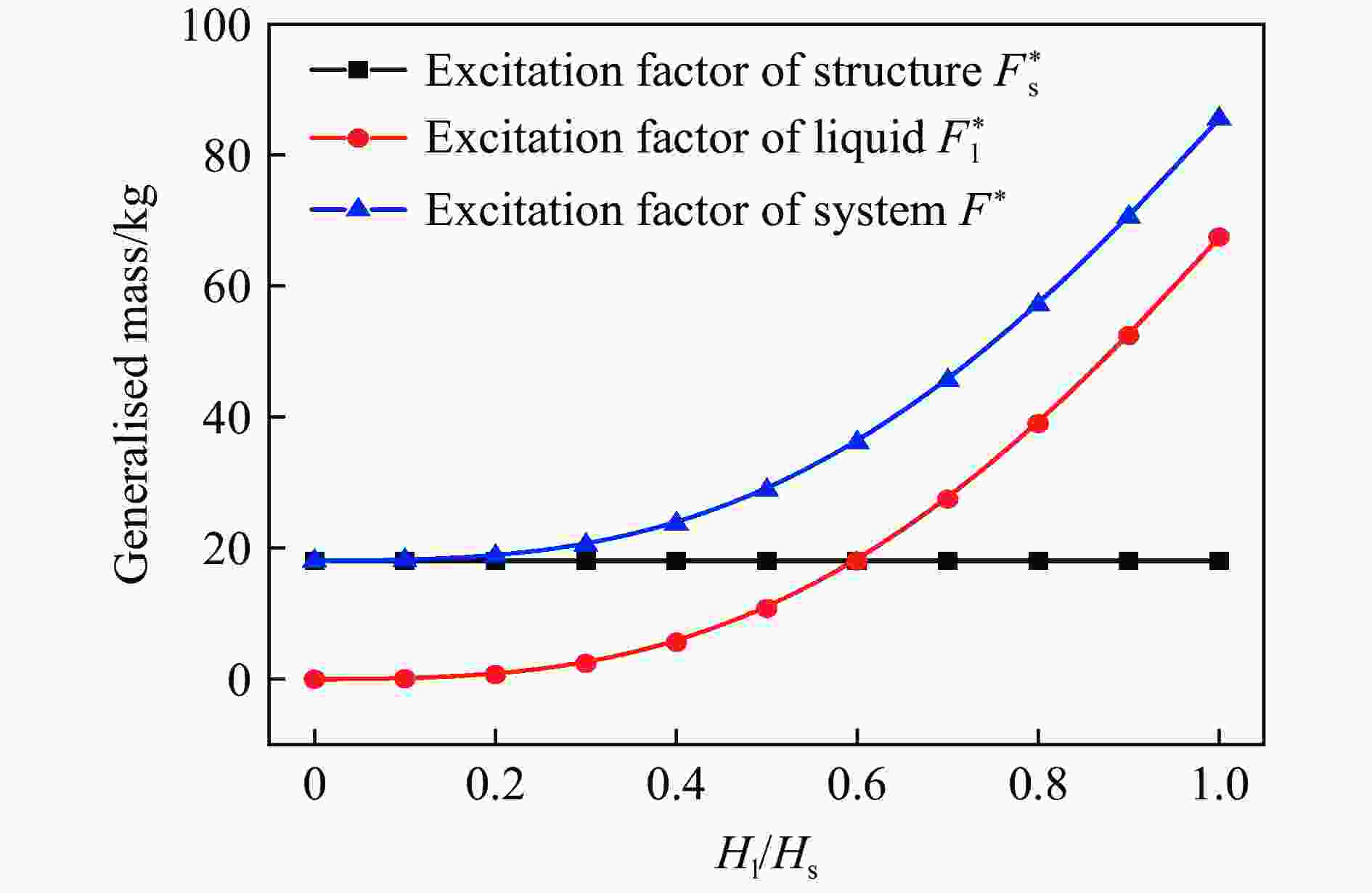
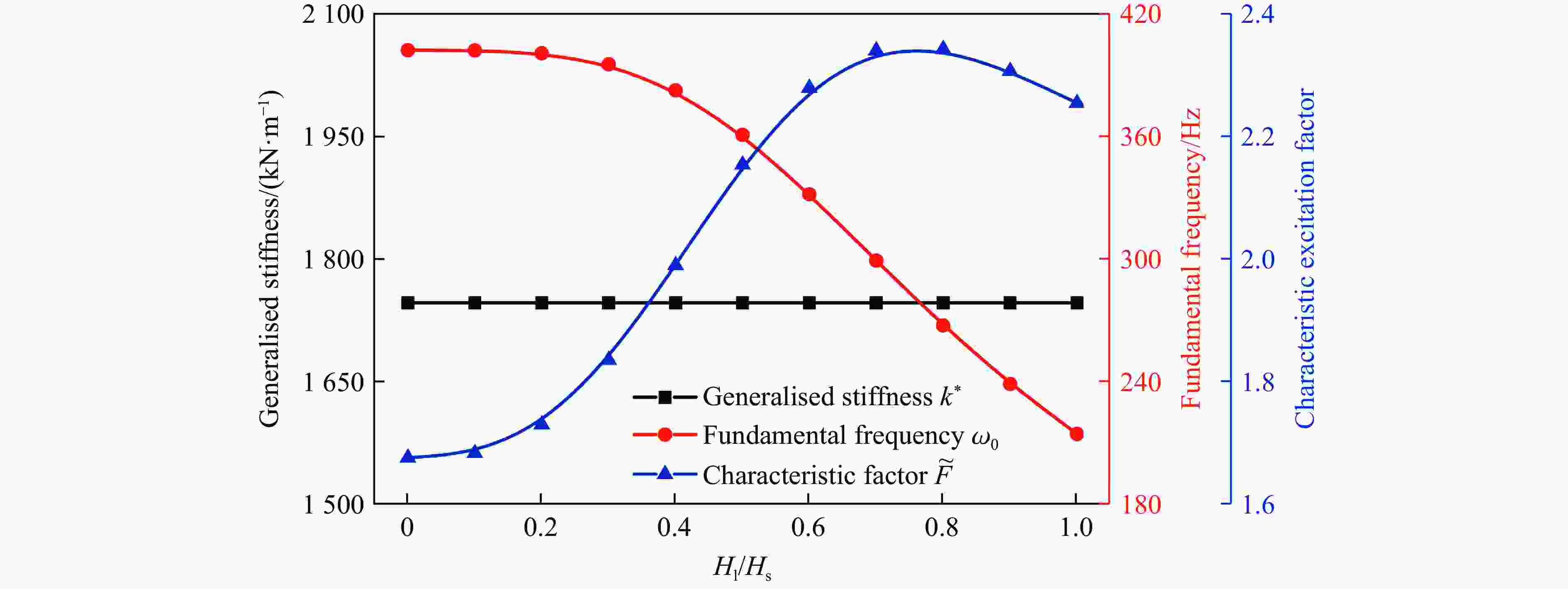
Table 3. Dynamic characteristic parameters of the LSS
ms*/kg ml*/kg m*/kg Fs*/kg Fl*/kg F*/kg $ \tilde F $ k*/(N·m−1) ω/Hz 10.79 1.19 11.98 18.08 5.87 23.95 2.00 1.75×106 381.82
下载: 导出CSV
-
[1] 钱七虎, 王明洋. 高等防护结构计算理论 [M]. 南京: 凤凰出版传媒集团, 2009.QIAN Q H, WANG M Y. Calculation theory for advanced protective structure [M]. Nanjing: Phoenix Science Press, 2009. [2] MA G W, ZHOU H Y, LU Y, et al. In-structure shock of underground structures: A theoretical approach [J]. Engineering Structures, 2010, 32(12): 3836–3844. DOI: 10.1016/j.engstruct.2010.08.026. [3] 周健南, 金丰年, 范华林, 等. 震后地下拱结构的抗冲击波动载能力评估 [J]. 工程力学, 2012, 29(2): 159–164, 171.ZHOU J N, JIN F N, FAN H L, et al. Residual dynamic resistance of seismic damaged underground arch [J]. Engineering Mechanics, 2012, 29(2): 159–164, 171. [4] 王羽, 高康华. 土中爆炸波与地下结构相互作用计算方法研究综述 [J]. 爆炸与冲击, 2015, 35(5): 703–710. DOI: 10.11883/1001-1455(2015)05-0703-08.WANG Y, GAO K H. Review on calculation methods for interaction between explosion waves in soil and underground structures [J]. Explosion and Shock Waves, 2015, 35(5): 703–710. DOI: 10.11883/1001-1455(2015)05-0703-08. [5] ZHOU H Y, CONG P L, WANG X J, et al. Global response of underground structures subjected to ground shock with consideration of rise time [J]. Soil Dynamics and Earthquake Engineering, 2021, 143: 106624. DOI: 10.1016/j.soildyn.2021.106624. [6] 程选生, 杜永峰. 混凝土矩形贮液结构——动力分析理论与数值仿真 [M]. 北京: 科学出版社, 2017. [7] 张浩天, 赵雪川, 宋春明, 等. 爆炸地震动下储液结构动力响应试验研究 [J]. 振动与冲击, 2022, 41(21): 97–108, 128. DOI: 10.13465/j.cnki.jvs.2022.21.012.ZHANG H T, ZHAO X C, SONG C M, et al. Test study on dynamic response of liquid storage structure under explosion ground motion [J]. Journal of Vibration and Shock, 2022, 41(21): 97–108, 128. DOI: 10.13465/j.cnki.jvs.2022.21.012. [8] ZHANG H T, SONG C M, WANG M Y, et al. On the dynamic response of rectangular liquid storage structure subjected to blast-induced ground shock [J]. Engineering Structures, 2023, 285: 116071. DOI: 10.1016/j.engstruct.2023.116071. [9] ZHANG H T, SONG C M, WANG M Y, et al. A geotechnical seismic isolation system based on marine sand cushion for attenuating ground shock effect: Experimental investigation [J]. Soil Dynamics and Earthquake Engineering, 2023, 168: 107854. DOI: 10.1016/j.soildyn.2023.107854. [10] WESTERGAARD H M. Water pressures on dams during earthquakes [J]. Transactions of the American Society of Civil Engineers, 1933, 98(2): 418–433. DOI: 10.1061/TACEAT.0004496. [11] HOSKINS L M, JACOBSEN L S. Water pressure in a tank caused by a simulated earthquake [J]. Bulletin of the Seismological Society of America, 1934, 24(1): 1–32. DOI: 10.1785/BSSA0240010001. [12] HOUSNER G W. Dynamic pressures on accelerated fluid containers [J]. Bulletin of the Seismological Society of America, 1957, 47(1): 15–35. DOI: 10.1785/BSSA0470010015. [13] HOUSNER G W. The dynamic behavior of water tanks [J]. Bulletin of the Seismological Society of America, 1963, 53(2): 381–387. DOI: 10.1785/BSSA0530020381. [14] VELETSOS A S. Seismic effects in flexible liquid storage tanks [C]// Proceedings of the International Association for Earthquake Engineering Fifth World Conference. Rome, 1974: 630–639. [15] VELETSOS A S. Seismic response and design of liquid storage tanks: Guidelines for the seismic design of oil and gas pipeline systems [M]. Technical Council on Lifeline Earthquake Engineering, ASCE, 1984. [16] HAROUN M A. Vibration studies and tests of liquid storage tanks [J]. Earthquake Engineering and Structural Dynamics, 1983, 11(2): 179–206. DOI: 10.1002/EQE.4290110204. [17] 居荣初, 曾心传. 弹性结构与液体的耦联振动理论 [M]. 北京: 地震出版社, 1983. [18] 魏发远, 黄玉盈, 金涛. 矩形水槽在任意地面运动激励下的响应 [J]. 华中理工大学学报, 1997, 25(6): 70–72, 80. DOI: 10.13245/j.hust.1997.06.023.WEI F Y, HUANG Y Y, JIN T. The response of a rectangular sink to random excitation due to ground movement [J]. Journal of Huazhong University of Science and Technology, 1997, 25(6): 70–72, 80. DOI: 10.13245/j.hust.1997.06.023. [19] 杜永峰, 史晓宇, 程选生. 钢筋混凝土矩形贮液结构的液固耦合振动 [J]. 甘肃科学学报, 2008, 20(2): 45–49. DOI: 10.3969/j.issn.1004-0366.2008.02.013.DU Y F, SHI X Y, CHENG X S. Vibration of reinforced concrete rectangular liquid-storage structures with liquid-structure interaction [J]. Journal of Gansu Sciences, 2008, 20(2): 45–49. DOI: 10.3969/j.issn.1004-0366.2008.02.013. [20] 程选生, 郑颖人. 弯剪型模型下弹性贮液结构的自振特性分析 [J]. 重庆大学学报, 2011, 34(12): 132–137.CHENG X S, ZHENG Y R. Free vibration characteristic analysis of the elastic liquid-storage tanks based on the bending shearing model [J]. Journal of Chongqing University, 2011, 34(12): 132–137. [21] CHEN J Z, KIANOUSH M R. Generalized SDOF system for seismic analysis of concrete rectangular liquid storage tanks [J]. Engineering Structures, 2009, 31(10): 2426–2435. DOI: 10.1016/j.engstruct.2009.05.019. [22] 程选生, 杜永峰. 弹性壁板下钢筋混凝土矩形贮液结构的液动压力 [J]. 工程力学, 2009, 26(6): 82–88.CHENG X S, DU Y F. The dynamic fluid pressure of reinforced concrete rectangular liquid-storage tanks with elastic walls [J]. Engineering Mechanics, 2009, 26(6): 82–88. [23] 程选生, 杜永峰. 弹性地基上矩形贮液结构的液-固耦合振动特性 [J]. 工程力学, 2011, 28(2): 186–192.CHENG X S, DU Y F. Vibration characteristic analysis of rectangular liquid-storage structures considering liquid-solid coupling on elastic foundation [J]. Engineering Mechanics, 2011, 28(2): 186–192. [24] HAROUN M A. Stress analysis of rectangular walls under seismically induced hydrodynamic loads [J]. Bulletin of the Seismological Society of America, 1984, 74(3): 1031–1041. DOI: 10.1785/BSSA0740031031. [25] KIM J K, KOH H M, KWAHK I J. Dynamic response of rectangular flexible fluid containers [J]. Journal of Engineering Mechanics, 1996, 122(9): 807–817. DOI: 10.1061/(ASCE)0733-9399(1996)122:9(807). [26] HASHEMI S, SAADATPOUR M M, KIANOUSH M R. Dynamic behavior of flexible rectangular fluid containers [J]. Thin-Walled Structures, 2013, 66: 23–38. DOI: 10.1016/j.tws.2013.02.001. [27] CLOUGH R W, PENZIEN J. Dynamics of structures [M]. 2nd ed. New York: McGraw-Hill, 1993. [28] 曹志远. 板壳振动理论 [M]. 北京: 中国铁道出版社, 1989. [29] 杜建国, 张洪海, 谢清粮. 基于反应谱分析的爆炸冲击震动信号的半正弦脉冲等效 [J]. 防护工程, 2009, 31(1): 11–14.DU J G, ZHANG H H, XIE Q L. Half-sine pulse equivalent of the explosion and shock signals based on the response spectrum analysis [J]. Protective Engineering, 2009, 31(1): 11–14. -
计量
- 文章访问数: 307
- HTML全文浏览量: 46
- PDF下载量: 82
- 被引次数: 0