Study on blast loadings of cylindrical charges air explosion
-
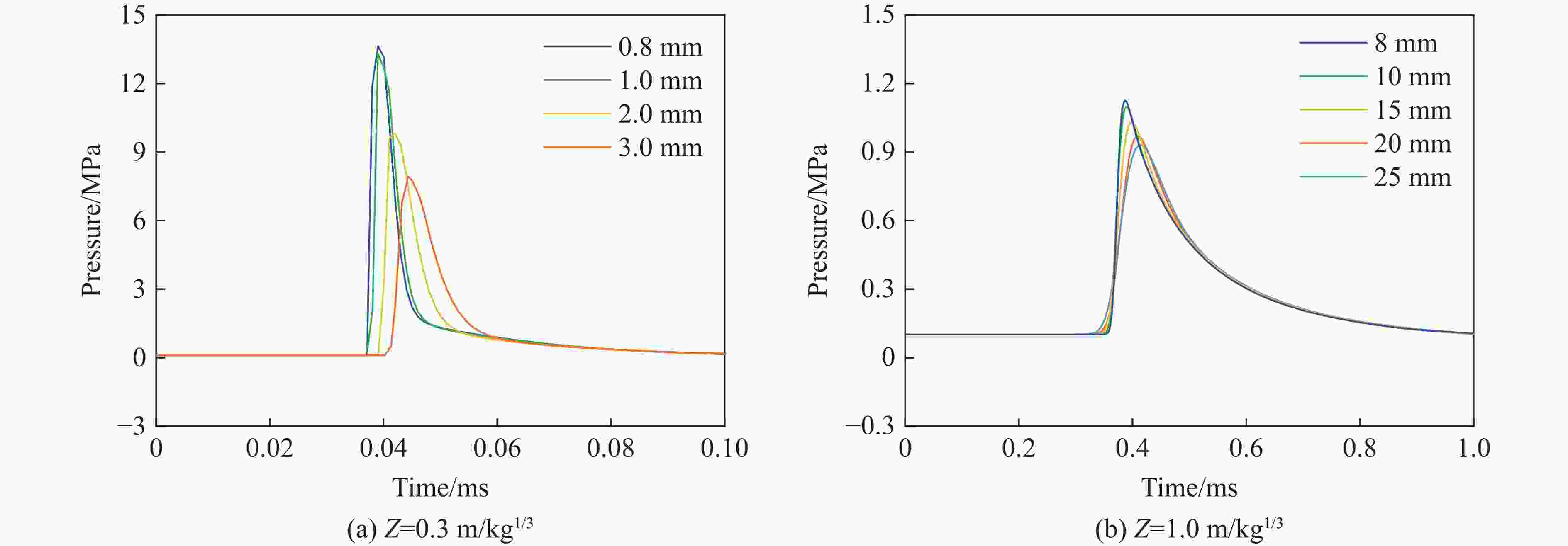
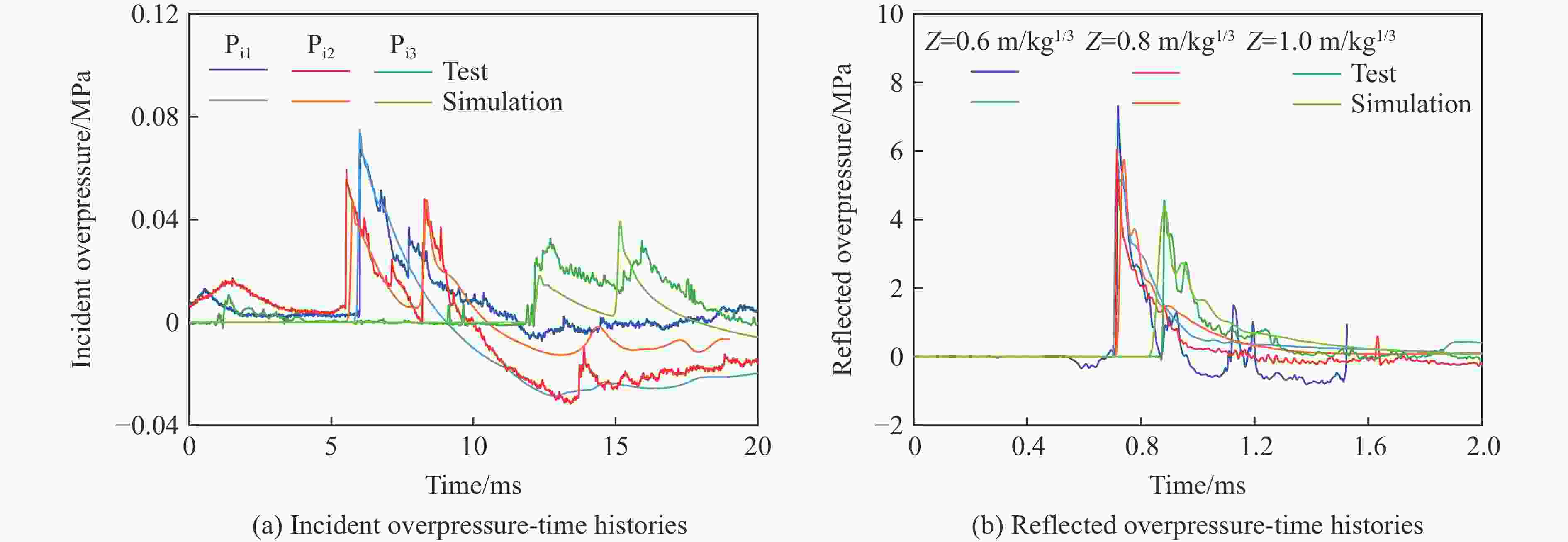
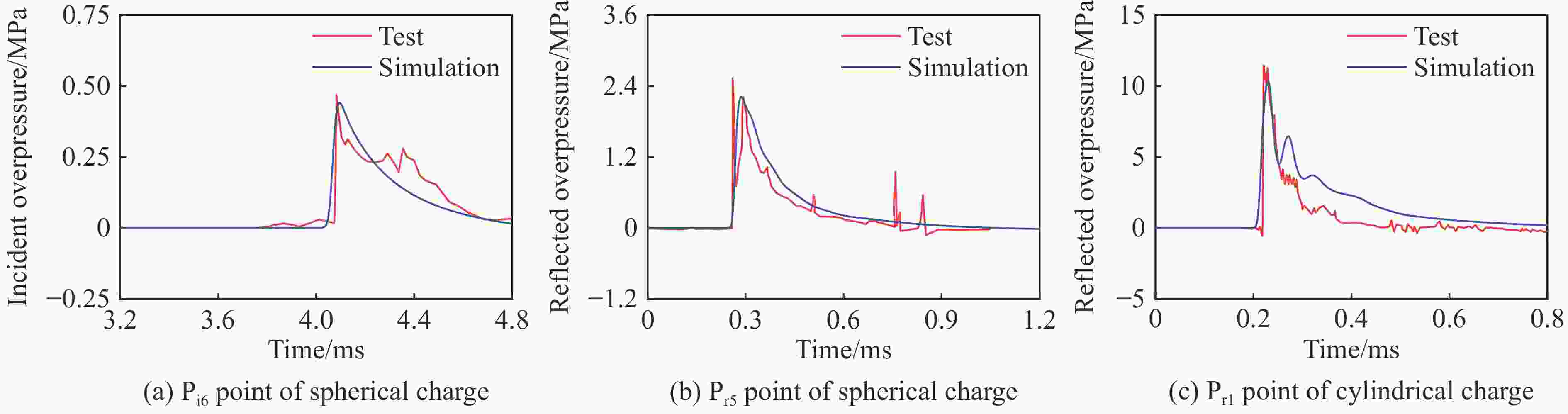
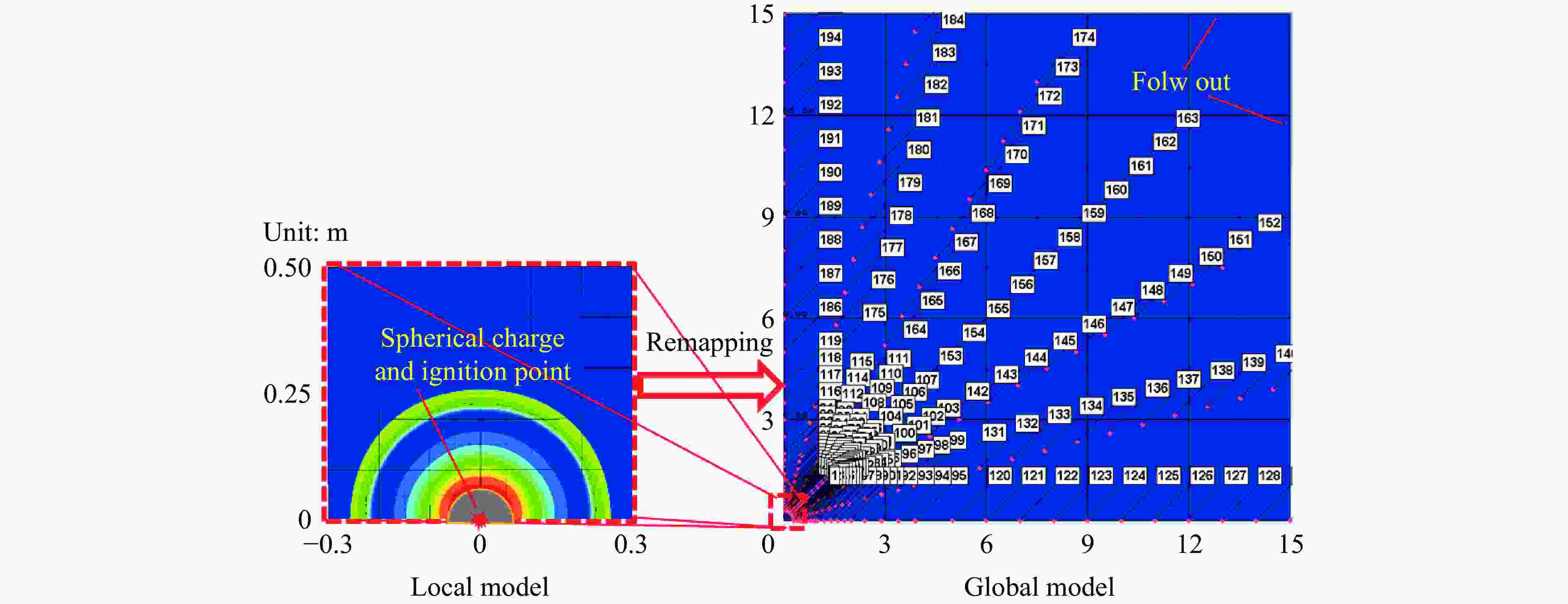
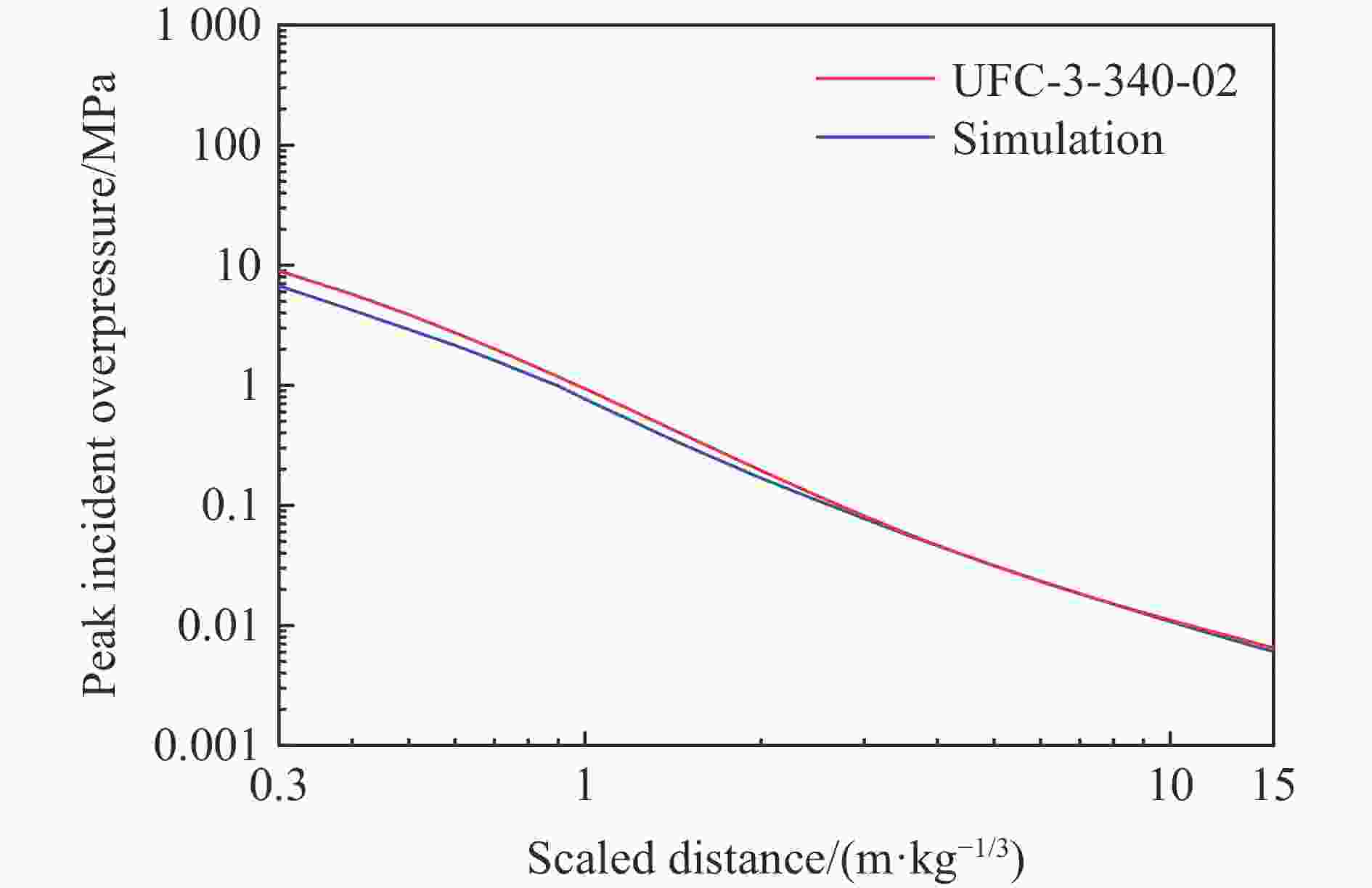
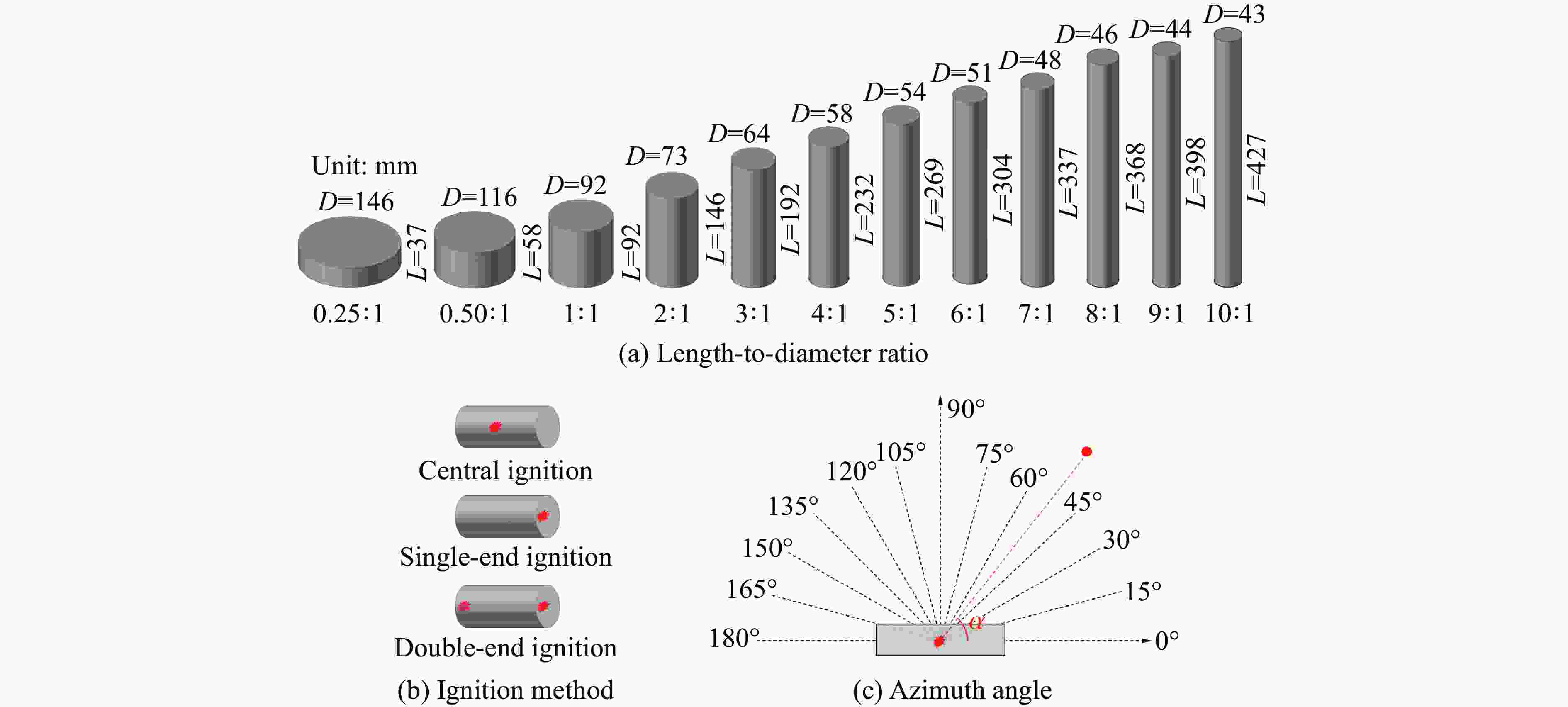
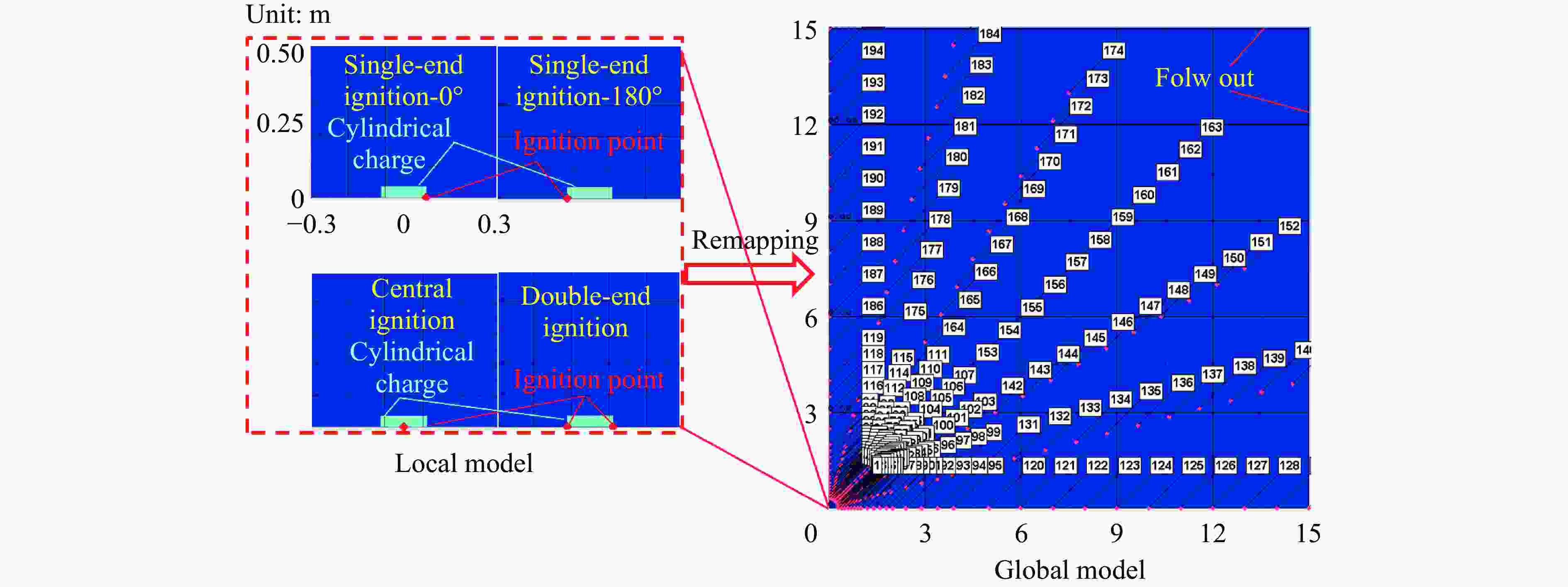
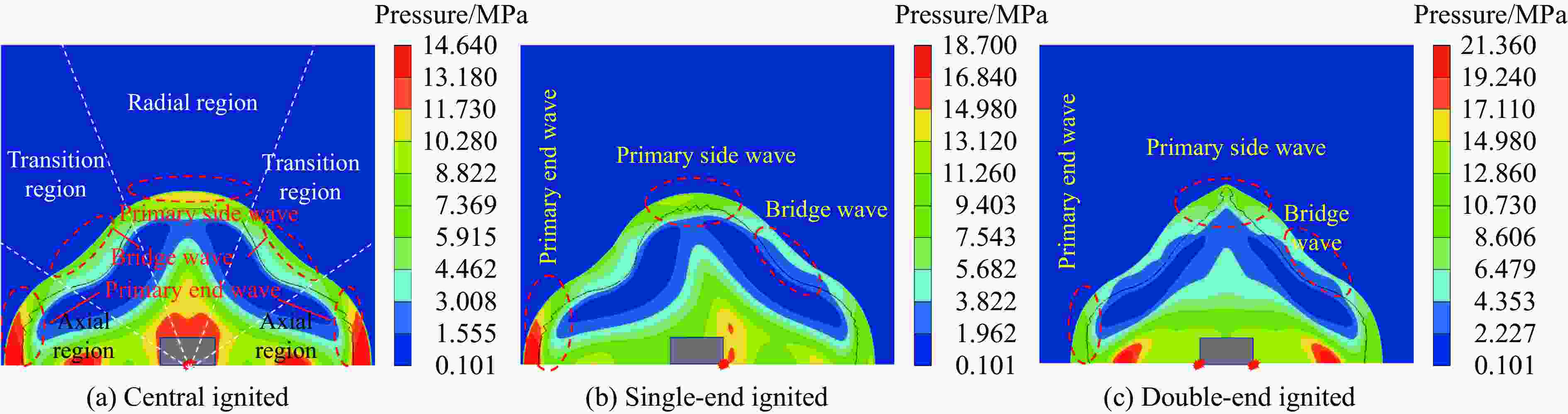
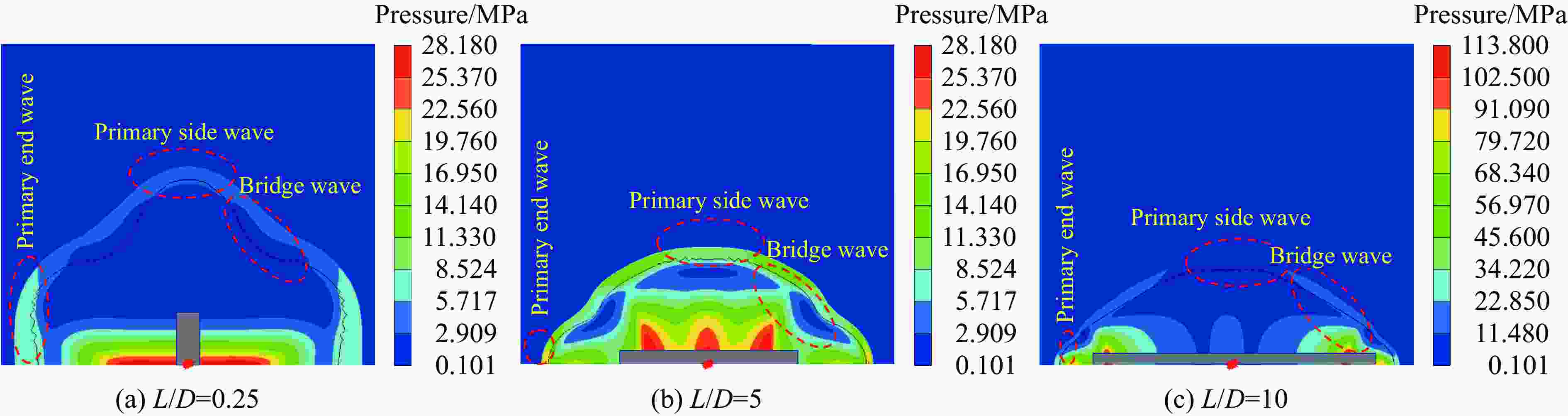
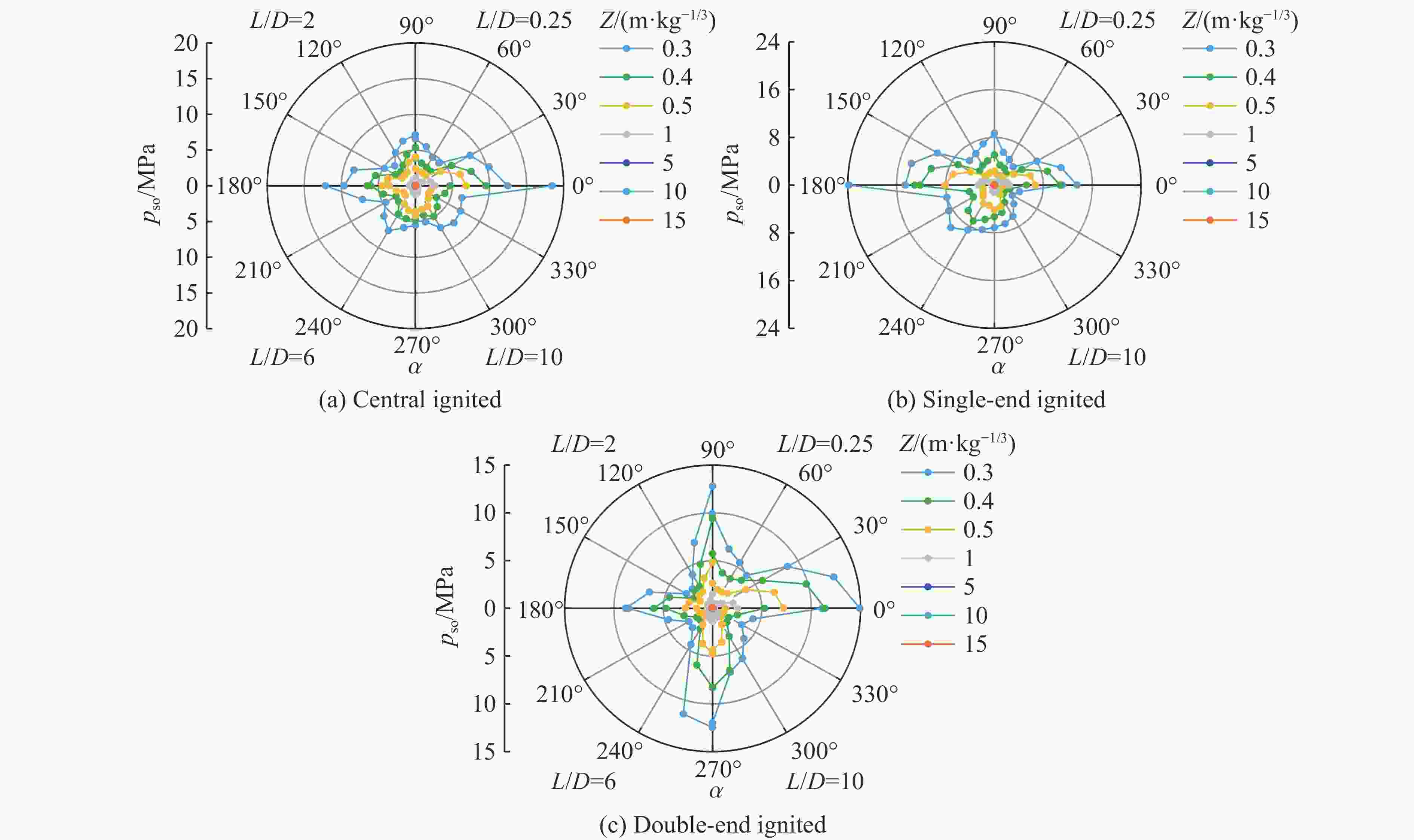
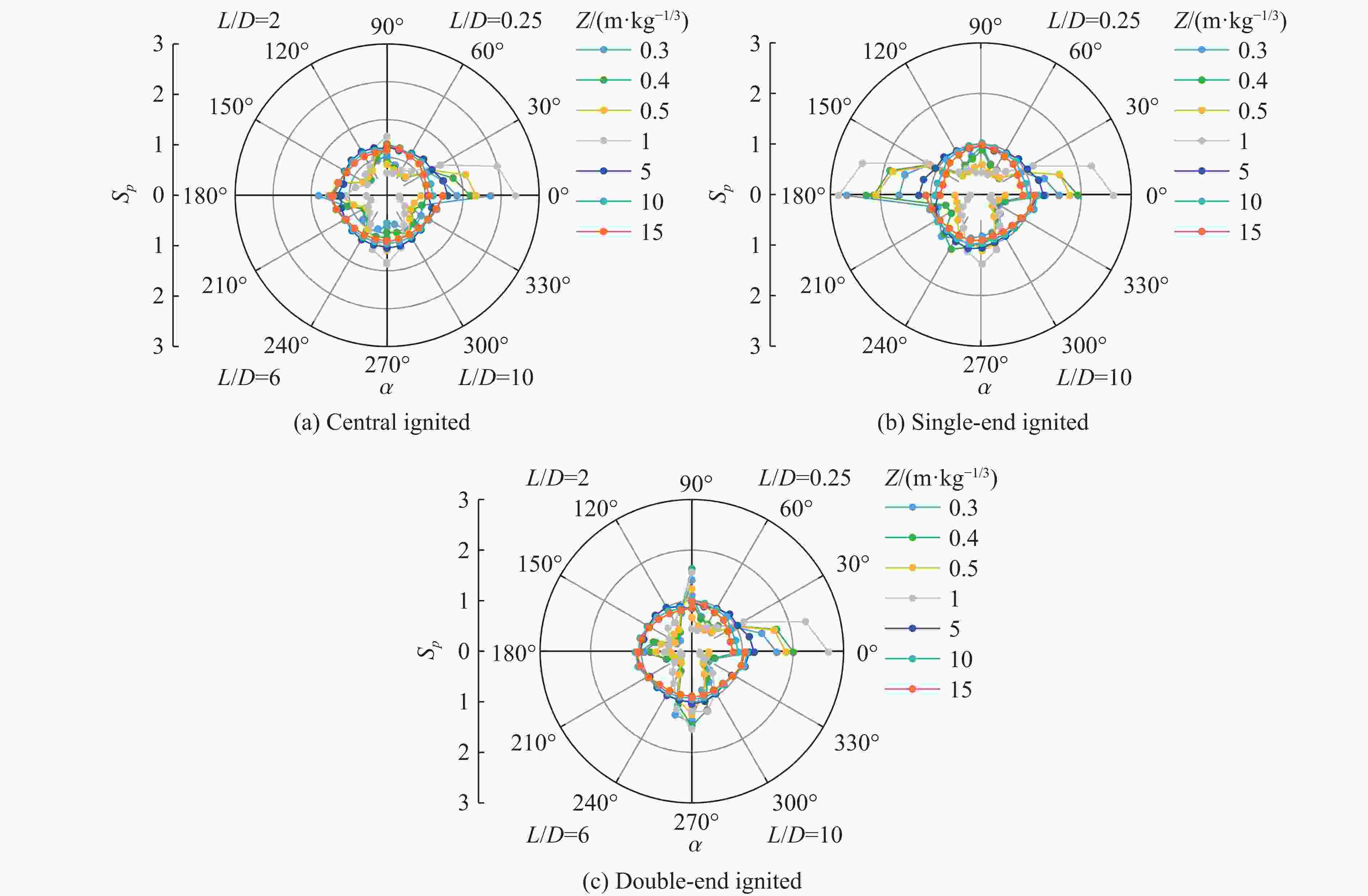
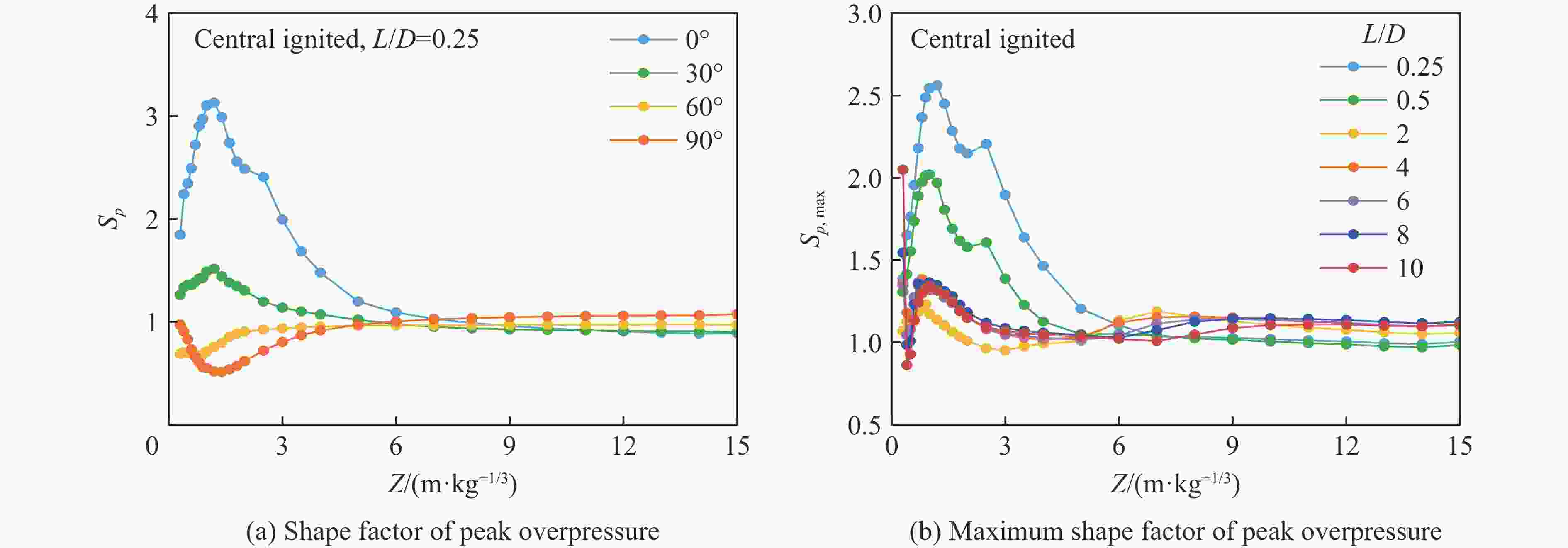
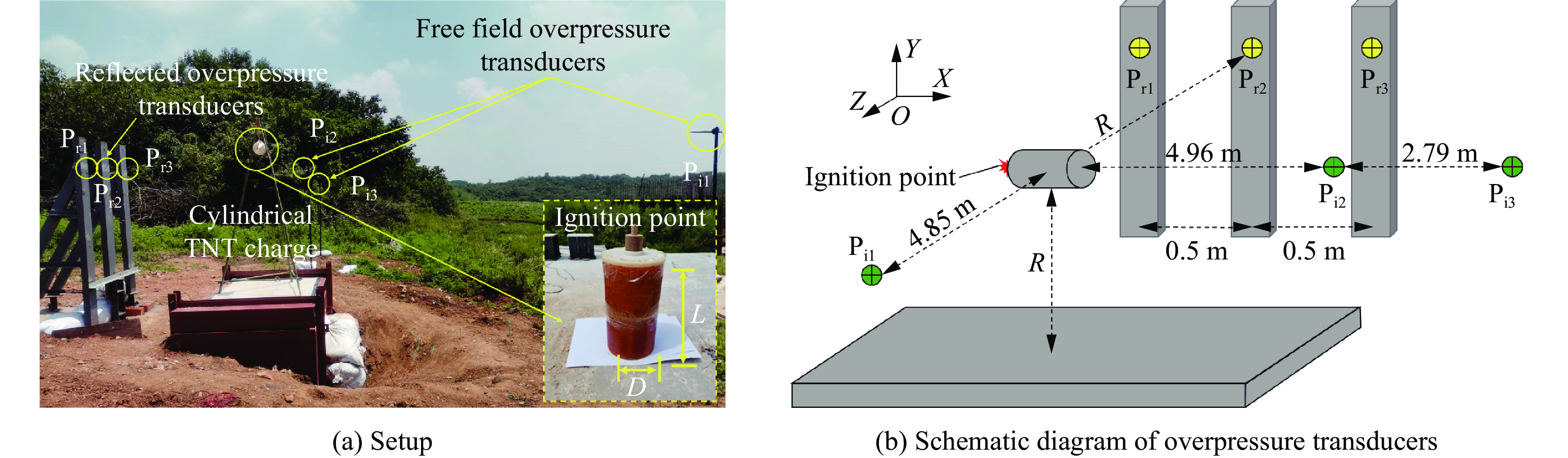
摘要: 受比例距离、装药长径比、起爆方式、方位角、冲击波入射角以及反射面相对位置等多种因素的影响，球形装药空中爆炸冲击波荷载的计算方法不适用于柱形装药。为探究柱形装药空中自由场爆炸冲击波入射和反射荷载，首先，开展柱形TNT装药单端起爆的空中爆炸试验，并基于显式动力学分析软件AUTODYN进行数值模拟，通过与试验和规范进行对比，验证了采用的有限元分析方法的适用性。进一步开展考虑比例距离、长径比、起爆方式、方位角和刚性反射等因素的1000余组柱形装药空中爆炸工况的数值模拟。基于模拟结果，揭示了柱形装药空中爆炸入射冲击波峰值超压和最大冲量及其形状因子的分布特征，提出峰值超压和最大冲量临界比例距离的判定准则和确定方法，阐明了刚性反射冲击波峰值超压和反射系数的变化规律。最后，提出柱形装药空中爆炸入射和反射冲击波荷载的计算方法，并得到360余组试验数据的验证。该方法可快速计算作用于建筑结构上的爆炸荷载，并为弹药毁伤效能评估、结构动态响应和破坏分析及其抗爆设计提供参考。Abstract: The existing specifications and studies mainly focus on the scenarios that the spherical charges are ignited at the central point and explosion is in free air, while the studies of the blast loadings of cylindrical charges air explosion, especially the reflected overpressure acting on the structure, are relatively limited. The blast loading calculation formula for spherical charge cannot be applied for cylindrical charge as attributed to the parametric influences such as scaled distance, length-to-diameter ratio, ignition method, azimuth angle, incident angle and relative location of reflected plane. To explore the incident and reflected blast loadings of cylindrical charges air explosion, firstly, three shots of explosion test of the single-end ignited cylindrical TNT charge were conducted. The corresponding numerical simulations are conducted based on the finite element program AUTODYN, and the applicability of the adopted finite element analysis method is verified by comparing with the experimental incident and reflected overpressure-time histories of spherical and cylindrical charges air explosion of tests, as well as the peak incident overpressure-scaled distance relationship of unified facilities criteria (UFC) 3-340-02 of spherical charges air explosion. Furthermore, the numerical simulations of more than 1000 sets of cylindrical charges air explosion scenarios considering the scaled distance, length-to-diameter ratio, ignition method, azimuth angle and rigid reflection are carried out based on validated finite element analysis method. The distribution characteristics of peak overpressure, maximal impulse of the incident blast wave and the corresponding shape factors are examined and discussed. The judging criteria and determination methods for the critical scaled distance of peak overpressure and maximal impulse are proposed by using data fitting, and the variation law of the reflected peak overpressure and the rigid reflection coefficient are revealed. Finally, a calculation method for the incident and reflected blast loadings of cylindrical charges air explosion is proposed and experimentally verified by 360 sets data. The method can rapidly predict the blast loadings on building structures, and provide reference for evaluating the ammunition damage efficiency, analyzing structural dynamic response and failure, as well as for the corresponding blast-resistant design.
-
Key words:
- cylindrical charge /
- air explosion /
- peak overpressure /
- maximal impulse /
- critical scaled distance
-
图 2 柱形装药空中爆炸试验有限元模型
Figure 2. Finite element model of cylindrical charges air explosion test
图 3 不同网格尺寸下的压力时程曲线
Figure 3. Pressure-time histories corresponding to different grid sizes
图 4 入射和反射超压时程曲线的试验和数值模拟结果对比
Figure 4. Comparisons of the test and simulated incident and reflected overpressure-time histories
图 9 柱形装药长径比、起爆方式和方位角
Figure 9. Length-to-diameter ratio, initiation method, and azimuth angle of cylindrical charges
图 10 柱形装药空中爆炸自由场有限元模型
Figure 10. Finite element model of cylindrical charges air explosion
图 11 柱形装药轴向和径向冲击波反射示意图
Figure 11. Schematic diagram of axial and radial blast wave reflection of cylindrical charge
图 12 典型柱形装药空中爆炸的反射场有限元模型
Figure 12. Typical finite element model for reflections of cylindrical charges air explosion
图 13 柱形装药3种起爆方式下的压力云图（L/D=1）
Figure 13. Pressure contours of cylindrical charge under three ignition methods (L/D=1)
图 14 典型长径比柱形装药中心起爆压力云图
Figure 14. Pressure contours of central ignited cylindrical charge with typical L/D
图 15 柱形装药中心起爆不同时刻的压力云图（L/D=1）
Figure 15. Instantaneous pressure contours of central ignited cylindrical charge (L/D=1)
图 16 典型长径比柱形装药3种起爆方式的峰值超压分布
Figure 16. Peak overpressure distributions of cylindrical charge with typical L/D and three ignition methods
图 17 典型长径比柱形装药3种起爆方式的峰值超压形状因子分布
Figure 17. Peak overpressure shape factor distributions of cylindrical charge with typical L/D and three ignition methods
图 18 典型峰值超压形状因子与最大峰值超压形状因子
Figure 18. Typical shape factor and maximum shape factor of peak overpressure
图 19 3种起爆方式下不同长径比柱形装药的峰值超压临界比例距离
Figure 19. Critical scaled distance of peak overpressure for cylindrical charge with different L/D under three ignition methods
图 20 典型长径比柱形装药3种起爆方式的最大冲量分布
Figure 20. Maximal impulse distributions of cylindrical charge with typical L/D and three ignition methods
图 21 典型长径比柱形装药3种起爆方式的最大冲量形状因子分布
Figure 21. Maximal impulse shape factor distributions of cylindrical charge with typical L/D and three ignition methods
图 22 典型最大冲量形状因子与最大的最大冲量形状因子
Figure 22. Typical shape factor and maximum shape factor of maximal impulse
图 23 3种起爆方式下不同长径比柱形装药的最大冲量临界比例距离
Figure 23. Critical scaled distance of maximal impulse for cylindrical charge with different L/D under three ignition methods
图 25 3种起爆方式下柱形装药轴向反射峰值超压与投影距离的关系
Figure 25. Dependence of axial reflected peak overpressure on projection distance of cylindrical charge with three ignition methods
图 26 典型长径比下柱形装药轴向反射峰值超压与投影距离的关系
Figure 26. Dependence of axial reflected peak overpressure on projection distance of cylindrical charge with typical L/Ds
图 27 典型长径比柱形装药中心起爆的轴向和径向超压反射系数
Figure 27. Axial and radial overpressure reflection coefficients of central ignited cylindrical charge with typical L/Ds
图 28 L/D=0.25柱形装药单/双端起爆的轴向和径向峰值超压反射系数
Figure 28. Axial and radial peak overpressure reflection coefficients of single/double-end ignited cylindrical charge with L/D=0.25
图 29 爆炸荷载试验与计算结果对比
Figure 29. Comparisons of test data and calculated results of blast loadings
表 1
$L/D{\text{≥}}1 $ 柱形装药入射峰值超压拟合公式系数Table 1. Fitted formula coefficients for peak incident overpressure of central ignited cylindrical charges with
$L/D{\text{≥}}1 $ 起爆方式 α/(°) 0.3 m/kg1/3≤Z≤1 m/kg1/3 1 m/kg1/3<Z≤15 m/kg1/3 A B C R2 A B C R2 中心起爆 0 173 9 399 0.943 7 −211 390 31 0.612 6 30 −33 503 −166 0.904 5 −200 424 40 0.902 7 60 −103 958 −491 0.988 3 −202 644 −11 0.969 0 90 −242 1 352 −141 0.926 4 281 501 −11 0.986 3 单端起爆 0 −56 1 013 −900 0.884 5 −491 619 22 0.616 4 30 −39 365 −96 0.800 2 −284 546 1 0.880 1 60 60 −131 693 0.940 7 −114 509 9 0.961 8 90 −225 1 438 −244 0.941 8 306 512 −19 0.976 8 120 −205 1 732 −1 360 0.977 9 −238 721 −16 0.969 6 150 −27 580 −261 0.943 1 −171 431 43 0.915 8 180 77 1 246 −1 057 0.909 9 −531 574 34 0.775 3 双端起爆 0 −25 865 −796 0.875 3 −887 1 096 −56 0.733 9 30 −29 304 −24 0.793 5 −313 593 4 0.914 4 60 29 22 602 0.954 3 −69 505 18 0.968 2 90 −255 2 054 −1 068 0.923 7 187 694 −74 0.932 8 
下载: 导出CSV
表 2 最大冲量临界比例距离拟合公式系数
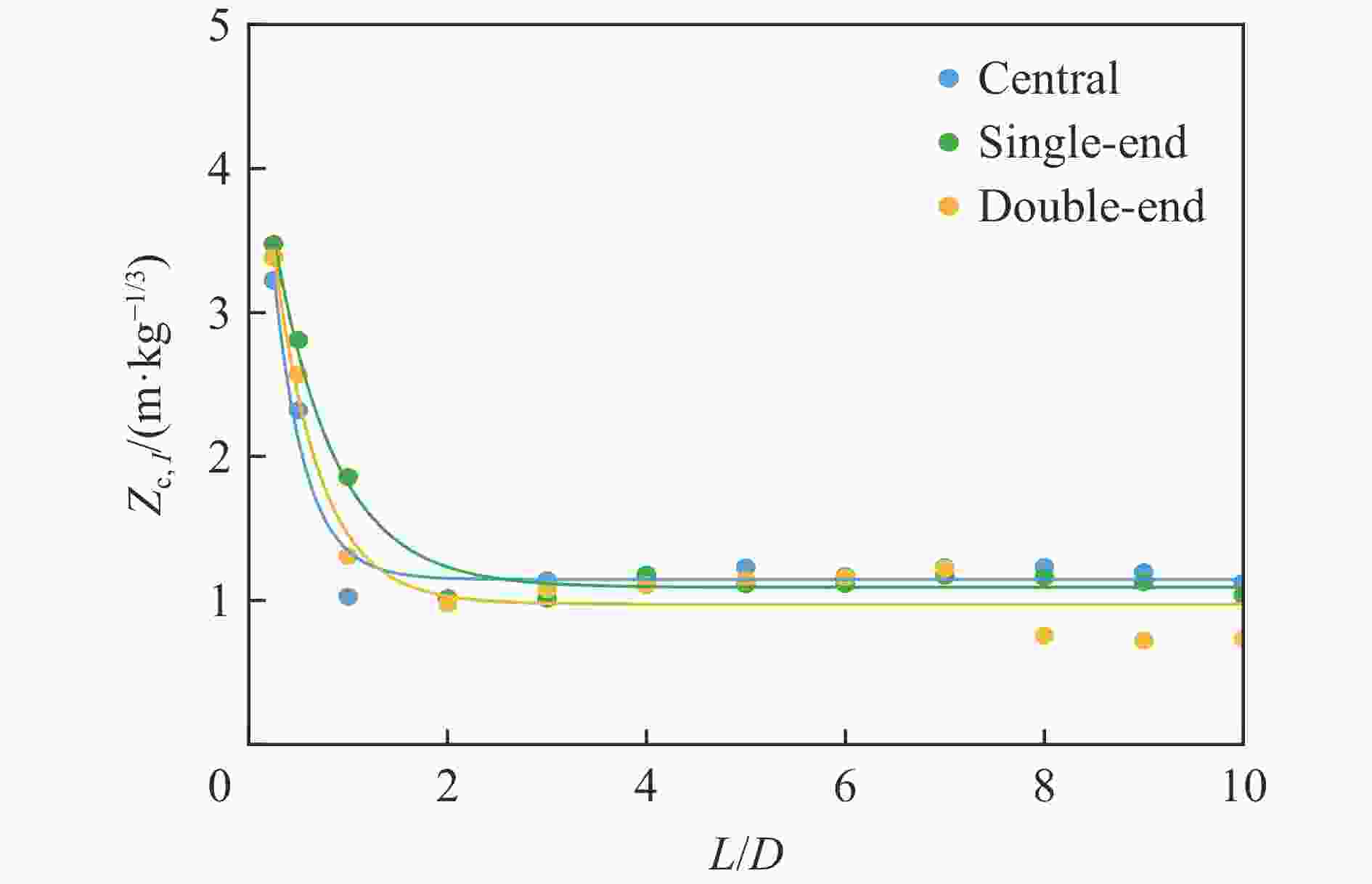
Table 2. Coefficients of fitted formula for the maximal impulse critical scaled distance
起爆方式 拟合公式系数 k a b c R2 中心起爆 2.13 0.25 1.14 0.32 0.945 0 单端起爆 2.48 0.24 1.09 0.61 0.981 2 双端起爆 2.60 0.23 0.97 0.46 0.927 8
下载: 导出CSV
表 3 最大冲量拟合公式系数
Table 3. Coefficients of the fitted formula for the maximal impulse
起爆方式 公式拟合系数 A1,1 A1,2 A1,1,1 A1,1,2 A1,2,1 A1,2,2 A1,3,1 A1,3,2 A1,4,1 A1,4,2 中心 2 088 −2 044 1 222 −1 043 −4 422 4 503 2 583 −2 715 −971 1 101 单端 341 −110 276 −257 186 −163 247 −236 −27 105 双端 640 −384 1 304 −783 −2077 1 352 1 026 −620 85 −190 起爆方式 A2,1 A2,2 A2,1,1 A2,1,2 A2,2,1 A2,2,2 A2,3,1 A2,3,2 A2,4,1 A2,4,2 中心 −543 568 −550 459 1 321 −1 436 −677 824 173 −293 单端 −135 21 −127 101 −43 22 −106 95 −40 −23 双端 −88 −123 −516 225 528 16 −154 −126 −174 250 起爆方式 A3,1 A3,2 A3,1,1 A3,1,2 A3,2,1 A3,2,2 A3,3,1 A3,3,2 A3,4,1 A3,4,2 中心 45 −50 60 −49 −110 134 42 −73 3 21 单端 18 −1 17 −12 7 −2 13 −11 11 2 双端 15 28 57 −16 −63 −33 12 34 25 −38
下载: 导出CSV
-
[1] US Department of the Army. Fundamentals of protective design for conventional weapons: TM 5-855-1 [S]. Washington, USA: US Department of the Army, 1986. [2] American Society of Civil Engineers. Blast protection of buildings: ASCE 59-11 [S]. Reston, Virginia, USA: American Society of Civil Engineers, 2011. [3] Canadian Standards Association. Design and assessment of buildings subjected to blast loads: CSA/S850-23 [S]. Toronto, Canda: Canadian Standards Association, 2023. [4] US Department of Defense. Structures to resist the effects of accidental explosions, with change 2: UFC 3-340-02 [S]. Washington, USA: US Department of Defense, 2014. [5] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 爆破安全规程: GB 6722-2014 [S]. 北京: 中国标准出版社, 2014. [6] STONER R G, BLEAKNEY W. The attenuation of spherical shock waves in air [J]. Journal of Applied Physics, 1948, 19(7): 670–678. DOI: 10.1063/1.1698189. [7] BRODE H L. Numerical solutions of spherical blast waves [J]. Journal of Applied Physics, 1955, 26(6): 766–775. DOI: 10.1063/1.1722085. [8] BAKER W E. Explosions in air [M]. Austin, USA: University of Texas Press, 1974: 6–10. [9] HENRYCH J, ABRAHAMSON G R. The dynamics of explosion and its use [M]. Amsterdam New York, USA: Elsevier Science Publishing Company, 1979: 218. [10] MILLS C A. The design of concrete structures to resist explosions and weapon effects [C]// The 1st International Conference on Concrete for Hazard Protections. Edinburgh, UK: European Cement Association, 1987: 11–15. [11] WU C Q, HAO H. Modeling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions [J]. International Journal of Impact Engineering, 2005, 31(6): 699–717. DOI: 10.1016/j.ijimpeng.2004.03.002. [12] KINNEY G F, GRAHAM K J, KENNETH J. Explosive shocks in air [M]. Berlin, Germany: Springer Verlag, 1985: 1–17. [13] SHI Y C, WANG N, CUI J, et al. Experimental and numerical investigation of charge shape effect on blast load induced by near-field explosions [J]. Process Safety and Environmental Protection, 2022, 165: 266–277. DOI: 10.1016/j.psep.2022.07.018. [14] ISMAIL M M, MURRAY S G. Study of the blast waves from the explosion of nonspherical charges [J]. Propellants, Explosives, Pyrotechnics, 1993, 18: 132–138. DOI: 10.1002/prep.19930180304. [15] SIMOENS B, LEFEBVRE M H, MINAMI F. Influence of different parameters on the TNT-equivalent of an explosion [J]. Central European Journal of Energetic Materials, 2011, 8(1): 53–67. [16] ANASTACIO A C, KNOCK C. Radial blast prediction for high explosive cylinders initiated at both ends [J]. Propellants, Explosives, Pyrotechnics, 2016, 41(4): 682–687. DOI: 10.1002/prep.201500302. [17] KNOCK C, DAVIES N. Predicting the peak pressure from the curved surface of detonating cylindrical charges [J]. Propellants, Explosives, Pyrotechnics, 2011, 36(3): 203–209. DOI: 10.1002/prep.201000001. [18] KNOCK C, DAVIES N. Predicting the impulse from the curved surface of detonating cylindrical charges [J]. Propellants, Explosives, Pyrotechnics, 2011, 36(2): 105–109. DOI: 10.1002/prep.201000002. [19] KNOCK C, DAVIES N, REEVES T. Predicting blast waves from the axial direction of a cylindrical charge [J]. Propellants, Explosives, Pyrotechnics, 2015, 40(2): 169–179. DOI: 10.1002/prep.201300188. [20] GAO C, KONG X Z, FANG Q, et al. Numerical investigation on free air blast loads generated from center-initiated cylindrical charges with varied aspect ratio in arbitrary orientation [J]. Defence Technology, 2022, 18(9): 1662–1678. DOI: 10.1016/j.dt.2021.07.013. [21] WU C Q, FATTORI G, WHITTAKER A, et al. Investigation of air-blast effects from spherical-and cylindrical-shaped charges [J]. International Journal of Protective Structures, 2010, 1(3): 345–362. DOI: 10.1260/2041-4196.1.3.345. [22] HU Y, CHEN L, FANG Q, et al. Blast loading model of the RC column under close-in explosion induced by the double-end-initiation explosive cylinder [J]. Engineering Structures, 2018, 175: 304–321. DOI: 10.1016/j.engstruct.2018.08.013. [23] SHERKAR P, SHIN J, WHITTAKER A, et al. Influence of charge shape and point of detonation on blast-resistant design [J]. Journal of Structural Engineering, 2016, 142(2): 1–11. DOI: 10.1061/(asce)st.1943-541x.0001371. [24] XIAO W F, ANDRAE M, GEBBEKEN N. Effect of charge shape and initiation configuration of explosive cylinders detonating in free air on blast-resistant design [J]. Journal of Structural Engineering, 2020, 146(8): 1–13. DOI: 10.1061/(asce)st.1943-541x.0002694. [25] THAM C Y. Numerical simulation on the interaction of blast waves with a series of aluminum cylinders at near-field [J]. International Journal of Impact Engineering, 2009, 36(1): 122–131. DOI: 10.1016/j.ijimpeng.2007.12.011. [26] SIMOENS B, LEFEBVRE M. Influence of the shape of an explosive charge: quantification of the modification of the pressure field [J]. Central European Journal of Energetic Materials, 2015, 12(2): 195–213. [27] PAPE R, MNISZEWSKI K R, LONGINOW A, et al. Explosion phenomena and effects of explosions on structures Ⅲ: methods of analysis (explosion damage to structures) and example cases [J]. Practice Periodical on Structural Design and Construction, 2010, 15(2): 153–169. DOI: 10.1061/(ASCE)SC.1943-5576.0000040. [28] KNOCK C, DAVIES N. Blast waves from cylindrical charges [J]. Shock Waves, 2013, 23(4): 337–343. DOI: 10.1007/s00193-013-0438-7. [29] YANG T C, LUO Y Z, HU G Q, et al. Probability distribution and determination of blast loading during structural blast resistant study [J]. Shock and Vibration, 2022. DOI: Artn 736728810.1155/2022/7367288. [30] WISOTSKI J, SNYER. W H. Characteristics of blast waves obtained from cylindrical high explosive charges: 80210, DRI-2286 [R]. Denver, USA: University of Denver, Denver Research Institute, 1965. [31] PLOOSTER M N. Blast effects from cylindrical explosive charges: experimental measurements: NWC TP 6382 [R]. China Lake, USA: Naval Report Centre, 1982. [32] SU Q, WU H, SUN H S, et al. Experimental and numerical studies on dynamic behavior of reinforced UHPC panel under medium-range explosions [J]. International Journal of Impact Engineering, 2021, 148: 1–23. DOI: 10.1016/j.ijimpeng.2020.103761. [33] TIAN S Z, YAN Q S, DU X L, et al. Experimental and numerical studies on the dynamic response of precast concrete slabs under blast load [J]. Journal of Building Engineering, 2023, 70: 1–18. DOI: 10.1016/j.jobe.2023.106425. [34] WHARTON R K, FORMBY S A, MERRIFIELD R. Airblast TNT equivalence for a range of commercial blasting explosives [J]. Journal of Hazardous Materials, 2000, 79(1): 31–39. DOI: 10.1016/S0304-3894(00)00168-0. -
计量
- 文章访问数: 335
- HTML全文浏览量: 88
- PDF下载量: 243
- 被引次数: 0