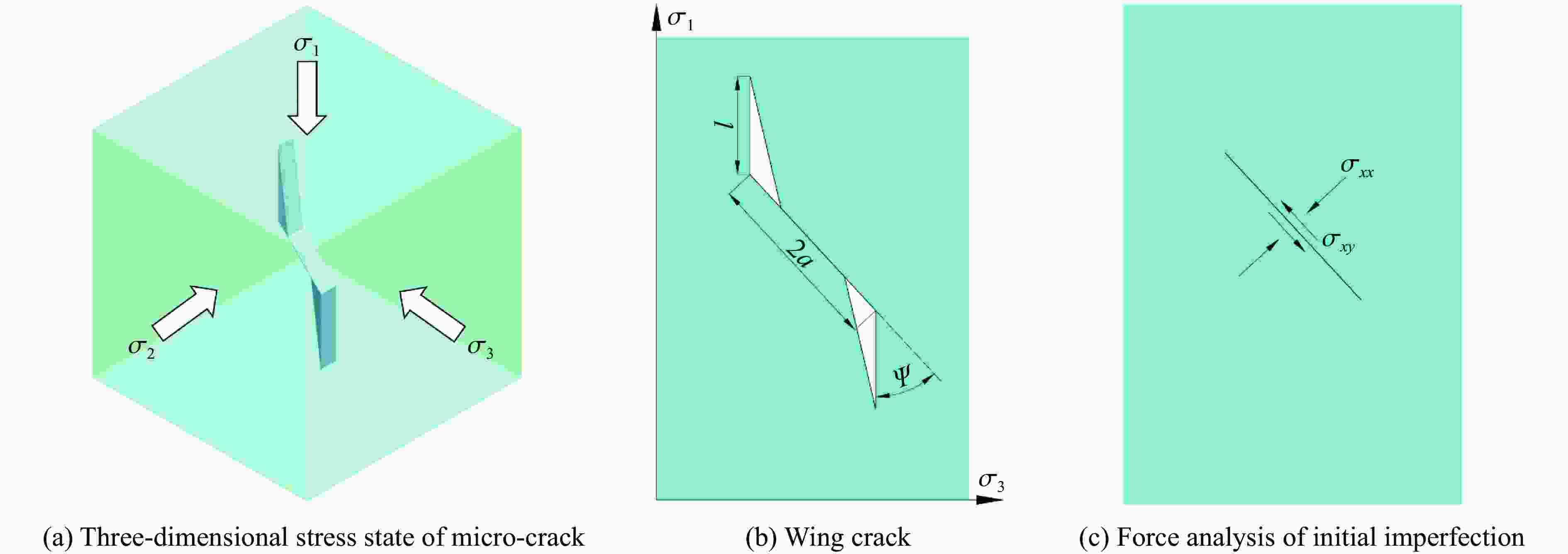
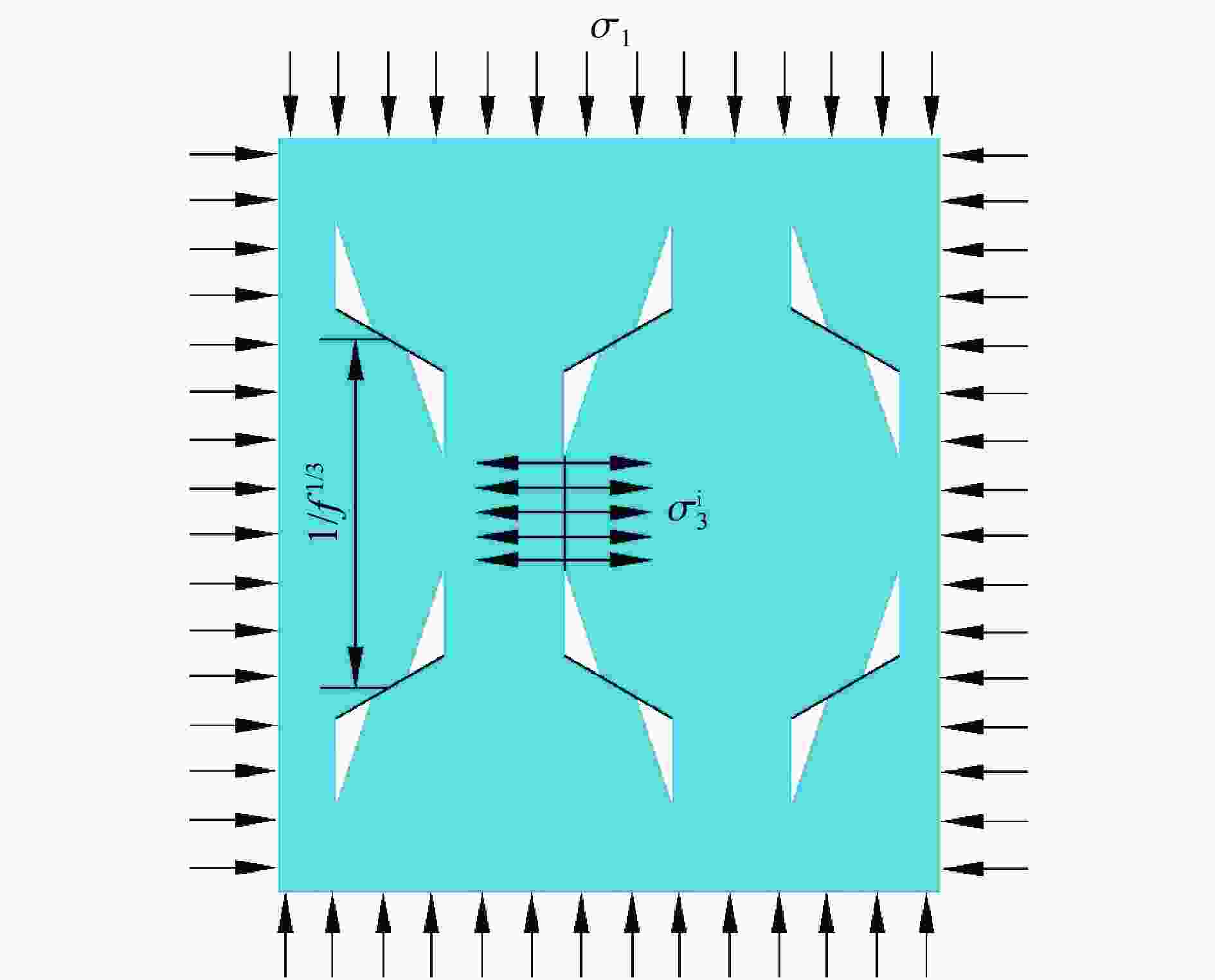
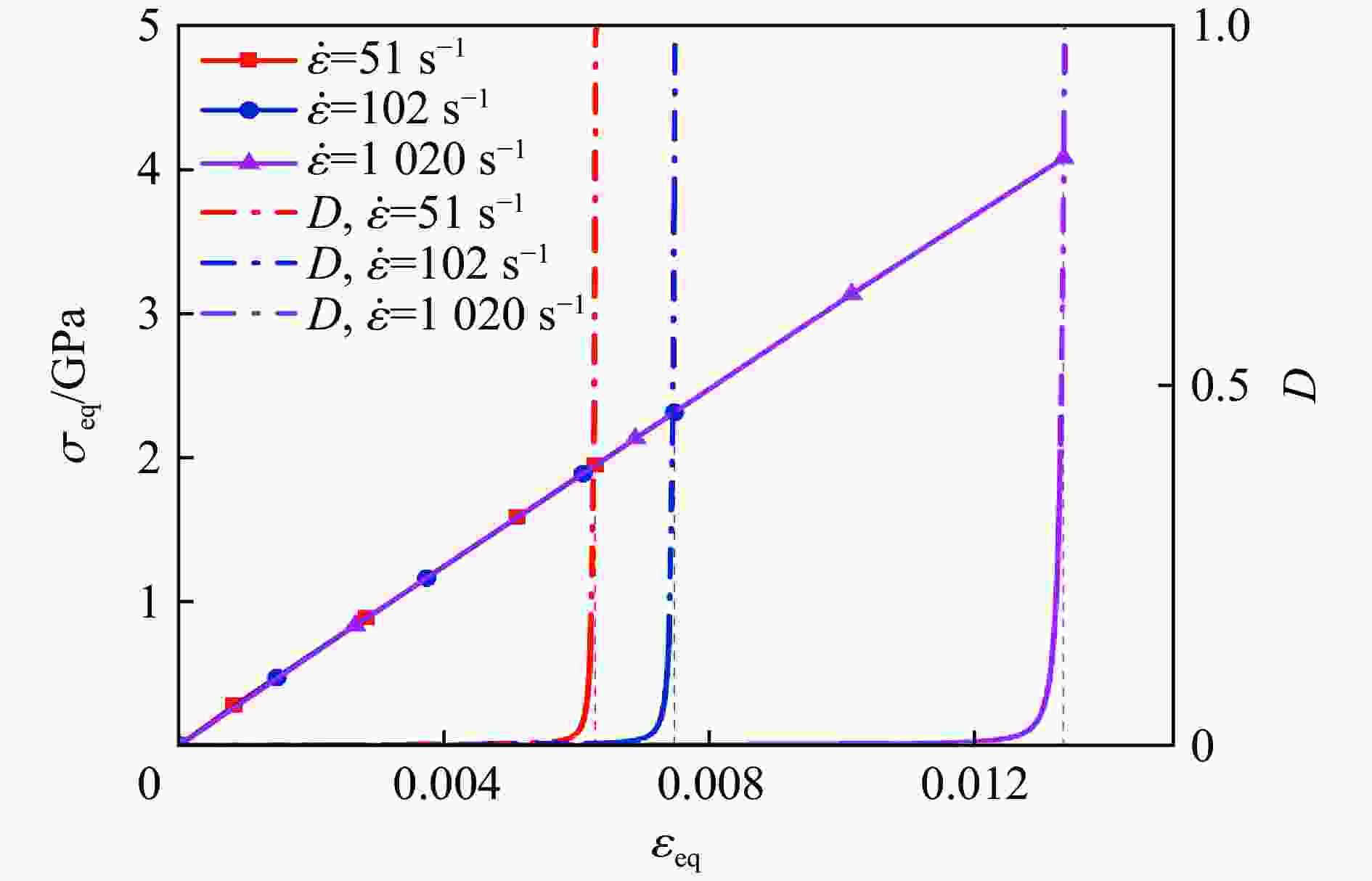
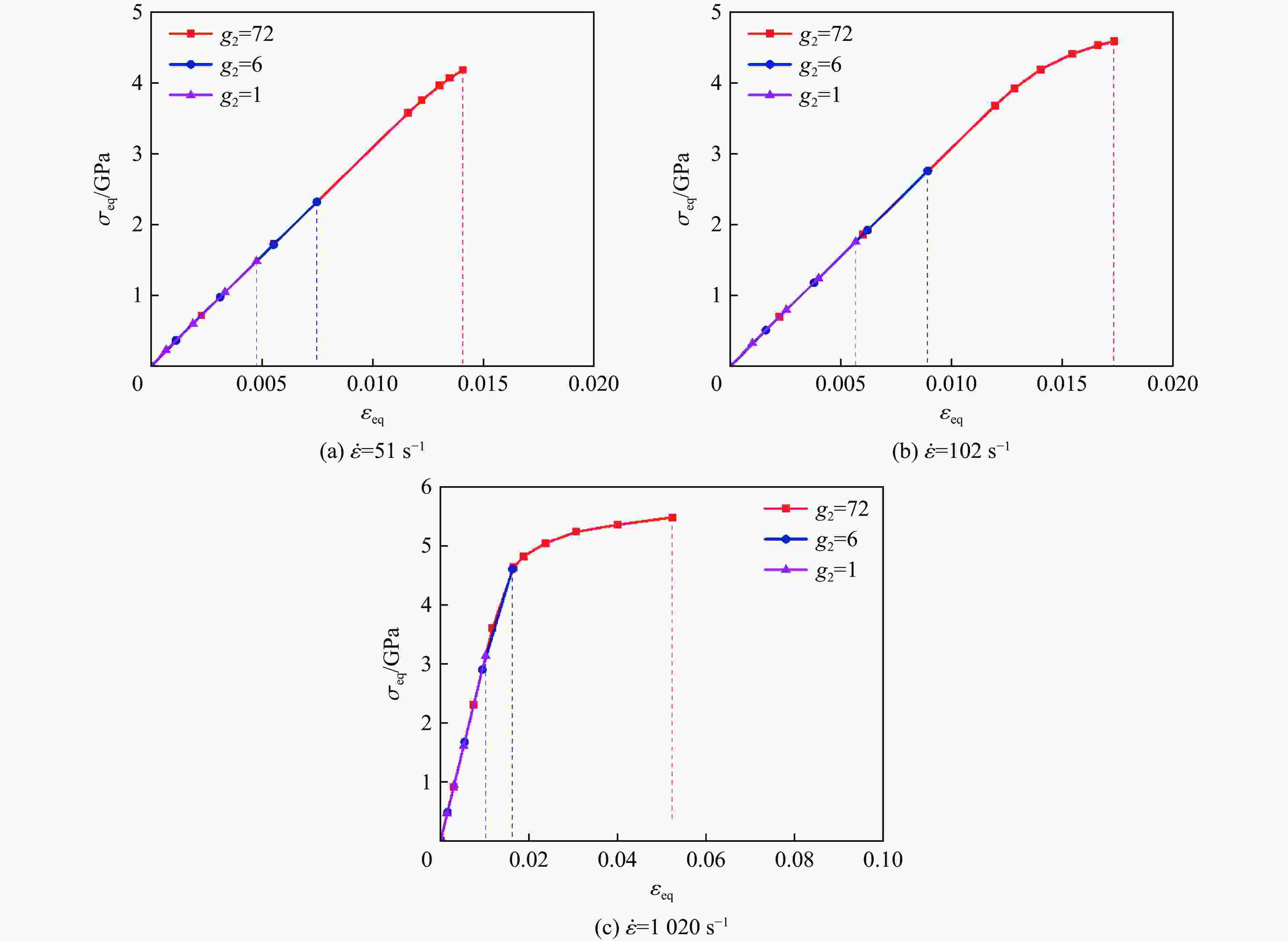
A constitutive model for ceramic materials including microstructural features and damage factor
-
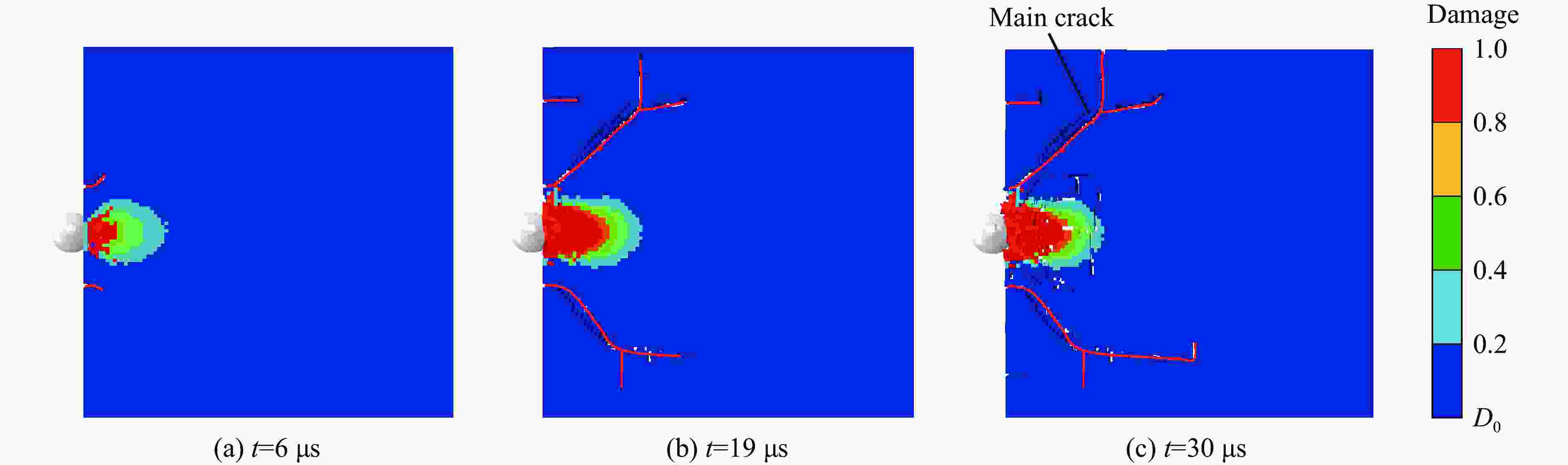
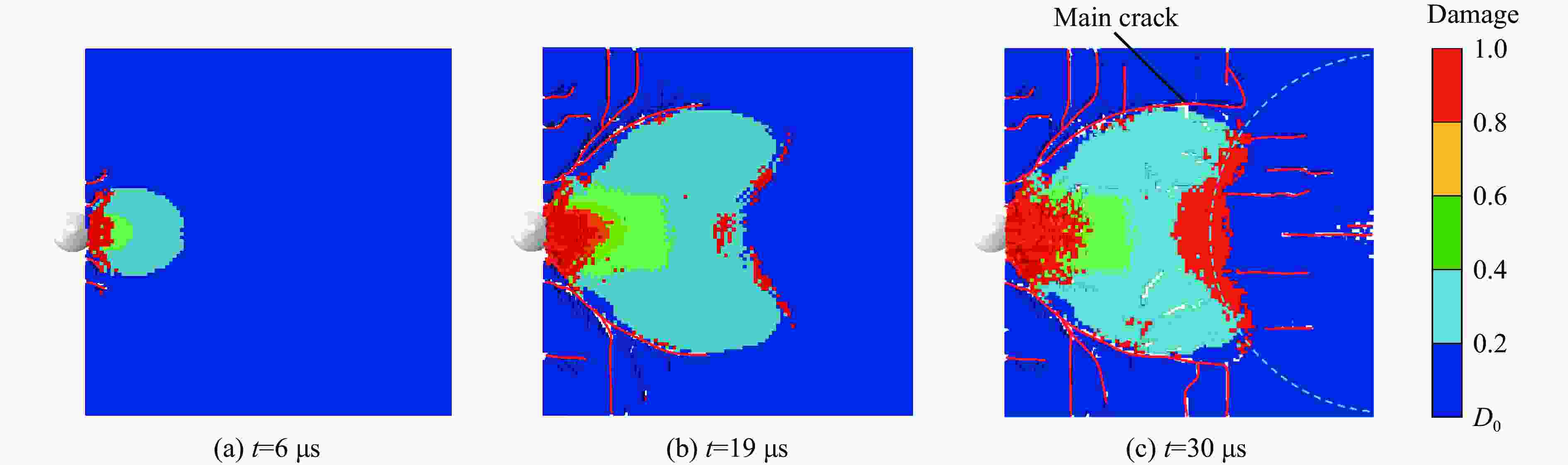
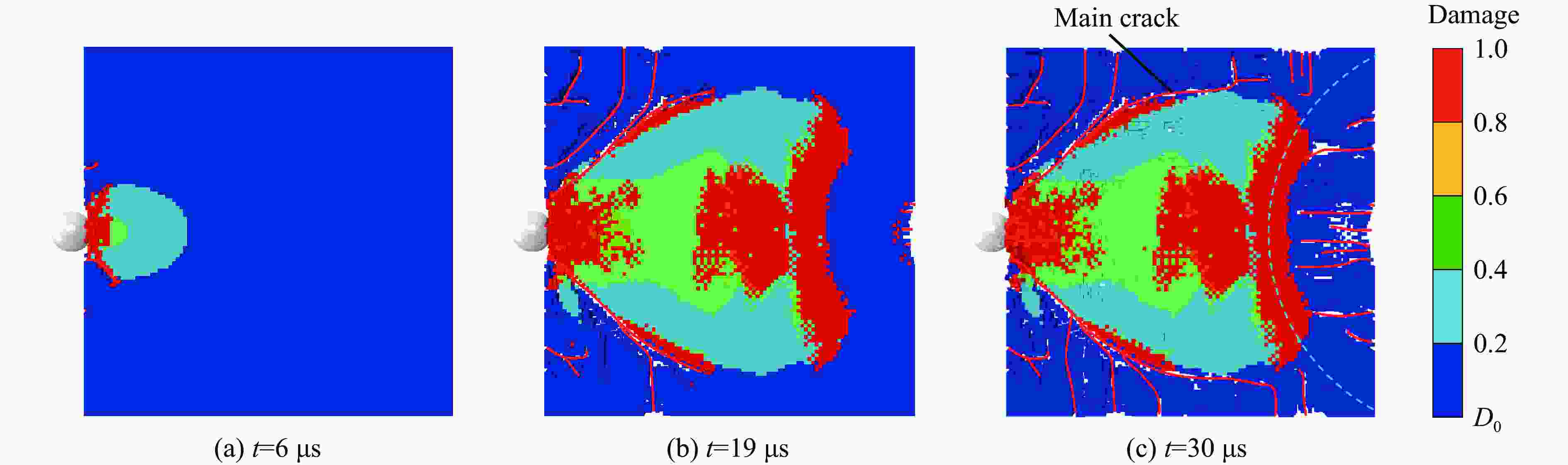
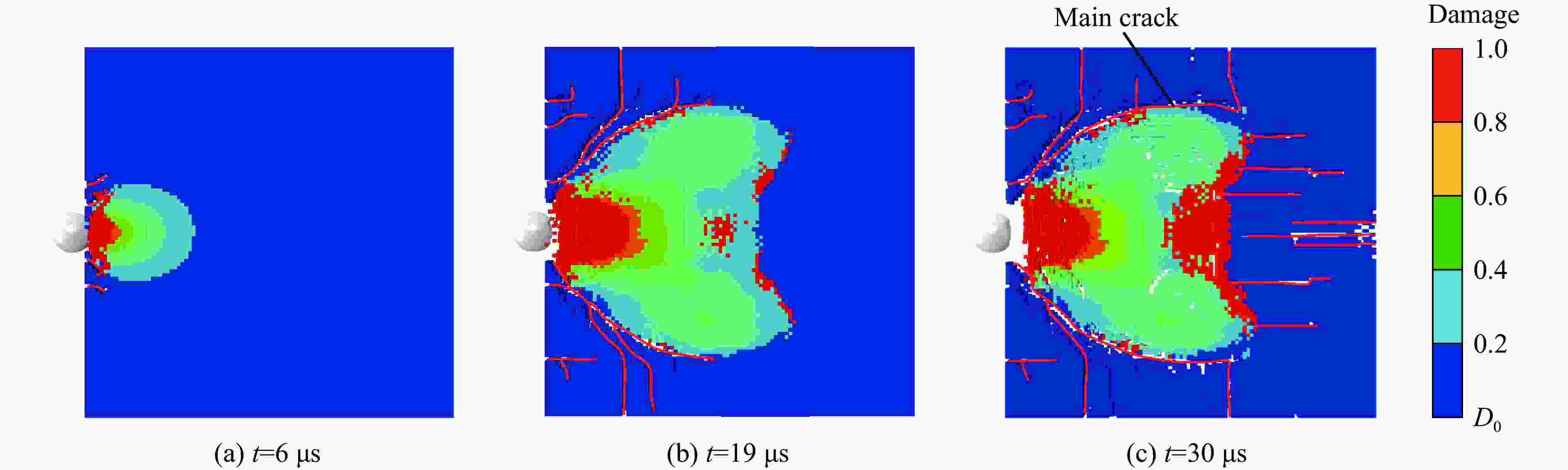
摘要: 为了研究不同微结构陶瓷材料的冲击破坏特征，以从微结构角度出发、描述陶瓷材料非弹性变形和断裂行为的Deshpande-Evan模型为基础构建本构模型，计算了无约束条件下材料的应力状态。为了验证改进模型的有效性，将VUMAT子程序编程方法将与ABAQUS有限元软件相结合，并将其应用于典型陶瓷材料（YAG透明陶瓷）冲击破坏过程的分析模拟。采用改进模型分析应变率、应力三轴度、晶粒尺寸及初始缺陷分布密度对YAG透明陶瓷动态力学行为和损伤演化机制的影响规律。结果表明：随着晶粒尺寸和裂纹分布密度的增加，YAG透明陶瓷破坏程度随之加剧，完全损伤区域面积也随之增加，晶粒尺寸对YAG透明陶瓷宏观破坏特征的影响程度要大于裂纹分布密度；YAG透明陶瓷失效强度以及断裂应变随着晶粒尺寸以及初始缺陷分布密度的增大而减小；随着应变率不断增加，YAG透明陶瓷在不同晶粒尺寸以及初始缺陷分布密度下的峰值应力和断裂应变均随之增加；裂纹扩展速度会随着晶粒尺寸的增加呈现出先增加而后平缓的趋势，裂纹扩展速度与初始缺陷分布密度系数成线性关系。改进模型可以描述YAG透明陶瓷微结构对其宏观破坏特征的影响，为进一步分析微结构对陶瓷材料宏观破坏特征的影响提供支撑。Abstract: In order to study the impact failure characteristics of ceramic materials with different microstructures, a constitutive model was constructed based on the Deshpande-Evan model which describes the inelastic deformation and fracture behavior of ceramic materials from the perspective of microstructure and the stress state of the material is calculated without considering the constraint condition. In order to verify the validity of the improved model, VUMAT subroutine programming method was used to combine it with ABAQUS finite element software, and it was applied to the analysis and simulation of the impact failure process of typical ceramic materials (YAG transparent ceramics). The effects of strain rate, stress triaxiality, grain size and crack distribution density on the dynamic mechanical behavior and damage evolution mechanism of YAG transparent ceramics were analyzed by using the improved model. The results show that with the increase of grain size and crack distribution density, the damage degree of YAG transparent ceramics increases, and the area of complete damage area increases. The influence of grain size on the macroscopic failure characteristics of YAG transparent ceramics is greater than that of crack distribution density. The failure strength and fracture strain of YAG transparent ceramics decrease with the increase of grain and crack distribution density. With the increase of the strain rate, the peak stress and fracture strain of YAG transparent ceramics under the influence of different factors (grain size as well as initial defect distribution density) increase. With the increase of grain size, the crack propagation speed of YAG transparent ceramics increases first and then flattens out, which is linearly related to the crack distribution density coefficient. The improved model can describe the influence of YAG transparent ceramic microstructure on its macroscopic failure characteristics, and provide support for further analysis of the influence of microstructure on the macroscopic failure characteristics of ceramic materials.
-
飞机座舱风挡、座舱盖和弦舱材料为高聚物材料, 在飞机飞行时需要承受一定的温度和载荷作用。在起飞和着陆时, 还有可能会遇到飞鸟的撞击, 军用飞机可能在空战中被非爆弹丸或高爆碎片击中, 这相当于对这些位置的材料施加一定的高速率载荷。同时, 由于飞机在低、高空飞行时, 环境温度相差很大, 高聚物材料的力学性能受外界温度的影响很大。因此, 开展对高聚物材料在高温和高应变率下的力学性能研究具有重要意义。
C.G’Sell等[1]对聚合物在常应变率下的变形行为进行了研究, 发现应变率影响材料的应变硬化现象。陈建桥等[2]、吴衡毅等[3]通过恒应变率的实验对有机玻璃进行了研究, 结果表明, 在较低应变率下, 有机玻璃的力学性能具有明显的应变率相关性。E.M.Arruda等[4]、O.S.Lee等[5]分别研究了准静态及中、高应变率下温度和应变率对PMMA材料力学性能的影响, 发现随着温度的升高, 材料的应力应变行为发生了显著变化, 同时伴随有热软化现象发生。G.W.Adams等[6]、Machida等[7]通过研究温度和应变率对PC材料力学性能的影响后发现:温度在293~338K之间时, 材料变形过程中储存的能量对实验温度的依赖性并不明显。S.M.Walley等[8]在一定的应变率范围内对一些高聚物材料进行了力学性能测试, 解释了在高应变率下由于绝热效应的原因, 使得材料出现应变软化行为。索涛等[9-10]对几种航空有机玻璃进行了研究, 认为在某一应变率和某一温度下, 由于试样内部的微裂纹使得有机玻璃表现出明显的应变软化行为; 在相同温度下, 随着应变率的升高, 有机玻璃的流动应力增大, 而破坏应变减小, 并建立了考虑温度效应的本构模型。
本文中对YB-2航空有机玻璃在不同温度下的准静态和动态力学行为进行系统的研究。分别采用Hopkinson分离式压杆和CSS44100型电子万能试验机对材料进行初始温度分别为218、253、293、343、373 K, 应变率分别为0.001、0.1、700、3 000 s-1下的压缩实验。同时, 结合实验数据, 基于朱-王-唐模型, 拟合考虑应变率效应以及温度效应的本构模型, 并给出模型预测和实验所得的应力应变曲线。
1. 实验过程与方法
1.1 导热时间的测定实验
有机玻璃是一种高分子材料, 对温度等环境比较敏感。由于聚合体材料的导热系数很低, 约是金属的1%, 即聚合体的导热系数为0.2 mm/min, 试样在加热或冷却的过程中, 如果加温或冷却的时间不充分, 试样表面温度和心部温度就会不一致, 导致实验结果不准确。因此, 在涉及温度的实验时, 为了确保实验中试样受热均匀和热平衡, 从而保证实验数据的准确性, 首先测试了YB-2有机玻璃在不同温度下试样表面和试样内部达到相同温度时所需要的时间。实验中, 采用正方体试样, 边长为10 mm。在试样中心沿着厚度方向钻孔, 孔的深度为5 mm。通过孔洞, 在试样心部引入一对热电偶。将另外一对热电偶缠绕在试样表面。用密闭的电热炉, 对试样进行加热或在密闭的容器中喷洒低温氮气对试样进行冷却。当经过标定的两组热电偶显示的温度相同时, 认为试样内部和外部的温度达到了平衡。
1.2 低应变率实验
低应变率压缩实验在CSS44100型电子万能试验机上进行, 压缩试样为直径6 mm、长4 mm的圆柱体, 如图 1所示。两种低应变率分别为0.1、0.001 s-1, 温度分别为218、253、293、343、373 K。实验前将压头降温或加热至相对应的实验温度后对试验机进行空压, 得到位移随着压力变化关系, 以此标定试验机刚度, 用于消除试样位移测量中试验机位移的影响。低温通过液氮循环获得, 高温实验采用电阻丝加热法对试样进行加热, 并用一个与试样相连的热电偶测量和显示温度, 通过电磁继电器的通断控制温度, 使之保持在实验值的±5 ℃误差范围内。
1.3 高应变率实验
700、3 000 s-1时的高应变率压缩实验是在一套直径12.7 mm的分离式Hopkinson压杆上进行的, 压杆所用材料为马氏体时效钢(18Ni(C250)), 实验装置见图 2。采取同低应变率下相同的试样。利用撞击杆撞击入射杆产生的应力波对放置于入射杆和透射杆之间的试样进行加载; 通过粘贴在两根杆子上与惠斯通电桥相连接的应变片采集输出的电压信号; 利用超动态应变仪和高频数据采集系统记录到实测波形, 并根据一维应力波原理可以得到材料的应力应变关系。高低应变下低温和高温的获得采用相同的方法。
2. 实验结果及分析
2.1 导热时间的测定
图 3(a)和(b)为加热或者冷却温度与保温时间的曲线以及不同的实验温度所需最短时间值。可以看出图 3(a)中, 当经过一定时间后, 无论是高温加热还是低温冷却, 试样内部和外部的温度达到一致, 记录加热或冷却的时间, 就得到了该温度下试样内外温度达到平衡所需的时间。从图 3(b)可以看出, 低温冷却试样内外温度平衡所需时间比高温时所需时间要短, 随着温度的逐渐升高, 平衡所需时间呈现逐渐变短的趋势。当温度高于有机玻璃的玻璃化转变温度后, 平衡时间变长。但如果温度继续升高, 平衡所需的时间几乎相同。
图 3 不同温度下保温时间曲线和保温所需最小时间Figure 3. Time-temperature curves and minimum times at different temperatures2.2 低应变率和高应变率压缩实验
YB-2航空有机玻璃有别于定向有机玻璃, 是未经过取向的高聚物, 分子链段的排列是随机的, 因此理论上材料体现出各向同性。在开始实验之前, 为了测试该材料的各向性能, 首先对其进行了考虑方向性的准静态压缩实验。试样分别取自于垂直于板材和平行于板材两个方向, 见图 1。实验结果(见图 4)表明:沿2个方向取样所测出的应力应变曲线基本吻合, 这说明材料力学各向同性。在后续的实验中采用的试样沿V方向取样。
图 5给出了在不同温度下试样的真实应力应变曲线。可以看出, 高分子材料的力学性能强烈依赖于温度和应变率。图 5(a)中, 当应变率为0.001 s-1时, 随着温度的升高, 材料的弹性模量呈现降低的趋势, 屈服强度减小, 塑性变形能力增加。在其余的3种应变率下(见图 5(b)~(d)), 材料呈现相似的趋势。在室温及以下的高应变率时, 材料的破坏应变随着温度的升高而增大, 此时, 材料为玻璃体呈现出典型的脆性破坏形式, 这是因为在低温高应变率下, 材料处于玻璃态, 且加载时间非常短暂, 材料的分子结构没有足够的时间发生弛豫, 因而断裂特性表现为脆性; 而当实验温度在材料的玻璃化转变温度(90 ℃)附近时, 材料处于高弹态, 其承载能力急剧下降, 变形能力增强, 不再呈现脆性破坏, 这是由于分子结构的活化能降低、自由体积增大, 因此受力后分子结构中的链段运动更加容易[11]。
图 6给出了同一温度下不同应变率时的应力应变曲线。在218 K时(见图 6(a)), 应变率对材料的弹性模量和屈服应力的影响并不明显, 但屈服应力仍呈现随应变率升高而升高的趋势, 破坏应变则反之。当温度升高时(见图 6(b)~(d)), 应变率对材料的弹性模量的影响逐渐变大, 屈服应力以及破坏应变呈现同218K时相似的趋势。4种应变率下, 材料均出现不同程度的应变软化。低应变率时, 由于加载脉冲宽度有限, 材料在实验中并未发生破坏。已有研究结果[12]表明:低温时, 聚合物处于玻璃态, 分子链的链段被冻结发生松弛的时间是无穷大, 此时, 加载速率(即应变率)的改变对聚合物材料变形的影响作用非常微弱, 表现为弹性模量对应变率的不敏感; 而在高温时, 聚合物处于高弹态, 其变形实际上是一种强迫高弹形变的过程, 分子链的链段已经被激活, 并且分子链的链段运动受到松弛时间的影响非常大。由于应变率的变化对松弛时间的影响很大, 因此在高温时弹性模量对应变率较为敏感。
图 7为不同应变率时温度-应力峰值曲线。当实验温度为218 K时, 不同应变率下试样的应力峰值差值较小。随着温度的升高, 应力峰值的差值变大, 在室温时应力峰值的差值达到最大。随后, 该差值又逐渐变小。这表明:在室温时材料的应变率敏感性达到最强。在高应变率加载下, 应变率对材料应力峰值的影响逐渐弱化。
3. YB-2有机玻璃的本构模型
朱兆祥等[13]对典型工程塑料进行的一系列研究发现:在变形小于8%, 应变率在10-4~103 s-1范围内, 朱-王-唐模型(ZWT)可以较好地描述高聚物材料的本构模型。该模型描述如下:
$$ \sigma(\varepsilon, \dot{\varepsilon})=E_{0} \varepsilon+\alpha \varepsilon^{2}+\beta \varepsilon^{2}+E_{1} \int_{0}^{t} \dot{\varepsilon} \exp \left(-\frac{t-\tau}{\theta_{1}}\right) \mathrm{d} t+E_{2} \int_{0}^{t} \dot{\varepsilon} \exp \left(-\frac{t-\tau}{\theta_{2}}\right) \mathrm{d} t $$ (1) 式中:E0、α和β为材料的弹性常数。2个积分项分别用来描述低应变率和高应变率下的黏弹性响应, E1、θ1和E2、θ2分别是所对应的Maxwell单元的弹性常数和松弛时间。
为描述温度对材料的影响, 索涛等[10]对朱-王-唐模型进行修正, 并分别对4种航空有机玻璃实验所得的真实应力应变曲线进行拟合, 实验与模型预测的曲线吻合较好。修正的模型中加入的温度效应项, 其形式为
/f0(ε, T0), 它随温度的升高而减小, 随应变的增大而增大。改进后的模型描述为:
$$ \sigma(\varepsilon, \dot{\varepsilon}, T)=\sigma(\varepsilon, \dot{\varepsilon}) f(\varepsilon, T) / f\left(\varepsilon, T_{0}\right) $$ (2) $$ f(\varepsilon, T)=a(\varepsilon) \exp [b(\varepsilon) T] $$ (3) 式中:
)为式(1)对应的温度和应变率下得到的应力值, T0为选定的参考温度。
根据公式(1)~(3)可得到温度影响项的表达式:
, 由实验数据拟合以多项式
给出。
基于该模型, 以293 K作为参考温度, 针对YB-2试样, 经过拟合实验曲线得到常温时的6个参数:E0=3.26 GPa、α=-20.12 GPa、E1=2.4 GPa、θ1=0.205 s、E2=2.622 GPa、θ2=6 μs。
在此基础上, 采用最小二乘法拟合可以得到YB-2航空有机玻璃温度效应影响项中b(ε)的估计表达式为:
$$ b(\varepsilon ) = 0.6429{\varepsilon ^2} - 0.1336\varepsilon - 0.004$$ (4) 对于拟合参数优度的评估, 我们将对回归参数的方差和置信区间进行分析。根据实验结果, 对公式(4)中各系数的方差和置信区间的分析如下:假定置信系数为0.95, 计算得出拟合函数的方差和置信区间见表 1。
表 1 温度影响项中各系数的方差和置信区间Table 1. Variances and confidence intervals of the coefficients for thermo-item参数 方差 置信区间 a 0.381 131 (0.527 425, 1.273 1) b 0.009 826 (-0.235 72, -0.103 88) c 0.000 295 (-0.004 56, -0.003 54) 图 8给出了拟合结果与实验结果的比较。不难看出, 图 8(a)~(c)中拟合曲线同实验曲线吻合较好; 对于图 8(d), 拟合曲线和实验曲线有较大差异, 这是因为在PMMA的热变形温度(70 ℃)左右时, 材料将开始发生玻璃态与高弹态之间的相态转变。而ZWT模型主要用来描述材料的黏弹性行为, 因此在拟合343 K下材料的变形行为时表现出较大的误差。总体来说, 改进后的ZWT模型可以较好的描述一定温度范围内材料的非线性黏弹性力学行为。
图 8 修正的ZWT模型拟合结果与实验结果的比较Figure 8. Comparison of prediction using modified ZWT model with experimental results4. 结论
通过对YB-2航空有机玻璃的研究得出以下结论:
(1) YB-2有机玻璃的力学性能强烈依赖于应变率和温度:在低应变率下, 随着温度的升高, 材料的弹性模量和流动应力逐渐减小, 弹性变形能力降低, 塑性变形能力增加; 在高应变率下, 材料的流动应力随着温度的升高逐渐减小, 破坏应变随着温度的升高而增大。在室温及以下时, 材料为玻璃体, 呈现出典型的脆性破坏, 弹性模量对应变率不敏感; 当实验温度在材料的玻璃化转变温度附近时, 高应变率下材料破坏不再呈现脆性破坏, 弹性模量对应变率较为敏感。
(2) 随着应变率的升高, 材料的流动应力显著升高, 但破坏应变减小。在室温时, 材料的应变率敏感性达到最强。在高应变率下, 材料的屈服强度受应变率的影响逐渐弱化。
(3) 加入温度效应的ZWT模型能够较好地拟合应变范围在8%以内的实验曲线, 但由于模型中未考虑损伤以及高分子高温下自由体积和复杂的分子链运动的影响, 因而不能较准确地描述应变软化以及大应变时的应变硬化现象。
-
图 1 陶瓷的典型微结构特征及缺陷
Figure 1. Typical microstructure characteristics and defects of ceramics
图 2 考虑微结构特征的陶瓷材料本构模型理论体系
Figure 2. Constitutive model theory system of ceramic materials considering microstructure characteristics
图 6 不同应变率下YAG透明陶瓷的应力-应变响应及损伤演化过程
Figure 6. Stress-strain response and damage evolution of YAG transparent ceramics at different strain rates
图 7 不同应力三轴度下YAG透明陶瓷的应力应变响应
Figure 7. Stress-strain response of YAG transparent ceramics under different stress triaxialities
图 8 不同晶粒度下YAG透明陶瓷的应力应变曲线
Figure 8. Stress-strain curves of YAG transparent ceramics with different grain sizes
图 9 不同裂纹分布密度下YAG透明陶瓷的应力应变曲线
Figure 9. Stress-strain curves of YAG transparent ceramics with different crack distribution densities
图 13 主裂纹扩展长度模拟结果与试验对比图
Figure 13. Comparison between simulation and test results of main crack propagation length
图 14 YAG透明陶瓷破坏特征，d=40 μm
Figure 14. Damage characteristics of YAG transparent ceramics while d=40 μm
图 15 YAG透明陶瓷破坏特征，d=100 μm
Figure 15. Damage characteristics of YAG transparent ceramics while d=100 μm
图 16 YAG透明陶瓷破坏特征，d=150 μm
Figure 16. Damage characteristics of YAG transparent ceramics while d=150 μm
图 18 YAG透明陶瓷破坏特征，g2=6
Figure 18. Damage characteristics of YAG transparent ceramics, g2=6
图 19 YAG透明陶瓷破坏特征，g2=10
Figure 19. Damage characteristics of YAG transparent ceramics, g2=10
图 20 YAG透明陶瓷破坏特征，g2=12
Figure 20. Damage characteristics of YAG transparent ceramics, g2=12
图 21 裂纹扩展速度与裂纹密度系数的关系
Figure 21. Relationship of crack propagation velocity with crack density coefficient
表 1 YAG透明陶瓷弹性阶段材料参数
Table 1. Material parameters of YAG transparent ceramics in elastic stage
密度/（kg·m3） 剪切模量/GPa 泊松比 $ {\sigma }_{\rm{Y}} $/GPa 4550 113 0.25 1.58 
下载: 导出CSV
表 2 YAG透明陶瓷塑性阶段材料参数
Table 2. Material parameters of transparent YAG ceramic in plastic stage
$ {\sigma }_{\rm{Y}} $/GPa $ {\varepsilon }_{\rm{Y}} $ $ {\dot{{ \varepsilon }}}_0 $/s−1 $ {\dot{\varepsilon }}_{\rm{t}} $/s−1 n M 1.58 5.6×10−3 1×10−3 1×106 34 0.1
下载: 导出CSV
Table 3. Material parameters of YAG transparent ceramics in crack propagation stage
d/μm 摩擦因数 KⅠC/（MPa·m1/2） β γ g1 g2 m $ {\dot{l}}_{0} $/（m·s−1） 100 0.75 1.27 0.45 2 0.5 6 30 0.01
下载: 导出CSV
-
[1] 胡泽望, 陈肖朴, 刘欣, 等. 微量SiO2添加对Pr: Lu3Al5O12陶瓷光学及闪烁性能的影响 [J]. 无机材料学报, 2020, 35(7): 796–802. DOI: 10.15541/jim20190418.HU Z W, CHEN X P, LIU X, et al. Trace SiO2 addition on optical and scintillation property of Pr: Lu3Al5O12 ceramics [J]. Journal of Inorganic Materials, 2020, 35(7): 796–802. DOI: 10.15541/jim20190418. [2] 卢绪高. 轧膜成型氮化硅陶瓷的组织结构与导热性能研究 [D]. 哈尔滨: 哈尔滨工业大学, 2019. [3] TAYLOR L M, CHEN E P, KUSZMAUL J S. Microcrack-induced damage accumulation in brittle rock under dynamic loading [J]. Computer Methods in Applied Mechanics and Engineering, 1986, 55(3): 301–320. DOI: 10.1016/0045-7825(86)90057-5. [4] RAJENDRAN A M, KROUPA J L. Impact damage model for ceramic materials [J]. Journal of Applied Physics, 1989, 66(8): 3560–3565. DOI: 10.1063/1.344085. [5] STEINBERG D J. Computer studies of the dynamic strength of ceramics [C]//Proceedings of the 18th International Symposium on Shock Waves. Senda: Springer, 1991: 415–422. DOI: 10.1007/978-3-642-77648-9_64. [6] JOHNSON G R, HOLMQUIST T J. A computational constitutive model for brittle materials subjected to large strains, high strain rates, and high pressures [M]// Shock Wave and High-Strain-Rate Phenomena in Materials. CRC Press, 1992: 1075–1082. DOI: 10.1115/1.4004326. [7] JOHNSON G R, HOLMQUIST T J. An improved computational constitutive model for brittle materials [J]. AIP Conference Proceedings, 1994, 309(1): 981–984. DOI: 10.1063/1.46199. [8] JOHNSON G R, HOLMQUIST T J, BEISSEL S R. Response of aluminum nitride (including a phase change) to large strains, high strain rates, and high pressures [J]. Journal of Applied Physics, 2003, 94(3): 1639–1646. DOI: 10.1063/1.1589177. [9] WILKINS M. Second progress report of light armor program [R]. Livermore: Lawrence Livermore National Laboratory, 1967. DOI: 10.2172/7156835. [10] CHAKRABORTY S, ISLAM R I, SHAW A, et al. A computational framework for modelling impact induced damage in ceramic and ceramic-metal composite structures [J]. Composite Structures, 2017, 164: 263–276. DOI: 10.1016/j.compstruct.2016.12.064. [11] REN H L, ZHUANG X Y, RABCZUK T. Implementation of GTN model in dual-horizon peridynamics [J]. Procedia Engineering, 2017, 197: 224–232. DOI: 10.1016/j.proeng.2017.08.099. [12] 唐瑞涛, 徐柳云, 文鹤鸣, 等. 陶瓷材料宏观动态新本构模型 [J]. 高压物理学报, 2020, 34(4): 044201. DOI: 10.11858/gywlxb.20190863.TANG R T, XU L Y, WEN H M, et al. A macroscopic dynamic constitutive model for ceramic materials [J]. Chinese Journal of High Pressure Physics, 2020, 34(4): 044201. DOI: 10.11858/gywlxb.20190863. [13] RAJENDRAN A M. Modeling the impact behavior of AD85 ceramic under multiaxial loading [J]. International Journal of Impact Engineering, 1994, 15(6): 749–768. DOI: 10.1016/0734-743x(94)90033-h. [14] RAJENDRAN A M, GROVE D J. Modeling the shock response of silicon carbide, boron carbide and titanium diboride [J]. International Journal of Impact Engineering, 1996, 18(6): 611–631. DOI: 10.1016/0734-743x(96)89122-6. [15] ESPINOSA H D, ZAVATTIERI P D, DWIVEDI S K. A finite deformation continuum\discrete model for the description of fragmentation and damage in brittle materials [J]. Journal of the Mechanics and Physics of Solids, 1998, 46(10): 1909–1942. DOI: 10.1016/s0022-5096(98)00027-1. [16] 任会兰, 宁建国. 冲击压缩下准脆性材料含微裂纹损伤的本构模型 [J]. 材料工程, 2007(3): 18–21. DOI: 10.3969/j.issn.1001-4381.2007.03.005.REN H L, NING J G. Micro-cracks damage constitutive model of quasi-brittle materials subjected to shock compression [J]. Journal of Materials Engineering, 2007(3): 18–21. DOI: 10.3969/j.issn.1001-4381.2007.03.005. [17] 任会兰, 宁建国. 强冲击载荷下氧化铝陶瓷的力学特性及本构模型 [J]. 北京理工大学学报, 2007, 27(9): 761–764, 796. DOI: 10.3969/j.issn.1001-0645.2007.09.003.REN H L, NING J G. Mechanical characteristics and constitutive model of alumina ceramic subjected to shock loading [J]. Transactions of Beijing Institute of Technology, 2007, 27(9): 761–764, 796. DOI: 10.3969/j.issn.1001-0645.2007.09.003. [18] ASHBY M F, SAMMIS C G. The damage mechanics of brittle solids in compression [J]. Pure and Applied Geophysics, 1990, 133(3): 489–521. DOI: 10.1007/BF00878002. [19] WANG D, ZHAO J, ZHOU Y H, et al. Extended finite element modeling of crack propagation in ceramic tool materials by considering the microstructural features [J]. Computational Materials Science, 2013, 77: 236–244. DOI: 10.1016/j.commatsci.2013.04.045. [20] VIGLIOTTI A, DESHPANDE V S, PASINI D. Non linear constitutive models for lattice materials [J]. Journal of the Mechanics and Physics of Solids, 2014, 64: 44–60. DOI: 10.1016/j.jmps.2013.10.015. [21] DESHPANDE V S, EVANS A G. Inelastic deformation and energy dissipation in ceramics: a mechanism-based constitutive model [J]. Journal of the Mechanics and Physics of Solids, 2008, 56(10): 3077–3100. DOI: 10.1016/j.jmps.2008.05.002. [22] DESHPANDE V S, GAMBLE E A N, COMPTON B G, et al. A constitutive description of the inelastic response of ceramics [J]. Journal of the American Ceramic Society, 2011, 94(S1): s204–s214. DOI: 10.1111/j.1551-2916.2011.04516.x. [23] LAHIRI S K, SHAW A, RAMACHANDRA L S. On performance of different material models in predicting response of ceramics under high velocity impact [J]. International Journal of Solids and Structures, 2016, 176-177: 96–107. DOI: 10.1016/j.ijsolstr.2019.05.024. [24] GAMBLE E A, COMPTON B G, DESHPANDE V S, et al. Damage development in an armor ceramic under quasi-static indentation [J]. Journal of the American Ceramic Society, 2011, 94(S1): s215–s225. DOI: 10.1111/j.1551-2916.2011.04472.x. [25] ASHBY M F, HALLAM S D. The failure of brittle solids containing small cracks under compressive stress states [J]. Acta Metallurgica, 1986, 34(3): 497–510. DOI: 10.1016/0001-6160(86)90086-6. [26] 韩国庆, 张先锋, 谈梦婷, 等. 边缘冲击(EOI)作用下透明陶瓷破坏特性研究 [J]. 爆炸与冲击, 2022, 42(5): 053102. DOI: 10.11883/bzycj-2021-0292.HAN G Q, ZHANG X F, TAN M T, et al. Failure characteristics of three transparent ceramics materials under the edge-on impact loading [J]. Explosion and Shock Waves, 2022, 42(5): 053102. DOI: 10.11883/bzycj-2021-0292. [27] 马坤, 李名锐, 陈春林, 等. 修正金属本构模型在超高速撞击模拟中的应用 [J]. 爆炸与冲击, 2022, 42(9): 091406. DOI: 10.11883/bzycj-2021-0315.MA K, LI M R, CHEN C L, et al. The application of a modified constitutive model of metals in the simulation of hypervelocity impact [J]. Explosion and Shock Waves, 2022, 42(9): 091406. DOI: 10.11883/bzycj-2021-0315. -
下载:
计量
- 文章访问数: 287
- HTML全文浏览量: 67
- PDF下载量: 164
- 被引次数: 0