融合先验知识的混凝土侵彻深度试验数据异常点检测算法

秦帅; 刘浩; 陈力; 张磊

doi:10.11883/bzycj-2023-0287

融合先验知识的混凝土侵彻深度试验数据异常点检测算法

doi: 10.11883/bzycj-2023-0287

秦帅^{1, 2,},
刘浩^{1, 3},
陈力¹,
张磊^1, ,

1.
军事科学院国防工程研究院，河南洛阳，471000
2.
哈尔滨工程大学计算机科学与技术学院，黑龙江哈尔滨，150001
3.
哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨，150001

基金项目: 国家自然科学基金（12172381）；中原科技创新领军人才项目（234200510016）

详细信息

作者简介:
秦　帅（1995－　），男，博士研究生，2013061315@hrbeu.edu.cn

通讯作者:
张　磊（1974－　），男，博士，研究员，ustczhanglei@163.com

中图分类号: O385
计量
- 文章访问数: 181
- HTML全文浏览量: 65
- PDF下载量: 80
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-14
- 修回日期: 2023-11-23
- 网络出版日期: 2023-11-24
- 刊出日期: 2024-03-14

Outlier detection algorithms for penetration depth data of concrete targets combined with prior knowledge

QIN Shuai^{1, 2
,},
LIU Hao^{1, 3},
CHEN Li¹,
ZHANG Lei^{1
, ,}

1.
Institute of Defense Engineering, AMS, Luoyang 471000, Henan, China
2.
College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, Heilongjiang, China
3.
College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China

摘要

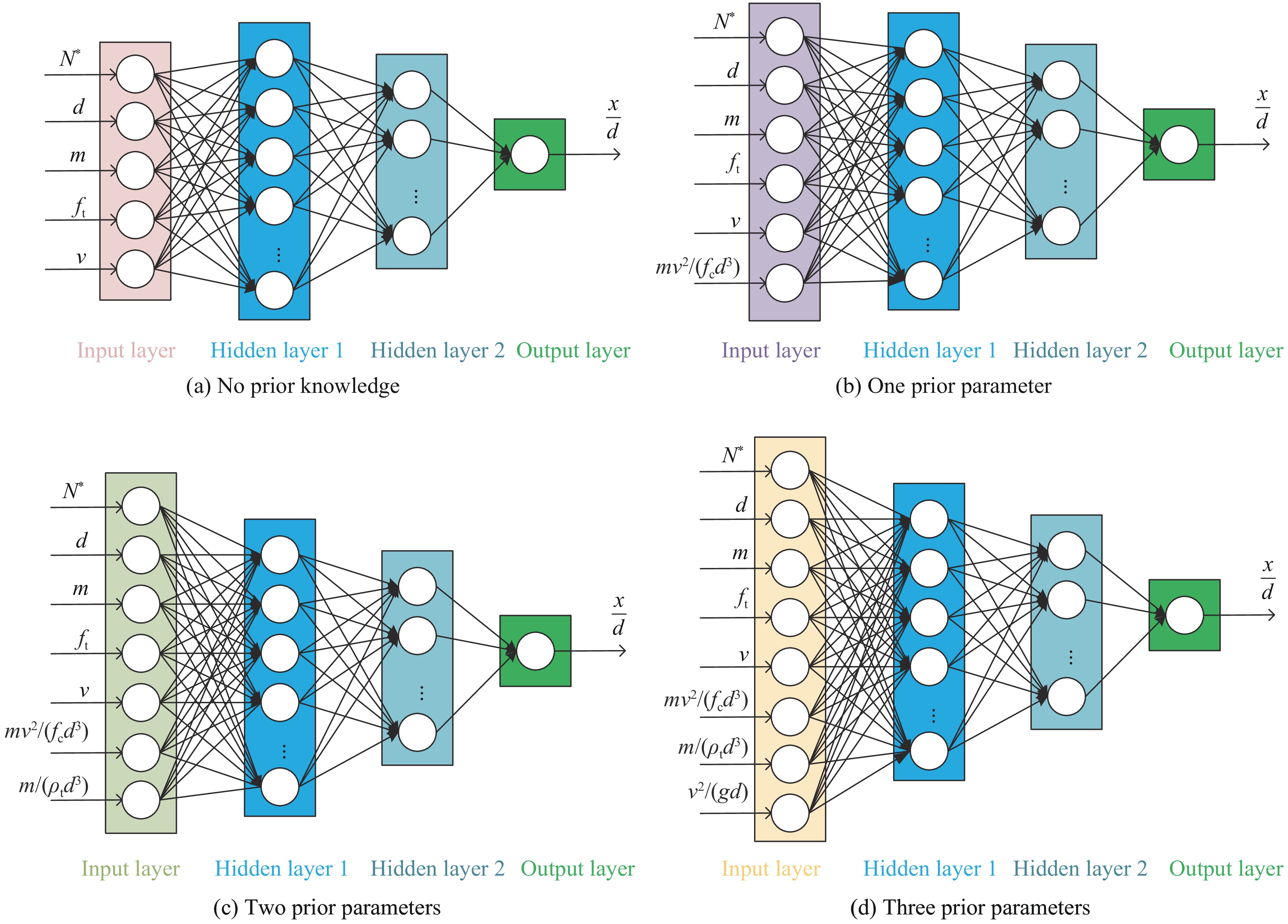
摘要: 为剔除混凝土侵彻深度试验数据异常点，提出了一种融合先验知识的异常检测算法。利用反向传播（back propagation, BP）神经网络模型拟合试验样本数据的分布，结合偏差指标筛选离群样本点，并通过经验算法评价模型异常检测性能。针对试验数据特点选择全量梯度下降结合动量优化方法，从而提高模型迭代训练的稳定性和效率，并且在构建模型过程中融合领域先验知识约束对样本数据的拟合，使得模型在训练过程中能反映附加特征的影响。结果表明，BP神经网络模型适合于刚性弹对混凝土侵彻试验数据异常点的检测，加入合理的领域先验知识可有效提高模型的检测精度。
- 混凝土侵彻 /
- 神经网络 /
- 先验知识 /
- 异常检测
Abstract: Data quality is the basis for the validity and accuracy of data-driven models, and there may be a large number of anomalies in the raw concrete targets penetration depth data. Therefore, to ensure the accuracy of the subsequent data-driven model, it is necessary to eliminate the outlier of the raw data. Compared with the traditional anomaly detection method, the anomaly detection method based on neural network models is more suitable for complex multi-dimensional and unevenly distributed concrete target penetration depth data. However, relying only on the neural network model to fit the raw experimental data ignores the abundant and effective expert prior knowledge, which will reduce the accuracy of the model, and even lead to wrong prediction results due to the limited amount of data of the training sample, data bad pixels, poor data distribution, etc. To this end, an algorithm for outlier detection of concrete target penetration depth data combined with prior knowledge was proposed. Firstly, the back propagation (BP) neural network model is used to fit the distribution of the experiment samples, then the outlier is screened out based on the deviation index, and at last, the anomaly detection performance of the model is evaluated by the empirical algorithm. Based on the characteristics of the experimental data, the batch gradient descent combined with the momentum optimization method is selected to improve the stability and efficiency during training. Furthermore, by adding domain prior knowledge with the BP neural network model to constrain the fitting of the sample data, the model can reflect the influence of additional features during training. The research results show that the BP neural network model is suitable for the outlier detection of the rigid projectile penetrating concrete experiment data. The fusion of reasonable prior knowledge can improve the detection accuracy and the convergence speed of the model, furthermore, integrating different prior knowledge will cause different results.
- concrete penetration /
- neural network /
- prior knowledge /
- anomaly detection

HTML全文

图 1 构建的4种神经网络模型基本结构

Figure 1. Basic structures of the four neural network models constructed

下载: 全尺寸图片幻灯片

图 2 4种神经网络模型预测的无量纲侵彻深度与真实无量纲侵彻深度的相对偏差

Figure 2. Relative deviations between the predicted dimensionless penetration depths by the four neural network models and the actual dimensionless penetration depth

下载: 全尺寸图片幻灯片

图 3 4种模型训练误差对比

Figure 3. Comparison of training losses of the four models

下载: 全尺寸图片幻灯片

表 1 试验数据示例

Table 1. Examples of experimental data

d/m	m/kg	v/(m·s⁻¹)	f_c/MPa	N^*	x/d
0.01292	0.064	371	13.8	1	9.83
0.0762	5.9	308	35.1	3	3.04
0.305	191.62	79	39.0	2	0.098
0.01292	0.064	1142	13.8	0	65.79
$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $

下载: 导出CSV

表 2 各速度区间数据分布

Table 2. Data distribution in each velocity range

速度区间/(m·s⁻¹)	样本数/个	速度区间/(m·s⁻¹)	样本数/个
[0, 400]	379	(800, 1200]	117
(400, 800]	542	(1200, 1700]	40

下载: 导出CSV

表 3 各质量区间数据分布

Table 3. Data distribution in each mass range

质量区间/kg	样本数/个	质量区间/kg	样本数/个
[0, 50]	991	(100, 500]	56
(50, 100]	31

下载: 导出CSV

表 4 异常数据示例

Table 4. Examples of outlier data

数据编号	d/m	m/kg	v/(m·s⁻¹)	f_c/MPa	N^*	x/d	备注
306	0.0127	0.0587	399	29.2	0	9.40
307	0.0127	0.0587	334.9	29.2	0	11.19	异常数据
308	0.0127	0.0587	453.8	29.2	0	11.04
569	0.05	4.5	417	135	2	9.9
571	0.05	4.5	460	135	2	11.2
573	0.05	4.5	456	135	2	10.8
577	0.05	4.5	456	135	2	5	异常数据
$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $

下载: 导出CSV

表 5 模型异常检测性能对比

Table 5. Comparison of the outlier detection performances of the models

模型	样本总数	模型剔除异常样本点数	经验算法评判异常样本点数	准确率
无融合先验知识	1078	128	87	0.6796
融合单先验参数	1078	113	78	0.6903
融合双先验参数	1078	115	86	0.7478
融合三先验参数	1078	112	82	0.7321

下载: 导出CSV

参考文献(23)

[1]	张磊, 吴昊, 赵强, 等. 基于数据挖掘技术的地下工程目标毁伤效应计算方法 [J]. 爆炸与冲击, 2021, 41(3): 031101. DOI: 10.11883/bzycj-2020-0114. ZHANG L, WU H, ZHAO Q, et al. Calculation method of damage effects of underground engineering objectives based on data mining technology [J]. Explosion and Shock Waves, 2021, 41(3): 031101. DOI: 10.11883/bzycj-2020-0114.
[2]	LI Q L, WANG Y, SHAO Y D, et al. A comparative study on the most effective machine learning model for blast loading prediction: from GBDT to Transformer [J]. Engineering Structures, 2023, 276: 115310. DOI: 10.1016/j.engstruct.2022.115310.
[3]	ALMUSTAFA M K, NEHDI M L. Machine learning model for predicting structural response of RC slabs exposed to blast loading [J]. Engineering Structures, 2020, 221: 111109. DOI: 10.1016/j.engstruct.2020.111109.
[4]	ALMUSTAFA M K, NEHDI M L. Machine learning model for predicting structural response of RC columns subjected to blast loading [J]. International Journal of Impact Engineering, 2022, 162: 104145. DOI: 10.1016/j.ijimpeng.2021.104145.
[5]	ZHAO C F, ZHU Y F, ZHOU Z H. Machine learning-based approaches for predicting the dynamic response of RC slabs under blast loads [J]. Engineering Structures, 2022, 273: 115104. DOI: 10.1016/j.engstruct.2022.115104.
[6]	NETO L B, SALEH M, PICKERD V, et al. Rapid mechanical evaluation of quadrangular steel plates subjected to localised blast loadings [J]. International Journal of Impact Engineering, 2020, 137: 103461. DOI: 10.1016/j.ijimpeng.2019.103461.
[7]	WANG H Z, BAH M J, HAMMAD M. Progress in outlier detection techniques: a survey [J]. IEEE Access, 2019, 7: 107964–108000. DOI: 10.1109/ACCESS.2019.2932769.
[8]	PANG G S, SHEN C H, CAO L B, et al. Deep learning for anomaly detection: a review [J]. ACM Computing Surveys, 2021, 54(2): 38. DOI: 10.1145/3439950.
[9]	MURALIDHAR N, ISLAM M R, MARWAH M, et al. Incorporating prior domain knowledge into deep neural networks [C]//2018 IEEE International Conference on Big Data. Seattle: IEEE, 2018: 36–45. DOI: 10.1109/BigData.2018.8621955.
[10]	ZHANG W E, SHENG Q Z, ALHAZMI A, et al. Adversarial attacks on deep-learning models in natural language processing: a survey [J]. ACM Transactions on Intelligent Systems and Technology, 2020, 11(3): 24. DOI: 10.1145/3374217.
[11]	VON RUEDEN L, MAYER S, BECKH K, et al. Informed machine learning: a taxonomy and survey of integrating prior knowledge into learning systems [J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(1): 614–633. DOI: 10.1109/TKDE.2021.3079836.
[12]	FORRESTAL M J, LUK V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid [J]. Journal of Applied Mechanics, 1988, 55(2): 275–279. DOI: 10.1115/1.3173672.
[13]	文鹤鸣. 混凝土靶板冲击响应的经验公式 [J]. 爆炸与冲击, 2003, 23(3): 267–274. WEN H M. Empirical equations for the impact response of concrete targets [J]. Explosion and Shock Waves, 2003, 23(3): 267–274.
[14]	CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics [J]. International Journal of Impact Engineering, 2002, 27(6): 619–637. DOI: 10.1016/S0734-743X(02)00005-2.
[15]	LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile [J]. International Journal of Impact Engineering, 2003, 28(1): 93–116. DOI: 10.1016/S0734-743X(02)00037-4.
[16]	任辉启, 穆朝民, 刘瑞朝, 等. 精确制导武器侵彻效应与工程防护[M]. 北京: 科学出版社, 2016: 54−58.
[17]	陈小伟. 穿甲/侵彻力学的理论建模与分析 [M]. 北京: 科学出版社, 2019.
[18]	王清华, 徐丰, 郭伟国. 基于ANN-GA协同寻优的动态拉伸试样尺寸优化方法 [J]. 爆炸与冲击, 2022, 42(1): 014201. DOI: 10.11883/bzycj-2021-0218. WANG Q H, XU F, GUO W G. A method of geometry optimization for dynamic tensile specimen based on artificial neural network and genetic algorithm [J]. Explosion and Shock Waves, 2022, 42(1): 014201. DOI: 10.11883/bzycj-2021-0218.
[19]	李秦超, 姚成宝, 程帅, 等. 神经网络状态方程在强爆炸冲击波数值模拟中的应用 [J]. 爆炸与冲击, 2023, 43(4): 044202. DOI: 10.11883/bzycj-2022-0222. LI Q C, YAO C B, CHENG S, et al. Application of the neural network equation of state in numerical simulation of intense blast wave [J]. Explosion and Shock Waves, 2023, 43(4): 044202. DOI: 10.11883/bzycj-2022-0222.
[20]	MUSTAPHA A, MOHAMED L, ALI K. An overview of gradient descent algorithm optimization in machine learning: Application in the ophthalmology field [C]//The 3rd International Conference on Smart Applications and Data Analysis. Marrakesh, Morocco: Springer, 2020: 349–359. DOI: 10.1007/978-3-030-45183-7_27.
[21]	ZHANG L, WANG J M, JIANG M W, et al. Evaluation method based on random forests for empirical algorithms of penetration effects [C]//2022 International Conference on Machine Learning, Cloud Computing and Intelligent Mining (MLCCIM). Xiamen, Fujian, China: IEEE, 2022: 73–78. DOI: 10.1109/MLCCIM55934.2022.00020.
[22]	FULLARD K, BARR P. Development of design guidance for low velocity impacts on concrete floors [J]. Nuclear Engineering and Design, 1989, 115(1): 113–120. DOI: 10.1016/0029-5493(89)90264-1.
[23]	YOUNG C W. Penetration equations [R]. Albuquerque, NM, United States: Sandia National Lab, 1997. DOI: 10.2172/562498.