A fast equivalent-isotropic-plate model for stiffened circular plates under pulse loading
-
摘要: 加筋板在爆炸与冲击防护中应用广泛，而其动力响应的快速求解一直是工程中关注的重点。对于径向均匀加筋的圆板，基于刚度叠加思想，提出了一种将其等效为各向同性平板的方法，用于分析其在脉冲载荷下弹性阶段的动力响应。结合理论推导与数值方法，显式地给出了简洁的等效平板厚度公式。经验证，提出的等效方法建立了加筋圆板与均质圆板间的内在联系，适用于多种加筋尺寸、材料及载荷形式。等效圆板与加筋圆板的最大挠度偏差不超过6%，低阶振动频率偏差不超过10%。相比于直接对加筋圆板进行计算，等效分析方法大大提高了求解效率，且保证了很高的计算精度，在冲击响应预测和结构优化等工程应用中具有重要意义。Abstract: Stiffened panels are widely used in the explosion and impact protection, thus a fast and accurate method for solving their dynamic response is highly desired in engineering. Based on the idea of stiffness superposition, a novel equivalent-isotropic-plate method is proposed in this paper to convert the radial and uniformly stiffened circular plate into an isotropic flat plate, so as to analyze its dynamic response in the elastic stage under uniform pulse loading. Since obtaining the dynamic response of an isotropic plate is mature and convenient, the equivalent analysis can overcome the computational difficulty of anisotropy in direct modeling, thus greatly improving the solving efficiency. Through the linear superposition of the plate and stiffener dynamic equations, a concise formula of the equivalent plate thickness is derived explicitly. The equivalent parameter in the formula is obtained with the assistance of simulation and numerical fitting, which directly measures the strengthening effect of the stiffeners on the plate. Employing the equivalent-isotropic-plate model, the overall dynamic response of a stiffened circular plate can be represented by that of an equivalent isotropic plate with acceptable accuracy, especially for low-order vibrations and center deflections. It is verified that the equivalent method can be successfully applied to a variety of stiffening types, materials, and load forms. The deviation of the maximum deflection response of the equivalent flat plate from that of the original stiffened circular plate does not exceed 6%, and the deviation of the response frequency does not exceed 10%. This completely meets the engineering requirements. The equivalent-isotropic-plate model verifies the feasibility of isotropic equivalence, and reveals the intrinsic connection between the radial stiffened circular plate and the homogeneous circular plate, which is of great significance in engineering applications such as response prediction and structural optimization.
-
Key words:
- stiffened plate /
- circular plate /
- dynamic response analysis /
- equivalent method /
- pulse loading
-
双层环肋圆柱壳作为一种典型结构，在潜艇中被广泛应用。由于作业环境恶劣，一旦发生撞击事故，会造成重大损失[1]。针对潜艇受到碰撞或潜艇搁浅的问题，梅志远等[2-3]、朱新阳等[4]对潜艇典型结构受撞损伤特征开展了数值模拟和模型试验研究。关于环肋圆柱壳结构撞击问题，Y.W.Kim等[5]利用能量法计算了环肋圆柱壳在阶跃冲击作用下的动态响应；孙清磊等[6]考虑静水压作用，对环肋圆柱壳受不同形状撞击体的撞击过程进行了数值模拟，探讨了不同撞头形状对结构变形吸能及碰撞力的影响规律。潜艇受撞击与导弹穿甲或侵彻问题不同，后者是金属在高速冲击和冲击产生高温的联合作用下瞬时被击穿形成破口的过程，破口周围的结构几乎不产生变形，穿甲机理包含力学和热力学作用[7]。而前者的撞击速度较低，撞击过程中热力学作用微小，可以忽略，且结构的变形范围不仅局限于接触区。目前，对圆柱壳受撞问题的研究，撞击物多为单一体，而实际中常会遇到多个物体同时或连续撞击的案例，而该类问题的研究却少见报道。本文中拟针对双层环肋圆柱壳受多物体撞击问题进行数值模拟和模型试验，对多物体撞击下的壳体结构损伤机理和典型特征开展研究，以期为相关工程设计提供参考。
1. 数值模拟
1.1 数值模型
选取双层环肋圆柱壳受撞一侧的半圆结构作为研究对象，由内、外层环肋圆柱壳通过实肋板连接而成。内外壳结构的特征参数如表 1所示，其中R为壳体半径，t为壳体板厚，L为壳体上环肋骨间距，F为环肋骨横剖面积，下标1、2分别代表外壳和内壳；撞击物为5只相同的实心钢球，半径为150 mm，每只钢球的质量为111 kg。
表 1 模型结构特征参数Table 1. Parameters of the model's structural characteristicsR1/t1 L1/√R1t1 F1/L1t1 R2/t2 L2/√R2t2 F2/L2t2 363.3 4.2 0.25 153.3 1.62 0.56 建模前首先对模型网格尺度对计算结果的影响进行分析，以单个物体(钢球)撞击双层壳体的环肋外壳为例，采用4种不同尺度的网格建立模型。从计算得到的撞击力和壳体变形能对比曲线，如图 1所示。从图中可以看出，模型网格特征长度为20和12 mm的计算结果基本吻合，表明前者能满足计算结果的稳定。根据结构受撞损伤的局部特性[8-9]，考虑计算效率，建模时在壳体受撞及附近区域采用特征长度为20 mm的网格，远离受撞区采用较粗网格。
图 1 不同网格特征长度数值模拟结果对比Figure 1. Comparison of calculation results between different element lengths采用MSC.Patran[10]建立的双层环肋半圆柱壳结构及撞击物(钢球)的数值模型如图 2所示，图中还给出了钢球的分布。模型中所有构件均采用壳单元模拟，单元数为50 388，节点数为50 479。通过在撞击物上施加11.71 m/s的初始速度来模拟5只钢球从距离圆柱壳顶端7 m的高度同时自由坠落撞击壳体，同时考虑撞击过程中重力加速度以及摩擦作用的影响，动、静摩擦力因数都取0.1。
图 2 双层环肋半圆柱壳结构和撞击物有限元模型Figure 2. Finite element models of double ring-stiffened cylindrical shell structure and colliding bodies为了与模型试验相对应，双层环肋半圆柱壳结构的材料采用普通船用Q235钢，计算时考虑材料的应变率敏感性，用弹塑性材料来模拟，相关材料参数如下：材料密度, 7 850 kg/m3; 屈服应力, 290 MPa; 弹性模量, 206 GPa; 泊松比, 0.3;最大塑性失效应变, 0.386;应变率敏感系数D=40.4, q=5[11]。实心钢球相对于壳体结构的刚度较大，变形可忽略不计，因此采用刚体材料来模拟。
1.2 数值模拟结果及损伤机理分析
采用MSC.Dytran的主从面自适应接触算法对壳体受撞损伤过程进行计算，并用MSC.Patran对计算结果进行后处理，对结构的动态响应过程进行分析。
1.2.1 结构损伤变形
图 3~4所示分别为钢球达到最大撞深时壳体上产生的等效应力和损伤变形分布，可以看出，外壳上5个撞击点形成的网状面内的壳板多处产生屈服，损伤变形主要以受撞点处的凹陷为主，此外，受撞点之间的壳板变形也较明显。远离受撞区的壳板等效应力和结构变形都很小。中间钢球造成的壳体损伤变形最大，最大撞击深度达到了122 mm，表明相同撞击条件下，沿圆柱壳板径向撞击造成的壳体损伤最严重。根据受撞壳体结构的特征参数可以推断，达到最大撞深时外壳板将会与内壳上的环向肋骨产生接触。
图 5所示为钢球达到最大撞深时受撞壳体内壳的等效应力分布，可以看出，内壳上产生的塑性变形区较小，主要集中在与外壳板发生接触区以及与实肋板相连的环向肋骨上，撞击造成的内壳变形很小，表明在受撞环境下双层环肋圆柱壳的外壳能够对内壳起到很好的防护作用。
1.2.2 撞击力变化
图 6所示为5只钢球产生的撞击力时程曲线，可以看出，撞击力曲线的非线性现象十分明显，0号球的撞击力峰值要大于其余4只球，表明相同条件下沿圆柱壳板径向撞击形成的撞击力最大。撞击位置相似的钢球产生的撞击力基本相同。
0号球的撞击力曲线出现了2个明显的峰值，从撞击过程的动态模拟中观察分析，第1个峰值是由于0号球位于圆柱壳弧顶端，5只钢球同一平面同时落下时，0号球首先与圆柱壳接触，撞击力随着接触面的增加而增加，随后其余4只球与圆柱壳接触，它们的撞击造成了圆柱壳的凹陷，使得0号球与撞击位置的壳板接触面减小，因此会出现撞击力的卸载；此时0号球仍然具有撞击速度，随着接触的继续增加，撞击力继续增加，直至0号球的撞击速度减为零，撞击力达到最大值，出现第2个峰值。从图中还可以看出，其余4只钢球的撞击力曲线在卸载过程中也受到了0号球撞击产生的影响，表明多物体撞击过程中的撞击力会相互影响，产生耦合现象，这也是其区别于单物体撞击的显著特征。
1.2.3 能量转换
壳体受撞过程遵守能量守恒定律，在整个过程中钢球的撞击动能绝大部分将会被耗散，转变成以下几种能量：受撞壳体的动能、结构变形能以及接触摩擦产生的热能，在计算中还有一部分会转变成模型的沙漏能。直接从中间钢球(0号球)与壳体即将接触时刻开始计起，图 7给出了整个过程中各种能量的变化曲线。可以看出，钢球的初始动能随着撞击过程的进行将会被耗散，损失的动能有97.3%转变成了受撞壳体的结构变形能。撞击引起的壳体运动很小，因此壳体动能很小，同时，数值模拟中的沙漏能也很小，都可以忽略不计。从图中还可以发现，钢球在撞击过程中发生了反弹现象，还剩余一部分的撞击动能，考虑重力影响，反弹后的钢球动能将会转变成重力势能，再次下落撞击壳体结构，最终转变成壳体结构的变形能。
2. 模型试验验证
2.1 试验模型
为了与数值模拟结果进行对比，开展了相应的模型试验。通过采用特定的装置和措施，使得5只钢球按照给定高度、分布方式坠落，撞击壳体的指定位置，受撞壳体结构模型及撞击钢球如图 8所示。
试验开始前，受撞圆柱壳模型放置在特定的试验池内，弧顶向上，两侧的纵边与试验池底钢板焊接来模拟刚性固定的边界条件。5只撞击钢球悬挂在受撞圆柱壳中间位置的弧顶正上方，距离弧顶7 m，通过连接在吊车上的电磁钩瞬间释放自由下落撞击壳体模型。壳体模型受撞过程中的撞击力是通过安装在钢球起吊端一侧的加速度传感器来测量的，通过动态测试仪器可以直接得到该过程中的加速度值，然后根据Fi=miai可以求出各个钢球的撞击力，式中Fi、mi和ai分别为i号钢球的撞击力、质量和加速度，加速度传感器分别安装在0~3号球上。
2.2 试验结果及对比分析
对壳体模型受撞损伤的过程进行了高速摄像，受撞瞬间的接触状态及受撞后发生的钢球反弹现象如图 9所示。从高速摄像可以观察到，撞击是在十几毫秒内完成的，时间极其短暂。壳体模型在瞬时撞击载荷作用下，受撞区结构产生了明显的变形，同时整体还产生了明显的振动现象。钢球发生了反弹现象，0号钢球反弹方向基本是垂直向上的，而1~4号钢球由于模型弧度的影响，反弹方向是稍微偏向外侧的。反弹后的钢球在重力作用下会再次撞击模型，但造成的二次结构损伤不是很明显。
2.2.1 撞击力对比
图 10所示为0号和1号球撞击力的模型试验结果与数值模拟结果对比图，可以看出，2种结果吻合得较好，两者撞击力峰值和变化趋势都有很好的相似性。与数值模拟结果相比，试验得到的0号球撞击力曲线同样存在2个较明显的峰值，模型试验首次峰值的量值和卸载时间都比数值模拟计算的更大，造成这种差异的原因可能是0号球与其余4只球之间的距离在模型试验和计算之间存在微小差异，导致其余4只球的撞击对0号球产生的影响不同，但对0号球的撞击力最大峰值的影响很小。
2.2.2 壳体结构变形对比
受撞后外壳和外壳环肋骨上产生的损伤变形的模型试验结果与数值模拟结果对比如图 11所示。首先，从结构损伤变形范围来看，2种结果都显示：损伤变形集中在外壳板上5个受撞击点形成的面内，变形在实肋板处存在较明显的终止现象。其次，从损伤模式来看，2种结果均显示：外壳板的变形模式主要包含2种变形模式，一种是5只钢球撞击点处的壳板凹陷，另一种是连接1~4号钢球相邻撞击点的外壳板屈曲变形，如图 11(a)所示。这部分是由相邻受撞区壳板凹陷变形引起的连接区壳板面内挤压而造成的，即多物体撞击产生的变形耦合现象，这也是其区别于单物体撞击的典型特征。此外，外壳内表面上的环肋骨随壳板变形产生了屈曲失稳、压皱和扭曲等变形模式。
采用激光跟踪仪对试验结束后的模型外壳板受撞损伤变形量进行了测量，图 12给出了外壳板上5只钢球撞击深度的试验测量结果和数值模拟结果。对比可以看出，0号球造成的撞深最大，试验测量和数值模拟计算分别为103.2和106.0 mm，两者比较接近；其余4只球撞深的2种结果差异较大。产生这种现象的原因可能有：(1)变形测量时的操作误差，例如激光定位时没有扫描到最大变形处；(2)模型的初始挠度误差；(3)撞击前钢球位置存在偏差，越靠近圆弧两侧，产生的撞深越小。上述原因也正是模型试验不确定性的表现，但从整体来看，模型试验和数值模拟结果吻合较好，有限元数值模拟能够较准确地反映壳体结构受多物体撞击的损伤特性。
3. 结论
针对双层环肋圆柱壳结构受到多物体撞击问题，分别开展了数值模拟计算和模型试验，通过对两者结果的比较，得到如下结论：
(1) 双层环肋圆柱壳结构同时受多物体撞击是一个瞬态动响应过程，在巨大瞬时冲击载荷作用下，受撞区壳板会迅速超越弹性变形而产生塑性变形；撞击的物体、速度、方向均相同的前提下，沿圆柱壳板径向撞击形成的撞深和撞击力最大。
(2) 多物体撞击会造成外壳板一定区域的损伤变形，当撞击物分布均匀、紧密时，壳板的损伤区域不仅包括与撞击物接触区，还包括连接这些部位的区域，后者是由多物体撞击引起的变形耦合而产生的，这也是区别于单物体撞击的典型特征。
(3) 多物体撞击产生的撞击力会相互干扰，导致其非线性特征更明显；
(4) 双层圆柱壳的外壳能对内壳起到较好的防护作用，在外壳没被撞穿的情况下，其结构变形会吸收绝大部分的撞击动能，可以通过优化外壳的吸能效率来达到双层壳体结构物内壳防撞的目的。
-
图 2 加强肋方向s1和s2的坐标变换
Figure 2. The coordinate transformation of the directions s1 and s2 of the stiffeners
图 3 LS-DYNA中十字形加筋圆板的壳单元网格划分
Figure 3. The mesh of cross-stiffened circular plate using shell element in LS-DYNA
图 4 不同厚度圆板在线性衰减脉冲（压力峰值50 kPa，衰减时间2 ms）作用下的最大响应挠度及拟合曲线
Figure 4. The maximum deflections and fitting curve of circular flat plates with different thicknesses under linear decaying pulse with the peak pressure of 50 kPa and the decay time of 2 ms
图 5 3种不同十字形加筋圆板的
h2s 和h2e 的关系Figure 5. The relations between
h2s andh2e for three different cross-stiffened circular plates
图 6 不同n、β设置下加筋圆板的等效参数K
Figure 6. The equivalent parameter K of the stiffened circular plates with different n and β
图 7 等效参数K(n, β)拟合函数图
Figure 7. The fitting function graphs of equivalent parameter K(n, β)
图 8 3种不同加筋圆板及其等效平板、等质量修正板、等质量分布修正板的中心挠度-时间曲线对比
Figure 8. Comparisons of the central deflection-time curves among three different stiffened circular plates and the corresponding equivalent plates, equal mass revised plates, equal mass distribution revised plates
图 9 不同时刻n4β0.07加筋圆板(左)与对应等效平板(右)的挠度分布云图
Figure 9. The deflection contour maps of the stiffened circular plate n4β0.07 (left) and the corresponding equivalent plate (right) at different times
图 10 不同n、β设置下加筋圆板及其等效平板（采用式(16)或式(19)）在同等线性衰减脉冲载荷下的响应情况对比
Figure 10. Comparisons of the dynamic response of the stiffened circular plates and the corresponding equivalent plates (by Eq.(16) or Eq. (19)) with different n and β under the same linear decaying pulse
图 12 不同线性衰减脉冲压力下的n4β0.07加筋圆板与对应等效平板的最大挠度
Figure 12. The maximum deflections of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the triangle decaying pulse with different pressure
图 13 矩形脉冲（RP）、线性衰减脉冲（LDP）和等腰三角脉冲（ITP）下的n4β0.07加筋圆板与对应等效平板的中心挠度-时间曲线
Figure 13. The central deflection-time curves of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the rectangle pulse (RP), linear decaying pulse (LDP), and isosceles triangular pulse (ITP)
-
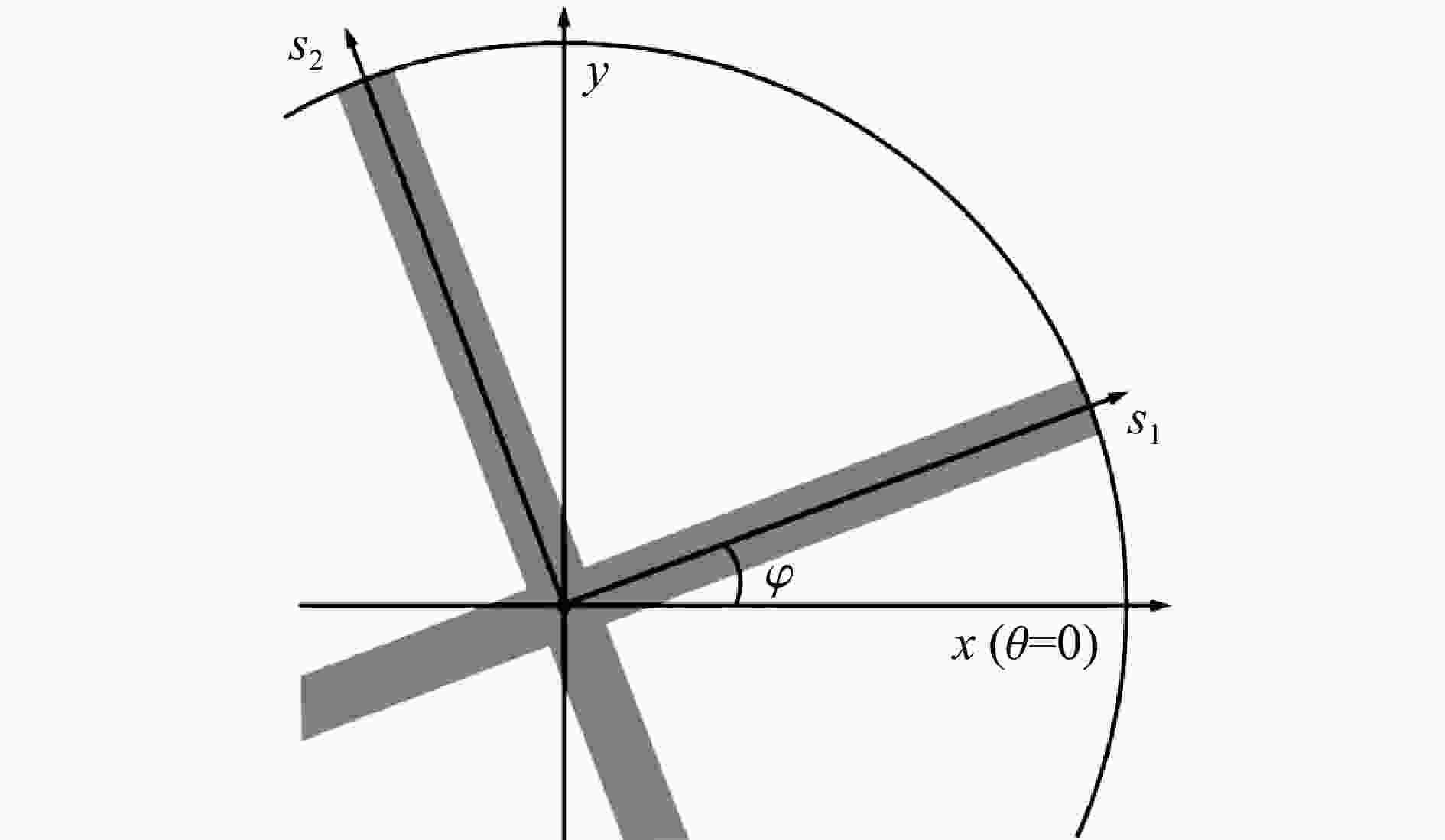
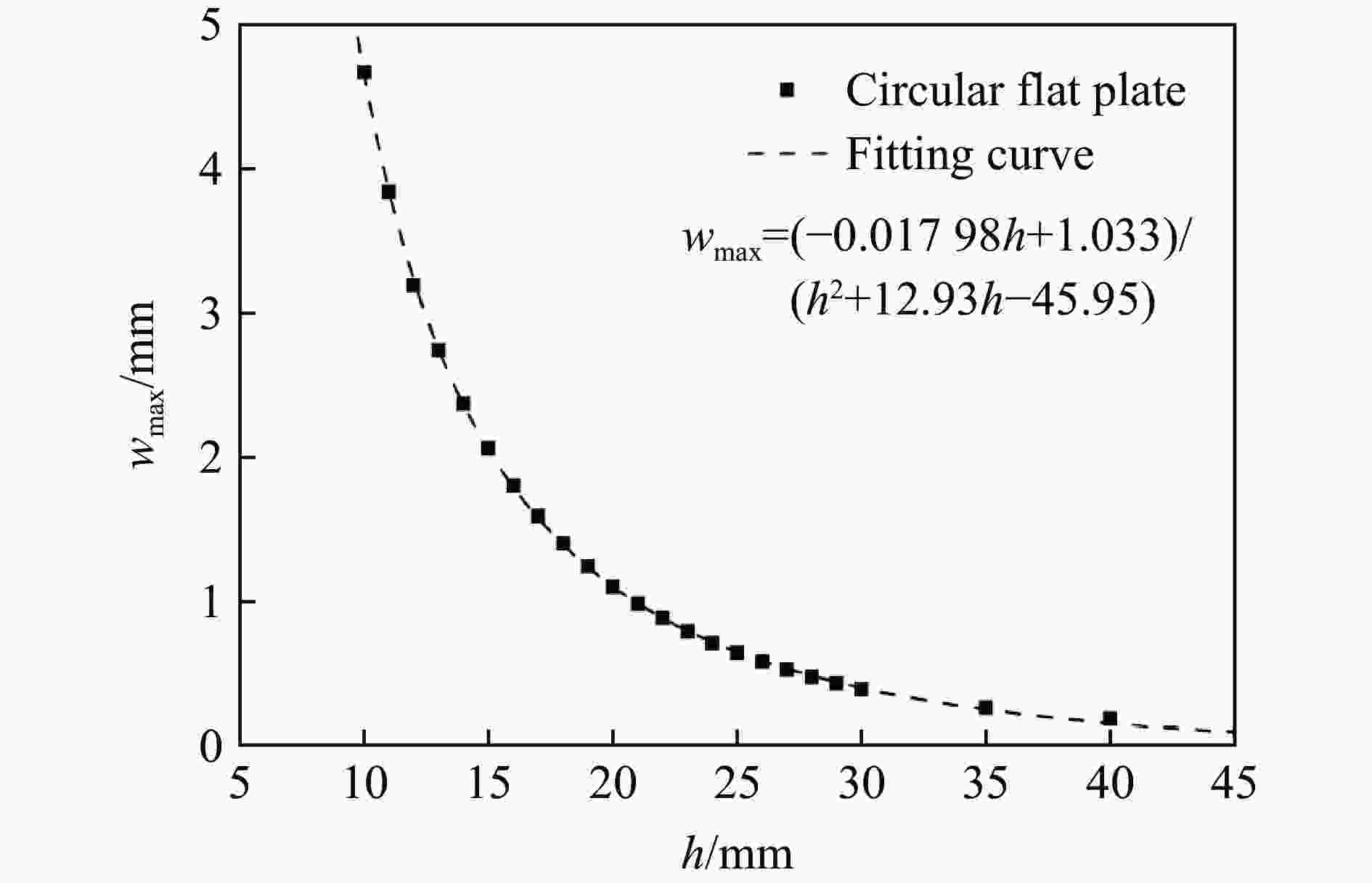
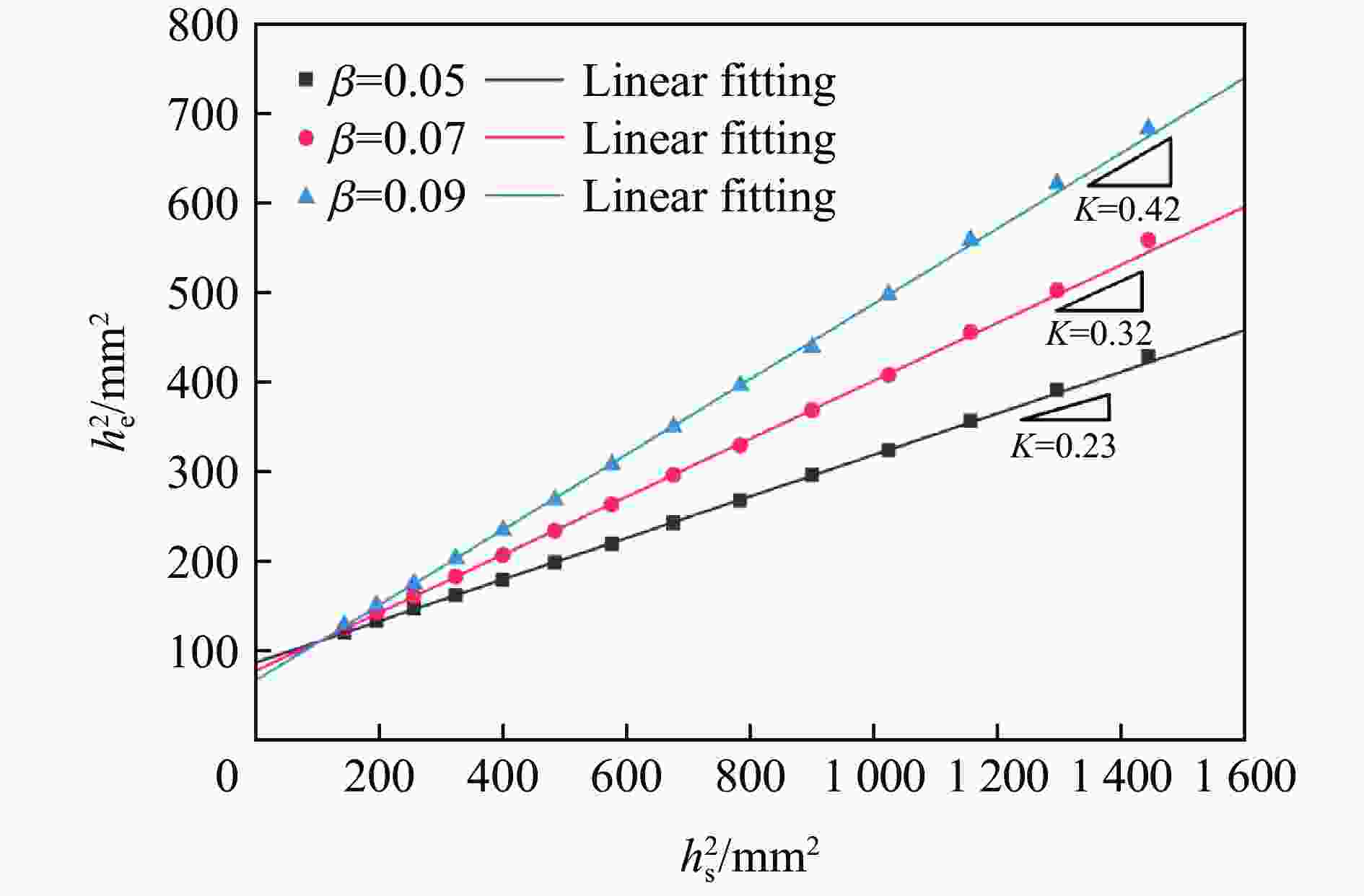
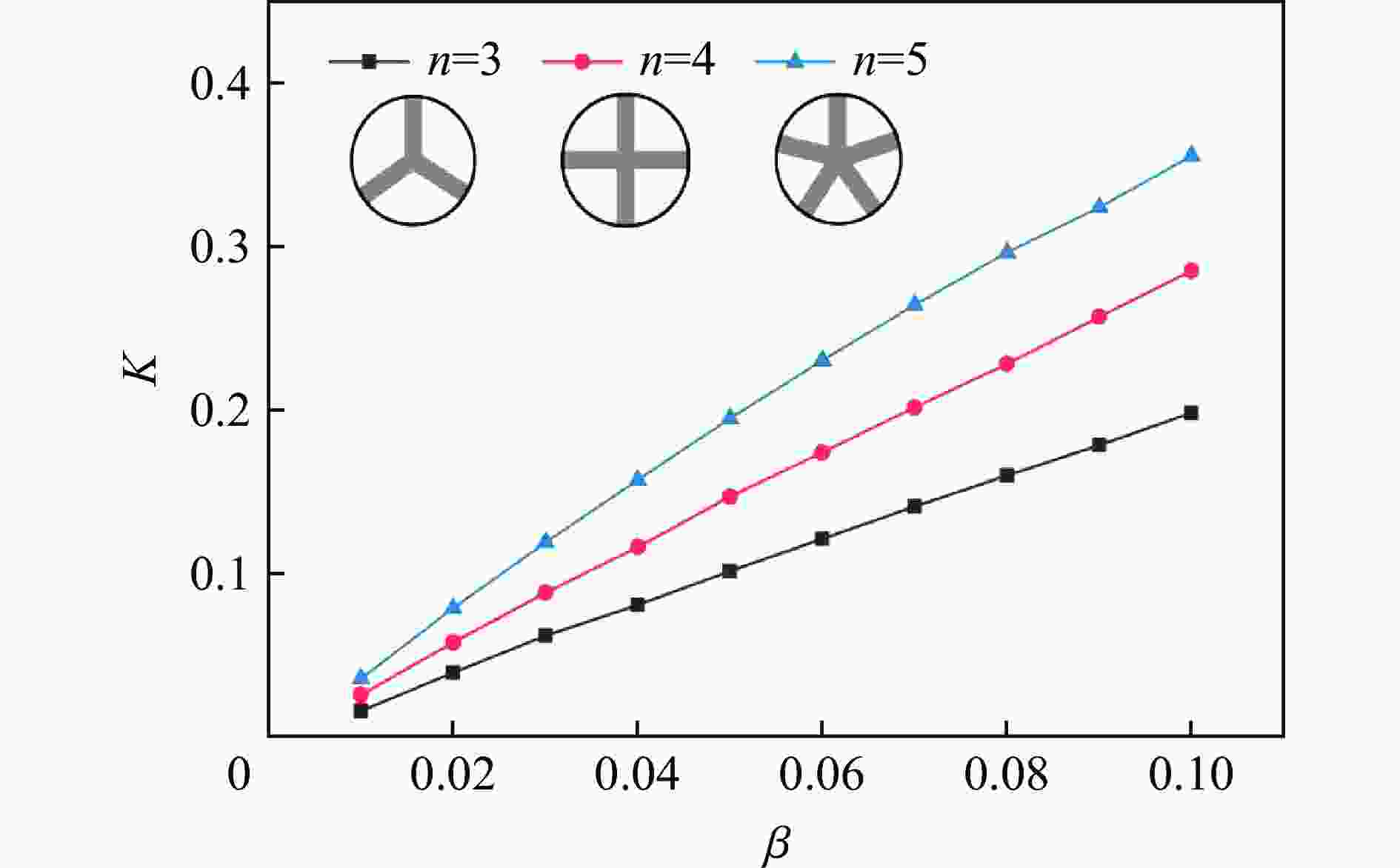
[1] TROITSKY M S. Stiffened plates: bending, stability, and vibrations [M]. Amsterdam: Elsevier, 1976. [2] SZILARD R. Theories and applications of plate analysis: classical, numerical, and engineering methods [M]. Hoboken: John Wiley & Sons, 2004. [3] KIM D K, LIM H L, YU S Y. A technical review on ultimate strength prediction of stiffened panels in axial compression [J]. Ocean Engineering, 2018, 170: 392–406. DOI: 10.1016/j.oceaneng.2018.10.022. [4] KARPOV V V, SEMENOV A A. Refined model of stiffened shells [J]. International Journal of Solids and Structures, 2020, 199: 43–56. DOI: 10.1016/j.ijsolstr.2020.03.019. [5] BALKAN D, DEMIR Ö, ARIKOĞLU A. Dynamic analysis of a stiffened composite plate under blast load: a new model and experimental validation [J]. International Journal of Impact Engineering, 2020, 143: 103591. DOI: 10.1016/j.ijimpeng.2020.103591. [6] 张涛, 刘土光, 赵耀, 等. 加筋板弹性大挠度的冲击响应分析 [J]. 爆炸与冲击, 2002, 22(4): 301–307. DOI: 10.3321/j.issn:1001-1455.2002.04.003.ZHANG T, LIU T G, ZHAO Y, et al. Large deflection dynamic response of stiffened plates under lateral impact loading [J]. Explosion and Shock Waves, 2002, 22(4): 301–307. DOI: 10.3321/j.issn:1001-1455.2002.04.003. [7] ISLAM A, SHEIKH A H, BENNETT T, et al. An innovative modeling strategy for flexural response of fiber-reinforced stiffened composite structures [J]. Thin-Walled Structures, 2022, 172: 108929. DOI: 10.1016/j.tws.2022.108929. [8] YU H D, ZHAO Z J, YANG D, et al. A new composite plate/plate element for stiffened plate structures via absolute nodal coordinate formulation [J]. Composite Structures, 2020, 247: 112431. DOI: 10.1016/j.compstruct.2020.112431. [9] SHEN Y J, HE X C, CHEN W, et al. Meshless simulation and experimental study on forced vibration of rectangular stiffened plate [J]. Journal of Sound and Vibration, 2022, 518: 116602. DOI: 10.1016/j.jsv.2021.116602. [10] KARPOV V V, SEMENOV A A. Structural anisotropy method for shells with orthogonal stiffeners [J]. Structures, 2021, 34: 3206–3221. DOI: 10.1016/j.istruc.2021.09.027. [11] ZHANG B, CHEN H L, LI M, et al. Equivalent static load method for hierarchical stiffened composite panel subjected to blast loading [J]. Engineering Structures, 2018, 171: 569–582. DOI: 10.1016/j.engstruct.2018.05.107. [12] XIA Y, FRISWELL M I, SAAVEDRA FLORES E I. Equivalent models of corrugated panels [J]. International Journal of Solids and Structures, 2012, 49(13): 1453–1462. DOI: 10.1016/j.ijsolstr.2012.02.023. [13] TIMOSHENKO S, WOINOWSKY-KRIEGER S. Theory of plates and shells [M]. New York: McGraw-Hill, 1959. [14] BATTAGLIA G, DI MATTEO A, PIRROTTA A, et al. Dynamic response of equivalent orthotropic plate model for stiffened plate: numerical-experimental assessment [J]. Procedia Engineering, 2017, 199: 1423–1428. DOI: 10.1016/j.proeng.2017.09.387. [15] XING Y F, LIU B. New exact solutions for free vibrations of thin orthotropic rectangular plates [J]. Composite Structures, 2009, 89(4): 567–574. DOI: 10.1016/j.compstruct.2008.11.010. [16] FERTIS D G, MIJATOV M M. Equivalent systems for variable thickness plates [J]. Journal of Engineering Mechanics, 1989, 115(10): 2287–2300. DOI: 10.1061/(ASCE)0733-9399(1989)115:10(2287). [17] SEO J K, KIM B J, RYU H S, et al. Validation of the equivalent plate thickness approach for ultimate strength analysis of stiffened panels with non-uniform plate thickness [J]. Thin-Walled Structures, 2011, 49(6): 753–761. DOI: 10.1016/j.tws.2011.02.001. [18] HUANG X R, WANG M, FENG Y J, et al. Finite deformation analysis of the elastic circular plates under pressure loading [J]. Thin-Walled Structures, 2023, 188: 110864. DOI: 10.1016/j.tws.2023.110864. -
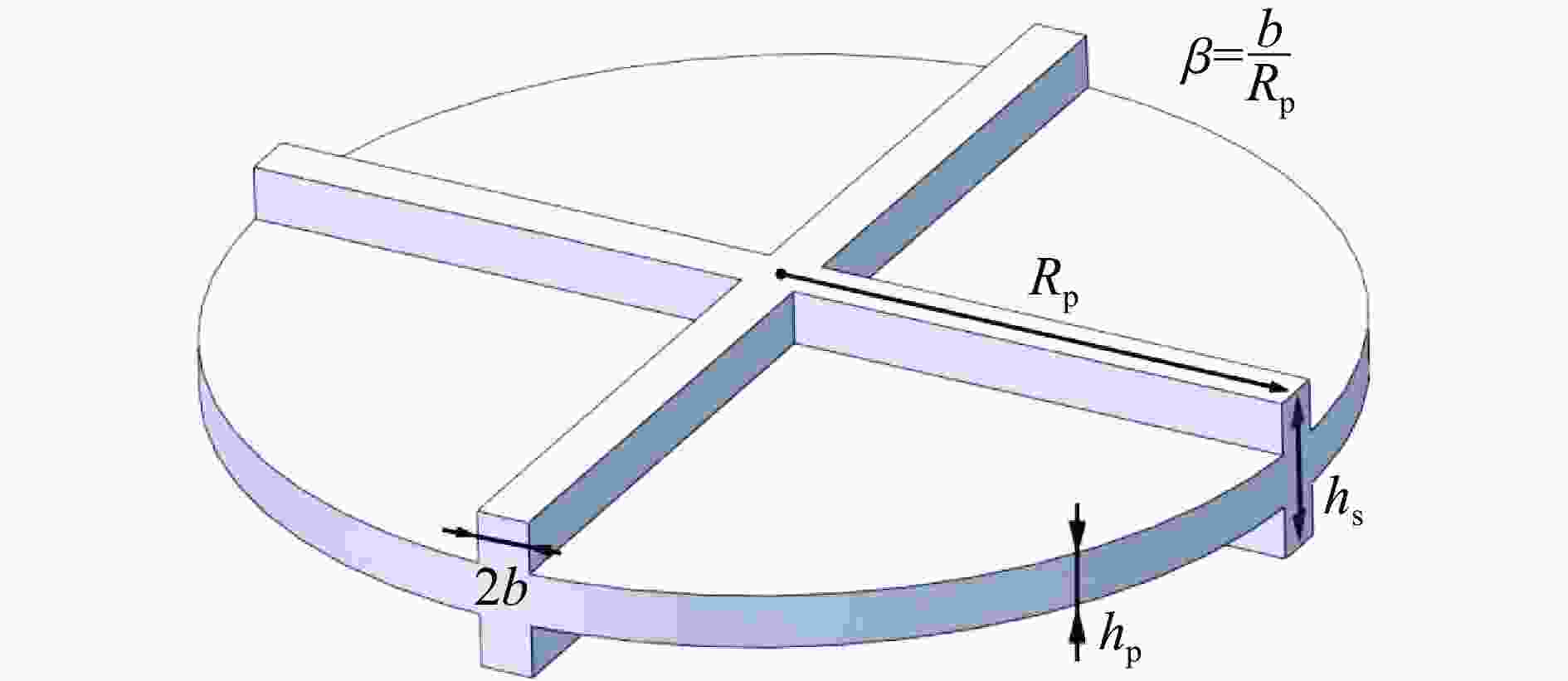
下载:
下载:
计量
- 文章访问数: 289
- HTML全文浏览量: 106
- PDF下载量: 131
- 被引次数: 0