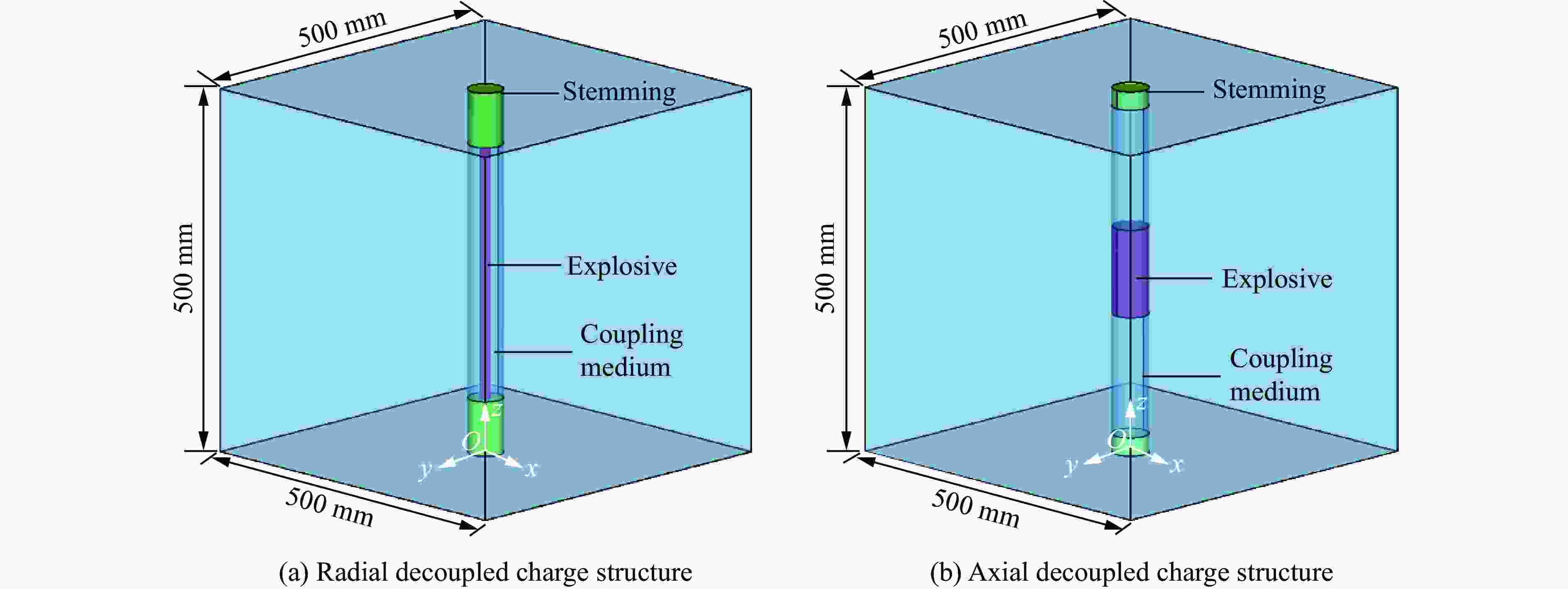
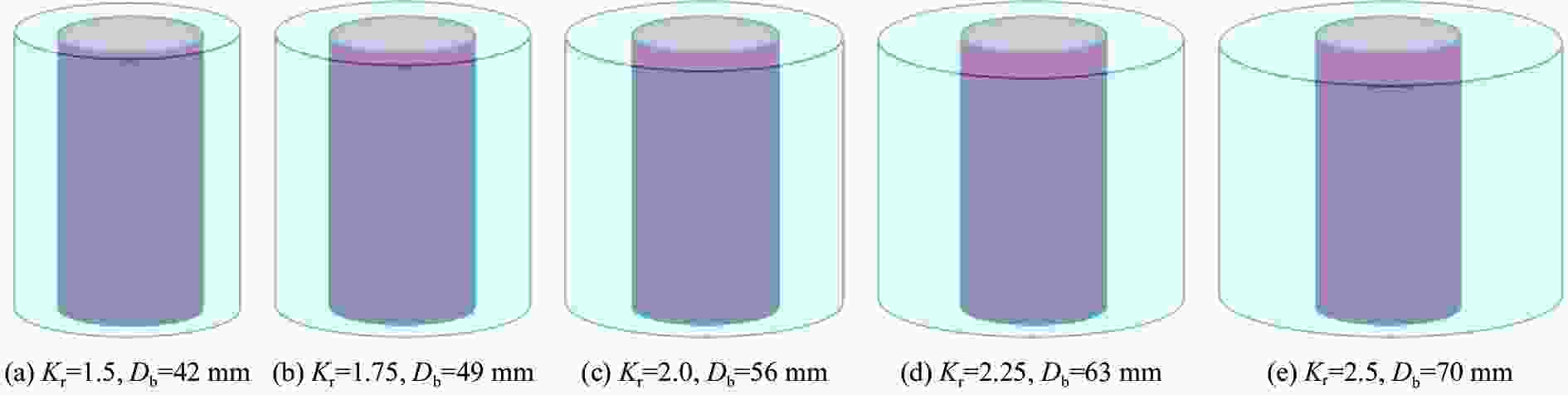
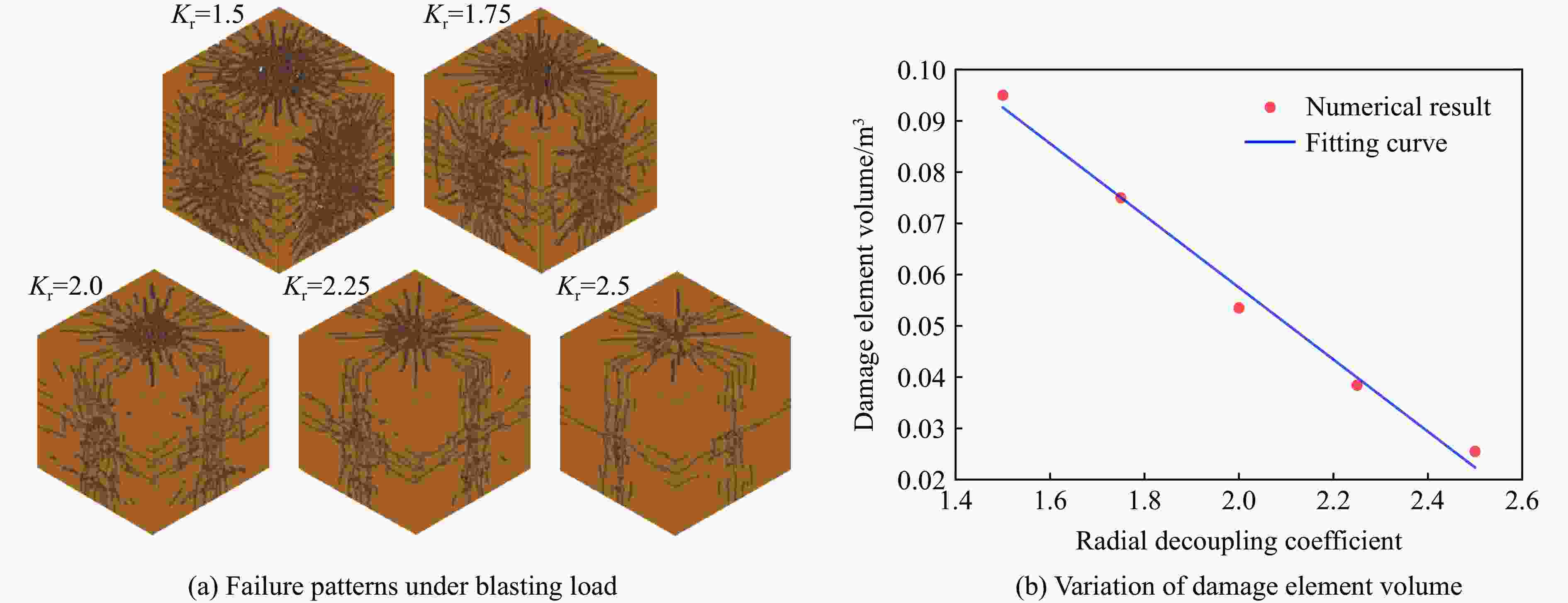
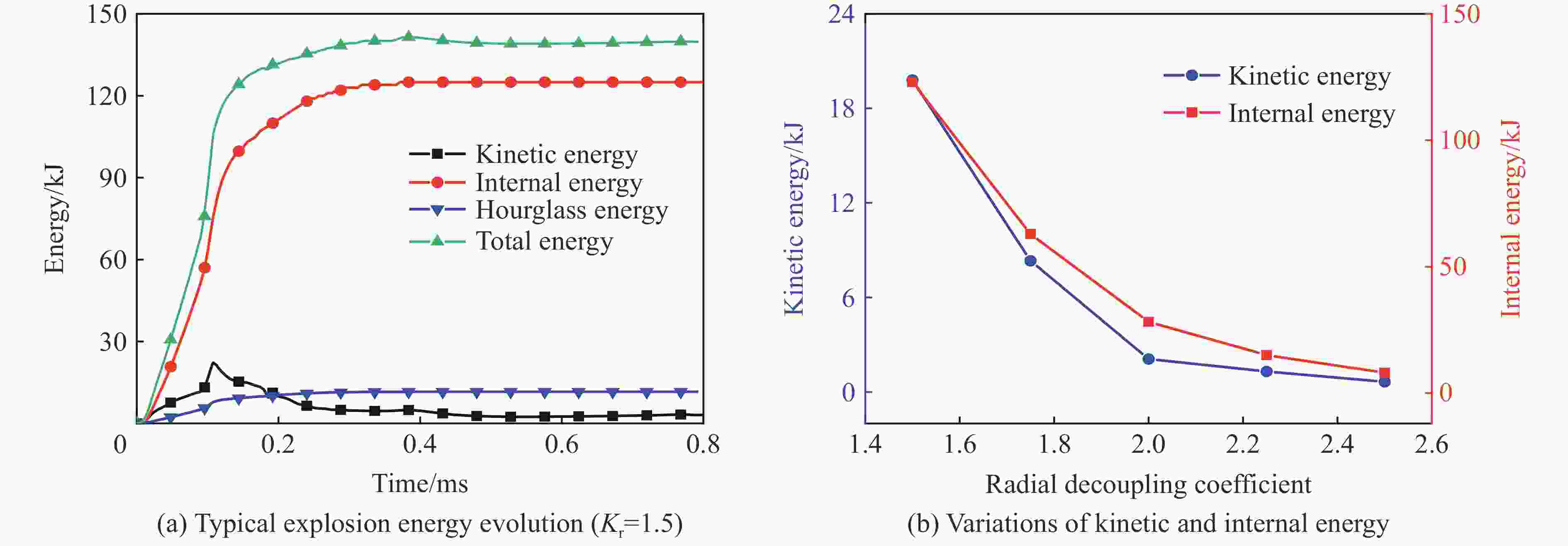
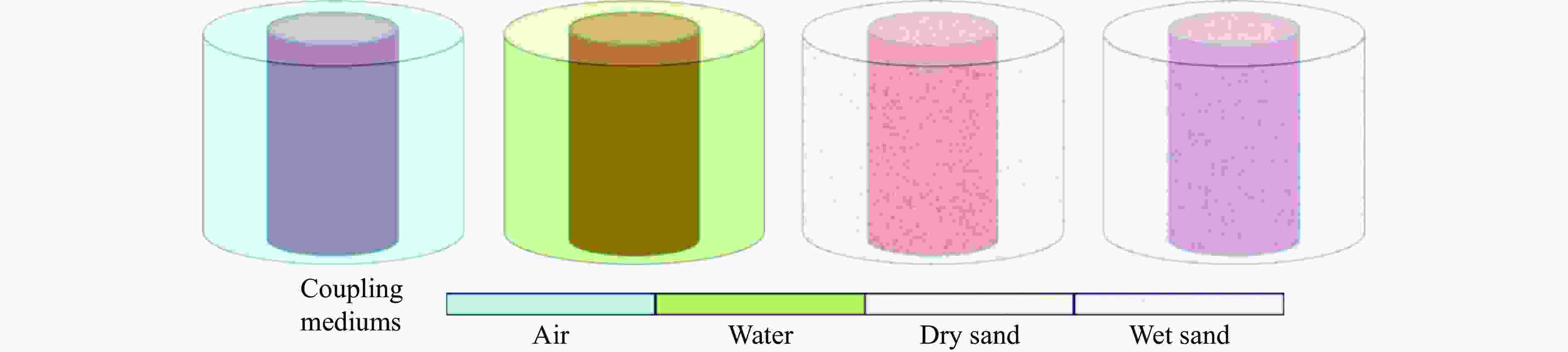
Size distribution characteristics of blast-induced rock fragmentation under decoupled charge structures
-
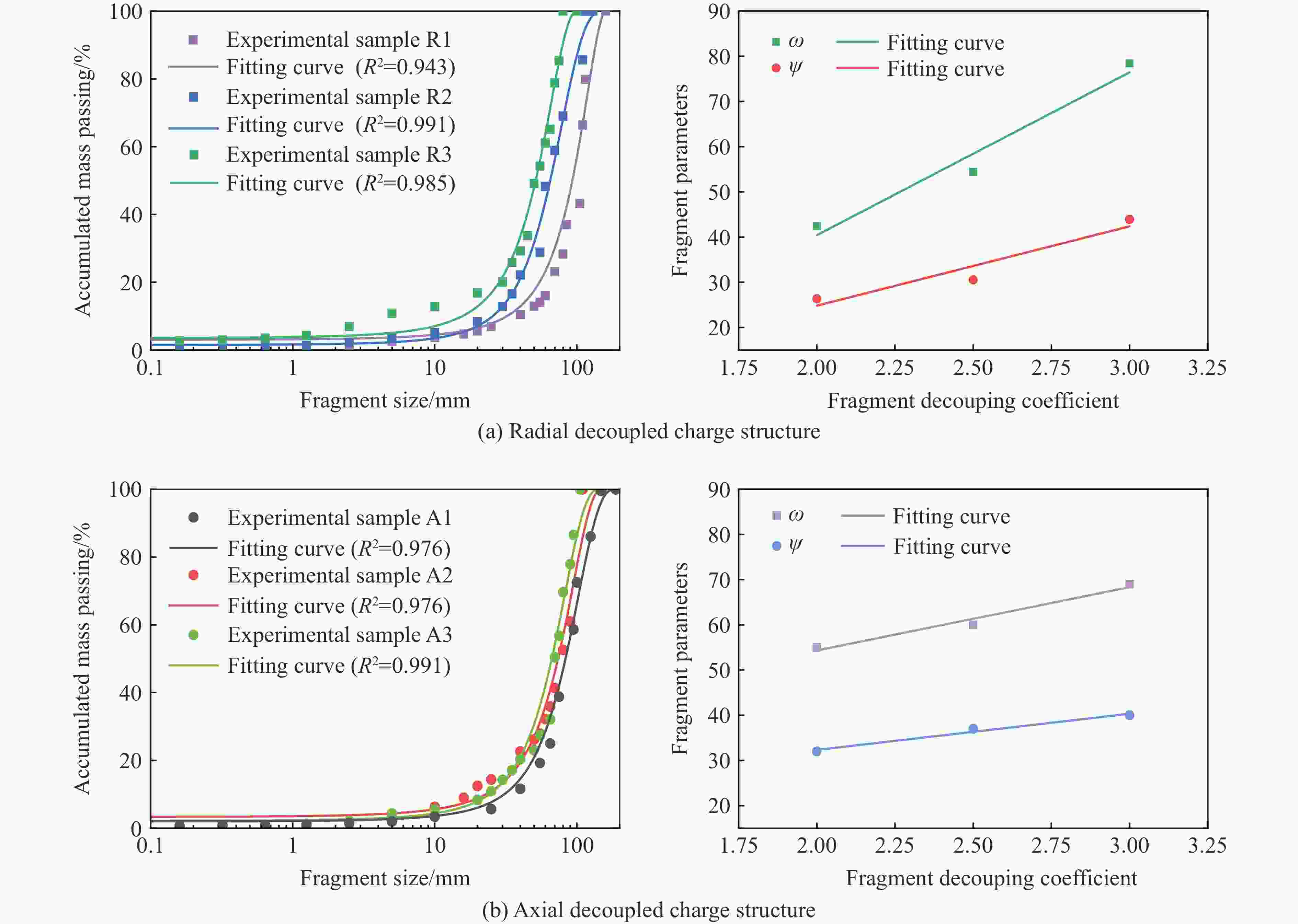
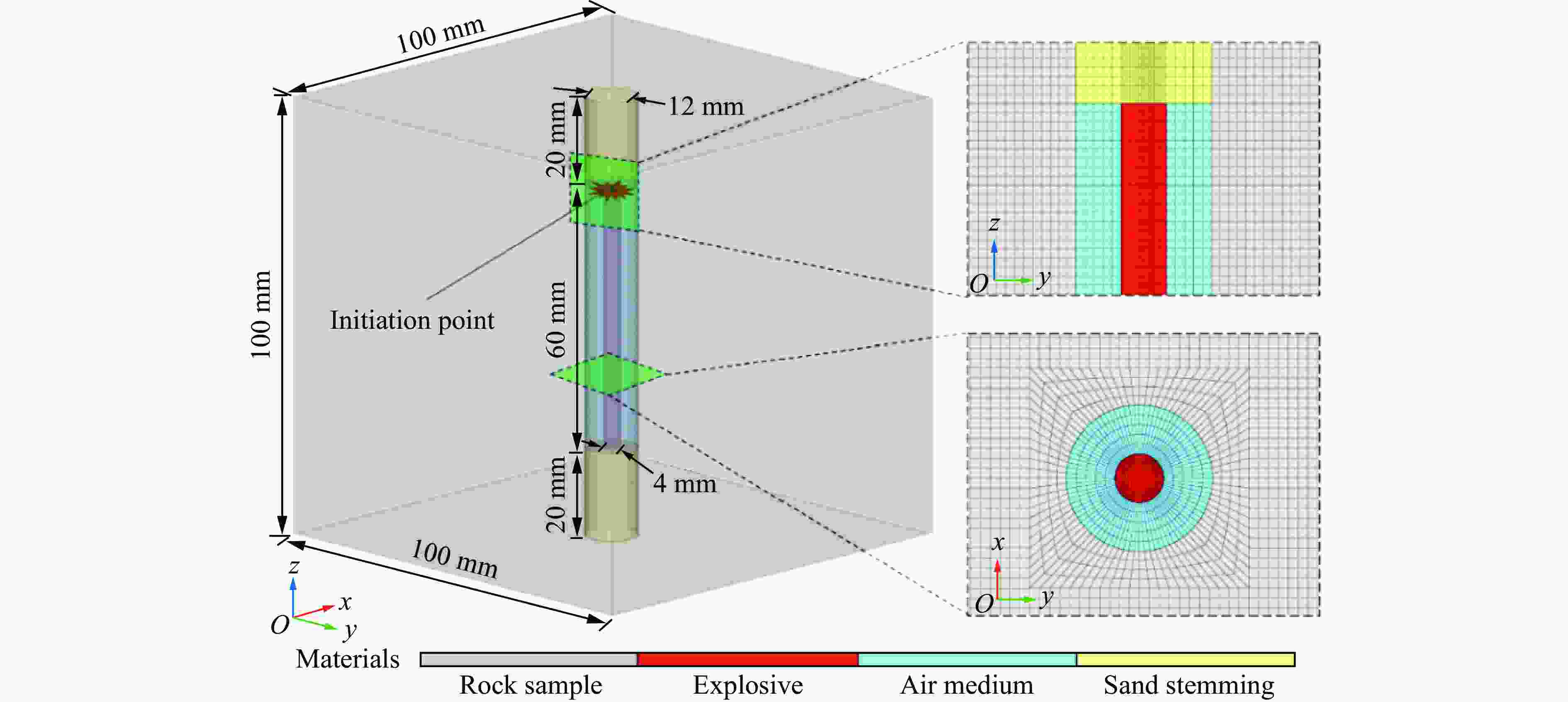
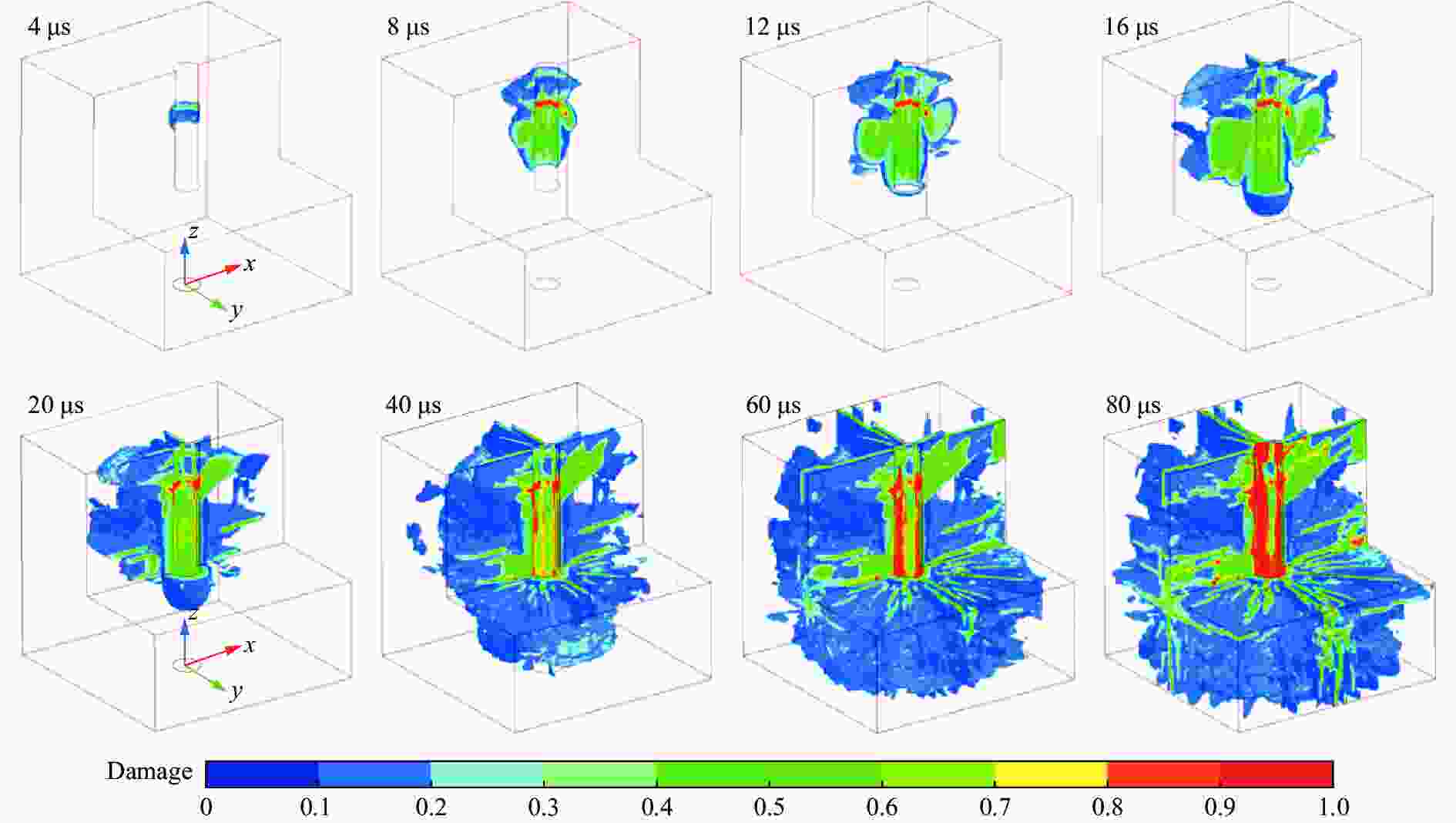
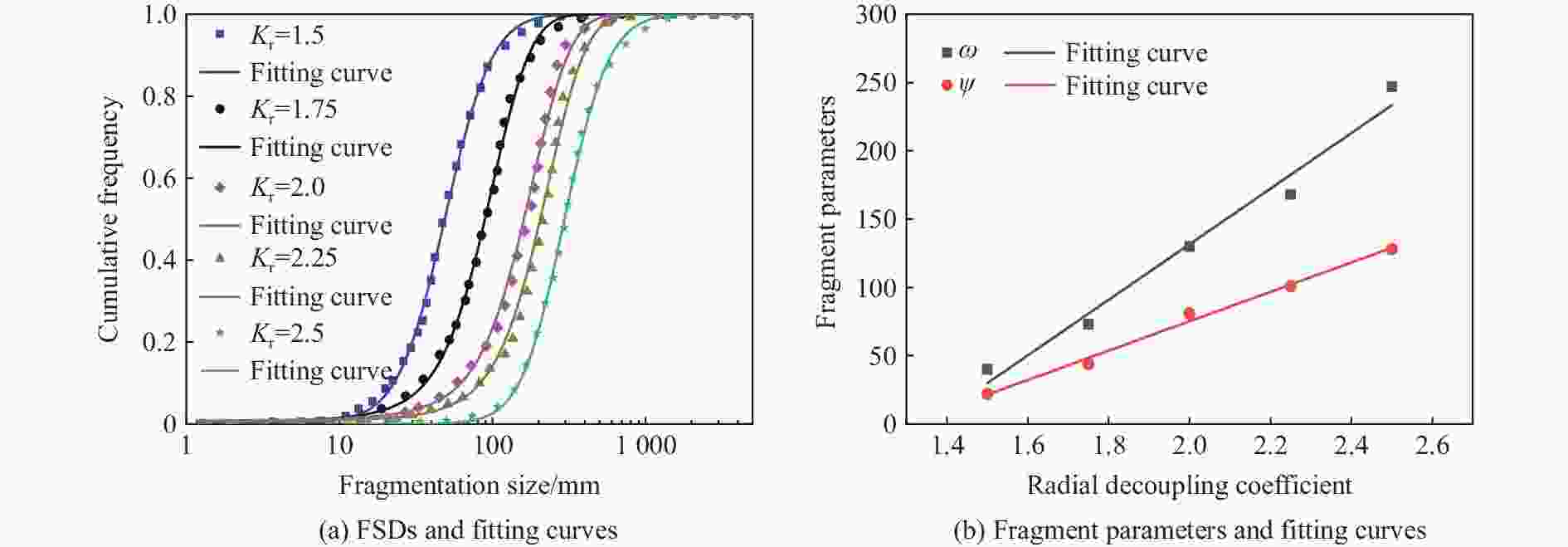
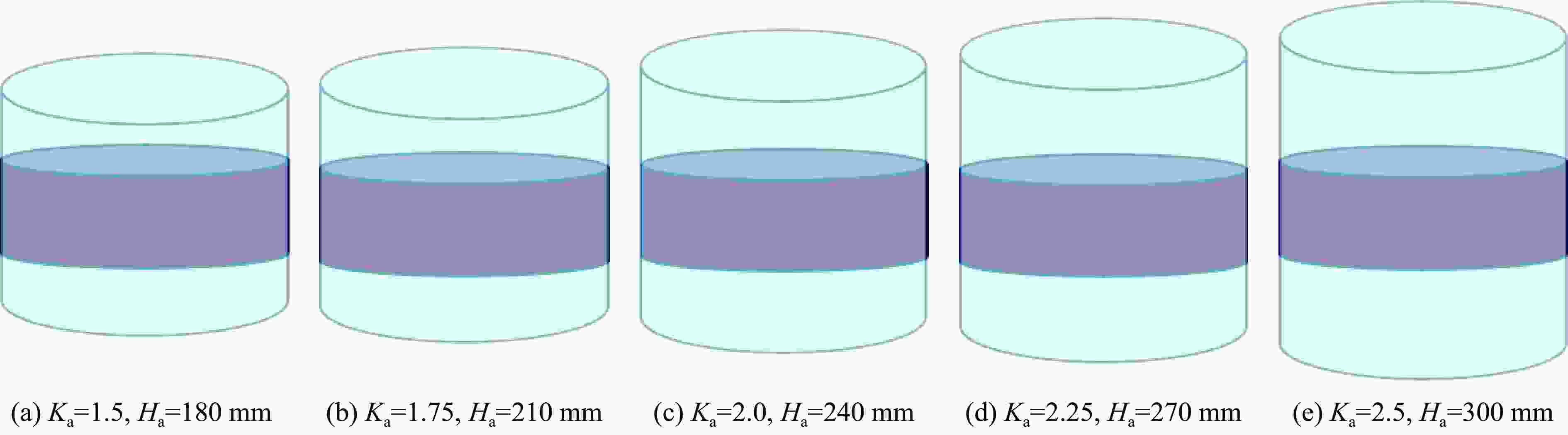
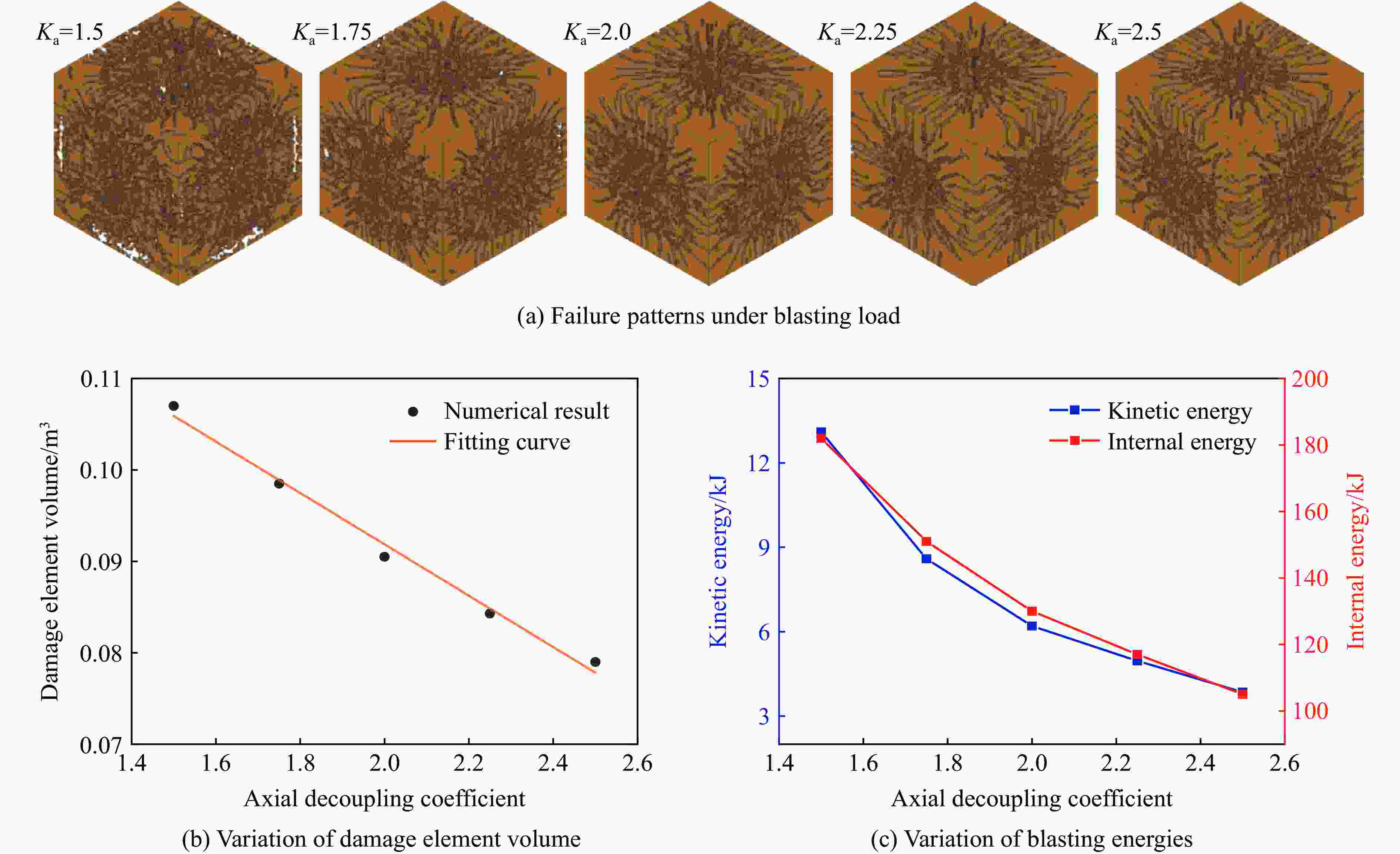
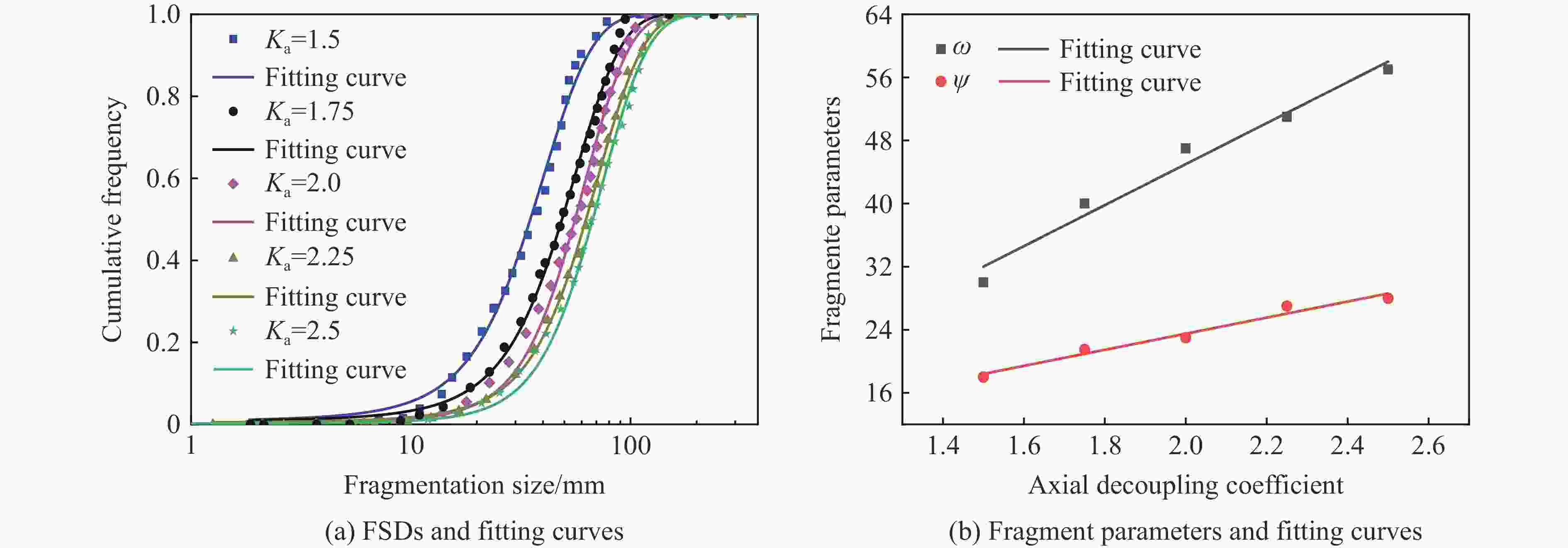
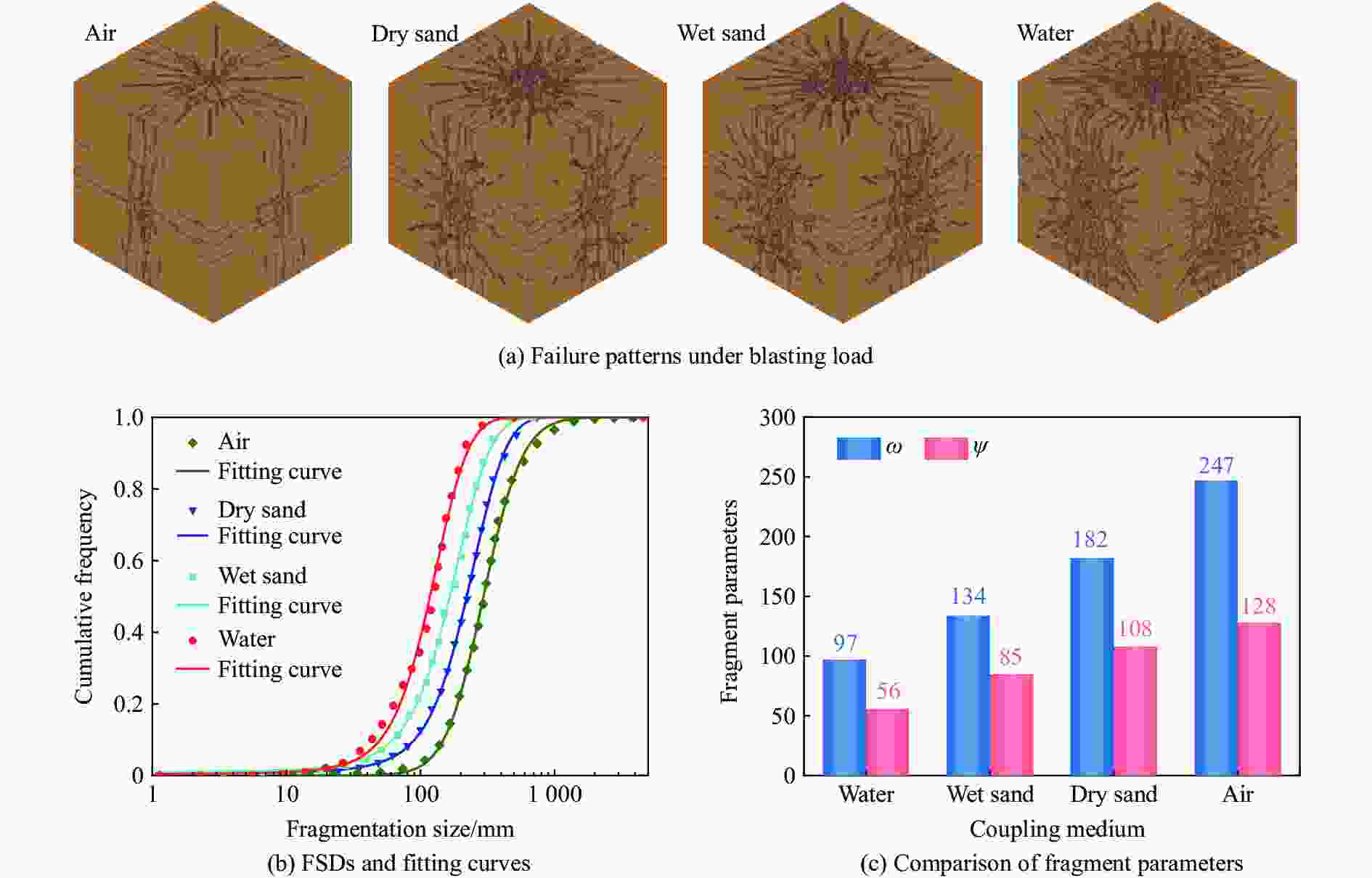
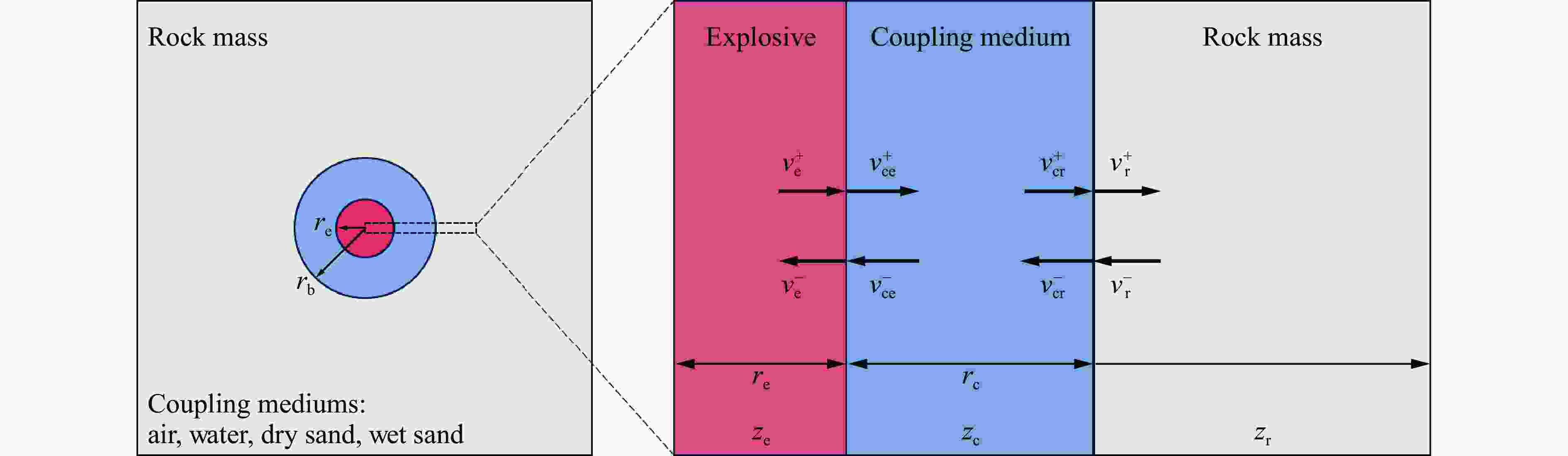
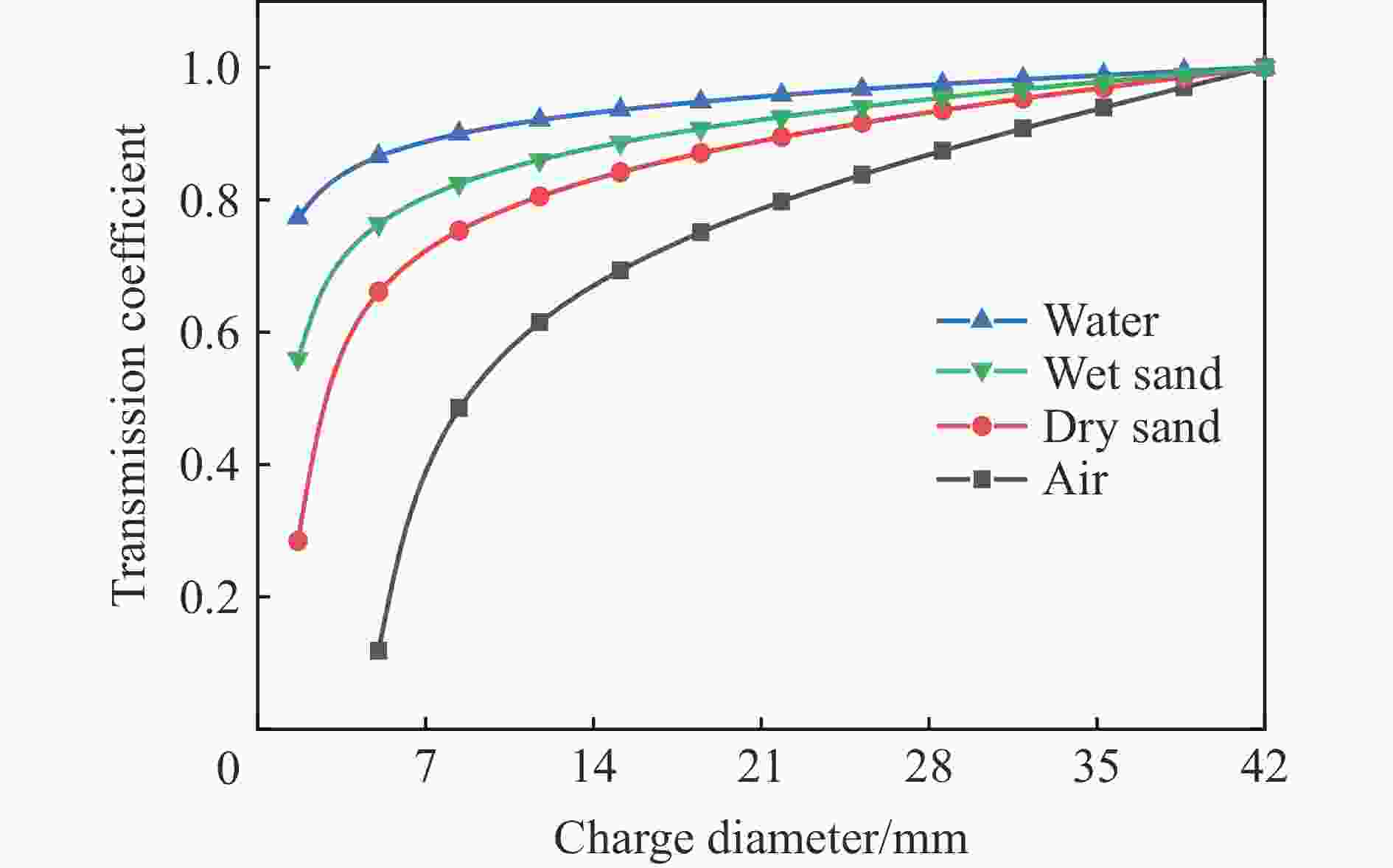
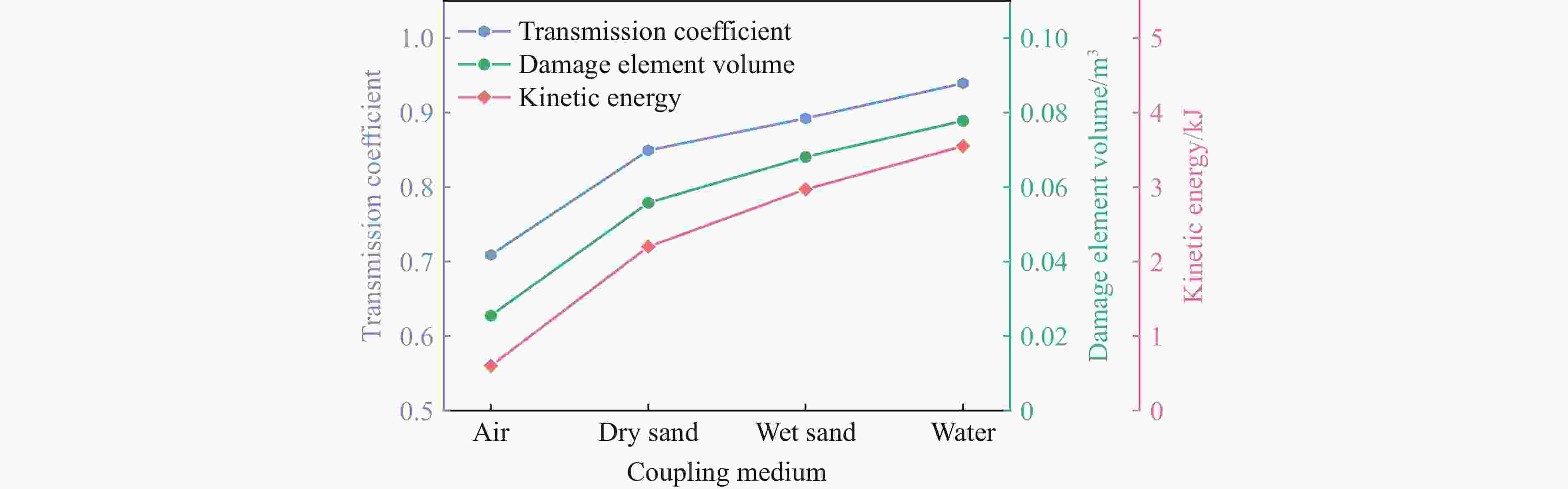
摘要: 通过不同装药结构下立方体红砂岩小型爆破实验，分析了岩石的损伤程度和破坏模式，同时引入三参数极值分布函数量化岩石爆破块体尺寸分布特征。此外，根据岩样R1的爆破实验结果进行了有限元数值模型验证，基于验证的模型展开了岩石单孔爆破损伤破裂行为的模拟，讨论了径向、轴向不耦合系数和耦合介质对岩石破碎效果的影响。结果表明，三参数极值分布函数可以较好地表征岩石爆破后破碎块体尺寸分布特征，块体平均尺寸随着不耦合系数的减小呈线性降低趋势，且破碎块度趋于均匀。通过比较不同耦合介质装药时岩石内部的能量分布特征和破坏体积发现，水作为耦合介质时，爆炸能量的传递效率最高，其次分别是湿砂和干砂，空气的能量传递效率最低。结合等效波阻法计算的理论应力透射系数可以很好地反映不耦合装药时岩石的破碎程度。Abstract: Decoupled charge structure is widely used in contour blasting for rock excavation engineering, and its efficacy in rock breaking is tied intricately to both the decoupling ratio and the transfer features of explosion energy. In this study, the analysis delves into the damage degree and failure patterns of cubic red sandstone samples through two groups of lab-scale blasting tests utilizing various charging modes. To precisely quantify the features of rock fragmentation size distribution (FSD) induced by blasting load, a three-parameter generalized extreme value (GEV) function was introduced. In addition, a three-dimensional finite element model was developed in ANSYS software. The numerical model was calibrated based on the tested results of sample R1 by comparing the fracture networks and FSD curves. This validated model was then deployed to model the rock fracture behavior under decoupled charge blasting, and the evolution of blasting cracks and explosion pressure inside the rock sample was reproduced. Moreover, the effects of axial and radial decoupled ratios and the choice of coupling medium on the rock fragmentation and fracture patterns were discussed. The results showed that the three-parameter GEV function can better characterize the rock fragmentation features resulting from blasting. Notably, the average size of the fragment decreases linearly with the decrease of the decoupling ratio, and the degree of fragmentation tends to be uniform. By comparing the energy distribution and damage levels of rock when using different coupling mediums, it was found that water as the coupling medium exhibits the highest efficiency in energy transfer, followed by wet sand and dry sand, and air has the lowest energy transfer efficiency. Furthermore, the theoretical stress transmission coefficient calculated by the equivalent wave impedance method can well reflect the rock fragmentation features and serve as a valuable reference for rock blasting in decoupled charge.
-
图 1 红砂岩小型爆破实验准备
Figure 1. Preparation for lab-scale blasting experiments on red sandstone samples
图 2 不同装药结构下岩石爆破破坏模式
Figure 2. Failure patterns of rock samples under blasting load with different decoupled charge structures
图 3 不同装药结构下岩石爆破块体尺寸分布
Figure 3. Size distribution of rock fragmentation induced by blasting load with different decoupled charge structures
图 7 爆破荷载下不同时刻岩石的压力分布
Figure 7. Explosion pressure distribution in rock mass under blasting load
图 8 不耦合装药下岩石爆破数值模拟结果与实验结果的比较
Figure 8. Comparison between numerical simulation results and experimental results of rock blasting under decoupled charges
图 9 岩石不同装药结构的几何模型
Figure 9. Geometry models of rock mass with different decoupled charge structures
图 10 装药直径固定为28 mm、炮孔直径不同的径向不耦合装药结构
Figure 10. Radial decoupled charge structures with a fixed charge diameter of 28 mm and different blast hole diameters
图 11 径向不耦合装药爆炸载荷下岩石的破裂特征
Figure 11. Fracture characteristics of rock mass under radially decoupled charge blasting
图 12 径向不耦合装药下爆炸能量的分布特征
Figure 12. Explosion energy distribution under radially decoupled charge blasting
图 13 径向不耦合装药爆炸载荷下岩石破碎块体尺寸的分布
Figure 13. Rock fragmentation size distribution under radially decoupled charge blasting
图 14 装药高度固定为120 mm、空气层高度不同的轴向不耦合装药结构
Figure 14. Axial decoupled charge structures with a fixed charge height of 120 mm and different air layer heights
图 15 轴向不耦合装药爆炸载荷下岩石的破裂特征
Figure 15. Fracture characteristics of rock mass under axially decoupled charge blasting
图 16 轴向不耦合装药爆炸载荷下岩石爆破块体尺寸的分布
Figure 16. Rock fragmentation size distribution under axially decoupled charge blasting
图 18 不同耦合介质装药下岩石破裂特征
Figure 18. Fracture features of rock mass under decoupled charge with different coupling media
图 19 径向不耦合装药下爆轰波的传播过程
Figure 19. Explosion wave propagation process under radial decoupled charges
图 20 不同耦合介质装药时应力波的传递效率
Figure 20. Transfer efficiency of stress wave of different coupling media charges
图 21 不同耦合介质装药时透射系数、损伤单元体积和动能的变化
Figure 21. Variations of transmission coefficient, damage element volume and kinetic energy for different coupling media
表 1 试样尺寸及装药结构
Table 1. Samples dimensions and charge structures
试样 试样长度/mm 试样宽度/mm 试样高度/mm 炮孔直径/mm 不耦合系数 装药结构 R1 100.29 100.34 100.37 12.00 3.0 径向不耦合 R2 100.38 99.81 99.73 10.00 2.5 R3 100.02 100.53 100.52 8.00 2.0 A1 99.81 100.14 100.12 10.00 3.0 轴向不耦合 A2 100.31 100.27 99.77 10.00 2.5 A3 99.63 99.86 100.11 10.00 2.0 
下载: 导出CSV
表 2 岩石RHT模型的材料参数
Table 2. Material parameters of the rock RHT model
参数名称 符号 值 来源 参数名称 符号 值 来源 密度/(kg·m−3) ρr 2360 实验测定 残余面参数 Af 1.62
试错法初始孔隙度 $ {\alpha }_{0}^{\mathrm{r}} $ 1.12 残余面参数 Nf 0.61 抗压强度/MPa fc 21.6 压缩屈服面参数 $ {G}_{\mathrm{c}}^{*} $ 0.53 压缩应变率指数 βc 0.047 理论计算 拉伸屈服面参数 $ {G}_{\mathrm{t}}^{*} $ 0.70 拉伸应变率指数 βt 0.048 最小损伤残余应变 $ {\varepsilon }_{\mathrm{p}}^{\mathrm{m}} $ 0.01 状态方程参数/GPa T1 17.33 孔隙压实压力/GPa pcomp 6.00 Hugoniot多项式系数/GPa A1 17.33 损伤因子 D1 0.04 默认取值 Hugoniot多项式系数/GPa A2 29.11 损伤因子 D2 1.00 Hugoniot多项式系数/GPa A3 17.79 孔隙度指数 NP 3.0 孔隙坍塌压力/MPa pcrush 14.4 参考压缩应变率/s−1 $ {\dot{\varepsilon }}_{0}^{\mathrm{c}} $ 3.0×10−5 洛德角相关因子 Q0 0.68 参考拉伸应变率/s−1 $ {\dot{\varepsilon }}_{0}^{\mathrm{t}} $ 3.0×10−6 洛德角相关因子 B 0.05 破坏压缩应变率/s−1 $ {\dot{\varepsilon }}_{\mathrm{c}} $ 3.0×1022 破坏面参数 A 1.99 破坏拉伸应变率/s−1 $ {\dot{\varepsilon }}_{\mathrm{t}} $ 3.0×1022 破坏面参数 N 0.59 Grüneisen系数 $ \gamma $ 0.0 相对抗剪强度 $ {F}_{\mathrm{s}}^{*} $ 0.45 理论计算 侵蚀塑性应变 $ {\varepsilon }_{\mathrm{s}}^{\mathrm{f}} $ 2.00 默认取值 相对抗拉强度 $ {F}_{\mathrm{t}}^{*} $ 0.10 剪切模量减小因子 ξr 0.50 状态方程参数 B0 1.68 状态方程参数/GPa T2 0.00 状态方程参数 B1 1.68 拉伸体积塑性应变分数 $ {p}_{\mathrm{t}}^{\mathrm{f}} $ 0.001 弹性剪切模量/GPa G 5.10
下载: 导出CSV
表 3 炸药材料参数
Table 3. Material parameters of the explosive
ρe/(kg·m−3) vOD/(m·s−1) pCJ/GPa Ae/GPa Be/GPa R1 R2 ωe $ {E}_{0}^{\mathrm{e}} $/GPa 790 1530 16.0 371 3.23 4.15 0.95 0.33 2.0
下载: 导出CSV
ρa/(kg·m−3) C0 C1 C2 C3 C4 C5 C6 $ {E}_{0}^{\mathrm{a}} $/(kJ·m−3) $ {V}_{0}^{\mathrm{a}} $ 1.29 0.0 0.0 0.0 0.0 0.4 0.4 0.0 250 1.0
下载: 导出CSV
ρds/(kg·m−3) Gds/MPa Kds/MPa pds/kPa ads0 ads1 ads2 1600 34.8 134 -3.4 0.0 0.0 0.3
下载: 导出CSV
表 6 水介质模型参数
Table 6. Material parameters for water
ρw/(kg·m−3) cw/(m·s−1) Ew/(kJ·m−3) S1 S2 S3 γw αw $ {V}_{0}^{\mathrm{w}} $ 1000 1480 1890 2.56 −1.98 1.23 0.35 0.0 1.0
下载: 导出CSV
$ {\rho }_{\mathrm{w}\mathrm{s}}^{} $(kg·m−3) $ {G}_{\mathrm{w}\mathrm{s}}^{} $/MPa $ {K}_{\mathrm{w}\mathrm{s}}^{} $/MPa $ {p}_{\mathrm{w}\mathrm{s}}^{} $/kPa $ {a}_{\mathrm{w}\mathrm{s}0}^{} $ $ {a}_{\mathrm{w}\mathrm{s}1}^{} $ $ {a}_{\mathrm{w}\mathrm{s}2}^{} $ 1800 63.8 126 −6.9 3.4×107 6.4×103 0.3
下载: 导出CSV
-
[1] LI H B, XIA X, LI J C, et al. Rock damage control in bedrock blasting excavation for a nuclear power plant [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 210–218. DOI: 10.1016/j.ijrmms.2010.11.016. [2] 付玉华, 李夕兵, 董陇军. 损伤条件下深部岩体巷道光面爆破参数研究 [J]. 岩土力学, 2010, 31(5): 1420–1426. DOI: 10.16285/j.rsm.2010.05.005.FU Y H, LI X B, DONG L J. Analysis of smooth blasting parameters for tunnels in deep damaged rock mass [J]. Rock and Soil Mechanics, 2010, 31(5): 1420–1426. DOI: 10.16285/j.rsm.2010.05.005. [3] LU W B, CHEN M, GENG X, et al. A study of excavation sequence and contour blasting method for underground powerhouses of hydropower stations [J]. Tunnelling and Underground Space Technology, 2012, 29: 31–39. DOI: 10.1016/j.tust.2011.12.008. [4] 叶志伟, 陈明, 魏东, 等. 不耦合装药爆破孔壁压力峰值的实验研究 [J]. 爆炸与冲击, 2021, 41(5): 055201. DOI: 10.11883/bzycj-2020-0004.YE Z W, CHEN M, WEI D, et al. Experimental study on the peak pressure of borehole wall in decoupling charge blasting [J]. Explosion and Shock Waves, 2021, 41(5): 055201. DOI: 10.11883/bzycj-2020-0004. [5] HUO X F, QIU X Y, SHI X Z, et al. Experimental and numerical investigation on the peak value and loading rate of borehole wall pressure in decoupled charge blasting [J]. International Journal of Rock Mechanics and Mining Sciences, 2023, 170: 105535. DOI: 10.1016/j.ijrmms.2023.105535. [6] LANGEFORS U, KIHLSTRÖ M B. The modern technique of rock blasting [M]. 3rd ed. New York: John Wiley and Sons Incorporation, 1963. [7] PAINE R S, HOLMES D K, CLARK H E. Controlling overbreak by presplitting [M]//CLARK G B. Mining Research. Amsterdam: Elsevier, 1962. [8] 张正宇, 卢文波, 刘美山, 等. 水利水电工程精细爆破概论 [M]. 北京: 中国水利水电出版社, 2009. [9] CHEN M, LU W B, YI C P. Blasting vibration criterion for a rock-anchored beam in an underground powerhouse [J]. Tunnelling and Underground Space Technology, 2007, 22(1): 69–79. DOI: 10.1016/j.tust.2006.03.005. [10] 王伟, 李小春. 不耦合装药下爆炸应力波传播规律的试验研究 [J]. 岩土力学, 2010, 31(6): 1723–1728. DOI: 10.16285/j.rsm.2010.06.004.WANG W, LI X C. Experimental study of propagation law of explosive stress wave under condition of decouple charge [J]. Rock and Soil Mechanics, 2010, 31(6): 1723–1728. DOI: 10.16285/j.rsm.2010.06.004. [11] 李桐, 陈明, 叶志伟, 等. 不同耦合介质爆破爆炸能量传递效率研究 [J]. 爆炸与冲击, 2021, 41(6): 062201. DOI: 10.11883/bzycj-2020-0381.LI T, CHEN M, YE Z W, et al. Study on the energy transfer efficiency of explosive blasting with different coupling medium [J]. Explosion and Shock Waves, 2021, 41(6): 062201. DOI: 10.11883/bzycj-2020-0381. [12] CHI L Y, WANG C, ZHANG Z X, et al. Experimental investigation of decoupled charge effect on rock fragmentation by blasting [J]. Rock Mechanics and Rock Engineering, 2022, 55(7): 3791–3806. DOI: 10.1007/s00603-022-02823-w. [13] YANG R S, DING C X, YANG L Y, et al. Study of decoupled charge blasting based on high-speed digital image correlation method [J]. Tunnelling and Underground Space Technology, 2019, 83: 51–59. DOI: 10.1016/j.tust.2018.09.031. [14] YANG J C, LIU Z X, LIU K W, et al. Study on the blasting damage of prestressed rock-like specimens with different coupling mediums [J]. International Journal of Impact Engineering, 2023, 181: 104758. DOI: 10.1016/j.ijimpeng.2023.104758. [15] LI X D, LIU K W, SHA Y Y, et al. Numerical investigation on rock fragmentation under decoupled charge blasting [J]. Computers and Geotechnics, 2023, 157: 105312. DOI: 10.1016/j.compgeo.2023.105312. [16] 王志亮, 李永池. 工程爆破中径向水不耦合系数效应数值仿真 [J]. 岩土力学, 2005, 26(12): 1926–1930. DOI: 10.16285/j.rsm.2005.12.013.WANG Z L, LI Y C. Numerical simulation on effects of radial water-decoupling coefficient in engineering blast [J]. Rock and Soil Mechanics, 2005, 26(12): 1926–1930. DOI: 10.16285/j.rsm.2005.12.013. [17] ZHU Z M, XIE H P, MOHANTY B. Numerical investigation of blasting-induced damage in cylindrical rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 111–121. DOI: 10.1016/j.ijrmms.2007.04.012. [18] YUAN W, WANG W, SU X B, et al. Experimental and numerical study on the effect of water-decoupling charge structure on the attenuation of blasting stress [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 124: 104133. DOI: 10.1016/j.ijrmms.2019.104133. [19] 袁增森, 徐振洋, 潘博, 等. 不同不耦合系数下花岗岩爆破损伤特性的离散元模拟 [J]. 高压物理学报, 2022, 36(1): 015301. DOI: 10.11858/gywlxb.20210804.YUAN Z S, XU Z Y, PAN B, et al. Discrete element simulation of blasting damage characteristics of granite under different decoupling coefficients [J]. Chinese Journal of High Pressure Physics, 2022, 36(1): 015301. DOI: 10.11858/gywlxb.20210804. [20] LI X D, LIU K W, SHA Y Y, et al. Investigation on radial fracturing around borehole under combined static stress and blasting [J]. Theoretical and Applied Fracture Mechanics, 2023, 127: 104038. DOI: 10.1016/j.tafmec.2023.104038. [21] SHEN W G, ZHAO T, CROSTA G B, et al. Analysis of impact-induced rock fragmentation using a discrete element approach [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 98: 33–38. DOI: 10.1016/j.ijrmms.2017.07.014. [22] 李洪超. 岩石RHT模型理论及主要参数确定方法研究 [D]. 北京: 中国矿业大学(北京), 2017.LI H C. The study of the rock RHT model and to determine the values of main parameters [D]. Beijing: China University of Mining & Technology, Beijing, 2017. [23] XIE L X, LU W B, ZHANG Q B, et al. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses [J]. Tunnelling and Underground Space Technology, 2017, 66: 19–33. DOI: 10.1016/j.tust.2017.03.009. [24] LI S L, LING T L, LIU D S, et al. Determination of rock mass parameters for the RHT model based on the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2023, 56(4): 2861–2877. DOI: 10.1007/s00603-022-03189-9. [25] BORRVALL T, SWEDEN L, RIEDEL W. The RHT concrete model in LS-DYNA [C]//Proceedings of the 8th European LS-DYNA Users Conference. Strasbourg, 2011. [26] 马泗洲, 刘科伟, 杨家彩, 等. 初始应力下岩体爆破损伤特性及破裂机理 [J]. 爆炸与冲击, 2023, 43(10): 105201. DOI: 10.11883/bzycj-2023-0151.MA S Z, LIU K W, YANG J C, et al. Blast-induced damage characteristics and fracture mechanism of rock mass under initial stress [J]. Explosion and Shock Waves, 2023, 43(10): 105201. DOI: 10.11883/bzycj-2023-0151. [27] DEHGHAN BANADAKI M M, MOHANTY B. Numerical simulation of stress wave induced fractures in rock [J]. International Journal of Impact Engineering, 2012, 40/41: 16–25. DOI: 10.1016/j.ijimpeng.2011.08.010. [28] LIU K W, QIU T, LI X D, et al. Deep rock blasting using decoupled charge with different coupling mediums [J]. International Journal of Geomechanics, 2023, 23(8): 04023112. DOI: 10.1061/IJGNAI.GMENG-8179. [29] TAO J, YANG X G, LI H T, et al. Numerical investigation of blast-induced rock fragmentation [J]. Computers and Geotechnics, 2020, 128: 103846. DOI: 10.1016/j.compgeo.2020.103846. [30] MA S Z, LIU K W, YANG J C. Investigation of blast-induced rock fragmentation and fracture characteristics with different decoupled charge structures [J]. International Journal of Impact Engineering, 2024, 185: 104855. DOI: 10.1016/j.ijimpeng.2023.104855. [31] WANG H C, WANG Z L, WANG J G, et al. Effect of confining pressure on damage accumulation of rock under repeated blast loading [J]. International Journal of Impact Engineering, 2021, 156: 103961. DOI: 10.1016/j.ijimpeng.2021.103961. [32] 白金泽. LS-DYNA3D理论基础与实例分析 [M]. 北京: 科学出版社, 2005: 167–170. [33] 李夕兵. 岩石动力学基础与应用 [M]. 北京: 科学出版社, 2014: 357–360. -
计量
- 文章访问数: 236
- HTML全文浏览量: 70
- PDF下载量: 118
- 被引次数: 0