Measurement of strength in a Zr-based bulk metallic glass under dynamic high-pressure loading
-
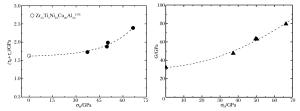
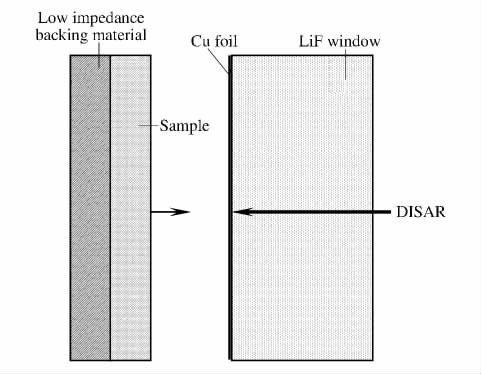
摘要: 为了研究Zr51Ti5Ni10Cu25Al9金属玻璃的高压强度特性，进行了平靶冲击实验。采用反向碰撞方式，运用DISAR技术测量金属玻璃样品/LiF窗口界面粒子速度剖面，分析粒子速度剖面获得了37~66GPa压力范围锆基金属玻璃的屈服强度和剪切模量。实验结果表明，在上述压力范围金属玻璃的屈服强度和剪切模量均显示出一定程度的压力硬化效应，分析表明金属玻璃冲击加载波阵面剪应力衰减并非由损伤/破坏或温度软化等因素导致。Abstract: To investigate the dynamic strength behaviors of a Zr-based bulk metallic glass(BMG), Zr51Ti5Ni10Cu25Al9(in atomic percent), a series of reverse-impact experiments were performed in the peak shock stress range from 37to 66GPa.A displacement interferometer system for any reflector(DISAR)was used to measure the particle velocity profiles at the sample/LiF window interface.By analyzing the measured particle velocity profiles, the yield strength and shear modulus of the Zr-based BMG were obtained.The experimental results show that both the yield strength and the shear modulus of the Zr-based BMG increase with the increasing of the shock stresses in the stress range considered here.And the shear stress relaxation across the shock wave front of the Zr-based BMG is not due to the shock-induced damage/failure or temperature softening.
-
Key words:
- solid mechanics /
- yield strength /
- DISAR /
- bulk metallic glass /
- shear modulus /
- shock wave
-
图 2 样品/窗口界面粒子速度剖面
Figure 2. Particle velocity profiles measured at sample/window interface
图 3 卸载过程的拉格朗日纵波和体波声速
Figure 3. Longitudinal and bulk Lagrangian wave speed during unloading
图 4 屈服强度和剪切模量随冲击压力的变化
Figure 4. Variation of yield strength and shear modulus with shock pressure
表 1 平靶冲击实验参数及结果
Table 1. Experimental conditions and results for four plate-impact experiments
No. ρ0/(g·cm-3) Hs/mm W/(km·s-1) σH/GPa (τH+τc)/GPa G/GPa 1 6.744 3.142 2.889 37.28 1.73 47.59 2 6.743 3.120 3.604 49.69 1.88 63.25 3 6.736 3.016 3.640 50.33 1.99 62.96 4 6.655 3.007 4.480 66.42 2.39 79.47 
下载: 导出CSV
-
[1] Inoue A. Stabilization of metallic supercooled liquid and bulk amorphous alloys[J]. Acta Materialia, 2000, 48(1): 279-306. doi: 10.1016/S1359-6454(99)00300-6 [2] Schuh C A, Hufnagel T C, Ramamurty U. Mechanical behavior of amorphous alloys[J]. Acta Materialia, 2007, 55(12): 4067-4109. doi: 10.1016/j.actamat.2007.01.052 [3] Trexler M M, Thadhani N N. Mechanical properties of bulk metallic glasses[J]. Progress in Materials Science, 2010, 55(8): 759-839. doi: 10.1016/j.pmatsci.2010.04.002 [4] Lu J, Ravichandran G. Pressure-dependent flow behavior of Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass[J]. Journal of Materials Research, 2003, 18(9): 2039-2049. doi: 10.1557/JMR.2003.0287 [5] Mashimo T, Togo H, Zhang Y, et al. Hugoniot-compression curve of a Zr-based bulk metallic glass[J]. Applied Physics Letters, 2006, 89(24): 241904. doi: 10.1063/1.2403931 [6] Xi F, Yu Y Y, Dai C D, et al. Shock compression response of a Zr-based bulk metallic glass up to 110GPa[J]. Journal of Applied Physics, 2010, 108(8): 083537. doi: 10.1063/1.3501044 [7] Turneaure S J, Dwivedi S K, Gupta Y M. Shock-wave induced tension and spall in a zirconium-based bulk amorphous alloy[J]. Journal of Applied Physics, 2007, 101(4): 043514. doi: 10.1063/1.2537982 [8] Yuan F P, Prakash V, Lewandowski J J. Spall strength and Hugoniot elastic limit of a zirconium-based bulk metallic glass under planar shock compression[J]. Journal of Materials Research, 2007, 22(2): 402-411. doi: 10.1557/jmr.2007.0053 [9] Yuan F P, Prakash V, Lewandowski J J. Shear yield and flow behavior of a zirconium-based bulk metallic glass[J]. Mechanics of Materials, 2010, 42(3): 248-255. doi: 10.1016/j.mechmat.2009.11.003 [10] Turneaure S J, Winey J M, Gupta Y M. Response of a Zr-based bulk amorphous alloy to shock wave compression[J]. Journal of Applied Physics, 2006, 100(6): 063522. doi: 10.1063/1.2345606 [11] 俞宇颖, 习锋, 戴诚达, 等.冲击加载下Zr51Ti5Ni10Cu25Al9金属玻璃的塑性行为[J].物理学报, 2012, 61(19): 196202. doi: 10.7498/aps.61.196202Yu Yu-ying, Xi Feng, Dai Cheng-da, et al. Plastic behavior of Zr51Ti5Ni10Cu25Al9 metallic glass under planar shock loading[J]. Acta Physica Sinica, 2012, 61(19): 196202. doi: 10.7498/aps.61.196202 [12] Arman B, Luo S N, Germann T C, et al. Dynamic response of Cu46Zr54 metallic glass to high-strain-rate shock loading: Plasticity, sapll and atomic-level structures[J]. Physical Review B, 2010, 81(14): 144201. doi: 10.1103/PhysRevB.81.144201 [13] Wang W H, Li F Y, Pan M X, et al. Elastic property and its response to pressure in a typical bulk metallic glass[J]. Acta Materialia, 2004, 52(3): 715-719. doi: 10.1016/j.actamat.2003.10.008 [14] Weng J D, Tan H, Wang X, et al. Optical-fiber interferometer for velocity measurements with picosecond resolution[J]. Applied Physics Letters, 2006, 89(1): 111101. doi: 10.1063/1.2335948 [15] Narsh S P. LASL Shock Hugoniot Data[M]. Berkeley: University of California Press, 1980: 296-297. [16] 谭华.实验冲击波物理导引[M].北京: 国防工业出版社, 2007: 163-167. [17] Yu Y Y, Tan H, Hu J B, et al. Determination of effective shear modulus of shock-compressed LY12Al from particle velocity profile measurements[J]. Journal of Applied Physics, 2008, 103(10): 103529. doi: 10.1063/1.2927492 [18] Asay J R, Chhabildas L C. Determination of the shear strength of shock compressed 6061-T6aluminum[C]//Meyers M M, Murr L E. Shock waves and high-strain-rate phenomena in metals. New York: Plenum, 1981: 417-431. [19] Wang J G, Zhao D Q, Pan M X, et al. Correlation between onset of yielding and free volume in metallic glasses[J]. Scripta Materialia, 2010, 62(7): 477-480. doi: 10.1016/j.scriptamat.2009.12.015 -
图(4) / 表(1)
计量
- 文章访问数: 1138
- HTML全文浏览量: 334
- PDF下载量: 13
- 被引次数: 0