Sensitivity analysis for impact resistance of steel plate concrete walls based on force vs. time-history analysis
-
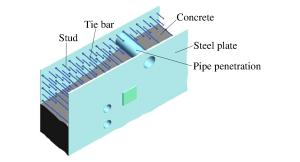
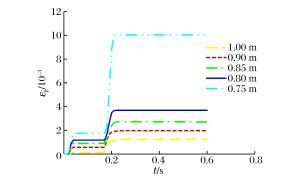
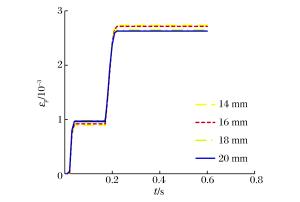
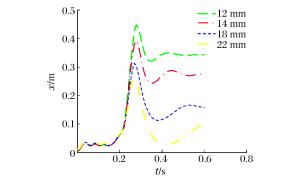
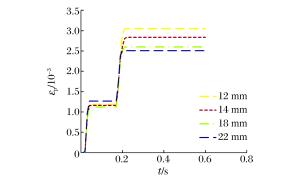
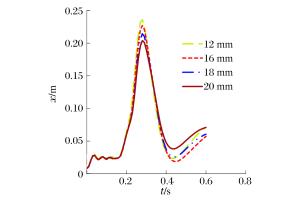
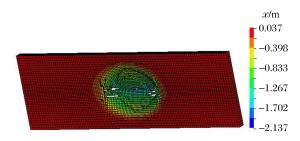
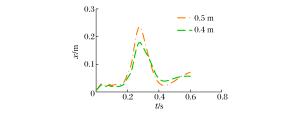
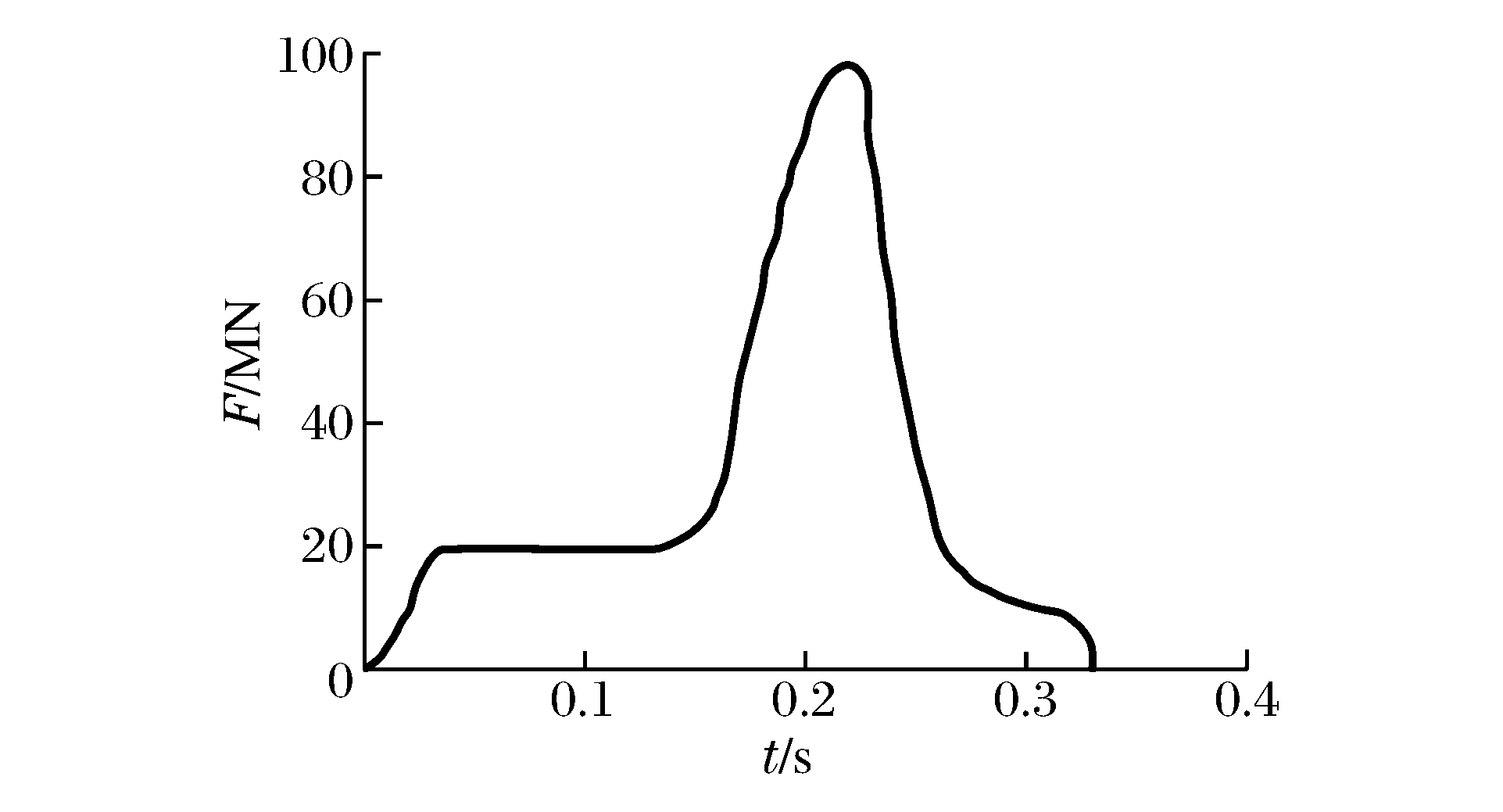
摘要: 选取由表面钢板、拉结筋、剪力钉及混凝土组成的钢板混凝土结构墙为研究对象，运用经典显式非线性动力分析软件ANSYS/LS-DYNA，基于荷载时程分析法进行了一系列影响钢板混凝土结构墙抗冲击性能的参数敏感性分析。这些参数包括：墙体厚度、钢板厚度、拉结筋直径与间距等。分析结果表明，以上参数均会影响墙体的抗冲击性能，尤其是墙体与钢板的厚度以及拉结筋的间距。本文的研究工作对于核电厂核岛厂房钢板混凝土结构外墙的设计具有一定的指导与参考意义。Abstract: In this paper, to study preventive ways against incidents involving the impact of steel plate concrete (SC) structures, the steel plate concrete (SC) walls composed of surface steel plates, tie-bars, shear studs and concretes were selected as the object of investigation. The impact analysis of the walls was performed using ANSYS/LS-DYNA, the FEM code, based on the force vs. time-history analysis, in which a series of numerical sensitivity studies were conducted to evaluate the effect of several parameters affecting the behavior of the SC wall. These parameters include the thickness of the wall, the thickness of the steel plate, and the diameter and space of tie bars. The results show that they all have an effect on the impact resistance of the SC wall. This is especially true with the thickness of the wall and the steel plate, and the spacing distance between the tie bars. These studies will serve as guidance and reference for the design of SC structures that are to be used in nuclear power plant buildings.
-
金属铍具有中子散射截面大、吸收截面小、硬度高、模量高、比强高、热学性能良好等特性，因此被广泛应用于航空航天、军事工业、医疗设备、焊接技术等多个技术领域，如中子反射层，反应堆第一壁材料、中子慢化剂，航空航天结构部件、精密仪表、光学器件及X射线管窗口等。国外已开展大量金属铍的变形行为研究，而国内开展的相关研究较少，且主要集中在常温静态拉伸性能方面，对其压缩力学行为尤其是动态压缩特性方面报道较少[1-9]。王零森等[1]研究了晶粒尺寸对铍静态拉伸力学性能的影响，发现随着晶粒度逐渐细化，铍材料的强度显著提高，而晶粒过粗或过细，延伸率均下降。许德美等[2-3]研究了组织缺陷对金属铍室温拉伸断裂行为的影响，其分析结果表明铍的“脆性”特征主要来源于杂质、片状晶体疏松和孔洞等初始缺陷，最关键因素是杂质的尺寸、间距和其在材料内部的分布形态。W.R.Blumenthal等[4-5]对不同制备工艺下的铍进行了较为系统的研究。实验结果表明，铍的压缩应力应变响应具有较强的应变率敏感性和一定的热软化效应，并指出孪生是高应变率下铍变形的主要机制。D.W.Brown等[6-8]系统开展了应变率对热压和轧制铍的力学性能和变形机理的研究工作，分析结果表明屈服强度对应变率不敏感，而加工硬化则受织构的影响具有较强的率相关性。T.Nicholas[9]和D.Breithaupt[10]研究了铍在常温102~103 s-1应变率下的动态压缩性能，结果表明铍具有良好的塑性，应变增大至0.25时样品才发生断裂。由此可见，国外开展的相关研究工作重点关注制备工艺、温度、应变率等条件对金属铍滑移及孪晶变形机制的影响研究，获得描述金属铍变形织构行为的本构模型参数。国内开展的研究则主要围绕金属铍静态拉伸应力状态下的“脆性”行为的微观变形机制，对其压缩行为研究工作较少，尤其是动态加载下温度、应变速率对其变形行为的影响未见相关研究报道。
本文中利用材料实验机及Hopkinson杆装置系统开展了热等静压金属铍在不同温度、应变率下的压缩力学行为研究，获得金属铍压缩载荷下强度、塑性与实验温度、应变率之间的对应关系。并采用Johnson-Cook本构模型对获得的应力应变曲线进行拟合，模型计算结果与实验结果吻合较好。
1. 实验材料及方法
铍在机加后表面会有较大的残余应力，为了消除残余应力对测量结果的影响[11]，室温力学实验前对样品进行了蚀刻处理，蚀刻剂配方为：H3PO4，750 mL；H2SO4，30 mL；Cr2O3，71 mg；H2O，200 mL。蚀刻方法为将铍试样放入酸洗液约50 s取出，用蒸馏水等清洗干净。
静态力学实验在CMT5105型材料试验机及其配置的高温真空炉中进行，高温炉温度控制精度为±3 ℃，真空度优于1×10-2 Pa，试样在1 h内加热到规定温度，保温15 min后开始实验，应变率为1.0×10-3 s-1，测试温度范围为室温至800 ℃。动态压缩实验采用∅10 mm的Hopkinson杆装置。试样为∅5 mm×5 mm的圆柱体，应变率范围为0.5×103~2.5×103 s-1, 在常温下进行。
2. 实验结果与分析
图 1所示为铍在不同温度下的准静态压缩实验结果。由图 1应力应变曲线可以看出，金属铍在室温至800 ℃的温度范围内压缩变形具有良好的塑性。屈服强度和流动应力随实验温度升高而降低，加工硬化行为也随之降低。图 2所示为不同固定应变下的流动应力随实验温度的变化。由图中可以看到，在室温至200 ℃时，不同固定应变下流动应力均下降较快，高于200 ℃时流动应力下降趋势变缓，呈线性下降特征。当实验温度高于400 ℃时，不同应变下的流动应力值基本一致，这表明此时材料的塑性变形行为趋于理性塑性流动。
图 1 金属铍在准静态条件下应力应变关系Figure 1. Relation between stress and strain under quasi-static condition
图 2 金属铍在准静态条件下流动应力随温度变化曲线Figure 2. Relation between flow stress and temprature under quasi-static condition图 3所示为铍的动态压缩实验结果。可以看出，铍的屈服强度和加工硬化行为随应变率增大而显著增大，在初始变形阶段，加工硬化行为呈现非线性特征，随变形量增大，转变为线性硬化。由文献[4]可知，准静态和动态加载下，金属铍的塑性变形控制机制有显著区别。与大多数对称性低、滑移系统少的密排六方晶系金属一样，由于晶体的取向不利于发生滑移，孪生成为铍塑性变形的重要方式。在初始变形阶段，变形机制由位错滑移控制，随着变形增大，位错滑移困难，通过孪生协调变形，尤其在动态加载过程中，晶粒内部将产生大量的孪晶，由于滑移与孪生机制的竞争导致了不同应变率、不同应变下金属铍屈服强度和加工硬化行为的显著区别。
3. 本构模型
Johnson-Cook模型是目前应用最广泛的本构模型之一，模型中将流动应力表述为应变硬化效应、应变率效应和温度软化效应的乘积，方程的基本形式如下：
σ=(A+Bεnp)(1+Cln˙ε˙ε0)(1−T∗m) (1) 式中:σ为Von-Mises流动应力，εp为等效塑性应变，A为准静态下的屈服应力，B为应变硬化系数，n为应变硬化指数，˙ε0为参考应变率(可取准静态应变率)，C为应变率敏感系数，T*为温度相关项，具体表达式为(T-Tr)/(Tm-Tr), Tr和Tm分别为参考温度和熔化温度，一般取Tr为300 K，m为热软化系数。由式(1)可见，Johnson-Cook本构模型忽略了材料变形历史的影响，即如果材料服从Johnson-Cook本构模型，则不同应变率下的应力应变曲线是相似的。
而由图 1~3中的应力应变曲线可以看到，不同温度或应变率下铍的应力应变曲线呈发散趋势，传统的Johnson-Cook本构模型已不适用。因此，本文中采用一个修正的Johnson-Cook本构模型对实验数据进行拟合，在应变硬化项中增加屈服强度温度相关线性函数，同时参考Zerrilli-Armstrong本构模型中描述hcp晶体结构材料变形硬化的函数关系式, 在幂指数应变硬化项中添加应变率指数硬化项和温度指数软化项，分别描述温度、变形历史对材料屈服强度和流动应力的影响，以及流动应力随应变率明显的增加趋势, 其表达式为：
σ=[A(1−A1T∗)+Bεnpea˙ε(B1+B2eβT∗)](1+Cln˙ε˙ε0) (2) 和传统Johnson-Cook模型相比，修正模型中增加了4个参数。取准静态应变率10-3 s-1为参考应变率，Tm=1 557 K。本构拟合参数为：A=424 MPa, B=1 010 MPa, A1=1.487, B1=0.107 3, B2=0.885 4, n=0.485, α=0.000 39, β=-13.83, C=0.015。
采用修正模型计算结果与实验结果对比如图 4所示，实线为采用修正Johnson-Cook本构模型的计算结果。可以看到，模型的计算结果与实验结果符合较好，修正后的Johnson-Cook本构模型能够较好地描述金属铍在不同温度、应变和应变率下的压缩变形行为。
图 4 修正Johnson-Cook模型计算结果与实验结果对比Figure 4. Comparison of experimental results with calculated results by modified Johnson-Cook model4. 结论
本文中研究了较宽温度范围和应变率下热等静压金属铍的压缩力学行为。结果表明铍的屈服强度和加工硬化行为随应变率的提高而显著增大，随温度的升高而降低。常温下其加工硬化行为在初始变形阶段呈现非线性特征，随变形增大转变为线性硬化。温度高于400 ℃时，其变形行为趋于理性塑性流动。考虑温度、变形历史对材料屈服强度和加工硬化的影响，对Johnson-Cook模型进行了修正，修正后的本构模型预测结果和实验结果吻合较好。
-
图 3 机身和机翼的撞击荷载时程曲线
Figure 3. Curves of impact force vs. time-history for fuselage and wings
图 4 机身和机翼的撞击面积时程曲线
Figure 4. Curves of impact area vs. time-history for fuselage and wings
图 5 波音707-320机身和机翼的均布荷载时程曲线
Figure 5. Curves of evenly distributed impact pressure vs. time-history for fuselage and wings of Boeing 707-320
图 6 波音707-320整个飞机的均布荷载时程曲线
Figure 6. Curve of evenly distributed impact pressure vs. time-history for the whole aircraft of Boeing 707-320
图 7 典型的钢板混凝土结构墙示意图
Figure 7. Schematic illustration of the typical steel plate concrete (SC) wall
图 9 不同加载模式的墙体最大位移时程曲线
Figure 9. Curves of max displacement vs. time-history of SC wall for different loads
图 10 不同加载模式的混凝土最大塑性应变时程曲线
Figure 10. Curves of max plastic strain vs. time-history of concrete for different loads
图 11 不同加载模式下混凝土的最大塑性应变云图
Figure 11. Contour plot of max plastic strain of concrete for different loads
图 12 不同厚度SC墙体的最大位移时程曲线
Figure 12. Curves of max displacement vs. time-history for SC wall with different thickness
图 13 不同厚度SC墙体的混凝土最大塑性应变时程曲线
Figure 13. Curves of max plastic strain vs. time-history for concrete of SC wall with different thickness
图 14 不同钢板厚度的墙体最大位移时程曲线
Figure 14. Curves of max displacement vs. time-history for SC wall of steel plates with different thickness
图 15 不同钢板厚度的混凝土最大塑性应变时程曲线
Figure 15. Curves of max plastic strain vs. time-history for concrete for steel plates with different thickness
图 16 不同钢板厚度的墙体最大位移时程曲线
Figure 16. Curves of max displacement vs. time-history for SC wall of steel plates with different thickness
图 17 不同钢板厚度的混凝土最大塑性应变时程曲线
Figure 17. Curves of max plastic strain vs. time-history for concrete of steel plates with different thickness
图 18 SC墙体14 mm厚背部钢板的等效应力云图
Figure 18. Contour plot of the equivalent stress of back face of 14mm steel plate for SC wall
图 19 SC墙体18 mm厚背部钢板的等效应力云图
Figure 19. Contour plot of the equivalent stress of back face of 18mm steel plate for SC wall
图 20 不同拉结筋直径的墙体最大位移时程曲线
Figure 20. Curves of max displacement vs. time-history for SC wall with different diameter of tie-bar
图 22 SC墙体背部的残余位移云图
Figure 22. Contour plot of residual displacement of SC wall back surface
图 23 SC墙体钢板的最大塑性应变云图
Figure 23. Contour plot of max plastic strain of SC wall steel plate
图 24 不同拉结筋间距的墙体最大位移时程曲线
Figure 24. Curves of max displacement vs. time-history for differently spaced tie-bar
表 1 钢板混凝土墙的材料参数
Table 1. Material parameters of steel plate concrete wall
材料 ρ/(kg·m-3) E/GPa υ fc/MPa ft/MPa 混凝土 2 400 35.2 0.2 46.0 4.2 钢板 7 800 206.0 0.3 400.0 400.0 拉结筋 7 800 206.0 0.3 330.0 330.0 剪力钉 7 800 206.0 0.3 330.0 330.0 
下载: 导出CSV
-
[1] US Nuclear Regulatory Commission.10CFR50.150 Aircraft impact assessment[S]. Washington, DC: US Nuclear Regulatory Commission, 2009. [2] ERIN Engineering and Research, Inc. NEI 07-13, Revision 8P, methodology for performing aircraft impact assessments for new plant designs[S]. Palo Alto, 2011. [3] Tsubota H, Koshika N, Mizuno J, et al. Scale model tests of multiple barriers against aircraft impact: Part 1. Experimental program and test results[C]//Transactions of the 15th International Conference on Structural Mechanics in Reactor Technology (SMiRT-15). Seoul, Korea, 1999: Ⅶ137-Ⅶ144. [4] Mizuno J, Koshika N, Sawamoto Y, et al. Investigations on impact resistance of steel plate reinforced concrete barriers against aircraft impact part 1: Test program and results[C]//Transactions of the 18th International Conference on Structural Mechanics in Reactor Technology, 2005: 2566-2579. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-EGVD200508001267.htm [5] Muhammad S, Zhu X Y, Pan R. Simulation analysis of impact tests of steel plate reinforced concrete and reinforced concrete slabs against aircraft impact and its validation with experimental results[J]. Nuclear Engineering and Design, 2014, 273:653-667. doi: 10.1016/j.nucengdes.2014.03.031 [6] 朱秀云, 潘蓉, 林皋, 等.基于荷载时程分析法的钢筋混凝土和钢板混凝土墙的冲击响应对比分析[J].振动与冲击, 2014, 33(22):172-177. http://www.cnki.com.cn/article/cjfdtotal-zdcj201422031.htmZhu Xiuyun, Pan Rong, Lin Gao, et al. Comparative analysis of impact response with reinforced concrete and steel plate concrete walls based on force time-history analysis method[J]. Journal of Vibration and Shock, 2014, 33(22):172-177. http://www.cnki.com.cn/article/cjfdtotal-zdcj201422031.htm [7] 潘蓉, 吴婧姝, 张心斌.钢板混凝土结构在核电工程中应用的发展状况[J].工业建筑.2014, 44(12):1-7. http://d.old.wanfangdata.com.cn/Periodical/gyjz201412001Pan Rong, Wu Jingshu, Zhang Xinbin. Application and development of steel plate reinforced concrete structure in nuclear power engineering[J]. Industrial Construction, 2014, 44(12):1-7. http://d.old.wanfangdata.com.cn/Periodical/gyjz201412001 [8] Hallquist J Q. LS-DYNA keyword user's manual, revision 971[M]. California: Livermore Software Technology Corportion, 2007. [9] 中国国家核安全局.HAD101/04.核电厂厂址选择的外部人为事件[S].北京: 中国法制出版社, 1989. [10] Mullapudi T R S, Summers P, Hwan M. Impact analysis of steel plated concrete wall[C]//Structures Congress 2012.ASCE, 2012: 1881-1893. [11] Arros J, Doumbalski N. Analysis of aircraft impact to concrete structures[J]. Nuclear Engineering and Design, 2007, 237(12/13):1241-1249. https://www.sciencedirect.com/science/article/pii/S0029549306005875 [12] Abu-Odeh A. Modeling and simulation of bogie impacts on concrete bridge rails using LS-DYNA[C]//10th International LS-DYNA Users Conference. 2008. [13] Comite Euro-International du Beton. CEB-FIP model code 1990[M]. Trowbridge, Wiltshire, U K: Redwood Books, 1993. [14] Wu Y C, Crawford J E, Magallanes J M. Performance of LS-DYNA concrete constitutive models[C]//12th International LS-DYNA Users Conference, 2012. [15] 朱秀云, 潘蓉, 林皋, 等.基于ANSYS/LS-DYNA的钢板混凝土墙冲击实验的有限元分析[J].爆炸与冲击, 2015, 35(2):222-228. doi: 10.11883/1001-1455(2015)02-0222-07Zhu Xiuyun, Pan Rong, Lin Gao, et al. FEM analysis of impact experiments with steel plate concrete walls based on ANSYS/LS-DYNA[J]. Explosion and Shock Waves, 2015, 35(2):222-228. doi: 10.11883/1001-1455(2015)02-0222-07 [16] Mizuno J, Koshika N, Morikawa H, et al. Investigations on impact resistance of steel plate reinforced concrete barriers against aircraft impact. Part 2: Simulation analyses of scale model impact tests[C]//Transactions of the 18th International Conference on Structural Mechanics in Reactor Technology, 2005: 2580-2590. 期刊类型引用(8)
1. 张震，姚颖康，贾永胜，谢全民，孙金山. 冲击荷载作用下地铁隧道盾构管片破坏特性. 地下空间与工程学报. 2024(02): 488-496 . 
百度学术2. 杨程风，闫俊伯，刘彦，吕中杰，黄风雷. 接触爆炸载荷下波纹钢加固钢筋混凝土板毁伤特征分析. 北京理工大学学报. 2022(05): 453-462 . 百度学术3. 朱立猛，高晓飞，张春巍. 无焊缝全螺栓连接双钢板混凝土组合剪力墙平面外抗冲击性能有限元分析. 振动与冲击. 2021(09): 166-174 . 百度学术4. 李晓昆，王小兵，刘敏，杨建华. 某核安全相关厂房中减振层有限元分析研究. 工业建筑. 2021(12): 37-40+63 . 百度学术5. 赵唯以，王琳，郭全全，高泽鹏. 双钢板混凝土组合结构抗冲击性能的研究进展. 钢结构(中英文). 2020(03): 26-36 . 百度学术6. 王秀振，钱永久，邵长江，宋帅. 结构地震需求QRNN重要性分析. 应用基础与工程科学学报. 2020(04): 953-965 . 百度学术7. 姚洪灿，谭平，周福霖. 商用飞机撞击刚性墙的荷载时程分析方法. 自然灾害学报. 2019(02): 49-59 . 百度学术8. 窦旭强，赵唯以，可飞，郭全全. 双钢板-混凝土组合剪力墙落锤冲击性能研究. 建筑结构学报. 2017(S1): 84-89 . 百度学术其他类型引用(9)
-
下载:
百度学术
计量
- 文章访问数: 6565
- HTML全文浏览量: 3056
- PDF下载量: 853
- 被引次数: 17