内爆加载金属界面不稳定性的数值分析

郝鹏程; 冯其京; 胡晓棉

doi:10.11883/1001-1455(2016)06-0739-06

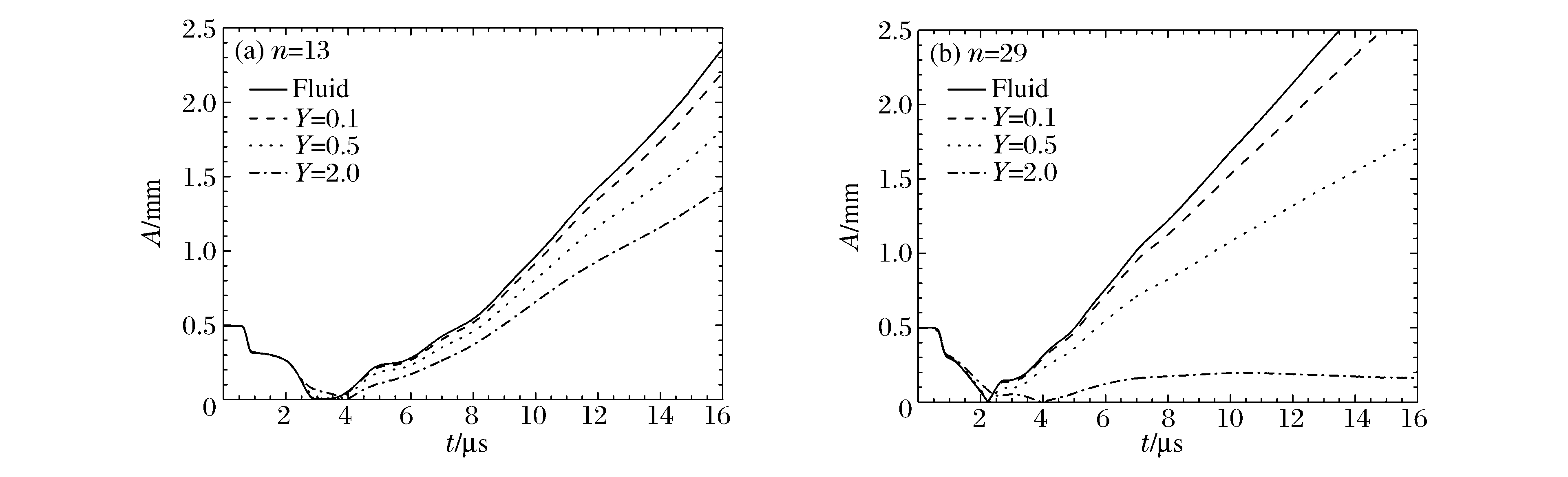
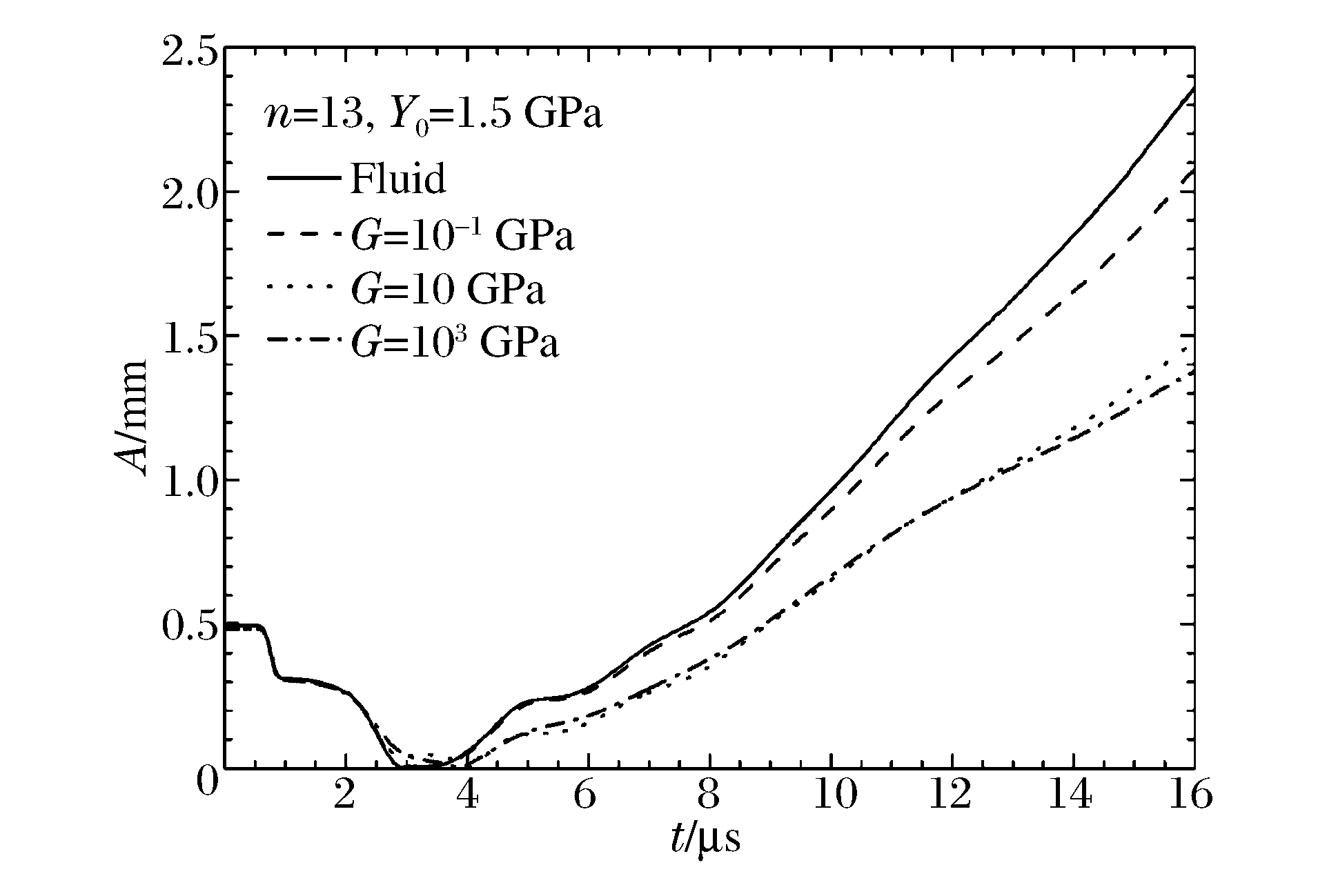
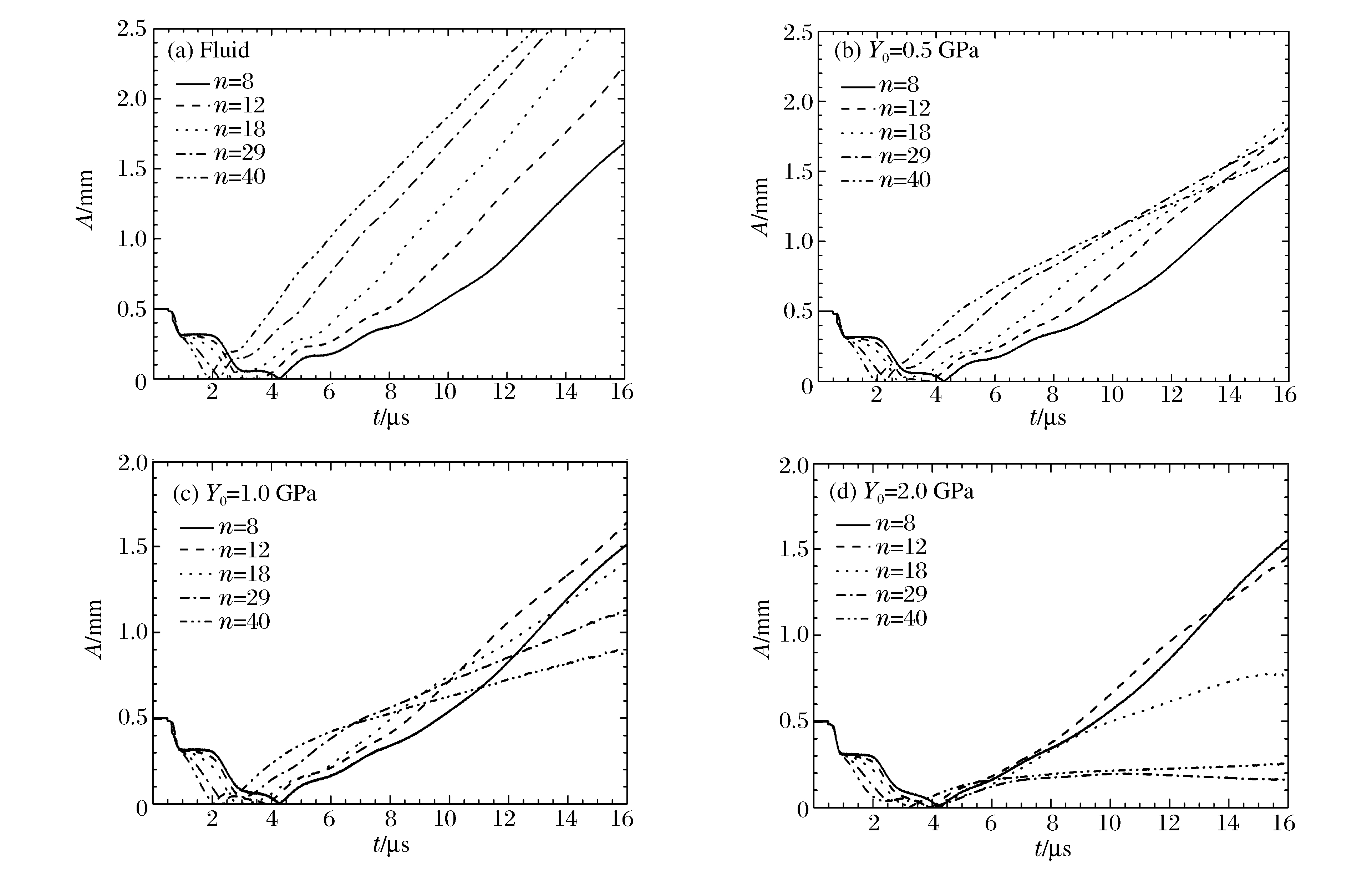
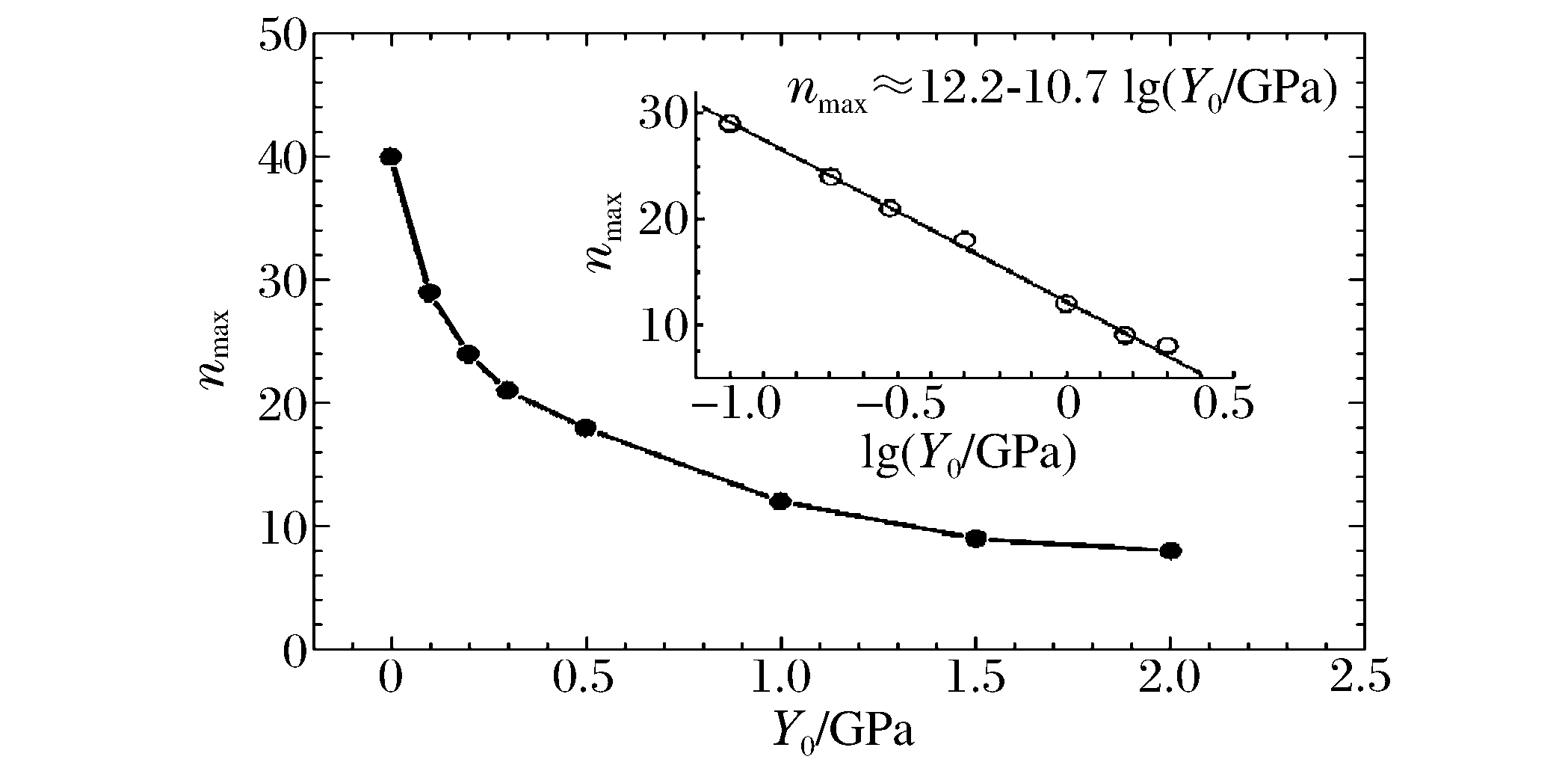
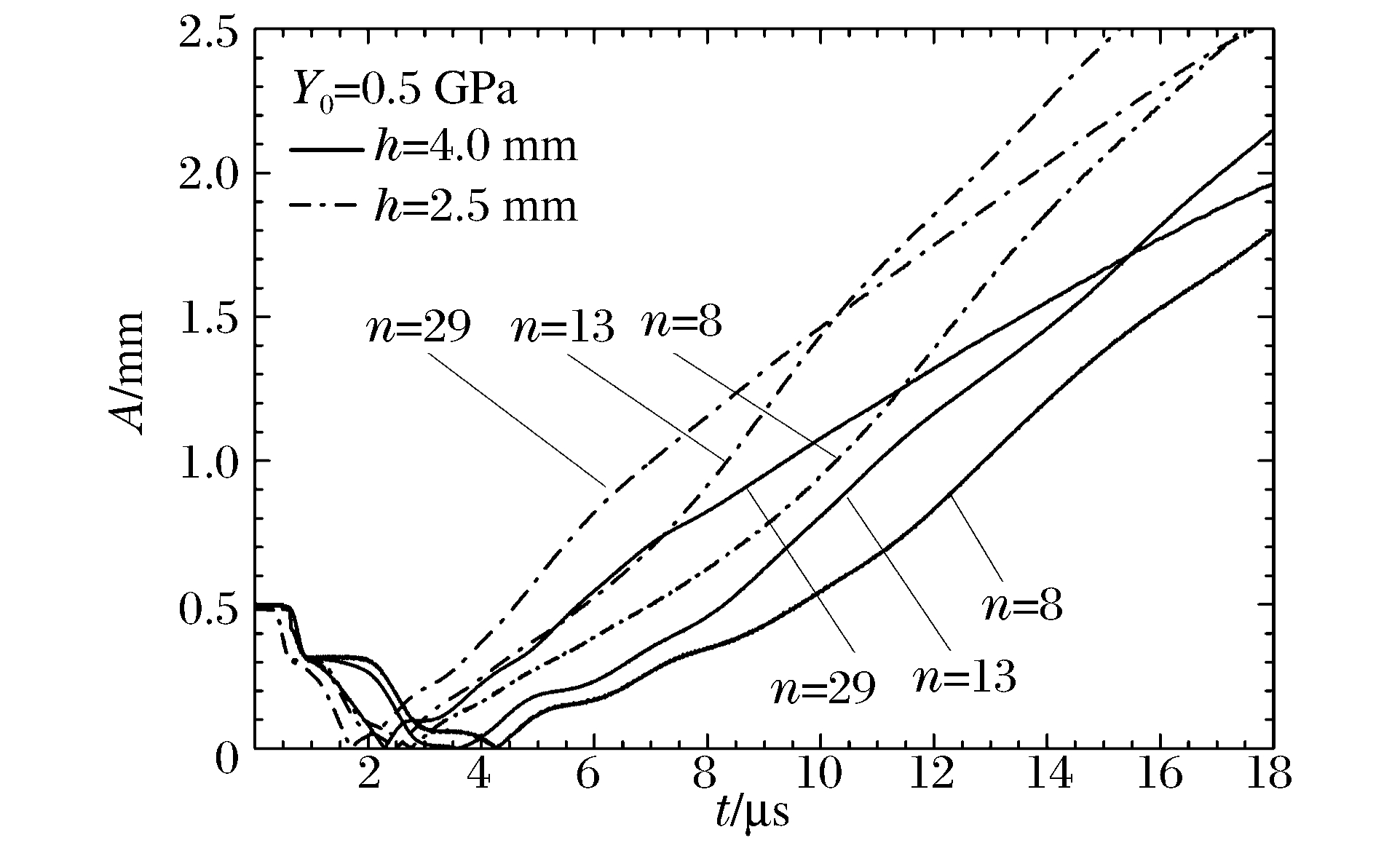
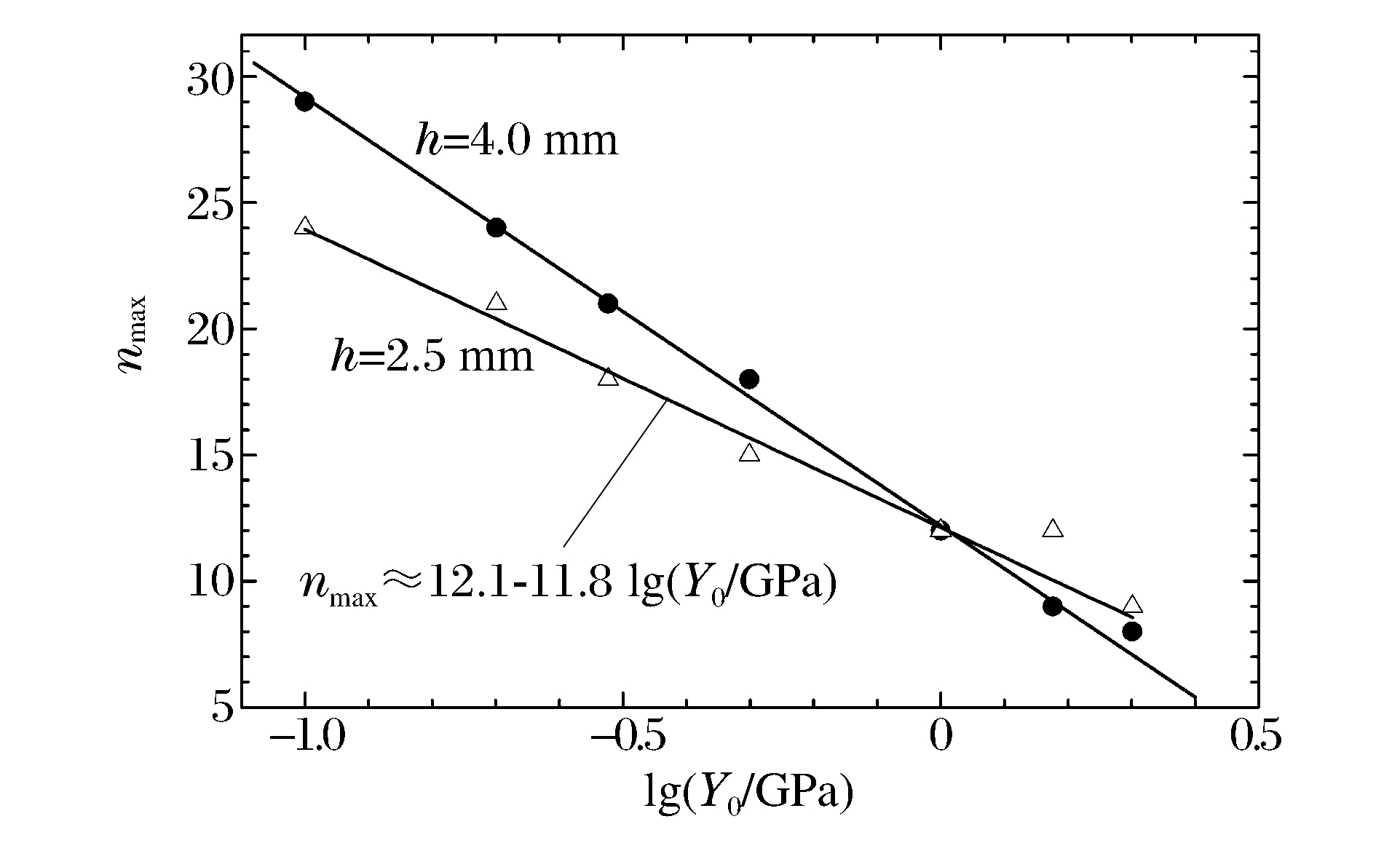
摘要: 采用自行研制的多介质弹塑性流体力学欧拉程序，对柱形内爆加载金属界面不稳定性进行了数值研究，数值模拟结果与文献实验数据吻合较好。数值结果表明：材料强度对界面不稳定性发展有不可忽略的抑制作用；材料屈服强度对较高模数不稳定性增长的抑制较强，而剪切模量对不稳定性发展的影响相似但敏感性相对较弱；金属界面不稳定性增长存在最不稳定模数，最不稳定模数随屈服强度增加而减小，并近似与屈服强度的对数呈线性关系；随着壳的厚度减小，扰动增长加快。

关键词:

Abstract: In this work the instability of the metal shell in the cylindrical implosion was studied numerically using a multi-component elastic-plastic hydrodynamic Eulerian code. Agreeing with those of the experiments, the numerical results show that the material strength restrains the growth of the interfacial perturbation with an effect not to be overlooked. The material yield strength has an obvious restraining effect on the higher mode of perturbation, while that of the shear module is similar but less sensitive. There exists a most instable mode number, which decreases as the yield strength increases and is approximately linear with the logarithm of the yield strength, and the perturbation grows faster as the shell grows thinner.

Key words:

图 1 柱形内爆计算模型

Figure 1. Computational model in cylindrical implosion

下载: 全尺寸图片幻灯片

图 2 金属壳外壁压力

Figure 2. Pressure on outer interface of metal shell

下载: 全尺寸图片幻灯片

图 3 金属壳内壁速度

Figure 3. Velocity on inner interface of metal shell

下载: 全尺寸图片幻灯片

图 4 密度等值云图(n=29)

Figure 4. Density contour plot

下载: 全尺寸图片幻灯片

图 5 金属界面扰动增长

Figure 5. Growth of metal interfacial perturbation amplitude

下载: 全尺寸图片幻灯片

图 6 材料屈服强度对界面扰动增长的影响

Figure 6. Effect of yield strength on perturbation growth

下载: 全尺寸图片幻灯片

图 7 材料剪切模量对界面扰动增长的影响

Figure 7. Effect of shear strength on perturbation growth

下载: 全尺寸图片幻灯片

图 8 不同屈服强度下扰动模数与扰动增长的关系

Figure 8. Effect of perturbation mode on perturbation growth under different yield strength

下载: 全尺寸图片幻灯片

图 9 最不稳定模数与屈服强度的关系

Figure 9. Relationship between yield strength and most instable mode

下载: 全尺寸图片幻灯片

图 10 不同金属壳厚度下的扰动增长

Figure 10. Effect of shell thickness on perturbation growth

下载: 全尺寸图片幻灯片

图 11 不同金属壳厚度下最不稳定模数与屈服强度的关系

Figure 11. Relationship between yield strength andmost instable mode with different shell thicknesses

下载: 全尺寸图片幻灯片

Piriz A R, Lopez Cela J J, Tahir N A, et al. Richtmyer-Meshkov instability in elastic-plastic media[J]. Physical Review E, 2008, 78(5):056401. doi: 10.1103/PhysRevE.78.056401

Piriz A R, Lopez Cela J J, Tahir N A. Linear analysis of incompressible Rayleigh-Taylor instability in solids[J]. Physical Review E, 2009, 80(4):046305. doi: 10.1103/PhysRevE.80.046305

Miles J W. Taylor instability of a flat plate[R]. San Diego: General Dynamics, GAMD-7335, 1966.

Drucker D C. "Taylor instability" of the surface of an elastic-plastic plate[C]//Nemat-Nasser C. Mechanics Today, Vol. 5. New York: Pergamon Press, 1980: 37-47.

Lebedev A I, Nizovtsev P N, Rayevsky V A. Rayleigh-Taylor instability in solids[C]//4th International Workshop on the Physics of Compressible Turbulent Mixing (IWPCTM). Cambridge, England, 1993.

Barnes J F, Blewett P J, McQueen R G, et al. Taylor instability in solids[J]. Journal of Applied Physics, 1974, 45(2):727-732. doi: 10.1063/1.1663310

Swegle J W, Robinson A C. Acceleration instability in elastic-plastic solids. I. Numerical simulations of plate acceleration[J]. Journal of Applied Physics, 1989, 66(7):2838-2858. doi: 10.1063/1.344190

Mikaelian K. Effect of viscosity on Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J]. Physical Review E, 1993, 47(1):375-383. doi: 10.1103/PhysRevE.47.375

Colvin J D, Legrand M, Remington B A, et al. A model for instability growth in accelerated solid metals[J]. Journal of Applied Physics, 2003, 93(9):5287-5301. doi: 10.1063/1.1565188

Atchison W L, Zocher M A, Kaul A M. Studies of material constitutive behavior using perturbation growth in explosive and magnetically driven liner systems[J]. Russian Journal of Physical Chemistry B, 2008, 2(3):387-401. doi: 10.1134/S199079310803010X

Dimonte G, Terrones G, Cheme F J, et al. Use of the Richtmyer-Meshkov instability to infer yield stress at high-energy density[J]. Physical Review Letters, 2011, 107(26):264502. doi: 10.1103/PhysRevLett.107.264502

Frachet V, Geleznikoff F, Guix R, et al. Rayleigh Taylor instability in cylindrical configuration[C]//2nd International Workshop on the Physics of Compressible Turbulent Mixing (IWPCTM). Pleasanton, CA, 1989.

Park H S, Lorenz K T, Cavallo R M, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate[J]. Physical Review Letters, 2010, 104(13):135504. doi: 10.1103/PhysRevLett.104.135504

刘军, 冯其京, 周海兵.柱面内爆驱动金属界面不稳定性的数值模拟研究[J].物理学报, 2014, 63(15):155201. doi: 10.7498/aps.63.155201

Liu Jun, Feng Qijing, Zhou Haibing. Simulation study of interface instability in metals driven by cylindrical implosion[J]. Acta Physica Sinica, 2014, 63(15):155201. doi: 10.7498/aps.63.155201

冯其京, 郝鹏程, 杭义洪, 等.聚能装药的欧拉数值模拟[J].爆炸与冲击, 2008, 28(2):138-143. doi: 10.3321/j.issn:1001-1455.2008.02.007

期刊类型引用(5)

1.	高士清，邹立勇，唐久棚，李季，林健宇. 高马赫数激波作用下单模界面的Richtmyer-Meshkov不稳定性数值模拟. 爆炸与冲击. 2024(07): 38-58 . 本站查看
2.	陈涵，甘元超，彭建祥，俞宇颖，胡建波. 固体界面不稳定性的研究现状、应用及挑战. 力学进展. 2024(04): 771-822 . 百度学术
3.	王涛，汪兵，林健宇，柏劲松，李平，钟敏，陶钢. 金属锡Rayleigh-Taylor不稳定性对模型参数敏感性的数值分析. 高压物理学报. 2020(02): 24-32 . 百度学术
4.	王涛，汪兵，林健宇，钟敏，柏劲松，李平，陶钢. 柱形汇聚几何中内爆驱动金属界面不稳定性. 爆炸与冲击. 2020(05): 4-15 . 本站查看
5.	李碧勇，彭建祥，谷岩，尹晓春，贺红亮. 高纯铜界面Rayleigh-Taylor不稳定性扰动增长的数值模拟. 兵工学报. 2020(09): 1809-1816 . 百度学术

其他类型引用(2)