An internal state variable viscoplastic constitutive model considering the evolution of microstructural characteristic length
-
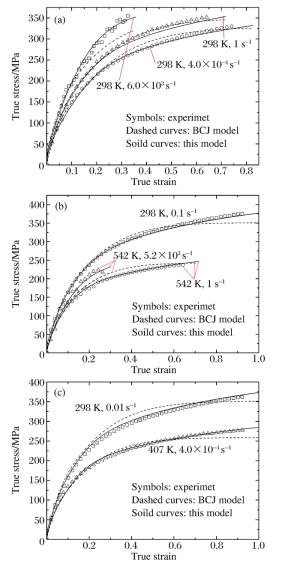
摘要: 在金属晶体材料高应变率大应变变形过程中,存在强烈的位错胞尺寸等微观结构特征长度细化现象,势必对材料加工硬化、宏观塑性流动应力产生重要影响。基于宏观塑性流动应力与位错胞尺寸成反比关系,提出了一种新型的BCJ本构模型。利用位错胞尺寸参数,修正了BCJ模型的流动法则、内变量演化方程,引入了考虑应变率和温度相关性的位错胞尺寸演化方程,建立了综合考虑微观结构特征长度演化、位错累积与湮灭的内变量黏塑性本构模型。应用本文模型,对OFHC铜应变率在10-4~103 s-1、温度在298~542 K、应变在0~1的实验应力-应变数据进行了预测。结果表明:在较宽应变率、温度和应变范围内,本文模型的预测数据与实验吻合很好;与BCJ模型相比,对不同加载条件下实验数据的预测精度均有较大程度的提高,最大平均相对误差从9.939%减小为5.525%。
-
关键词:
- 固体力学 /
- 新型内变量黏塑性本构模型 /
- 位错胞尺寸 /
- 高应变率大应变变形 /
- 微观结构特征长度
Abstract: During high strain rate and large strain deformation of crystalline metals, there exist phenomena of continuous refinement of microstructural characteristic length, like the size of dislocation cells, which occurs intensively and would have significant influence on the work hardening and macroscopic flow stress. In this work, based on the inverse relation between macroscopic flow stress and and the cell size, a new type of BCJ constitutive model was proposed. The flow rule and evolution equations for internal state variables in BCJ model were modified by involving the cell size parameter; the evolution equation for the cell size considering the dependence of the strain rate and the temperature was introduced into the model; and an internal state variable viscoplastic constitutive model that considers the evolution of microstructural characteristic length, accumulation and annihilation of dislocations was then established. The new constitutive model was illustrated by predicting the experimental stress-strain data of OFHC Cu over a wide range of strain rates (10-4 -103 s-1), temperatures (298-542 K) and strains (0-1). The results show that the predicted data agree very well with the experimental data. Compared with the BCJ model, the predictive accuracies of the proposed model in various loading conditions are obviously improved, the maximum average relative error is reduced from 9.939% to 5.525%. -
表 1 参数识别的实验数据
Table 1. Experimental data for parameters identification
Curve Strain rate/s-1 Temperature/K 1 4.0×10-4 298 2 4.0×10-4 407 3 0.01 298 4 0.1 298 5 1 298 6 1 542 7 5.2×103 542 8 6.0×103 298 表 2 参数取值范围和优化识别的材料参数
Table 2. Value domains and identified material parameters
Material
parametersEstimated
low limitEstimated
upper limitIdentified
valuesC1/MPa 1.659×10-7 1 214.336 6.591×10-7 C2/K -5 052.155 2 994.571 -4 170.1 C3/MPa 0.017 5 21.747 2.519 C4/K 1.2 2 200.608 593.5 C5/s-1 2.760×10-4 1 628.508 1 622.224 C6/K -9 072.0 7 917.029 3 786.757 C7/MPa-1 0.010 7 0.139 0.113 C8/K -3.072 1 005.614 355.623 C9/MPa 46.528 892.555 880.38 C10/K 0.041 1 842.039 0.053 9 C11/(s·MPa)-1 2.200×10-6 0.018 1 2.500×10-6 C12/K 26.956 7 507.226 3 656.84 C13/MPa-1 0.003 28 3.244 2.297 C14/K -1 425.544 1 598.282 507.016 C15/MPa 327.923 1 104.828 880.835 C16/K 0.179 516.232 0.187 C17/(s·MPa)-1 1.468×10-5 0.009 34 3.168×10-4 C18/K 0.588 2 612.062 29.848 δ0/mm 0.03 0.16 0.058 4 δr0/mm 0.001 30 1.121 ar 1.0 120 10.239 ξr 0.001 290 3.406 νr 1.000×10-4 200 0.033 3 δs0/mm 0.001 0.36 0.017 6 as 1.0 180 80.011 ξs 0.001 50 43.767 νs 1.000×10-4 80 0.025 6 Fitness value — — 2 165.292 表 3 模型预测数据的平均相对误差
Table 3. Relative error of constitutive model predictions
Strain rate
/s-1Temperature
/KRelative error/% BCJ model This model 4.0×10-4 298 2.468 1.626 4.0×10-4 407 3.934 1.923 0.01 298 4.952 2.266 0.1 298 3.383 0.956 1 298 1.861 2.042 1 542 6.494 3.369 5.2×103 542 9.939 5.525 6.0×103 298 6.777 2.603 -
[1] Manes A, Serpellini F, Pagani M, et al. Perforation and penetration of aluminium target plates by armour piercing bullets[J]. International Journal of Impact Engineering, 2014, 69(4):39-54. http://www.sciencedirect.com/science/article/pii/S0734743X14000499 [2] 汤铁钢, 刘仓理.高应变率拉伸加载下无氧铜的本构模型[J].爆炸与冲击, 2013, 33(6):581-586. doi: 10.3969/j.issn.1001-1455.2013.06.004Tang Tiegang, Liu Cangli. On the constitutive model for oxygen-free high-conductivity copper under high strain-rate tension[J]. Explosion and Shock Waves, 2013, 33(6):581-586. doi: 10.3969/j.issn.1001-1455.2013.06.004 [3] Zerilli F J, Armstrong R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations[J]. Journal of Applied Physics, 1987, 61(5):1816-1825. doi: 10.1063/1.338024 [4] Huh H, Ahn K, Lim J H, et al. Evaluation of dynamic hardening models for BCC, FCC, and HCP metals at a wide range of strain rates[J]. Journal of Materials Processing Technology, 2014, 214(7):1326-1340. doi: 10.1016/j.jmatprotec.2014.02.004 [5] Follansbee P S, Kocks U F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable[J]. Acta Metallurgica, 1988, 36(1):81-93. doi: 10.1016/0001-6160(88)90030-2 [6] Banerjee B. The mechanical threshold stress model for various tempers of AISI 4340 steel[J]. International Journal of Solids and Structures, 2007, 44(3/4):834-859. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cond-mat%2f0510330 [7] Bammann D J, Chiesa M L, Johnson G C. A state variable damage model for temperature and strain rate dependent metal[C]//Rajendran A M, Batra R C. Constitutive laws: Experiments and numerical implementation. Barcelona: International Center for Numerical Methods in Engineering (CIMNE), 1995: 84-97. [8] Tanner A B. Modeling temperature and strain rate history in effects in OFHU Cu[D]. Ann Arbor: Georgia Institute of Technology, 1998. http://www.researchgate.net/publication/252105952_Modeling_temperature_and_strain_rate_history_in_effects_in_OFHU_Cu [9] Molinari A, Ravichandran G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length[J]. Mechanics of Materials, 2005, 37(7):737-752. doi: 10.1016/j.mechmat.2004.07.005 [10] Sevillano J G, van Houtte P, Aernoudt E. Large strain work hardening and textures[J]. Progress in Materials Science, 1980, 25(2):69-412. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0211046481/ [11] Thompson A W. Substructure strengthening mechanisms[J]. Metallurgical Transactions: A, 1977, 8(6):833-842. doi: 10.1007/BF02661564 [12] Ananthan V S, Leffers T, Hansen N, et al. Cell and band structures in cold rolled polycrystalline copper[J]. Materials Science and Technology, 1991, 7(12):1069-1075. doi: 10.1179/mst.1991.7.12.1069 [13] Luo Z P, Zhang H W, Hansen N, et al. Quantification of the microstructures of high purity nickel subjected to dynamic plastic deformation[J]. Acta Materialia, 2012, 60(3):1322-1333. doi: 10.1016/j.actamat.2011.11.035 [14] Staker M R, Holt D L. The dislocation cell size and dislocation density in copper deformed at temperatures between 25 and 700 ℃[J]. Acta Metallurgica, 1972, 20(4):569-579. doi: 10.1016/0001-6160(72)90012-0 [15] Lee W S, Lin C F, Chen T H, et al. Dynamic mechanical behaviour and dislocation substructure evolution of Inconel 718 over wide temperature range[J]. Materials Science and Engineering: A, 2011, 528(19/20):6279-6286. http://www.sciencedirect.com/science/article/pii/S0921509311005223 [16] Holt D L. Dislocation cell formation in metals[J]. Journal of Applied Physics, 1970, 41(8):3197-3201. doi: 10.1063/1.1659399 [17] Huang M, Li Z, Tong J. The influence of dislocation climb on the mechanical behavior of polycrystals and grain size effect at elevated temperature[J]. International Journal of Plasticity, 2014, 61:112-127. doi: 10.1016/j.ijplas.2014.06.002 [18] Devincre B, Hoc T, Kubin L. Dislocation Mean Free Paths and Strain Hardening of Crystals[J]. Science, 2008, 320(5884):1745-1748. doi: 10.1126/science.1156101 [19] Kolupaeva S, Semenov M. The stored energy of plastic deformation in crystals of face-centered cubic metals[J]. IOP Conference Series: Materials Science and Engineering, 2015, 71(1):12-77. http://www.researchgate.net/publication/276237736_The_stored_energy_of_plastic_deformation_in_crystals_of_face-_centered_cubic_metals [20] Lee W S, Chen T H. Effects of strain rate and temperature on dynamic mechanical behaviour and microstructural evolution in aluminium-scandium (Al-Sc) alloy[J]. Materials Science and Technology, 2008, 24(10):1271-1282. doi: 10.1179/174328408X323078 [21] 谭阳, 迟毅林, 黄亚宇, 等.Bammann-Chiesa-Johnsonn粘塑性本构模型材料参数的一种识别方法[J].计算力学学报, 2015(4):490-495. http://www.cjcm.net/ch/reader/view_abstract.aspx?file_no=20150408&flag=1Tan Yang, Chi Yilin, Huang Yayu, et al. An approach for identification of material parameters in Bammann-Chiesa-Johnson viscoplastic constitutive model[J]. Chinese Journal of Computational Mechanics, 2015(4):490-495. http://www.cjcm.net/ch/reader/view_abstract.aspx?file_no=20150408&flag=1 -







 下载:
下载: