金属热黏塑性本构关系的研究进展

王强; 王建军; 张晓琼; 张天辉; 王怀坤; 吴桂英

doi:10.11883/bzycj-2021-0443

金属热黏塑性本构关系的研究进展

doi: 10.11883/bzycj-2021-0443

太原理工大学机械与运载工程学院，山西太原 030024

基金项目: 国家自然科学基金（11902272, 12172245）

详细信息

作者简介:
王　强（1995－　），男，博士研究生，wangqiang0004@link.tyut.edu.cn

通讯作者:
王建军（1987－　），男，博士，副研究员，wangjianjun@tyut.edu.cn

中图分类号: O347.3
计量
- 文章访问数: 1712
- HTML全文浏览量: 990
- PDF下载量: 202
- 被引次数: 7
出版历程
- 收稿日期: 2021-10-28
- 修回日期: 2022-03-22
- 网络出版日期: 2022-03-29
- 刊出日期: 2022-09-29

Advances in the research of metallic thermo-viscoplastic constitutive relationships

College of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China

摘要

摘要: 金属材料的塑性流动行为依赖于温度和应变率，温度和应变率敏感性是金属材料塑性流动的最重要的本质特性之一，建立合适的热黏塑性本构关系来准确描述金属塑性流动行为的温度和应变率依赖性，是金属材料能被广泛应用的必要前提。为此，对金属热黏塑性本构关系的最新研究进展进行了综述，介绍了常见的几种金属热黏塑性本构关系并进行了详细讨论，给出了各本构关系的优势与不足，最后系统介绍了包含金属塑性流动行为中出现的第三型应变时效、或K-W锁位错结构引起的流动应力随温度变化出现的反常应力峰以及拉压不对称等行为的金属热黏塑性本构关系的研究进展。
- 热黏塑性 /
- 本构关系 /
- 应变率效应 /
- 温度效应
Abstract: The studies of the plastic flow behaviour of metallic materials show that the plastic deformation process of metallic materials is dependent on temperature and strain rate, so the temperature and strain rate sensitivities are the most important essential properties of plastic deformation of metallic materials. It is therefore necessary to establish appropriate thermo-viscoplastic constitutive relations to accurately describe the temperature and strain rate dependences of the plastic flow behaviour of metals over a wide range of temperatures and strain rates. Advantages and disadvantages of these constitutive relationships are first reviewed in the present paper. With the increasing applications of metallic materials and the emergence of new materials, the 3rd type strain aging, K-W lock induced anomalous stress peak, and tensile-compression asymmetry are often observed in the plastic flow behaviour of metals. Due to the occurrence of those phenomena, the traditional metal thermo-viscoplastic constitutive relations may no longer be applicable. In view of the significant roles played by the 3rd type strain aging, K-W lock dislocation structure-induced anomalous stress peaks, and tensile-compression asymmetry in the plastic flow behaviour of metals, especially in high temperature loading, it is necessary to take those particular phenomena into account in the framework of the thermo-viscoplastic constitutive relationship of metals. Thus, a large variety of constitutive relation, which considers the interaction of strain, temperature and strain rate, has been established to predict the deformation behaviors of metals. In this context, this paper presents a systematic review of the thermo-viscoplastic constitutive relationships of metals, which includes the anomalous stress peaks in the flow stresses with temperature due to the 3rd type strain aging or K-W-locked dislocation structures, and the tensile-compression asymmetry. In addition, the forms of these thermo-viscoplastic constitutive relationship considering the 3rd type strain aging, K-W lock dislocation structure-induced anomalous stress peaks and tensile-compression asymmetry in the flow stress of metals, are discussed and analysed.
- thermal-viscosity plasticity /
- constitutive relationship /
- strain-rate effect /
- temperature effect

HTML全文

材料的本构关系研究是理论与应用力学领域的重要课题^[1]。在工程应用中，选择合适的本构关系来描述材料的力学行为，是进行工程结构承载与失效分析的前提。在航空航天工程、军事工业等领域中，材料常处于高温、高应变率的极端环境，对处于这种极端环境下的结构进行数值分析，需要首先建立准确的材料热黏性本构关系^[2]。

金属的塑性流动是指金属在外力作用下产生非弹性变形或屈服后的应力与应变关系。金属材料的塑性流动与温度密切相关，温度升高，金属的流动应力减小，即热软化，如图1所示^[3]。金属的塑性流动实际上主要是位错越过各种障碍的运动过程，通常，阻碍位错运动的障碍分为两种：短程障碍和长程障碍。短程障碍可通过热激活克服，而长程障碍对温度不敏感。因此，对应的金属流动应力通常可由热激活部分和非热部分组成。

图 1 不同应变率下93W-Ni-Fe的流动应力随温度的变化曲线^[4]

Figure 1. Flow stress-temperature curves of 93W-Ni-Fe at different strain rates^[4]

下载: 全尺寸图片幻灯片

同时，流动应力的应变率效应也是材料中普遍存在的现象，不仅反映在力学性能和破坏模式的差异上，也体现在材料微观机制随应变率的变化差异上，例如，屈服强度的变化和加工硬化的差异。许多学者针对多种已在工程领域中被广泛应用的金属材料进行了研究，探索了应变率对其流动应力的影响机制，如2024-T351铝^[5-6]、6061-T6铝合金^[7-8]、OFHC铜^[9-10]、4340钢^[11-12]、Ti-6Al-4V合金^[13-14]。为了研究材料在不同变形率下的服役性能，揭示材料的变形机制，需要针对金属材料的应变率效应开展系统研究，可为设计性能更优异的新材料提供试验和理论基础。

随着金属材料的广泛应用，需要建立材料的热黏塑性本构关系为其工程应用提供理论依据。描述金属塑性流动行为的本构关系的发展已有很长的历史，现有的本构关系通常被分为经验型/唯象本构关系和物理概念本构关系^[3]。唯象本构关系主要包括Johnson-Cook本构关系（J-C模型）^{[11, 15]}、K-H本构关系（K-H模型）^[16]等，物理概念本构关系主要包括Zerilli-Armstrong本构关系（Z-A模型）^[17]、力学阈值应力本构关系（MTS模型）^[10]、Bonder-Partom本构关系（B-P模型）^[18]等。材料热黏塑性本构关系不仅是理论与应用力学领域的重要研究课题，且随着计算机技术的兴起，也成为了计算力学的重要组成部分。

为了系统地介绍可以描述在不同温度、不同应变率下金属塑性流动行为的热黏塑性本构关系，本文中首先介绍几种常见的金属热黏塑性本构关系，详细讨论其优势、不足以及其修正形式，然后系统介绍考虑了第三型应变时效的金属热黏塑性本构关系、考虑K-W锁位错结构引起的反常应力峰的金属热黏塑性本构关系以及考虑拉压不对称性的金属热黏塑性本构关系的研究进展。

1. 常见金属热黏塑性本构关系及其修正形式

金属热黏塑性本构关系的发展已有数十年的历史，已建立了数种常见的金属热黏塑性本构关系。在工程应用中，如何选用合适的热黏塑性本构关系成为关注的重点。为此，本节将对几种常见的金属热黏塑性本构关系及其优缺点进行分析，并介绍其修正形式。现有的金属热黏塑性本构关系分为唯象本构关系（或经验型本构关系）和物理概念本构关系，唯象本构关系通常具有更简洁的形式，因此在工程中应用广泛^[19]，而物理概念本构关系是基于金属材料的塑性变形机理建立起来的，适用范围更广。

1.1 唯象本构关系

1.1.1 Johnson-Cook本构关系

J-C本构关系是Johnson等^[11]于1983年建立的一种唯象本构关系。J-C本构关系由于形式简单、参数容易获得而被广泛应用，并被嵌入ABAQUS、ANSYS等商用有限元软件中。J-C本构关系认为金属的等效流动应力可表示为等效应变函数、等效应变率函数和温度函数的乘积，具体形式为^[20]：

$\sigma {\text{ = }}\left( {A + B{\varepsilon ^n}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\left( {1 - {T^{ * m}}} \right)$

(1)

式中： $\sigma$ 为等效流动应力； $\varepsilon$ 为等效塑性应变； ${\dot \varepsilon ^ * }{\text{ = }}\dot \varepsilon /{\dot \varepsilon _0}$ 为无量纲塑性应变率，其中 $\dot \varepsilon$ 为塑性应变率， ${\dot \varepsilon _0}$ 为参考应变率； ${T^*} = \left( {T - {T_{\text{r}}}} \right)/\left( {{T_{\text{m}}} - {T_{\text{r}}}} \right)$ 为无量纲温度，其中T为绝对温度，T_m为熔化温度，T_r为室温；A、B、n、C和m为材料常数，其中，A为参考温度和参考应变率下的屈服应力，B为应变硬化系数，n为应变硬化指数，C和m分别代表应变率硬化系数和热软化系数的材料常数。

J-C本构关系形式简单，其材料常数通过少量试验即可获得，但其对一些金属的塑性流动行为的预测结果并不理想，难以实现本构关系形式简单和预测精度高之间的平衡。通常认为J-C本构关系的缺点包括以下两个方面：

（1）对于一些金属材料，其流动应力随对数应变率呈非线性关系，这使得J-C本构关系不能准确描述这些金属材料塑性流动行为的应变率敏感性，同样，对于一些金属材料，J-C本构关系不能准确描述其塑性流动行为的温度敏感性，如图2所示；

图 2 不同应变率下，流动应力随温度变化的模型预测结果与试验结果比较^[23]

Figure 2. Comparison of model predictions and experimental results of flow stress variation with temperature at different strain rates^[23]

下载: 全尺寸图片幻灯片

（2）对于金属塑性流动行为中的等效应变、等效应变率和温度对流动应力的影响为非独立的现象，J-C本构关系同样不再适用^[21-22]。

针对J-C本构关系的缺点，学者们建立了多种修正的J-C本构关系。对于J-C本构关系的第一类缺点，Holmquist等^[24]通过对OFHC铜的泰勒冲击试验发现，应变率对材料强度的影响不是J-C本构关系所描述的为对数应变率的线性函数，而是应变率指数函数。为了更好地描述这种行为，将J-C本构关系中的应变率项修正为无量纲塑性应变率的幂函数：

$\sigma = \left( {A + B{\varepsilon ^n}} \right) {{{\dot \varepsilon }^{ * C}}} \left( {1 - {T^{ * m}}} \right)$

(2)

然而，由于该修正关系对应变率敏感性的加强有限，因此没有得到广泛应用。

当应变率大于10³ s⁻¹时，多数金属材料的屈服强度会随着应变率的增加而显著提升^[10]，Rule等^[25]提出了一个修正的J-C本构关系（RJC）来描述7075-T6铝的塑性行为。该修正的J-C本构关系在应变率项中增加了 ${C_4}\left( {\dfrac{1}{{{C_5} - \ln {{\dot \varepsilon }^ * }}} - \dfrac{1}{{{C_5}}}} \right)$ （C₄和C₅为附加的经验系数）。在高速率情况下， $1/\left( {{C_5} - \ln {{\dot \varepsilon }^ * }} \right)$ 项可以显著增加应变率敏感性，C₄控制着该修正的J-C本构关系与J-C本构关系之间的差距。

为了增加应变率敏感性，Kang等^[26]在J-C本构关系的应变率项中引入了对数应变率的二次型项：

$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + {C_1}\ln {{\dot \varepsilon }^ * } + {C_2}{{\left( {\ln {{\dot \varepsilon }^ * }} \right)}^2}} \right]\left( {1 - {T^ * }^m} \right)$

(3)

式中：C₁和C₂为经验系数。

对于J-C本构关系的第二类缺点，Vural等^[27]通过试验发现，实际的应变硬化项下降的速度比J-C本构关系的预测值更快，这是由J-C本构关系中的温度软化项决定的。为了描述这一现象，其在耦合温度和应变硬化项的同时，在应变率敏感项部分加入了温度效应，以便能更好地反映温度对应变率敏感性的影响。其形式为：

$\sigma = \left\{ {A + {B_0}\left[ {1 - {{\left( {\frac{{T - {T_0}}}{{{T_{\text{m}}} - {T_0}}}} \right)}^p}} \right]{\varepsilon ^n}} \right\}\left[ {1 + \left( {{c_1}T_{\text{r}}^{ * p} + {c_2}H} \right)\ln {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} } \right]\left[ {1 - {{\left( {\frac{{T - {T_0}}}{{{T_{\text{r}}} - {T_0}}}} \right)}^p}} \right]$

(4)

式中：

$H\left( {\dot \varepsilon ,{{\dot \varepsilon }_{\text{t}}},k'} \right) = \frac{1}{2} + \frac{1}{2}\tanh \left( {k'\ln {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\text{t}}}}}} } \right)$

(5)

c₁和c₂分别为准静态应变率范围内（ $\dot \varepsilon \text{＜} {\dot \varepsilon _{\rm{t}}}$ ）的率敏感度和动态应变率范围内的率敏感度（ $\dot \varepsilon \text{＞} {\dot \varepsilon _{\rm{t}}}$ ）， ${\dot \varepsilon _{\rm{t}}}$ 为将准静态变形与动态变形分离开的过渡应变率，T_r为室温，T₀为参考温度，H为Heaviside阶跃函数的近似， $k'$ 为比例因子^[21]，B₀、p为材料常数。图3所示为2139-T8铝合金单轴拉伸的试验结果与修正的J-C本构关系预测结果的比较。

图 3 试验应力-应变曲线与修正的J-C本构关系预测结果的比较^[27]

Figure 3. Comparison betwwen experimental stress-strain curves with MJC model predictions^[27]

下载: 全尺寸图片幻灯片

Lin等^[28]通过对2124-T851铝合金和高强合金钢在宽温度、宽应变率范围内的拉伸塑性流动行为进行分析，提出了一个考虑温度和应变率耦合效应的J-C本构关系^[29]：

$\begin{split}\sigma =& \left( {A + {B_1}\varepsilon + {B_2}{\varepsilon ^2}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\times\\ &\exp \left[ {\left( {{\lambda _1} + {\lambda _2}\ln {{\dot \varepsilon }^ * }} \right)\left( {T - {T_{\text{r}}}} \right)} \right] \end{split}$

(6)

式中：B₁、B₂、 ${\lambda _1}$ 和 ${\lambda _2}$ 为材料常数。

此外，还有许多学者针对金属材料的热黏塑性流动行为建立了修正的J-C本构关系^{[23, 30-32]}，极大地拓宽了J-C本构的使用范围。例如，Dou等^[33]不仅考虑了应变、应变率和温度效应，而且考虑了应力状态效应，提出了一个塑性模型，确定了Ti-6Al-4V合金在宽温度范围(93～1073 K)和宽应变率范围（10⁻³～6.5×10³ s⁻¹）下，不同应力状态(单轴拉伸、压缩和简单剪切)下的塑性行为和微观机制。

1.1.2 Khan-Huang（K-H）本构关系和Khan-Huang-Liang（K-H-L）本构关系

Khan等^[16]建立了可以描述金属在大应变率范围内的力学行为的K-H本构关系。K-H本构关系将应力偏量的第二不变量J₂表示为等效塑性应变函数与塑性变形率的第二不变量 $D_2^{\text{p}}$ 函数的乘积：

${J_2} = {f_1}\left( \varepsilon \right){f_2}\left( {D_2^{\text{p}}} \right)$

(7)

这个表达式可以进一步简化为 $\sigma {\text{ = }}{g_1}\left( \varepsilon \right){g_2}\left( {\dot \varepsilon } \right)$ ，其中， ${g_1}$ 描述了参考应变率下的应力与塑性应变的相关性， ${g_2}$ 表示了应力对应变率的依赖性，即^[34]：

${g_1}\left( \varepsilon \right) = {\sigma _0} + {E_\infty }\varepsilon - a{{\text{e}}^{ - \alpha \varepsilon }}$

(8)

${g_2}\left( {\dot \varepsilon } \right) = 1\Biggr/\left( {1 - \frac{{\ln {\dot \varepsilon } }}{{\ln {D_0^{\text{p}}} }}} \right)$

(9)

式中： ${\sigma _0}$ 、 ${E_\infty }$ 、a和 $\alpha$ 为材料常数。

Yu等^[35]使用K-H本构关系描述了双相600钢（DP600）在10⁻⁴～1.6×10³ s⁻¹应变率范围内的塑性流动行为，结果表明，在较高应变率下，该本构关系不能很好地预测DP600的流动应力，因此提出了一种修正的K-H本构关系：

$\sigma = f\left( {\varepsilon ,\dot \varepsilon } \right) = {\sigma _0}{\hat f_2}\left( {\dot \varepsilon } \right) + {E_\infty }\varepsilon - a{{\text{e}}^{ - \alpha \varepsilon }}$

(10)

${\hat f_2}\left( {\dot \varepsilon } \right) = 1 + D{\left( {\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)^{{m_1}}}$

(11)

式中：D和m₁为材料常数。

Khan等^[36]对钽、含2.5%钨的钽合金以及AerMet 100钢3种BCC金属进行了不同温度和不同应变率下的试验，发现J-C本构关系和Z-A本构关系无法准确描述这3种材料的加工硬化随应变率变化的塑性流动行为。因此，为了更好地预测这3种BCC材料的加工硬化行为，他们耦合了应变和应变率对加工硬化的影响，建立了修正的K-H本构关系：

${J}_{2}={f}_{\text{l}}\left(\varepsilon,{D}_{2}^{\text{p}}\right){f}_{2}\left(T\right)$

(12)

式中： ${f_{\text{l}}}$ 描述了应变和应变率对加工硬化行为的耦合效应。K-H-L本构关系具体形式为：

$\sigma = \left[ {A + B{{\left( {1 - \frac{{\ln {\dot \varepsilon } }}{{\ln {D_0^{\text{p}}} }}} \right)}^{{n_{\text{1}}}}}{\varepsilon ^{{n_{\text{0}}}}}} \right]\left( {1 - {T^{*m}}} \right){\dot \varepsilon ^C}$

(13)

式中：n₀和n₁为材料常数； $D_0^{\text{p}}$ 取10⁶ s⁻¹，是任意选择的上限应变率。该本构关系可以通过材料常数n₁来描述随应变率增加加工硬化行为弱化的现象。

考虑了晶粒尺寸对金属流动应力的影响，Khan等^[36]在K-H-L本构关系中加入了Hall-Petch关系 ${\sigma _{\text{y}}} = {a_1} + {k_1}/\sqrt d$ ，获得了粗晶多晶材料的本构关系^[37]，其中 ${\sigma _{\text{y}}}$ 为屈服应力，d为多晶平均晶粒尺寸，a₁和k₁为材料常数。修正后的本构关系为：

$\sigma = \left[ {\left( {a{}_1 + \frac{{{k_1}}}{{\sqrt d }}} \right) + B{{\left( {1 - \frac{{\ln {\dot \varepsilon } }}{{\ln {D_0^{\text{p}}} }}} \right)}^{{n_1}}}{\varepsilon ^{{n_0}}}} \right]\left( {1 - {T^{ * m}}} \right){\dot \varepsilon ^C}$

(14)

针对Ti-6Al-4V合金的塑性流动行为，Khan等^[13]建立了一个修正的K-H-L本构关系，并与J-C本构关系的预测结果以及试验结果进行了对比，结果表明，修正后的K-H-L本构关系比J-C本构关系对Ti-6Al-4V合金塑性流动行为有更好的预测结果，如图4所示。修正后的K-H-L本构关系为：

图 4 不同应变率下，Ti-6Al-4V(296 K)的准静态和动态加载试验结果与K-H-L和J-C本构关系预测结果的比较^[13]

Figure 4. Quasi-static and dynamic loading experimental results of Ti-6Al-4V (at a temperature of 296 K) for different strain rates with correlations using K-H-L and J-C models^[13]

下载: 全尺寸图片幻灯片

$\sigma = \left[ {A + B{{\left( {1 - \frac{{\ln {\dot \varepsilon } }}{{\ln {D_0^{\text{p}}} }}} \right)}^{{n_1}}}} {\varepsilon ^{{n_0}}}\right]{\left( {\frac{{{T_{\text{m}}} - T}}{{{T_{\text{m}}} - {T_{\text{r}}}}}} \right)^m}{\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }^ * }}}} \right)^C}$

(15)

为了描述晶粒细化引起的不同多晶金属的塑性流动行为，Farrokh等^[38]基于K-H-L本构关系^{[13, ]}，建立了与晶粒尺寸和温度相关的金属热黏塑性本构关系：

$\sigma {\text{ = }}\left\{ {\left( {{a_1} + \frac{{{k_1}}}{{\sqrt d }}} \right) + B{{\left( {\frac{d}{{{d_0}}}} \right)}^{{n_2}}}{{\left[ {\left( {1 - \frac{{\ln {\dot \varepsilon } }}{{\ln {D_0^{\text{p}}} }}} \right) {\frac{{{T_{\text{m}}}}}{T}} } \right]}^{{n_1}}}{{ \varepsilon }^{{n_0}}}} \right\}{\left( {\frac{{{T_{\text{m}}} - T}}{{{T_{\text{m}}} - {T_{\text{r}}}}}} \right)^m}{\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }^ * }}}} \right)^C}$

(16)

式中：d₀为被测材料粗晶状态的平均晶粒度，n₂为材料常数。图5中给出了K-H-L本构关系对不同晶粒尺寸纳米晶铝在不同应变率下的流动应力预测结果。

图 5 不同晶粒尺寸纳米晶铝在不同应变率下的流动应力-应变试验结果与K-H-L本构关系预测结果^[38]

Figure 5. Observed and calculated responses for nanocrystalline aluminium at different strain rates by using KHL model for various grain sizes^[38]

下载: 全尺寸图片幻灯片

1.1.3 其他唯象模型

FCC金属的真实应力-应变曲线可以通过指数形式表示，Voce^[39]和Kocks^[40]建立了V-K本构关系。该指数律最初由Voce^[39]于1948年提出，之后被许多研究者进行了扩展，其表达式为：

$\sigma = {\sigma _{\text{s}}} + {\left( {{\sigma _0} - {\sigma _{\text{s}}}} \right)\exp \left( { - \frac{\varepsilon }{{{\varepsilon _{\text{r}}}}}} \right)}$

(17)

式中： ${\sigma _{\text{s}}}$ 为饱和应力， ${\sigma _0}$ 为初始屈服应力。

考虑温度和应变率对饱和应力 ${\sigma _{\text{s}}}$ 的影响，Kocks^[40]提出了饱和应力 ${\sigma _{\text{s}}}$ 的表达式：

${\sigma _{\text{s}}} = {\sigma _{{\text{s0}}}}{\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{{\text{s0}}}}}}} \right)^{kT/{A_{\text{s}}}}}$

(18)

式中： ${A_{\text{s}}} = \mu {b^3}A$ ，k为玻尔兹曼常数， $\mu$ 为与温度相关的剪切模量，b为Burgers矢量， ${\dot \varepsilon _{{\text{s}}0}}$ 、A和 ${\sigma _{{\text{s0}}}}$ 为材料参数， ${\sigma _{{\text{s0}}}}$ 为温度为0 K下的饱和阈值应力。初始屈服应力可表示为^[40]：

${\sigma _0}{\text{ = }}{\sigma _{{\text{k}}0}}{\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{{\text{k0}}}}}}} \right)^{kT/{A_0}}}$

(19)

式中： ${A_0} = A'\mu {b^3}$ ， ${\dot \varepsilon _{{\text{k0}}}}$ 和 $A'$ 为材料参数。松弛应变 ${\varepsilon _{\text{r}}}$ 为：

${\varepsilon _{\text{r}}}\left( {\dot \varepsilon ,T} \right) = \frac{{{\sigma _{\text{s}}}\left( {\dot \varepsilon ,T} \right) - {\sigma _0}\left( {\dot \varepsilon ,T} \right)}}{{{\theta _0}}}$

(20)

式中： ${\theta _0}$ 为初始加工硬化率。

Molinari等^[41]基于微观结构的演化，建立了一个描述金属在宽温度域宽应变率范围下塑性流动行为的唯象本构关系（M-R本构关系）：

$\frac{{{\delta _{\text{r}}}}}{{{\delta _{{\text{r0}}}}}} = {\left[ {1 - {{\left( {{k_{\text{r}}} {\frac{T}{{{T_{{\text{r0}}}}}}} \lg {\frac{{{{\dot \varepsilon }_{{\text{r0}}}}}}{{\dot \varepsilon }}} } \right)}^{{p_{\text{r}}}}}} \right]^{{q_{\text{r}}}}}$

(21)

$\frac{{{\delta _{\text{s}}}}}{{{\delta _{{\text{s0}}}}}} = \frac{1}{{{{\left[ {1 - {{\left( {{k_{\text{s}}} {\dfrac{T}{{{T_{{\text{s0}}}}}}} \lg {\dfrac{{{{\dot \varepsilon }_{{\text{r0}}}}}}{{\dot \varepsilon }}} } \right)}^{{p_{\text{s}}}}}} \right]}^{{q_{\text{s}}}}}}}$

(22)

式中： ${\delta _{\text{r}}}$ 为一个无量纲特征长度尺度细化率参数， ${\delta _{\text{s}}}$ 为较大应变下特征长度尺度的饱和尺寸， ${\delta _{{\text{r0}}}}$ 和 ${\delta _{{\text{s0}}}}$ 分别为 ${\delta _{\text{r}}}$ 和 ${\delta _{\text{s}}}$ 的参考值，k_r、p_r和q_r以及k_s、p_s和q_s为描述微观结构细化和稳态特征长度对应变率和温度依赖性的常数。T_r0、T_s0和 ${\dot \varepsilon _{{\text{r0}}}}$ 、 ${\dot \varepsilon _{{\text{s0}}}}$ 为参考温度和参考应变率。图6中给出了利用M-R本构关系预测铜在冲击载荷下的塑性流动行为。Naderi等^[42]将V-K本构关系和M-R本构关系结合起来描述了22MnB5硼钢在等温变形下的应变、应变率和温度的依赖性。然而，该研究的不足在于只考虑了相对较低的应变率情况（小于10 s⁻¹）。

图 6 不同温度和应变率下铜的真实应力-真实应变曲线与预测结果的对比^[41]

Figure 6. Comparison of true stress - true strain curves and model predictions for copper at different temperatures and strain rates^[41]

下载: 全尺寸图片幻灯片

为了能直观地了解各唯象本构关系的主要特性及其表达式，表1中给出了各种唯象型本构关系的主要特征，表2中给出了各种唯象型本构关系的方程形式。

表 1 唯象型本构关系的模型对比

Table 1. Comparison of phenomenological constitutive relations

本构关系	年份	模型	应变率范围/s⁻¹	主要特征
J-C	1983	Johnson-Cook^[20]	>10⁴	（1）形式简单，材料常数容易获得（2）考虑了应变率效应（3）考虑了温度效应（4）不能准确描述流动应力随对数应变率呈非线性关系的金属材料的塑性流动行为的应变率敏感性（5）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	1991	Holmquist^[24]	10⁻³～500	（1）应变率项修正为幂函数（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象（3）对高应变率范围内的应变率敏感性的加强描述依旧有限
	1998	Rule-Jones^[25]	>10³	（1）高速率情况下，可以更好地描述应变率敏感性的作用（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	1999	Kang-Cho^[26]	10⁻³～5000	（1）应变率项中引入了对数应变率的二次型项（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象（3）对高应变率范围内的应变率敏感性的加强描述依旧有限
	2009	Vural-Cairo^[27]	10⁻²～10⁴	（1）在应变和应变率项中加入了温度效应（2）可以描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	2010	Lin-Xia^[28]	10⁻²～10	（1）考虑温度和应变率耦合效应（2）应变项为抛物线形式
K-H	1992	Khan-Huang^[16]	10⁻⁵～10⁴	（1）考虑了应变率效应（2）假定依赖于J₂不变量（3）没有考虑温度效应
	2009	Yu-Guo^[35]	10⁻⁴～1.6×10³	没有考虑温度效应
	1999	Khan-Liang^[36]	10⁻⁶～10⁴	（1）考虑了应变率对应变硬化的影响。（2）应变率项为幂函数形式
	2000	Khan-Zhang^[37]	10⁻⁴～10³	（1）考虑了晶粒尺寸对金属流动应力的影响（2）考虑了应变率对应变硬化的影响（3）应变率项为幂函数形式
	2004	Farrokh-Khan^[38]	10⁻⁴～10³	（1）可以描述晶粒细化引起的不同多晶金属的塑性流动行为（2）考虑了应变率对应变硬化的影响（3）应变率项为幂函数形式
其他	1976	Voce-Kocks^[39-40]	10	考虑温度和应变率对饱和应力 ${\sigma _{\rm{s}}}$ 的影响
其他	2005	Molinari-Ravichandran^[41]	10⁻³～8.5×10⁴	考虑了微观结构的演化

下载: 导出CSV

| 显示表格

表 2 唯象型本构关系的方程形式

Table 2. Equations of phenomenological constitutive relationships relations

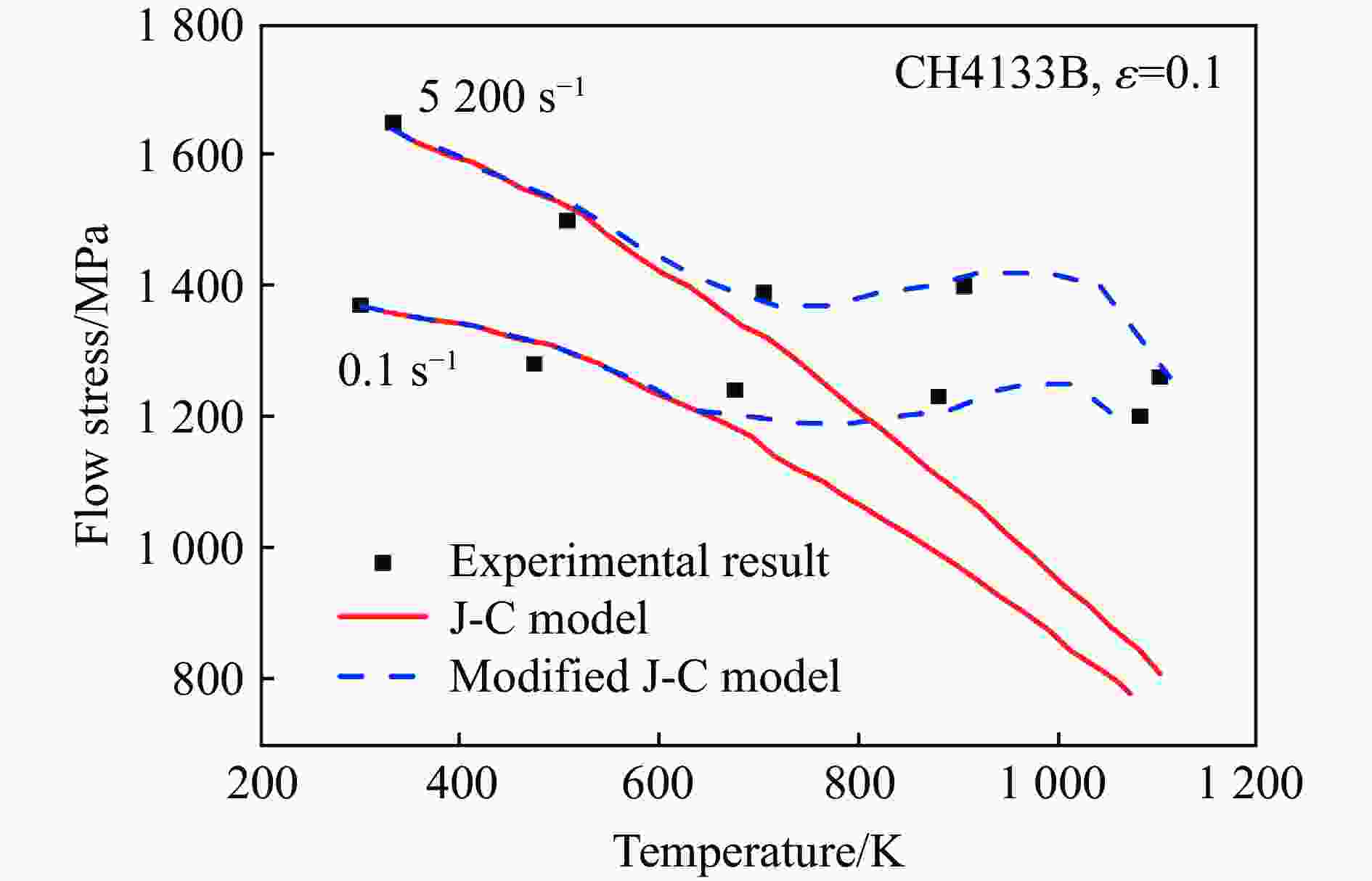
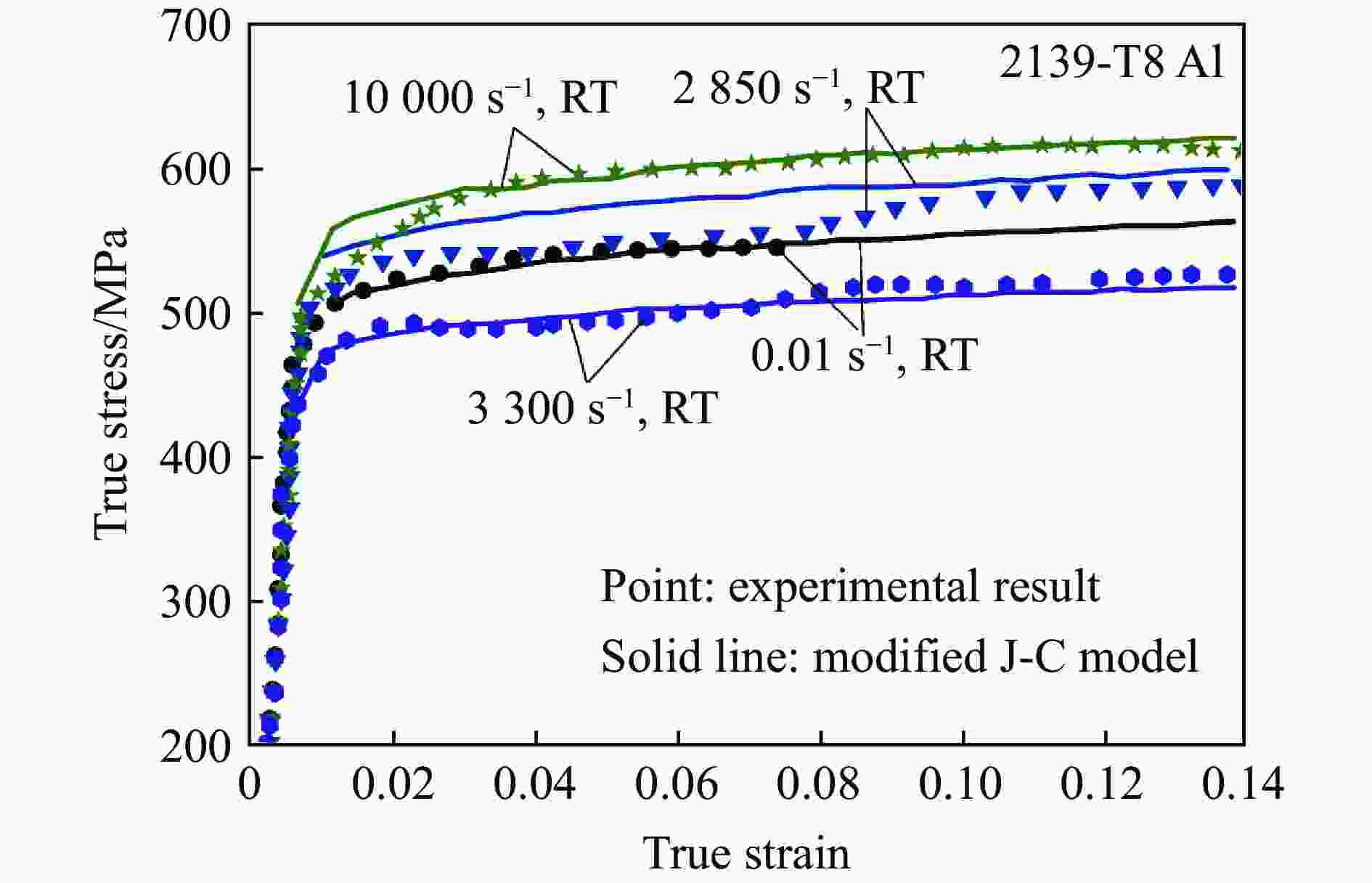
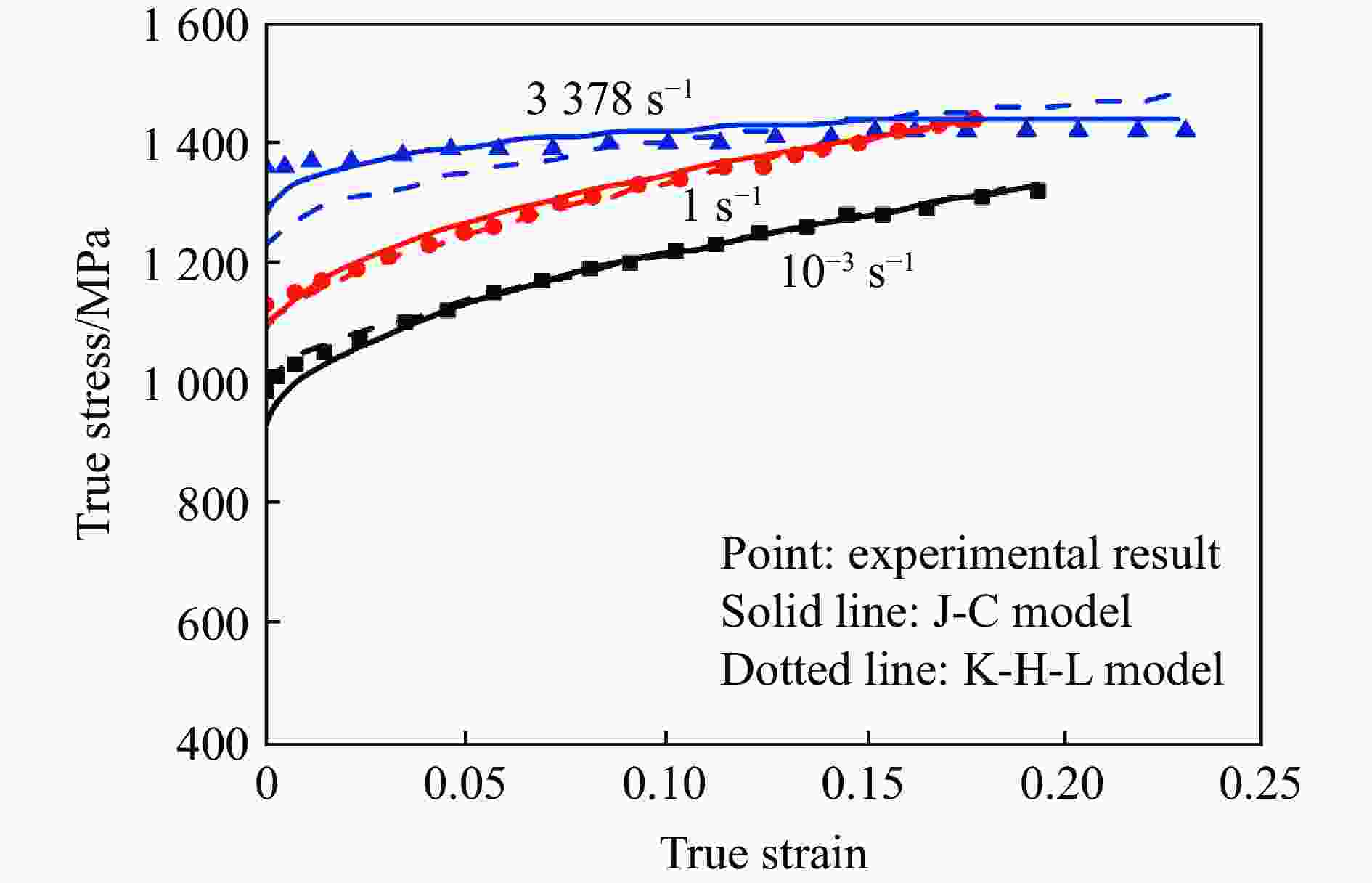
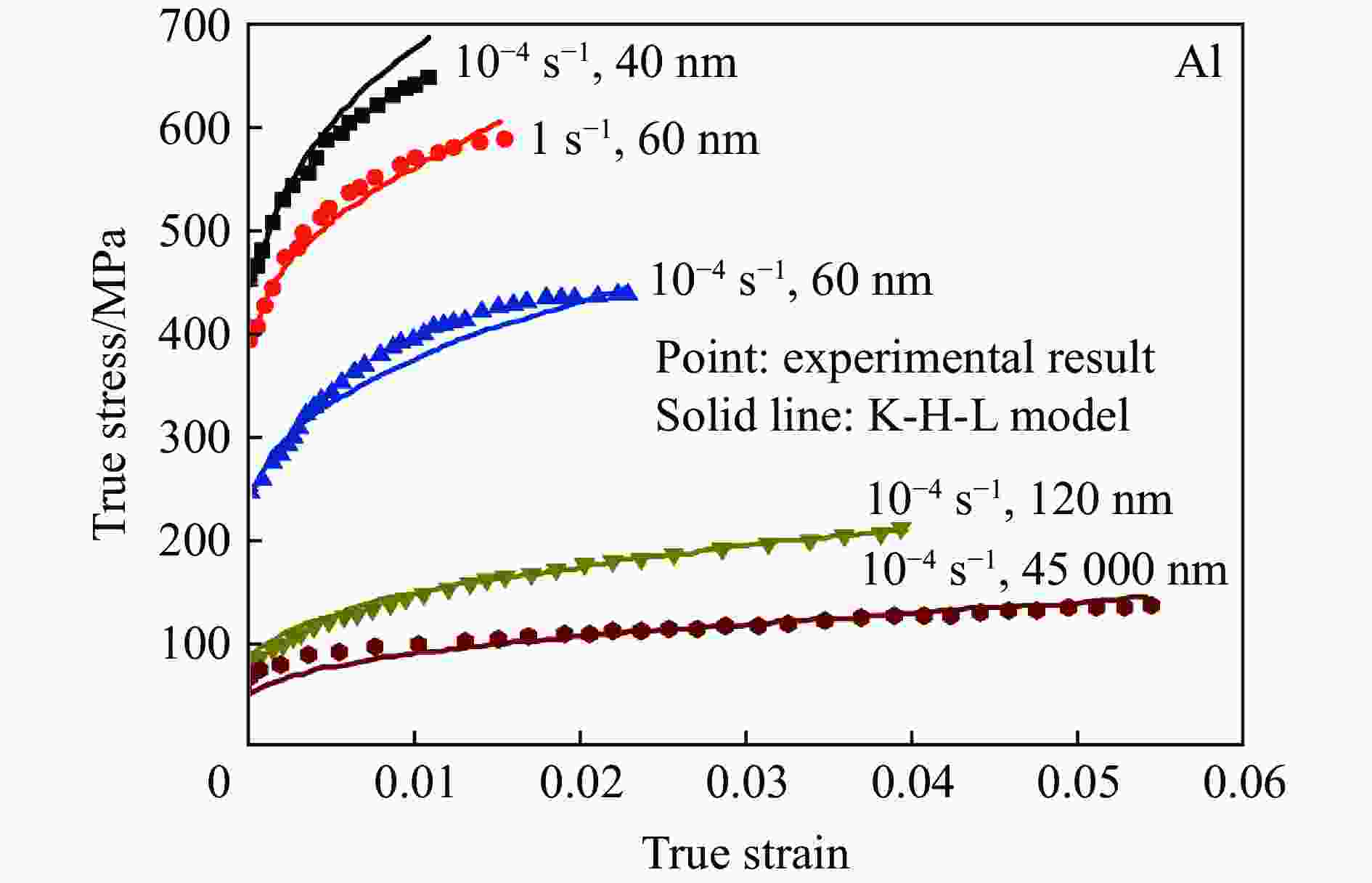
模型	方程形式
Johnson-Cook^[20]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\left( {1 - {T^{ * m}}} \right)$
Holmquist^[24]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left( {{{\dot \varepsilon }^{ * C}}} \right)\left( {1 - {T^{ * m}}} \right)$
Rule-Jones^[25]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + C\ln {{\dot \varepsilon }^ * } + {C_4}\left( {\dfrac{1}{{{C_5} - \ln {{\dot \varepsilon }^ * }}} - \dfrac{1}{{{C_5}}}} \right)} \right]\left( {1 - {T^{ * m}}} \right)$
Kang-Cho^[26]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + {C_1}\ln {{\dot \varepsilon }^ * } + {C_2}{{\left( {\ln {{\dot \varepsilon }^ * }} \right)}^2}} \right]\left( {1 - {T^{ * m}}} \right)$
Vural-Cairo^[27]	$\sigma = \left\{ {A + {B_0}\left[ {1 - {{\left( {\dfrac{{T - {T_0}}}{{{T_{\text{m}}} - {T_0}}}} \right)}^p}} \right]{\varepsilon ^n}} \right\}\left[ {1 + \left( {{c_1}T_{\text{r}}^{ * p} + {c_2}H} \right)\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]\left[ {1 - {{\left( {\dfrac{{T - {T_0}}}{{{T_{\text{r}}} - {T_0}}}} \right)}^p}} \right]$
Lin-Xia^[28]	$\sigma = \left( {A + {B_1}\varepsilon + {B_2}{\varepsilon ^2}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\exp \left[ {\left( {{\lambda _1} + {\lambda _2}\ln {{\dot \varepsilon }^ * }} \right)\left( {T - {T_{\text{r}}}} \right)} \right]$
Khan-Huang^[16]	${J_2} = {f_1}\left( \varepsilon \right){f_2}\left( {D_2^{\text{p}}} \right)$
Yu-Guo^[35]	$\sigma = f\left( {\varepsilon ,\dot \varepsilon } \right) = {\sigma _0}{\hat f_2}\left( {\dot \varepsilon } \right) + {E_\infty }\varepsilon - a{{\text{e}}^{ - \alpha \varepsilon }}$
Khan-Liang^[36]	$\sigma = \left[ {A + B{ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right)}^{ {n_1} } }{\varepsilon ^{ {n_0} } } } \right]\left( {1 - {T^{*m} } } \right){\dot \varepsilon ^C}$
Khan-Zhang^[37]	$\sigma = \left[ { \left({a{}_1 + \dfrac{ { {k_1} } }{ {\sqrt d } } }\right) + B{ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right)}^{ {n_1} } }{\varepsilon ^{ {n_0} } } } \right]\left( {1 - {T^{ * m} } } \right){\dot \varepsilon ^C}$
Farrokh-Khan^[38]	$\sigma {\text{ = } }\left\{ {\left( { {a_1} + \dfrac{ { {k_1} } }{ {\sqrt d } } } \right) + B{ {\left( {\dfrac{d}{ { {d_0} } } } \right)}^{ {n_2} } }{ {\left[ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right) {\dfrac{ { {T_{\text{m} } } } }{T} } } \right]}^{ {n_1} } }{ {\left( \varepsilon \right)}^{ {n_0} } } } \right\}{\left( {\dfrac{ { {T_{\text{m} } } - T} }{ { {T_{\text{m} } } - {T_{\text{r} } } } } } \right)^m}{\left( {\dfrac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }^ * } } } } \right)^C}$
Voce-Kocks^[39-40]	$\sigma = {\sigma _{\text{s}}} + \left[ {\left( {{\sigma _0} - {\sigma _{\text{s}}}} \right)\exp \left( { - \dfrac{\varepsilon }{{{\varepsilon _{\text{r}}}}}} \right)} \right]$
Molinari-Ravichandran^[41]	$\dfrac{ { {\delta _{\text{r} } } } }{ { {\delta _{ {\text{r0} } } } } } = {\left[ {1 - { {\left( { {k_{\text{r} } } {\dfrac{T}{ { {T_{ {\text{r0} } } } } } } \lg {\dfrac{ { { {\dot \varepsilon }_{ {\text{r0} } } } } }{ {\dot \varepsilon } } } } \right)}^{ {p_{\text{r} } } } } } \right]^{ {q_{\text{r} } } } }\text{，}\dfrac{ { {\delta _{\text{s} } } } }{ { {\delta _{ {\text{s0} } } } } } = \dfrac{1}{ { { {\left[ {1 - { {\left( { {k_{\text{s} } } {\dfrac{T}{ { {T_{ {\text{s0} } } } } } } \lg {\dfrac{ { { {\dot \varepsilon }_{ {\text{r0} } } } } }{ {\dot \varepsilon } } } } \right)}^{ {p_{\text{s} } } } } } \right] }^{ {q_{\text{s} } } } } } }$

下载: 导出CSV

| 显示表格

1.2 物理概念本构关系

1.2.1 Bodner-Partom（B-P）本构关系

Bodner等^[18]于1975年建立了考虑应变硬化和黏性影响的大变形弹-黏-塑性本构关系。尽管该本构关系对应变率不是很敏感，且没有考虑温度效应，但B-P本构关系的优势在于其坚实的物理基础。该本构关系将材料的总变形率分为弹性和塑性两部分，即：

${d_{ij}} = d_{ij}^{\text{e}} + d_{ij}^{\text{p}}$

(23)

式中： ${d_{ij}}$ 为速度梯度的对称部分。根据广义胡克定律^[15]，变形率的弹性部分与柯西应力率张量有关：

$d_{ij}^{\text{e}} = \frac{{{{\dot t}_{ij}}}}{G} - \frac{{\lambda {{\dot t}_{kk}}{\delta _{ij}}}}{{2G\left( {3\lambda + 2G} \right)}}$

(24)

式中：G为弹性剪切模量， ${\dot t_{ij}}$ 为柯西应力率张量， $\lambda$ 为Lamé常数。塑性变形率 $d_{ij}^{\text{p}}$ 与Cauchy应力张量 ${s_{ij}}$ 的偏量部分有关：

$d_{ij}^{\text{p}} = \gamma {s_{ij}}$

(25)

式中： $\gamma$ 为材料参数。等式两边取平方，得到 ${\gamma ^2}{\text{ = }}D_2^{\text{p}}/{J_2}$ 或 $D_2^{\text{p}} = f\left( {{J_2}} \right)$ ，f为J₂的函数。Bodner等^[18]适当考虑了该函数的特殊形式：

$D_2^{\text{p}} = D_0^2\exp \left[ { - {\frac{{n + 1}}{n}}{{\left( {\frac{{{Z^2}}}{{3{J_2}}}} \right)}^n}} \right]$

(26)

式中：D₀为最大应变率，Z为一个内部变量，表示材料的变形历史。应变率敏感度由参数n控制。Z假定为塑性功W_p的函数：

$Z = {Z_1} + \left( {{Z_0} - {Z_1}} \right)\exp \left( { - m\frac{{{W_{\text{p}}}}}{{{Z_0}}}} \right)$

(27)

式中：Z₀、Z₁和m为本构常数。

Huang等^[43]使用B-P本构关系描述了1100-0铝在应变率为10⁻⁵～10⁴ s⁻¹范围内的塑性流动行为。结果表明，B-P本构关系可以准确描述1100-0铝的应变率敏感性和在大塑性变形下的加工硬化。

由于B-P本构关系没有考虑温度效应，所以Chen等^[44]在B-P本构关系中引入了热软化效应来描述30CrMnSiA钢的塑性流动行为，其形式为：

${A^2} = \frac{1}{3}\left[ {Z\exp \left( {{C_1}{T^{ * m}}} \right)} \right]\sqrt[{n}]{{\frac{{n + 1}}{n}}}$

(28)

式中：A、C₁和n为本构常数。

图7所示为B-P本构关系预测得到的30CrMnSiA在温度升高时流动应力的软化。马鑫等^[45]用B-P本构关系描述了Sn-Pb共晶合金在10⁻⁵～10⁻² s⁻¹应变率范围内、−55～125 ℃温度下的拉伸行为，其结果如图8所示。

图 7 30CrMnSiA热软化情况的理论和试验值的比较^[44]

Figure 7. Comparison between theoretical and experimental values on thermal softening of 30CrMnSiA^[44]

下载: 全尺寸图片幻灯片

图 8 Sn60Pb40合金的计算结果与试验结果的比较^[45]

Figure 8. Comparison of calculated results and experimental results for Sn60Pb40 alloy^[45]

下载: 全尺寸图片幻灯片

1.2.2 Zerilli-Armstrong（Z-A）本构关系

Zerilli^[17]于1987年基于位错力学建立了Z-A本构关系，该本构关系考虑了应变硬化、应变率硬化和晶粒尺寸对金属材料流动应力的影响。由于温度和应变率对面心立方体金属材料（face-centered cubic，FCC）和体心立方体金属材料（body-centered cubic，BCC）的影响不同，例如BCC金属比FCC金属表现出更高的温度敏感性和应变率敏感性，所以FCC和BCC两类金属材料的Z-A型本构关系形式也不同。对于FCC金属，位错必须克服林位错的阻碍；对于BCC金属，位错必须克服Peierls-Nabarro障碍。因此，对于FCC金属，Z-A本构关系的形式为：

$\sigma = {\sigma _{\text{a}}} + B{\varepsilon ^{1/2}}\exp \left( { - \alpha T} \right)$

(29)

对于BCC金属，Z-A本构关系的形式为：

$\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^n}$

(30)

式中： ${\sigma _{\text{a}}}$ 为流动应力的非热分量，主要由溶质和晶界等因素确定， ${\sigma _{\text{a}}} = {\sigma _{\text{G}}} + {k_1}{d^{ - 1/2}}$ ，其中 ${\sigma _{\text{G}}}$ 为考虑溶质和初始位错密度影响的屈服应力部分，k₁为晶粒尺寸系数，表征微结构应力强度； $\alpha {\text{ = }}{\alpha _0} - {\alpha _1}\ln \dot \varepsilon$ ， $\beta {\text{ = }}{\beta _0} - {\beta _1}\ln \dot \varepsilon$ ，B、B₀、 ${\alpha _0}$ 、 ${\alpha _1}$ 、 ${\beta _0}$ 、 ${\beta _1}$ 和 ${\sigma _{\text{G}}}$ 为由试验确定的材料参数。

鉴于HCP（hexagonal close-packed，HCP）材料表现出与FCC和BCC金属类似的应变率敏感性和温度依赖性，例如钛金属^[46]，Zerilli等^[47]将Z-A本构关系的FCC形式和BCC形式统一，建立了一个新的本构关系，描述了Ti-6Al-4V合金和HY-100合金的塑性流动行为，其表达式为：

$\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^{^{1/2}}}\exp \left( { - \alpha T} \right)$

(31)

Z-A本构关系中的参数在各种条件和整个变形过程中被视为常数，但是这种情况与实际情况是不符合的。因此Zhang等^[48]建立了一个修正的Z-A本构关系，描述了新开发的镍基高温合金IC10在宽温域(293～1073 K)和宽应变率(10⁻⁵～10⁻² s⁻¹)下的塑性响应，该本构关系考虑了温度、应变率和变形过程对参数的影响。修正后的本构关系表达式为：

对于FCC：

$\sigma = {\sigma _{\text{a}}} + {C_1}{\varepsilon ^{1/2}}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\frac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\}$

(32)

对于BCC：

$\sigma = {\sigma _{\text{a}}} + {C_2}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\frac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\} + {C_5}{\varepsilon ^n}$

(33)

式中：位错密度 $r\left( \varepsilon \right) = {\rho _0} + M\varepsilon$ 随着塑性应变线性增加，其中M为相对于位错密度增长速率的材料常数， ${\rho _0}$ 为初始位错密度， ${C_i}$ 、 ${C''_3}$ 和 ${C'_4}$ 为材料常数， $H\left( T \right)$ 为温度的函数。

除此之外，许多学者对Z-A本构关系进行了修正以适应某些特定的材料。例如，Samantaray等^[49]在Z-A本构关系的基础上，考虑了温度与应变、温度与应变率的耦合效应对流动应力的影响，建立了一个新的本构关系，描述了Ti改性奥氏体不锈钢(D9合金)在1073～1473 K温度范围、10⁻³～1 s⁻¹应变率范围内的塑性流动行为，其本构形式为：

$\sigma = \left( {{C_1} + {C_2}{\varepsilon ^n}} \right)\exp \left[ { - \left( {{C_3} + {C_4}\varepsilon } \right){T^ * } + \left( {{C_5} + {C_6}{T^ * }} \right)\ln {{\dot \varepsilon }^ * }} \right]$

(34)

式中：C₁、C₂、C₃、C₄、C₅和C₆为材料常数。

Abed等^[50]通过试验发现，Z-A本构关系在预测热激活应力时，假定应力-温度呈指数关系。但是这种指数形式并不适用于所有类型的金属，特别是在高温下，这会导致Z-A本构关系的热激活应力在任何温度下都不会消失，该假设与热激活理论相悖。因此，Abed等^[50]建立了Z-A本构关系的修正形式。

对于FCC：

$\sigma = {C_2}{\varepsilon ^{0.5}}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_6}$

(35)

对于BCC：

$\sigma = {C_1}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_5}{\varepsilon ^n} + {C_6}$

(36)

式中： $X = {C_4}T\ln \left( {1/{{\dot \varepsilon }^ * }} \right)$ ；C₁、C₃和C₄为与微观结构相关的材料参数；C₆为一个附加的应力，与溶质、原始位错密度以及晶粒尺寸相关。

1.2.3 力学阈值应力（mechanical threshold stress，MTS）本构关系

在Z-A本构关系中，流动应力的应变率相关性被分成两个区：滑移区和拖曳区^[34]，将FCC金属的流动应力在应变率超过10³ s⁻¹时的快速增长解释为变形机制的转变：从滑移区向拖曳区转变。然而Follansbee等^{[10, 51]}通过试验观察，认为应变率敏感性的上升应归因于结构演化的速率敏感性，因此，为了描述材料的高应变率行为，发展了MTS本构关系，其形式为：

$\sigma = {\sigma _{\text{a}}} + \left( {\hat \sigma - {\sigma _{\text{a}}}} \right){\left[ {1 - {{\left( {\frac{{kT}}{{{g_0}\mu {b^3}}}\ln \frac{{{{\dot \varepsilon }_0}}}{{\dot \varepsilon }}} \right)}^{1/q}}} \right]^{1/p}}$

(37)

式中： $\hat \sigma$ 为力学阈值应力，即0 K时的流动应力，在常应变下是应变率的函数； ${\sigma _{\text{a}}}$ 为非热应力；k为玻尔兹曼常数； $\mu$ 为剪切模量（与温度相关）；g₀为总的热激活能；p和q为代表势垒形状的参数。

MTS本构关系中考虑了应变、应变率和温度对流动应力的影响，所以需要大量的试验才能确定所需的材料参数，因此使用起来比较麻烦。Follansbee^[52]于1988年总结回顾了MTS本构关系的研究进展，加入了变形孪晶和多重强化机制，给出了MTS本构关系的更一般的形式：

$\sigma = {\sigma _{\text{a}}} + \sum\limits_{i = 1}^n {{S_i}} \left( {\dot \varepsilon ,T} \right){\hat \sigma _{\text{t}}}\mu \left( T \right)/{\mu _0}$

(38)

式中：S_i为与温度和应变率相关的因子， ${\hat \sigma _{\text{t}}}$ 为热应力，一般取n=2。

由于MTS本构关系可以很好地预测高应变率范围（10³～10⁴ s⁻¹）内的流动行为，因此被研究人员用来模拟各种金属在宽应变率范围内的塑性变形行为^[53]。

Banerjee等^[54]对不同退火的4340钢进行了泰勒冲击试验，并使用MTS本构关系预测了其在高温高应变率下的塑性流动行为。此外，学者们也将MTS本构关系嵌入有限元程序，用来模拟金属材料在高应变率下的变形行为，如Maudlin等^[55]采用Taylor冲击试验、扭转试验、平板撞击和斜撞击试验的数据，在EPIC-2和PINON程序上对MTS进行了评估，发现在剪应变小于0.2的情况下，MTS模型有很好的精度^[34]。

1.2.4 Nemat-Nasser-Li（N-N-L）本构关系

为了描述钽和钽钨合金在宽温度域、宽应变率范围、大变形条件下的塑性流动行为，Nemat-Nasser等^[56]建立了一种金属热黏塑性本构关系，其表达式为：

$\sigma {\text{ = }}{\sigma _0}{\varepsilon ^n} + \hat \sigma {\left\{ {1 - {{\left[ { - \frac{{kT}}{{{{G'}_0}}}\left( {\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]}^{1/q}}} \right\}^{1/p}}$

(39)

式中：k为玻尔兹曼常数， $\hat \sigma$ 为阻碍位错运动的阈值应力， ${G'_0}$ 为参考吉布斯自由能。在此基础上，Nemat-Nasser等^[57]考虑位错密度随应变和温度的变化，建立了一个可以描述FCC金属塑性流动行为的物理概念型本构关系，其表达式为：

$\sigma \left( {\dot \varepsilon ,\varepsilon ,T} \right) = {\sigma ^0}{\left\{ {1 - {{\left[ { - \frac{{kT}}{{{G'_0}}}\left( {\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}} + \ln \left( {1 + a\left( T \right){\varepsilon ^{1/2}}} \right)} \right)} \right]}^{1/2}}} \right\}^{3/2}}\left[ {1 + a\left( T \right){\varepsilon ^{1/2}}} \right] + \sigma _{\text{a}}^0{\varepsilon ^{{n_1}}}$

(40)

${\sigma ^0}{\text{ = }}\frac{{{{G'}_0}}}{{b\lambda '{l_0}}},\qquad\quad {\dot \varepsilon _0} = b{\rho _{\text{m}}}{\omega _0}{l_0},\qquad\quad a\left( T \right) = {a_0}\left[ {1 - {{\left( {T/{T_{\text{m}}}} \right)}^2}} \right]$

(41)

式中： $a\left( T \right)$ 和n₁为试验得到的参数； ${G'_0} = \hat \sigma b\lambda 'l$ ，其中 $\hat \sigma$ 为绝对温度为0时的热应力； $\lambda '$ 、 ${l_0}$ 为初始温度下的平均势垒宽度和初始位错间距； $\omega {}_0$ 为试探频率；a₀的值取决于初始平均位错间距。图9中给出了N-N-L本构关系对OFHC铜的预测结果与试验结果的对比，发现在整个应变率和温度范围内，理论预测与试验结果具有良好的一致性。

图 9 不同应变率和温度下，退火OFHC铜的N-N-L本构关系预测结果与试验结果的比较^[57]

Figure 9. Comparison of model prediction predictions with experimental results for annealed OFHC copperat different strain rates and temperatures using N-N-L constitutive model^[57]

下载: 全尺寸图片幻灯片

Guo等^[58]利用N-N-L本构关系描述了3003 Al-Mn合金的塑性流动行为，结果如图10所示。此外，N-N-L本构关系也被用于钼^[59]和钛^[60]等金属塑性流动行为的预测。

图 10 不同应变率下N-N-L模型预测与试验结果的比较^[58]

Figure 10. Comparison between N-N-L model predictions with experimental results at different strain rate^[58]

下载: 全尺寸图片幻灯片

1.2.5 其他物理概念本构模型

除上述几种常见的物理概念本构关系外，学者们建立了其他的物理概念本构关系以描述金属材料的温度依赖性和应变率敏感性。例如，Rusinek等^[61]基于Klepaczko^[62]的研究建立了一种热黏塑性本构关系（R-K本构关系），用于描述金属铝薄板在10⁻⁴～10³ s⁻¹应变率下的应变、应变率和温度与流动应力之间的关系。该本构关系中添加了一个有效应力，对应于应变硬化和热激活过程。其表达式为：

$\sigma = \frac{{E\left( T \right)}}{{{E_0}}}\left[ {{B_0}\theta _{\text{m}}^{ - v}{{\left( {{\varepsilon _0} + {\varepsilon _{\text{p}}}} \right)}^{n\left( {1 - {D_2}{\theta _{\text{n}}}} \right)}} + \sigma _0^*{{\left( {1 - {D_1}{\theta _{\text{m}}}} \right)}^m}} \right]$

(42)

式中： ${\theta _{\text{m}}} = \dfrac{T}{{{T_{\text{m}}}}}\lg \left( {\dfrac{{{{\dot \varepsilon }_{\max }}}}{{{{\dot \varepsilon }}}}} \right)$ 和 ${\theta _{\text{n}}} = \dfrac{T}{{{T_{\text{m}}}}}\lg \left( {\dfrac{{{{\dot \varepsilon }}}}{{{{\dot \varepsilon }_{\min }}}}} \right)$ 为两个用应变率修正的温度；B₀为塑性模量；v为温度敏感性指数；n为硬化系数； $m = {\left( {\dfrac{{\partial \lg \sigma }}{{\partial \lg \dot \varepsilon }}} \right)_{\varepsilon ,T}}$ ；在T=0 K时，有效应力 $\sigma _0^ *$ 、D₁和D₂为材料常数；E和E₀分别为当前温度和0 K温度下的弹性模量； ${\dot \varepsilon _{\max }}$ 为应变率的上限，并在临界温度下达到最小应变率 ${\dot \varepsilon _{\min }}$ 。然而，之后的研究证明R-K本构关系不能准确描述金属热黏塑性行为的某些方面，于是Rusinek等^[63]通过在流动应力 $\sigma$ 中添加一个第三项来扩展该本构关系的应用范围，新项 ${\sigma _{{\text{ns}}}}$ 解释了铝合金中观察到的负应变率敏感性，其修正形式为：

${\sigma _{{\text{ns}}}}\left( {\dot \varepsilon ,T} \right) = \sigma _0^{{\text{ns}}} {\lg \left( {\frac{{{{\dot \varepsilon }_{{\text{trans}}}}}}{{\dot \varepsilon }}} \right)} \left[ {1 - {D_3}\left( {\frac{{{T_{\text{m}}}}}{T}} \right)\lg \left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\max }}}}} \right)} \right]$

(43)

式中： $\sigma _0^{{\text{ns}}}$ 和D₃为材料常数， ${\dot \varepsilon _{{\text{trans}}}}$ 表示正应变率敏感性和负应变率敏感性之间的过渡。Rusinek等^[64]又基于对OFHC铜的研究，对R-K本构关系进行了修正，修正后的本构关系（M-R-K）中，von Mises应力为：

$\sigma = \frac{{E\left( T \right)}}{{{E_0}}}\left( {{\sigma _{\text{a}}} + {\sigma _{{\text{th}}}}} \right) + {\sigma _{{\text{vs}}}}$

(44)

式中： ${\sigma _{\text{a}}}$ 为等效非热应力，等效热应力 ${\sigma _{{\text{th}}}}$ 为：

${\sigma _{{\text{th}}}} = \sigma _{{\text{th}}}^0{\left[ {1 - {\xi _1}\left( {\frac{T}{{{T_{\text{m}}}}}} \right)\lg \left( {\frac{{{{\dot \varepsilon }_{\max }}}}{{\dot \varepsilon }}} \right)} \right]^{1/{\xi _2}}}$

(45)

式中： ${\xi _1}$ 和 ${\xi _2}$ 为描述材料温度和速率敏感性的材料常数， $\sigma _{{\text{th}}}^0\left( {\varepsilon ,\dot \varepsilon ,T} \right) = B\left( {\dot \varepsilon ,T} \right){\left( \varepsilon \right)^{n\left( {\dot \varepsilon ,T} \right)}}$ 。黏性阻力分量 ${\sigma _{{\text{vs}}}}$ 为Taylor因子、阻力系数和移动位错密度的函数。Voyiadjis等^[65]利用修正后的R-K本构关系对2024-T3铝合金在低速射孔试验中的温度敏感性进行了预测，本构关系的预测结果与试验结果的对比如图11所示。

图 11 用M-R-K本构关系描述的流动应力随塑性应变的变化^[65]

Figure 11. Change of the flow stress with plastic strain described using the M-R-K model^[65]

下载: 全尺寸图片幻灯片

Sung等^[66]提出了Hollomon和Voce本构方程，建立了一个包含3个函数的乘法型本构关系，描述了3种双相钢的塑性流动行为，其形式为：

$\sigma = \sigma \left( {\varepsilon ,\dot \varepsilon ,T} \right) = f\left( {\varepsilon ,T} \right)g\left( {\dot \varepsilon } \right)h\left( T \right)$

(46)

式中：函数f通过Hollomon和Voce应变硬化方程的线性组合来揭示应变硬化率的温度敏感性，形式为：

$f\left( {\varepsilon ,T} \right) = \alpha \left( T \right){f_{\text{h}}} + \left[ {1 - \alpha \left( T \right){f_{\text{v}}}} \right] \tag{47a}$

$\alpha \left( T \right) = {\alpha _1} - {\alpha _2}\left( {T - {T_0}} \right) \tag{47b}$

${f_{\text{h}}} = H{\varepsilon ^n} \tag{47c}$

${f_{\text{v}}} = V\left( {1 - A{{\text{e}}^{B\varepsilon }}} \right) \tag{47d}$

式中： ${\alpha _1}$ 、 ${\alpha _2}$ 、H、n、A、B和V为材料常数。

Gao等^[67]基于位错运动的热激活机制，建立了一种可以描述FCC金属动态塑性行为的热黏塑性本构关系，该本构关系中本构参数与材料的微观结构特征直接相关，其形式为：

$\sigma {\text{ = }}{\sigma _{\text{a}}} + \hat Y{\varepsilon ^n}\exp \left( {{c_3}T\ln {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{{\text{s0}}}}}}} } \right){\left[ {1 - {{\left( { - {c_4}T\ln {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} } \right)}^{1/q}}} \right]^{1/p}}$

(48)

式中： $\hat Y{\text{ = }}\lambda {\hat \sigma _{{\text{s0}}}}$ 为实际参考热应力，其中 ${\hat \sigma _{{\text{s0}}}}$ 为参考饱和阈值应力； ${c_3} = k/ \left( {{g_{{\text{s0}}}}\mu {b^3}} \right)$ ， ${c_4} = k/ \left( {{g_0}\mu {b^3}} \right)$ ，其中 ${g_{{\text{s0}}}}$ 为常数； ${\dot \varepsilon _0}$ 为参考应变率， ${\dot \varepsilon _{{\text{s0}}}}$ 为饱和参考应变率， ${g_0}$ 为归一化自由能。

为了能直观地了解各物理概念本构关系的主要特性和其表达式，表3～4分别给出了上述各种物理概念本构关系的主要特点和本构方程的具体形式。

表 3 物理概念本构关系的模型对比

Table 3. Comparison of physically based constitutive relations

本构关系	年份	模型	应变率范围/s⁻¹	本构关系的主要特征
B-P	1975	Bodner-Partom^[18]	10⁻³～1	（1）将材料的总变形率分为弹性和塑性两部分（2）通过塑性功项合并应变硬化效应（3）没有考虑温度效应
Z-A	1987	Zerilli-Armstrong^[17]	4×10³	（1）考虑了晶粒尺寸的影响（2）基于热激活理论
	2009	Zhang-Wen^[48]	10⁻⁵～10⁻²	考虑了温度、应变率和变形过程对Z-A模型中参数的影响
	2009	Samantaray-Mandal^[49]	10⁻³～1	考虑了温度与应变、温度与应变率的耦合效应对流动应力的影响
	2005	Abed-Voyiadjis^[50]	10⁻⁴～10⁴	（1）可用于预测等温和绝热塑性变形的应力应变曲线（2）将模型参数准确的与微观结构物理参数联系起来
M-T-S	1988	Follansbee^[10,51]	10⁻⁴～10⁴	（1）认为应变率敏感性的上升应归因于结构演化的速率敏感性（2）考虑了阈值应力
N-N-L	1998	Nemat-Nasser-Li^[57]	10⁻³～10⁴	考虑了位错密度随应变和温度的变化
其他	2001	Rusinek-Klepaczko^[61,62]	10⁻⁴～10³	考虑了应变率历史效应对金属材料塑性流动行为的影响
	2009	Rusinek-Rodrguez-Martnez^[63]	10⁻⁴～10⁴	（1）添加一个第三项来扩展该本构关系的应用范围（2）考虑负应变率敏感性和粘性阻力
	2010	Sung^[66]	10⁻³～10	通过Hollomon和Voce应变硬化方程的线性组合来揭示应变硬化率的温度敏感
	2010	Gao-Zhang^[67]	10⁻³～10⁴	考虑FCC金属变形过程中微观结构的演变建立阈值应力与应变、温度和应变率的关系

下载: 导出CSV

| 显示表格

表 4 物理概念本构关系的方程形式

Table 4. Equations of physically based constitutive relations

模型	方程形式
Bodner-Partom^[18]	$D_2^{\text{p}} = D_0^2\exp \left[ { - \left( {\dfrac{{n + 1}}{n}} \right){{\left( {\dfrac{{{Z^2}}}{{3{J_2}}}} \right)}^n}} \right]$
Zerilli-Armstrong^[17]	对于FCC: $\sigma = {\sigma _{\text{a}}} + B{\varepsilon ^{1/2}}\exp \left( { - \alpha T} \right)$ 和 $\alpha {\text{ = }}{\alpha _0} - {\alpha _1}\ln \dot \varepsilon$ 对于BCC： $\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^n}$ 和 $\beta {\text{ = }}{\beta _0} - {\beta _1}\ln \dot \varepsilon$ 对于HCP： $\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^{^{1/2}}}\exp \left( { - \alpha T} \right)$
Zhang-Wen^[48]	对于FCC： $\sigma = {\sigma _{\text{a}}} + {C_1}{\varepsilon ^{1/2}}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\}$ 对于BCC： $\sigma = {\sigma _{\text{a}}} + {C_2}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\} + {C_5}{\varepsilon ^n}$
Samantaray-Mandal^[49]	$\sigma = \left( {{C_1} + {C_2}{\varepsilon ^n}} \right)\exp \left[ { - \left( {{C_3} + {C_4}\varepsilon } \right){T^ * } + \left( {{C_5} + {C_6}{T^ * }} \right)\ln {{\dot \varepsilon }^ * }} \right]$
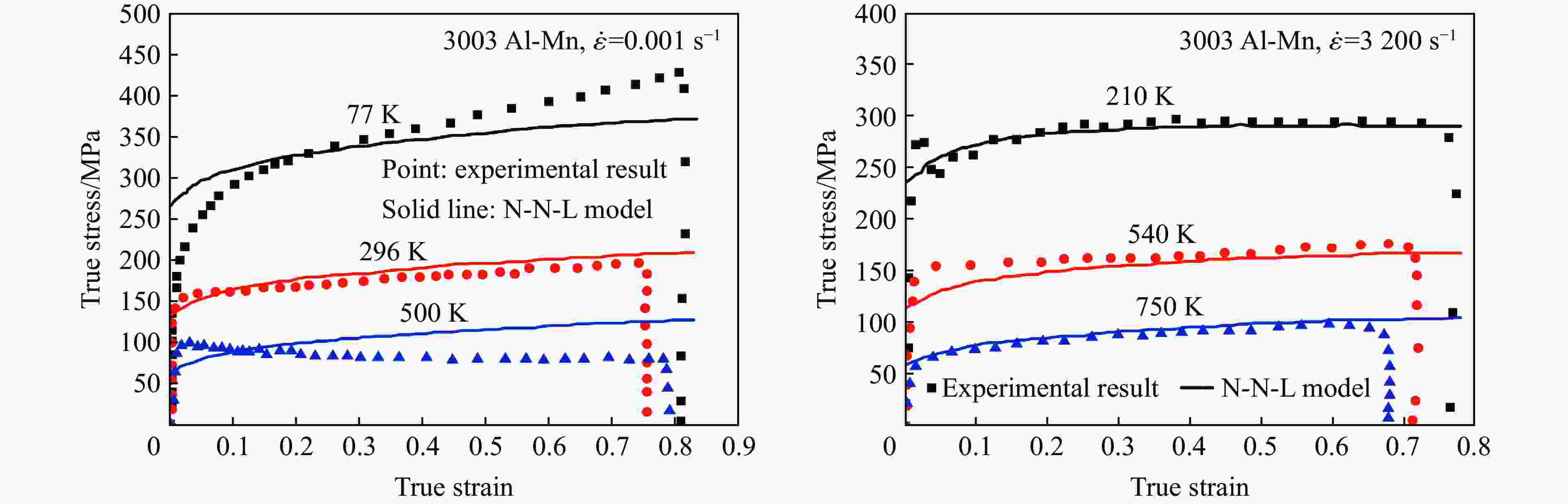
Abed-Voyiadjis^[50]	对于FCC： $\sigma = {C_2}{\varepsilon ^{0.5}}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_6}$ 和 $X = {C_4}T\ln \left( {1/{{\dot \varepsilon }^ * }} \right)$ 对于BCC： $\sigma = {C_1}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_5}{\varepsilon ^n} + {C_6}$
Follansbee^[10,51]	$\sigma = {\sigma _{\text{a}}} + \left( {\hat \sigma - {\sigma _{\text{a}}}} \right){\left[ {1 - {{\left( {\dfrac{{kT}}{{{g_0}\mu {b^3}}}\ln \dfrac{{{{\dot \varepsilon }_0}}}{{\dot \varepsilon }}} \right)}^{1/q}}} \right]^{1/p}}$
Nemat-Nasser-Li^[57]	$\sigma \left( {\dot \varepsilon ,\varepsilon ,T} \right) = {\sigma ^0}{\left\{ {1 - {{\left[ { - \dfrac{{kT}}{{{G'_0}}}\left( {\ln \dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}} + \ln \left( {1 + a\left( T \right){\varepsilon ^{1/2}}} \right)} \right)} \right]}^{\tfrac{1}{2}}}} \right\}^{\tfrac{3}{2}}}\left[ {1 + a\left( T \right){\varepsilon ^{\tfrac{1}{2}}}} \right] + \sigma _{\text{a}}^0{\varepsilon ^{{n_1}}}$
Rusinek-Klepaczko^[61,62]	$\sigma = \dfrac{{E\left( T \right)}}{{{E_0}}}\left[ {{B_0}\theta _{\text{m}}^{ - v}{{\left( {{\varepsilon _0} + {\varepsilon _{\text{p}}}} \right)}^{n\left( {1 - {D_2}{\theta _n}} \right)}} + \sigma _0^*{{\left( {1 - {D_1}{\theta _{\text{m}}}} \right)}^m}} \right]$
Rusinek-Rodrguez-Martnez^[63]	${\sigma _{{\text{ns}}}}\left( {\dot \varepsilon ,T} \right) = \sigma _0^{{\text{ns}}} \left[ {\lg \left( {\dfrac{{{{\dot \varepsilon }_{{\text{trans}}}}}}{{\dot \varepsilon }}} \right)} \right] \left[ {1 - {D_3}\left( {\dfrac{{{T_{\text{m}}}}}{T}} \right)\lg \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\max }}}}} \right)} \right]$
Sung^[66]	$\sigma = \sigma \left( {\varepsilon ,\dot \varepsilon ,T} \right) = f\left( {\varepsilon ,T} \right)g\left( {\dot \varepsilon } \right)h\left( T \right)$
Gao-Zhang^[67]	$\sigma {\text{ = }}{\sigma _{\text{a}}} + \hat Y{\varepsilon ^n}\exp \left[ {{c_3}T\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{{\text{s0}}}}}}} \right)} \right]{\left\{ {1 - {{\left[ { - {c_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]}^{1/q}}} \right\}^{1/p}}$

下载: 导出CSV

| 显示表格

此外，Xu等^[68-70]近年来也对常见的各种金属热黏塑性本构关系的描述和预测能力进行了详细的研究和对比。主要针对B-P、N-N-L、Z-A、V-A和R-K等5种物理概念本构关系以及J-C和K-H-L等2种唯象本构关系，介绍了各本构关系参数的确定方法，分别用于描述典型FCC金属铜^[69]和钨基复合材料93W-4.9Ni-2.1Fe^[70]在宽应变率宽温度范围内的塑性行为，分析了各本构关系在描述加工硬化、温度和应变速率影响时的灵活性。

2. 包含第三型应变时效的金属热黏塑性本构关系

在宽温域、宽应变率范围内对金属材料的塑性流动行为进行测试时，会发现：在某应变率下，金属材料的流动应力-应变曲线随着试验温度升高整体或较大部分反而上升，表现在对应的流动应力-温度曲线上为出现一反常应力峰值^[71-72]，如图12所示。考虑到这种现象在形式上有别于“静态应变时效”和锯齿屈服PLC动态应变时效，郭伟国等^[73]，Wang等^[74-75]和Xiao等^[76]将这一现象称为“第三型应变时效”（third type SA，简称3rd SA）。第三型应变时效现象的出现具有普遍性，在单晶、多晶(BCC, HCP, FCC)等各类金属^[77-79]中都出现这一现象。

图 12 DH36钢流动应力随温度变化曲线上出现的反常应力峰^[71]

Figure 12. Anomalous stress peaks in the flow stress curves of DH36 steel with temperature^[71]

下载: 全尺寸图片幻灯片

第三型应变时效现象的出现使得常见的金属热黏塑性本构关系不能很好地描述金属材料在第三型应变时效出现的温度区域内的塑性流动行为。为此，学者们通过对第三型应变时效的表现形式和微观机理的研究来建立考虑第三型应变时效的金属热黏塑性本构关系^[80-86]。Gilat等^[81]在基于位错热激活理论建立的金属热黏塑性本构关系的基础上，增加了考虑局部溶质原子浓度的第三型应变时效项，利用建立的包含第三型应变时效的金属热黏塑性本构关系，可以很好地描述1020钢在不同温度、不同应变率下的塑性流动行为。Cheng等^[82]基于N-N-L本构关系考虑第三型应变时效过程中溶质原子浓度的变化，建立了包含第三型应变时效的金属热黏塑性本构关系，其最终形式如下：

$\sigma {\text{ = }}{\sigma '_0}{\left\{ {1 - {{\left[ { - \frac{{kT}}{{{F'_0}\sqrt {C'/{C'_0}} }}\left( {\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]}^{1/q}}} \right\}^{1/p}} \left\{ {1 + {a_0}\left[ {1 - {{\left( {\frac{T}{{{T_{\text{m}}}}}} \right)}^2}} \right]{\varepsilon ^{{n_0}}}} \right\} + \sigma _{\text{a}}^0{\varepsilon ^{{n_1}}}$

(49)

$\frac{{C'}}{{{C'_0}}} = 1 + {\left[ {\frac{{\sigma - \sigma _{\text{a}}^0{\varepsilon ^{{n_1}}}}}{{{\sigma _1}C'/{C'_0}}}\frac{\varepsilon }{{{\varepsilon _1}}}\exp \left( {1 - \frac{\varepsilon }{{{\varepsilon _1}}}} \right)} \right]^{{n_2}}} \left\{ {1 - \exp \left[ { - {{\left( {\frac{\varOmega }{\varepsilon }\exp \left( { - \frac{{Q - {Q_i}}}{{kT}}} \right)} \right)}^\alpha }} \right]} \right\}$

(50)

式中： $C'$ 为位错线上溶质原子的浓度； ${F'_0}$ 为溶质浓度为 ${C'_0}$ 时的活化能；a₀和n₀为材料参数； $\sigma _{\text{a}}^0$ 为一个带有压力大小的常数；n₁为一个常数；Q_i为溶质原子与位错间的相互作用能； $\alpha$ 、 ${\sigma '_0}$ 、 ${\sigma _1}$ 、 ${\varepsilon _1}$ 、n₁、n₂和 $\varOmega$ 都为常数， $\varOmega = \beta b{\rho _{\text{m}}}l{\nu '_0} = {\dot \varepsilon _0}\left( {{{\nu '}_0}/{\nu _0}} \right)$ ，其中 ${\nu '_0}$ 为溶质原子的试探频率， $\ \beta$ 为指向因子。郭扬波等^[87]考虑位错与位错芯内的溶质原子(位错芯气团)的相互作用，在Z-A热黏塑性本构关系的基础上，加入位错和位错芯气团的相互作用的影响，建立了一种可定量描述第三型应变时效现象的本构关系，所建立的本构关系的表达式如下：

$\sigma = \left\{ {\begin{array}{*{20}{l}} {\sigma _0}\sqrt {\dfrac{{C'}}{{{C'_0}}}} \exp \left( { - {c_0}T + {c_1}T\ln \dot \varepsilon + d\dfrac{{kT}}{{{{G'}_0}\sqrt {C'/{C'_0}} }}\ln {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} } \right) + {B_0} + \sigma _0^{\text{I}}{\varepsilon ^n}&T \text{＜} {T_{\text{C}}} \\ {B_0} + \sigma _0^{\text{I}}{\varepsilon ^n}&T \text{≥} {T_{\text{C}}} \end{array}} \right.$

(51)

$\frac{{C'}}{{{C'_0}}} = 1 + N{\varepsilon ^m} \left\{ {1 - \exp \left[ { - {{\left( {\frac{\varOmega }{{\dot \varepsilon }}\exp \left( { - \frac{{Q - {Q_i}}}{{kT}}} \right)} \right)}^a}} \right]} \right\}$

(52)

式中： ${C'_0}$ 为位错线上溶质原子的初始浓度； ${G'_0}$ 为位错线上溶质原子浓度为 ${C'_0}$ 、外部功为零时，克服障碍所需的全部自由能；K、 $\sigma _0^{\text{I}}$ 、n、c₀、c₁、 $\alpha$ 、 ${\sigma _0}$ 和 $\varOmega$ 均为常数， ${B_0} = {\sigma _{\text{G}}} + {k_1}{d^{ - 1/2}}$ ， ${\sigma _0} = {G'_0}/\left( {{A_0}b} \right)$ 。

以上3种金属热黏塑性本构关系均是考虑了第三型应变时效过程中的微观机理建立起来的，被认为是具有物理概念的包含第三型应变时效的本构关系，但是，其形式复杂，材料参数较难获得，因而未得到广泛应用。为此，学者们将更多注意力放在了第三型应变时效的经验型本构关系。Hong^[80]和Lee等^[83]考虑到第三型应变时效在高温和低温下未出现而在中温区最为明显，提出了正态分布形式的第三型应变项的表达式：

${\sigma _{\text{D}}} = \sigma _{\text{D}}^0\exp \left[ { - \frac{{{{\left( {T - \overline T} \right)}^2}}}{{{T_{\text{W}}}}}} \right]$

(53)

式中： $\sigma _{\text{D}}^0$ 为 ${\sigma _{\text{D}}}$ 的最大值， $\overline T$ 为该最大值出现的温度，T_W为第三型应变时效出现的温度宽度。考虑到随着应变率的增大，第三型应变时效会移向更高的温度，Hong^[80]和Lee等^[83]认为 $\overline T$ 为应变率的函数，其表达式如下：

$\frac{1}{\overline T}=C_1\ln \dot{\varepsilon} +C_2$

(54)

式中：C₁和C₂为材料常数。Lee等^[84]在Nemat-Nasser等^[56]建立的物理概念热黏塑性本构关系的基础上，增加了第三型应变时效项来描述3种热等静压高温合金的塑性流动行为，其中，第三型应变时效项的表达式为：

${\sigma _{\text{D}}} = \sigma _{\text{D}}^0\exp \left[ { - \frac{{{{\left( {T - \overline T} \right)}^2}}}{{T_{\text{W}}^2}}} \right]{\varepsilon ^c}$

(55)

其中并未考虑第三型应变时效现象的应变率效应。孟卫华等^[88-89]和Su等^[90]同样在Nemat-Nasser等^[56]建立的物理概念热黏塑性本构关系的基础上，增加了第三型应变时效项来描述DH-36钢的拉伸和压缩塑性流动行为，考虑到第三型应变时效现象的应变率效应，通过对在很宽应变率范围内的试验结果进行进行分析，认为第三型应变时效项中的特征参数 ${\sigma _{\text{D}}}$ 、 $\overline T$ 和T_W与对数应变率呈线性关系，表达式为：

${\hat \sigma _{\text{D}}} = \sigma _{\text{D}}^0\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}\text{，}\qquad\quad \overline T = {T_1}\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}} + {T_2}\text{，}\qquad\quad \Delta T = \Delta {T_1}\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}} + \Delta {T_2}$

(56)

式中： $\sigma _{\text{D}}^0$ 、T₁、T₂、 $\Delta {T_1}$ 、 $\Delta {T_2}$ 为材料常数。Guo等 ^[85]则通过对试验结果分析，认为特征参数 $\overline T$ 与对数应变率呈反比例关系，表达式如下：

$\overline T = {T_1}\Biggr/\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}$

(57)

为了能准确地给出特征参数 $\sigma _{\text{D}}^0$ 、 $\overline T$ 和T_W与应变率的关系，Wang等^[74]基于运动位错与扩散溶质原子的相互作用建立了特征参数 $\sigma _{\text{D}}^0$ 、 $\overline T$ 和T_W与应变率的表达式：

${T_{\text{W}}} = \frac{{{T_1}}}{{\ln \dfrac{{\dot \varepsilon }}{A} - m\ln \varepsilon }}$

(58)

$\xi = \frac{{{T_2}}}{{\ln \dfrac{{\dot \varepsilon }}{A} - m\ln \varepsilon }}$

(59)

${\hat \sigma _{\text{D}}} = \hat \sigma _{\text{D}}^1\ln \frac{{\dot \varepsilon }}{A} + \hat \sigma _{\text{D}}^2$

(60)

式中：T₁、A、m、T₂、 $\hat \sigma _{\text{D}}^1$ 、 $\hat \sigma _{\text{D}}^2$ 为材料常数。

Song等^[86]和Voyiadjis等^[91]基于修正的Voyiadjis-Abed热黏塑性本构关系增加第三型应变时效项，增加的第三型应变时效项表达式如下：

$\sigma _{\text{D}}^0 = \chi {\sigma _{\text{w}}}\left( {\varepsilon ,\dot \varepsilon ,T} \right)$

(61)

$\chi \left( T \right) = \frac{1}{4}\left( {1 + \tanh \frac{{T - {T_{\text{l}}}}}{\xi }} \right)\left( {1 - \tanh \frac{{T - {T_{\text{u}}}}}{\xi }} \right)$

(62)

${\sigma _{\text{w}}} = \left( {\varepsilon ,\dot \varepsilon ,T} \right) = {a_{\text{w}}}\exp \left\{ { - \frac{{{{\left[ {T - W\left( {\dot \varepsilon } \right)} \right]}^2}}}{{{b_{\text{w}}}}}} \right\}$

(63)

式中： ${a_{\text{w}}}$ 和 ${b_{\text{w}}}$ 均为应变的幂函数， $W\left( {\dot \varepsilon } \right)$ 为应变率的幂函数，T_u和T_l分别为活跃的第三型应变时效温度范围的上限和下限， $\xi$ 为温度参数， $\ \chi$ 为定义第三型应变时效温度范围的系数。

第三型应变时效现象的出现，使常见的金属热黏塑性本构关系不能很好地描述金属塑性流动行为，为此，学者们建立了多种包含第三型应变时效的金属热黏塑性本构关系，可分为两类：具有物理概念的本构关系和经验型的本构关系。具有物理概念的本构关系是基于第三型应变时效微观机理，即运动位错与溶质原子的相互作用建立起来的，其形式通常较复杂，材料参数不易获得。经验型的本构关系在常见金属热黏塑性本构关系的基础上增加了第三型应变时效项，由于其形式简单、参数容易获得，近年来受到了广泛关注。经验型的本构关系中的第三型应变时效项通常采用正态分布形式，但是其中的特征参数与应变率的关系式有一定差异。

3. 包含K-W锁位错结构引起的反常应力峰的金属热黏塑性本构关系

在对 $\gamma '$ 相增强的镍基高温合金的塑性流动行为的研究中发现： $\gamma '$ 相增强的镍基高温合金流动应力在随温度变化的曲线上，会出现一反常应力峰，如图13所示。该反常应力峰的出现被认为是由镍基高温合金中 $\gamma '$ 相中的K-W 锁位错结构引起的。学者们在观察和分析交滑移锁形成过程的基础上，成功发展出很多与K-W锁的形成和解锁相关的超弯折模型。K-W锁的形成过程为被压缩的超不全位错首先滑移到立方面上，然后扩展到一相交的八面体上，以非平面锁的形式锁住整个位错。超弯折模型的基础为Orowan公式，包含Sun模型^[92]、Hirsch模型^[93-94]、ELU模型^[95]和自解锁机制模型^[96]。

图 13 镍基高温合金的拉伸强度随温度的变化^[97-98]

Figure 13. Tensile strength of nickel base superalloy as a function of temperature^[97-98]

下载: 全尺寸图片幻灯片

为了描述 $\gamma '$ 相增强的镍基高温合金DD407的力学行为，Wang等^[99]建立了一个考虑屈服应力的异常温度依赖性及其应变率效应的本构关系。根据反常应力峰的特点，Wang等^[23]修正了Johnson-Cook本构关系以描述镍基高温合金GH4133B的塑性流动行为。结合反相界面能的温度依赖性和经典的颗粒剪切理论，Li等^[100]建立了一个温度依赖的屈服强度模型来描述 $\gamma '$ 增强高温合金的屈服强度随温度的变化。

Wang等^[99]基于镍基单晶高温合金的微观结构——一种含有 $\gamma$ 基体相和 $\gamma '$ 增强相的双相结构，建立了包含K-W锁位错结构引起的反常应力峰的屈服强度与温度和应变率的关系。考虑 $\gamma$ 相和 $\gamma '$ 相的影响，高温合金的流动应力可表示为^[101-102]：

${\sigma ^n} = \sigma _{\text{m}}^n + \sigma _{\text{p}}^n$

(64)

式中： $\sigma$ 为 $\gamma '$ 增强高温合金的流动应力， ${\sigma _{\text{m}}}$ 为 $\gamma$ 相的流动应力， ${\sigma _{\text{p}}}$ 为 $\gamma '$ 相的流动应力，n为在1和2之间变化的指数^[103-104]。 $\gamma$ 基体相的流动应力可表示为：

${\sigma _{\rm{m}}} = {\sigma _{\rm{O}}} + {\sigma _{\rm{S}}}$

(65)

式中： ${\sigma _{\rm{O}}}$ 为Orowan的阻力部分， ${\sigma _{\text{S}}}$ 为固溶阻力部分。 ${\sigma _{\rm{O}}}$ 可以表示为^[105]：

${\sigma _{\rm{O}}} = \frac{{Gb}}{{l'\beta }}$

(66)

式中：G为剪切模量，b为Burgers矢量， $l'$ 为基体通道的尺寸， $\ \beta$ 为基于基体各向同性的取向常数。固溶阻力可以表示为：

${\sigma _{\text{S}}} = A{\dot \varepsilon ^{1/m}}\exp \left( {\frac{Q}{{mkT}}} \right)$

(67)

式中：k为玻尔兹曼常数， $Q$ 为位错运动的激活自由能，A和m为材料常数。

位错从八面体平面向立方体平面的交叉滑移，导致K-W锁的形成，是屈服应力与温度正相关的根本原因。由于热激活滑移更倾向于立方体平面，导致材料在超过峰值应力^[106]对应的温度时发生软化。为了描述由K-W锁引起的对位错运动的额外阻力的大小，可用正态分布来定量描述K-W锁形成的概率随温度的变化， $\gamma '$ 相的流动应力^[99]具体表达式如下：

${\sigma _{\text{p}}} = C\exp \left[ { - \frac{{{{\left( {T - {T_{{\text{KW}}}}} \right)}^2}}}{{{\zeta ^2}}}} \right]$

(68)

式中：T_KW、 $\zeta$ 和C为K-W锁引起的反常应力峰值的特征参数，T_KW为K-W 锁产生的阻力最大时的温度，即峰值温度， $\zeta$ 为应力峰的宽度，C为应力峰的高度。T_KW、 $\zeta$ 和C为应变率的函数：

${T_{{\text{KW}}}} = \frac{E}{{F - \ln \dot \varepsilon }}\text{，}\qquad\quad \xi = \frac{D}{{F - \ln \dot \varepsilon }}\text{，}\qquad\quad C = {C_0} - {C_1}n\ln \dot \varepsilon$

(69)

式中：E、D、F、C₀和C₁为材料常数。

王建军等^[3]所建立的包含K-W锁位错结构引起的反常应力峰的本构关系可以很好地描述 $\gamma '$ 相增强的镍基高温合金屈服应力随温度和应变率的变化，但未考虑塑性变形的影响。近期，Wang等^[107]在对镍基高温合金K403在宽温度域、宽应变率范围内的塑性流动行为进行测试时发现：高温合金K403的流动应力随温度变化会出现两个反常应力峰，如图14所示，通过系统分析，认为这两个反常应力峰分别由第三型应变时效和K-W锁位错结构引起。为了能准确描述高温合金K403的塑性流动行为，在文献[99]建立的 $\gamma '$ 相增强的镍基高温合金的本构关系的基础上，在 $\gamma$ 相的流动应力（ ${\sigma _{\text{m}}}$ ）中增加了第三型应变时效项，在固溶阻力部分（ ${\sigma _{\text{S}}}$ ）增加了非热部分。因此， $\gamma '$ 相增强的镍基高温合金热黏塑性本构关系的最终表达式为：

图 14 高温合金K403在不同应变率下的流动应力随温度的变化

Figure 14. Flow stress of superalloy K403 as function of temperature at different strain rates

下载: 全尺寸图片幻灯片

$\sigma = {\left( {\sigma _{\text{m}}^n + \sigma _{\text{p}}^n} \right)^{1/n}}$

(70)

${\sigma _{\text{m}}} = {\sigma _{\text{O}}} + {\sigma _{\text{S}}} + {\sigma _{{\text{SA}}}}$

(71)

${\sigma _{\text{O}}} = \frac{{Gb}}{{l'\beta }}$

(72)

${\sigma _{\text{S}}} = A{\dot \varepsilon ^{1/m}}\exp \left( {\frac{{Q'}}{{mkT}}} \right) + B{\varepsilon ^a}$

(73)

${\sigma _{{\text{SA}}}} = {\hat \sigma _{{\text{SA}}}}\exp \left[ { - {{\left( {\frac{{T - {T_{{\rm{SA}}}}}}{\xi }} \right)}^2}} \right]$

(74)

${T_{{\text{SA}}}} = \frac{{{T_1}}}{{\ln \dfrac{{\dot \varepsilon }}{F} - m\ln \varepsilon }}$

(75)

$\xi =\frac{T_2}{\ln\dfrac{\dot {\varepsilon}}{F}-m \ln \varepsilon}$

(76)

${\hat \sigma _{\text{D}}} = \hat \sigma _{\text{D}}^1\ln \frac{{\dot \varepsilon }}{F} + \hat \sigma _{\text{D}}^2$

(77)

${\sigma _{\text{p}}} = C\exp \left[ { - \frac{{{{\left( {T - {T_{{\text{KW}}}}} \right)}^2}}}{{{\zeta ^2}}}} \right]$

(78)

$T = {T_0} + \Delta T = {T_0} + \frac{\eta }{{\rho {C_{\text{V}}}}}\int_0^\varepsilon {\sigma {\text{d}}\varepsilon }$

(79)

$\eta = \left\{ {\begin{array}{*{20}{l}} 0 \\ {0.316\lg \dot \varepsilon + 0.95} \\ {0.95} \end{array}\begin{array}{*{20}{l}} {\dot \varepsilon \text{≤} {{10}^{ - 3}}\;{\rm{s}}^{-1}} \\ {{{10}^{ - 3}}\;{\rm{s}}^{-1} \text{＜} \dot \varepsilon \text{＜} 1.0\;{\rm{s}}^{-1}} \\ {\dot \varepsilon \text{≥} 1.0\;{\rm{s}}^{-1}} \end{array}} \right.$

(80)

如图14所示，所建立的 $\gamma '$ 相增强的镍基高温合金的热黏塑性本构关系可以准确地预测高温合金K403在宽温度域、宽应变率范围内的塑性流动行为。

4. 考虑拉压不对称性的金属热黏塑性本构关系

在钛合金和其他HCP金属中经常观察到拉伸和压缩之间的强度差，即拉/压不对称^[108-109]。Khan等^[109]研究了电子束单熔体Ti-6Al-4V合金在不同应变率下的拉伸和压缩行为，发现Ti-6Al-4V合金的拉伸和压缩行为不仅在屈服应力水平上有明显差异，而且在加工硬化速率上也有显著差异。Li等^[110]研究了激光立体成形Ti-6Al-4V合金(LSF Ti-6Al-4V)在宽温度域和宽应变率下的拉伸和压缩行为，发现拉伸和压缩力学行为在屈服应力和加工硬化速率上也存在显著差异。

在结构分析中，通常采用经典J₂塑性理论来描述金属合金的塑性响应，该理论认为应力偏量的第一不变量和第三不变量对流动应力没有影响。然而，对于金属塑性流动行为中出现的拉/压不对称行为，J₂塑性理论不再适用。岩土力学界早就认识到将静水压力(与应力偏量的第1个不变量有关)和Lode角参数(与应力偏量的第三个不变量有关)纳入本构关系的必要性^[111-112]。Richmond等^[113]进行了初步研究，证明了静水压力对铝合金屈服的影响；Gao等^[114]揭示了应力状态对5083铝合金的塑性响应有很强的影响，为应力状态相关的塑性模型的发展提供了蓝图；Khan等^[115]提出了应变率和温度依赖的屈服准则来描述Ti-6Al-4V合金的各向异性屈服行为和拉压不对称特性；Tuninetti等^[116]研究了Ti-6Al-4V合金的拉压不对称、各向异性屈服和各向异性应变硬化行为，基于宏观正交各向异性屈服准则CPB06，建立了考虑拉压不对称、各向异性屈服和各向异性应变硬化的弹塑性本构关系。

在Ti-6Al-4V合金中经常观察到的流动应力拉/压不对称通常归因于滑移系统^[117-118]和机械孪晶^[119]的不同。LSF Ti-6Al-4V合金的屈服应力和加工硬化速率具有显著的拉/压不对称，且其拉/压不对称与温度和应变速率有关^[110]。本文中将基于LSF Ti-6Al-4V合金的塑性流动行为，建立一个考虑拉/压不对称以及温度和应变速率依赖性的金属热黏塑性本构关系。

金属的流动应力为 $\sigma {\text{ = }}\sqrt {\dfrac{3}{2}{\sigma _{ij}}{\sigma _{ij}}}$ ，即位错运动的阻力，可分为热激活部分和非热部分^{[74, 114]}：

$\sigma = {\sigma _{{\text{th}}}} + {\sigma _{\text{a}}}$

(81)

式中： ${\sigma _{\text{a}}}$ 为等效非热应力， ${\sigma _{{\text{th}}}}$ 为与应变、应变率和温度有关的等效热激活应力。

剪切应变率可以表示为运动位错密度及其变化率的函数^[120-121]:

$\dot \gamma=b\rho_{\rm{m}} v+b\dot \rho_{\rm{m}} l$

(82)

式中： $\dot \gamma$ 为塑性剪切应变率， ${\rho _{\text{m}}}$ 为运动位错密度，v为位错平均速度，l为位错平均间距。宏观尺度的塑性应变率张量 $\dot \varepsilon _{_{ij}}^{\text{p}}$ 可以表示为:

$\dot \varepsilon _{ij}^{\text{p}} = \dot \gamma {M_{ij}}$

(83)

式中： ${M_{ij}}$ 为对称施密特方向张量，定义为：

${M_{ij}} =\frac{1}{2}(n_i\otimes s_j+s_i\otimes n_j)$

(84)

式中：n和s分别为滑移方向的单位向量和滑移平面上的单位法向量。通过求解式(82)～(83)，可得等效塑性应变率为：

$\dot \varepsilon = \sqrt {\frac{2}{3}{{\dot \varepsilon }_{ij}}{{\dot \varepsilon }_{ij}}} = \tilde mb{\rho _{\text{m}}}v + \tilde mb{\dot \rho _{\text{m}}}l$

(85)

式中： $\tilde m = \sqrt {\dfrac{2}{3}{M_{ij}}{M_{ij}}}$ 为施密特取向因子。当运动位错密度假定为恒定时，式(84)将与Orowan方程相同。

为了描述运动位错密度的演化，Kubin等^[122]提出了如下方程：

$\frac{{{\text{d}}{\rho _{\text{m}}}}}{{{\text{d}}\varepsilon }} = \frac{{{C_1}}}{{{b^2}}} - {C_2}{\rho _{\text{m}}} - \frac{{{C_3}}}{b}\sqrt {{\rho _{\text{f}}}}$

(86)

式中：常数系数C₁与运动位错的增殖有关，常数系数C₂表示运动位错的相互湮灭和俘获，常数系数C₃表示运动位错通过与林位错的相互作用而被固定。林位错密度 ${\rho _{\text{f}}}$ 可以认为在高应变率下是恒定的。通过求解方程(86)，得到：

${\rho _{\text{m}}} = - \frac{{{C_5}\exp \left( { - {C_2}{\varepsilon _{\text{p}}}} \right)}}{{{C_2}}} + {C_4}$

(87)

式中： ${C_4} = \left( {\dfrac{{{C_1}}}{{{b^2}}} - \dfrac{{{C_3}\sqrt {{\rho _{\text{f}}}} }}{b}} \right)\Biggr/{C_2}$ 和C₅为常数。方程（87）可以进一步写成以下形式：

${\dot \rho _{\text{m}}} = {C_5}\exp \left( { - {C_2}\varepsilon } \right)\dot \varepsilon$

(88)

平均位错速度v可以通过热激活来确定，Bammann等^[121]提出了热激活形式的平均位错速度的一般表达式：

$v = {v_0}\exp \left( { - \frac{{G'}}{{kT}}} \right)$

(89)

式中：v₀为参考位错速度，k为玻尔兹曼常数， $G'$ 为吉布斯自由能， $G'$ 不仅与应力有关，还与温度和应变速率有关。Kocks^[123]将 $G'$ 与热流动应力联系起来，表达式如下：

$G' = {G'_0}{\left[ {1 - {{\left( {\frac{{{\sigma _{{\text{th}}}}}}{{{\sigma _{{\text{s0}}}}}}} \right)}^p}} \right]^q}$

(90)

式中： ${\sigma _{{\text{s0}}}}$ 为温度为0 K时的阈值应力， ${G'_0}$ 为温度为0 K时的参考吉布斯自由能。

利用式(85)～(89)，求解 $G'$ ，可得：

$G'=KT\left\{\ln \frac{B[1-D\exp (C\varepsilon)]}{1-A\exp(C\varepsilon)}-\ln\dot \varepsilon\right\}$

(91)

式中：C=−C₂和 $D = \dfrac{{{C_5}}}{{{C_2}{C_4}}}$ 为常数， $A = \tilde mbl{C_5}$ ， $B = \tilde mb{v_0}{C_4}$ 。考虑Ti-6Al-4V合金在拉伸和压缩时滑移系统的激活是不同的，因此，对于拉伸和压缩载荷情况，A和B的值不同，与应力状态有关。联立式(90)～(91)，可得热激活应力：

${\sigma _{{\text{th}}}} = {\sigma _{{\text{s0}}}}{\left\{ {1 - {{\left[ {\frac{{kT}}{{{G'_0}}}\left( {\ln \frac{{B\left( {1 - D\exp \left( {C\varepsilon } \right)} \right)}}{{1 - A\exp \left( {C\varepsilon } \right)}} - \ln \dot \varepsilon } \right)} \right]}^{1/q}}} \right\}^{1/p}}$

(92)

Hoge等^[124]建立了激活体积 $V_0^ *$ 与塑性应变的关系：

$V_0^ * = {\left( {a + b\varepsilon _{\text{p}}^m} \right)^{ - 1}}$

(93)

式中：a、b、m为材料常数。式(94)中的参考吉布斯自由能 ${G'_0}$ 可表示为^[125]：

${G'_0} = \hat \tau {V^ * } = \frac{1}{{\tilde m}}{\sigma _{{\text{s0}}}}V_0^ *$

(94)

联立式(93)～(94)，可得：

${\sigma _{{\text{s0}}}} = \frac{{\tilde m{G'_0}}}{{V_0^ * }} = \tilde m{G'_0}\left( {a + b{\varepsilon ^m}} \right) = {\sigma _0}\left( {1 + {K_1}{\varepsilon ^m}} \right)$

(95)

式中： ${\sigma _0}{\text{ = }}\tilde m{G'_0}a$ ， ${K_1} = b/a$ 。由于拉伸和压缩中激活的滑移系不同， ${\sigma _0}$ 的值也不同。

非热应力与温度和应变速率无关，它是由对位错的长程障碍的阻碍作用引起的，可表示为^[126-127]：

${\sigma _{\text{a}}} = {\sigma _{\text{G}}} + {\sigma _{\text{S}}} + {K_2}{\varepsilon ^n}$

(96)

式中： ${\sigma _{\text{G}}}$ 为初始缺陷引起的应力，K₂为应变硬化系数，n为应变硬化指数。 ${\sigma _{\text{S}}}$ 为由晶粒尺寸效应引起的应力。孪晶是LSF Ti-6Al-4V合金的变形机制之一，孪晶细化晶粒提高了晶粒的抗滑移性和加工硬化率。由于孪晶对应变速率和温度的敏感性很低，因此将孪晶对流动应力的贡献纳入到非热应力中^[127]。Meyers等^[128]提出，在大多数情况下，孪晶的粒度依赖性服从Hall-Petch关系，且孪晶的斜率大于滑移的斜率。因此， ${\sigma _{\text{S}}}$ 可以表示为：

${\sigma _{\text{S}}} = {k_{{d}}}{d^{ - 1/2}} + {k_{\lambda}}{\lambda ''^{ - 1/2}}$

(97)

式中：d为晶粒直径， $\lambda ''$ 为相邻孪晶界间的平均间距， ${k_{{d}}}$ 和 ${k_{\lambda}}$ 分别为斜率系数。Lu等^[129]考虑到孪晶界和晶界在相反位错运动中的相似作用，对于 ${V^{ * - 1}}$ 将Hall-Petch关系推广为同时包含晶界和孪晶界效应的公式：

${V^{ * - 1}} - V_1^{{ * - 1}} = {k_{{d}}}{d^{ - 1/2}} + {k_{\lambda}}{\lambda ''^{ - 1/2}}$

(98)

式中： ${V^ * }$ 为试验测量的表观活化体积， $V_1^ *$ 为与晶粒内或孪晶内位错机制有关的活化体积。如式(95)所示，根据激活体积与塑性应变相关，Gao等^[127]用幂函数 ${K_2}{\varepsilon ^n}$ 来表示激活体积，则非热应力可简化为：

${\sigma _{\text{a}}} = {\sigma _{\text{G}}} + {K_2}{\varepsilon ^n}$

(99)

结合式(83)～(84)、(91)、(94)、(98)，可以得到流动应力的关系式：

$\sigma = {\sigma _{\text{G}}} + {K_2}{\varepsilon ^n} + {\sigma _0}\left( {1 + {K_1}{\varepsilon ^m}} \right){\left\{ {1 - {{\left[ {\frac{{kT}}{{{G'_0}}}\left( {\ln \frac{{B\left( {1 - D\exp \left( {C\varepsilon } \right)} \right)}}{{1 - A\exp \left( {C\varepsilon } \right)}} - \ln \dot \varepsilon } \right)} \right]}^{1/q}}} \right\}^{1/p}}$

(100)

$T = {T_0} + \Delta T = {T_0} + \frac{\eta }{{\rho {C_{\text{V}}}}}\int_0^\varepsilon {\sigma {\text{d}}\varepsilon }$

(101)

(102)

式中： ${\sigma _{\text{G}}}$ 、n、 ${\sigma _0}$ 、K₁、K₂、m、 $K/{G'_0}$ 、A、B、C、D、p和q为本构关系参数。参数K、 ${\sigma _0}$ 、A和B的值在拉伸和压缩情况下不同，为此，可将其表示为Lode参数的指数函数^[115]：

$K = K'\exp \left[ { - {C_{\text{K}}}\left( {L + 1} \right)} \right]$

(103)

${\sigma _0} = {\sigma '_0}\exp \left[ { - {C_{{\sigma _0}}}\left( {L + 1} \right)} \right]$

(104)

$A = A'\exp \left[ { - {C_{\text{A}}}\left( {L + 1} \right)} \right]$

(105)

$B = B'\exp \left[ { - {C_{\text{B}}}\left( {L + 1} \right)} \right]$

(106)

式中： $K'$ 、 ${\sigma '_0}$ 、 $A'$ 、 $B'$ 、C_K、 ${C_{{\sigma _0}}}$ 、C_A和C_B为材料常数。

图15为所建立的金属热黏塑性本构关系的预测结果与不同温度和应变率下LSF Ti-6Al-4V拉伸和压缩应力-应变曲线的对比，可以看出，所建立的考虑拉/压不对称行为的金属热黏塑性本构关系可以很好地描述LSF Ti-6Al-4V拉伸和压缩塑性流动行为。

图 15 考虑拉压不对称行为的金属热黏塑性本构关系预测结果与试验结果的对比

Figure 15. Comparison between the predicted and experimental results of thermo-viscoplastic constitutive relationships of metal considering the asymmetrical behavior of tension and compression

下载: 全尺寸图片幻灯片

5. 总　结

热黏塑性本构关系能够描述最普遍情况下金属材料的变形行为，可预测金属材料在一定的温度和应变率范围内的塑性流动行为。传统唯象本构关系缺乏对物理机制的足够认识，所以无法准确描述材料塑性变形与微观结构演化的关系；而物理型本构关系考虑了材料在变形过程中的热变形机理。此外，由位错及其相互作用引起的加工硬化和温度升高引起的动态软化将导致热变形过程中特有的变形机制，所以能充分地描述这两种效应在金属热黏塑性本构关系中的作用，也是一个重要的研究领域。

由于第三型应变时效引起的反常应力峰、K-W锁位错结构引起的反常应力峰以及拉压不对称行为的出现，使得常见的金属热黏塑性本构关系不再适用。为此，学者们针对3种现象的微观机理、宏观特征等建立了考虑这3种反常行为的金属热黏塑性本构关系，进一步完善了金属热黏塑性本构关系。

图 1 不同应变率下93W-Ni-Fe的流动应力随温度的变化曲线^[4]

Figure 1. Flow stress-temperature curves of 93W-Ni-Fe at different strain rates^[4]

下载: 全尺寸图片幻灯片

图 2 不同应变率下，流动应力随温度变化的模型预测结果与试验结果比较^[23]

Figure 2. Comparison of model predictions and experimental results of flow stress variation with temperature at different strain rates^[23]

下载: 全尺寸图片幻灯片

图 3 试验应力-应变曲线与修正的J-C本构关系预测结果的比较^[27]

Figure 3. Comparison betwwen experimental stress-strain curves with MJC model predictions^[27]

下载: 全尺寸图片幻灯片

图 4 不同应变率下，Ti-6Al-4V(296 K)的准静态和动态加载试验结果与K-H-L和J-C本构关系预测结果的比较^[13]

Figure 4. Quasi-static and dynamic loading experimental results of Ti-6Al-4V (at a temperature of 296 K) for different strain rates with correlations using K-H-L and J-C models^[13]

下载: 全尺寸图片幻灯片

图 5 不同晶粒尺寸纳米晶铝在不同应变率下的流动应力-应变试验结果与K-H-L本构关系预测结果^[38]

Figure 5. Observed and calculated responses for nanocrystalline aluminium at different strain rates by using KHL model for various grain sizes^[38]

下载: 全尺寸图片幻灯片

图 6 不同温度和应变率下铜的真实应力-真实应变曲线与预测结果的对比^[41]

Figure 6. Comparison of true stress - true strain curves and model predictions for copper at different temperatures and strain rates^[41]

下载: 全尺寸图片幻灯片

图 7 30CrMnSiA热软化情况的理论和试验值的比较^[44]

Figure 7. Comparison between theoretical and experimental values on thermal softening of 30CrMnSiA^[44]

下载: 全尺寸图片幻灯片

图 8 Sn60Pb40合金的计算结果与试验结果的比较^[45]

Figure 8. Comparison of calculated results and experimental results for Sn60Pb40 alloy^[45]

下载: 全尺寸图片幻灯片

图 9 不同应变率和温度下，退火OFHC铜的N-N-L本构关系预测结果与试验结果的比较^[57]

Figure 9. Comparison of model prediction predictions with experimental results for annealed OFHC copperat different strain rates and temperatures using N-N-L constitutive model^[57]

下载: 全尺寸图片幻灯片

图 10 不同应变率下N-N-L模型预测与试验结果的比较^[58]

Figure 10. Comparison between N-N-L model predictions with experimental results at different strain rate^[58]

下载: 全尺寸图片幻灯片

图 11 用M-R-K本构关系描述的流动应力随塑性应变的变化^[65]

Figure 11. Change of the flow stress with plastic strain described using the M-R-K model^[65]

下载: 全尺寸图片幻灯片

图 12 DH36钢流动应力随温度变化曲线上出现的反常应力峰^[71]

Figure 12. Anomalous stress peaks in the flow stress curves of DH36 steel with temperature^[71]

下载: 全尺寸图片幻灯片

图 13 镍基高温合金的拉伸强度随温度的变化^[97-98]

Figure 13. Tensile strength of nickel base superalloy as a function of temperature^[97-98]

下载: 全尺寸图片幻灯片

图 14 高温合金K403在不同应变率下的流动应力随温度的变化

Figure 14. Flow stress of superalloy K403 as function of temperature at different strain rates

下载: 全尺寸图片幻灯片

图 15 考虑拉压不对称行为的金属热黏塑性本构关系预测结果与试验结果的对比

Figure 15. Comparison between the predicted and experimental results of thermo-viscoplastic constitutive relationships of metal considering the asymmetrical behavior of tension and compression

下载: 全尺寸图片幻灯片

表 1 唯象型本构关系的模型对比

Table 1. Comparison of phenomenological constitutive relations

本构关系	年份	模型	应变率范围/s⁻¹	主要特征
J-C	1983	Johnson-Cook^[20]	>10⁴	（1）形式简单，材料常数容易获得（2）考虑了应变率效应（3）考虑了温度效应（4）不能准确描述流动应力随对数应变率呈非线性关系的金属材料的塑性流动行为的应变率敏感性（5）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	1991	Holmquist^[24]	10⁻³～500	（1）应变率项修正为幂函数（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象（3）对高应变率范围内的应变率敏感性的加强描述依旧有限
	1998	Rule-Jones^[25]	>10³	（1）高速率情况下，可以更好地描述应变率敏感性的作用（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	1999	Kang-Cho^[26]	10⁻³～5000	（1）应变率项中引入了对数应变率的二次型项（2）不能描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象（3）对高应变率范围内的应变率敏感性的加强描述依旧有限
	2009	Vural-Cairo^[27]	10⁻²～10⁴	（1）在应变和应变率项中加入了温度效应（2）可以描述对于金属塑性流动行为中的应变、应变率和温度对流动应力的影响为非独立的现象
	2010	Lin-Xia^[28]	10⁻²～10	（1）考虑温度和应变率耦合效应（2）应变项为抛物线形式
K-H	1992	Khan-Huang^[16]	10⁻⁵～10⁴	（1）考虑了应变率效应（2）假定依赖于J₂不变量（3）没有考虑温度效应
	2009	Yu-Guo^[35]	10⁻⁴～1.6×10³	没有考虑温度效应
	1999	Khan-Liang^[36]	10⁻⁶～10⁴	（1）考虑了应变率对应变硬化的影响。（2）应变率项为幂函数形式
	2000	Khan-Zhang^[37]	10⁻⁴～10³	（1）考虑了晶粒尺寸对金属流动应力的影响（2）考虑了应变率对应变硬化的影响（3）应变率项为幂函数形式
	2004	Farrokh-Khan^[38]	10⁻⁴～10³	（1）可以描述晶粒细化引起的不同多晶金属的塑性流动行为（2）考虑了应变率对应变硬化的影响（3）应变率项为幂函数形式
其他	1976	Voce-Kocks^[39-40]	10	考虑温度和应变率对饱和应力 ${\sigma _{\rm{s}}}$ 的影响
其他	2005	Molinari-Ravichandran^[41]	10⁻³～8.5×10⁴	考虑了微观结构的演化

下载: 导出CSV

表 2 唯象型本构关系的方程形式

Table 2. Equations of phenomenological constitutive relationships relations

模型	方程形式
Johnson-Cook^[20]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\left( {1 - {T^{ * m}}} \right)$
Holmquist^[24]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left( {{{\dot \varepsilon }^{ * C}}} \right)\left( {1 - {T^{ * m}}} \right)$
Rule-Jones^[25]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + C\ln {{\dot \varepsilon }^ * } + {C_4}\left( {\dfrac{1}{{{C_5} - \ln {{\dot \varepsilon }^ * }}} - \dfrac{1}{{{C_5}}}} \right)} \right]\left( {1 - {T^{ * m}}} \right)$
Kang-Cho^[26]	$\sigma = \left( {A + B{\varepsilon ^n}} \right)\left[ {1 + {C_1}\ln {{\dot \varepsilon }^ * } + {C_2}{{\left( {\ln {{\dot \varepsilon }^ * }} \right)}^2}} \right]\left( {1 - {T^{ * m}}} \right)$
Vural-Cairo^[27]	$\sigma = \left\{ {A + {B_0}\left[ {1 - {{\left( {\dfrac{{T - {T_0}}}{{{T_{\text{m}}} - {T_0}}}} \right)}^p}} \right]{\varepsilon ^n}} \right\}\left[ {1 + \left( {{c_1}T_{\text{r}}^{ * p} + {c_2}H} \right)\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]\left[ {1 - {{\left( {\dfrac{{T - {T_0}}}{{{T_{\text{r}}} - {T_0}}}} \right)}^p}} \right]$
Lin-Xia^[28]	$\sigma = \left( {A + {B_1}\varepsilon + {B_2}{\varepsilon ^2}} \right)\left( {1 + C\ln {{\dot \varepsilon }^ * }} \right)\exp \left[ {\left( {{\lambda _1} + {\lambda _2}\ln {{\dot \varepsilon }^ * }} \right)\left( {T - {T_{\text{r}}}} \right)} \right]$
Khan-Huang^[16]	${J_2} = {f_1}\left( \varepsilon \right){f_2}\left( {D_2^{\text{p}}} \right)$
Yu-Guo^[35]	$\sigma = f\left( {\varepsilon ,\dot \varepsilon } \right) = {\sigma _0}{\hat f_2}\left( {\dot \varepsilon } \right) + {E_\infty }\varepsilon - a{{\text{e}}^{ - \alpha \varepsilon }}$
Khan-Liang^[36]	$\sigma = \left[ {A + B{ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right)}^{ {n_1} } }{\varepsilon ^{ {n_0} } } } \right]\left( {1 - {T^{*m} } } \right){\dot \varepsilon ^C}$
Khan-Zhang^[37]	$\sigma = \left[ { \left({a{}_1 + \dfrac{ { {k_1} } }{ {\sqrt d } } }\right) + B{ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right)}^{ {n_1} } }{\varepsilon ^{ {n_0} } } } \right]\left( {1 - {T^{ * m} } } \right){\dot \varepsilon ^C}$
Farrokh-Khan^[38]	$\sigma {\text{ = } }\left\{ {\left( { {a_1} + \dfrac{ { {k_1} } }{ {\sqrt d } } } \right) + B{ {\left( {\dfrac{d}{ { {d_0} } } } \right)}^{ {n_2} } }{ {\left[ {\left( {1 - \dfrac{ {\ln {\dot \varepsilon } } }{ {\ln {D_0^{\text{p} } } } } } \right) {\dfrac{ { {T_{\text{m} } } } }{T} } } \right]}^{ {n_1} } }{ {\left( \varepsilon \right)}^{ {n_0} } } } \right\}{\left( {\dfrac{ { {T_{\text{m} } } - T} }{ { {T_{\text{m} } } - {T_{\text{r} } } } } } \right)^m}{\left( {\dfrac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }^ * } } } } \right)^C}$
Voce-Kocks^[39-40]	$\sigma = {\sigma _{\text{s}}} + \left[ {\left( {{\sigma _0} - {\sigma _{\text{s}}}} \right)\exp \left( { - \dfrac{\varepsilon }{{{\varepsilon _{\text{r}}}}}} \right)} \right]$
Molinari-Ravichandran^[41]	$\dfrac{ { {\delta _{\text{r} } } } }{ { {\delta _{ {\text{r0} } } } } } = {\left[ {1 - { {\left( { {k_{\text{r} } } {\dfrac{T}{ { {T_{ {\text{r0} } } } } } } \lg {\dfrac{ { { {\dot \varepsilon }_{ {\text{r0} } } } } }{ {\dot \varepsilon } } } } \right)}^{ {p_{\text{r} } } } } } \right]^{ {q_{\text{r} } } } }\text{，}\dfrac{ { {\delta _{\text{s} } } } }{ { {\delta _{ {\text{s0} } } } } } = \dfrac{1}{ { { {\left[ {1 - { {\left( { {k_{\text{s} } } {\dfrac{T}{ { {T_{ {\text{s0} } } } } } } \lg {\dfrac{ { { {\dot \varepsilon }_{ {\text{r0} } } } } }{ {\dot \varepsilon } } } } \right)}^{ {p_{\text{s} } } } } } \right] }^{ {q_{\text{s} } } } } } }$

下载: 导出CSV

表 3 物理概念本构关系的模型对比

Table 3. Comparison of physically based constitutive relations

本构关系	年份	模型	应变率范围/s⁻¹	本构关系的主要特征
B-P	1975	Bodner-Partom^[18]	10⁻³～1	（1）将材料的总变形率分为弹性和塑性两部分（2）通过塑性功项合并应变硬化效应（3）没有考虑温度效应
Z-A	1987	Zerilli-Armstrong^[17]	4×10³	（1）考虑了晶粒尺寸的影响（2）基于热激活理论
	2009	Zhang-Wen^[48]	10⁻⁵～10⁻²	考虑了温度、应变率和变形过程对Z-A模型中参数的影响
	2009	Samantaray-Mandal^[49]	10⁻³～1	考虑了温度与应变、温度与应变率的耦合效应对流动应力的影响
	2005	Abed-Voyiadjis^[50]	10⁻⁴～10⁴	（1）可用于预测等温和绝热塑性变形的应力应变曲线（2）将模型参数准确的与微观结构物理参数联系起来
M-T-S	1988	Follansbee^[10,51]	10⁻⁴～10⁴	（1）认为应变率敏感性的上升应归因于结构演化的速率敏感性（2）考虑了阈值应力
N-N-L	1998	Nemat-Nasser-Li^[57]	10⁻³～10⁴	考虑了位错密度随应变和温度的变化
其他	2001	Rusinek-Klepaczko^[61,62]	10⁻⁴～10³	考虑了应变率历史效应对金属材料塑性流动行为的影响
	2009	Rusinek-Rodrguez-Martnez^[63]	10⁻⁴～10⁴	（1）添加一个第三项来扩展该本构关系的应用范围（2）考虑负应变率敏感性和粘性阻力
	2010	Sung^[66]	10⁻³～10	通过Hollomon和Voce应变硬化方程的线性组合来揭示应变硬化率的温度敏感
	2010	Gao-Zhang^[67]	10⁻³～10⁴	考虑FCC金属变形过程中微观结构的演变建立阈值应力与应变、温度和应变率的关系

下载: 导出CSV

表 4 物理概念本构关系的方程形式

Table 4. Equations of physically based constitutive relations

模型	方程形式
Bodner-Partom^[18]	$D_2^{\text{p}} = D_0^2\exp \left[ { - \left( {\dfrac{{n + 1}}{n}} \right){{\left( {\dfrac{{{Z^2}}}{{3{J_2}}}} \right)}^n}} \right]$
Zerilli-Armstrong^[17]	对于FCC: $\sigma = {\sigma _{\text{a}}} + B{\varepsilon ^{1/2}}\exp \left( { - \alpha T} \right)$ 和 $\alpha {\text{ = }}{\alpha _0} - {\alpha _1}\ln \dot \varepsilon$ 对于BCC： $\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^n}$ 和 $\beta {\text{ = }}{\beta _0} - {\beta _1}\ln \dot \varepsilon$ 对于HCP： $\sigma = {\sigma _{\text{a}}} + B\exp \left( { - \beta T} \right) + {B_0}{\varepsilon ^{^{1/2}}}\exp \left( { - \alpha T} \right)$
Zhang-Wen^[48]	对于FCC： $\sigma = {\sigma _{\text{a}}} + {C_1}{\varepsilon ^{1/2}}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\}$ 对于BCC： $\sigma = {\sigma _{\text{a}}} + {C_2}\exp \left\{ {\left[ { - {C''_3}T + {C'_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{r\left( \varepsilon \right)r\left( {\dot \varepsilon } \right)}}} \right)} \right]H\left( T \right)} \right\} + {C_5}{\varepsilon ^n}$
Samantaray-Mandal^[49]	$\sigma = \left( {{C_1} + {C_2}{\varepsilon ^n}} \right)\exp \left[ { - \left( {{C_3} + {C_4}\varepsilon } \right){T^ * } + \left( {{C_5} + {C_6}{T^ * }} \right)\ln {{\dot \varepsilon }^ * }} \right]$
Abed-Voyiadjis^[50]	对于FCC： $\sigma = {C_2}{\varepsilon ^{0.5}}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_6}$ 和 $X = {C_4}T\ln \left( {1/{{\dot \varepsilon }^ * }} \right)$ 对于BCC： $\sigma = {C_1}\left( {1 - {X^{1/2}} - X + {X^{3/2}}} \right) + {C_5}{\varepsilon ^n} + {C_6}$
Follansbee^[10,51]	$\sigma = {\sigma _{\text{a}}} + \left( {\hat \sigma - {\sigma _{\text{a}}}} \right){\left[ {1 - {{\left( {\dfrac{{kT}}{{{g_0}\mu {b^3}}}\ln \dfrac{{{{\dot \varepsilon }_0}}}{{\dot \varepsilon }}} \right)}^{1/q}}} \right]^{1/p}}$
Nemat-Nasser-Li^[57]	$\sigma \left( {\dot \varepsilon ,\varepsilon ,T} \right) = {\sigma ^0}{\left\{ {1 - {{\left[ { - \dfrac{{kT}}{{{G'_0}}}\left( {\ln \dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}} + \ln \left( {1 + a\left( T \right){\varepsilon ^{1/2}}} \right)} \right)} \right]}^{\tfrac{1}{2}}}} \right\}^{\tfrac{3}{2}}}\left[ {1 + a\left( T \right){\varepsilon ^{\tfrac{1}{2}}}} \right] + \sigma _{\text{a}}^0{\varepsilon ^{{n_1}}}$
Rusinek-Klepaczko^[61,62]	$\sigma = \dfrac{{E\left( T \right)}}{{{E_0}}}\left[ {{B_0}\theta _{\text{m}}^{ - v}{{\left( {{\varepsilon _0} + {\varepsilon _{\text{p}}}} \right)}^{n\left( {1 - {D_2}{\theta _n}} \right)}} + \sigma _0^*{{\left( {1 - {D_1}{\theta _{\text{m}}}} \right)}^m}} \right]$
Rusinek-Rodrguez-Martnez^[63]	${\sigma _{{\text{ns}}}}\left( {\dot \varepsilon ,T} \right) = \sigma _0^{{\text{ns}}} \left[ {\lg \left( {\dfrac{{{{\dot \varepsilon }_{{\text{trans}}}}}}{{\dot \varepsilon }}} \right)} \right] \left[ {1 - {D_3}\left( {\dfrac{{{T_{\text{m}}}}}{T}} \right)\lg \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\max }}}}} \right)} \right]$
Sung^[66]	$\sigma = \sigma \left( {\varepsilon ,\dot \varepsilon ,T} \right) = f\left( {\varepsilon ,T} \right)g\left( {\dot \varepsilon } \right)h\left( T \right)$
Gao-Zhang^[67]	$\sigma {\text{ = }}{\sigma _{\text{a}}} + \hat Y{\varepsilon ^n}\exp \left[ {{c_3}T\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{{\text{s0}}}}}}} \right)} \right]{\left\{ {1 - {{\left[ { - {c_4}T\ln \left( {\dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)} \right]}^{1/q}}} \right\}^{1/p}}$

下载: 导出CSV

参考文献(129)

[1]	李永池, 谭福利, 姚磊, 等. 含损伤材料的热粘塑性本构关系及其应用 [J]. 爆炸与冲击, 2004, 24(4): 289–298. LI Y C, TAN F L, YAO L, et al. Thermo-viscoplastic constitutive relation of damaged materials with application [J]. Explosion and Shock Waves, 2004, 24(4): 289–298.
[2]	REMINGTON B A, BAZAN G, BELAK J, et al. Materials science under extreme conditions of pressure and strain rate [J]. Metallurgical and Materials Transactions A, 2004, 35(9): 2587–2607. DOI: 10.1007/s11661-004-0205-6.
[3]	王建军. 典型金属塑性流动中反常应力峰及其本构关系 [D]. 西安: 西北工业大学, 2017: 47–100. DOI: 10.7666/d.D01601051. WANG J J. Anomalous stress peak in the plastic flow of typical metals and its constitutive model [D]. Xi’an: Northwestern Polytechnical University, 2017: 47–100. DOI: 10.7666/d.D01601051.
[4]	CHENG J Y, NEMAT-NASSER S, GUO W G. A unified constitutive model for strain-rate and temperature dependent behavior of molybdenum [J]. Mechanics of Materials, 2001, 33(11): 603–616. DOI: 10.1016/S0167-6636(01)00076-X.
[5]	SEIDT J D, GILAT A. Plastic deformation of 2024-T351 aluminum plate over a wide range of loading conditions [J]. International Journal of Solids and Structures, 2013, 50(10): 1781–1790. DOI: 10.1016/j.ijsolstr.2013.02.006.
[6]	WIERZBICKI T, BAO Y B, LEE Y W, et al. Calibration and evaluation of seven fracture models [J]. International Journal of Mechanical Sciences, 2005, 47(4/5): 719–743. DOI: 10.1016/j.ijmecsci.2005.03.003.
[7]	WILKINS M L, STREIT R D, REAUGH J E. Cumulative-strain-damage model of ductile fracture: simulation and prediction of engineering fracture tests [R]. San Leandro: Lawrence Livermore National Laboratory, 1980. DOI: 10.2172/6628920.
[8]	GILIOLI A, MANES A, GIGLIO M, et al. Predicting ballistic impact failure of aluminium 6061-T6 with the rate-independent Bao-Wierzbicki fracture model [J]. International Journal of Impact Engineering, 2015, 76: 207–220. DOI: 10.1016/j.ijimpeng.2014.10.004.
[9]	BAIG M, KHAN A S, CHOI S H, et al. Shear and multiaxial responses of oxygen free high conductivity (OFHC) copper over wide range of strain-rates and temperatures and constitutive modeling [J]. International Journal of Plasticity, 2013, 40: 65–80. DOI: 10.1016/j.ijplas.2012.07.004.
[10]	FOLLANSBEE P S, KOCKS U F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable [J]. Acta Metallurgica, 1988, 36(1): 81–93. DOI: 10.1016/0001-6160(88)90030-2.
[11]	JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceedings of the 7th International Symposium on Ballistics. The Hague, Netherlands, 1983: 541–547.
[12]	JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. DOI: 10.1016/0013-7944(85)90052-9.
[13]	KHAN A S, SUH Y S, KAZMI R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys [J]. International Journal of Plasticity, 2004, 20(12): 2233–2248. DOI: 10.1016/j.ijplas.2003.06.005.
[14]	NEMAT-NASSER S, GUO W G, NESTERENKO V F, et al. Dynamic response of conventional and hot isostatically pressed Ti-6Al-4V alloys: experiments and modeling [J]. Mechanics of Materials, 2001, 33(8): 425–439. DOI: 10.1016/S0167-6636(01)00063-1.
[15]	LIANG R Q, KHAN A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures [J]. International Journal of Plasticity, 1999, 15(9): 963–980. DOI: 10.1016/S0749-6419(99)00021-2.
[16]	KHAN A S, HUANG S J. Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10⁻⁵−10⁴ s⁻¹ [J]. International Journal of Plasticity, 1992, 8(4): 397–424. DOI: 10.1016/0749-6419(92)90057-J.
[17]	ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825. DOI: 10.1063/1.338024.
[18]	BODNER S R, PARTOM Y. Constitutive equations for elastic-viscoplastic strain-hardening materials [J]. Journal of Applied Mechanics, 1975, 42(2): 385–389. DOI: 10.1115/1.3423586.
[19]	王礼立. 冲击动力学进展 [M]. 合肥: 中国科学技术大学出版社, 1992: 58–87.
[20]	LEMAITRE J, CHABOCHE J L, MAJI A K. Mechanics of Solid Materials [J]. Journal of Engineering Mechanics, 1993, 119(3): 642–643. DOI: 10.1061/(ASCE)0733-9399(1993)119:3(642.2).
[21]	SALVADO F C, TEIXEIRA-DIAS F, WALLEY S M, et al. A review on the strain rate dependency of the dynamic viscoplastic response of FCC metals [J]. Progress in Materials Science, 2017, 88: 186–231. DOI: 10.1016/j.pmatsci.2017.04.004.
[22]	GAMBIRASIO L, RIZZI E. An enhanced Johnson-Cook strength model for splitting strain rate and temperature effects on lower yield stress and plastic flow [J]. Computational Materials Science, 2016, 113: 231–265. DOI: 10.1016/j.commatsci.2015.11.034.
[23]	WANG J J, GUO W G, LI P H, et al. Modified Johnson-Cook description of wide temperature and strain rate measurements made on a nickel-base superalloy [J]. Materials at High Temperatures, 2017, 34(3): 157–165. DOI: 10.1080/09603409.2016.1252164.
[24]	HOLMQUIST T J, JOHNSON G R. Determination of constants and comparison of results for various constitutive models [J]. Journal de Physique Ⅳ, 1991, 1(C3): 853–860. DOI: 10.1051/jp4:19913119.
[25]	RULE W K, JONES S E. A revised form for the Johnson-Cook strength model [J]. International Journal of Impact Engineering, 1998, 21(8): 609–624. DOI: 10.1016/S0734-743X(97)00081-X.
[26]	KANG W J, CHO S S, HUH H, et al. Modified Johnson-Cook model for vehicle body crashworthiness simulation [J]. International Journal of Vehicle Design, 1999, 21(4/5): 424–435. DOI: 10.1504/ijvd.1999.005594.
[27]	VURAL M, CARO J. Experimental analysis and constitutive modeling for the newly developed 2139-T8 alloy [J]. Materials Science and Engineering:A, 2009, 520(1/2): 56–65. DOI: 10.1016/j.msea.2009.05.026.
[28]	LIN Y C, XIA Y C, CHEN X M, et al. Constitutive descriptions for hot compressed 2124-T851 aluminum alloy over a wide range of temperature and strain rate [J]. Computational Materials Science, 2010, 50(1): 227–233. DOI: 10.1016/j.commatsci.2010.08.003.
[29]	LIN Y C, CHEN X M, LIU G. A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel [J]. Materials Science and Engineering: A, 2010, 527(26): 6980–6986. DOI: 10.1016/j.msea.2010.07.061.
[30]	SHIN H, KIM J B. A phenomenological constitutive equation to describe various flow stress behaviors of materials in wide strain rate and temperature regimes [J]. Journal of Engineering Materials and Technology, 2010, 132(2): 021009. DOI: 10.1115/1.4000225.
[31]	WANG Y, ZHOU Y X, XIA Y M. A constitutive description of tensile behavior for brass over a wide range of strain rates [J]. Materials Science and Engineering: A, 2004, 372(1/2): 186–190. DOI: 10.1016/j.msea.2003.12.009.
[32]	HOU Q Y, WANG J T. A modified Johnson-Cook constitutive model for Mg-Gd-Y alloy extended to a wide range of temperatures [J]. Computational Materials Science, 2010, 50(1): 147–152. DOI: 10.1016/j.commatsci.2010.07.018.
[33]	DOU W, XU Z J, HU H Z, et al. A generalized plasticity model incorporating stress state, strain rate and temperature effects [J]. International Journal of Impact Engineering, 2021, 155: 103897. DOI: 10.1016/j.ijimpeng.2021.103897.
[34]	刘旭红, 黄西成, 陈裕泽, 等. 强动载荷下金属材料塑性变形本构模型评述 [J]. 力学进展, 2007, 37(3): 361–374. DOI: 10.3321/j.issn:1000-0992.2007.03.004. LIU X H, HUANG X C, CHEN Y Z, et al. A review on constitutive models for plastic deformation of metal materials under dynamic loading [J]. Advances in Mechanics, 2007, 37(3): 361–374. DOI: 10.3321/j.issn:1000-0992.2007.03.004.
[35]	YU H D, GUO Y J, ZHANG K Z, et al. Constitutive model on the description of plastic behavior of DP600 steel at strain rate from 10⁻⁴ to 10³ s⁻¹ [J]. Computational Materials Science, 2009, 46(1): 36–41. DOI: 10.1016/j.commatsci.2009.01.025.
[36]	KHAN A S, LIANG R Q. Behaviors of three BCC metal over a wide range of strain rates and temperatures: experiments and modeling [J]. International Journal of Plasticity, 1999, 15(10): 1089–1109. DOI: 10.1016/S0749-6419(99)00030-3.
[37]	KHAN A S, ZHANG H Y, TAKACS L. Mechanical response and modeling of fully compacted nanocrystalline iron and copper [J]. International Journal of Plasticity, 2000, 16(12): 1459–1476. DOI: 10.1016/S0749-6419(00)00023-1.
[38]	FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: synthesis, experiment, and constitutive modeling [J]. International Journal of Plasticity, 2009, 25(5): 715–732. DOI: 10.1016/j.ijplas.2008.08.001.
[39]	VOCE E. The relationship between stress and strain for homogeneous deformation [J]. Journal of the Institute of Metals, 1948, 74: 537–562.
[40]	KOCKS U F. Laws for work-hardening and low-temperature creep [J]. Journal of Engineering Materials and Technology, 1976, 98(1): 76–85. DOI: 10.1115/1.3443340.
[41]	MOLINARI A, RAVICHANDRAN G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length [J]. Mechanics of Materials, 2005, 37(7): 737–752. DOI: 10.1016/j.mechmat.2004.07.005.
[42]	NADERI M, DURRENBERGER L, MOLINARI A, et al. Constitutive relationships for 22MnB5 boron steel deformed isothermally at high temperatures [J]. Materials Science and Engineering: A, 2008, 478(1/2): 130–139. DOI: 10.1016/j.msea.2007.05.094.
[43]	HUANG S, KHAN A S. Modeling the mechanical behaviour of 1100-0 aluminum at different strain rates by the bodner-partom model [J]. International Journal of Plasticity, 1992, 8(5): 501–517. DOI: 10.1016/0749-6419(92)90028-B.
[44]	CHEN S Y, HUANG C G, WANG C K, et al. Mechanical properties and constitutive relationships of 30CrMnSiA steel heated at high rate [J]. Materials Science and Engineering: A, 2008, 483/484: 105–108. DOI: 10.1016/j.msea.2006.09.132.
[45]	马鑫, 王莉, 方洪渊, 等. Sn-Pb共晶钎料合金的Bodner-Partom本构方程 [J]. 应用力学学报, 1998, 15(2): 89–92; 148. MA X, WANG L, FANG H Y, et al. Viscoplastic constitutive equations for Tin-Lead eutectic solder alloy [J]. Chinese Journal of Applied Mechanics, 1998, 15(2): 89–92; 148.
[46]	HOLT W H, MOCK JR W, ZERILLI F J, et al. Experimental and computational study of the impact deformation of titanium Taylor cylinder specimens [J]. Mechanics of Materials, 1994, 17(2/3): 195–201. DOI: 10.1016/0167-6636(94)90059-0.
[47]	ZERILLI F J, ARMSTRONG R W. Constitutive equation for HCP metals and high strength alloy steels [C]//ASME International Mechanical Engineering Congress and Exposition. San Francisco, CA: ASME, 1995.
[48]	ZHANG H J, WEN W D, CUI H T, et al. A modified Zerilli-Armstrong model for alloy IC10 over a wide range of temperatures and strain rates [J]. Materials Science and Engineering: A, 2009, 527(1/2): 328–333. DOI: 10.1016/j.msea.2009.08.008.
[49]	SAMANTARAY D, MANDAL S, BORAH U, et al. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel [J]. Materials Science and Engineering: A, 2009, 526(1/2): 1–6. DOI: 10.1016/j.msea.2009.08.009.
[50]	ABED F H, VOYIADJIS G Z. A consistent modified Zerilli-Armstrong flow stress model for BCC and FCC metals for elevated temperatures [J]. Acta Mechanica, 2005, 175(1): 1–18. DOI: 10.1007/s00707-004-0203-1.
[51]	CHAWLA K K. Metallurgical applications of shock-wave and high-strain-rate phenomena: L. E. Murr, K. P. Staudhammer, and M. A. Meyers (eds. ), (Marcel Dekker, New York, 1986), 1120 pages, $145.00 [J]. Metallography, 1987, 20(2): 249–250. DOI: 10.1016/0026-0800(87)90034-6.
[52]	FOLLANSBEE P S. Recent results and continued development of the MTS (mechanical threshold stress) model [R]. Los Alamos: Los Alamos National Laboratory, 1988.
[53]	DARIDON L, OUSSOUADDI O, AHZI S. Influence of the material constitutive models on the adiabatic shear band spacing: MTS, power law and Johnson-Cook models [J]. International Journal of Solids and Structures, 2004, 41(11/12): 3109–3124. DOI: 10.1016/j.ijsolstr.2004.01.008.
[54]	BANERJEE B. The mechanical threshold stress model for various tempers of AISI 4340 steel [J]. International Journal of Solids and Structures, 2007, 44(3/4): 834–859. DOI: 10.1016/j.ijsolstr.2006.05.022.
[55]	MAUDLIN P J, DAVIDSON R F, HENNINGER R J. Implementation and assessment of the mechanical-threshold-stress model using the EPIC2 and PINON computer codes [R]. Los Alamos: Los Alamos National Laboratory, 1990. DOI: 10.2172/6537785.
[56]	NEMAT-NASSER S, ISAACS J B. Direct measurement of isothermal flow stress of metals at elevated temperatures and high strain rates with application to Ta and Ta-W alloys [J]. Acta Materialia, 1997, 45(3): 907–919. DOI: 10.1016/S1359-6454(96)00243-1.
[57]	NEMAT-NASSER S, LI Y L. Flow stress of f. c. c. polycrystals with application to OFHC Cu [J]. Acta Materialia, 1998, 46(2): 565–577. DOI: 10.1016/S1359-6454(97)00230-9.
[58]	GUO W G, ZHANG X Q, SU J, et al. The characteristics of plastic flow and a physically-based model for 3003 Al-Mn alloy upon a wide range of strain rates and temperatures [J]. European Journal of Mechanics—A/Solids, 2011, 30(1): 54–62. DOI: 10.1016/j.euromechsol.2010.09.001.
[59]	NEMAT-NASSER S, GUO W G, LIU M Q. Experimentally-based micromechanical modeling of dynamic response of molybdenum [J]. Scripta Materialia, 1999, 40(7): 859–872. DOI: 10.1016/S1359-6462(99)00041-X.
[60]	NEMAT-NASSER S, GUO W G, CHENG J Y. Mechanical properties and deformation mechanisms of a commercially pure titanium [J]. Acta Materialia, 1999, 47(13): 3705–3720. DOI: 10.1016/S1359-6454(99)00203-7.
[61]	RUSINEK A, KLEPACZKO J R. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress [J]. International Journal of Plasticity, 2001, 17(1): 87–115. DOI: 10.1016/S0749-6419(00)00020-6.
[62]	KLEPACZKO J. Thermally activated flow and strain rate history effects for some polycrystalline f. c. c. metals [J]. Materials Science and Engineering, 1975, 18(1): 121–135. DOI: 10.1016/0025-5416(75)90078-6.
[63]	RUSINEK A, RODRÍGUEZ-MARTÍNEZ J A. Thermo-viscoplastic constitutive relation for aluminium alloys, modeling of negative strain rate sensitivity and viscous drag effects [J]. Materials & Design, 2009, 30(10): 4377–4390. DOI: 10.1016/j.matdes.2009.04.011.
[64]	RUSINEK A, RODRÍGUEZ-MARTÍNEZ J A, ARIAS A. A thermo-viscoplastic constitutive model for FCC metals with application to OFHC copper [J]. International Journal of Mechanical Sciences, 2010, 52(2): 120–135. DOI: 10.1016/j.ijmecsci.2009.07.001.
[65]	VOYIADJIS G Z, ABED F H. Microstructural based models for BCC and FCC metals with temperature and strain rate dependency [J]. Mechanics of Materials, 2005, 37(2/3): 355–378. DOI: 10.1016/j.mechmat.2004.02.003.
[66]	SUNG J H, KIM J H, WAGONER R H. A plastic constitutive equation incorporating strain, strain-rate, and temperature [J]. International Journal of Plasticity, 2010, 26(12): 1746–1771. DOI: 10.1016/j.ijplas.2010.02.005.
[67]	GAO C Y, ZHANG L C. A constitutive model for dynamic plasticity of FCC metals [J]. Materials Science and Engineering: A, 2010, 527(13/14): 3138–3143. DOI: 10.1016/j.msea.2010.01.083.
[68]	XU Z J, HUANG F L. Comparison of physically based constitutive models characterizing armor steel over wide temperature and strain rate ranges [J]. Modelling and Simulation in Materials Science and Engineering, 2012, 20(1): 015005. DOI: 10.1088/0965-0393/20/1/015005.
[69]	XU Z J, HUANG F L. Comparison of constitutive models for FCC metals over wide temperature and strain rate ranges with application to pure copper [J]. International Journal of Impact Engineering, 2015, 79: 65–74. DOI: 10.1016/j.ijimpeng.2014.10.003.
[70]	XU Z J, HUANG F L. Thermomechanical behavior and constitutive modeling of tungsten-based composite over wide temperature and strain rate ranges [J]. International Journal of Plasticity, 2013, 40: 163–184. DOI: 10.1016/j.ijplas.2012.08.004.
[71]	NEMAT-NASSER S, GUO W G. Thermomechanical response of DH-36 structural steel over a wide range of strain rates and temperatures [J]. Mechanics of Materials, 2003, 35(11): 1023–1047. DOI: 10.1016/S0167-6636(02)00323-X.
[72]	NEMAT-NASSER S, GUO W G. Thermomechanical response of HSLA-65 steel plates: experiments and modeling [J]. Mechanics of Materials, 2005, 37(2/3): 379–405. DOI: 10.1016/j.mechmat.2003.08.017.
[73]	郭伟国, 左红星, 孟卫华, 等. 第三种应变时效与机械波谱关联性探讨 [J]. 材料科学与工艺, 2012, 20(1): 128–134. DOI: 10.11951/j.issn.1005-0299.20120126. GUO W G, ZUO H X, MENG W H, et al. Discussion of the relevancy of the third-type strain aging and mechanical spectroscopy [J]. Materials Science and Technology, 2012, 20(1): 128–134. DOI: 10.11951/j.issn.1005-0299.20120126.
[74]	WANG J J, GUO W G, GAO X S, et al. The third-type of strain aging and the constitutive modeling of a Q235B steel over a wide range of temperatures and strain rates [J]. International Journal of Plasticity, 2015, 65: 85–107. DOI: 10.1016/j.ijplas.2014.08.017.
[75]	王建军, 袁康博, 张晓琼, 等. 第三型应变时效的提出与研究进展 [J]. 爆炸与冲击, 2021, 41(5): 051101. DOI: 10.11883/bzycj-2020-0422. WANG J J, YUAN K B, ZHANG X Q, et al. Proposition and research progress of the third-type strain aging [J]. Explosion and Shock Waves, 2021, 41(5): 051101. DOI: 10.11883/bzycj-2020-0422.
[76]	XIAO J Y, WANG J J, GUO W G, et al. The influence of heat treatment and strain rate on the third type strain ageing phenomenon [J]. Materials at High Temperatures, 2019, 36(2): 104–110. DOI: 10.1080/09603409.2018.1467108.
[77]	WEAVER M L, NOEBE R D, KAUFMAN M J. The influence of C and Si on the flow behavior of NiAl single crystals [J]. Scripta Materialia, 1996, 34(6): 941–948. DOI: 10.1016/1359-6462(95)00590-0.
[78]	VARADHAN S, BEAUDOIN A J, FRESSENGEAS C. Lattice incompatibility and strain-aging in single crystals [J]. Journal of the Mechanics and Physics of Solids, 2009, 57(10): 1733–1748. DOI: 10.1016/j.jmps.2009.06.007.
[79]	WEAVER M L, NOEBE R D, LEWANDOWSKI J J, et al. Observations of static strain-aging in polycrystalline NiAl [J]. Intermetallics, 1996, 4(7): 533–542. DOI: 10.1016/0966-9795(96)00040-4.
[80]	HONG S I. Influence of dynamic strain aging on the apparent activation volume for deformation [J]. Materials Science and Engineering, 1985, 76: 77–81. DOI: 10.1016/0025-5416(85)90082-5.
[81]	GILAT A, WU X R. Plastic deformation of 1020 steel over a wide range of strain rates and temperatures [J]. International Journal of Plasticity, 1997, 13(6/7): 611–632. DOI: 10.1016/S0749-6419(97)00028-4.
[82]	CHENG J Y, NEMAT-NASSER S. A model for experimentally-observed high-strain-rate dynamic strain aging in titanium [J]. Acta Materialia, 2000, 48(12): 3131–3144. DOI: 10.1016/S1359-6454(00)00124-5.
[83]	LEE K W, KIM S K, KIM K T, et al. Ductility and strain rate sensitivity of Zircaloy-4 nuclear fuel claddings [J]. Journal of Nuclear Materials, 2001, 295(1): 21–26. DOI: 10.1016/S0022-3115(01)00509-8.
[84]	LEE K O, LEE S B. Modeling of materials behavior at various temperatures of hot isostatically pressed superalloys [J]. Materials Science and Engineering: A, 2012, 541: 81–87. DOI: 10.1016/j.msea.2012.02.005.
[85]	GUO W G, GAO X S. On the constitutive modeling of a structural steel over a range of strain rates and temperatures [J]. Materials Science and Engineering: A, 2013, 561: 468–476. DOI: 10.1016/j.msea.2012.10.065.
[86]	SONG Y, VOYIADJIS G Z. Constitutive modeling of dynamic strain aging for HCP metals [J]. European Journal of Mechanics—A/Solids, 2020, 83: 104034. DOI: 10.1016/j.euromechsol.2020.104034.
[87]	郭扬波, 唐志平, 程经毅. 一种基于位错机制的动态应变时效模型 [J]. 固体力学学报, 2002, 23(3): 249–256. DOI: 10.3969/j.issn.0254-7805.2002.03.001. GUO Y B, TANG Z P, CHENG J Y. A dislocation-mechanics-based constitutive model for dynamic strain aging [J]. Acta Mechanica Solida Sinica, 2002, 23(3): 249–256. DOI: 10.3969/j.issn.0254-7805.2002.03.001.
[88]	孟卫华, 郭伟国, 苏静, 等. DH-36钢的塑性流动统一本构关系研究 [J]. 力学学报, 2011, 43(5): 958–962. DOI: 10.6052/0459-1879-2011-5-lxxb2010-676. MENG W H, GUO W G, SU J, et al. Study of plastic flow unified constitutive relation for steel DH-36 [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 958–962. DOI: 10.6052/0459-1879-2011-5-lxxb2010-676.
[89]	孟卫华, 郭伟国, 王建军, 等. DH36钢拉伸塑性流动特性及本构关系 [J]. 爆炸与冲击, 2013, 33(4): 438–443. DOI: 10.11883/1001-1455(2013)04-0438-06. MENG W H, GUO W G, WANG J J, et al. Tensile plasticity flow characteristics of DH36 steel and its constitutive relation [J]. Explosion and Shock Waves, 2013, 33(4): 438–443. DOI: 10.11883/1001-1455(2013)04-0438-06.
[90]	SU J, GUO W, MENG W, et al. Plastic behavior and constitutive relations of DH-36 steel over a wide spectrum of strain rates and temperatures under tension [J]. Mechanics of Materials, 2013, 65: 76–87. DOI: 10.1016/j.mechmat.2013.06.002.
[91]	VOYIADJIS G Z, SONG Y. A physically based constitutive model for dynamic strain aging in Inconel 718 alloy at a wide range of temperatures and strain rates [J]. Acta Mechanica, 2020, 231(1): 19–34. DOI: 10.1007/s00707-019-02508-6.
[92]	SUN Y Q, HAZZLEDINE P M. A TEM weak-beam study of dislocations in γ' in a deformed Ni-based superalloy [J]. Philosophical Magazine A, 1988, 58(4): 603–617. DOI: 10.1080/01418618808209940.
[93]	HIRSCH P B. A new theory of the anomalous yield stress in L12 alloys [J]. Philosophical Magazine A, 1992, 65(3): 569–612. DOI: 10.1080/01418619208201539.
[94]	HIRSCH P B. A model of the anomalous yield stress for (111) slip in L12 alloys [J]. Progress in Materials Science, 1992, 36: 63–88. DOI: 10.1016/0079-6425(92)90005-R.
[95]	LOUCHET F. Stress anomaly in L1₂ alloys: the ‘extended-locking /unzipping’ model [J]. Materials Science and Engineering: A, 1997, 234: 275–278. DOI: 10.1016/S0921-5093(97)00197-4.
[96]	CAILLARD D, PAIDAR V. A model for the anomalous mechanical properties of nickel-base L12 ordered alloys—Ⅰ. Dislocations dynamics [J]. Acta Materialia, 1996, 44(7): 2759–2771. DOI: 10.1016/1359-6454(95)00388-6.
[97]	LUO Z P, WU Z T, MILLER D J. The dislocation microstructure of a nickel-base single-crystal superalloy after tensile fracture [J]. Materials Science and Engineering: A, 2003, 354(1/2): 358–368. DOI: 10.1016/S0921-5093(03)00039-X.
[98]	MACLACHLAN D W, KNOWLES D M. Modelling and prediction of the stress rupture behaviour of single crystal superalloys [J]. Materials Science and Engineering: A, 2001, 302(2): 275–285. DOI: 10.1016/S0921-5093(00)01829-3.
[99]	WANG J J, GUO W G, SU Y, et al. Anomalous behaviors of a single-crystal Nickel-base superalloy over a wide range of temperatures and strain rates [J]. Mechanics of Materials, 2016, 94: 79–90. DOI: 10.1016/j.mechmat.2015.11.015.
[100]	LI W G, MA J Z, KOU H B, et al. Modeling the effect of temperature on the yield strength of precipitation strengthening Ni-base superalloys [J]. International Journal of Plasticity, 2019, 116: 143–158. DOI: 10.1016/j.ijplas.2019.01.002.
[101]	KOPPENAAL T J, KUHLMANN-WILSDORF D. The effect of prestressing on the strength of neutron-irradiated copper single crystals [J]. Applied Physics Letters, 1964, 4(3): 59–61. DOI: 10.1063/1.1753962.
[102]	NEMBACH E, CHOW C K. Experimental investigation into the relation between γ′ particle dispersion and the yield stress of PE 16 [J]. Materials Science and Engineering, 1978, 36(2): 271–279. DOI: 10.1016/0025-5416(78)90080-0.
[103]	REPPICH B, SCHEPP P, WEHNER G. Some new aspects concerning particle hardening mechanisms in γ' precipitating nickel-base alloys—Ⅱ. Experiments [J]. Acta Metallurgica, 1982, 30(1): 95–104. DOI: 10.1016/0001-6160(82)90049-9.
[104]	FOREMAN A J E, MAKIN M J. Dislocation movement through random arrays of obstacles [J]. Canadian Journal of Physics, 1967, 45(2): 511–517. DOI: 10.1139/p67-044.
[105]	POLLOCK T M, ARGON A S. Creep resistance of CMSX-3 nickel base superalloy single crystals [J]. Acta Metallurgica et Materialia, 1992, 40(1): 1–30. DOI: 10.1016/0956-7151(92)90195-K.
[106]	REED R C. The superalloys: fundamentals and applications [M]. Cambridge: Cambridge University Press, 2006. DOI: 10.1017/CBO9780511541285.
[107]	WANG J J, WANG R F, MENG W H, et al. Double-humped temperature dependence of plastic behaviour of K403 superalloy and its constitutive model [J]. Materials at High Temperatures, 2022, 39(1): 55–67. DOI: 10.1080/09603409.2021.2007009.
[108]	GILLES G, HAMMAMI W, LIBERTIAUX V, et al. Experimental characterization and elasto-plastic modeling of the quasi-static mechanical response of TA-6 V at room temperature [J]. International Journal of Solids and Structures, 2011, 48(9): 1277–1289. DOI: 10.1016/j.ijsolstr.2011.01.011.
[109]	KHAN A S, YU S J. Deformation induced anisotropic responses of Ti-6Al-4V alloy. Part Ⅰ: experiments [J]. International Journal of Plasticity, 2012, 38: 1–13. DOI: 10.1016/j.ijplas.2012.03.015.
[110]	LI P H, GUO W G, YUAN K B, et al. Effects of processing defects on the dynamic tensile mechanical behavior of laser-solid-formed Ti-6Al-4 V [J]. Materials Characterization, 2018, 140: 15–29. DOI: 10.1016/j.matchar.2018.03.032.
[111]	DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design [J]. Quarterly of Applied Mathematics, 1952, 10(2): 157–165. DOI: 10.1090/qam/48291.
[112]	BARDET J P. Lode dependences for isotropic pressure-sensitive elastoplastic materials [J]. Journal of Applied Mechanics, 1990, 57(3): 498–506. DOI: 10.1115/1.2897051.
[113]	RICHMOND O, SPITZIG W A. Pressure dependence and dilatancy of plastic flow [J]. Theoretical and Applied Mechanics, 1980(1): 377–386.
[114]	GAO X S, ZHANG T T, HAYDEN M, et al. Effects of the stress state on plasticity and ductile failure of an aluminum 5083 alloy [J]. International Journal of Plasticity, 2009, 25(12): 2366–2382. DOI: 10.1016/j.ijplas.2009.03.006.
[115]	KHAN A S, YU S J, LIU H W. Deformation induced anisotropic responses of Ti-6Al-4V alloy. Part Ⅱ: a strain rate and temperature dependent anisotropic yield criterion [J]. International Journal of Plasticity, 2012, 38: 14–26. DOI: 10.1016/j.ijplas.2012.03.013.
[116]	TUNINETTI V, GILLES G, MILIS O, et al. Anisotropy and tension-compression asymmetry modeling of the room temperature plastic response of Ti-6Al-4V [J]. International Journal of Plasticity, 2015, 67: 53–68. DOI: 10.1016/j.ijplas.2014.10.003.
[117]	LOWDEN M A W, HUTCHINSON W B. Texture strengthening and strength differential in titanium-6Al-4V [J]. Metallurgical Transactions A, 1975, 6(3): 441–448. DOI: 10.1007/BF02658401.
[118]	JONES I P, HUTCHINSON W B. Stress-state dependence of slip in titanium-6Al-4V and other H. C. P. metals [J]. Acta Metallurgica, 1981, 29(6): 951–968. DOI: 10.1016/0001-6160(81)90049-3.
[119]	PRAKASH D G L, DING R, MOAT R J, et al. Deformation twinning in Ti-6Al-4 V during low strain rate deformation to moderate strains at room temperature [J]. Materials Science and Engineering: A, 2010, 527(21/22): 5734–5744. DOI: 10.1016/j.msea.2010.05.039.
[120]	AIFANTIS E C. The physics of plastic deformation [J]. International Journal of Plasticity, 1987, 3(3): 211–247. DOI: 10.1016/0749-6419(87)90021-0.
[121]	BAMMANN D J, AIFANTIS E C. A model for finite-deformation plasticity [J]. Acta Mechanica, 1987, 69(1): 97–117. DOI: 10.1007/BF01175716.
[122]	KUBIN L P, ESTRIN Y. Evolution of dislocation densities and the critical conditions for the Portevin-Le Chtelier effect [J]. Acta Metallurgica et Materialia, 1990, 38(5): 697–708. DOI: 10.1016/0956-7151(90)90021-8.
[123]	KOCKS U F, ARGONr A S, ASHBY M F. Thermodynamics and kinetics of slip [J]. Progress in Materials Science, 1975, 19: 141–145.
[124]	HOGE K G, MUKHERJEE A K. The temperature and strain rate dependence of the flow stress of tantalum [J]. Journal of Materials Science, 1977, 12(8): 1666–1672. DOI: 10.1007/BF00542818.
[125]	YAN S L, YANG H, LI H W, et al. A unified model for coupling constitutive behavior and micro-defects evolution of aluminum alloys under high-strain-rate deformation [J]. International Journal of Plasticity, 2016, 85: 203–229. DOI: 10.1016/j.ijplas.2016.07.011.
[126]	GAO C Y, ZHANG L C. Constitutive modelling of plasticity of FCC metals under extremely high strain rates [J]. International Journal of Plasticity, 2012, 32/33: 121–133. DOI: 10.1016/j.ijplas.2011.12.001.
[127]	GAO C Y, ZHANG L C, YAN H X. A new constitutive model for HCP metals [J]. Materials Science and Engineering: A, 2011, 528(13/14): 4445–4452. DOI: 10.1016/j.msea.2011.02.053.
[128]	MEYERS M A, VÖHRINGER O, LUBARDA V A. The onset of twinning in metals: a constitutive description [J]. Acta Materialia, 2001, 49(19): 4025–4039. DOI: 10.1016/S1359-6454(01)00300-7.
[129]	LU L, DAO M, ZHU T, et al. Size dependence of rate-controlling deformation mechanisms in nanotwinned copper [J]. Scripta Materialia, 2009, 60(12): 1062–1066. DOI: 10.1016/j.scriptamat.2008.12.039.

施引文献

期刊类型引用(3)

1.	李祥辉，张兴渝，胡家豪，刘洋，马伯翰，王永刚，蒋招绣. AISI 4340钢靶大塑性模型及断裂起始模型参数研究. 兵工学报. 2025(01): 301-316 . 百度学术
2.	张斌，张青平，陈建良，颜怡霞，何丽灵，李继承，郝志明，李明海. 运载撞击事故场景下复杂结构冲击响应数值模拟分析. 包装工程. 2024(19): 102-107 . 百度学术
3.	钱迪鑫，王立人，夏春明. 基于机器学习的GH4169合金Johnson-Cook本构参数反演方法. 机械工程材料. 2024(12): 100-105 . 百度学术