An experimental technique for medium strain-rate loading by a progressive cam
-
摘要: 研制了一种可以实现多次加载的凸轮递进式中应变率压缩实验系统。该实验装置采用伺服电机驱动蓄能飞轮转动,后蓄能飞轮带动加载凸轮压缩加载杆的方法,实现对试样中应变率的压缩;同时在一级压缩即将结束时步进电机迅速推动蓄能飞轮贴近加载凸轮,实现多级压缩。试样的动态压缩载荷通过两侧杆上粘贴的应变片所记录的应变信号得到;试样变形过程通过激光干涉测速系统测得的试样两侧杆端的运动速度信号得到。以纸蜂窝试样为例,基于研制的中应变率实验系统,并结合高速摄影图片,研究了厚度10 mm、直径14.5 mm的纸蜂窝试样在应变率3.5 s−1下的动态压缩力学性能,得到了单级压缩和两级压缩过程中纸蜂窝试样的应力-应变曲线和变形过程,并讨论了该实验系统的可靠性。此实验系统可以实现多级递进式中应变率加载;纸蜂窝试样在中等应变率下的峰值强度和平台应力对高应变率下的动态压缩实验数据和低应变率下的准静态实验数据进行了较好地衔接;试样的失效模式主要为准弹性变形后的外壁屈曲和面内剪切。Abstract: A medium strain rate compression experimental system based on a progressive cam was developed to realize multiple medium strain rate loading. The developed experimental system uses the servo motor to drive the energy storage flywheel to rotate at a certain speed, and when the clutch is started, the energy storage flywheel can drive the loading cam to rotate. The loading cam pushes the loading guide bar and the input bar to compress the sample. When the loading cam rotates one circle, a single medium strain-rate compression is completed. At the same time, when the first stage compression is about to end, the stepper motor rapidly pushes the energy storage flywheel close to the loading cam for the next compression, and the cycles repeat to achieve multiple medium strain rate compression. The load and deformation of the material during compression were measured by strain gauges and a velocity interferometer system for any reflector (VISAR), respectively. The strain gauges were affixed to the input bar and the support bar, respectively. The strain signals of the bars during compression were recorded by the strain gauges and the forces exerted on the sample were obtained based on these strain signals. Two fiber optic probes of the VISAR system were used to measure the velocities of the input bar and the support bar during compression. Based on the two velocity curves measured, the velocity difference curve between the two ends of the sample was obtained, and then the deformation of the sample was gained by integrating the velocity difference. The stress-strain curves were obtained from the load- and deformation-time curves. Taking the paper honeycomb sample as an example, the reliability of the developed medium strain rate experimental system was discussed based on the high-speed images. The dynamic compressive mechanical properties of the paper honeycomb samples with the thickness of 10 mm and the diameter of 14.5 mm at the strain rate of 3.5 s−1 were studied. The stress-strain curves and deformation processes of the paper honeycomb samples during single compression and double compression were obtained. The experimental system could realize multistage progressive medium strain rate loading. The peak strength and plateau stress of the paper honeycomb samples at medium strain rates well connect the dynamic compression results at high strain rates with the quasi-static compression results at low strain rates. The failure modes of the samples are mainly out-of-plane buckling and in-plane shear after quasi-elastic deformation.
-
Key words:
- medium strain rate /
- paper honeycomb /
- mechanical performance /
- compression experiment
-
应变率是表征材料动力学性能的重要参数之一,目前研究大多位于低应变率范围和高应变率范围。低应变率(10−5~10−2 s−1)下材料的压缩/拉伸力学性能的研究通常采用万能试验机来实现[1-2];高应变率(102~104 s−1)下材料动态性能的研究通常采用落锤、霍普金森杆来完成[3-5]。然而,中等应变率下,即10−2~102 s−1区间,材料相关实验研究难以开展。其原因在于:(1)此应变率区间超出了准静态实验系统的响应速度。Huh等[6]采用具有不同固有频率的伺服液压试样夹进行中应变率拉伸实验,拉伸实验曲线的振荡受试样夹的响应频率影响较大。当试样夹响应频率为2500和4800 Hz时,测试载荷振荡厉害;当固有频率达到13000 Hz时,伺服液压系统可以测试得到较稳定的载荷数据,但是更高速度的冲击仍然是一个挑战。(2) 此应变率区间需要产生比高应变率下大得多的变形,需要较长的加载时间,这对霍普金森杆实验系统也是一个挑战。然而,中等应变率范围是材料的力学行为从高应变率下的波动效应向低应变率下的准平衡状态过渡的关键区域,相关研究具有重要的科学意义。
高应变率下材料的动态行为反映的是在波动效应作用下材料的局部响应,而低应变率(应变率10−5~10−3 s−1)下材料的力学行为反映的是准静态下材料或结构的准平衡性能。因此,中应变率加载过程中,材料的力学行为包含从短程的波动效应、到长程的振动效应、再向准静态的材料和结构的准平衡作用转化的多种作用,这一应变率区域是多种机制转化的过渡区域。对其进行研究,可探讨新型材料尺度转换率等多种相关的基础理论,非常值得进行深入探索。中等应变率的加载手段主要包括凸轮加载[7-8]、摆锤[9-10]、异形杆[11]以及伺服液压试验机[12-13],这些装置都存在一定不足。例如:实验装置体积大、结构复杂并需要特殊加工、加载时间较短(0.3~12 ms),等等。因此,开发具有较好通用性的中应变率加载的实验装置显得尤为重要。
因为纸蜂窝在冲击防护过程中一般需要承受较大的变形和一定的加载速率,因此选择纸蜂窝为研究对象。蜂窝材料和结构以其较高的比强度和刚度、承载性能、吸能和隔音等特点广泛应用于飞机、船舶、高速列车、包装、缓冲衬垫等领域[14-16]。金属铝、钢等材质为基体的蜂窝材料的破坏行为被广泛研究,其应变率效应[17-18]、尺寸效应[19-20]、惯性效应[21]和相关机制得到了较充分的揭示。纸蜂窝材料与金属蜂窝材料结构类似,变形过程也可分为3个阶段:线性阶段、应力平台阶段、致密阶段[22-23]。Wang[23]研究了多种类型纸蜂窝的动态冲击性能,发现结构的阻尼性能与蜂窝的密度、壁厚和壁长有关,并随密度、壁厚和壁长的增大而增强。Heimbs等[24]研究了应变率对纸蜂窝性能的影响,发现应变率从10 s−1升至300 s−1时,应力提高了30%。Shan等[25]采用实验和数值模拟方法,探究了不同尺寸的纸蜂窝在不同应变率下的强度和冲击失效过程,发现当纸蜂窝厚度大于2 mm时,屈服强度具有明显的尺寸效应和应变率效应,并且结构的失效过程主要为蜂窝壁的屈曲。范成年等[26]探索了双层复合纸蜂窝结构的力学性能,发现双层纸蜂窝的失效过程中包含2个压缩平台,且双层纸蜂窝的变形时间长于单层纸蜂窝,同时吸能性能优于单层纸蜂窝。但是,这些研究主要针对高应变率加载下材料和结构的变形过程,对应的变形量不是很大。
本文中,基于新近研制的一种凸轮递进式加载的中等应变率实验系统,对纸蜂窝进行中等应变率下动态加载实验,检验实验系统的可靠性,并探索中等应变率下纸蜂窝的失效特征。
1. 实验系统
1.1 实验原理
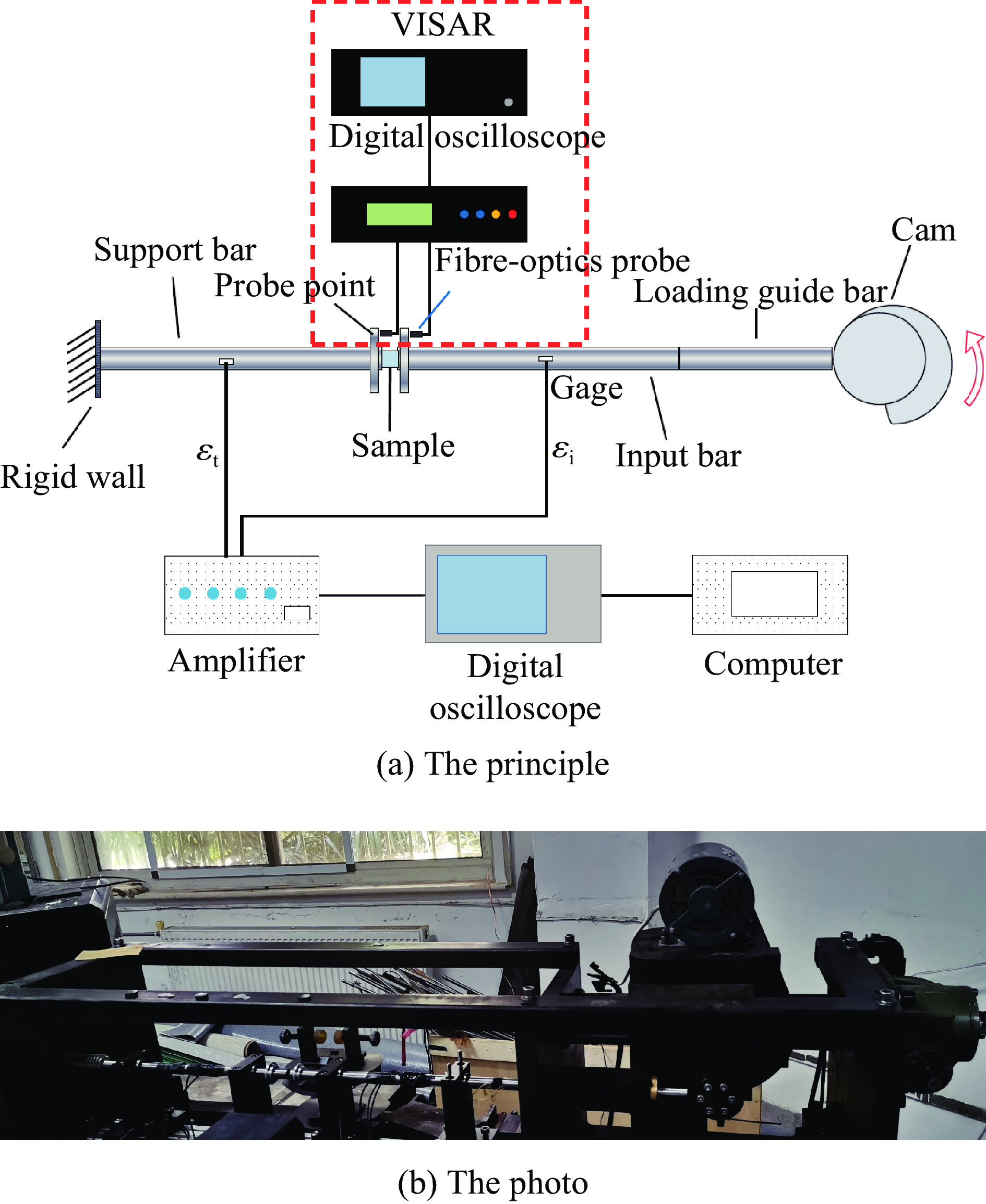
图1所示为实验设备示意图[27]。如图1(a)所示,该实验系统由伺服电机、蓄能飞轮1、加载离合器、蓄能飞轮2、加载凸轮、凸轮相位检测装置、步进电机、导向装置、加载导向杆、加载杆、支撑杆、试样和激光干涉速度测试探头等组件构成。实验中,首先打开伺服电机,使它以较高的转速ω0旋转。伺服电机通过传动皮带带动蓄能飞轮1以转速ω1旋转,完成第1次减速。蓄能飞轮1通过齿轮带动蓄能飞轮2以转速ω2旋转,完成第2次减速。蓄能飞轮2带有加载离合器,与加载凸轮同轴。此时加载离合器与轴分离,蓄能飞轮2处于虚转状态,保持较大的转动动能。
如图1(b)所示,加载凸轮是半径由r1逐渐增大到r2的偏心凸轮,其初始段在转角θ0(例如15°)范围内半径保持r1不变,以使压缩加载初期的凸轮顺利启动。实验时,加载杆最初与加载凸轮的半径最小处接触。根据相位检测装置的相位监控信号,启动加载离合器,使蓄能飞轮2与加载凸轮的轴接合,蓄能飞轮2将带动加载凸轮以转速ω2旋转,加载凸轮通过加载杆对试件施加动态压缩加载。在凸轮旋转过程中,凸轮相位检测装置实时检测加载凸轮转角。当加载凸轮即将旋转一周时,启动步进电机,推动蓄能飞轮2整体迅速跟进,使其与加载凸轮紧密接触,进入下一个加载周期。如此往复,以实现多级递进式加载。同时,也可基于相位监控信息在任意转角θ处断开离合器,终止加载。图1(b)中:θ1为凸轮倒角区域对应的角度,α为加载导向杆与法线n的夹角,τ为切线方向。
1.2 测试原理
在中等应变率实验过程中,试样两侧钢杆通常会产生同等程度的变形,此时采用传统霍普金森压杆(split Hopkinson pressure bar, SHPB)实验的数据采集方法已经无法获得试样的变形,因此本实验系统分别采用激光干涉速度测试系统(velocity interferometer system for any reflector, VISAR)和应变采集系统来获得压缩过程中试样的载荷信号和变形信号,测试原理如图2(a)所示。实验中,在加载杆和支撑杆上分别粘贴应变片,测量加载过程中两杆上的应变波形,得到加载端应变历程εi和支撑端的应变历程εt,通过两杆的变形分别获取试样两端的应力信号。利用激光干涉速度测试探头测量两杆夹持试件端面的位移ds,采用VISAR测量试件2个端面的运动速度,由此进行试件应变的计算。结合两杆上的应变波形和试件两端的速度波形,确定在某一恒定应变率下试件的轴向应变εs和应力σs。实验过程中可以通过调节伺服电机转速,改变蓄能飞轮的转速,进而改变加载速率。实验设备如图2(b)所示,目前实验装置所采用的凸轮的r1和r2分别为40 和50 mm;伺服电机和蓄能飞轮最大转速分别为2800和560 r/min,对应的平均应变率范围为0.5~15 s−1(厚度10 mm纸蜂窝试样);同时采用更高转速的伺服电机可以实现更高的应变率。实验系统中加载导向杆长为300 mm,加载杆长为400 mm,支撑杆长为400 mm;杆直径均为20 mm。不同材料和结构设计出的试样尺寸是不一致的,主要设计原则是:加载过程中,加载杆和支撑杆保持弹性。此时,试样极限强度对应的荷载应小于加载杆和支撑杆的弹性极限,即σmaxAs<σe,bA0,其中σmax为试样极限强度,σe,b为加载杆和支撑杆的弹性极限,A0为加载杆和支撑杆的横截面积,As为试件的横截面积。为了保证加载过程中试样两端应力平衡,试样的长径比d/Ls应小于1(其中,d为试样直径,Ls为试样长度);随加载速率的升高,试样的长径比适当减小。考虑加载过程中试样的泊松效应,为保证加载过程中整个试样受压,所设计的试样直径应略小于加载杆直径。例如,本实验中可以采用直径为16 mm、长度为10~15 mm的圆柱试样。
试件轴向应力的计算公式为:
σs = E0A02As(εt(t)+εi(t)) (1) 式中:E0为加载杆和支撑杆的弹性模量,εi 和εt分别为加载杆和支撑杆的应变信号。
试件应变率的计算,有2种方法:(1)根据加载凸轮的转速进行估计;(2)根据试件2个端面的运动速度VISAR测试结果进行计算。第1种方法主要用于实验前加载凸轮的选型、实验转速设计和试样厚度的设计。后者反映了实验过程中试样的真实应变,用于试样应力-应变关系曲线的计算;同时,也可以对前者计算的应变率进行修正,以得到更满足要求的实验应变率。由加载凸轮的转速计算应变率:
˙ε = ξr2−r1Lsω22π ,或˙ε = εsω22π−θ (2) 式中:ξ为变形传递系数,与凸轮、加载杆、支撑杆的材料参数和尺寸相关,可借助VISAR系统进行标定。此计算公式反映了凸轮转速、凸轮尺寸变化与试样尺寸的关系,其中,r2−r1为加载杆的最大理论行程并受凸轮尺寸控制,此时计算的应变率与试件的应变率有区别。
由VISAR系统测试得到的速度计算应变率:
˙εs = dεsdt=(vi(t)−vt(t))/Ls (3) 式中:vi和vt分别为试件在加载杆和支撑杆端的速度。由此,试件轴向应变为:
εs=∫t0˙εsdt (4) 由式(1)、(3)可知,对强度较高的材料应适当减小试样直径;通过减小试样厚度可以提高加载应变率。
2. 实 验
2.1 纸蜂窝试样
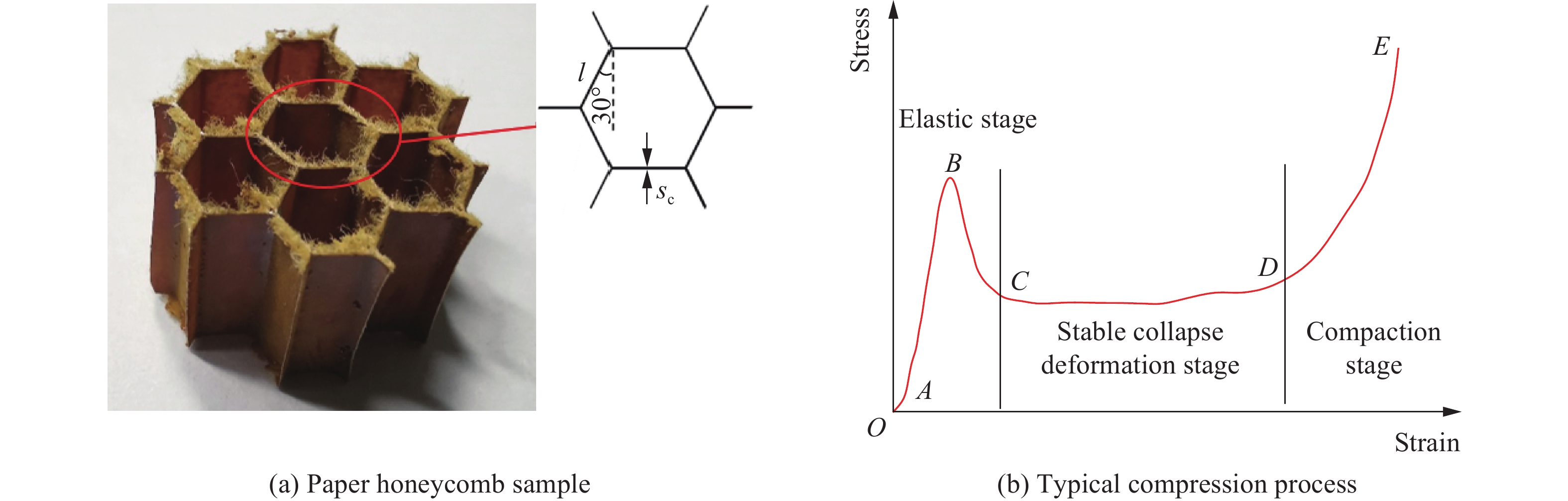
实验所用的Aramid纸蜂窝具有规则六边形蜂窝单元的典型蜂窝芯结构,密度为1100 kg/m3,每个蜂窝单元的边长l为2.75 mm,壁厚sc为0.1 mm,蜂窝单元壁角度γ为30°。如图3所示,将纸蜂窝制成直径为14.5 mm包含7个完整蜂窝单元的试样,试样的厚度为(10±0.3) mm。图3为纸蜂窝典型压缩曲线,压缩过程共包含3个阶段:弹性变形、稳定塌陷变形以及致密阶段。利用图2所示的中等应变率实验系统对纸蜂窝试样进行压缩实验,同时为了跟踪试样破坏过程,采用CCD (charge-coupled device)相机实时拍摄,拍摄时间间隔为5 ms。
2.2 实验系统讨论
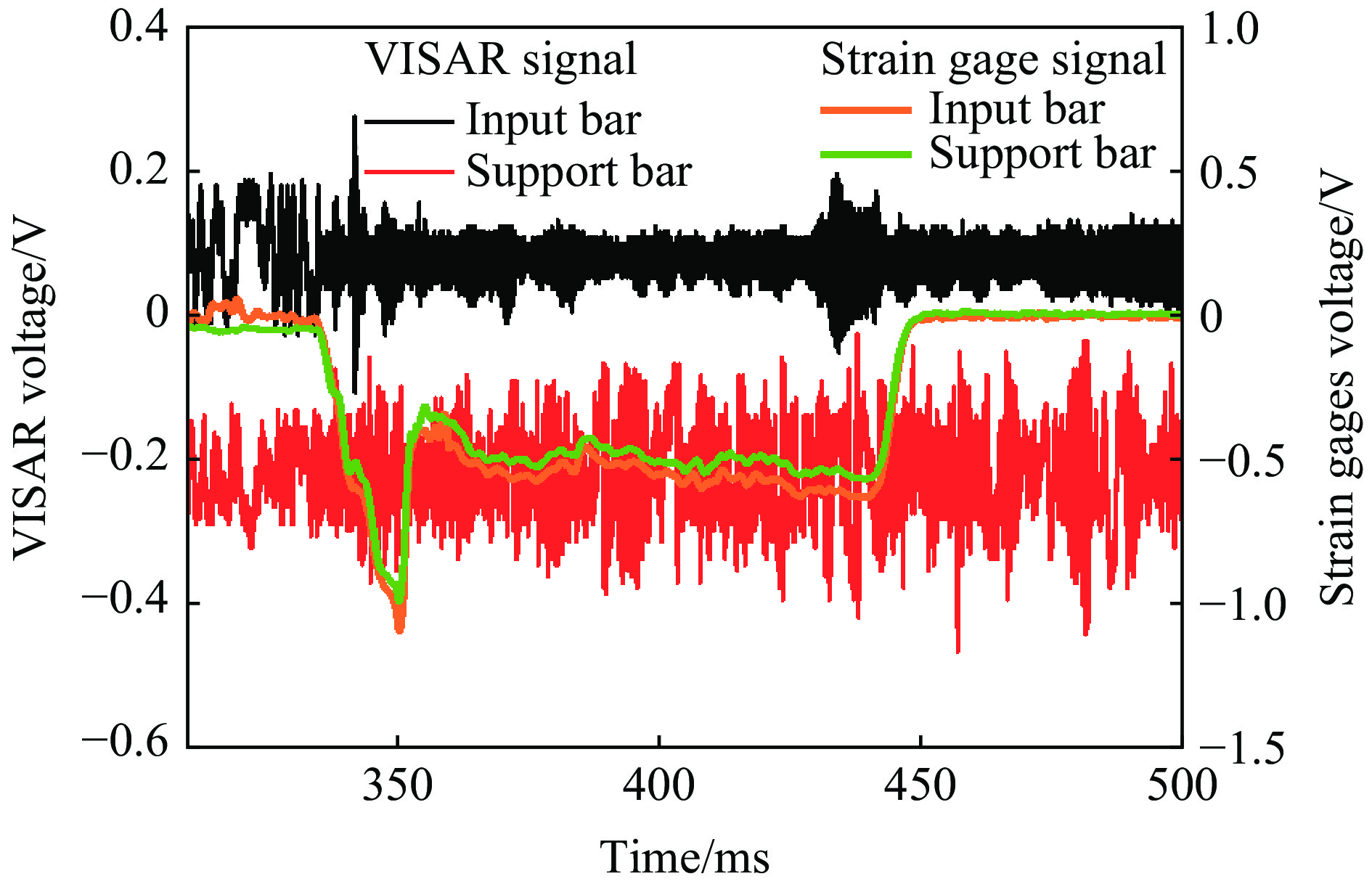
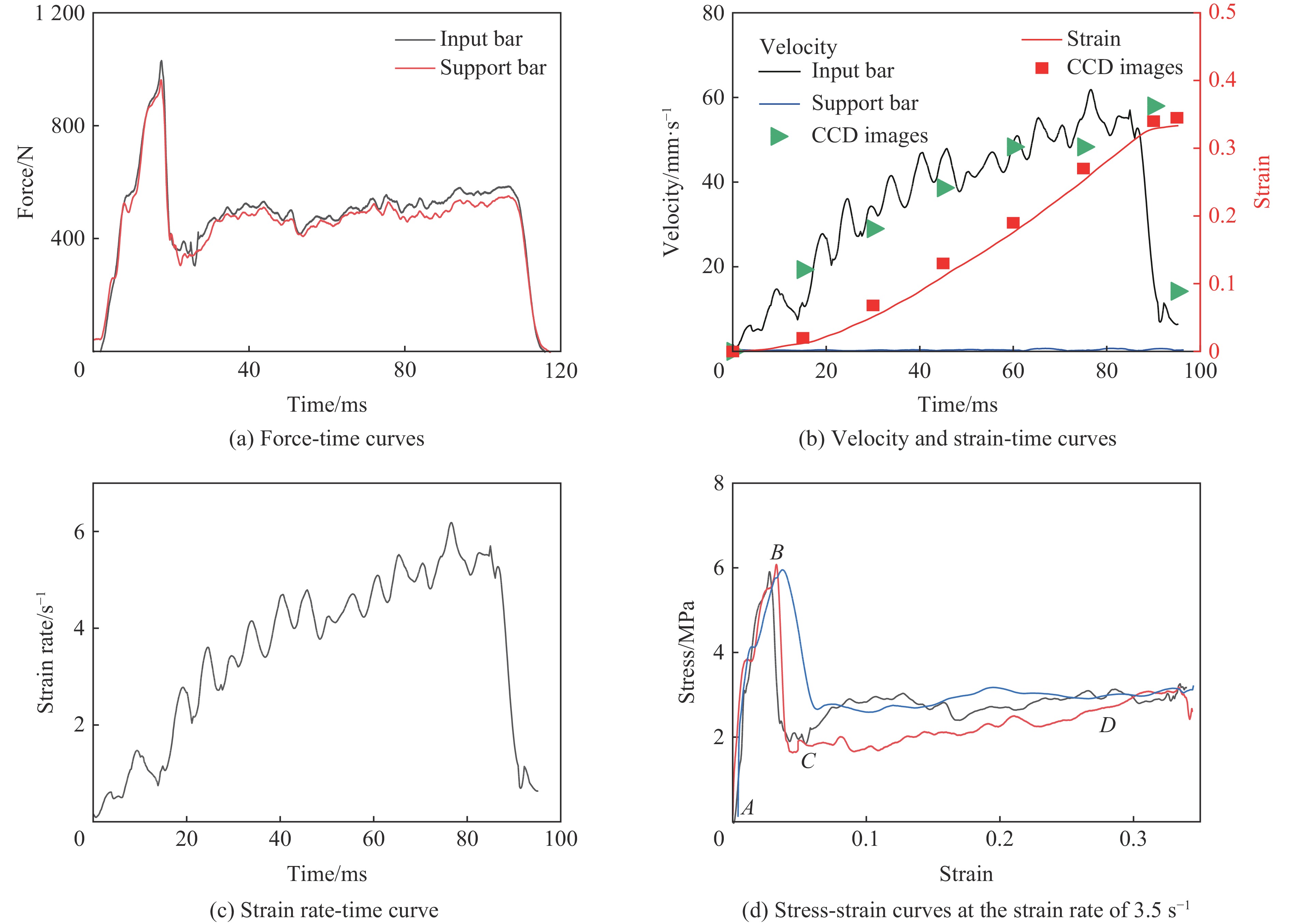
图4为蓄能飞轮转速为280 r/min时加载杆和支撑杆上的应变片以及VISAR测速系统得到的典型信号及数据分析结果。图中黑色和红色曲线分别为VISAR测速系统得到的试件前后表面的速度干涉图像,橘红色和绿色曲线分别为加载杆和支撑杆上应变片测试得到的原始波形。由此信号计算得到的试样两端的载荷-时间曲线如图5(a)所示,整个压缩过程中试样的两端载荷基本平衡。
对VISAR信号进行时频分析,可以得到试件前后表面的速度-时间曲线,分别如图5(b)中黑色和蓝色曲线所示。加载端的运动速度随着加载过程的进行持续升高,加载速度最高约为50 mm/s。在凸轮旋转一周后,即加载结束时,加载端速度迅速降低。支撑端的运动由杆件的变形和宏观运动构成,支撑杆的另一端为固定端,支撑杆一般不发生较大的宏观运动。由于纸蜂窝试件强度较低,压缩过程中支撑杆所受的载荷较小,其变形和宏观运动相对于加载杆均非常小,因此支撑杆端可视为不发生运动,如图5(b)中蓝线所示。由CCD图像分析计算得到的加载杆端的速度变化过程和试样应变如图5(b)散点所示,由此可见:VISAR测量的速度变化过程与CCD图片计算结果基本一致。表明通过VISAR测量杆端的运动具有较高的准确性和可靠性。由于支撑杆端测试得到的速度很低,为简化分析过程,实际数据分析忽略支撑杆端的运动速度,则式(3)可以简化为
˙εs=vi(t)/vi(t)LsLs 。计算得到的应变率-时间曲线如图5(c)所示,整个加载过程的平均应变率ˉ˙εs 约为3.5 s−1。由式(2),系统的变形传递系数ξ可标定为4.7。同时,由式(4)可以计算试样的变形,计算结果如图5(b)中红色曲线所示。随着加载过程的发展,试样变形持续增大,其数值与CCD图像分析计算得到的应变基本一致,这进一步验证了实验方法的可靠性和有效性。由压缩过程中纸蜂窝试样的载荷-时间曲线和变形-时间曲线,即可获得试样的应力-应变曲线。图5(d)为在3.5 s−1的应变率下纸蜂窝试样的3次实验的应力-应变曲线,准弹性阶段(AB)基本一致,实验结果具有较好的重复性;坍塌阶段(BC)、应力平台阶段(CD)存在一定差异,这与试样坍塌过程和坍塌模式有关。3. 结果与讨论
3.1 应力-应变关系
图6为蓄能飞轮转速为280 r/min时纸蜂窝试样的单级压缩和两级压缩过程中的应力-应变曲线及CCD图片。从图6(a)可以看出,应力-应变曲线可以分为3个阶段:准弹性阶段(AB)、坍塌阶段(BC)和应力平台阶段(CD),该过程与纸蜂窝典型波形趋势基本一致。在压缩开始时,纸蜂窝处于准弹性变形阶段(图片(1)~(2)),随着变形增大,强度提高;随着变形进一步增大,纸蜂窝试样开始出现外壁屈曲变形(黄色椭圆标记)和局部面内剪切(红色椭圆标记)而发生坍塌(图片(3)),应力迅速降低,但结构仍具有一定的承载能力;随着加载的持续进行,变形进入应力平台阶段,在这一阶段,试样的载荷基本保持不变,试样发生连续稳定的坍塌(图片(4)~(6))。此次压缩过程的平均应变率可以通过CCD图片和速度-时间曲线关系获得,加载过程的平均应变率约为3.5 s−1。
图6(b)中图片(1)~(5)对应第1级压缩过程,图片(6)~(8)对应第2级压缩过程。其中第1级压缩过程与单级压缩过程基本一致,主要包括3个阶段:准弹性阶段(AB)、坍塌阶段(BC)和应力平台阶段(CD)。在准弹性阶段(AB),试样主要发生弹性变形(图片(1)和(2));在坍塌阶段BC试样产生面内剪切破坏和外壁屈曲变形(图片(3));在阶段CD,试样持续发生坍塌变形(图片(4)和(5))。在第1级压缩结束后,应力会卸载至零,即阶段DE。第2级压缩时,随着加载进行,应力逐渐升高(阶段EF)并进入稳定坍塌阶段(阶段FG),压缩结束后应力发生卸载(阶段GH)。由图6(b)中图片(6)~(8)可以看出,两级压缩过程中试样持续发生坍塌,平台应力基本保持稳定。整个加载过程的平均应变率约为3.5 s−1。
3.2 与准静态和动态压缩实验结果的比较
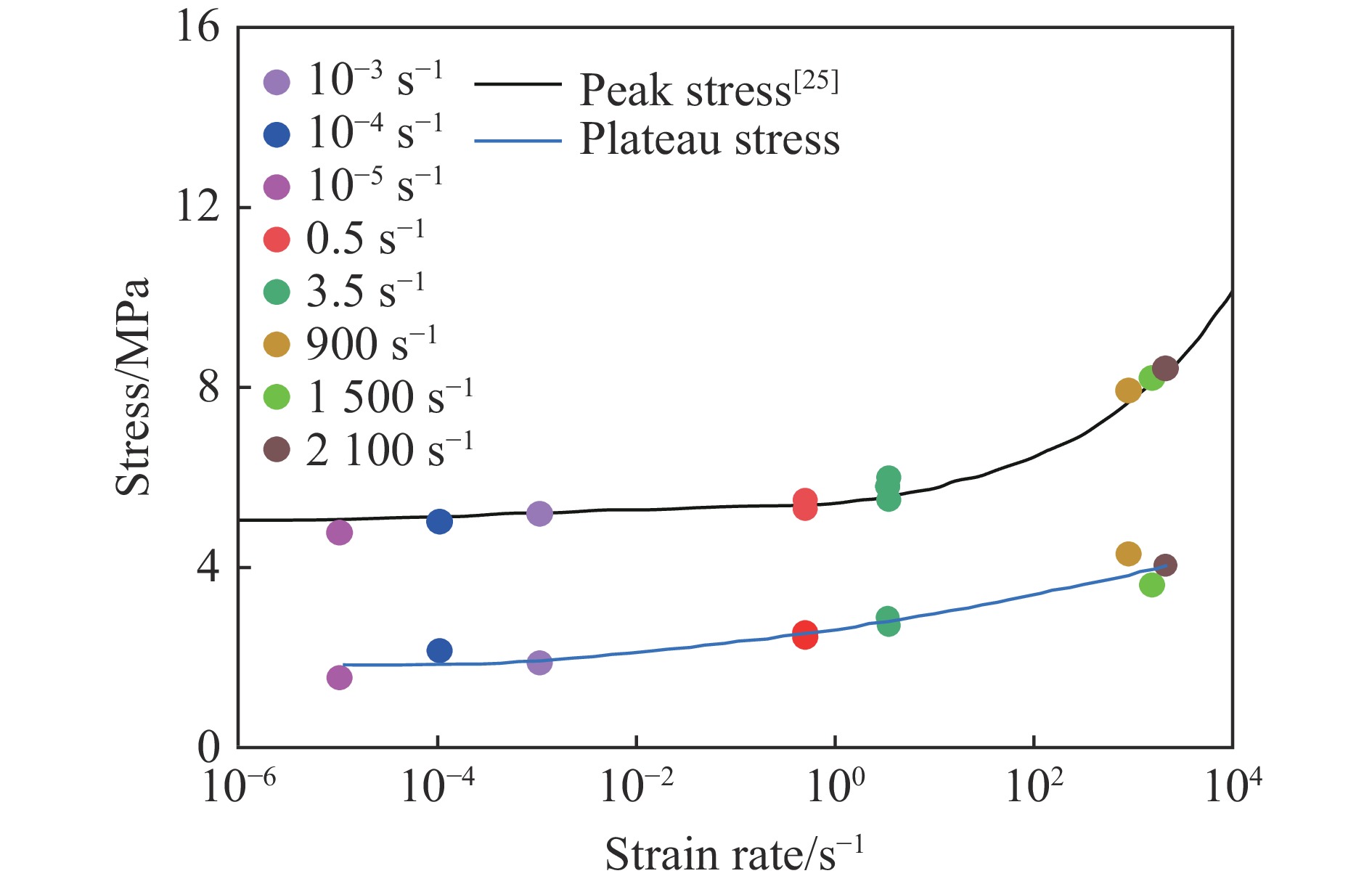
Shan等[25]基于MTS万能试验机和SHPB实验装置,研究了不同厚度的纸蜂窝在准静态和高应变率下的力学性能。图7为厚度10 mm的纸蜂窝试样在不同应变率下的应力-应变曲线。在不同应变率下,纸蜂窝试样的应力-应变曲线均可分为3个阶段:准弹性阶段(AB)、坍塌阶段(BD)和应力平台阶段(CD)。中等应变率下纸蜂窝的峰值强度约为5.8 MPa,介于准静态和高应变率之间,进一步验证了纸蜂窝试样的应变率效应,峰值强度随着应变率的升高而增大。同时,在稳定坍塌阶段的应力平台明显更稳定,应力值也处于准静态和高应变率实验数据之间。对于可以产生大变形的纸蜂窝试样,多级递进式压缩弥补了单次压缩中变形量的不足,增加试样的变形时间和变形量,使纸蜂窝试样可以发生持续稳定的坍塌。
峰值应力和平台应力是反映材料承载能力的重要参数,纸蜂窝试样在压缩过程中的峰值应力和平台应力与应变率的关系如图8所示。由图中散点分布可以看出,试样的峰值应力随应变率的升高而显著增大,应变率从10−5 s−1升至0.5、3.5和2100 s−1时,峰值应力分别增大了11.11%、23.42%和77.13%,中应变率下的峰值强度很好地衔接了准静态压缩实验结果和SHPB动态压缩实验结果。蜂窝结构的峰值应力与应变率的关系[25,28-29]为:
σyd=C0σys(sc/l)5/3(1+C1˙ε)p (5) 式中:σys为纸蜂窝单元壁的屈服应力,C0和p为无量纲系数,C1为一个具有时间维度的系数。Shan等[25]对不同厚度的纸蜂窝试样在不同应变率下的实验结果峰值应力进行了拟合,其中10 mm厚纸蜂窝试样的拟合结果如图8中黑色实线所示,C0=7.23,C1=0.103×10−3 s,p=0.28。本文中,纸蜂窝试样在应变率0.5和3.5 s−1下的峰值应力也满足此拟合结果。
基于式(5)对平台应力与应变率的关系进行拟合,拟合结果如图8中蓝色实线所示,其中C0p=492.65,C1p =0.057 s,pp =2.44。平台应力整体上也呈现出随应变率的升高而增大的趋势,但在高应变率下平台期应力波动较大,平台应力随应变率的升高并非单调变化。
4. 结 语
(1)研制了一种递进式凸轮中应变率实验系统,此系统应用凸轮递进旋转对试样施加动态载荷,应用VISAR测试系统对试样两端的运动速度进行测试,由此得到试样的应力-应变关系。此过程中,加载速率通过凸轮的转速来控制,试样的较大变形通过凸轮系统的递进运动产生较大位移来实现。结合CCD图像处理对该中等应变率实验系统的可靠性进行了讨论,结果表明此实验系统可以实现多级递进式中应变率加载。利用本文中研制的递进式凸轮中应变率实验系统,可以对高应变率下的动态波动效应与较低应变率下的准静态过程之间的过渡区域进行深入研究。
(2)对纸蜂窝试样在应变率3.5 s−1下的动力学性能进行了实验研究,得到了该试样在中应变率压缩下的应力-应变关系,以及峰值强度和平台应力的应变率效应,且获得的峰值强度和平台应力可将SHPB动态实验数据和MTS准静态实验数据进行较好地衔接。CCD图像结果表明纸蜂窝试样在准弹性变形后存在外壁屈曲和面内剪切2种失稳模式,这2种失稳模式是导致纸蜂窝失稳坍塌的主要机制。
感谢洛阳纳智机电有限公司的宋晓勇高级工程师在中等应变率设备的设计、制作和调试过程中给与的大力协助。
-
-
[1] HUANG J, XU S, YI H, et al. Size effect on the compression breakage strengths of glass particles [J]. Powder Technology, 2014, 268: 86–94. DOI: 10.1016/j.powtec.2014.08.037. [2] 薛晓, 乔禹, 王鹏飞, 等. 碳纳米管纤维的动态拉伸力学性能研究 [J]. 实验力学, 2020, 35(5): 811–819. DOI: 10.7520/1001-4888-19-213.XUE X, QIAO Y, WANG P F, et al. Dynamic tensile mechanical properties of carbon nanotube fiber [J]. Journal of Experimental Mechanics, 2020, 35(5): 811–819. DOI: 10.7520/1001-4888-19-213. [3] MIAO C H, XU S L, SONG Y P, et al. Influence of stress state on dynamic breakage of quartz glass spheres subjected to lower velocity impacting [J]. Powder Technology, 2022, 397: 117081. DOI: 10.1016/j.powtec.2021.117081. [4] 袁良柱, 苗春贺, 单俊芳, 等. 冲击下混凝土试样应变率效应和惯性效应探讨 [J]. 爆炸与冲击, 2022, 42(1): 013101. DOI: 10.11883/bzycj-2021-0114.YUAN L Z, MIAO C H, SHAN J F, et al. On strain-rate and inertia effects of concrete samples under impact [J]. Explosion and Shock Waves, 2022, 42(1): 013101. DOI: 10.11883/bzycj-2021-0114. [5] 郑监, 卢芳云. 金属梁在预应力下的冲击响应 [J]. 爆炸与冲击, 2021, 41(3): 031401. DOI: 10.11883/bzycj-2020-0328.ZHENG J, LU F Y. On impact response of a prestressed metal beam [J]. Explosion and Shock Waves, 2021, 41(3): 031401. DOI: 10.11883/bzycj-2020-0328. [6] HUH H, LIM J H, PARK S H. High speed tensile test of steel sheets for the stress-strain curve at the intermediate strain rate [J]. International Journal of Automotive Technology, 2009, 10(2): 195–204. DOI: 10.1007/s12239-009-0023-3. [7] FROUSTEY C, LAMBERT M, CHARLES J L, et al. Design of an impact loading machine based on a flywheel device: application to the fatigue resistance of the high rate pre-straining sensitivity of aluminium alloys [J]. Experimental Mechanics, 2007, 47(6): 709–721. DOI: 10.1007/s11340-007-9082-4. [8] COLE B N, STURGES J L. The flying wedge: a method for high strain rate tensile testing. Part 2: characteristics of the device [J]. International Journal of Impact Engineering, 2003, 28(8): 891–908. DOI: 10.1016/S0734-743X(03)00003-4. [9] PETITEAU J C, OTHMAN R, GUÉGAN P, et al. A drop-bar setup for the compressive testing of rubber-like materials in the intermediate strain rate range [J]. Strain, 2014, 50(6): 555–562. DOI: 10.1111/str.12113. [10] PEROGAMVROS N, MITROPOULOS T, LAMPEAS G. Drop tower adaptation for medium strain rate tensile testing [J]. Experimental Mechanics, 2016, 56(3): 419–436. DOI: 10.1007/s11340-015-0112-3. [11] WHITTINGTON W R, OPPEDAL A L, FRANCIS D K, et al. A novel intermediate strain rate testing device: the serpentine transmitted bar [J]. International Journal of Impact Engineering, 2015, 81: 1–7. DOI: 10.1016/j.ijimpeng.2015.02.009. [12] ZHU D, RAJAN S D, MOBASHER B, et al. Modal analysis of a servo-hydraulic high speed machine and its application to dynamic tensile testing at an intermediate strain rate [J]. Experimental Mechanics, 2011, 51(8): 1347–1363. DOI: 10.1007/s11340-010-9443-2. [13] OTHMAN R, GUÉGAN P, CHALLITA G, et al. A modified servo-hydraulic machine for testing at intermediate strain rates [J]. International Journal of Impact Engineering, 2009, 36(3): 460–467. DOI: 10.1016/j.ijimpeng.2008.06.003. [14] LI Z, WANG T, JIANG Y, et al. Design-oriented crushing analysis of hexagonal honeycomb core under in-plane compression [J]. Composite Structures, 2018, 187: 429–438. DOI: 10.1016/j.compstruct.2017.12.066. [15] ZHOU H, XU P, XIE S C, et al. Mechanical performance and energy absorption properties of structures combining two Nomex honeycombs [J]. Composite Structures, 2018, 185: 524–536. DOI: 10.1016/j.compstruct.2017.11.059. [16] WANG Z G, LI Z D, XIONG W. Experimental investigation on bending behavior of honeycomb sandwich panel with ceramic tile face-sheet [J]. Composites Part B: Engineering, 2019, 164: 280–286. DOI: 10.1016/j.compositesb.2018.10.077. [17] WANG Z G, TIAN H Q, LU Z J, et al. High-speed axial impact of aluminum honeycomb: experiments and simulations [J]. Composites Part B: Engineering, 2014, 56: 1–8. DOI: 10.1016/j.compositesb.2013.07.013. [18] SIBEAUD J M, THAMIÉ L, PUILLET C. Hypervelocity impact on honeycomb target structures: experiments and modeling [J]. International Journal of Impact Engineering, 2008, 35(12): 1799–1807. DOI: 10.1016/j.ijimpeng.2008.07.037. [19] ZHOU X L, ZHOU H F, LI X Y, et al. Size effects on tensile and compressive strengths in metallic glass nanowires [J]. Journal of the Mechanics and Physics of Solids, 2015, 84: 130–144. DOI: 10.1016/j.jmps.2015.07.018. [20] ZHOU Q, MAYER R R. Characterization of aluminum honeycomb material failure in large deformation compression, shear, and tearing [J]. Journal of Engineering Materials and Technology, 2002, 124(4): 412–420. DOI: 10.1115/1.1491575. [21] HOU B, ZHAO H, PATTOFATTO S, et al. Inertia effects on the progressive crushing of aluminium honeycombs under impact loading [J]. International Journal of Solids and Structures, 2012, 49(19/20): 2754–2762. DOI: 10.1016/j.ijsolstr.2012.05.005. [22] WANG Z G, LI Z D, XIONG W. Numerical study on three-point bending behavior of honeycomb sandwich with ceramic tile [J]. Composites Part B: Engineering, 2019, 167: 63–70. DOI: 10.1016/j.compositesb.2018.11.108. [23] WANG D M. Impact behavior and energy absorption of paper honeycomb sandwich panels [J]. International Journal of Impact Engineering, 2009, 36(1): 110–114. DOI: 10.1016/j.ijimpeng.2008.03.002. [24] HEIMBS S, SCHMEER S, MIDDENDORF P, et al. Strain rate effects in phenolic composites and phenolic-impregnated honeycomb structures [J]. Composites Science and Technology, 2007, 67(13): 2827–2837. DOI: 10.1016/j.compscitech.2007.01.027. [25] SHAN J F, XU S L, ZHOU L J, et al. Dynamic fracture of aramid paper honeycomb subjected to impact loading [J]. Composite Structures, 2019, 223: 110962. DOI: 10.1016/j.compstruct.2019.110962. [26] 范成年, 张磊, 单俊芳, 等. 复合纸蜂窝结构的力学性能与吸能特性研究 [J]. 实验力学, 2021, 36(5): 627–637. DOI: 10.7520/1001-4888-21-001.FAN C N, ZHANG L, SHAN J F, et al. The mechanical performance and energy absorption properties of composite paper honeycomb structures [J]. Journal of Experimental Mechanics, 2021, 36(5): 627–637. DOI: 10.7520/1001-4888-21-001. [27] 徐松林, 单俊芳, 周李姜, 等. 对试样进行中等应变速率压缩的实验装置: CN109781555A [P]. 2019-05-21. 北京: 北京集佳知识产权代理有限公司, 2019. [28] RUAN D, LU G, CHEN F L, et al. Compressive behaviour of aluminium foams at low and medium strain rates [J]. Composite Structures, 2002, 57(1): 331–336. DOI: 10.1016/S0263-8223(02)00100-9. [29] XU S Q, RUAN D, BEYNON J H, et al. Experimental investigation of the dynamic behavior of aluminum foams [J]. Materials Science Forum, 2010, 654/655/656: 950–953. DOI: 10.4028/www.scientific.net/MSF.654-656.950. 期刊类型引用(1)
1. 马昊,陈美多,袁良柱,王鹏飞,徐松林. 中等应变率下纸蜂窝结构的力学性能研究. 高压物理学报. 2024(04): 102-113 .  百度学术
百度学术其他类型引用(0)
-








 下载:
下载:















 下载:
下载:


 百度学术
百度学术






