脉冲载荷下加筋圆板的各向同性快速等效方法

焦重熙; 钟巍; 王霂; 梅晰洁; 邱信明

doi:10.11883/bzycj-2023-0308

摘要: 加筋板在爆炸与冲击防护中应用广泛，而其动力响应的快速求解一直是工程中关注的重点。对于径向均匀加筋的圆板，基于刚度叠加思想，提出了一种将其等效为各向同性平板的方法，用于分析其在脉冲载荷下弹性阶段的动力响应。结合理论推导与数值方法，显式地给出了简洁的等效平板厚度公式。经验证，提出的等效方法建立了加筋圆板与均质圆板间的内在联系，适用于多种加筋尺寸、材料及载荷形式。等效圆板与加筋圆板的最大挠度偏差不超过6%，低阶振动频率偏差不超过10%。相比于直接对加筋圆板进行计算，等效分析方法大大提高了求解效率，且保证了很高的计算精度，在冲击响应预测和结构优化等工程应用中具有重要意义。

关键词:

Abstract: Stiffened panels are widely used in the explosion and impact protection, thus a fast and accurate method for solving their dynamic response is highly desired in engineering. Based on the idea of stiffness superposition, a novel equivalent-isotropic-plate method is proposed in this paper to convert the radial and uniformly stiffened circular plate into an isotropic flat plate, so as to analyze its dynamic response in the elastic stage under uniform pulse loading. Since obtaining the dynamic response of an isotropic plate is mature and convenient, the equivalent analysis can overcome the computational difficulty of anisotropy in direct modeling, thus greatly improving the solving efficiency. Through the linear superposition of the plate and stiffener dynamic equations, a concise formula of the equivalent plate thickness is derived explicitly. The equivalent parameter in the formula is obtained with the assistance of simulation and numerical fitting, which directly measures the strengthening effect of the stiffeners on the plate. Employing the equivalent-isotropic-plate model, the overall dynamic response of a stiffened circular plate can be represented by that of an equivalent isotropic plate with acceptable accuracy, especially for low-order vibrations and center deflections. It is verified that the equivalent method can be successfully applied to a variety of stiffening types, materials, and load forms. The deviation of the maximum deflection response of the equivalent flat plate from that of the original stiffened circular plate does not exceed 6%, and the deviation of the response frequency does not exceed 10%. This completely meets the engineering requirements. The equivalent-isotropic-plate model verifies the feasibility of isotropic equivalence, and reveals the intrinsic connection between the radial stiffened circular plate and the homogeneous circular plate, which is of great significance in engineering applications such as response prediction and structural optimization.

Key words:

相比于传统平板结构，加筋板能够在较小的体积下实现较高的结构刚度与承载能力，且结构简单，易于生产制造，因此，其在汽车、船舶、建筑、航空航天等众多领域都有着广泛的应用，特别在冲击与爆炸防护方面有着较高的应用价值。国内外已有加筋板相关的众多研究^[1-3]，其中加筋板在冲击作用下动力响应分析是研究重点之一。理论方面，多数研究将平板与加强肋分离，进而分别建立其动力学微分方程，再根据界面连续条件与受力平衡建立平板和加强肋的联系，从而导出问题的控制方程^[4-6]。但由于这一求解过程将涉及到大量的数学推导，且受到微分方程的非线性限制，因此很难给出问题的解析解，多数只能通过有限差分等方法给出数值解或半解析解。另一途径是基于有限元方法建立新的更准确的加筋板数值求解模型，如考虑翘曲等非线性效应的特殊单元^[7]、平板与加强肋的复合单元^[8]、加筋板无网格方法^[9]，等等。有限元方法能够处理复杂多样的加筋板类型，有着很高的适用性，但需要占用较高的计算资源，且要预先完成加筋板的建模和单元划分等前处理工作，不适于工程现场分析等需要快速应用的场景。而且有限元方法仅能够给出指定问题的数值解答，每算例均需仿真，不能抽象出一类问题中内含的本质物理规律。

因为直接对加筋板进行理论或数值分析比较复杂，可以考虑将加筋板等效为平板进行研究。在工程领域，尤其需要无需求解复杂方程的快速分析方法。一般来说，可以通过本构分析等方式将加筋板等效为各向异性平板，特别是正交加筋的情况，可以将其等效为正交异性平板。如，Karpov等^[10]提出了一种刚度涂抹法（smeared stiffener method），能够将正交加筋板（壳）等同于具有相同刚度的正交异性均匀板（壳）；Zhang等^[11]建立了多级加筋板的等效理论，能够将其均匀化为平板，同时保持结构的拉伸刚度和弯曲刚度不变；Xia等^[12]建立了波纹加筋板的等效模型，并给出了等效刚度参数的解析解。除了基于本构关系的严格推导外，一个经典的方法是Timoshenko等在20世纪50年代提出的加筋板等效模型（equivalent plate model, EPM方法）^[13]。该方法的思路非常简单：在线弹性小变形假设下，加筋板的刚度可以近似为平板刚度和加强肋刚度的线性叠加。若加筋板为正交加筋，则可以方便地将其等效为正交异性板，给出两个正交方向的弯曲刚度。该方法提供了加筋板弯曲刚度和扭转刚度的直接近似，同时公式中也保持了加筋板的原始几何参数，一定程度上揭示了加筋板和平板间的内在联系。Battaglia等^[14]对EPM预测单向加筋板动力响应的准确性进行了实验评估。结果表明，EPM在低阶响应和模态预测方面具有良好的性能，能够满足工程精度要求。

等效分析能够给出加筋板与各向异性板之间的等价关系，但为获得各向异性平板的动力响应解仍然无法避免求解复杂方程^[15]。实际上，均质平板动力响应问题可以给出简单的解析解，那么加筋板在一定条件下可以等效为各向同性平板吗？过去曾有研究尝试过，如Fertis等^[16]基于渐进分析给出了变厚度板的精确等效模型，也可以用于加筋板的等效分析。然而计算复杂性限制了其应用范围。另一种简单思路是根据等效前后体积不变直接给出等效平板厚度^[17]，但这种等效粗糙而不够准确。

本文中，首先将在EPM方法的基础上，将刚度叠加的等效思想用于径向均匀加筋圆板，通过理论推导与数值方法给出加筋圆板的各向同性等效模型及等效厚度计算公式；然后借助有限元仿真，验证该各向同性等效方法的合理性；最后，将给出此等效方法对不同加筋尺寸、材料、载荷类型的适用性及对于加筋圆板最大响应挠度的预测准确度。

1. 理论推导

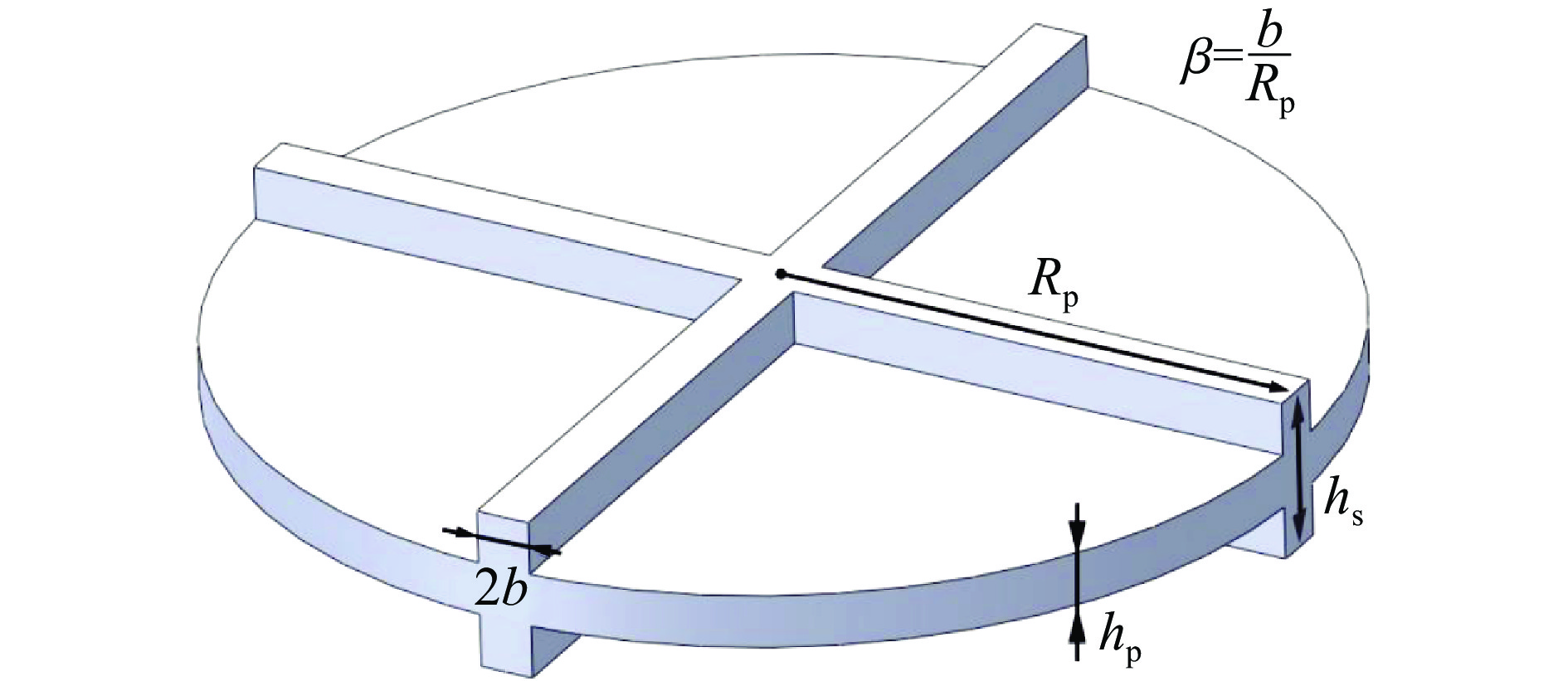
基于Timoshenko等提出的EPM等效理论^[13]，将建立适用于圆形加筋板的基本等效模型，并给出等效厚度表达式。为保证加筋板能够等效为各向同性平板，这里将限制等效方法的应用对象为径向均匀加筋板，且由线弹性材料构成。以图1中的十字形加筋圆板为例，均匀加筋板的各条肋夹角需要保持一致，且正反两面的肋厚相同。在此假设下，加筋板的中性层仍能够维持在板中面位置处，不会因肋厚而发生改变。假设加筋板的平板与加强肋均由同种线弹性材料构成，材料弹性模量为E，密度为ρ。几何尺寸上，圆板半径为R_p，厚度h_p；加筋板肋宽为2b，肋厚（包含板厚部分）为h_s。为便于后续理论分析，这里定义无量纲宽度β=b/R_p。为保持圆板的轴对称性，加强肋无量纲宽度β应小于0.1，这一条件也适用于绝大多数工程应用场景。

图 1 十字形加筋圆板几何尺寸

Figure 1. Geometry illustration of cross-stiffened circular plate

下载: 全尺寸图片幻灯片

在叠加等效的思想下，加筋圆板可以拆分为厚为h_p的平板与高为h_s的加强肋2个部分。若加筋板上表面受到均布脉冲载荷p(t)作用，则分解在平板和加强肋上分别为p_p和p_s，且各个载荷间满足平衡关系：p(A_s+A_p)=p_sA_s+p_pA_p。式中A_s为所有加强肋上表面积，A_p为平板区域上表面积。显然A_s+A_p为加筋板整体的上表面积。考虑到轴对称性，平板部分的动力学控制方程在极坐标(r, θ)下可以表示为：

$\frac{{{D_{\text{p}}}}}{{\rho {h_{\text{p}}}}}{\left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}}} \right)^2}{w_{\text{p}}} + \frac{{{\partial ^2}{w_{\text{p}}}}}{{\partial {t^2}}} = \frac{{{p_{\text{p}}}}}{{\rho {h_{\text{p}}}}}$

(1)

式中：D_p为平板弯曲刚度，w_p为平板挠度。由于肋宽及肋厚尺寸相对于板半径较小，因此加强肋可以采用Euler梁模型进行分析，其控制方程为：

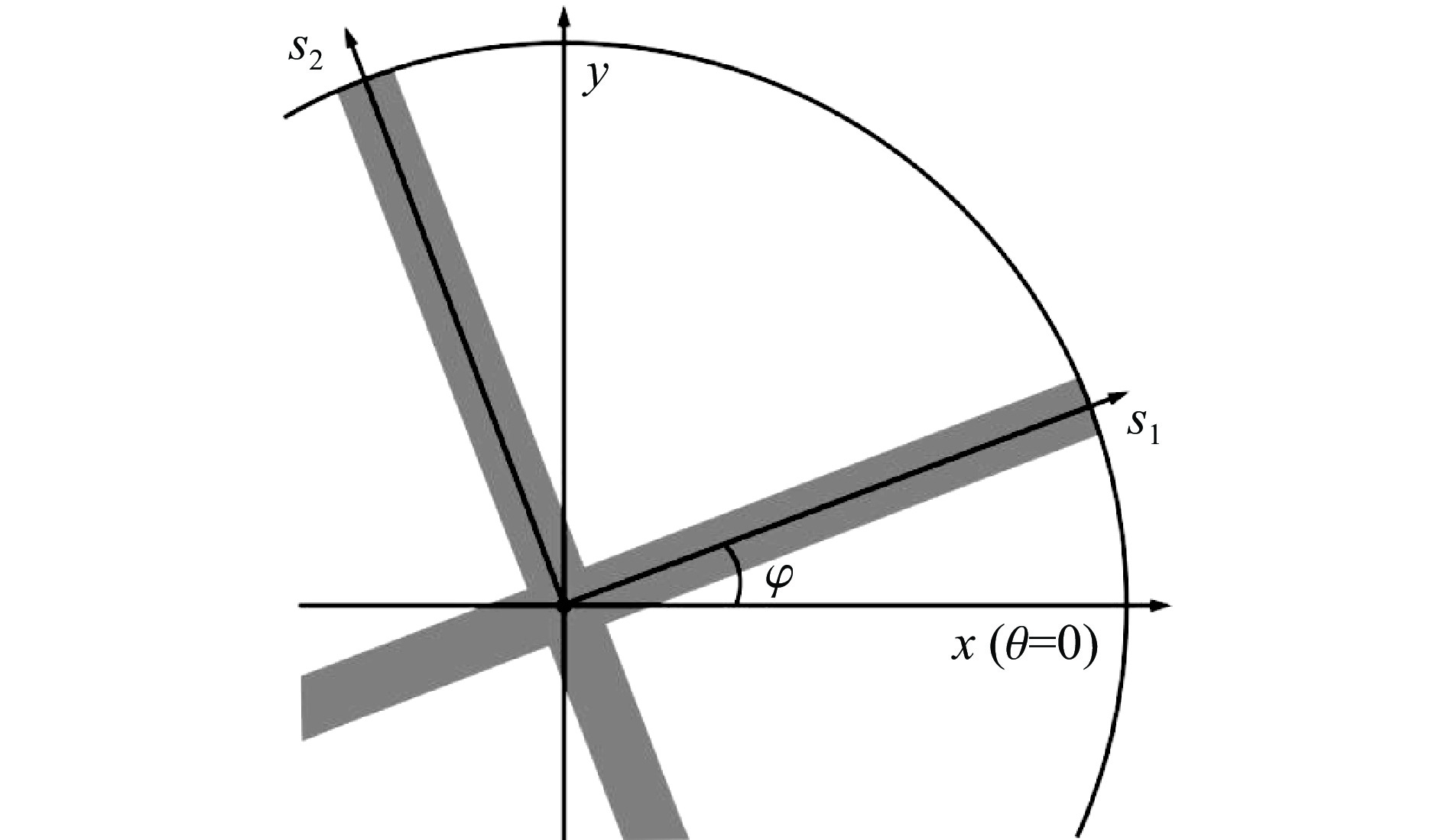
$\frac{{E{I_{\text{s}}}}}{{\rho S}}\frac{{{\partial ^4}{w_{\text{s}}}}}{{\partial {s^4}}} + \frac{{{\partial ^2}{w_{\text{s}}}}}{{\partial {t^2}}} = \frac{{{p_{\text{s}}}}}{{\rho {h_{\text{s}}}}}$

(2)

式中：w_s、S和I_s分别为加强肋的挠度、横截面积和惯性矩。该表达式中含有关于s的方向导数，取决于加强肋在平板上的布置方向。通过坐标转换关系可以将关于s的偏导数变换到极坐标(r, θ)下，如图2所示。

图 2 加强肋方向s₁和s₂的坐标变换

Figure 2. The coordinate transformation of the directions s₁ and s₂ of the stiffeners

下载: 全尺寸图片幻灯片

以图2中十字形加筋圆板为例，不妨假设其中一条肋与轴线θ = 0的夹角为 $\varphi$ ，方向坐标为s₁。作为坐标系转换的桥梁，坐标s₁首先被变换到图中(x, y)坐标系下，其一阶导数和二阶导数分别为：

$\frac{\partial }{{\partial {s_1}}} = \frac{\partial }{{\partial x}}\cos \varphi + \frac{\partial }{{\partial y}}\sin \varphi$

(3)

$\frac{{{\partial ^2}}}{{\partial s_1^2}} = \frac{{{\partial ^2}}}{{\partial {x^2}}}{\cos ^2}\varphi + \frac{{{\partial ^2}}}{{\partial {y^2}}}{\sin ^2}\varphi + 2\frac{{{\partial ^2}}}{{\partial x\partial y}}\cos \varphi \sin \varphi$

(4)

同理，设与该肋正交的另一条肋方向坐标为s₂。变换到(x, y)坐标系下，s₂的一阶导数和二阶导数分别为：

$\frac{\partial }{{\partial {s_2}}} = - \frac{\partial }{{\partial x}}\sin \varphi + \frac{\partial }{{\partial y}}\cos \varphi$

(5)

$\frac{{{\partial ^2}}}{{\partial s_2^2}} = \frac{{{\partial ^2}}}{{\partial {x^2}}}{\sin ^2}\varphi + \frac{{{\partial ^2}}}{{\partial {y^2}}}{\cos ^2}\varphi - 2\frac{{{\partial ^2}}}{{\partial x\partial y}}\cos \varphi \sin \varphi$

(6)

十字形加筋圆板共4条肋，另外2条肋的偏导数坐标变换结果与式(4)和(6)相同。因此，4条肋的方向导数叠加可以得到整体在(x, y)坐标系下的表达式：

$\sum\limits_{i = 1}^4 {\frac{{{\partial ^2}}}{{\partial s_i^2}}} = 2\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right)$

(7)

尽管式(7)是在十字形加筋圆板构型中推导得到的，但可以验证该式对于加筋数更多的均匀加筋圆板仍能够成立，仅在系数上存在差异，这并不影响后续的理论推导。(x, y)坐标系与(r, θ)坐标系的偏导数存在变换关系：

$\left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x}}} \\ {\dfrac{\partial }{{\partial y}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta } \\ {\sin \theta }&{\cos \theta } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial r}}} \\ {\dfrac{1}{r}\dfrac{\partial }{{\partial \theta }}} \end{array}} \right]$

(8)

因此，对于轴对称问题，式(7)中关于x和y的调和导数可以变换到(r, θ)坐标系下，即：

$\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}}$

(9)

以上推导完成了对于加强肋方向导数的坐标变换，按照这一基本思路即可完成平板控制方程(1)与加强肋控制方程(2)的线性叠加。

若等效各向同性平板存在，则等效平板的挠度w_e可以近似等于加筋板各部分的挠度，即w_e=w_p=w_s。因此，w_e满足的方程可以表达为式(1)与式(2)的加权线性叠加：

$\left( {K\frac{{E{I_{\text{s}}}}}{{\rho S}} + J\frac{{{D_{\text{p}}}}}{{\rho {h_{\text{p}}}}}} \right){\left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}}} \right)^2}{w_{\text{e}}} + \left( {K + J} \right)\frac{{{\partial ^2}{w_{\text{e}}}}}{{\partial {t^2}}} = K\frac{{{p_{\text{s}}}}}{{\rho {h_{\text{s}}}}} + J\frac{{{p_{\text{p}}}}}{{\rho {h_{\text{p}}}}}$

(10)

式中：K和J为权重系数，受到肋数量以及几何尺寸等因素的影响。假设等效平板受到与原加筋板相同的脉冲载荷p作用，则根据薄板控制方程基本形式，式(10)也可以等价地写为：

$\frac{{{D_{\text{e}}}}}{{\rho {h_{\text{e}}}}}{\left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}}} \right)^2}{w_{\text{e}}} + \frac{{{\partial ^2}{w_{\text{e}}}}}{{\partial {t^2}}} = \frac{p}{{\rho {h_{\text{e}}}}}$

(11)

式中：D_e、h_e和w_e分别为等效平板的弯曲刚度、厚度和挠度。由式(10)～(11)可以导出关于等效平板参数的关系式：

$K\frac{{EI}_{\mathrm{s}}}{\rho S}+J\frac{{D}_{\mathrm{p}}}{\rho h_{\mathrm{p}}}=\frac{D_{\mathrm{e}}}{\rho h_{\mathrm{e}}}\text{，}K+J=1\text{，}K\frac{p_{\mathrm{s}}}{\rho h_{\mathrm{s}}}+J\frac{p_{\mathrm{p}}}{\rho h_{\mathrm{p}}}=\frac{p}{\rho h_{\mathrm{e}}}$

(12)

其中：

${{I} _{\text{s}}} = \frac{{{bh} _{\text{s}}^3}}{{12}},\;\;S = {{bh} _{\text{s}}}, \;\;{{D} _{\text{p}}} = \frac{{{Eh} _{\text{p}}^3}}{{12\left( {1 - {\upsilon ^2}} \right)}} ,\;\;{{D} _{\text{e}}} = \frac{{{Eh} _{\text{e}}^3}}{{12\left( {1 - {\upsilon ^2}} \right)}}$

(13)

这里υ是材料泊松比，对大多数金属，0.2<υ<0.3，因此可以近似取1−υ²≈1以简化运算。由式(12)～(13)，可以得到等效平板的厚度：

$h_{\text{e}}^2 = \left( {1 - K} \right)h_{\text{p}}^2 + Kh_{\text{s}}^2$

(14)

可见，等效平板厚度与加筋板各部分厚度之间是简单的加权平方和关系，这揭示了加筋板与均质平板间的本质联系。由于推导过程不涉及到方程的求解，因此该等效厚度仅取决于加筋板的几何参数，而与材料、边界条件等无关，从而能大大简化求解过程，便于工程应用。式(14)中包含了一个重要的权重系数K，其取值范围为0～1，反映肋对加筋板的强化作用。当K=0时为未加筋状态，h_e=h_p；当K=1时对应肋布满平板表面的状态，h_e=h_s。其他K值涉及到加筋板的具体几何参数，需要通过数值方法确定。

2. 等效参数确定

将使用ANSYS LS-DYNA对加筋圆板进行数值模拟，探究其他几何参数对等效公式的影响，从而给出系数K的具体确定方法。

以十字形加筋圆板为例，结构整体（包括平板与加强肋部分）均采用SHELL163三角形单元进行网格划分，单元尺寸限制在30 mm以内，如图3所示。图中蓝色与红色区域单元厚度不同，分别对应加筋圆板的肋厚h_s和板厚h_p。由于等效方法仅限于弹性变形过程，因此设置为线弹性材料，在ANSYS LS-DYNA中选择Linear-Elastic-Isotropic。设置材料弹性模量E=72 GPa，泊松比υ=0.23，密度ρ=2500 kg/m³，与铝合金和普通玻璃相似。此外，由于等效理论并不涉及到边界条件，本文中加筋板边缘均采取固支条件。在几何尺寸选择上，不失一般性，本节及后续模型中圆板尺寸固定为R_p=0.5 m，h_p=10 mm。加筋板表面采用线性衰减脉冲压力加载，即t=0 ms时，p=50 kPa；t =2 ms时，p=0 kPa。已确保加筋板变形全过程在弹性范围内。

图 3 LS-DYNA中十字形加筋圆板的壳单元网格划分

Figure 3. The mesh of cross-stiffened circular plate using shell element in LS-DYNA

下载: 全尺寸图片幻灯片

在探究参数K的具体表达之前，将首先验证式(14)所给厚度关系的正确性。为获取加筋圆板的等效平板厚度，根据加筋圆板仿真结果进行反向推导。即首先由数值模拟获得加筋圆板的最大挠度值，随后根据均质圆板理论，找出对应此最大挠度的圆板厚度，过程中保证等效圆板与加筋圆板的载荷及边界条件相同。

要根据最大挠度反推圆板的厚度需要有圆板在脉冲载荷下的位移时程曲线，且能够显式地包含圆板几何参数。然而，在目前的研究背景下还无法完全解析地给出圆板动力学微分方程的解。因此，本文中采用半解析求解的理论方法^[18]，给出线性衰减脉冲下弹性圆板的挠度响应，即位移时程曲线。通过改变圆板厚度，可进一步提取不同位移时程曲线的第1个位移峰值，获得多个离散的数据点，如图4所示。由于这一过程是半解析的，因此没有办法给出最大挠度和圆板厚度之间的显式表达式，但可以根据这些数据点给出一条拟合曲线，具体表达式为：

图 4 不同厚度圆板在线性衰减脉冲（压力峰值50 kPa，衰减时间2 ms）作用下的最大响应挠度及拟合曲线

Figure 4. The maximum deflections and fitting curve of circular flat plates with different thicknesses under linear decaying pulse with the peak pressure of 50 kPa and the decay time of 2 ms

下载: 全尺寸图片幻灯片

$w_{\max }=\frac{-0.017\;98 h+1.033}{h^{2}+12.93 h-45.95}$

(15)

利用这一拟合函数即可根据最大挠度反推出圆板厚度。

事实上，等效理论的推导是基于加强肋和平板挠度的微分方程，此处将最大响应挠度作为等效标准是合理的。如上所述，计算肋宽β=0.05, 0.07, 0.09的3种十字形加筋圆板在不同肋厚设置下所对应的等效平板厚度，如图5所示。可见不同β下加筋板的 $h_{\mathrm{s}}^2$ 和 $h_{\mathrm{e}}^2$ 基本为线性关系，验证了式(14)，且参数K不受h_s的影响。由式(14)，拟合直线的斜率即待求的参数K，具体数值已标注在图中。显然更宽的加强肋对板的强化作用更大，因而对应更大的K值。另外3条拟合直线交点大致在（100,100）处，即对应肋厚h_s=h_p的情况，此时等效平板厚度就是h_p，与事实相符合。为便于讨论，后续的加筋圆板模型均保持肋厚h_s为30 mm。

图 5 3种不同十字形加筋圆板的

$h_{\mathrm{s}}^2$ 和

$h_{\mathrm{e}}^2$ 的关系

Figure 5. The relations between

$h_{\mathrm{s}}^2$ and

$h_{\mathrm{e}}^2$ for three different cross-stiffened circular plates

下载: 全尺寸图片幻灯片

图5中仅展示了肋宽β对于参数K的影响，且是针对十字形加筋圆板（n=4）的。除此之外，等效方法也可适用于其他加筋数目的情况。图6中给出了n=3, 4, 5的加筋圆板在不同肋宽β（≤0.1）下的K值。可以发现，K与β基本呈线性关系，也与n成比例。因此，采用表达式K=Cnβ对数据拟合得到：

图 6 不同n、β设置下加筋圆板的等效参数K

Figure 6. The equivalent parameter K of the stiffened circular plates with different n and β

下载: 全尺寸图片幻灯片

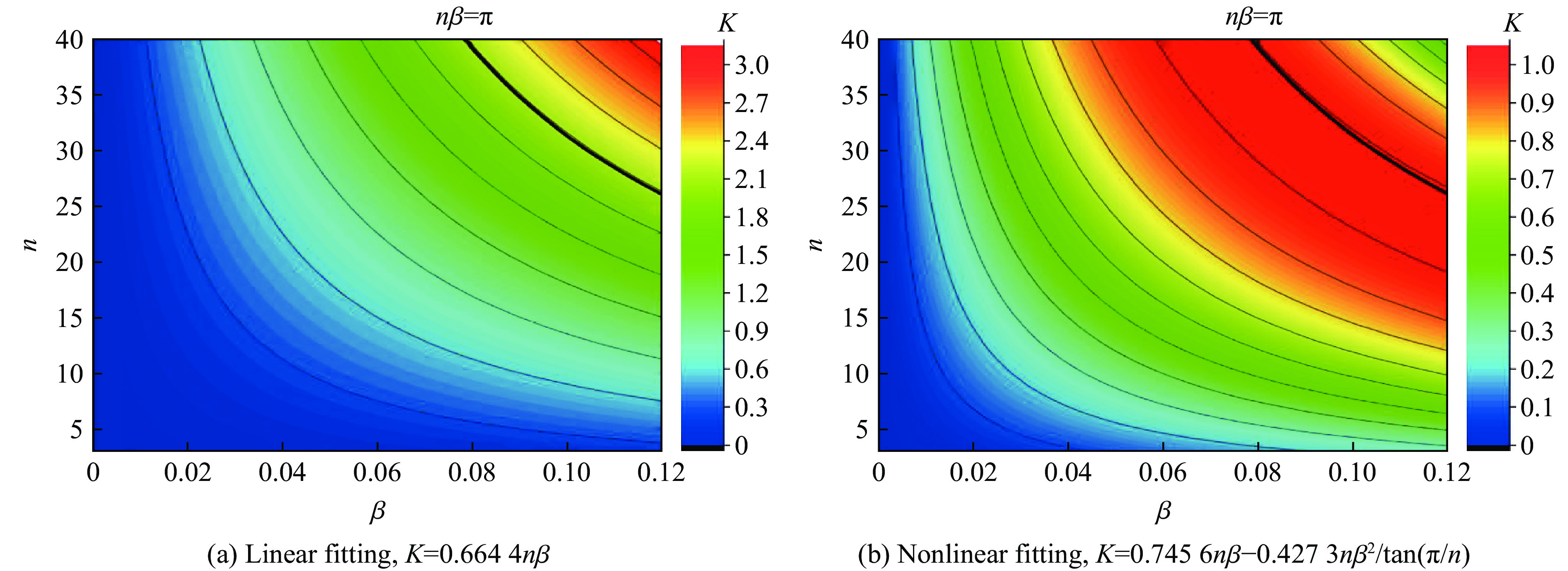
$K = 0.664\;4n\beta \qquad\quad R^2=0.979$

(16)

式(16)的等值线图如图7(a)所示。实际上，该式只是K的线性近似表达，仅适用于n和β较小的情况。仔细观察图6，可以发现当n=5时，K会随β的增加而逐渐呈现非线性，增长趋势逐渐平缓。当n或β不断增加时，加强肋逐渐覆盖圆板表面，可以预见K不再与n和β保持线性，而是逐渐趋于1。而采用式(16)会出现参数K>1，这显然是不合理的。

图 7 等效参数K(n, β)拟合函数图

Figure 7. The fitting function graphs of equivalent parameter K(n, β)

下载: 全尺寸图片幻灯片

为了给出K(n, β)表达式中的非线性项，考虑从加筋面积的计算公式入手。当加强肋数量较少，或宽度较小时，加筋面积占比接近0，此时参数K=0。反之，当加筋面积占比接近1时，参数K也会趋于1，两者在变化趋势上应是类似的。由几何分析，可以用n和β表示加筋面积占比：

$A\left( {n,{\text{ }}\beta } \right) = \left( {\arcsin \beta + \beta \sqrt {1 - {\beta ^2}} - {{{\beta ^2}} / {\tan {\frac{{\text{π}}}{n}} }}} \right)\frac{n}{{\text{π}}}$

(17)

将式(17)中各项关于β进行Taylor展开，只取关于β的前二阶项，可得：

$A\left( {n,\beta } \right) = \left( {2n\beta - {{n{\beta ^2}} / {\tan {\frac{\text{π}}{n}} }}} \right)\frac{1}{{\text{π}}}$

(18)

式(18)括号中的第1项是关于n和β的线性项，对应于式(16)；而括号中的第2项，即K(n, β)的非线性项，该非线性项一定程度上反映了矩形加强肋在圆板中心重叠的面积，具有实际物理意义。非线性的影响随着n和β的增加而增大。当β～ tan(π/n)时，非线性项与线性项的量级相同，其影响将不可忽略。若限定等效方法使用范围为β≤0.1，则加筋数n>4时线性拟合式(16)将不再适用。在加入非线性项后重新对数据进行拟合，可以得到：

$K = 0.745\;6n\beta-{{0.427\;3n{\beta ^2}} / {\tan {\frac{\text{π}}{n}} }} \qquad\quad R^2 = 0.995$

(19)

式(19)的图像绘制在图7(b)中。可以发现，在考虑非线性项的影响后，式(19)的拟合精度相较式(16)有所提高。令式(18)等于1，可以近似得到nβ=π，即加强肋覆盖圆板所有表面时的临界线，在图7中以黑色实线标出。理论上当加筋圆板参数满足nβ=π时应有K=1，如前文所述，但式(16)不能满足这一条件；而若采用式(19)，最大值K≈1且就在临界线附近，与预期相符。此外，由于非线性项的存在，式(19)存在下降阶段。但由于此区域已经超出了临界线，因此不在公式的适用范围内，不需要考虑。

至此，式(14)与式(19)完全确定了径向均匀加筋圆板的等效厚度公式。在给定加筋圆板的几何参数后，可以根据公式快速而又简单地给出其等效各向同性圆板的厚度。

3. 适用性验证

利用已给出的等效平板厚度公式，将对等效方法的适用性展开讨论。

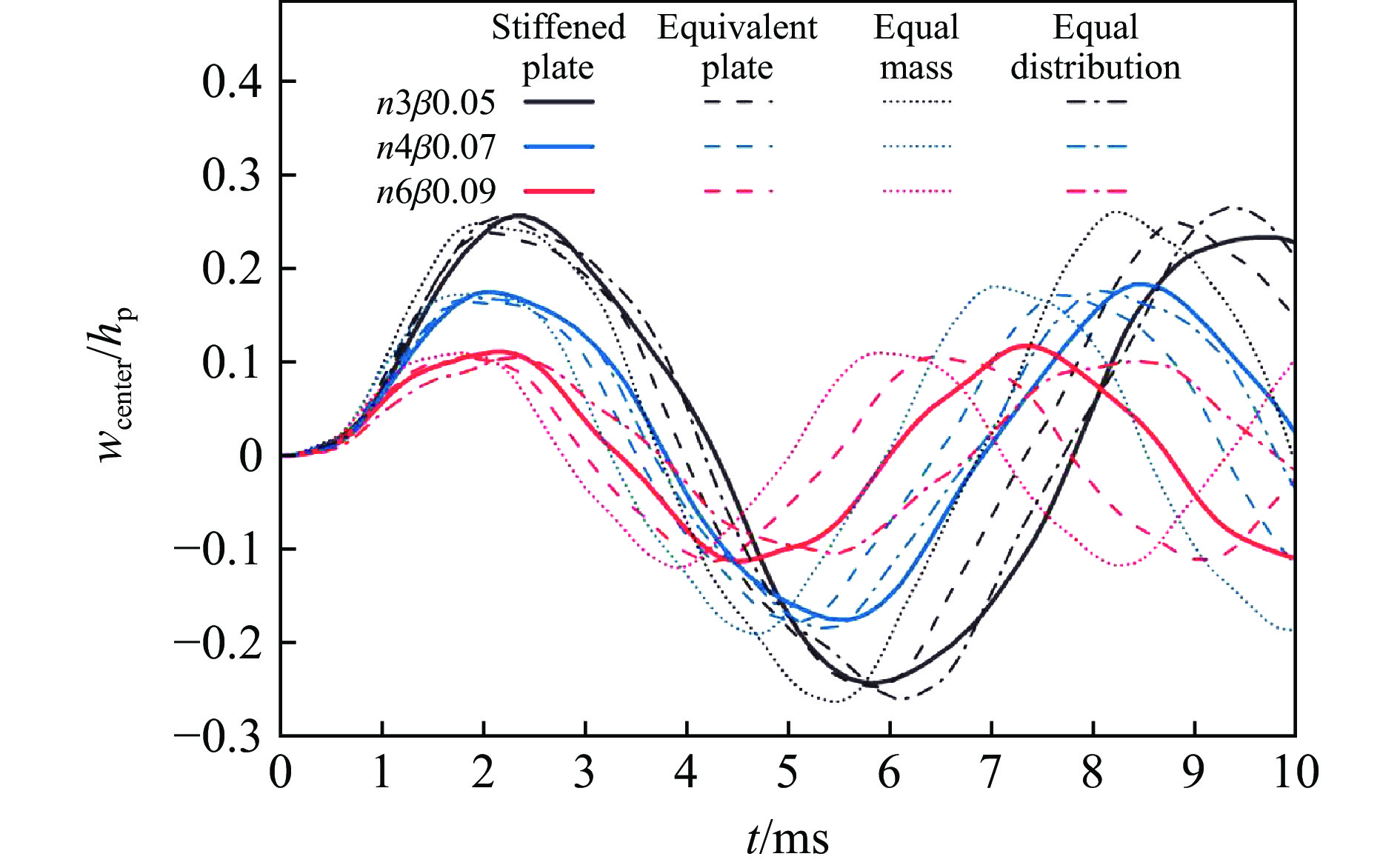
首先，选取n3β0.05、n4β0.07和n6β0.09等3种不同加筋圆板作为样本；然后，根据等效方法获得对应的等效平板，系数K使用式(19)进行计算；最后，通过有限元仿真给出二者在线性衰减脉冲载荷（压力峰值50 kPa，衰减时间2 ms）下的中心挠度-时间曲线，如图8所示。图中的中心挠度w_center已使用板厚进行无量纲化，实线为加筋圆板，虚线为等效平板。可以发现，3种加筋圆板的挠度-时间曲线与对应等效平板曲线的相似度较高。一般情况下，加筋板在第1个响应周期内即可达到最大挠度，而后振动幅度逐渐衰减。在第1个响应周期内，加筋板中心挠度的最大值与最小值和对应等效平板的相差不大，两者偏差在2%左右，等效性很好。而在响应频率方面，等效平板的频率要稍高于加筋圆板约5%。在第1个响应周期后二者曲线会发生一定的偏离，等效平板会更早地到达第2个挠度响应峰值。这主要是加筋圆板与等效平板在总质量及质量分布上的不同引起的。n3β0.05、n4β0.07和n6β0.09等3种加筋圆板的体积分别为0.0093、0.0106和0.0128 m³，而等效平板体积分别为0.0108、0.0127和0.0156 m³。如果采用同种材料，则等效平板质量均高于对应加筋圆板。通过调整等效后平板的密度，使得等效前后质量保持不变，可以给出等质量修正板的挠度时间曲线，如图8中的点线所示。可以发现，等质量修正板的响应频率会高于未修正的等效平板，而响应幅值基本变化不大。另外，考虑到加筋圆板质量更多地集中在加筋区域，可以对等效平板进行质量分布的修正。类似的，通过调整密度，使等效平板的质量分布比例与对应加筋圆板相同，但整体质量不做改动。等质量分布修正板的挠度时间曲线如图8中的点划线所示。可以发现，通过模拟加筋圆板的质量分布可使得等效平板振动频率更低，能够一定程度补偿等效方法带来的振动频率偏高问题。但实际上，2种质量修正均不一定能够使等效平板的频率更接近对应的加筋圆板。比如：n6β0.09等质量分布修正后的振动频率就要小于原结构，振动频率误差依然很高；3种结构在总质量修正后的频率误差甚至会更高。所以，在该等效方法基础上强行对质量进行修正的意义不大。尽管质量不同会带来一定的预测偏差，但误差范围是可以接受的。

图 8 3种不同加筋圆板及其等效平板、等质量修正板、等质量分布修正板的中心挠度-时间曲线对比

Figure 8. Comparisons of the central deflection-time curves among three different stiffened circular plates and the corresponding equivalent plates, equal mass revised plates, equal mass distribution revised plates

下载: 全尺寸图片幻灯片

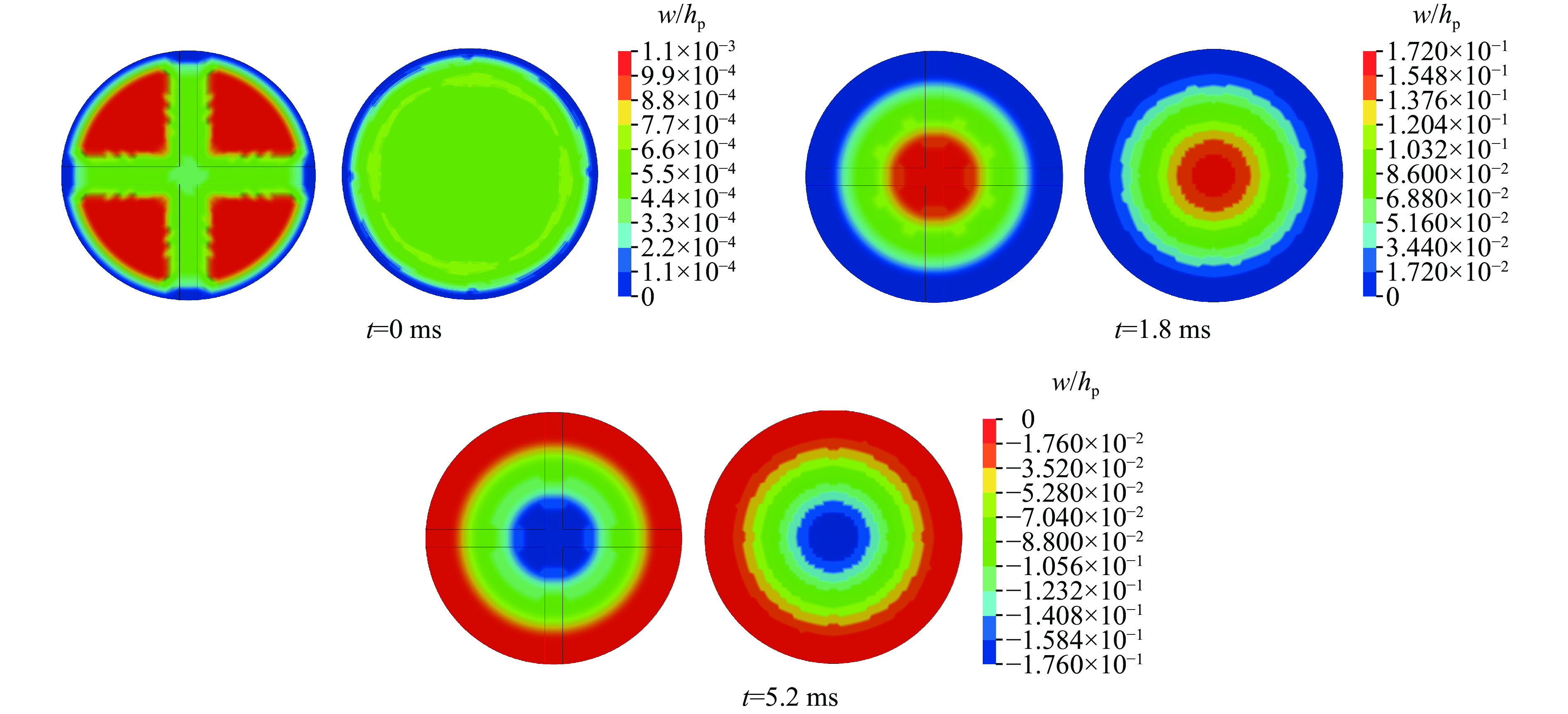
此外，图9给出了n4β0.07加筋圆板与对应等效平板在t=0, 1.8, 5.2 ms时刻的挠度分布云图，分别对应图8中载荷刚施加于表面、第一响应峰、第一响应谷的时刻。由于加强肋的存在，载荷刚施加时加筋圆板与对应等效平板的挠度分布并不相同，加筋圆板的最大挠度集中在未加肋区域，等效平板的挠度较小且分布更均匀。而在t=1.8 ms和t=5.2 ms时刻二者的云图基本相同，最大挠度均集中在板中间，其他区域的挠度数值也非常接近。总体来看，在低阶振动频率和最大挠度预测方面，采用本文中提出的等效方法对加筋圆板进行等效研究是行之有效的。

图 9 不同时刻n4β0.07加筋圆板(左)与对应等效平板(右)的挠度分布云图

Figure 9. The deflection contour maps of the stiffened circular plate n4β0.07 (left) and the corresponding equivalent plate (right) at different times

下载: 全尺寸图片幻灯片

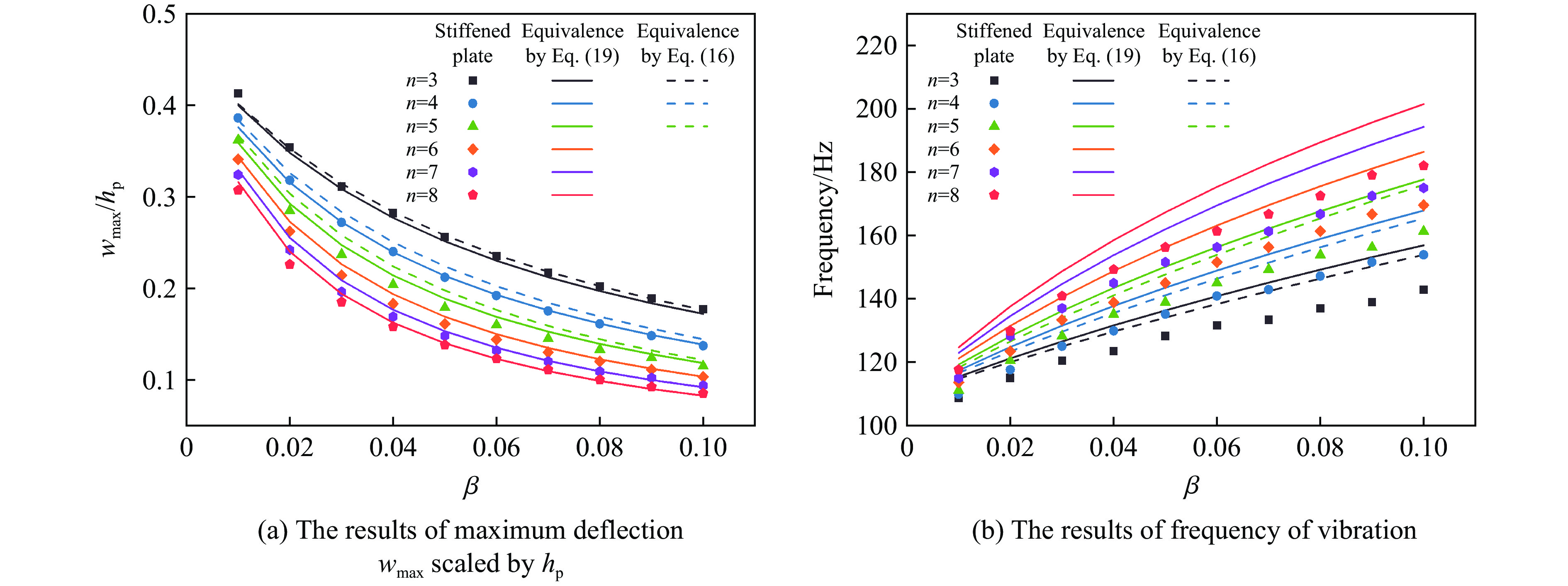
除工程中常见的加筋数量n=3, 4, 5外，本文的等效方法对于加筋数目更多的结构也具有很好的适用性。图10中给出了n=3～8，β=0.01～0.1的加筋圆板及其等效平板在与前文相同的线性衰减脉冲下的最大挠度w_max和振动频率。此外，采用系数K的线性表达式(16)对n=3, 4, 5的加筋圆板进行了等效，结果以虚线绘制在图10中。从图10(a)中可以看到，尽管式(19)是由加筋数为n =3, 4, 5仿真数据拟合得到，但该公式对于n更大的加筋圆板的最大挠度预测能力依然很高，且对于不同的n和β，加筋圆板和等效平板之间的最大偏差不超过6%。但如果采用式(16)进行等效，最大挠度误差会随着加筋数n的增加而增大。当n≤4时，误差能够控制在6%以内，但当n=5时误差已增长到10%左右。因此对于加筋数大于4的结构，更建议采用式(19)进行等效。对于低阶振动频率的等效性，在图10(b)中，由于加筋板和平板在质量分布和几何外形等方面存在本质不同，不论采用表达式(16)或(19)，等效平板的响应频率均要高于加筋板。具体数值上，等效平板与加筋圆板的振动频率误差在10%左右，表达式(16)的等效结果要稍好于表达式(19)，但区别并不是很大。

图 10 不同n、β设置下加筋圆板及其等效平板（采用式(16)或式(19)）在同等线性衰减脉冲载荷下的响应情况对比

Figure 10. Comparisons of the dynamic response of the stiffened circular plates and the corresponding equivalent plates (by Eq.(16) or Eq. (19)) with different n and β under the same linear decaying pulse

下载: 全尺寸图片幻灯片

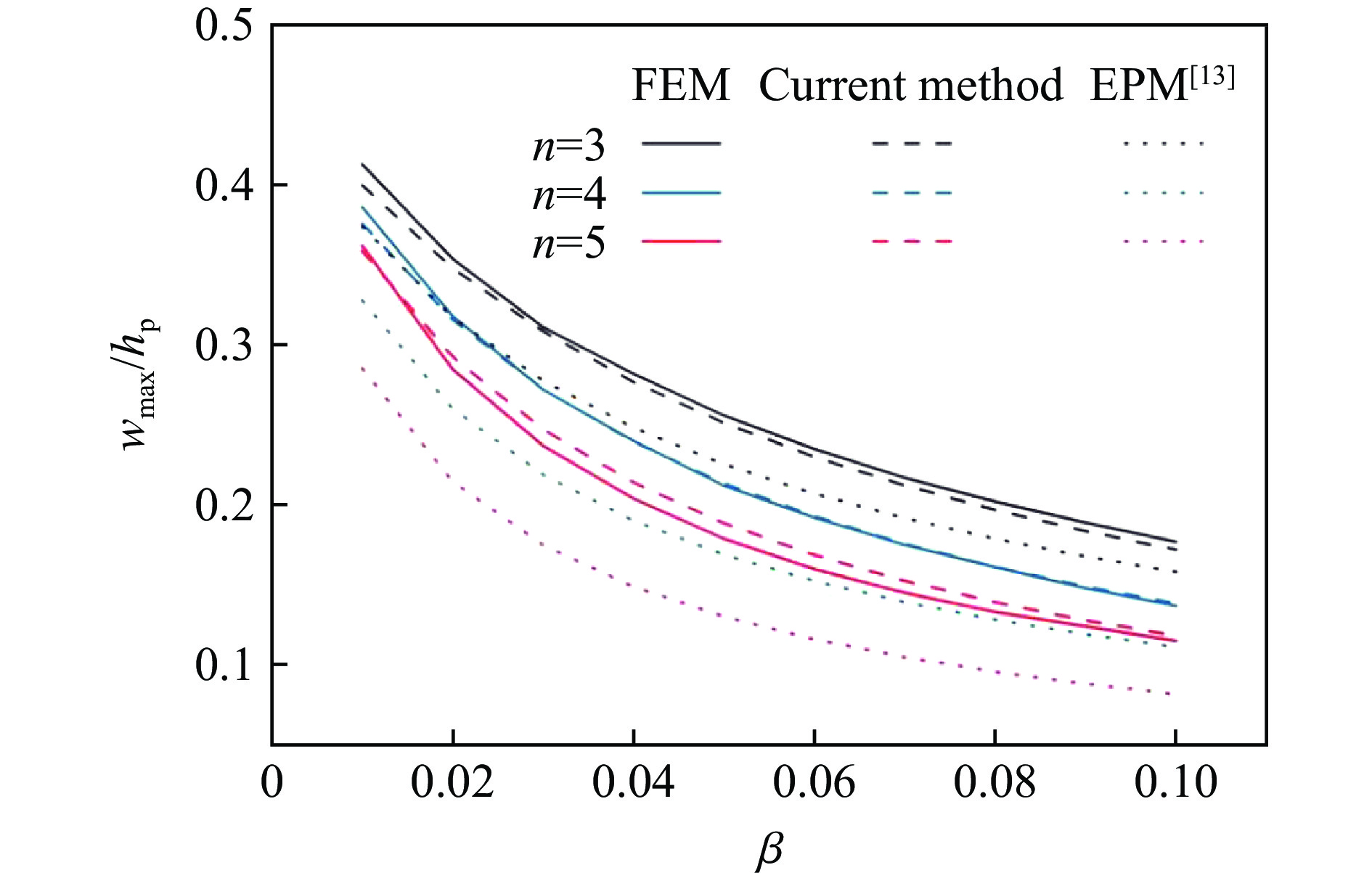
另外，本文中提出的等效方法与Timoshenko等提出的EPM等效理论^[13]相比准确性也更高。实际上，Timoshenko等^[13]仅讨论了矩形加筋板，但依然可以按其思想推导出圆形加筋板的等效公式。根据第1节中所给的坐标系变换关系，可将矩形板变换到圆板，给出EPM方法下的圆板等效厚度公式：

${h^3_\text{e}} = {h^3_\text{p}} + \frac{{{n^2}\beta }}{{2{\text{π}}}}{h^3_\text{s}}$

(20)

可以发现式(20)较本文中提出的等效方法更简洁，不同的是，该公式给出的等效厚度与加筋圆板各厚度之间是三次方关系。图11中展示了本文等效方法（采用式(19)）与EPM方法获得的等效圆板在相同线性衰减脉冲载荷下的最大挠度，加筋数量不超过5。可以发现，EPM的等效误差较大，而且明显随着加筋数量的增加而增大，最大误差在20%左右。这一误差主要源于EPM是在准静态条件下建立的，而且主要适用于矩形板等间距加筋的情况，在圆板等效方面肯定会稍显不足。

图 11 本文等效方法与Timoshenko等^[13]提出的EPM对n=3, 4, 5加筋圆板的最大挠度等效情况对比

Figure 11. Comparison of the maximum deflections of the stiffened circular plate (n=3, 4, 5) using current equivalent method and the EPM proposed by Timoshenko, et al^[13]

下载: 全尺寸图片幻灯片

总体来看，本研究提出的等效方法对于轴对称均匀加筋圆板具有普适性，且关于K的拟合公式(19)能够正确反映各加强肋对于圆形平板的强化作用。在最大挠度预测方面误差不超过6%，在低阶振动频率预测方面误差不超过10%。

前文研究的加筋板均为同种材料，且载荷的脉冲大小和类型固定。实际上等效理论的推导过程与材料和载荷无关，因此方法本身不受材料与载荷参数的限制。以n4β0.07加筋圆板为例，加筋板边缘保持固支，验证不同载荷及材料下方法的适用性。

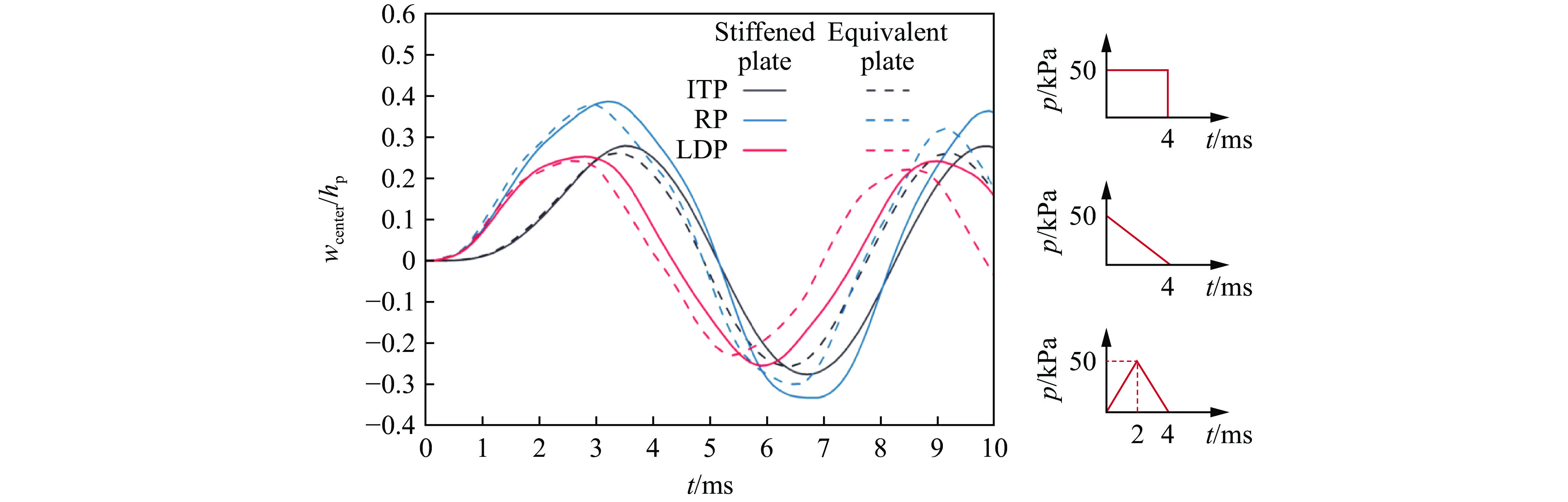
仍然采用线性衰减脉冲，但t=0 ms时的压力调整为1～500 kPa不等，脉冲衰减时间为2 ms，仿真获得的加筋圆板及其等效平板的最大挠度值如图12所示。可见，在p=150 kPa之前最大挠度基本与脉冲压力保持线性关系，且加筋圆板与等效平板在相同载荷下的最大挠度基本一致。而在150 kPa后，最大挠度与脉冲压力之间不再保持线性关系，且挠度达到了板厚同等量级，此时为大变形阶段。可以发现，等效平板能够捕捉到最大挠度-脉冲压力之间从线性到非线性的变化，且误差能够保持在10%以内。尽管本文的等效方法是建立在小挠度模型上的，但完全可以拓展到大挠度变形问题中。这并不是巧合，对于考虑几何非线性的平板大挠度有限变形方程（冯卡门方程），刚度项只存在于方程的线性项中，因此几何非线性项并不会影响到刚度叠加原理。除了脉冲载荷大小，本文的等效方法可适用于多种脉冲载荷形式。采用矩形或等腰三角脉冲进行加载，获得加筋圆板及其等效平板的中心挠度-时间曲线，如图13所示。显然，尽管载荷类型不同会导致加筋圆板的响应情况存在差别，但采用等效方法给出的曲线与加筋圆板的差距较小，最大挠度差异不超过5%。

图 12 不同线性衰减脉冲压力下的n4β0.07加筋圆板与对应等效平板的最大挠度

Figure 12. The maximum deflections of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the triangle decaying pulse with different pressure

下载: 全尺寸图片幻灯片

图 13 矩形脉冲（RP）、线性衰减脉冲（LDP）和等腰三角脉冲（ITP）下的n4β0.07加筋圆板与对应等效平板的中心挠度-时间曲线

Figure 13. The central deflection-time curves of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the rectangle pulse (RP), linear decaying pulse (LDP), and isosceles triangular pulse (ITP)

下载: 全尺寸图片幻灯片

材料适用性方面，除了前文使用的类铝合金材料，本文中又分析了镁合金（E = 45 GPa，υ = 0.35，ρ = 1700 kg/m³）和合金钢（E = 210 GPa，υ = 0.25, ρ = 7900 kg/m³）2种材料。载荷仍为线性衰减脉冲（压力峰值50 kPa，衰减时间2ms）固定不变。3种材料加筋圆板及对应等效平板的中心挠度-时间曲线如图14所示。容易看出，材料尽管不同，等效平板的响应曲线与加筋圆板基本一致，最大挠度预测误差不超过6%。说明本文等效方法基本不受材料参数的影响，具有普适性。

图 14 铝合金、镁合金、合金钢n4β0.07加筋圆板与对应等效平板的中心挠度-时间曲线

Figure 14. The central deflection-time curves of the stiffened circular plate n4β0.07 and the corresponding equivalent plate made of different materials: aluminum alloy, magnesium alloy and alloy steel

下载: 全尺寸图片幻灯片

4. 结　论

基于Timoshenko等提出的加筋板等效求解方法中的刚度叠加思想，提出了一种适合径向均匀加筋圆板的等效模型，能够在线弹性范围内将其等效为各向同性圆板，从而大大简化问题求解过程。通过理论推导给出了等效厚度基本表达式(14)；并通过仿真与数值方法给出了等效参数K的具体表达式，二者构成了等效方法的核心。其中，等效参数K定量反映了肋数与肋宽对加筋圆板的强化作用。本文提供了K的2个拟合函数：式(16)可用于加筋数目n和肋宽β较小的情况（n≤4，β≤0.1），简单易用；而式(19)包含有非线性项，精度更高，适用于更广泛的加筋情况。通过有限元验证，提出的等效方法适用于工程中常见均匀加筋圆板（n≤8，β≤0.1），小挠度变形时最大挠度预测误差小于6%（若采用式(16)则要求n≤4，式(19)可至n=8），而大挠度变形问题最大挠度预测误差小于10%。等效平板响应频率稍快于对应加筋圆板，但式(16)及式(19)的频率误差均在10%以内，对第一响应周期内的等效分析影响不大。此外，经验证该等效方法不受材料参数以及载荷大小、类型的限制，且能够用于平板大挠度变形的情况，适用范围广泛，能够满足工程中快速等效分析的需求。也可以反向使用，在保持最大挠度不变的情况下给出平板对应的加筋板，以节省结构材料。

总之，本文中提出的等效方法揭示了加筋圆板与均质平板之间内在联系，表达式简洁、物理概念清楚、计算较为准确且效率高。尽管本文的等效理论限制在弹性范围内，但也有着一定的工程意义。如对于玻璃这类弹脆性材料，其在冲击响应过程中不存在塑性变形阶段，一旦达到弹性极限即发生破坏，因此只需要在弹性阶段内对其进行分析。在城市建筑中，玻璃幕墙结构往往是含有框架的。由于铝合金的弹性模量、泊松比均与普通玻璃相近，在弹性响应范围内，可以将这一结构视为加筋板。冲击载荷下往往玻璃优先发生破坏，因此本文的等效方法可用于爆炸脉冲下玻璃幕墙的响应问题，在响应挠度预测和结构优化等工程应用中具有一定价值。

图 1 十字形加筋圆板几何尺寸

Figure 1. Geometry illustration of cross-stiffened circular plate

下载: 全尺寸图片幻灯片

图 2 加强肋方向s₁和s₂的坐标变换

Figure 2. The coordinate transformation of the directions s₁ and s₂ of the stiffeners

下载: 全尺寸图片幻灯片

图 3 LS-DYNA中十字形加筋圆板的壳单元网格划分

Figure 3. The mesh of cross-stiffened circular plate using shell element in LS-DYNA

下载: 全尺寸图片幻灯片

图 4 不同厚度圆板在线性衰减脉冲（压力峰值50 kPa，衰减时间2 ms）作用下的最大响应挠度及拟合曲线

Figure 4. The maximum deflections and fitting curve of circular flat plates with different thicknesses under linear decaying pulse with the peak pressure of 50 kPa and the decay time of 2 ms

下载: 全尺寸图片幻灯片

图 5 3种不同十字形加筋圆板的 $h_{\mathrm{s}}^2$ 和 $h_{\mathrm{e}}^2$ 的关系

Figure 5. The relations between $h_{\mathrm{s}}^2$ and $h_{\mathrm{e}}^2$ for three different cross-stiffened circular plates

下载: 全尺寸图片幻灯片

图 6 不同n、β设置下加筋圆板的等效参数K

Figure 6. The equivalent parameter K of the stiffened circular plates with different n and β

下载: 全尺寸图片幻灯片

图 7 等效参数K(n, β)拟合函数图

Figure 7. The fitting function graphs of equivalent parameter K(n, β)

下载: 全尺寸图片幻灯片

图 8 3种不同加筋圆板及其等效平板、等质量修正板、等质量分布修正板的中心挠度-时间曲线对比

Figure 8. Comparisons of the central deflection-time curves among three different stiffened circular plates and the corresponding equivalent plates, equal mass revised plates, equal mass distribution revised plates

下载: 全尺寸图片幻灯片

图 9 不同时刻n4β0.07加筋圆板(左)与对应等效平板(右)的挠度分布云图

Figure 9. The deflection contour maps of the stiffened circular plate n4β0.07 (left) and the corresponding equivalent plate (right) at different times

下载: 全尺寸图片幻灯片

图 10 不同n、β设置下加筋圆板及其等效平板（采用式(16)或式(19)）在同等线性衰减脉冲载荷下的响应情况对比

Figure 10. Comparisons of the dynamic response of the stiffened circular plates and the corresponding equivalent plates (by Eq.(16) or Eq. (19)) with different n and β under the same linear decaying pulse

下载: 全尺寸图片幻灯片

图 11 本文等效方法与Timoshenko等^[13]提出的EPM对n=3, 4, 5加筋圆板的最大挠度等效情况对比

Figure 11. Comparison of the maximum deflections of the stiffened circular plate (n=3, 4, 5) using current equivalent method and the EPM proposed by Timoshenko, et al^[13]

下载: 全尺寸图片幻灯片

图 12 不同线性衰减脉冲压力下的n4β0.07加筋圆板与对应等效平板的最大挠度

Figure 12. The maximum deflections of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the triangle decaying pulse with different pressure

下载: 全尺寸图片幻灯片

图 13 矩形脉冲（RP）、线性衰减脉冲（LDP）和等腰三角脉冲（ITP）下的n4β0.07加筋圆板与对应等效平板的中心挠度-时间曲线

Figure 13. The central deflection-time curves of the stiffened circular plate n4β0.07 and the corresponding equivalent plate under the rectangle pulse (RP), linear decaying pulse (LDP), and isosceles triangular pulse (ITP)

下载: 全尺寸图片幻灯片

图 14 铝合金、镁合金、合金钢n4β0.07加筋圆板与对应等效平板的中心挠度-时间曲线

Figure 14. The central deflection-time curves of the stiffened circular plate n4β0.07 and the corresponding equivalent plate made of different materials: aluminum alloy, magnesium alloy and alloy steel

下载: 全尺寸图片幻灯片

[1]	TROITSKY M S. Stiffened plates: bending, stability, and vibrations [M]. Amsterdam: Elsevier, 1976.
[2]	SZILARD R. Theories and applications of plate analysis: classical, numerical, and engineering methods [M]. Hoboken: John Wiley & Sons, 2004.
[3]	KIM D K, LIM H L, YU S Y. A technical review on ultimate strength prediction of stiffened panels in axial compression [J]. Ocean Engineering, 2018, 170: 392–406. DOI: 10.1016/j.oceaneng.2018.10.022.
[4]	KARPOV V V, SEMENOV A A. Refined model of stiffened shells [J]. International Journal of Solids and Structures, 2020, 199: 43–56. DOI: 10.1016/j.ijsolstr.2020.03.019.
[5]	BALKAN D, DEMIR Ö, ARIKOĞLU A. Dynamic analysis of a stiffened composite plate under blast load: a new model and experimental validation [J]. International Journal of Impact Engineering, 2020, 143: 103591. DOI: 10.1016/j.ijimpeng.2020.103591.
[6]	张涛, 刘土光, 赵耀, 等. 加筋板弹性大挠度的冲击响应分析 [J]. 爆炸与冲击, 2002, 22(4): 301–307. DOI: 10.3321/j.issn:1001-1455.2002.04.003. ZHANG T, LIU T G, ZHAO Y, et al. Large deflection dynamic response of stiffened plates under lateral impact loading [J]. Explosion and Shock Waves, 2002, 22(4): 301–307. DOI: 10.3321/j.issn:1001-1455.2002.04.003.
[7]	ISLAM A, SHEIKH A H, BENNETT T, et al. An innovative modeling strategy for flexural response of fiber-reinforced stiffened composite structures [J]. Thin-Walled Structures, 2022, 172: 108929. DOI: 10.1016/j.tws.2022.108929.
[8]	YU H D, ZHAO Z J, YANG D, et al. A new composite plate/plate element for stiffened plate structures via absolute nodal coordinate formulation [J]. Composite Structures, 2020, 247: 112431. DOI: 10.1016/j.compstruct.2020.112431.
[9]	SHEN Y J, HE X C, CHEN W, et al. Meshless simulation and experimental study on forced vibration of rectangular stiffened plate [J]. Journal of Sound and Vibration, 2022, 518: 116602. DOI: 10.1016/j.jsv.2021.116602.
[10]	KARPOV V V, SEMENOV A A. Structural anisotropy method for shells with orthogonal stiffeners [J]. Structures, 2021, 34: 3206–3221. DOI: 10.1016/j.istruc.2021.09.027.
[11]	ZHANG B, CHEN H L, LI M, et al. Equivalent static load method for hierarchical stiffened composite panel subjected to blast loading [J]. Engineering Structures, 2018, 171: 569–582. DOI: 10.1016/j.engstruct.2018.05.107.
[12]	XIA Y, FRISWELL M I, SAAVEDRA FLORES E I. Equivalent models of corrugated panels [J]. International Journal of Solids and Structures, 2012, 49(13): 1453–1462. DOI: 10.1016/j.ijsolstr.2012.02.023.
[13]	TIMOSHENKO S, WOINOWSKY-KRIEGER S. Theory of plates and shells [M]. New York: McGraw-Hill, 1959.
[14]	BATTAGLIA G, DI MATTEO A, PIRROTTA A, et al. Dynamic response of equivalent orthotropic plate model for stiffened plate: numerical-experimental assessment [J]. Procedia Engineering, 2017, 199: 1423–1428. DOI: 10.1016/j.proeng.2017.09.387.
[15]	XING Y F, LIU B. New exact solutions for free vibrations of thin orthotropic rectangular plates [J]. Composite Structures, 2009, 89(4): 567–574. DOI: 10.1016/j.compstruct.2008.11.010.
[16]	FERTIS D G, MIJATOV M M. Equivalent systems for variable thickness plates [J]. Journal of Engineering Mechanics, 1989, 115(10): 2287–2300. DOI: 10.1061/(ASCE)0733-9399(1989)115:10(2287).
[17]	SEO J K, KIM B J, RYU H S, et al. Validation of the equivalent plate thickness approach for ultimate strength analysis of stiffened panels with non-uniform plate thickness [J]. Thin-Walled Structures, 2011, 49(6): 753–761. DOI: 10.1016/j.tws.2011.02.001.
[18]	HUANG X R, WANG M, FENG Y J, et al. Finite deformation analysis of the elastic circular plates under pressure loading [J]. Thin-Walled Structures, 2023, 188: 110864. DOI: 10.1016/j.tws.2023.110864.