A study on dynamic mechanical properties of Al0.3CoCrFeNi high-entropy alloy considering crystal orientation
-
摘要: 鉴于高熵合金材料（high-entropy alloy, HEA）在高应变率动态响应下呈现不同的破坏模式及力学性能，其潜在机理从宏观角度已不能够完全解释，需从微观角度研究其动态响应过程中的原子结构变化、位错分布变化、演变机理及变形机制，为优化HEA防护材料的加工工艺、制备方法等提供参考。利用分子动力学模拟的方法，设计了[100]、[110]和[111]等3种取向结构的Al0.3CoCrFeNi高熵合金在不同应变率下的压缩、拉伸及冲击试验，分析了动态响应过程中原子结构变化、位错分布变化、演变机理及变形机制。压缩试验中：[110]取向结构的Al0.3CoCrFeNi高熵合金的屈服强度最高，[111]的次之，[100]的最低；[100]取向结构的Al0.3CoCrFeNi高熵合金主要的变形机制为孪晶变形，[110]的为滑移变形，[111]的为位错变形。拉伸试验中：[111]取向结构的Al0.3CoCrFeNi高熵合金的屈服强度最高，[100]的次之，[110]的最低；[100]取向结构Al0.3CoCrFeNi高熵合金拉伸过程中孪晶结构较多，[110]取向结构的Al0.3CoCrFeNi高熵合金产生较规则的密排六方结构滑移面，[111]取向结构的Al0.3CoCrFeNi高熵合金不会产生任何滑移面。随着应变率的升高，3种取向结构的Al0.3CoCrFeNi高熵合金压缩和拉伸屈服强度均大幅度提高，对应伸长量增大。较低应变率（1×109 s−1）下的塑性变形机制主要为滑移变形，但滑移系较少；中应变率（1×1010 s−1）下的塑性变形机制是以滑移为主的变形机制，但滑移系较多；高应变率（1×1011 s−1）下的塑性变形机制是由原子排列无序化的非晶原子诱导的变形。[110]取向结构的Al0.3CoCrFeNi高熵合金的抗冲击性能最好，与其具有最高的屈服强度，并且在屈服结束阶段也能保持最高的应力有关。Abstract: High-entropy alloy (HEA) materials exhibit different failure modes and mechanical properties under high strain rate dynamic response. Because its potential mechanism cannot be fully explained from a macro perspective, it is necessary to study the atomic structure change, dislocation distribution change, evolution mechanism and deformation mechanism in the dynamic response process from a microscopic perspective. This study provides a reference for optimizing the processing technology and preparation method of HEA protective materials. The molecular dynamics simulation is adopted to design the compression, tensile at different strain rates and impact tests of [110], [111] and [100] three oriented Al0.3CoCrFeNi HEA. The atomic structure changes, dislocation distribution change, evolution mechanism and deformation mechanism in the dynamic response process are then analyzed. In the compression test: the yield strength of Al0.3CoCrFeNi high-entropy alloy with [110] orientation structure is the highest, followed by [111] and [100]. The main deformation mechanism of the [100] orientation structure is twin deformation, [110] orientation structure is slip deformation, and [111] orientation structure is dislocation deformation. In the tensile test: the yield strength of Al0.3CoCrFeNi high-entropy alloy with [111] orientation structure is the highest, followed by [100] and [110]. [100] orientation structure presents more twin structure during the tensile process; [110] exhibits more regular hexagonal close-packed structure slip surface; while [111] does not produce any slip surface. With the increase of strain rate, the compressive and tensile yield strength increased greatly, and the corresponding elongation increased, too. The plastic deformation mechanism at low strain rate (1×109 s−1) is mainly slip deformation, but the number of slip systems is small. The plastic deformation mechanism at medium strain rate (1×1010 s−1) is mainly slip deformation mechanism, but many slip systems appear. The plastic deformation mechanism at high strain rate (1×1011 s−1) is induced by amorphous atoms with disordered atomic arrangement. The Al0.3CoCrFeNi high-entropy alloy with [110] orientation structure has the best impact resistance, which is attributed to its highest yield strength and the highest stress at the end of the yield stage.
-
金属材料的动态力学性能一直是冲击防护领域关注的重点，广泛的动态响应研究[1-5]表明，金属材料在不同应变率下产生的破坏模式具有明显的区别[3-4, 6-8]，且金属材料的屈服强度及应变硬化具有明显的应变率效应[9-11]。
大量研究结果揭示了金属动态力学性能，探索了一系列高应变率加载作用下的应力-应变变化规律，但并不能从内在本质上解释产生这种规律的原因及潜在的机理，特别是对金属材料在高应变率加载作用下所产生的不同破坏模式及力学性能的机理研究不足，这对防护结构的设计及材料的研究带来了巨大的阻碍[12]。以上差异现象形成的原因从宏观角度已不能够完全解释，因此，需从微观角度研究动态响应过程中发生的原子结构变化、位错分布变化、演变机理及变形机制，从而揭示高应变率加载作用下动态力学性能的潜在机理。
目前，对金属材料在高应变率加载作用下的微观结构演化及变形机制还未清晰，造成相关研究较少的主要原因是缺乏对高应变率加载作用下材料微观变形的表征手段，不能够对高应变率下材料微观变形的全过程进行分析。分子动力学作为一种微观尺度模拟手段，广泛应用于金属材料微观力学性能和缺陷演化行为的研究，可从微观的角度分析变形过程中应力、应变、能量和缺陷的变化趋势，探讨材料的屈服和断裂机制[13-15]。因此，可采用分子动力学模拟的手段进行动态响应过程中微观原子结构变化、位错分布变化、演变机理及变形机制的研究。
高熵合金（high-entropy alloy, HEA）[16-17]的组成成分与传统合金材料不同，通常含有5种或更多种主元素，每种元素的物质的量浓度相近，并表现出高构型熵。由于成分复杂，HEA表现出4种核心效应，包括高熵、严重晶格畸变、缓慢扩散和鸡尾酒效应[18]。大量试验研究[19-25]表明，HEA具有优异的机械性能，如高强度、良好的延展性和优异的断裂韧性，由于其优异的力学性能，特别是优异的应变硬化能力，HEA在弹道防护领域应用潜力巨大[26]。最经典的高熵合金材料Al0.3CoCrFeNi，其组成结构及力学性能已被广泛研究[27-33]，Diao等[28]、Kireeva等[29]和Yasuda等[31]研究发现，相同Al0.3CoCrFeNi高熵合金材料的力学性能并不完全一致，例如拉伸屈服应力和拉伸量等有所差异。产生此现象的原因是Al0.3CoCrFeNi高熵合金微观组成结构复杂，由多种取向结构的原子晶体结构组成。各研究中制备工艺有较大差异，导致所获得的Al0.3CoCrFeNi高熵合金由多种复杂晶体取向的单晶结构构成[34-37]，而以上研究并未对不同晶体取向结构的影响进行深入研究。并且，现实中绝大多数动态冲击及加载会导致复杂的三维空间变化状态，使得应力及变形分析变得困难或不可能。通过对HEA材料进行原子级的单晶小尺度模拟研究（位错动力学、分子动力学或晶体塑性模型等），可揭示真实的变形机制，并从低维尺度向高维尺度提供研究基础[38]。因此，研究单晶的力学特性，可揭示复杂多晶的变形机制，为宏观模型多维度分析提供指导。
对于单质的不同取向的研究开展得较早，且相对广泛。Huang等[39]通过分子动力学模拟揭示了[110]、[100]及[111]等3种晶体取向对单晶Fe力学性能和微观形变的影响。Zhang等[40]对沿[001]和[110]方向取向的Fe纳米柱在300 K的恒温条件下进行了拉伸模拟试验，结果显示，2种不同取向的Fe纳米柱的拉伸变形机制不同。Dash等[41]研究评估了单晶Ta沿[100]、[110]和[111]等3个晶体取向的应力-应变曲线和屈服强度的变化，并分析了应变硬化能力，揭示了材料在高速冲击载荷下的动态力学响应行为。根据实际应用，对化合物的研究也相继展开。Islam等[42]研究了[100]、[110]和[111]等3种不同晶体取向结构的闪锌矿（ZnTe）的力学性能和断裂机制，[110]取向的ZnTe在高应变率下发生异常变形，出现了不寻常的短程和长程有序晶体结构，具有明显的应变率敏感性。Xu等[43]研究了晶体取向（[100]、[110]和[111]）对单晶尖晶石（MgAl2O4）纳米线拉伸变形力学性能的影响，发现MgAl2O4的弹性模量和极限抗拉强度等力学性能明显依赖于晶体取向。随着新型材料高熵合金的发展，关于其相关的研究目前在快速发展[9, 12, 34-37, 44]，对于晶体取向影响的探索也在全面展开。Qi等[45]利用纳米压痕技术研究了[001]、[110]和[111]等3种晶体取向对CoCrFeMnNi高熵合金的力学响应和微观结构演变的影响。Zhang等[46]在3个取向（[100]、[110]和[111]）上对单晶体心立方（body-centered cubic, BCC）AlCrFeCoNi纳米柱进行了原位单轴压缩，发现其位错机制依赖于纳米柱的晶体取向。
目前，针对不同取向结构对Al0.3CoCrFeNi高熵合金动态力学性能的影响还缺乏系统的研究。因此，为深入了解Al0.3CoCrFeNi高熵合金在动态响应过程中的微观演变过程，迫切需对其单一取向晶体结构的纳米柱进行高应变率加载下的力学性能研究，以便探索其动态力学性能。
本文中，采用分子动力学模拟的方法，针对Al0.3CoCrFeNi高熵合金，设计[100]、[110]和[111]等3种不同取向结构的纳米柱，对该纳米柱进行不同应变率的压缩、拉伸及冲击试验，分析动态响应过程中原子结构变化、位错分布变化、演变机理及变形机制，探讨影响其性能变化的微观机理，以期为优化高熵合金防护材料的加工工艺、制备方法等提供参考。
1. 模型的建立与分析方法
利用大规模原子/分子大型并行模拟器（large-scale atomic/molecular massively parallel simulator，LAMMPS）[47]，对Al0.3CoCrFeNi高熵合金纳米柱进行了一系列大规模原子的单轴压缩、拉伸及冲击模拟，积分时间步长为1 fs。为建立具有[100]、[110]和[111]等3种不同取向HEA样品的原子构型，首先构建面心立方（face-centered cubic，FCC）晶体结构的Cr单晶，然后用Co、Fe、Ni和Al等4种原子随机替换单晶中的Cr原子，同时确保原子数n比例n(Al)∶n(Co)∶n(Fe)∶n(Ni)∶n(Cr) = 0.3∶1∶1∶1∶1。
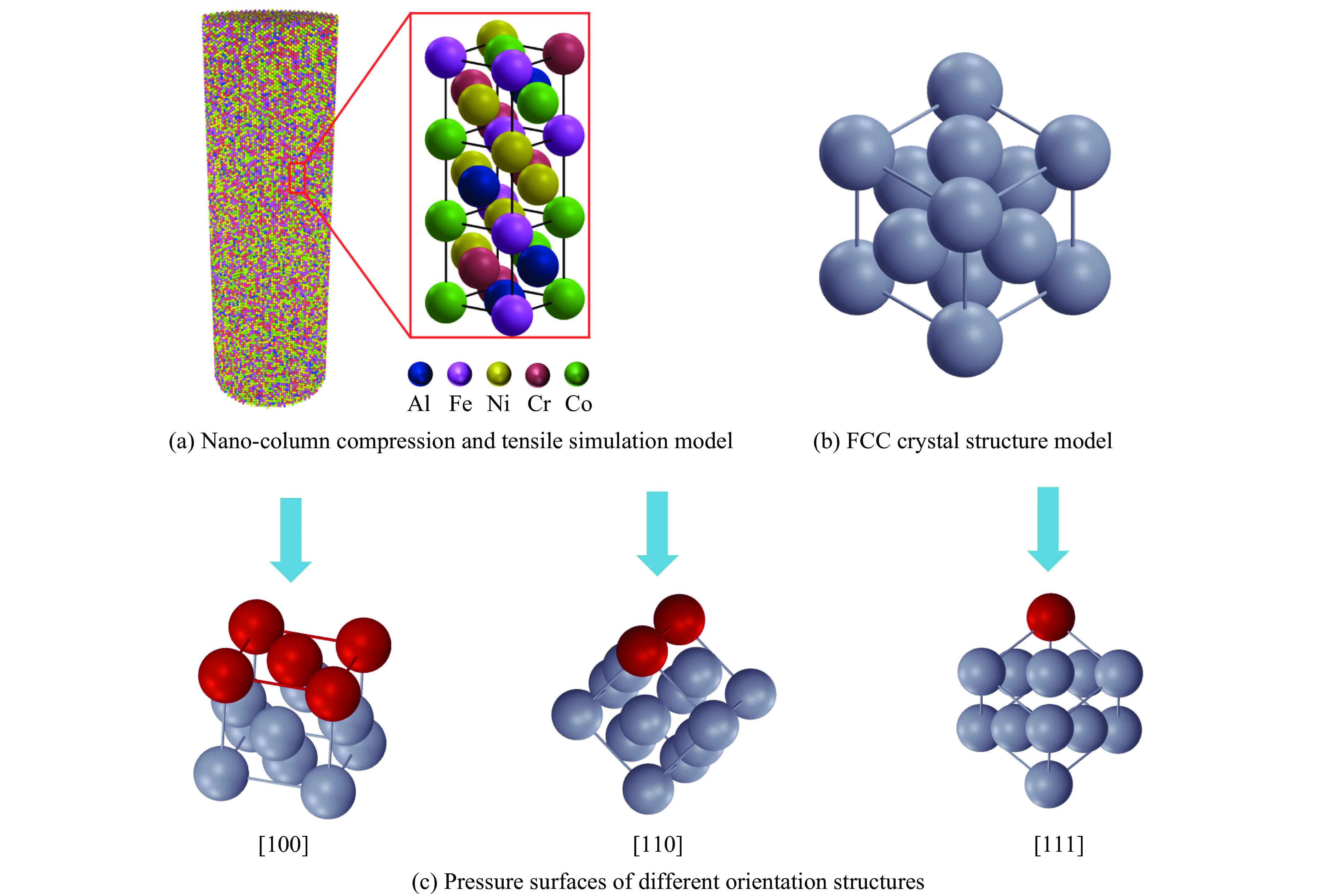
构建的[100]取向结构的Al0.3CoCrFeNi高熵合金纳米柱直径为10 nm、长径比为3.0，如图1(a)所示，它是由图1(b)所示的FCC原子结构组成的纳米柱。
[100]、[110]和[111]等3种不同取向是指FCC晶体结构的受力面的晶向指数分别为[100]、[110]和[111]，如图1(c)所示。[100]取向结构的受压面是FCC晶体结构的一个面，对应5个原子，[110]取向结构的受压面是FCC晶体结构的一条线，对应2个原子，[111]取向结构的受压面是FCC晶体结构的一个点，对应1个原子。
对HEA中原子间的相互作用采用嵌入原子势方法（embedded atom method，EAM）来描述[48]，该方法基于密度泛函理论，通过有效介质理论和准原子近似理论提出。EAM中将每一个原子看作基体中的外部杂质，得出整个体系的总势能等于相互作用能与嵌入能之和：
E=∑iFi(ρi)+12∑i≠jϕij(rij)ρi=∑i≠jφij(rij) (1) 式中：E为总势能；
∑iFi(ρi) 为嵌入能项，Fi(ρi) 为嵌入能函数，ρi 为除原子i外其余原子在原子i处产生的电子云密度之和；12∑i≠jϕij(rij) 为相互作用能项，ϕij(rij) 为第i个原子与第j个原子间的对势作用函数，rij为第i个原子与第j个原子之间的距离，φij(rij) 为电子云密度函数。对于冲击模拟试验，还需要利用Lennard-Jones (L-J)势[49]来描述刚性球体中的原子与HEA靶板中的原子之间的相互作用，包括Al-Co、Cr-Co、Fe-Co、Co-Co和Ni-Co相互作用力：
Vij(r)=4εij[(σijr)12−(σijr)6]εij=√εiiεjj, σij=σii+σjj2 (2) 式中：Vij(r)为原子i与原子j之间的势能，
εij 为势阱的深度，σij 为原子i与原子j之间的平衡位置，εii 和εjj 为同类原子之间相互作用的L-J势参数，即Al-Al、Cr-Cr、Fe-Fe、Co-Co和Ni-Ni之间相互作用的L-J势参数；σii 和σjj 为同类原子之间的平衡位置，即Al-Al、Cr-Cr、Fe-Fe、Co-Co和Ni-Ni之间的平衡位置。不同原子对的参数如表1所示。表 1 不同原子对之间相互作用的Lennard-Jones参数Table 1. Lennard-Jones parameters of the interactions between different atom pairs原子对 ε/eV σ/Å Al-Co 0.0469 2.578 Cr-Co 0.0466 2.456 Fe-Co 0.0477 2.448 Co-Co 0.0043 2.584 Ni-Co 0.0474 2.428 在压缩及拉伸模拟中，纳米柱都通过能量最小化和在等压等温（constant number of atoms, pressure, and temperature, NPT）系综下自由弛豫100 ps来达到平衡，以确保300 K的恒定温度和沿纳米柱轴向的零压力。平衡后，所有Al0.3CoCrFeNi高熵合金纳米柱分别在1×109、1×1010和1×1011 s−1的恒定应变率下，在等温等体积（constant number of atoms, volume, and temperature, NVT）系综和300 K温度下沿其轴向被压缩和拉伸。
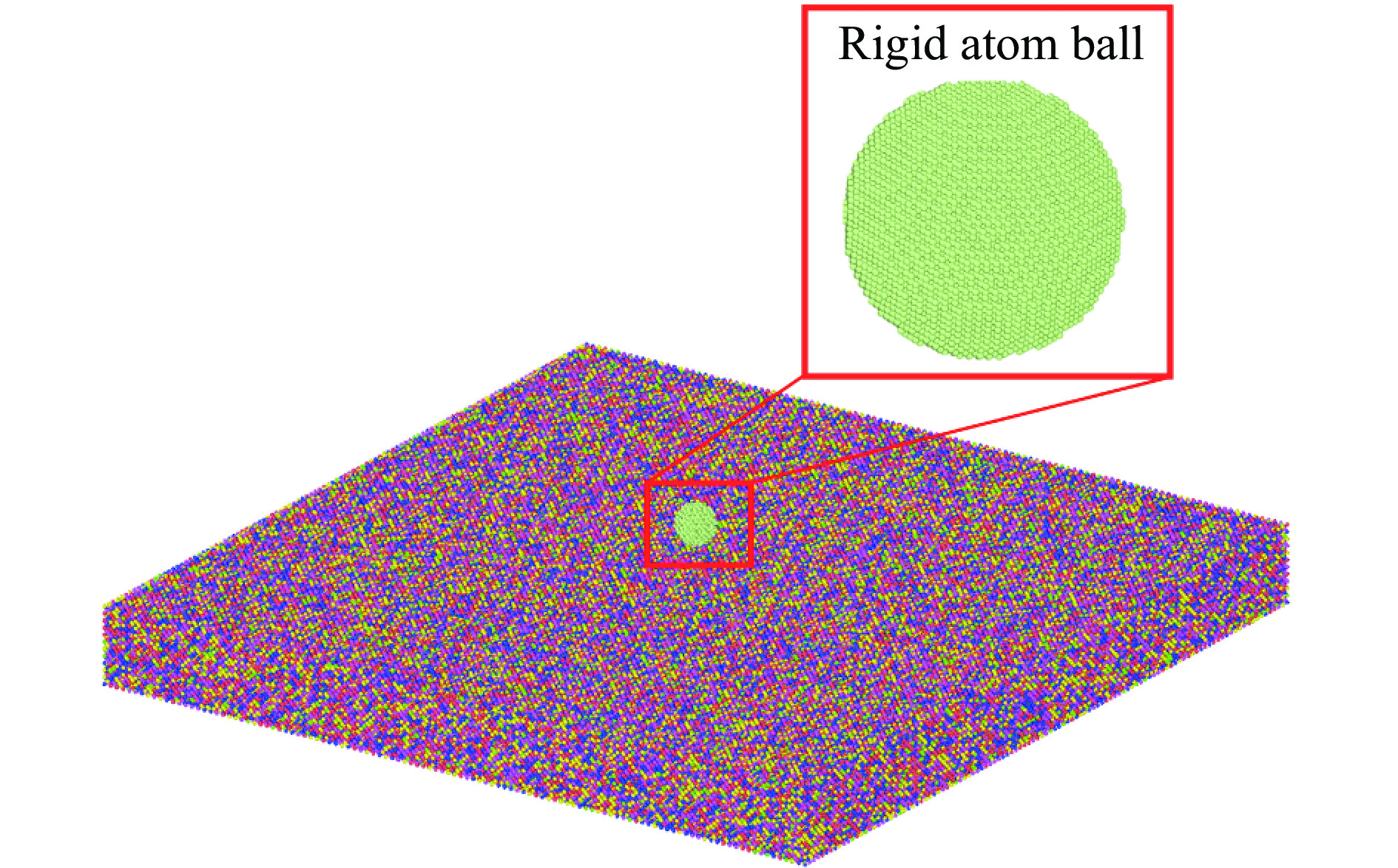
冲击模拟所用的方形靶板模型如图2所示，边长为20 nm，厚度为4 nm，刚性球为Co原子球，直径为1 nm。在冲击模拟中，纳米靶板通过能量最小化和在NVT系综下自由弛豫 100 ps来达到平衡，以确保300 K的恒定温度和沿纳米柱轴向的零压力。平衡后，刚性球以100 Å/ps的速度，在等体积等能量（constant number of atoms, volume, and energy, NVE）系综和300 K温度下对HEA靶板进行撞击。
图 2 刚性球冲击Al0.3CoCrFeNi纳米靶板模型Figure 2. A model for a rigid ball impacting an Al0.3CoCrFeNi nano-target采用共同邻域分析（common neighborhood analysis, CNA）法[50]识别变形过程中原子结构的变化和缺陷，采用位错提取算法（dislocation extraction algorithm, DXA）[51-52]进行位错分布分析。
值得注意的是，真实的压缩、拉伸及冲击试验的尺度在毫米到厘米的范围内，而分子动力学模拟的尺寸以纳米为单位，这种尺寸差异不影响分子动力学模拟所揭示的微观机理，且规模差异不影响键合强度和层错能的计算。因此，分子动力学模拟可以捕捉关键点以解释试验中观察到的结果。
2. 模拟结果
2.1 应力-应变曲线
2.1.1 不同取向结构的Al0.3CoCrFeNi高熵合金的应力-应变曲线
不同取向结构的Al0.3CoCrFeNi高熵合金在1×109 s−1应变率下的压缩及拉伸应力-应变曲线如图3所示。不同取向结构的Al0.3CoCrFeNi高熵合金，无论是在压缩还是拉伸过程中，都经历了弹性变形、屈服变形和塑性变形3个阶段，这与之前报道的模拟结果[34, 36]一致。Al0.3CoCrFeNi高熵合金纳米柱的应力-应变曲线所表现出的高应力值受Hall-Petch关系[53]的影响，即材料尺寸越小，强度越高，可达吉帕量级，与其他试验[39]及模拟结果[46, 54-55]相同。各个变形阶段临界点的应力和变形量见表2。
图 3 不同取向结构Al0.3CoCrFeNi高熵合金压缩及拉伸应力-应变曲线Figure 3. Compressive and tensile stress-strain curves of Al0.3CoCrFeNi high-entropy alloys with different orientation structures表 2 不同取向结构的Al0.3CoCrFeNi高熵合金在压缩及拉伸过程中各个变形阶段临界点的应力和变形量Table 2. The stress and deformation at the critical point of each deformation stage of Al0.3CoCrFeNi HEA with different orientation structures during compressive and tensile processes分界点 应力/GPa 应变/% 压缩 拉伸 压缩 拉伸 [100] [110] [111] [100] [110] [111] [100] [110] [111] [100] [110] [111] 弹性变形与屈服阶段分界点 5.38 18.41 16.63 10.28 6.14 10.45 5.5 4.8 5.3 10.0 4.5 5.0 屈服与塑性变形阶段分界点 1.55 2.43 1.23 3.51 2.30 3.74 8.4 6.2 6.8 12.8 5.6 6.6 从图3和表2可以看出，在不同取向结构的Al0.3CoCrFeNi高熵合金压缩和拉伸过程中，第1阶段，即弹性变形阶段，对应图3中的线性部分，应力-应变曲线呈现出线性关系，服从胡克定律；弹性变形阶段结束后，便进入第2阶段，即屈服变形阶段，应力-应变曲线出现迅速下降，在小的应变变化范围内，对应出现应力低谷峰值；继续加载过程中，应力-应变曲线出现应力波动，即进入塑性变形阶段，在此阶段，没有明显的应力升高或降低，属于不均匀的塑性变形[35]。
在压缩过程中，[110]取向结构的HEA展示出最大的屈服应力，为18.41 GPa，对应4.8%的应变，亦为最小的应变；[110]取向结构的HEA在屈服阶段结束时刻应力为2.43 GPa，在三者中展现出最高的应力，在6.2%的应变下最早进入塑性变形阶段。[111]取向结构的HEA的压缩屈服应力和屈服阶段结束时刻的最低应力分别为16.63 GPa和1.23 GPa，略低于[110]取向结构的HEA的相应值，然而相对应的应变分别为5.3%和6.8%，稍高于[110]取向结构的HEA的相应值。[100]取向结构的HEA的最大屈服应力仅为5.38 GPa，远小于[110]和[111]取向结构的HEA的最大屈服应力，对应的应变为5.5%，稍大于前两者的相应应变，这与在加载过程中滑移系能否充分滑动相关[44, 56]，这充分体现了晶体结构对HEA材料力学性能的影响较大。在压缩过程中，[110]取向结构的HEA表现出较好的力学性能，[111]取向结构的次之，[100]取向结构的最差。
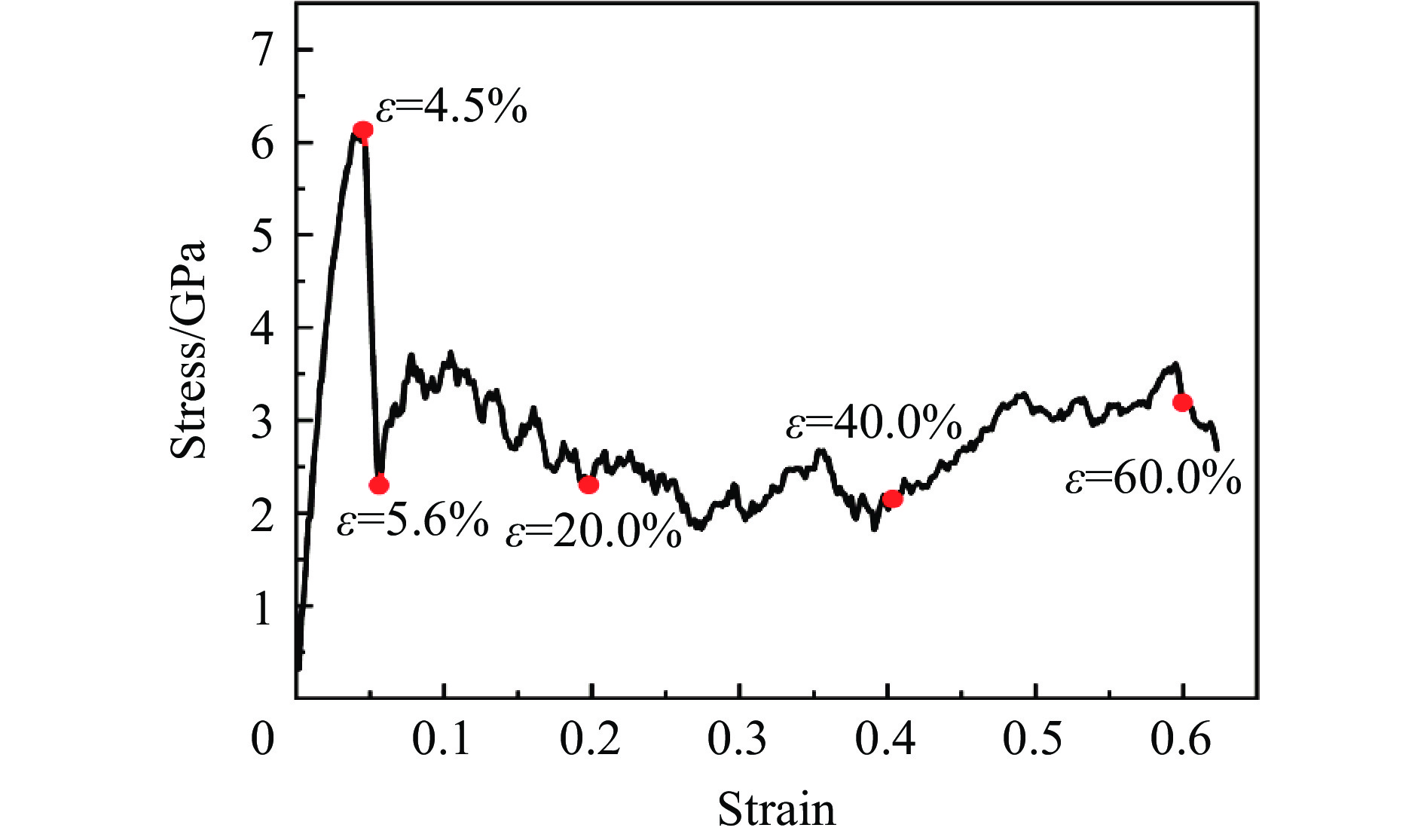
在拉伸过程中，不同取向结构的HEA的应力-应变曲线与压缩过程的区别较大，[100]、[110]和[111]取向结构的屈服应力分别为10.28、6.14和10.45 GPa，对应的应变分别为10.0%、4.5%和5.0%。第2阶段（即屈服阶段）结束时的应力分别为3.51、2.30和3.74 GPa，对应的应变分别为12.8%、5.6%和6.6%。拉伸过程中的力学性能，[110]取向结构的最差，[100]取向结构的稍好，而[111]取向结构的最好。
综上，不同取向结构的Al0.3CoCrFeNi高熵合金的应力-应变曲线都会出现弹性变形阶段、屈服阶段和塑性变形阶段，但三者力学性能差异较大，[110]取向结构的HEA具有良好的抗压性能，而抗拉性能较差；[100]取向结构的HEA具有良好的抗拉性能，而抗压性能较差；[111]取向结构的HEA抗压与抗拉性能都相对较好，较为均衡。
2.1.2 不同应变率下Al0.3CoCrFeNi高熵合金的应力-应变曲线
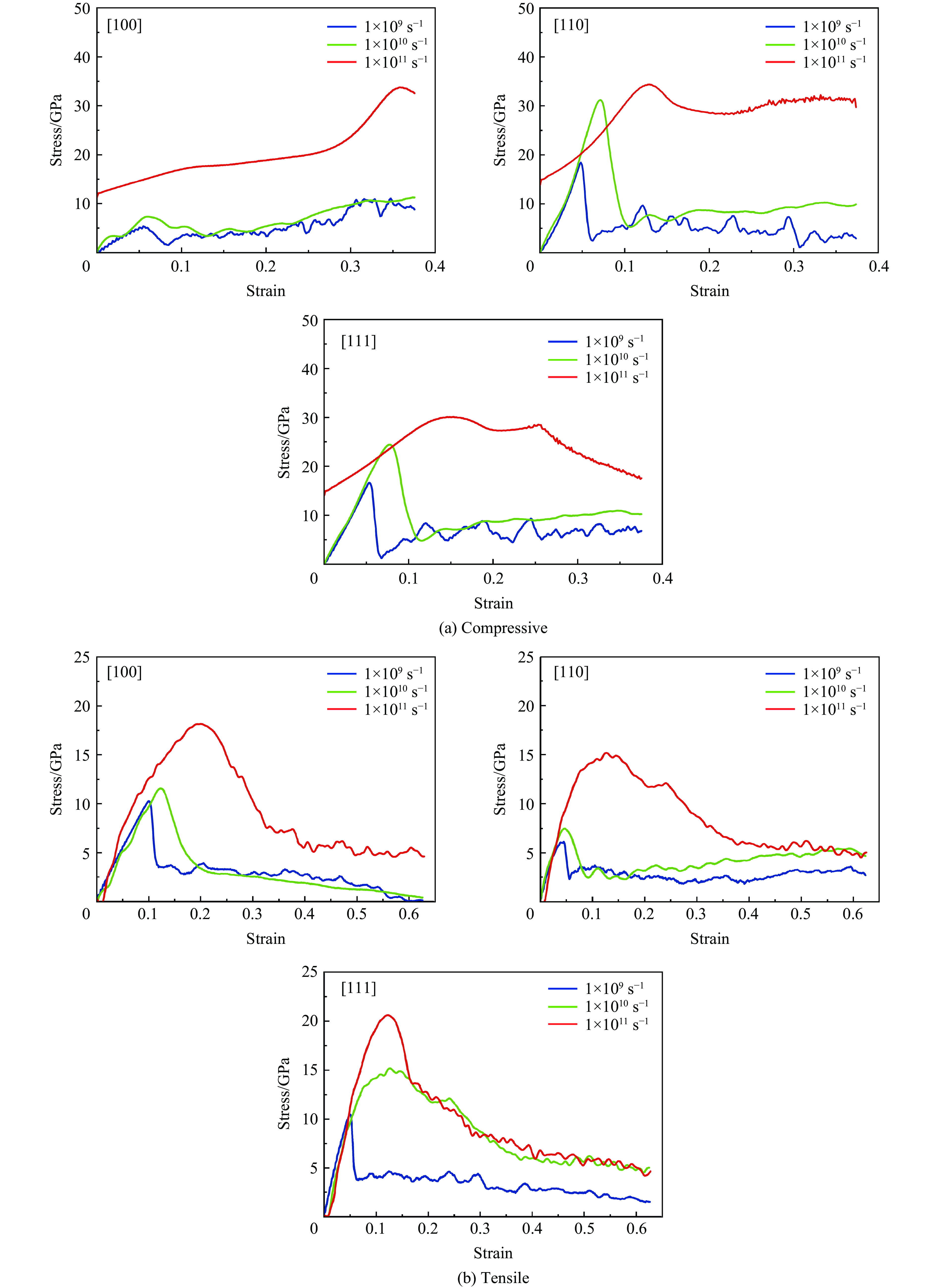
不同应变率下Al0.3CoCrFeNi高熵合金的应力-应变曲线如图4所示，不同晶体取向Al0.3CoCrFeNi高熵合金在不同应变率下的屈服应力总结见表3。
图 4 不同应变率下的Al0.3CoCrFeNi高熵合金压缩及拉伸应力-应变曲线Figure 4. Compressive and tensile stress-strain curves of Al0.3CoCrFeNi high-entropy alloys at different strain rates表 3 不同应变率下不同取向结构的Al0.3CoCrFeNi高熵合金的屈服应力及应变Table 3. Yield stresses and strains of Al0.3CoCrFeNi high-entropy alloys with different orientation structures at different strain rates模拟试验 晶体取向 1×109 s−1 1×1010 s−1 1×1011 s−1 屈服应力/GPa 应变/% 屈服应力/GPa 应变/% 屈服应力/GPa 应变/% 压缩 [100] 5.38 5.5 7.34 6.0 33.70 36.0 [110] 18.41 4.8 31.22 7.1 34.38 13.7 [111] 16.63 5.3 24.43 7.8 30.11 15.3 拉伸 [100] 10.28 10.0 11.57 12.2 18.16 20.0 [110] 6.14 4.5 7.50 4.7 15.19 12.6 [111] 10.45 5.0 15.19 12.6 20.62 12.2 分别对[100]、[110]和[111]等3种取向结构的Al0.3CoCrFeNi高熵合金体系进行了3种不同应变率（1×109、1×1010和1×1011 s−1）下的压缩及拉伸试验，对比了其应力-应变曲线的不同。图4和表3的压缩拉伸应力-应变数据显示，随着应变率的提高，3种取向结构的Al0.3CoCrFeNi高熵合金的屈服应力都明显增大，且对应的应变也增大。当应变率较高，如1×1011 s−1时，应力-应变曲线会发生较明显的变化，此现象与已报道的模拟研究[37, 57]一致。高应变率下，[100]、[110]和[111]等3种取向结构的压缩屈服强度分别为33.70、34.38和30.11 GPa，对应的应变分别为36.0%、13.7%和15.3%，拉伸屈服强度分别为18.16、15.19和20.62 GPa，对应的应变分别为20.0%、12.6%和12.2%，远高于1×109和1×1010 s−1应变率下的屈服强度和应变。
在1×1010或1×1011 s−1同一应变率下，不同取向结构的Al0.3CoCrFeNi高熵合金的应力-应变曲线与1×109 s−1应变率下呈现的规律一致。
2.2 变形机制及微观演变
2.2.1 [100]取向结构的压缩模拟变形机制及微观演变
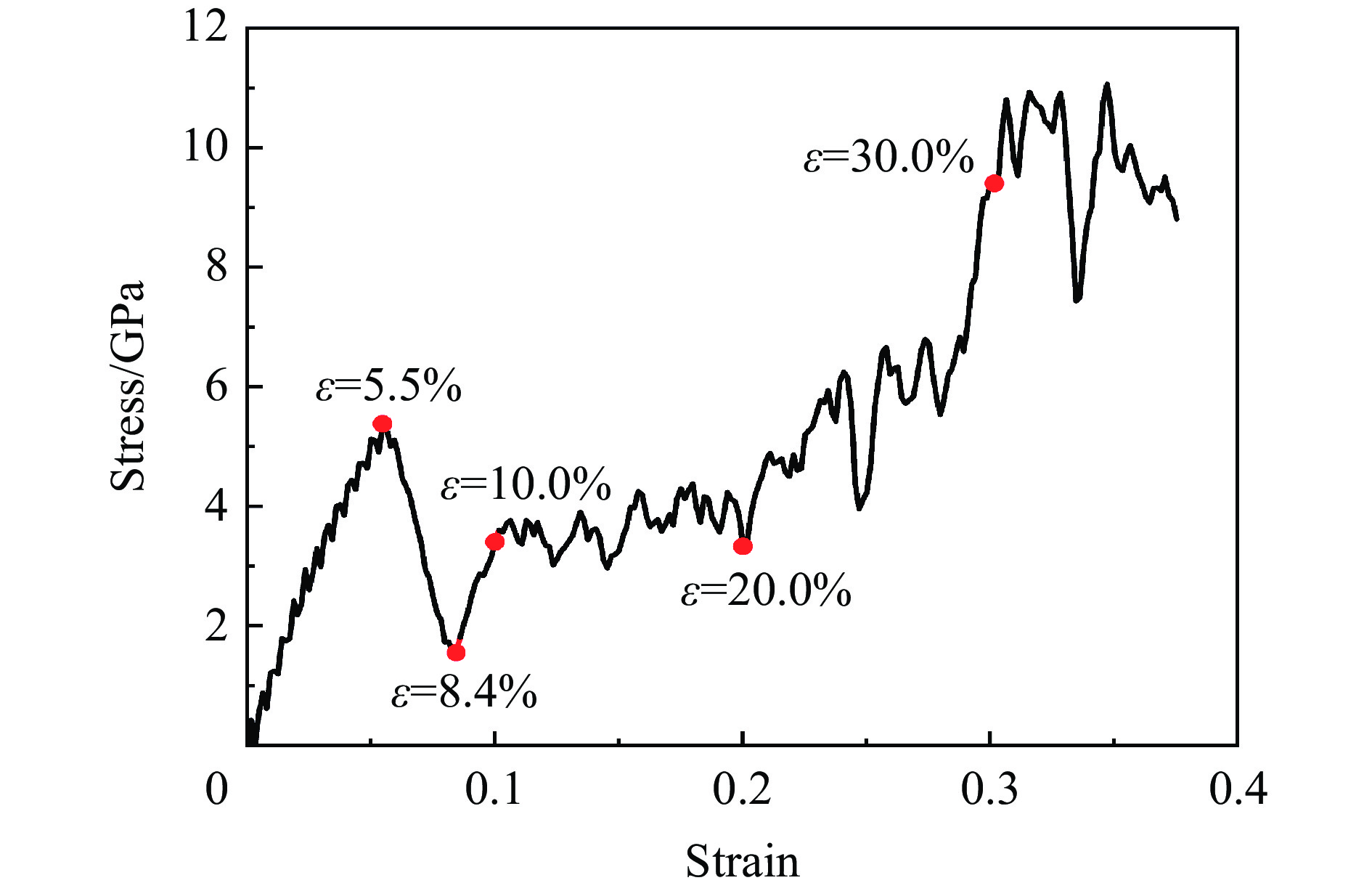
图5为[100]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线，截取了应变为5.5%（屈服强度点）、8.4%（屈服阶段最低点）、10.0%、20.0%及30.0%的晶体结构图和位错分布图进行分析，如图6～7所示，图中以不同颜色的球体区分不同的原子结构，不同颜色的线条区分不同种类的位错线。
图 5 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟应力-应变曲线Figure 5. Compression simulation stress-strain curve of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure
图 6 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟晶体结构演变Figure 6. Simulated crystal structure evolution of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure during compression
图 7 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟位错分布Figure 7. Simulated dislocation distribution of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure during compression如图6(a)和7(a)所示晶体结构及位错线状态，当应变为5.5%时，即Al0.3CoCrFeNi高熵合金压缩状态结束弹性变形阶段进入屈服阶段时刻，此时原子晶体结构基本保持最初的FCC结构，没有产生位错线，说明在弹性阶段变形过程中，HEA内部不发生晶体结构的改变，应力的提高全部是由原子间距的缩小所产生的抵抗力所致。
图6(b)和7(b)为应变8.4%所对应的原子状态，此刻为屈服阶段结束，即将进入不均匀塑性变形阶段。明显观察到原子结构的变化，层状HCP原子结构产生，并按照同一方向延伸扩展。在HCP原子结构的边界处，Al0.3CoCrFeNi高熵合金纳米柱体沿HCP延伸的方向发生滑移错动，如图6(b)粉色圆中部分所示。在HCP结构内部和延伸方向处，产生了大量的位错线，如图7(b)所示。金属晶体结构会沿着某一个面和某一方向产生滑移，称滑移面和滑移方向，滑移面和滑移方向共同称为滑移系，滑移错动的产生会使应力下降[58]。
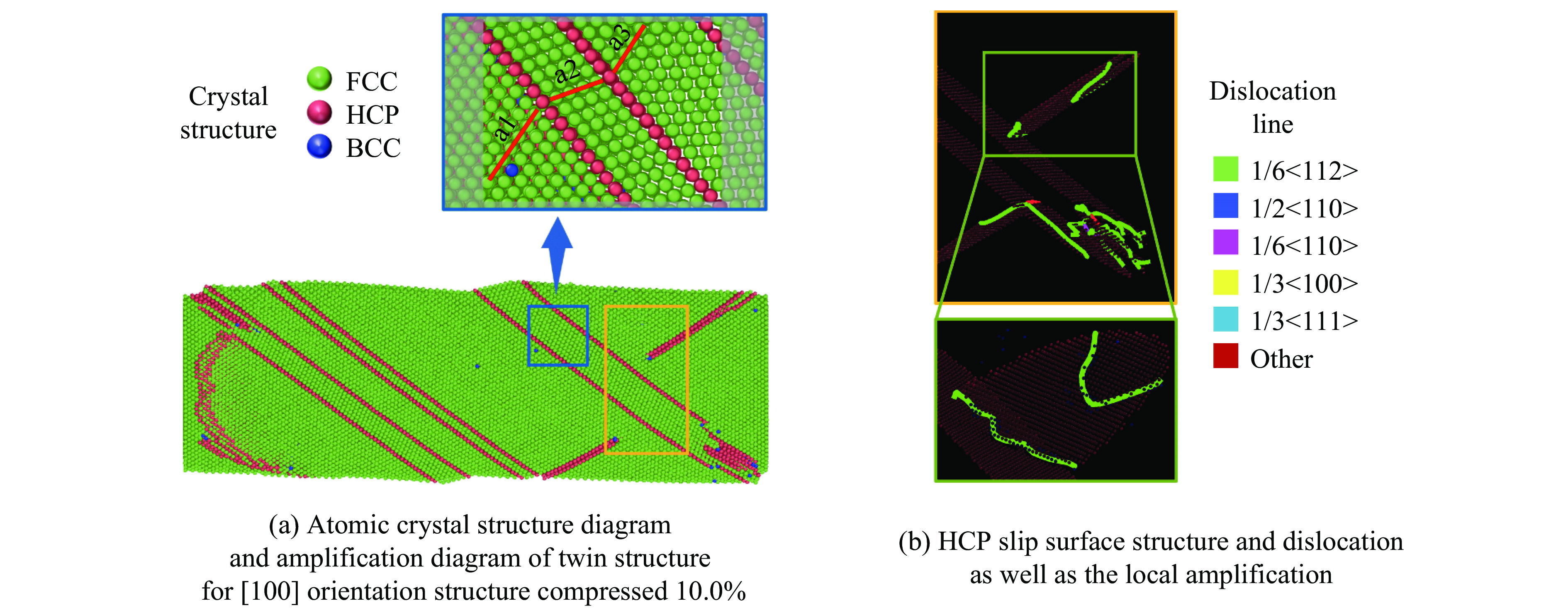
继续加载进入塑性变形阶段，应变为10.0%时，少许层状HCP原子结构排列整齐，如图6(c)所示。2层HCP原子结构与周围FCC原子结构共同构成孪晶结构，其原子排列方式如图8(a)所示，观察到沿着HCP原子结构边界，两边的FCC原子结构呈对称排列（a1与a2方向对称排列，a2与a3方向对称排列），其边界被称为孪晶界。孪晶结构的产生有利于加强材料的塑性性能[59-60]，分别定义图中2个孪晶界为L1和L2。图6(c)中HCP结构与纳米圆柱呈现出45°与35°夹角，其主要分别对应FCC结构的主要滑移系[46]，Al0.3CoCrFeNi高熵合金纳米柱以此角度方向发生明显错动现象。沿纳米柱滑移的平面为滑移面，即为HCP结构所组成的平面，如图8(b)所示。大量位错线在滑移面上产生，如图8(b)交叉滑移平面所示，在滑移交叉处极易产生位错线。
图 8 孪晶和位错现象的放大图Figure 8. Amplification diagrams of twinning and dislocation phenomenon图6(c)～(e)为Al0.3CoCrFeNi高熵合金压缩塑性阶段的原子结构图，随着应变的不断增大，观察到孪晶界L1和L2不断迁移，间距不断缩小，最终在应变30%时合并湮灭。正是该阶段内孪晶不断的产生、生长、湮灭，导致了应力-应变曲线的波动，最终导致HEA压缩过程中的不均匀变形。图7(c)～(e)为Al0.3CoCrFeNi高熵合金压缩塑性阶段位错线分布情况，随着应变的增大，HCP孪晶结构不断湮灭，以及滑移面逐渐消失，位错线也不断减少，原子结构趋于整齐排列。整个压缩过程所产生的位错线大部分为
1/6<112> 种类，其为孪晶系统中典型的位错类型，其可诱导锯齿状的应力-应变曲线变化[57]。HCP原子结构及孪晶结构的合并、湮灭及消失的过程如图9所示。HCP原子结构的合并首先开始于部分原子的移动，如图9(a)的180 ps和图9(b) 的182 ps所示，原子移动的地方产生位错，其原子移动方式与之前试验报道过的[61]一致。其湮灭开始于纳米圆柱边界，逐渐向内部扩展，如184 ps所示。
综上，在[100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟过程中，其主要的变形机制为孪晶变形，产生的位错线长程有序，大多为典型孪晶结构的
1/6<112> 型。弹性阶段应力的增加全部是由原子间距缩小产生的抵抗力所致，屈服阶段应力的下降是由于滑移错动的产生，塑性阶段应力的上下波动是由于孪晶结构的出现、发展及湮灭导致的。2.2.2 [110]取向结构的压缩模拟变形机制及微观演变
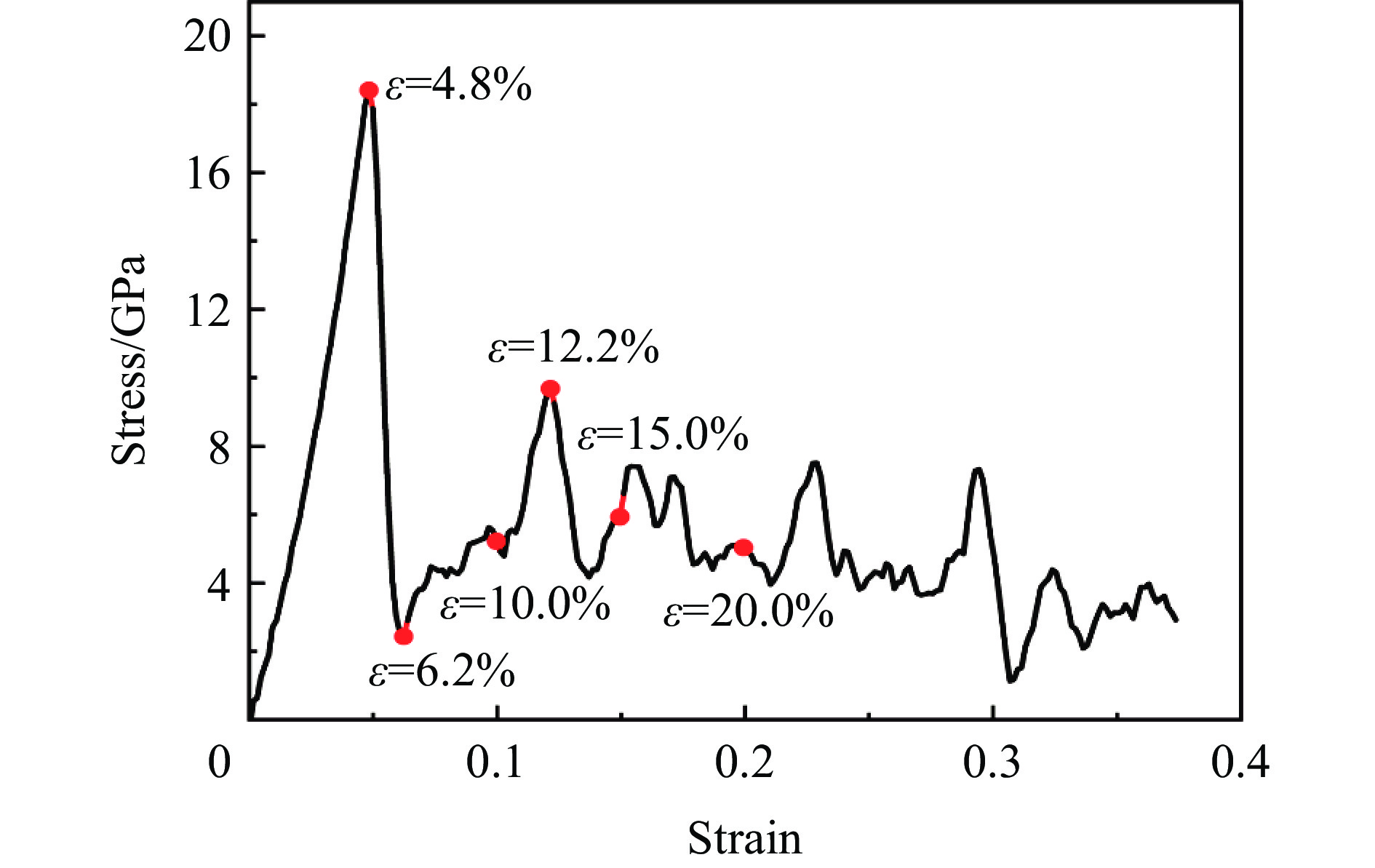
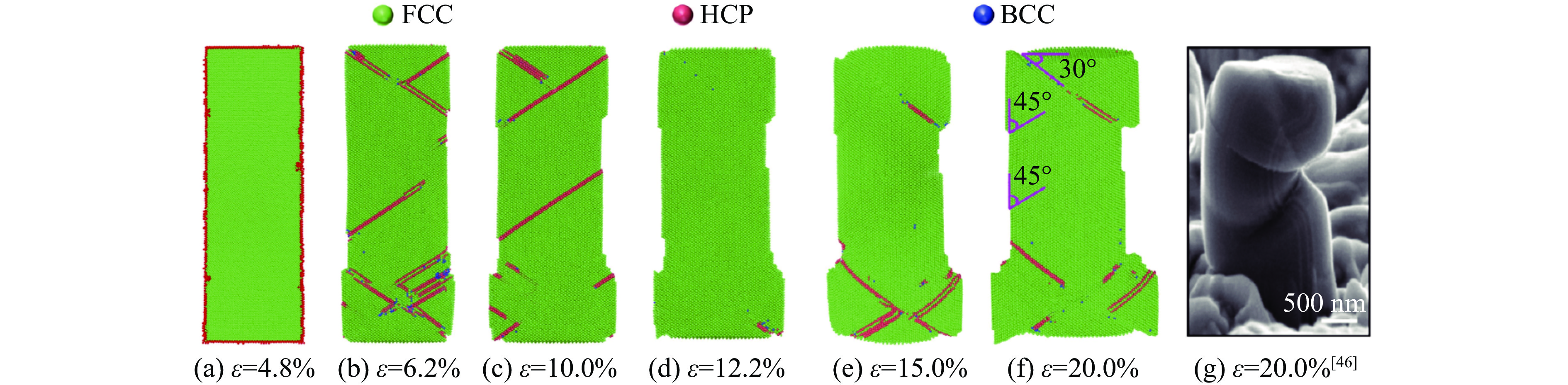
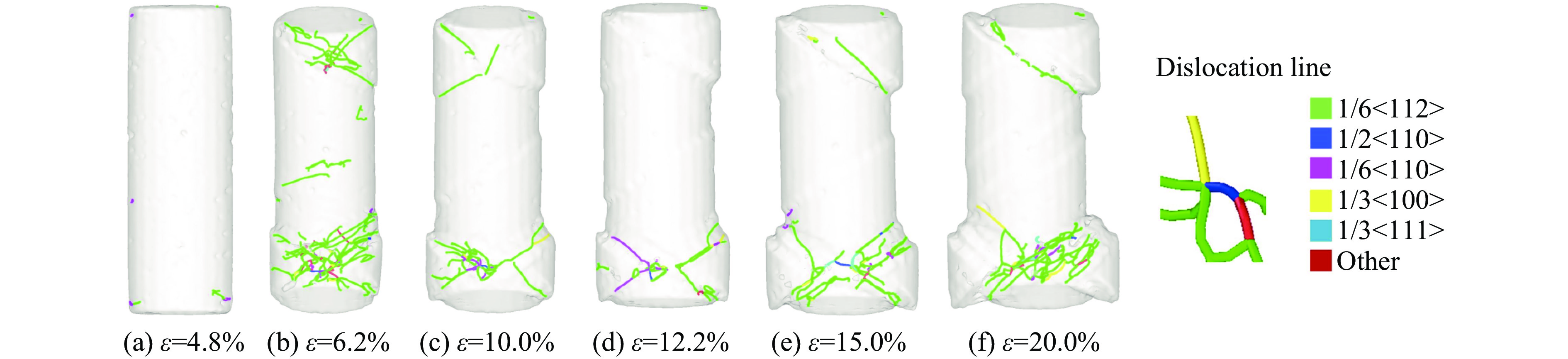
图10为[110]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线，截取了应变4.8%（屈服强度点）、6.2%（屈服阶段最低点）、10.0%、12.2%（塑性阶段最高点）、15.0%及20.0%的晶体结构图和位错分布图进行分析，如图11～12所示，图11(g)为已报道相关试验结果[46]，模拟结果与试验结果相似，证明模拟结果的可靠性高。
图 10 [110]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线模拟结果Figure 10. Simulated stress-strain curve of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 12 [110]取向结构Al0.3CoCrFeNi高熵合金的压缩位错分布的模拟结果Figure 12. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression图11(a)和(d)分别为屈服强度高点及塑性阶段最高点，其原子结构都大部分为FCC结构，且应力高的原因与[100]取向结构的图6(a)相同，都是由于原子间距离缩小导致的，塑性阶段最高点之所以比屈服强度应力低，是由于变形过程中已经产生了部分滑移，在结构内部产生了位错线，如图12(b)～(d)所示。
图11(b)～(c)显示，在应变6.2%～10.0%之间，HEA纳米柱的顶部与底部沿HCP滑移方向发生了明显的交叉滑移，其滑移方向分别为与顶部呈30°以及与纳米柱呈45°。在应变为20.0%时，其滑移方向与顶部呈30°方向的滑移系占据优势，发生大的滑移错动，明显的滑移可解释其在塑性变形阶段保持较低的应力值。
综上，在[110]取向结构Al0.3CoCrFeNi高熵合金的弹性变形及屈服阶段，其变形机制及应力产生的原因与[100]取向结构的大致相同，但其在塑性阶段产生了次高点并在压缩过程中形成了明显清晰的滑移现象，此阶段的变形机制为滑移变形，表明在随后的塑性变形阶段具有较低的应力，如图11(b)～(f)及图12(b)～(f)所示。
2.2.3 [111]取向结构的压缩模拟变形机制及微观演变
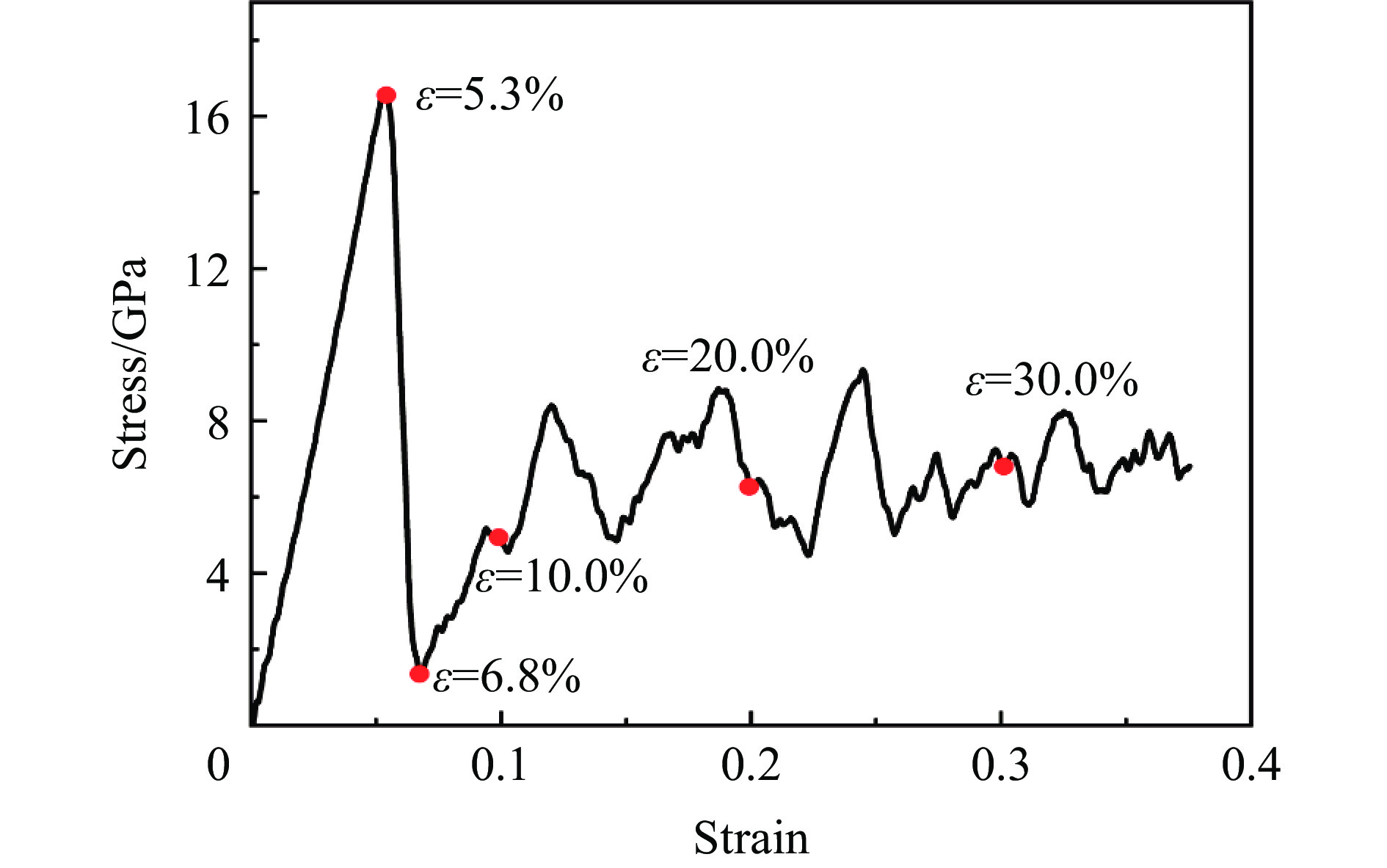
图13为[111]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线，截取了应变5.3%（屈服强度点）、6.8%（屈服阶段最低点）、10.0%、20.0%及30.0%的晶体结构图和位错分布图进行分析，如图14～15所示。
图 13 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线模拟结果Figure 13. Simulated stress-strain curve of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 14 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩晶体结构演变的模拟结果Figure 14. Simulated crystal structure evolutions of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 15 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩位错分布模拟结果Figure 15. Simulated dislocation distributions of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression在弹性变形与屈服阶段，其变化趋势与[100]取向结构和[110]取向结构的大致相同，如图14(a)～(b)和15(a)～(b)所示。然而在塑性变形阶段，图14(c)～(e)显示并没有产生明显的滑移现象，只是纳米柱直径变大。图15(b)～(g)显示[111]取向结构Al0.3CoCrFeNi高熵合金纳米柱压缩过程中形成大量长程位错线，且较密集，取应变为6.8%和30.0%纳米柱中的部分位错线进行局部放大，如图15(c)和(g)所示，可以观察到HCP结构零散破碎，并且大量位错线错综复杂，难以形成完整的HCP原子结构平面。HCP结构不断破碎湮灭，并且未能够形成完整的滑移平面，亦不会产生滑移系，因此，[111]取向结构Al0.3CoCrFeNi高熵合金压缩过程中在塑性变形阶段可保持较高的应力范围。
综上，[111]取向结构Al0.3CoCrFeNi高熵合金压缩模拟过程中，在弹性变形及屈服阶段，其变形机制及应力产生的原因与[100]和[110]取向结构的大致相同，但其在塑性阶段并没有滑移系的产生，可保持较高的应力范围。
2.2.4 不同取向结构的Al0.3CoCrFeNi高熵合金压缩模拟变形机制及微观演变对比
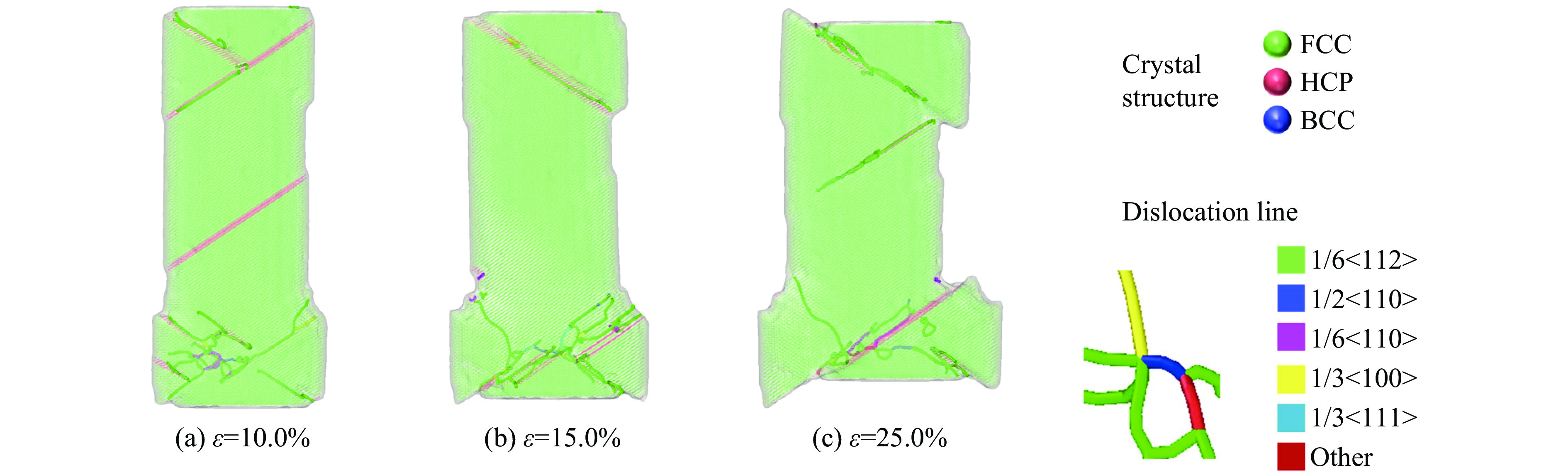
根据2.2.1~2.2.3节的不向取向结构的压缩模拟变形机制及微观演变分析可知，不同取向结构的HEA压缩过程中主要的差异体现在塑性变形阶段，图16～18即为不同取向结构Al0.3CoCrFeNi高熵合金的压缩变形机制及微观演变数值模拟结果对比，截取了应变10.0%、15.0%及25.0%的晶体结构和位错分布融合图进行分析。
图 16 [100]取向结构Al0.3CoCrFeNi高熵合金压缩过程中原子晶体结构及位错分布模拟结果融合对比Figure 16. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 17 [110]取向结构Al0.3CoCrFeNi高熵合金压缩过程中原子晶体结构及位错分布模拟结果融合对比Figure 17. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 18 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟原子晶体结构及位错分布融合对比Figure 18. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression在相同应变下，不同取向结构的Al0.3CoCrFeNi高熵合金的晶体结构具有明显的区别。[100]取向结构的Al0.3CoCrFeNi高熵合金压缩过程中孪晶结构较多，[110]取向结构的HCP结构会沿着滑移系产生较大的位错滑移，而[111]取向结构的不会产生任何滑移系，但会有大量长程位错生成。这可解释图3中不同取向结构的Al0.3CoCrFeNi高熵合金的压缩及拉伸应力-应变曲线塑性变形阶段应力值差异的原因。
除此之外，不同取向结构Al0.3CoCrFeNi高熵合金的变形机制也发生了改变。[100]取向结构Al0.3CoCrFeNi高熵合金主要的变形机制为孪晶变形，在30.0%应变后，孪晶会逐渐湮灭，整体呈现有序FCC结构，具有较高的应力值；[110]取向结构Al0.3CoCrFeNi高熵合金主要的变形机制为滑移变形，在三者中会表现出较低的应力值；[111]取向结构Al0.3CoCrFeNi高熵合金主要的变形机制为位错变形，具有位错强化性质，可保持较高的应力值。
2.2.5 [100]取向结构的拉伸模拟变形机制及微观演变
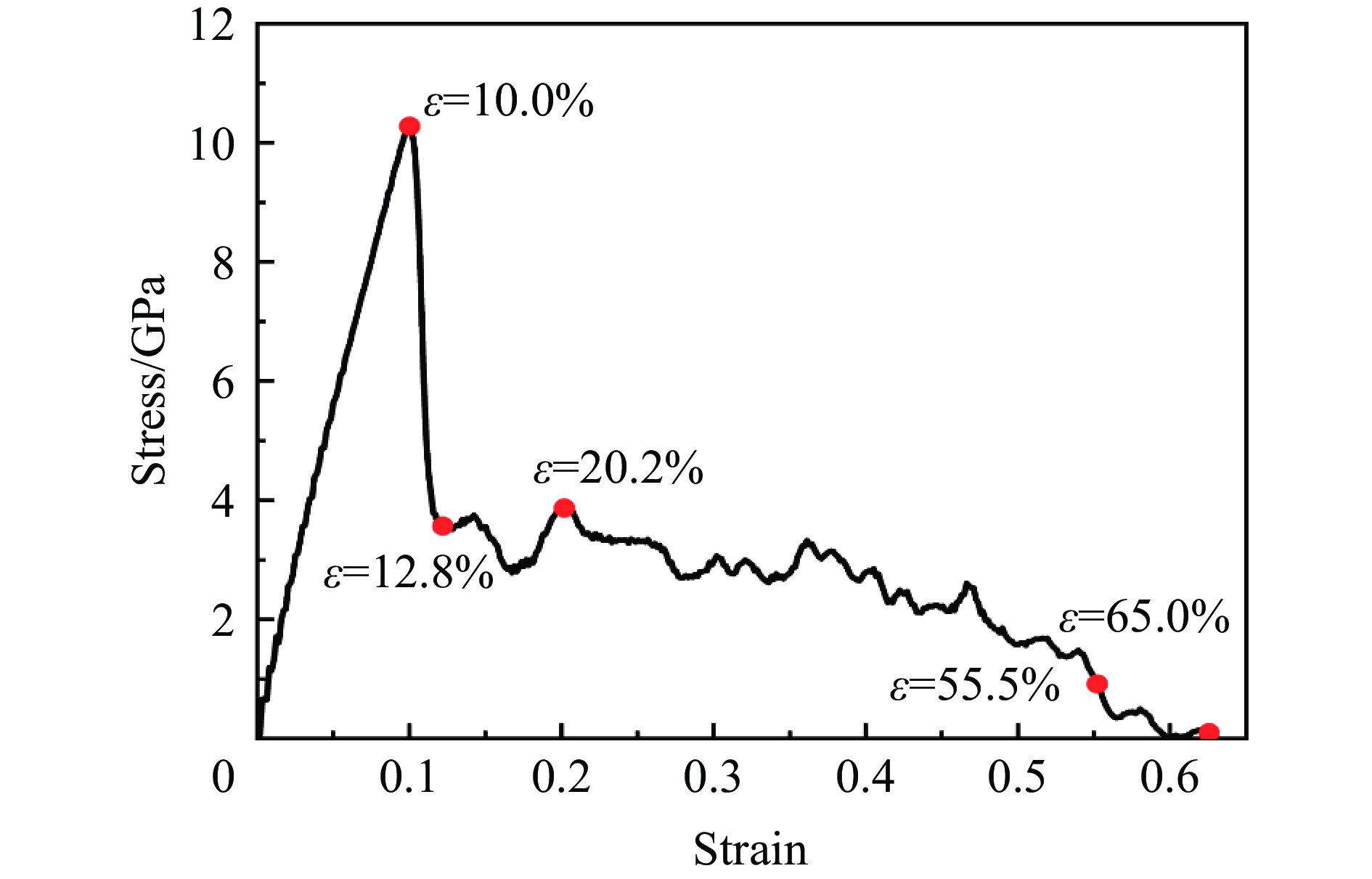
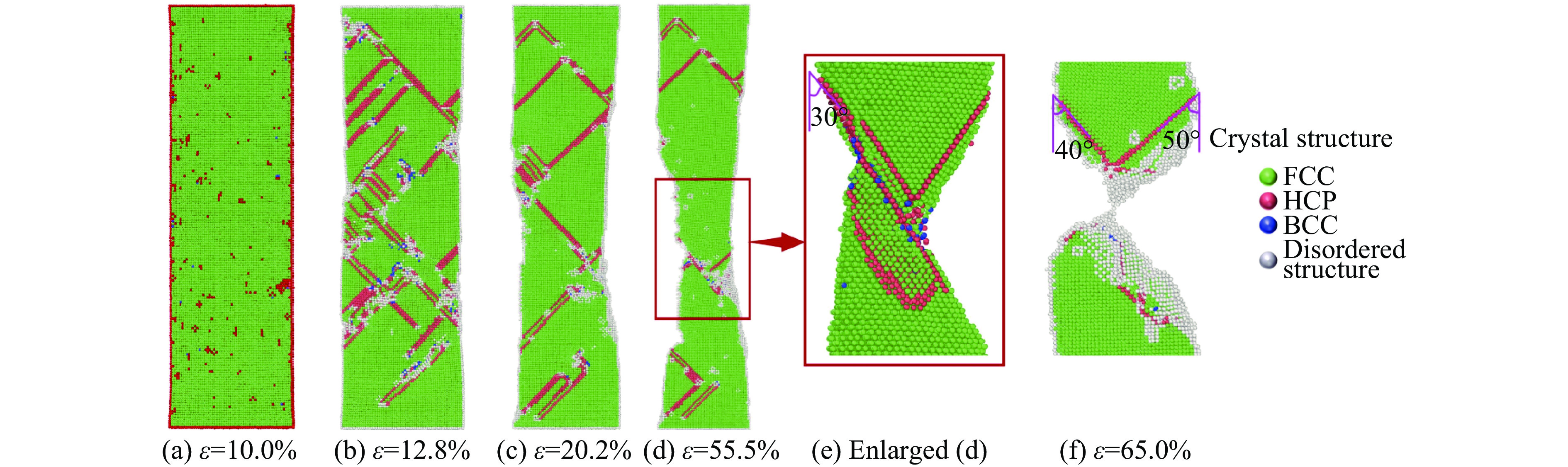
图19为[100]取向结构Al0.3CoCrFeNi高熵合金的拉伸应力-应变曲线图，截取了应变10.0%（屈服强度点）、12.8%（屈服阶段最低点）、20.2%（塑性阶段高点）、55.5%（颈缩形成点）及65.0%（拉伸断裂点）的晶体结构图和位错分布图进行分析，如图20所示。
图 19 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线Figure 19. Simulated stress-strain diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 20 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变Figure 20. Simulated crystal structure evolution diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under tension弹性变形阶段，拉伸与压缩过程规律一致，图20(a)所示晶体结构基本保持最初FCC结构，不产生晶体结构变化和位错，应力的增加全部是由原子间距的增加所产生的抵抗力所致。
屈服阶段，与压缩过程相比，形成了较多的HCP晶体结构，其错综复杂排列，部分无序结构在其中产生，如图20(b)所示。
随着应变的增大，当应变为20.2%时，在Al0.3CoCrFeNi高熵合金纳米柱中间部分产生收缩（图20(c)），图20(d)显示当应变为55.5%时，产生明显颈缩，在其边界部分，产生大量无序结构，图20(e)为颈缩部分放大图，观察到颈缩是由于沿着两个交叉的HCP面滑移产生的，周围边界原子以适应伸长量的变化，变化为无序结构。当应变为65.0%时，滑移至最后一个原子分离，即发生了断裂，如图20(f)所示。图19的应力-应变曲线显示，颈缩的产生使应力不断下降，直至断裂。
2.2.6 [110]取向结构的拉伸模拟变形机制及微观演变
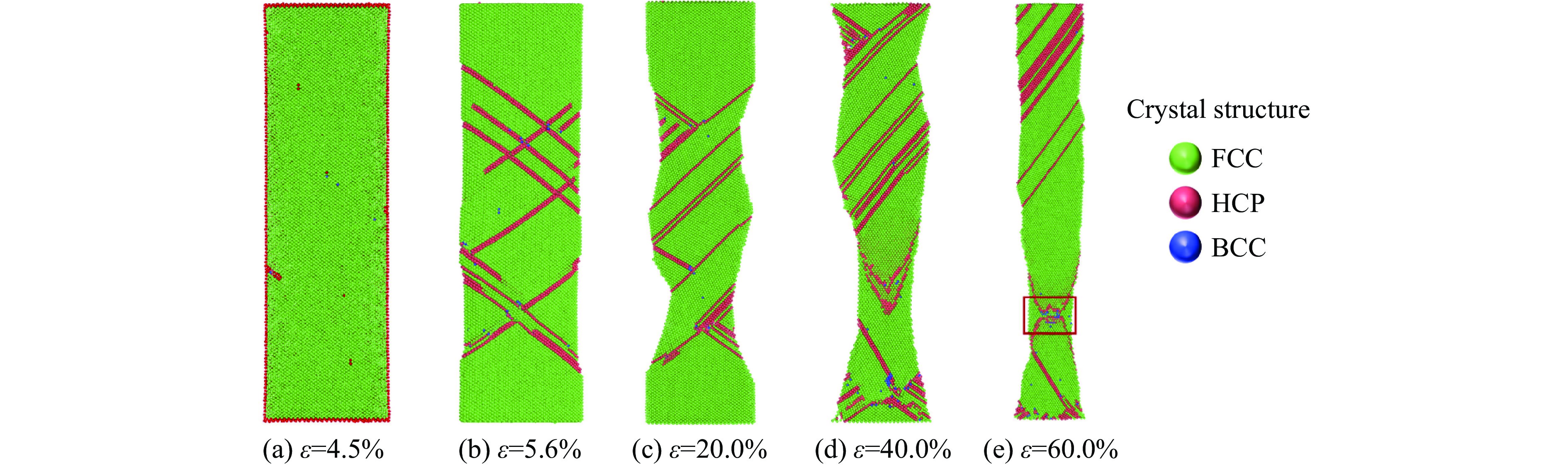
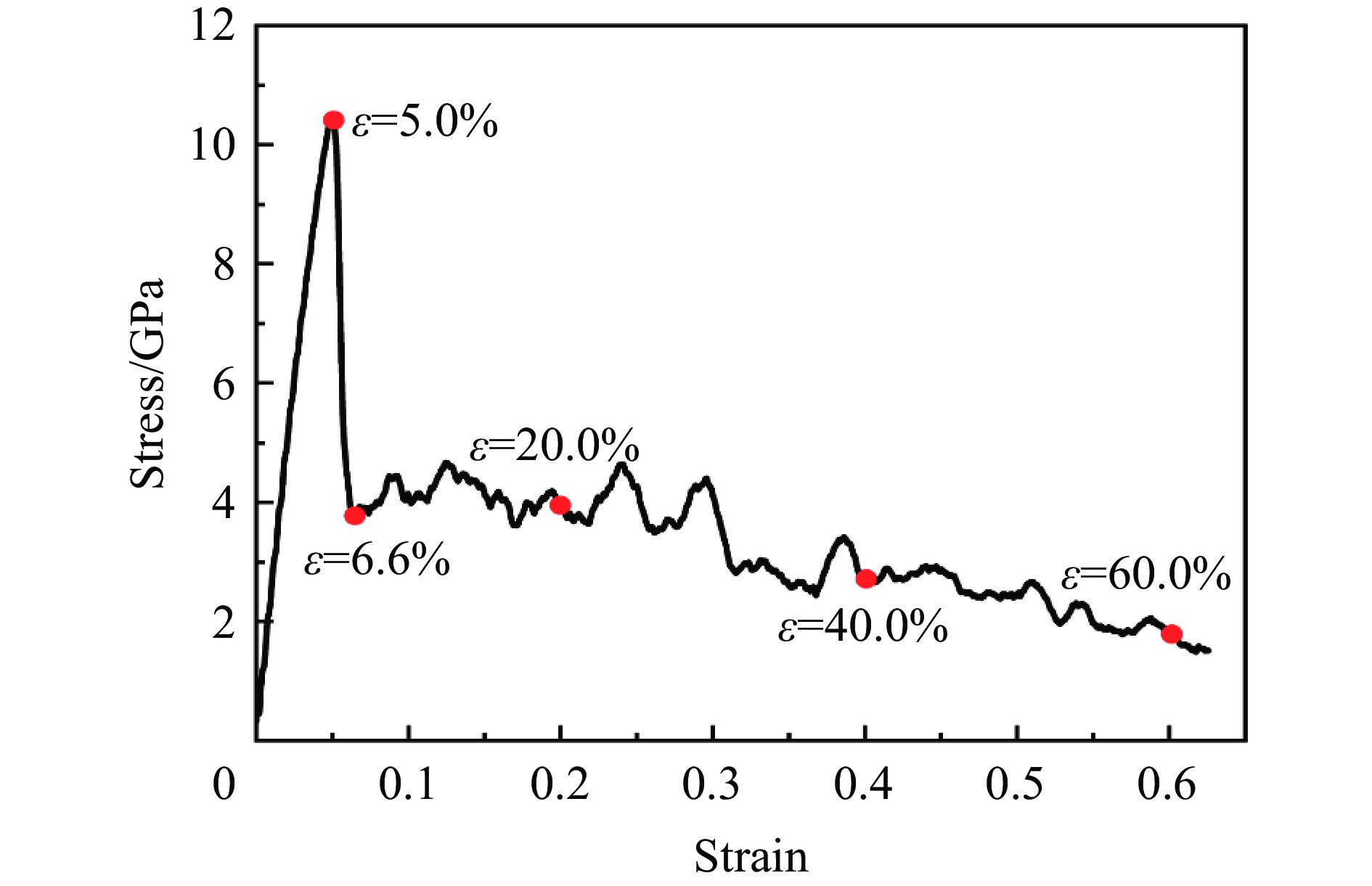
图21为[110]取向结构Al0.3CoCrFeNi高熵合金的拉伸应力-应变曲线，截取了应变4.5%（屈服强度点）、5.6%（屈服阶段最低点）、20.0%（颈缩形成点）、40.0%及60.0%的晶体结构图和位错分布图进行分析，如图22所示。
图 21 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线Figure 21. Simulated stress-strain curve of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 22 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变Figure 22. Simulated crystal structure evolution of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under tension弹性阶段与上述[100]取向结构规律一致。随着不断的拉伸，形成较为规则的HCP滑移面，产生孪晶结构，在应变为20.0%时，观察到明显的颈缩。[110]取向结构的Al0.3CoCrFeNi高熵合金在拉伸过程中，应力较低，表明晶体结构取向对应力的影响较大。
2.2.7 [111]取向结构的拉伸模拟变形机制及微观演变
图23为[111]取向结构Al0.3CoCrFeNi高熵合金的拉伸应力-应变曲线，截取了应变5.0%（屈服强度点）、6.6%（屈服阶段最低点）、20.0%（颈缩形成点）、40.0%及60.0%的晶体结构图和位错分布图进行分析，如图24所示。
图 23 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线Figure 23. Tension simulation stress-strain diagram of [111]-oriented Al0.3CoCrFeNi high-entropy alloy
图 24 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变Figure 24. Simulated crystal structure evolution of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under tension正如[111]取向结构的压缩过程，在弹性变形与屈服阶段，其变化趋势与[100]取向结构和[110]取向结构的大致相同，如图24(a)～(b)所示。然而，在塑性变形阶段，图24(c)～(e)显示并没有产生明显的滑移现象，只是纳米柱直径变小。在拉伸变形过程中，HCP结构同样零散破碎，难以形成完整的HCP原子结构平面。因此，HCP结构不断破碎湮灭，且未能形成完整的滑移平面，也不会产生滑移系，而颈缩是由2个交叉的HCP结构面在界面产生的缺口造成的。
2.2.8 不同取向结构的Al0.3CoCrFeNi高熵合金拉伸模拟变形机制及微观演变对比
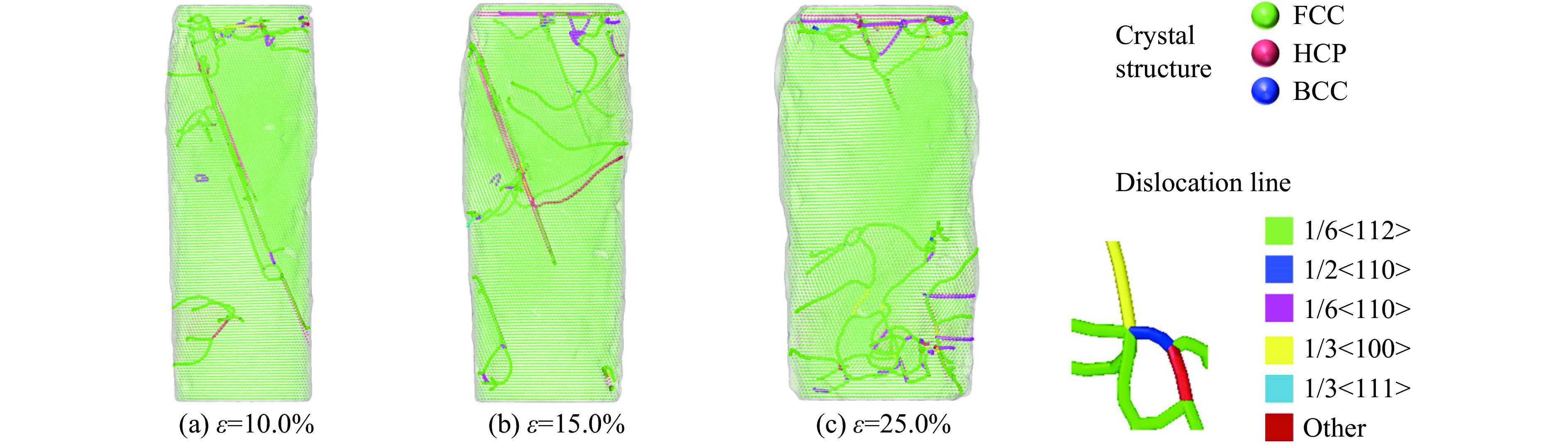
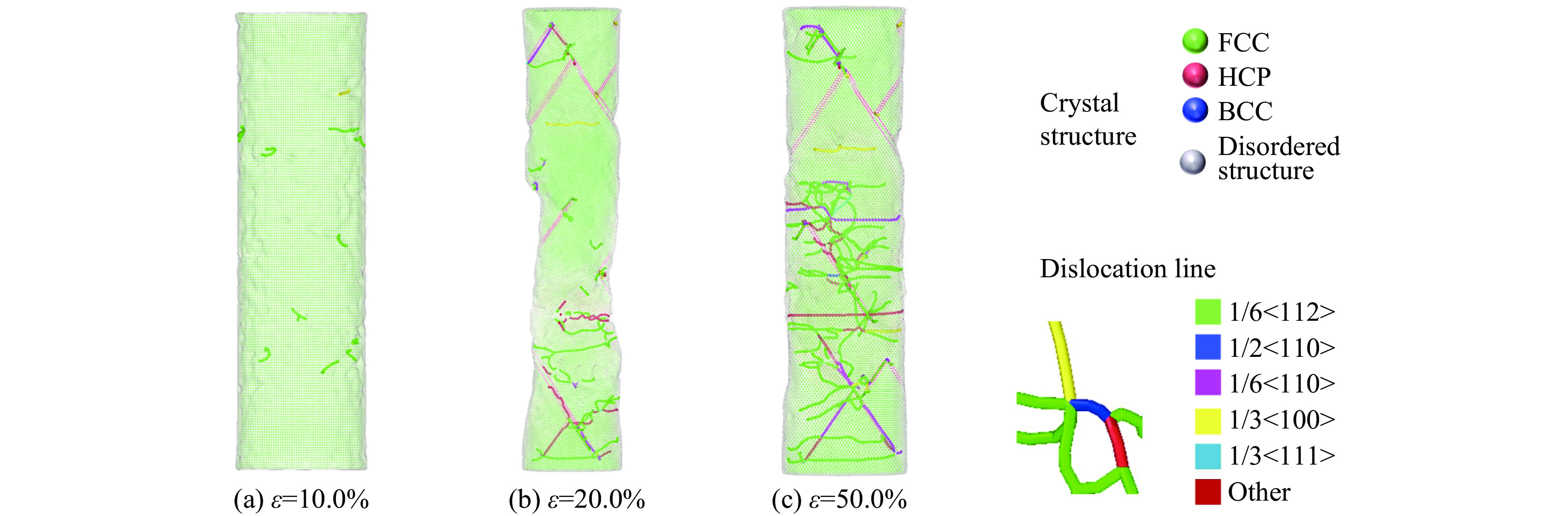
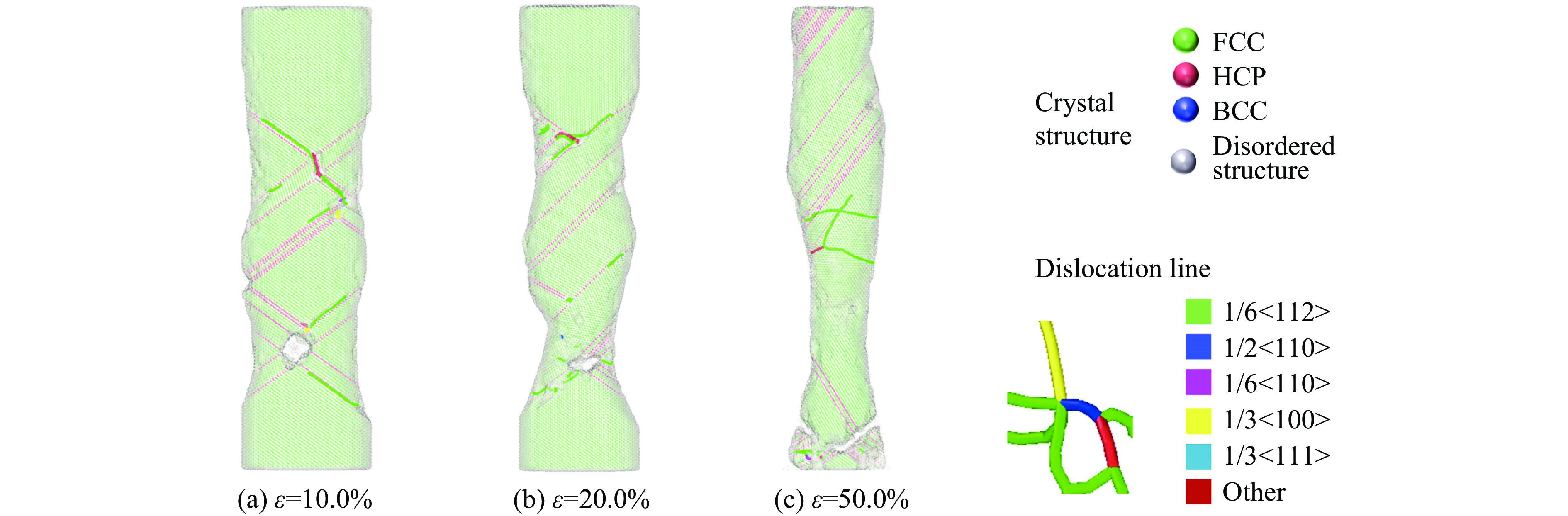
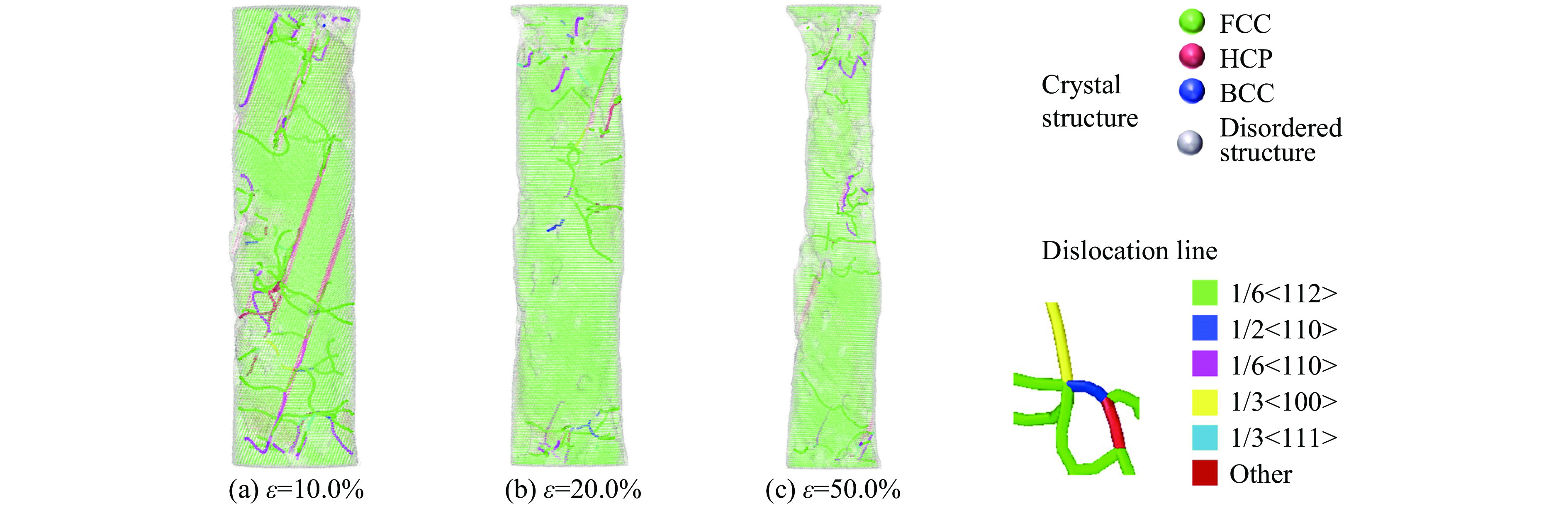
根据2.2.5~2.2.7节的不同取向结构的拉伸模拟变形机制及微观演变分析可知，与压缩情况相同，不同取向结构的HEA在拉伸过程中主要的不同在塑性变形阶段，图25～27即为不同取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟变形机制及微观演变对比图，截取了应变10.0%、20.0%及50.0%的晶体结构图和位错分布融合图进行分析。
图 25 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比Figure 25. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy
图 26 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比Figure 26. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [110]-oriented Al0.3CoCrFeNi high-entropy alloy
图 27 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比Figure 27. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [111]-oriented Al0.3CoCrFeNi high-entropy alloy在相同应变下，可观察到不同取向结构的Al0.3CoCrFeNi高熵合金的晶体结构具有明显的区别，[100]取向结构的Al0.3CoCrFeNi高熵合金拉伸过程中孪晶结构较多，且产生较多的位错线，[110]取向结构的产生相对规则的HCP结构滑移面，沿着滑移系产生较大的位错滑移，较早出现颈缩现象，而[111]取向结构的不会产生任何滑移系，位错线大多产生于结构内部，而不是从界面开始而扩展，且纳米柱直径变化较不均匀，没有太明显的颈缩发生点。
2.3 不同应变率下的变形机制及微观演变
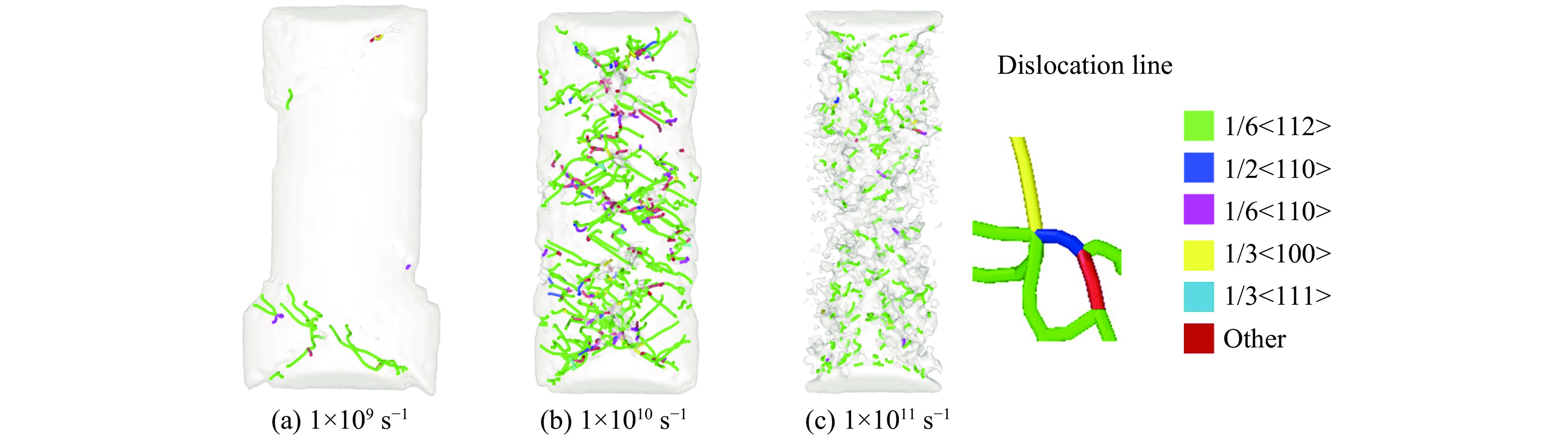
图28～31为了不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟原子晶体结构及位错分布图。截取了应变为15.0%和25.0%的2个状态进行分析。
图 28 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩15.0%的原子晶体结构模拟结果Figure 28. Simulated atomic crystal structures of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 15.0% at different strain rates
图 29 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩15.0%的位错分布模拟结果Figure 29. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 15.0% at different strain rates
图 30 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩25.0%的原子晶体结构模拟结果Figure 30. Simulated atomic crystal structures of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 25.0% at different strain rates
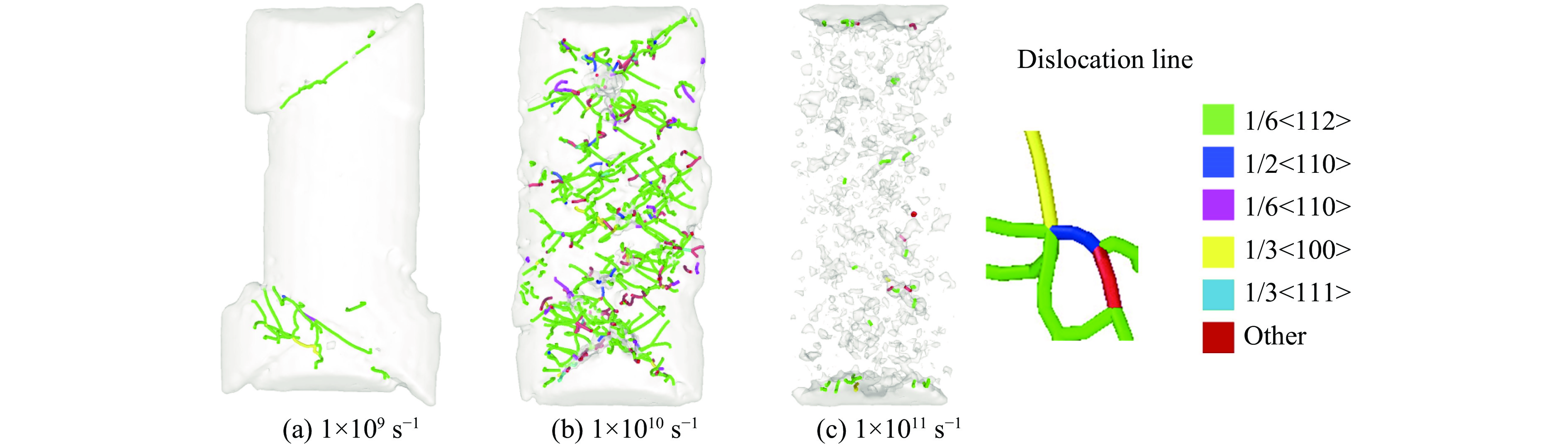
图 31 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩25.0%的位错分布模拟结果Figure 31. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 25.0%at different strain rates图28～31显示，应变率对Al0.3CoCrFeNi高熵合金的压缩塑性变形阶段产生影响，其晶体结构的变化及位错线的分布有明显差异。图28(a)和30(a)显示，在较低应变率（1×109 s−1）下，形成整齐有序完整的HCP结构面，并产生少量位错线，如图29(a)和31(a)所示，此时塑性变形机制主要是沿HCP面滑移，但滑移系数量较少，对应图4(a)中应力-应变曲线呈现出上下波动的锯齿状；图28(b)和30(b)显示，随应变率的提高（1×1010 s−1），大量滑移系上的原子开始沿滑移方向移动，形成密集的HCP结构面并发生交错滑移，在纳米柱内部同时产生大量的位错线，如图29(b)和31(b)所示，此时其主要的变形机制同样是以滑移为主的变形机制，但滑移系较多，出现大面积的交叉滑移现象并出现了密集的滑移平面，对应图4(a)中应力-应变曲线变得较为平滑；图28(c)和30(c)显示，在高应变率（1×1011 s−1）下，不再产生HCP原子结构类型，从边界处形成大量的无序原子结构，构成非晶原子结构，向纳米柱内部扩展，形成大量短程无序的密集位错线，如图29(c)和31(c)所示，其变形机制由原子排列无序化的非晶原子结构诱导。
高应变率下产生高的屈服强度和应变，如图4所示，结合图28～31，该现象可归因于如下3个因素。
(1)热激活位错没有足够的时间穿过能量势垒。从能量学的角度看，晶体运动产生位错，位错的运动需要克服一定的能量势垒，在应变率较高时，位错克服能量势垒的时间较短，激活的位错难以轻松移动，从而需要更大应力来驱动晶体结构的变形，同时需要更大的应变来适应大变形[33]。
(2)黏性声子拖曳对位错运动的强烈影响。在高的应变率下，其原子间的黏性摩擦力对位错运动的阻力较大，从而也使得其应力值较高。尤其是在压缩变形初始启动时的应力值较大，在短时间内产生大的变形量需要高的应力，3种取向结构的应力均约为15 GPa[62]。
(3)原子键的断裂及位错应力的提高。高应变率使原子运动速率增加，导致原子间的相对位移还未产生缺陷和位错，就发生了大量原子键的断裂，从而形成无序结构，而大量原子键的断裂需要高的应力，因此会有应力的显著提高；并且位错运动所需的临界切应力也会随着应变率的提高而增大[57]。
2.4 刚性球冲击模拟试验
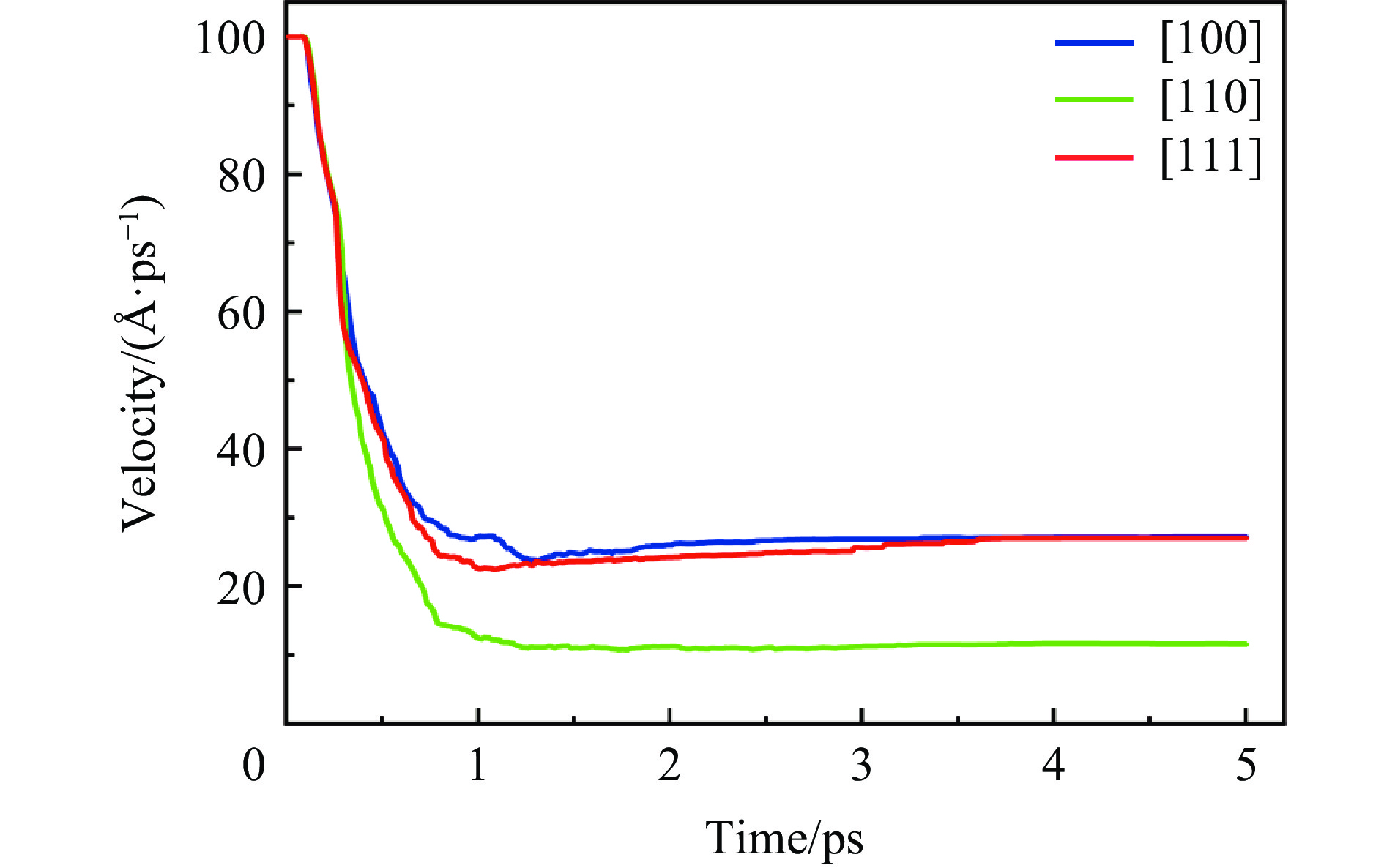
为进一步探究不同取向结构所组成Al0.3CoCrFeNi高熵合金的动态力学性能，进行了刚性球冲击数值模拟，刚性球的剩余速度变化曲线如图32所示。
图 32 撞击不同取向结构Al0.3CoCrFeNi高熵合金靶板的刚性球剩余速度的变化Figure 32. Residual velocity changes of rigid balls impacting differently-oriented Al0.3CoCrFeNi high-entropy alloy target plates图32显示，刚性球穿透[110]取向结构的Al0.3CoCrFeNi高熵合金靶板后的剩余速度最小，为10.74 Å/ps，说明[110]取向结构的Al0.3CoCrFeNi高熵合金靶板的抗冲击性能最好；而刚性球穿透[100]与[110]取向结构的Al0.3CoCrFeNi高熵合金靶板后的剩余速度分别为23.64和22.38 Å/ps，说明这2种取向结构的Al0.3CoCrFeNi高熵合金的抗冲击性能差异不大。
为探究[110]取向结构的Al0.3CoCrFeNi高熵合金靶板抗冲击性能良好的内在原因，截取3种取向结构Al0.3CoCrFeNi高熵合金靶板冲击过程中的晶体结构及位错分布图进行分析。
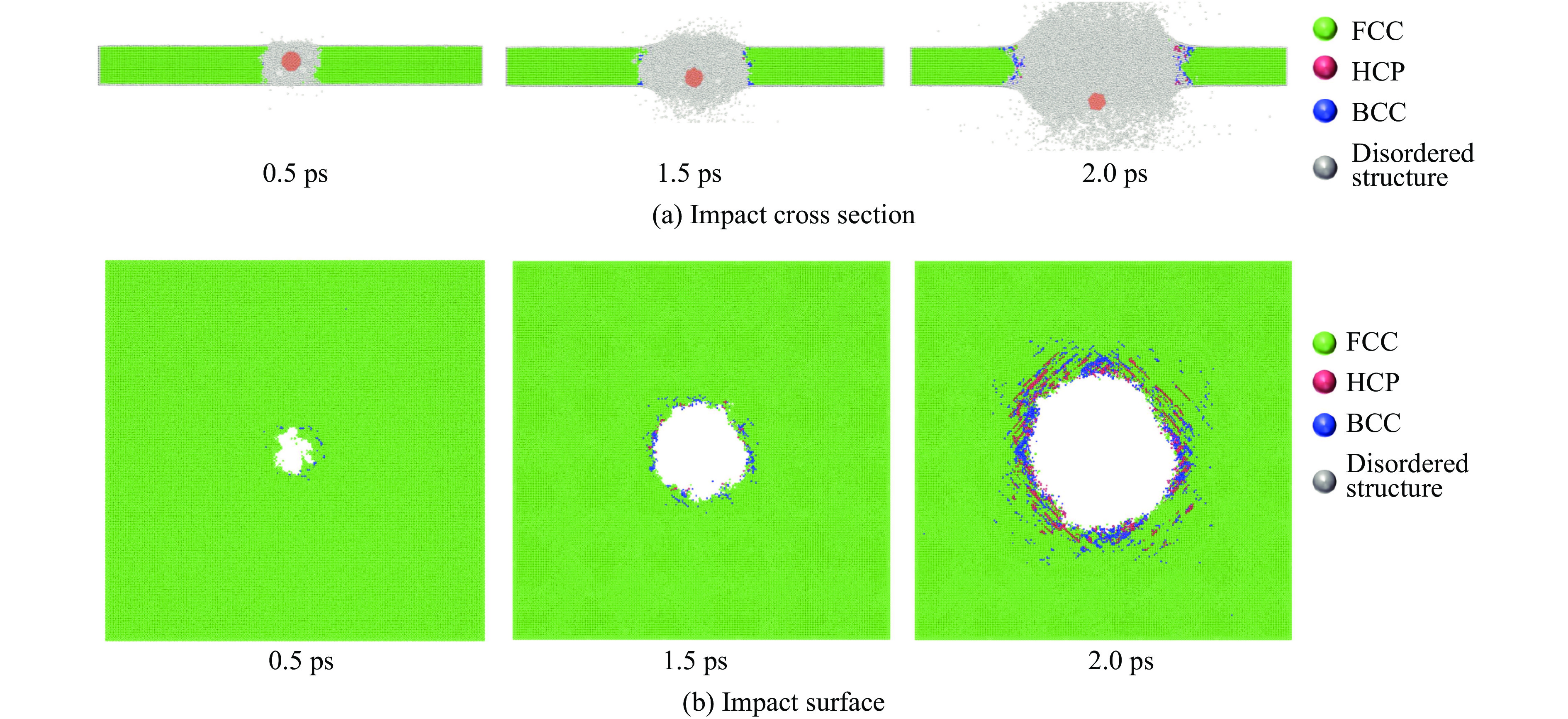
图33为[100]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布图。
图 33 [100]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布Figure 33. Crystal structure distribution of a [100]-oriented Al0.3CoCrFeNi high-entropy alloy target plate impacted by a rigid ball图33表示，当刚性球初始撞击到HEA靶板后（0.5 ps），便在撞击区域周围形成了无序结构。由2.3节中对图28～31高应变率压缩下晶体结构变化的分析可知，无序结构是由于原子高速运动导致原子键断裂造成的。刚性球继续冲击过程中，无序化区域继续扩大，大量无序化原子向靶前靶后方向分散，待刚性球完全穿透靶板后，无序化区域扩大至极限，在无序化原子周围形成环状分布的BCC与HCP原子结构，可推测从远离穿透孔至穿透孔方向，晶体结构的变化为原始FCC结构→BCC与HCP结构的混合→无序原子结构。
图34为[110]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布。
图 34 [110]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布Figure 34. Crystal structure distribution of a [110]-oriented Al0.3CoCrFeNi HEA target plate impacted by a rigid ball图34表示，[110]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击下晶体结构分布的变化趋势与[100]取向结构的大致相同，然而该靶板被刚性球完全穿透所需的时间更长，为4.5 ps，其原子分散程度更大。由图34中被刚性球完全穿透后靶板迎冲击面原子结构分布图（4.5 ps时刻）可以看出，在穿透孔附近的FCC原子结构呈现出稀疏波纹路（黄色波纹线），这与刚性球穿透靶板所产生的压缩波相关，该压缩波向靶四周扩散。
图35为[111]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布图。
图 35 [111]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布Figure 35. Crystal structure distribution of a [111]-oriented Al0.3CoCrFeNi HEA target plate impacted by a rigid ball图35表示，Al0.3CoCrFeNi高熵合金靶板被刚性球完全穿透后（2.5 ps），在穿透孔周围形成大量HCP有序结构，其中夹杂着少量BCC结构，原子结构变化涉及的区域更宽泛更广。
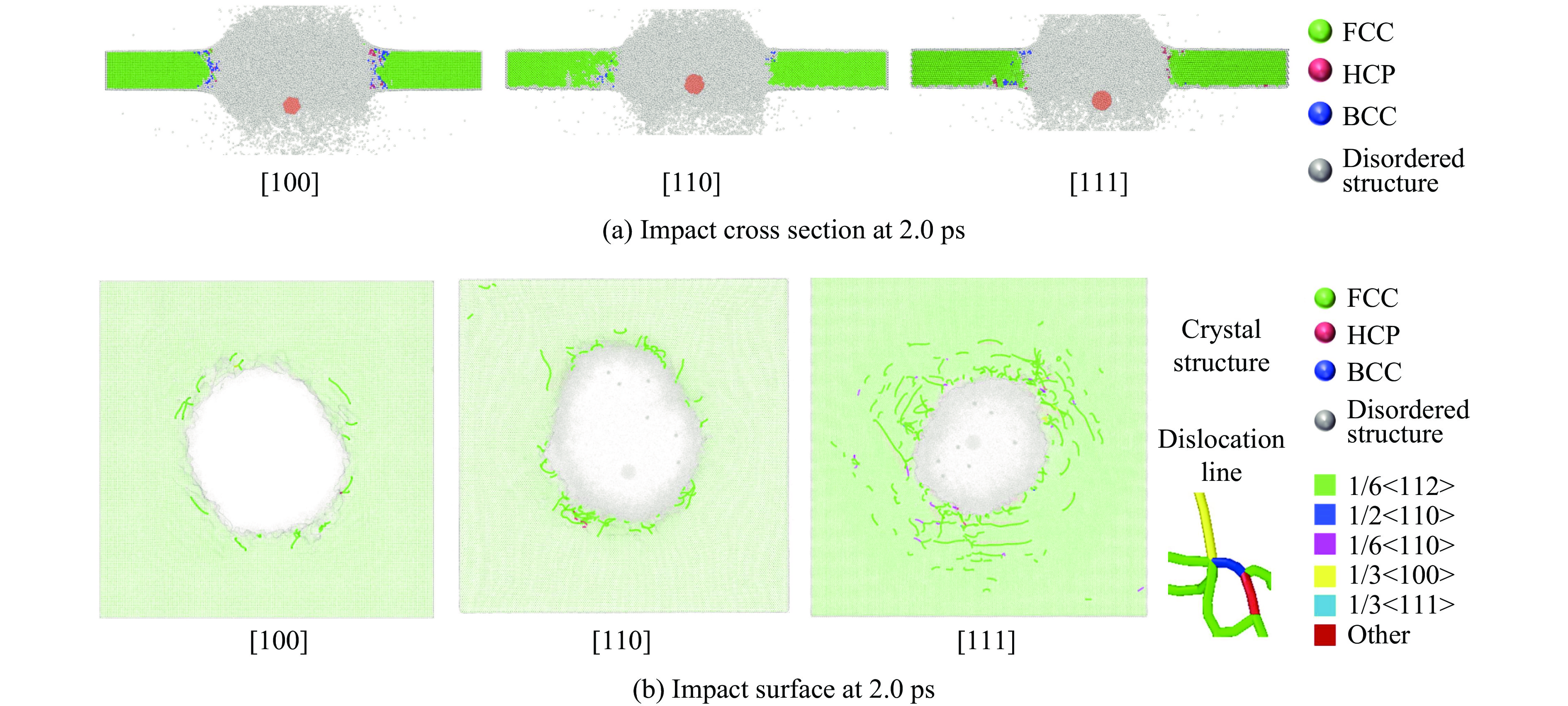
为更清晰地看出不同取向结构靶板冲击过程中原子结构变化的差别，在图36中给出显示了不同取向结构的原子晶体结构和位错线分布融合图。
图 36 不同取向结构Al0.3CoCrFeNi高熵合金靶板在刚性球撞击后的晶体结构及位错分布融合对比Figure 36. Comparison of atomic crystal structure and dislocation distribution fusion of differently-oriented Al0.3CoCrFeNi HEA target plates after impact by a rigid ball图36(a)显示，2.0 ps时，刚性球已完全穿透[100]取向结构的Al0.3CoCrFeNi高熵合金靶板，刚刚穿透[111]取向结构的靶板，还没有穿透[110]取向结构的靶板。图36(b)显示，[111]取向结构的靶板在穿透孔周围产生大量位错线，表明其周围变形较严重。
在刚性球冲击过程中，不可避免地产生局部温升，此对晶体结构产生一定的影响，在一些材料中会观察到绝热剪切带[12, 63-64]的产生。然而，本文的数值模拟中对刚性球撞击3种取向结构的Al0.3CoCrFeNi高熵合金靶板采用相同的外部条件，且考虑了撞击温度升高所带来的影响，图37展示了刚性球撞击后在2.0 ps时的局部温度分布，可以观察到，3种取向结构的Al0.3CoCrFeNi高熵合金靶板均产生了局部温升。在本文的模拟中，并未观察到绝热剪切带的产生，因此，局部温升现象并未对刚性球冲击不同取向结构的Al0.3CoCrFeNi高熵合金的模拟结果产生影响。
图 37 刚性球撞击不同取向结构Al0.3CoCrFeNi高熵合金的局部原子温度分布Figure 37. Local atomic temperature distribution of plates of Al0.3CoCrFeNi high entropy alloys with different orientation structures impacted by rigid balls综上，[110]取向结构的Al0.3CoCrFeNi高熵合金靶板具有较高的抗冲击能力，此与其具有良好的压缩性能有关，特别是在高应变率下的压缩性能。与[100]和[111]取向结构的Al0.3CoCrFeNi高熵合金靶板相比，[110]取向结构的靶板具有最高的屈服强度，并在屈服结束阶段也能保持最高的应力，因此能够抵御高速冲击。
3. 结 论
采用分子动力学模拟的方法，针对Al0.3CoCrFeNi高熵合金的单一取向的单晶结构，探究了[100]、[110]和[111]等3种不同取向结构的动态力学性能，得到以下结论。
(1)不同取向结构Al0.3CoCrFeNi高熵合金的动态力学性能及微观演变差异较大。三者的压缩和拉伸应力-应变曲线都会出现弹性变形阶段、屈服阶段和塑性变形阶段，但屈服强度和对应伸长量明显不同。压缩模拟试验中，[100]、[111]和[110]等3种不同取向结构的屈服强度依次升高，这是由不同取向结构中原子间距缩小所产生的抵抗力不同所致。塑性变形阶段，三者的应力变化趋势不同，这与不同的原子结构变化及变形机制密切相关，[100]取向结构主要的变形机制为孪晶变形，[110]取向结构主要的变形机制为滑移变形，[111]取向结构主要的变形机制为位错变形。拉伸模拟试验中，[111]、[100]、[110]等3种不同取向结构的屈服强度依次降低。塑性变形阶段，[100]取向结构在拉伸过程中的孪晶结构较多，伴有较多位错线，[110]取向结构产生相对规则的HCP结构滑移面，沿着滑移系产生较大的位错滑移，[111]取向结构不会产生任何滑移系。
(2)随着应变率的提高，Al0.3CoCrFeNi高熵合金的应力-应变曲线区别较大，且变形机制发生明显变化。随着应变率的提高，Al0.3CoCrFeNi高熵合金的屈服强度大幅度提高，对应伸长量也增大；在较低应变率（1×109 s−1）下，塑性变形机制主要是沿HCP面滑移变形，但滑移系数量较少。随应变率的提高（1×1010 s−1），其主要的变形机制同样是以滑移为主的变形机制，但滑移系较多，出现大面积的交叉滑移现象并出现了密集的滑移平面。在高应变率（1×1011 s−1）下，其变形机制由原子排列无序化的非晶原子结构诱导。
(3)在3种取向结构的Al0.3CoCrFeNi高熵合金中，[110]取向结构的抗冲击性能最好，与该结构取向的Al0.3CoCrFeNi高熵合金在高应变率下具有最高的屈服强度，并在屈服结束阶段也能保持最高的应力相关，并且冲击过程中形成大量的无序化原子结构，与它在高应变率（1×1011 s−1）压缩下，产生大量无序化原子结构现象相一致。
-
图 2 刚性球冲击Al0.3CoCrFeNi纳米靶板模型
Figure 2. A model for a rigid ball impacting an Al0.3CoCrFeNi nano-target
图 3 不同取向结构Al0.3CoCrFeNi高熵合金压缩及拉伸应力-应变曲线
Figure 3. Compressive and tensile stress-strain curves of Al0.3CoCrFeNi high-entropy alloys with different orientation structures
图 4 不同应变率下的Al0.3CoCrFeNi高熵合金压缩及拉伸应力-应变曲线
Figure 4. Compressive and tensile stress-strain curves of Al0.3CoCrFeNi high-entropy alloys at different strain rates
图 5 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟应力-应变曲线
Figure 5. Compression simulation stress-strain curve of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure
图 6 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟晶体结构演变
Figure 6. Simulated crystal structure evolution of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure during compression
图 7 [100]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟位错分布
Figure 7. Simulated dislocation distribution of Al0.3CoCrFeNi high-entropy alloy with [100] orientation structure during compression
图 8 孪晶和位错现象的放大图
Figure 8. Amplification diagrams of twinning and dislocation phenomenon
图 10 [110]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线模拟结果
Figure 10. Simulated stress-strain curve of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 12 [110]取向结构Al0.3CoCrFeNi高熵合金的压缩位错分布的模拟结果
Figure 12. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 13 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩应力-应变曲线模拟结果
Figure 13. Simulated stress-strain curve of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 14 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩晶体结构演变的模拟结果
Figure 14. Simulated crystal structure evolutions of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 15 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩位错分布模拟结果
Figure 15. Simulated dislocation distributions of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 16 [100]取向结构Al0.3CoCrFeNi高熵合金压缩过程中原子晶体结构及位错分布模拟结果融合对比
Figure 16. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 17 [110]取向结构Al0.3CoCrFeNi高熵合金压缩过程中原子晶体结构及位错分布模拟结果融合对比
Figure 17. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 18 [111]取向结构Al0.3CoCrFeNi高熵合金的压缩模拟原子晶体结构及位错分布融合对比
Figure 18. Comparison of simulated atomic crystal structures and dislocation distribution fusion contrast of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under compression
图 19 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线
Figure 19. Simulated stress-strain diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 20 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变
Figure 20. Simulated crystal structure evolution diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 21 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线
Figure 21. Simulated stress-strain curve of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 22 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变
Figure 22. Simulated crystal structure evolution of [110]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 23 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟应力-应变曲线
Figure 23. Tension simulation stress-strain diagram of [111]-oriented Al0.3CoCrFeNi high-entropy alloy
图 24 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟晶体结构演变
Figure 24. Simulated crystal structure evolution of [111]-oriented Al0.3CoCrFeNi high-entropy alloy under tension
图 25 [100]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比
Figure 25. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [100]-oriented Al0.3CoCrFeNi high-entropy alloy
图 26 [110]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比
Figure 26. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [110]-oriented Al0.3CoCrFeNi high-entropy alloy
图 27 [111]取向结构Al0.3CoCrFeNi高熵合金的拉伸模拟原子晶体结构及位错分布融合对比
Figure 27. Tension simulation of atomic crystal structure and dislocation distribution fusion contrast diagram of [111]-oriented Al0.3CoCrFeNi high-entropy alloy
图 28 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩15.0%的原子晶体结构模拟结果
Figure 28. Simulated atomic crystal structures of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 15.0% at different strain rates
图 29 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩15.0%的位错分布模拟结果
Figure 29. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 15.0% at different strain rates
图 30 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩25.0%的原子晶体结构模拟结果
Figure 30. Simulated atomic crystal structures of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 25.0% at different strain rates
图 31 不同应变率下[110]取向结构Al0.3CoCrFeNi高熵合金压缩25.0%的位错分布模拟结果
Figure 31. Simulated dislocation distributions of [110]-oriented Al0.3CoCrFeNi high-entropy alloy compressed by 25.0%at different strain rates
图 32 撞击不同取向结构Al0.3CoCrFeNi高熵合金靶板的刚性球剩余速度的变化
Figure 32. Residual velocity changes of rigid balls impacting differently-oriented Al0.3CoCrFeNi high-entropy alloy target plates
图 33 [100]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布
Figure 33. Crystal structure distribution of a [100]-oriented Al0.3CoCrFeNi high-entropy alloy target plate impacted by a rigid ball
图 34 [110]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布
Figure 34. Crystal structure distribution of a [110]-oriented Al0.3CoCrFeNi HEA target plate impacted by a rigid ball
图 35 [111]取向结构的Al0.3CoCrFeNi高熵合金靶板在刚性球冲击过程中的晶体结构分布
Figure 35. Crystal structure distribution of a [111]-oriented Al0.3CoCrFeNi HEA target plate impacted by a rigid ball
图 36 不同取向结构Al0.3CoCrFeNi高熵合金靶板在刚性球撞击后的晶体结构及位错分布融合对比
Figure 36. Comparison of atomic crystal structure and dislocation distribution fusion of differently-oriented Al0.3CoCrFeNi HEA target plates after impact by a rigid ball
图 37 刚性球撞击不同取向结构Al0.3CoCrFeNi高熵合金的局部原子温度分布
Figure 37. Local atomic temperature distribution of plates of Al0.3CoCrFeNi high entropy alloys with different orientation structures impacted by rigid balls
表 1 不同原子对之间相互作用的Lennard-Jones参数
Table 1. Lennard-Jones parameters of the interactions between different atom pairs
原子对 ε/eV σ/Å Al-Co 0.0469 2.578 Cr-Co 0.0466 2.456 Fe-Co 0.0477 2.448 Co-Co 0.0043 2.584 Ni-Co 0.0474 2.428 
下载: 导出CSV
表 2 不同取向结构的Al0.3CoCrFeNi高熵合金在压缩及拉伸过程中各个变形阶段临界点的应力和变形量
Table 2. The stress and deformation at the critical point of each deformation stage of Al0.3CoCrFeNi HEA with different orientation structures during compressive and tensile processes
分界点 应力/GPa 应变/% 压缩 拉伸 压缩 拉伸 [100] [110] [111] [100] [110] [111] [100] [110] [111] [100] [110] [111] 弹性变形与屈服阶段分界点 5.38 18.41 16.63 10.28 6.14 10.45 5.5 4.8 5.3 10.0 4.5 5.0 屈服与塑性变形阶段分界点 1.55 2.43 1.23 3.51 2.30 3.74 8.4 6.2 6.8 12.8 5.6 6.6
下载: 导出CSV
表 3 不同应变率下不同取向结构的Al0.3CoCrFeNi高熵合金的屈服应力及应变
Table 3. Yield stresses and strains of Al0.3CoCrFeNi high-entropy alloys with different orientation structures at different strain rates
模拟试验 晶体取向 1×109 s−1 1×1010 s−1 1×1011 s−1 屈服应力/GPa 应变/% 屈服应力/GPa 应变/% 屈服应力/GPa 应变/% 压缩 [100] 5.38 5.5 7.34 6.0 33.70 36.0 [110] 18.41 4.8 31.22 7.1 34.38 13.7 [111] 16.63 5.3 24.43 7.8 30.11 15.3 拉伸 [100] 10.28 10.0 11.57 12.2 18.16 20.0 [110] 6.14 4.5 7.50 4.7 15.19 12.6 [111] 10.45 5.0 15.19 12.6 20.62 12.2
下载: 导出CSV
-
[1] CHENG J C, ZHANG S, LIU Q, et al. Ballistic impact experiments and modeling on impact cratering, deformation and damage of 2024-T4 aluminum alloy [J]. International Journal of Mechanical Sciences, 2022, 224: 107312. DOI: 10.1016/j.ijmecsci.2022.107312. [2] RANAWEERA P, BAMBACH M R, WEERASINGHE D, et al. Ballistic impact response of monolithic steel and tri-metallic steel-titanium-aluminium armour to nonrigid NATO FMJ M80 projectiles [J]. Thin-Walled Structures, 2023, 182: 110200. DOI: 10.1016/j.tws.2022.110200. [3] LI L, ZHANG Q C, LU T J. Ballistic penetration of deforming metallic plates: experimental and numerical investigation [J]. International Journal of Impact Engineering, 2022, 170: 104359. DOI: 10.1016/j.ijimpeng.2022.104359. [4] DUBEY R, JAYAGANTHAN R, RUAN D, et al. Ballistic perforation and penetration of 6xxx-series aluminium alloys: A review [J]. International Journal of Impact Engineering, 2023, 172: 104426. DOI: 10.1016/j.ijimpeng.2022.104426. [5] FAIDZI M K, ABDULLAH S, ABDULLAH M F, et al. Computational analysis on the different core configurations for metal sandwich panel under high velocity impact [J]. Soft Computing, 2021, 25(16): 10561–10574. DOI: 10.1007/s00500-021-06015-6. [6] LIU J, ZHENG B L, ZHANG K, et al. Ballistic performance and energy absorption characteristics of thin nickel-based alloy plates at elevated temperatures [J]. International Journal of Impact Engineering, 2019, 126: 160–171. DOI: 10.1016/j.ijimpeng.2018.12.012. [7] REN J, XU Y X, LIU J X, et al. Effect of strength and ductility on anti-penetration performance of low-carbon alloy steel against blunt-nosed cylindrical projectiles [J]. Materials Science and Engineering: A, 2017, 682: 312–322. DOI: 10.1016/j.msea.2016.11.012. [8] DENG Y F, HU A, XIAO X K, et al. Experimental and numerical investigation on the ballistic resistance of ZK61m magnesium alloy plates struck by blunt and ogival projectiles [J]. International Journal of Impact Engineering, 2021, 158: 104021. DOI: 10.1016/j.ijimpeng.2021.104021. [9] CHOUDHURI D, JANNOTTI P A, MUSKERI S, et al. Ballistic response of a FCC-B2 eutectic AlCoCrFeNi2.1 high entropy alloy [J]. Journal of Dynamic Behavior of Materials, 2019, 5(4): 495–503. DOI: 10.1007/s40870-019-00220-z. [10] ZHANG Y, ZUO T T, TANG Z, et al. Microstructures and properties of high-entropy alloys [J]. Progress in Materials Science, 2014, 61: 1–93. DOI: 10.1016/j.pmatsci.2013.10.001. [11] SADEGHILARIDJANI M, MUSKERI S, HASANNAEIMI V, et al. Strain rate sensitivity of a novel refractory high entropy alloy: intrinsic versus extrinsic effects [J]. Materials Science and Engineering: A, 2019, 766: 138326. DOI: 10.1016/j.msea.2019.138326. [12] LI Z Z, ZHAO S T, ALOTAIBI S M, et al. Adiabatic shear localization in the CrMnFeCoNi high-entropy alloy [J]. Acta Materialia, 2018, 151: 424–431. DOI: 10.1016/j.actamat.2018.03.040. [13] 张平, 李远田, 张金勇, 等. Si对AlCoCrFeNi高熵合金热腐蚀行为的影响 [J]. 稀有金属材料与工程, 2021, 50(10): 3640–3647.ZHANG P, LI Y T, ZHANG J Y, et al. Effect of Si addition on hot corrosion behavior of AlCoCrFeNi high entropy alloys [J]. Rare Metal Materials and Engineering, 2021, 50(10): 3640–3647. [14] 吴炳乾, 饶湖常, 张冲, 等. Si含量对FeCoCr0.5NiBSi x高熵合金涂层组织结构和耐磨性的影响 [J]. 表面技术, 2015, 44(12): 85–91. DOI: 10.16490/j.cnki.issn.1001-3660.2015.12.014.WU B Q, RAO H C, ZHANG C, et al. Effect of silicon content on the microstructure and wear resistance of FeCoCr0.5NiBSi x high-entropy alloy coatings [J]. Surface Technology, 2015, 44(12): 85–91. DOI: 10.16490/j.cnki.issn.1001-3660.2015.12.014. [15] 王根, 李新梅. 第一性原理计算Cu、Co含量对CoCuFeNi系高熵合金的影响 [J]. 功能材料, 2020, 51(3): 3189–3195. DOI: 10.3969/j.issn.1001-9731.2020.03.029.WANG G, LI X M. Effects of Cu, Co contents on CoCuFeNi system high-entropy alloys by the first principle calculation [J]. Journal of Functional Materials, 2020, 51(3): 3189–3195. DOI: 10.3969/j.issn.1001-9731.2020.03.029. [16] CANTOR B, CHANG I T H, KNIGHT P, et al. Microstructural development in equiatomic multicomponent alloys [J]. Materials Science and Engineering: A, 2004, 375/376/377: 213–218. DOI: 10.1016/j.msea.2003.10.257. [17] YEH J W, CHEN S K, LIN S J, et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes [J]. Advanced Engineering Materials, 2004, 6(5): 299–303. DOI: 10.1002/adem.200300567. [18] TSAI M H, YEH J W. High-entropy alloys: a critical review [J]. Materials Research Letters, 2014, 2(3): 107–123. DOI: 10.1080/21663831.2014.912690. [19] DENG Y, TASAN C C, PRADEEP K G, et al. Design of a twinning-induced plasticity high entropy alloy [J]. Acta Materialia, 2015, 94: 124–133. DOI: 10.1016/j.actamat.2015.04.014. [20] LEI Z F, LIU X J, WU Y, et al. Enhanced strength and ductility in a high-entropy alloy via ordered oxygen complexes [J]. Nature, 2018, 563(7732): 546–550. DOI: 10.1038/s41586-018-0685-y. [21] GLUDOVATZ B, HOHENWARTER A, CATOOR D, et al. A fracture-resistant high-entropy alloy for cryogenic applications [J]. Science, 2014, 345(6201): 1153–1158. DOI: 10.1126/science.1254581. [22] FU Z Q, JIANG L, WARDINI J L, et al. A high-entropy alloy with hierarchical nanoprecipitates and ultrahigh strength [J]. Science Advances, 2018, 4(10): eaat8712. DOI: 10.1126/sciadv.aat8712. [23] ZHANG Z J, MAO M M, WANG J W, et al. Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi [J]. Nature Communications, 2015, 6: 10143. DOI: 10.1038/ncomms10143. [24] DING Q Q, ZHANG Y, CHEN X, et al. Tuning element distribution, structure and properties by composition in high-entropy alloys [J]. Nature, 2019, 574(7777): 223–227. DOI: 10.1038/s41586-019-1617-1. [25] ZOU Y, MA H, SPOLENAK R. Ultrastrong ductile and stable high-entropy alloys at small scales [J]. Nature Communications, 2015, 6: 7748. DOI: 10.1038/ncomms8748. [26] TANG Y Q, LI D Y. Dynamic response of high-entropy alloys to ballistic impact [J]. Science Advances, 2022, 8(32): eabp9096. DOI: 10.1126/sciadv.abp9096. [27] ANDREOLI A F, HAN X L, KABAN I. In situ studies of non-equilibrium crystallization of Al x CoCrFeNi ( x=0.3, 1) high-entropy alloys [J]. Journal of Alloys and Compounds, 2022, 922: 166209. DOI: 10.1016/j.jallcom.2022.166209. [28] DIAO H Y, MA D, FENG R, et al. Novel NiAl-strengthened high entropy alloys with balanced tensile strength and ductility [J]. Materials Science and Engineering: A, 2019, 742: 636–647. DOI: 10.1016/j.msea.2018.11.055. [29] KIREEVA I V, CHUMLYAKOV Y I, POBEDENNAYA Z V, et al. Effect of V-phase particles on the orientation and temperature dependence of the mechanical behaviour of Al0.3CoCrFeNi high-entropy alloy single crystals [J]. Materials Science and Engineering: A, 2020, 772: 138772. DOI: 10.1016/j.msea.2019.138772. [30] ZHANG J L, QIU R S, TAN X N, et al. The precipitation behavior in Al0.3CoCrFeNi high-entropy alloy affected by deformation and annealing [J]. Metals, 2023, 13(1): 157. DOI: 10.3390/met13010157. [31] YASUDA H Y, SHIGENO K, NAGASE T. Dynamic strain aging of Al0.3CoCrFeNi high entropy alloy single crystals [J]. Scripta Materialia, 2015, 108: 80–83. DOI: 10.1016/j.scriptamat.2015.06.022. [32] KIREEVA I V, CHUMLYAKOV Y I, POBEDENNAYA Z V, et al. The orientation dependence of critical shear stresses in Al0.3CoCrFeNi high-entropy alloy single crystals [J]. Technical Physics Letters, 2017, 43(7): 615–618. DOI: 10.1134/S1063785017070082. [33] MUSKERI S, GWALANI B, JHA S, et al. Excellent ballistic impact resistance of Al0.3CoCrFeNi multi-principal element alloy with unique bimodal microstructure [J]. Scientific Reports, 2021, 11(1): 22715. DOI: 10.1038/s41598-021-02209-y. [34] 张荣, 祁文军, 张爽. Al x CoCrFeNi拉伸力学性能的分子动力学模拟 [J]. 钢铁钒钛, 2022, 43(6): 173–179. DOI: 10.7513/j.issn.1004-7638.2022.06.026.ZHANG R, QI W J, ZHANG S. Molecular dynamics simulation of tensile mechanical properties of Al x CoCrFeNi [J]. Iron Steel Vanadium Titanium, 2022, 43(6): 173–179. DOI: 10.7513/j.issn.1004-7638.2022.06.026. [35] 李健, 郭晓璇, 马胜国, 等. AlCrFeCuNi高熵合金力学性能的分子动力学模拟 [J]. 高压物理学报, 2020, 34(1): 011301. DOI: 10.11858/gywlxb.20190762.LI J, GUO X X, MA S G, et al. Mechanical properties of AlCrFeCuNi high entropy alloy: a molecular dynamics study [J]. Chinese Journal of High Pressure Physics, 2020, 34(1): 011301. DOI: 10.11858/gywlxb.20190762. [36] 张路明. AlxCoCrFeNi高熵合金力学性能的分子动力学模拟 [D]. 太原: 太原理工大学, 2022.ZHANG L M. Mechanical properties of Al xCoCrFeNi high-entropy alloy: a molecular dynamics study [D]. Taiyuan: Taiyuan University of Technology, 2022. [37] 尹宗军, 苏蓉, 方传智, 等. FeNiCrCoCu高熵合金拉伸行为特征研究: 分子动力学模拟 [J]. 南阳师范学院学报, 2023, 22(3): 29–33. DOI: 10.3969/j.issn.1671-6132.2023.03.005.YIN Z J, SU R, FANG C Z, et al. Study on tensile behavior characteristics of FeNiCrCoCu high entropy alloys: molecular dynamics simulation [J]. Journal of Nanyang Normal University, 2023, 22(3): 29–33. DOI: 10.3969/j.issn.1671-6132.2023.03.005. [38] BARTON N R, BERNIER J V, BECKER R, et al. A multiscale strength model for extreme loading conditions [J]. Journal of Applied Physics, 2011, 109(7): 073501. DOI: 10.1063/1.3553718. [39] HUANG X, DING J, SONG K, et al. Crystal orientation effect on the irradiation mechanical properties and deformation mechanism of α-Fe: molecular dynamic simulations [J]. Journal of Materials Engineering and Performance, 2023, 32(18): 8063–8074. DOI: 10.1007/s11665-022-07730-3. [40] ZHANG Y, YU D J, WANG K M. Atomistic simulation of the orientation-dependent plastic deformation mechanisms of iron nanopillars [J]. Journal of Materials Science & Technology, 2012, 28(2): 164–168. DOI: 10.1016/S1005-0302(12)60037-1. [41] DASH M K, CHIU Y L, JONES I P, et al. Quasi-static compression of shock loaded, single crystal tantalum micropillars [J]. Materials Science and Engineering:A, 2023, 881: 145415. DOI: 10.1016/j.msea.2023.145415. [42] ISLAM A S M J, ISLAM M S, HASAN M S, et al. Anisotropic crystal orientations dependent mechanical properties and fracture mechanisms in zinc blende ZnTe nanowires [J]. RSC Advances, 2023, 13(33): 22800–22813. DOI: 10.1039/D3RA03825D. [43] XU W W, DÁVILA L P. Effects of crystal orientation and diameter on the mechanical properties of single-crystal MgAl2O4 spinel nanowires [J]. Nanotechnology, 2019, 30(5): 055701. DOI: 10.1088/1361-6528/aaef11. [44] SHI K W, CHENG J C, CUI L, et al. Ballistic impact response of Fe40Mn20Cr20Ni20 high-entropy alloys [J]. Journal of Applied Physics, 2022, 132(20): 205105. DOI: 10.1063/5.0130634. [45] QI Y M, XU H M, HE T W, et al. Effect of crystallographic orientation on mechanical properties of single-crystal CoCrFeMnNi high-entropy alloy [J]. Materials Science and Engineering: A, 2021, 814: 141196. DOI: 10.1016/j.msea.2021.141196. [46] ZHANG Q, HUANG R R, ZHANG X, et al. Deformation mechanisms and remarkable strain hardening in single-crystalline high-entropy-alloy micropillars/nanopillars [J]. Nano Letters, 2021, 21(8): 3671–3679. DOI: 10.1021/acs.nanolett.1c00444. [47] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1–19. DOI: 10.1006/jcph.1995.1039. [48] FARKAS D, CARO A. Model interatomic potentials for Fe-Ni-Cr-Co-Al high-entropy alloys [J]. Journal of Materials Research, 2020, 35(22): 3031–3040. DOI: 10.1557/jmr.2020.294. [49] JONES J E. On the determination of molecular fields: II. from the equation of state of a gas [J]. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1924, 106(738): 463–477. DOI: 10.1098/rspa.1924.0082. [50] FAKEN D, JÓNSSON H. Systematic analysis of local atomic structure combined with 3D computer graphics [J]. Computational Materials Science, 1994, 2(2): 279–286. DOI: 10.1016/0927-0256(94)90109-0. [51] HONEYCUTT J D, ANDERSEN H C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters [J]. The Journal of Physical Chemistry, 1987, 91(19): 4950–4963. DOI: 10.1021/j100303a014. [52] STUKOWSKI A. Structure identification methods for atomistic simulations of crystalline materials [J]. Modelling and Simulation in Materials Science and Engineering, 2012, 20(4): 045021. DOI: 10.1088/0965-0393/20/4/045021. [53] CORDERO Z C, KNIGHT B E, SCHUH C A. Six decades of the Hall-Petch effect: a survey of grain-size strengthening studies on pure metals [J]. International Materials Reviews, 2016, 61(8): 495–512. DOI: 10.1080/09506608.2016.1191808. [54] DEWAPRIYA M A N, MILLER R E. Energy absorption mechanisms of nanoscopic multilayer structures under ballistic impact loading [J]. Computational Materials Science, 2021, 195: 110504. DOI: 10.1016/j.commatsci.2021.110504. [55] CHENG Y J, DONG J L, LI F C, et al. Scaling law for impact resistance of amorphous alloys connecting atomistic molecular dynamics with macroscale experiments [J]. ACS Applied Materials and Interfaces, 2023, 15(10): 13449–13459. DOI: 10.1021/acsami.2c19719. [56] LI Z M, PRADEEP K G, DENG Y, et al. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off [J]. Nature, 2016, 534(7606): 227–230. DOI: 10.1038/nature17981. [57] 叶天舟, 姚欢, 巫英伟, 等. FeCrAl合金拉伸力学性能分子动力学研究 [J]. 稀有金属材料与工程, 2023, 52(2): 777–784. DOI: 10.12442/j.issn.1002-185X.20220441.YE T Z, YAO H, WU Y W, et al. Molecular dynamics study on tensile mechanical properties of FeCrAl alloy [J]. Rare Metal Materials and Engineering, 2023, 52(2): 777–784. DOI: 10.12442/j.issn.1002-185X.20220441. [58] GAO X Z, LU Y P, ZHANG B, et al. Microstructural origins of high strength and high ductility in an AlCoCrFeNi2.1 eutectic high-entropy alloy [J]. Acta Materialia, 2017, 141: 59–66. DOI: 10.1016/j.actamat.2017.07.041. [59] ZHANG D D, ZHANG J Y, KUANG J, et al. Superior strength-ductility synergy and strain hardenability of Al/Ta co-doped NiCoCr twinned medium entropy alloy for cryogenic applications [J]. Acta Materialia, 2021, 220: 117288. DOI: 10.1016/j.actamat.2021.117288. [60] DE COOMAN B C, ESTRIN Y, KIM S K. Twinning-induced plasticity (TWIP) steels [J]. Acta Materialia, 2018, 142: 283–362. DOI: 10.1016/j.actamat.2017.06.046. [61] SUN X H, WU D X, ZOU L F, et al. Dislocation-induced stop-and-go kinetics of interfacial transformations [J]. Nature, 2022, 607(7920): 708–713. DOI: 10.1038/s41586-022-04880-1. [62] GANGIREDDY S, GWALANI B, SONI V, et al. Contrasting mechanical behavior in precipitation hardenable AlXCoCrFeNi high entropy alloy microstructures: single phase FCC vs. dual phase FCC-BCC [J]. Materials Science and Engineering: A, 2019, 739: 158–166. DOI: 10.1016/j.msea.2018.10.021. [63] ZHANG Z R, ZHANG H, TANG Y, et al. Microstructure, mechanical properties and energetic characteristics of a novel high-entropy alloy HfZrTiTa0.53 [J]. Materials & Design, 2017, 133: 435–443. DOI: 10.1016/j.matdes.2017.08.022. [64] BHAV S B, SUKUMAR G, PRAKASA R P, et al. Superior ballistic performance of high-nitrogen steels against deformable and non-deformable projectiles [J]. Materials Science and Engineering: A, 2019, 751: 115–127. DOI: 10.1016/j.msea.2019.02.044. 期刊类型引用(2)
1. 李海峰，门建兵，金文，刘旭东. Ta-Hf-Nb-Zr体系高熵合金J-C模型及应用试验. 爆炸与冲击. 2025(03): 55-65 . 
本站查看2. 陈嘉琳，李述涛，安明，艾天淳，马上，陈叶青. 晶界类型对Al_(0.3)CoCrFeNi高熵合金压缩力学性能的影响及机制研究. 力学学报. 2025(03): 658-670 . 
百度学术其他类型引用(0)
-
下载:
百度学术
计量
- 文章访问数: 622
- HTML全文浏览量: 511
- PDF下载量: 176
- 被引次数: 2