Experimental research on optimizing the flow fieldof pulse gas flow generator
-
摘要: 为了分析脉冲气流发生器在不同喷嘴结构下的脉冲气流特征及其流场的变化规律，利用高速摄影技术, 通过控制闪光光源，得到不同喷嘴结构产生的冲击波及脉冲气流流场的实验图像及其影响。采用多项式拟合的方法获得冲击波超压值、速度随距离变化的衰减规律；通过图像处理技术，获取脉冲气流的有效数据，采用一阶指数衰减方程拟合出脉冲气流位移、速度随时间的变化规律。该实验方法及数据处理技术可以认知不同结构脉冲气流发生器产生的冲击波、脉冲气流的相关参数。Abstract: In order to investigate the characteristics of pulse gas flow generator with different nozzle structures and analyze those of the flow field and their tendencies to change, we achieved the shock wave profiles generated by the gas flow generators and obtained experimental photos of flow field by using high-speed photography technology and controlling the light sources. Next, we studied the influence of different nozzles on air flow patterns using the polynomial fitting method to acquire the overpressure of shock wave, the attenuation rules of velocity corresponding with change of distance. Moreover, taking advantage of image processing technology, we collected effective data of the air flow from experimental images and, according to the first order exponential decay equation, we deduced the gas flow displacements and the variation rules of velocity corresponding with changes of time. Our results will help to better understand and use the relevant parameters of shock wave and gas flow and thus provide effective reference to optimized design for the equipment.
-
Key words:
- fluid mechanics /
- vortex ring /
- image processing /
- pulse gas flow generator /
- shock wave
-
图 6 没有安装喷嘴时冲击波及脉冲气流的流场图
Figure 6. Shock wave and gas flow measuredwith no nozzle installed
图 7 安装喷嘴1时冲击波及脉冲气流的流场图
Figure 7. Shock wave and gas flow measuredwith nozzle 1 installed
表 1 冲击波超压值和正相作用时间的测试结果
Table 1. Overpressure and positive time of shock wave measured in experiment
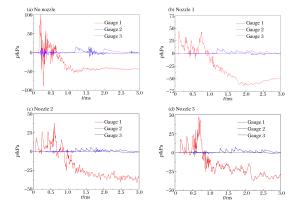
方案 n p/kPa t+/ms p/kPa t+/ms p/kPa t+/ms 传感器1 传感器2 传感器3 无喷嘴 1 75.69 - 15.91 - 10.09 0.63 喷嘴1 1 40.00 0.75 10.00 0.97 6.00 0.78 2 40.00 8.18 5.62 3 25.00 5.62 3.69 4 50.00 5.86 4.45 喷嘴2 1 22.76 0.70 5.60 0.57 3.33 0.87 2 29.57 5.37 2.96 3 32.70 5.30 3.13 4 40.85 5.65 2.70 5 17.28 4.23 1.72 喷嘴3 1 20.80 0.61 5.30 0.88 3.12 0.86 2 22.41 4.73 2.88 3 29.15 4.97 3.72 4 38.07 7.23 3.66 
下载: 导出CSV
表 2 冲击波超压拟合曲线的常数
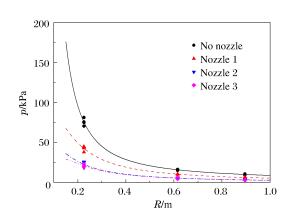
Table 2. Experimental parameters ofshock wave overpressure fitting curves
方案 A1 A2 A3 无喷嘴 7.593 0.600 0.325 喷嘴1 3.415 2.130 -0.168 喷嘴2 1.805 1.157 -0.092 喷嘴3 1.532 1.264 -0.125
下载: 导出CSV
表 3 冲击波正相冲量与脉冲气流速度
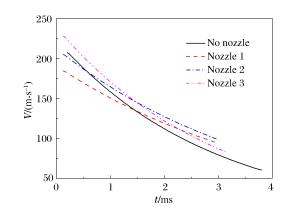
Table 3. Shock wave positive impulsesand pulse gas velocities
方案 R/m I+/(Pa·s) v/(m·s-1) 0.225 - 180.0 无喷嘴 0.615 2.50 45.5 0.895 2.02 - 0.225 12.22 156.4 喷嘴1 0.615 2.99 64.4 0.895 1.86 - 0.225 8.20 166.8 喷嘴2 0.615 1.82 67.0 0.895 1.19 - 0.225 8.33 176.9 喷嘴3 0.615 2.14 46.0 0.895 1.26 -
下载: 导出CSV
表 4 脉冲气流位移拟合曲线的常数
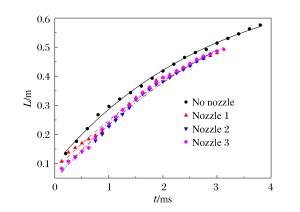
Table 4. Experimental parameters for fitting curvesof pulse gas flow displacement
方案 B0 B1 B2/10-3 无喷嘴 0.747 -0.649 2.90 喷嘴1 0.888 -0.809 4.24 喷嘴2 0.877 -0.831 3.91 喷嘴3 0.752 -0.712 2.98
下载: 导出CSV
-
[1] Lucey G, Jasper L. Vortex ring generator[R]. Adelphi, MD: Army Research Laboratory, 1998. [2] Shusser M, Gharib M. Energy and velocity of a forming vortex ring[J]. Physics of Fluids (1994-present), 2000, 12(3):618-621. doi: 10.1063/1.870268 [3] Gharib M, Rambod E, Shariff K. A universal time scale for vortex ring formation[J]. Journal of Fluid Mechanics, 1998, 360:121-140. doi: 10.1017/S0022112097008410 [4] Linden P F, Turner J S. The formation of optimal vortex rings, and the efficiency of propulsion devices[J]. Journal of Fluid Mechanics, 2001, 427:61-72. doi: 10.1017/S0022112000002263 [5] Dabiri J O, Gharib M. Delay of vortex ring pinchoff by an imposed bulk counterflow[J]. Physics of Fluids (1994-present), 2004, 16(4):L28-L30. doi: 10.1063/1.1669353 [6] Mohseni K, Ran H, Colonius T. Numerical experiments on vortex ring formation[J]. Journal of Fluid Mechanics, 2001, 430:267-282. doi: 10.1017/S0022112000003025 [7] Saffman P G. Vortex dynamics[M]. Cambridge University Press, 1992. [8] Widnall S E, Bliss D B, Tsai C Y. The instability of short waves on a vortex ring[J]. Journal of Fluid Mechanics, 1974, 66(1):35-47. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=190dd6f8f7e7fdabd97b89579415e990 [9] Widnall S E, Tsai C Y. The instability of the thin vortex ring of constant vorticity[J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1977, 287(1344):273-305. doi: 10.1098/rsta.1977.0146 [10] Fraenkel L E. Examples of steady vortex rings of small cross-section in an ideal fluid[J]. Journal of Fluid Mechanics, 1972, 51(1):119-135. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=S0022112072001107 [11] Maxworthy T. Turbulent vortex rings[J]. Journal of Fluid Mechanics, 1974, 64(2):227-240. doi: 10.1017/S0022112074002370 [12] Stanaway S K, Cantwell B J, Spalart P R. A numerical study of viscous vortex rings using a spectral method[R]. NASA STI/Recon Technical Report N, 1988. https://www.researchgate.net/publication/24295723_A_numerical_study_of_viscous_vortex_rings_using_a_spectral_method [13] Jassim E, Abdi M A, Muzychka Y. Computational fluid dynamics study for flow of natural gas through high-pressure supersonic nozzles: Part 1. Real gas effects and shockwave[J]. Petroleum Science and Technology, 2008, 26(15):1757-1772. doi: 10.1080/10916460701287847 [14] Ryzhov O S. Shockwave formation in laval nozzles[J]. Journal of Applied Mathematics and Mechanics, 1963, 27(2):453-494. doi: 10.1016/0021-8928(63)90013-3 [15] Brezhnev A L, Chernov I A. On the formation of shock waves in laval nozzles[J]. Journal of Applied Mathematics and Mechanics, 1981, 45(4):486-493. doi: 10.1016/0021-8928(81)90092-7 [16] Akhmetov D G. Vortex rings[M]. Berlin: Springer, 2009. [17] Maxworthy T. Some experimental studies of vortex rings[J]. Journal of Fluid Mechanics, 1977, 81(3):465-495. doi: 10.1017/S0022112077002171 -
计量
- 文章访问数: 4359
- HTML全文浏览量: 1265
- PDF下载量: 383
- 被引次数: 0